文章快速检索     高级检索
  气体物理  2016, Vol. 1 Issue (3): 47-52  
0

引用本文  

余奕甫, 时晓天, 王强. 低空大展弦比无人机翼梢磁梯度测量探头气动特性及影响[J]. 气体物理, 2016, 1(3): 47-52.
Yu Y F, Shi X T, Wang Q. Aerodynamic characteristics and influence of an airborne magnetic gradient measuring probe on the wing-tip of a high aspect ratio uav at low altitude[J]. Physics of Gases, 2016, 1(3): 47-52.

基金项目

国家自然科学基金(11102198)

第一作者简介

余奕甫(1985-)男, 江苏淮安, 工学硕士, 中国航天空气动力技术研究院, 主要从事气动计算与分析研究.通信地址:北京市丰台区云岗西路17号7201-56(100074). E-mail: uyifu308@126.com.

文章历史

收稿日期：2016-02-10
修回日期：2016-02-25
Contents              Abstract              Full text              Figures/Tables              PDF
低空大展弦比无人机翼梢磁梯度测量探头气动特性及影响
余奕甫 , 时晓天 , 王强     
中国航天空气动力技术研究院, 北京 100074
收稿日期：2016-02-10；修回日期：2016-02-25
基金项目：国家自然科学基金(11102198)
第一作者简介：余奕甫(1985-)男, 江苏淮安, 工学硕士, 中国航天空气动力技术研究院, 主要从事气动计算与分析研究.通信地址:北京市丰台区云岗西路17号7201-56(100074). E-mail: uyifu308@126.com..
摘要：针对一种低空大展弦比无人机, 文章进行全机和翼梢磁梯度测量探头数值模拟.全机计算给出翼梢磁梯度测量探头对全机气动特性和操稳特性的影响; 翼梢磁梯度测量探头计算实现了气动外形优化设计, 在保持全机操稳特性的前提下, 最大程度地减小全机气动阻力增量.结果表明, 磁梯度测量探头对全机气动阻力增量在9%之内, 俯仰力矩变化在5%之内, 对全机操稳特性的影响不大, 气动外形优化设计基本满足该低空大展弦比无人机的安全飞行技术要求.
关键词：无人机    磁梯度测量探头    优化设计    数值模拟    气动阻力    
Aerodynamic Characteristics and Influence of an Airborne Magnetic Gradient Measuring Probe on the Wing-Tip of a High Aspect Ratio UAV at Low Altitude
YU Yi-fu , SHI Xiao-tian , WANG Qiang     
China Academy of Aerospace Aerodynamics, Beijing 100074, China
Abstract: For a high aspect ratio UAV at low altitude, the flows around both the full vehicle and the airborne magnetic gradient measuring probe on its wing-tip were numerically simulated, respectively. The calculation of the full vehicle obtained the influences of the wing-tip airborne magnetic gradient measuring probe on the full vehicle aerodynamic characteristics and its control and stability; the calculation of the wing-tip airborne magnetic gradient measuring probe implemented its optimization design of aerodynamic configuration, and the aerodynamic drag increment of the full vehicle decreased at the furthest on the premise of keeping the full vehicle control and stability. Results show that the aerodynamic drag increment of the full vehicle related to the airborne magnetic gradient measuring probe is controlled within 9% and the variation of pitching moment is within 5%. The full vehicle control and stability is scarcely influenced by the airborne magnetic gradient measuring probe, and its optimization design of aerodynamic configuration mainly meet the technique requirement of the safe flight of the high aspect ratio UAV at low altitude.
Key words: UAV    airborne magnetic gradient measuring probe    optimization design    numerical simulation    aerodynamic drag    
引言

航空磁梯度测量的实用化是航空磁探测技术的一大进展, 近几年由于磁力仪灵敏度和飞机磁补偿技术的提高, 航空磁梯度系统呈现出急剧增加的趋势[1-2].目前, 大多数航空磁探测服务商都提供磁梯度测量服务, 这在航空磁探测中已占据主要位置.

固定翼航空磁梯度测量装置是重要的航空磁探测设备.固定翼无人机磁梯度测量作为一种低成本易操作无危险的空中移动探测技术, 很好地满足了当今高效率资源勘查的需要[3].通常, 磁梯度测量装置会对搭载无人机的气动特性产生一定影响, 如气动阻力等.获得并分析这些影响的规律, 进而对其气动外形加以优化, 是十分必要的.

本文采用数值模拟方法, 对一种低空大展弦比无人机的翼梢磁梯度测量探头绕流场进行了计算分析, 开展了气动外形优化设计, 以期为航空资源勘查无人机的安全飞行提供参考.

1 翼梢磁梯度测量探头气动外形设计

固定翼无人机磁探测主要利用能够高速飞行的特点, 在短时间内进行大范围的搜索, 克服复杂地形带来的飞行安全隐患等因素.这种航空磁探测方法将航空磁探测设备安装在无人机上, 通过探测地面或水中目标的磁性异常信号, 来探测并识别目标[4-7].

图 1为固定翼无人机搭载某种典型磁梯度测量探头的全机效果图.两个三分量磁梯度测量探头安装在机翼的两侧翼梢, 向前水平伸出; 两个两分量磁梯度测量探头分别安装在机头和机尾.这样, 由各探头测得的磁场值就可表示出机身中间点处的总磁场和磁场梯度.一方面, 要保证探头的结构强度和彼此之间的距离足够大; 另一方面, 还要保证无人机的安全飞行.

图 1 无人机搭载某种磁梯度测量探头的全机效果图 Fig.1 Whole machine effect of the UAV equipped with a magnetic gradient measuring probe

根据航空磁探测资源勘查的要求, 考虑图 1所示的低空大展弦比无人机, 在此无人机基础上略去进气道及推进螺旋桨, 在左右机翼翼梢处各侧向伸出一组航空磁探测设备, 且磁梯度测量探头通过3根不同尺寸的支杆连接于翼尖.同时, 为了保持全机操稳特性, 需最大程度地减小探头带来的气动阻力增量[8-9].如图 2所示, 采用水滴状外形对探头进行整流减阻, 3根支杆的剖面采用一定相对厚度的对称翼型, 也起到了整流减阻的作用.为了满足探头导线的要求, 前支杆整流剖面的厚度和尺寸较大, 辅助支杆整流剖面的厚度和尺寸较小.

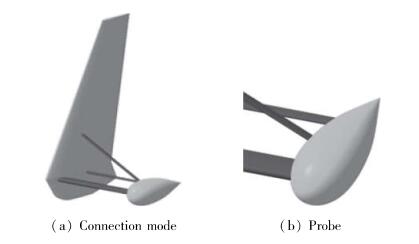
图 2 磁梯度测量探头与翼尖连接方式 Fig.2 Connection mode of the magnetic gradient measuring probe and tip of the wing
2 数值模拟方法

流动控制方程为积分形式的三维可压缩Reynolds平均Navier-Stokes方程, 即[7]

$\frac{\partial }{\partial t}\iiint_{V}{\mathit{\boldsymbol{Q}}\rm{d}V}\rm{+}\iint_{\mathit{S}}{\mathit{\boldsymbol{f}}\cdot \mathit{\boldsymbol{n}}\rm{d}\mathit{S}}\rm{=0}.$

其中, V为控制体体积; S为控制体表面; Q为守恒变量向量; f为通过表面S的通量向量, 包含3个方向的无黏通量和黏性通量; n为表面S的法向单位向量.此外, 湍流模型采用一方程Spalart-Allmaras湍流模型[10].

对于远场边界, 要求源自物形附近的扰动波不会反射回流场内部.假定远场边界附近为局部一维流动, 根据特征线理论, 可利用一维流动中的两个Riemann不变量处理法向流动, 而两个切向流动可通过流场内部变量向外插值获得.特别地, 来流入口边界设给定速度边界条件, 下游出口边界设压力边界条件.对于物面边界, 采用无滑移无穿透边界条件, 物面为绝热壁且法向压力梯度为0.

基于积分形式的Navier-Stokes方程, 采用有限体积法, 通过通量项的差分和插值, 在每个网格单元上离散得到以网格单元中心物理量为未知量的代数方程组进行求解.空间离散方式采用Jameson提出的显式中心差分格式, 时间推进方式采用隐式LU-SGS方法[11].

数值模拟的网格采用包含边界层的结构网格或非结构网格, 分别进行全机计算和翼梢磁梯度测量探头计算.全机计算的网格为结构网格, 单元总数约为5×106个, 法向第1层网格高度为10-4m(见图 3).翼梢磁梯度测量探头计算的网格为非结构网格, 法向第1层网格高度也为10-4m(见图 4).

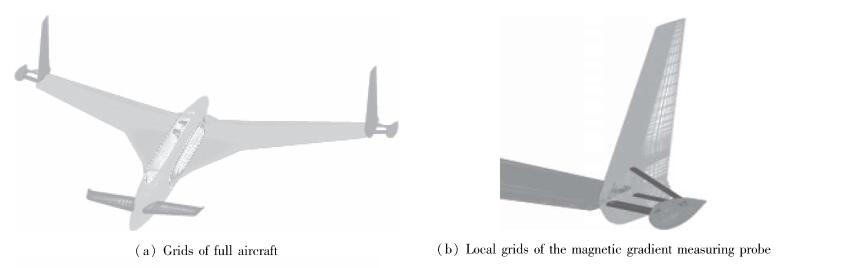
图 3 全机计算整体网格及局部网格 Fig.3 Grids and local grids of the aircraft
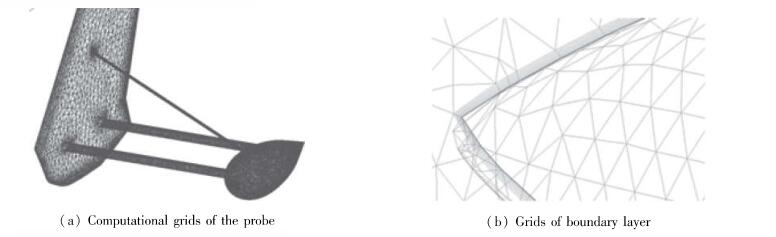
图 4 翼梢磁梯度测量探头整体网格及局部网格 Fig.4 Integrated grids and local grids for the probe of the magnetic gradient measuring of the wing tip
3 计算结果与分析

选取的低空大展弦比无人机的参考面积为9.44m2, 参考弦长为1.5283m.为了便于对比分析, 考虑全机和翼梢磁梯度测量探头两种绕流情形, 并使来流条件网格密度等参数基本相同.主要飞行参数为：来流速度为40m/s, 飞行高度为1000m, 计算Reynolds数Re=2×107, 飞行攻角α = 0, 3, 6°, 飞行侧滑角β = 0, 5, 15°.主要气动性能的评估要求是, 安装探头后对全机配平特性的影响足够小.

3.1 全机情形

在不同的飞行攻角和飞行侧滑角下进行无探头和有探头两组计算, 给出轴向力Ca, 法向力Cn, 俯仰力矩Cmz, 偏航力矩Cmy, 滚转力矩Cmx, 升力系数Cl, 阻力系数Cd, 压心位置Cp等气动特性参数. 表 1为无探头计算结果, 表 2为有探头计算结果.

下载CSV 表 1 无探头全机气动特性计算结果 Tab.1 Calculation results of aerodynamic characteristics of the whole aircraft without probe
下载CSV 表 2 有探头全机气动特性计算结果 Tab.2 Calculation results of the aerodynamic characteristics of the whole aircraft with probe

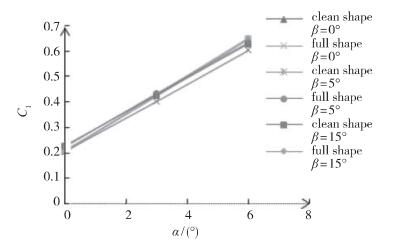
从表中对比可以看出, 探头及其连接支杆由于尺寸相对较小, 对全机的升力系数和俯仰力矩影响较小.由于已对探头外形及其连接支杆进行了整流设计, 计算结果表明, 连接探头后, 全机气动阻力增量在9%之内, 对升力系数的影响在7%之内, 对滚转力矩和偏航力矩的影响均在10%之内. 图 5和图 6分别为阻力系数和升力系数随攻角的变化曲线, 直观显示了连接探头后对气动特性的影响, 该变化基本可以保证无人机安全飞行.

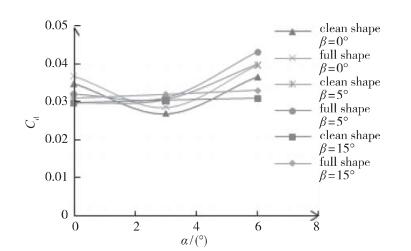
图 5 全机计算阻力系数随攻角的变化 Fig.5 Variation of drag coefficient Cd with angle of attack α
图 6 全机计算升力系数随攻角的变化 Fig.6 Variation of lift coefficient Cl with angle of attack α

在攻角为3°, 侧滑角为15°的飞行状态下, 连接探头后, 全机气动阻力增量约为5.26%, 升力系数增量在1.5%之内, 压心位置相对平均气动弦长(1.519m)后移约1%, 对滚转力矩和偏航力矩的影响均在2.0%之内, 对俯仰力矩的影响在2.7%之内. 图 7和图 8为飞行状态下无探头和有探头时全机表面压力分布等值云图, 整体特征基本相近.

图 7 无探头全机表面压力分布(α=3°，β=15°) Fig.7 Pressure distribution on the surface of the whole aircraft without probe
图 8 有探头全机表面压力分布(α=3°，β=15°) Fig.8 Pressure distribution on the surface of the whole aircraft with probe

进一步计算全机的翼根弯矩可知, 无探头时为-0.434, 有探头时为-0.440, 增加了约1.4%, 处于可以接受的范围之内.

3.2 翼梢磁梯度测量探头情形

经过整流设计的磁探头设备外形由于连接支杆有一定厚度, 对阻力影响不可忽略. 表 3为在攻角为0°, 无侧滑飞行状态下的阻力系数和阻力随弦长的变化关系, 翼型剖面的绝对厚度为32mm.可以看出, 通过局部数值模拟可以快速优化连接支杆的气动布局, 达到减小全机气动阻力的目的.

下载CSV 表 3 翼梢磁梯度测量探头情形阻力系数和阻力 Tab.3 Drag and drag coefficient of the magnetic gradient measuring probe on wing tip

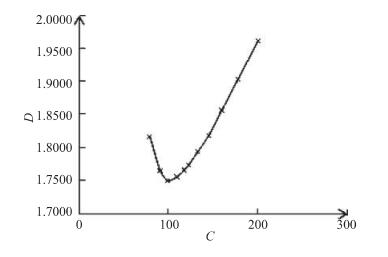
图 9为翼型剖面阻力预测结果, 对于一定绝对厚度的翼型, 支杆弦长为100mm时, 翼型阻力值最小.因此, 基于减阻因素和导线通过的要求, 整流外形剖面翼型弦长定为100mm.

图 9 翼型阻力随弦长变化的曲线 Fig.9 Variation curve of the airfoil drag

探杆展长有两种方案, 方案1展长L = 600mm和方案2展长L = 400mm.从已有的计算结果(见表 4)可以看出, 相对于无磁探头设备外形, 方案1气动阻力增加5%, 方案2气动阻力增加4%;两种方案升力变化在5%以内.如图 10所示, 在计算攻角为3°, 侧滑角为15°的巡航状态下, 方案2经过探头整流罩的气流没有影响到飞机垂尾的气动特性.基于减小探杆根部弯矩及减小翼根弯矩, 降低探杆抖振风险及其掉落带来对无人机本体控制的风险, 最终确定探杆展长为L = 400mm.

下载CSV 表 4 翼梢磁梯度测量探头情形气动特性参数 Tab.4 Aerodynamic characteristic parameters of the magnetic gradient probe on the wing tip
图 10 探头设备局部流线与压力分布 Fig.10 Local flow line and pressure distribution on the probe
4 结论

(1) 根据数值模拟的结果, 通过整流设计的磁梯度测量探头及其连接支杆对全机气动阻力的增加量在可以接受的范围内, 满足飞机巡航要求.

(2) 磁梯度测量探头设备的增加对全机巡航状态下气动压心位置变化在1%左右, 升力影响在7%以内, 对无人机操稳特性影响较小.

(3) 通过磁探头设备局部数值模拟, 优化连接支杆剖面翼型弦长及支杆展长, 使其对全机气动阻力的增量贡献达到最小, 以保障无人机巡航的可靠性和安全性.

参考文献
[1]
熊盛青. 发展中国航空物探技术有关问题的思考[J]. 中国地质, 2009, 36(6): 1366-1374.
Xiong S Q. The strategic consideration of the development of China's airborne geophysical technology[J]. Geology in China, 2009, 36(6): 1366-1374. (in Chinese)
[2]
熊盛青. 我国航空重磁勘探技术现状与发展趋势[J]. 地球物理学进展, 2009, 24(1): 113-117.
Xiong S Q. The present situation and development of airborne gravity and magnetic survey techniques in China[J]. Progress in Geophysics, 2009, 24(1): 113-117. (in Chinese)
[3]
Fahlstrom P G, Gleason T J.无人机系统[M].吴汉平, 译.北京:电子工业出版社, 2003: 2-4.
Fahlstrom P G, Gleason T J. Introduction to UAV systems[M]. Wu H P, translated.Beijing: Publishing House of Electronics Industry, 2003: 2-4(in Chinese).
[4]
Luyendyk A P. Processing of airborne magnetic data[J]. AGSO Journal of Australian Geology and Geophysics, 1997, 17(2): 31-38.
[5]
Foster M R, Jines W R, van der Weg K. Statistical estimation of systematic errors at intersections of lines of aeromagnetic survey data[J]. Journal of Geophysical Research, 1970, 75(8): 1507-1511. DOI:10.1029/JB075i008p01507
[6]
Barnard J A. The use of unmanned aircraft in oil, gas and mineral E+P activities[A]. //2008 SEG Annual Meeting[C].Las Vegas, 2008.
[7]
Zhong L, Makino Y. CFD-based aerodynamic optimization for complex aircraft configuration[J]. Computational Fluid Dynamics Journal, 2004, 13(1): 304-310.
[8]
Mason W H, Knill D L, Giunta A A, et al. Getting the full benefits of CFD in conceptual design[R]. AIAA 1998-2513, 1998.
[9]
王世安, 尹贵鲁. CFD在飞机设计中的应用[J]. 航空科学技术, 2002, 6: 33-36.
Wang S A, Yin G L. The application of CFD in aircraft design[J]. Aeronautical Science and Technology, 2002, 6: 33-36. DOI:10.3969/j.issn.1007-5453.2002.03.010 (in Chinese)
[10]
Baldwin B S, Barth T J. A one-equation turbulence transport model for high Reynolds number wall-bounded flows[R]. NASA TM 102847, 1990.
[11]
Yin C C, Li J F, Miao Z. Application on wing design of large plane with high-powered computation[J]. Large Plane and High Precision Computation, 2010, 1: 1-10.