引言

目前, 航天再入飞行器主要有钝体升力体和细长体3类.钝体的典型代表为飞船返回舱, 升阻比一般在0.3以下; 升力体的典型代表为航天飞机, 升阻比一般在1.5以上; 细长体的气动性能介于两者之间, 升阻比一般在0.8左右, 也受到一定的关注, 如欧洲最近成功完成飞行试验的IXV (Intermediate eXperimental Vehicle) ^[1].对于这些典型的航天飞行器再入大气层时, 要经历高超声速至亚跨声速的全流域全空域飞行, 其动态特性问题十分重要, 对飞行姿态控制和飞行安全等都有重要影响, 因而备受关注.如美国“阿波罗”Apollo飞船在研制过程中, 动稳定性就占有重要地位, 分别用9套模型在14座风洞中进行了亚跨超和高超声速风洞试验共约700多小时^[2], 但钝体类航天飞行器的动态特性问题并没有完全解决, 一般仅能给出动态失稳现象的唯象描述和工程分析方法, 缺乏理论分析.美国为替代航天飞机退役后的航天运输能力, 近期基于“阿波罗”Apollo飞船研制的“猎户座”CEV (Crew Exploration Vehicle) ^[3], 在投放试验中由于多次出现动态失稳现象而失败, 经过Langley的深入研究才得以解决, 并于2014年12月5日飞行试验成功.

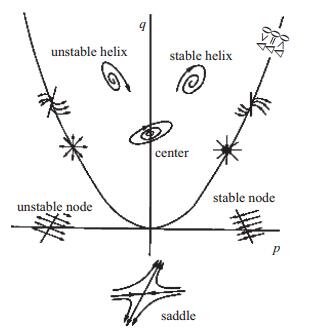
经过数十年的积累, 人们已认识到航天飞行器的动态特性与其绕流流场结构密切相关, 如飞船返回舱等钝体类航天飞行器, 以较大的配平攻角再入大气层, 后体有大尺度的分离和再附, 流场中存在复杂的波系结构^[3](见图 1).钝体气流分离效应后体气流再附效应船尾近尾涡流效应和动态迟滞效应等对飞船返回舱的动态特性都有重要影响.而飞行器的绕流流场结构, 是由飞行器的气动布局构型和Mach数(M)Reynolds数(Re)攻角(α)等流动参数控制.关于飞行器构型对动态特性的影响, 已有研究成果, 如“联盟号”和“神舟号”载人飞船返回舱在光体倒锥上增加稳定翼^[4], 就是为了改变后体分离拓扑形态, 从而改善返回舱的稳定性.对于特定的飞行器布局构型, 当某一个流动参数变化时, 其绕流流场结构形态随之而变, 从而导致飞行姿态的变化, 乃至可能诱发飞行姿态的突变.流动主控方程(Navier-Stokes方程)是一耗散系统, 其流场结构变化诱导的飞行器姿态变化, 可出现如下情况:

(1) 回到稳定飞行状态, 称为点吸引子.

(2) 演化为周期运动或多周期运动(Hopf分叉), 称为周期吸引子或极限环吸引子; 或演化为准周期运动, 称为准周期吸引子.

(3) 运动形态发生突变(鞍结点分叉), 它与准周期运动都是混沌运动的前兆^[5].

(4) 演化为混沌运动, 称为奇异吸引子(奇怪吸引子).

这启示我们, 可以引入微分方程的定性理论(分叉理论)，结合非定常数值模拟, 来分析航天飞行器再入大气层时的动态稳定性问题.本文开展了此项工作, 着重研究了钝体和细长体航天飞行器不同布局构型和再入时Mach数变化对飞行器动态特性的影响.对于升力体类航天飞行器, 由于一般具有较强的控制能力, 动态特性的影响较小, 故而未予研究.

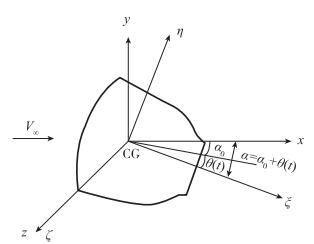
1 数学模型与分叉理论分析 1.1 数学分析模型

本文只研究钝体类和细长体类轴对称航天飞行器绕重心做单自由度俯仰振荡的运动情况, 其坐标系统见图 2.

设ξ-η-ζ是与飞行器相固连的正交坐标系(体轴系), ξ轴和飞行器的体轴重合, η，ζ两轴构成俯仰对称平面.

设x-y-z是惯性静止坐标系(风轴系), x轴与来流方向一致.

记α₀为平衡攻角, α(t)为攻角，θ(t)为俯仰角，t为时间，记θ(t)=α(t)-α₀.此时, 描述飞船返回舱俯仰振荡运动和非定常动态绕流以及所受俯仰力矩的无量纲化的耦合方程组为^[6]

$ \mathit{I\ddot \theta }{\rm{ = }}{\mathit{C}_{\rm{m}}}{\rm{ + }}{\mathit{C}_{\rm{ \mathsf{ μ} }}}\mathit{\dot \theta }\;\mathit{, } $

(1)

$ \frac{{\partial \mathit{U}}}{{\partial \mathit{t}}} + \frac{{\partial \mathit{E}}}{{\partial \mathit{x}}} + \frac{{\partial \mathit{F}}}{{\partial \mathit{y}}} + \frac{{\partial \mathit{G}}}{{\partial \mathit{z}}} = \frac{{\partial {\mathit{E}_\mathit{v}}}}{{\partial \mathit{x}}} + \frac{{\partial {\mathit{F}_\mathit{v}}}}{{\partial \mathit{y}}} + \frac{{\partial {\mathit{G}_\mathit{v}}}}{{\partial \mathit{z}}}\;, $

(2)

$ {\mathit{C}_{\rm{m}}}\mathit{\boldsymbol{k}}{\rm{ = }}\smallint {\smallint _{{\rm{wall}}}}{\mathit{\boldsymbol{r}}_{\rm{b}}}{\rm{ \times ( - }}\mathit{p}\mathit{\boldsymbol{n}}{\rm{ + }}\mathit{\sigma }{\mathit{\boldsymbol{\tau }}_{\rm{b}}}{\rm{)d}}\mathit{s}\mathit{.} $

(3)

式(1) 为描述飞行器单自由度俯仰运动方程. I表示无量纲的转动惯量, 右端项包括气动俯仰力矩系数C_m和机械阻尼力矩系数C_μ.在自由飞行中C_μ为0, 在风洞实验中应当计及它的贡献. ${\mathit{\dot \theta }} $，${\mathit{\ddot \theta }} $分别表示俯仰角θ对时间的1阶和2阶导数.式(2) 为非定常Navier-Stokes方程, 空间离散采用原始变量NND格式, 时间离散采用双时间步方法; 式(3) 为俯仰力矩系数的积分关系式，其中下标b指壁面.非定常计算方法的详细描述及方程中各符号的含义可参考文献[6-8].

对任意非定常运动, Etkin等^[9]认为, 非定常气动力和力矩是状态变量的泛函.据此, 可给出动态俯仰力矩系数表达式:

$ {\mathit{C}_{\rm{m}}}{\rm{(}}\mathit{t}{\rm{) = }}{\mathit{C}_{\rm{m}}}{\rm{(}}\mathit{\theta }, \mathit{\dot \theta }{\rm{, }}\mathit{\ddot \theta }{\rm{, }} \cdots {\rm{)}}\;{\rm{.}} $

(4)

在多数情况下, 可只保留到1阶导数项；但在某些情况下, 为了保证足够的精确度, 必须保留到2阶导数项.数十年的工程应用表明, 这一假设在实际应用中的适用范围极为广泛.将式(4) 保留至2阶导数, 并将无量纲的转动惯量I吸收到C_m和C_μ中, 且吸收后的俯仰力矩系数和机械阻尼力矩系数仍用C_m和C_μ表示, 代入式(1), 易得:

$ \mathit{\ddot \theta } = {\mathit{C}_{\rm{m}}}(\mathit{\theta }, \mathit{\dot \theta }, \mathit{\ddot \theta }) + {\mathit{C}_\mathit{\mu }}(\mathit{\theta }, \mathit{\dot \theta })\mathit{\dot \theta }\;. $

(5)

将俯仰力矩系数在平衡攻角α₀处展开, 可得:

$ \begin{array}{l} {C_{\rm{m}}}(\theta, \dot \theta, \ddot \theta ) = {\left( {{C_{\rm{m}}}} \right)_0} + {\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \theta }}} \right)_0}\theta + {\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \dot \theta }}} \right)_0}\dot \theta + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \ddot \theta }}} \right)_0}\ddot \theta + G(\theta, \dot \theta, \ddot \theta ). \end{array} $

(6)

其中, 下标0表示在平衡攻角处的定态俯仰力矩, 故有(C_m)0=0.非线性项$G(\theta, \dot \theta, \ddot \theta ) $为关于$ \theta, \dot \theta, \ddot \theta $的高阶项, 假定当$ {({\theta ^2}, {{\dot \theta }^2}, {{\ddot \theta }^2})^{1/2}} \to 0$时, 非线性项$G(\theta, \dot \theta, \ddot \theta ) $比$ {({\theta ^2}, {{\dot \theta }^2}, {{\ddot \theta }^2})^{1/2}}$更高阶地趋于0, 即非线性项满足Perron定理^[10].将式(6) 代入式(5), 即得:

$ \begin{array}{l} \;\;\;\;\;\left[{1-\;{{\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \ddot \theta }}} \right)}_0}} \right]\ddot \theta = {\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \theta }}} \right)_0}\theta + \\ \left[{{{\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \dot \theta }}} \right)}_0} + {C_\mu }\left( {0, 0} \right)} \right]\dot \theta + G(\theta, \dot \theta, \ddot \theta ). \end{array} $

(7)

令$ \mathit{x} = \dot \theta, y = \theta, $代入式(7) 得到:

$ \left\{ \begin{array}{l} \dot x = ax + by + g\\ \dot y = cx + dy \end{array} \right.. $

(8)

式(8) 中,

$ \begin{array}{l} \mathit{a} = \left[{{{\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \dot \theta }}} \right)}_0} + {C_\mu }\left( {0, 0} \right)} \right]/\left[{1-{{\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \ddot \theta }}} \right)}_0}} \right], \\ \;\;\;\;\;\;\;\;\;b = {\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \theta }}} \right)_0}/\left[{1-{{\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \ddot \theta }}} \right)}_0}} \right], \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;c = 1, d = 0, \\ \;\;\;\;\;\;\;g = G(\theta, \dot \theta, \ddot \theta )/\left[{1-{{\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \ddot \theta }}} \right)}_0}} \right]. \end{array} $

其中,

$ {\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \theta }}} \right)_0}, {\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \dot \theta }}} \right)_0}和{\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \ddot \theta }}} \right)_0} $

分别称为静导数动导数和2阶动导数.飞行器一般是静稳定的, 有

$ {\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \theta }}} \right)_0} < 0; $

2阶动导数的量值远小于1, 即

$ \left| {{{\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \ddot \theta }}} \right)}_0}} \right| \ll 1. $

至此, 就建立了描述单自由度俯仰运动的非线性平面自治动力系统(8).该动力系统的平衡点对应于飞行器在平衡攻角处的定态绕流, 此时有${(\theta, \dot \theta, \ddot \theta )_0} = \left( {0, 0, 0} \right). $

假设上述非线性系统式(8) 的非线性项满足Perron定理, 根据动力学方法^[10-11], 可以用非线性系统的一次近似系统式(9) 来分析其平衡解的稳定性.

$ \left\{ \begin{array}{l} \dot x = ax + by\\ \dot y = cx + dy \end{array} \right.. $

(9)

设:

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\lambda \left( {{M_\infty }} \right) = - p = \left( {a + d} \right) + \\ \;\;\;\;\left[{{{\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \dot \theta }}} \right)}_0} + {C_\mu }\left( {0, 0} \right)} \right]/\left[{1-{{\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \ddot \theta }}} \right)}_0}} \right], \\ \mathit{q} = \mathit{ad} - bc = - b = - {\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \theta }}} \right)_0}/\left[{1-{{\left( {\frac{{\partial {C_{\rm{m}}}}}{{\partial \ddot \theta }}} \right)}_0}} \right], \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Delta = }{\mathit{p}^{\rm{2}}} - 4q = {\lambda ^2} + 4b. \end{array} $

则一次近似系统式(9) 的Jacobian矩阵的特征值为: ${{{\bar{\lambda }}}_{1, 2}}=\left( \lambda \pm \sqrt{\mathit{\Delta }} \right)/2 $.根据非线性动力学系统的有关定理^[10-11], 可知在p-q平面上各类平衡点(也称奇点或临界点)的区域如图 3所示.下面将通过判断飞行器的配平姿态(平衡点或奇点)落入p-q平面相图的何区域, 来判断奇点的性态, 从而预示奇点周围轨线的形状.

1.2 随参数变化相平面上的奇点唯一时的分叉分析(情形1)

这是较为普遍的情形, 即飞行器再入大气层时, 随弹道下降，Mach数降低, 飞行器的配平攻角始终只有1个(在不同Mach数下, 配平攻角的大小会有所不同, 但数量总是1个).此时, 随参数Mach数变化, 在相平面上奇点(即配平攻角)数目不发生改变, 但奇点的性态可能发生变化.显而易见, 这样一来, 奇点周围轨线的形状, 就仅由奇点的性态决定, 而没有其他奇点对其发生干扰.只要分析奇点的性态(判断奇点落入p-q相平面的何区域)即可预示轨线的走向.以下来分析奇点的性态.一般Δ＜0, 而参数λ有λ＜0，λ=0和λ＞0这3种可能, 并且随来流Mach数变化, λ有可能出现变号.这样, 一次近似系统的Jacobian矩阵的特征值为一对共轭复根, 可进一步得到以下结论:

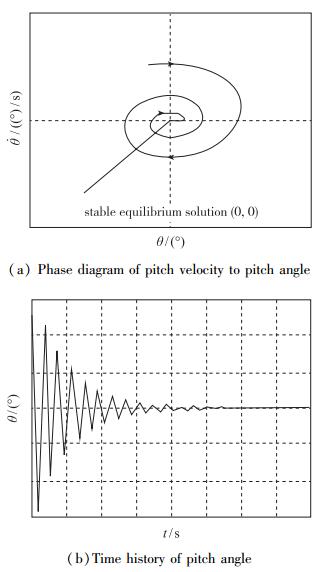
(1) 若λ＜0, Δ＜0, 易得到p＞0, q＞0, 则在$(\dot{\theta }, \theta) $相平面上, 平衡点(奇点)为稳定的螺旋点, 也称焦点.在平衡点(0, 0) 附近, 非线性动力系统(8) 的轨线为稳定的螺旋点形态，见图 4(a).俯仰振荡角的时间历程曲线是收敛的, 即随时间t增加, θ是减小的, 最后趋于0，见图 4(b).因此, λ＜0和Δ＜0可作为平衡点(奇点)的动稳定性的判据.

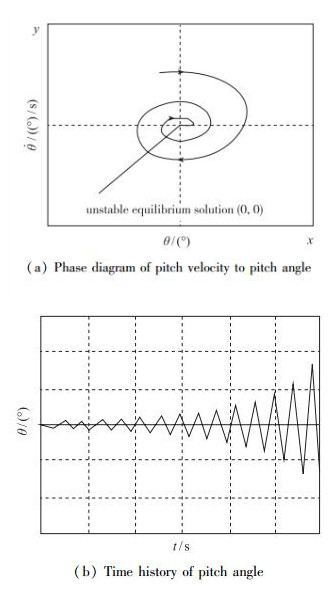
(2) 若λ＞0, Δ＜0, 可得到p＜0, q＞0, 则在$(\dot{\theta }, \theta) $相平面上, 平衡点为不稳定的螺旋点, 在平衡点(0, 0) 附近, 非线性动力系统(8) 的轨线为不稳定的螺旋点形态，见图 5(a).俯仰振荡角的时间历程曲线是发散的, 即随时间t增加, θ是增大的，见图 5(b).

(3) 若λ=0, Δ＜0, 可以得到p=0, q＞0, 非线性动力系统(8) 的一次近似系统Jacobian矩阵的特征值${{{\bar{\lambda }}}_{1, 2}}=\left( \lambda \pm \sqrt{\mathit{\Delta }} \right)/2 $, 在λ=λ_cr=0时, 满足:

① 特征值的实部Re[λ₁(λ_cr), λ₂(λ_cr)]=0;

② 特征值的虚部Im[λ₁(λ_cr), λ₂(λ_cr)]≠0;

③ 因为Δ＜0, 则Re$ \left[{{{\bar{\lambda }}}_{1}}\left( \lambda \right), {{{\bar{\lambda }}}_{2}}\left( \lambda \right) \right]=\frac{1}{2}\lambda $, 故有:

$ \frac{\rm{dRe}\left[{{{\bar{\lambda }}}_{1}}\left( \lambda \right), {{{\bar{\lambda }}}_{2}}\left( \lambda \right) \right]}{\rm{d}\lambda }\left| _{\lambda ={{\lambda }_{\rm{cr}}}=0}=\frac{1}{2}\ne 0. \right. $

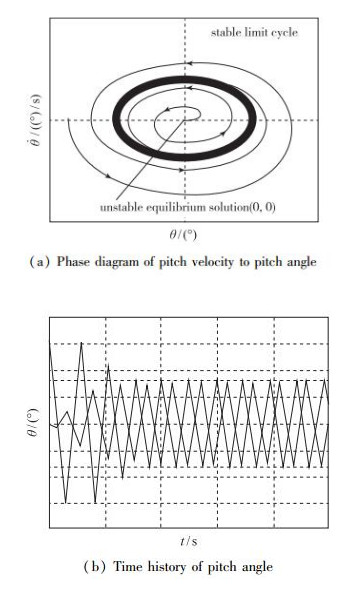
于是, 在λ=λ_cr=0时, 系统的特征值满足Hopf分叉的3个条件^[10-11], 其中第3个条件称为Hopf分叉的横截条件(transversality condition).即随参数M变化, λ的符号经过λ=0发生改变时, 动力系统(8) 将发生Hopf分叉, 在$ (\dot{\theta }, \theta )$相平面上, 平衡点(0, 0) 的性态改变, 出现稳定的极限环，见图 6(a).俯仰振荡角的时间历程曲线在达到稳定后既不收敛也不发散, 即随时间t增加, θ出现周期振荡，见图 6(b).

这样, 理论上就获得了单自由度俯仰运动发生动态Hopf分叉失稳, 极限环振荡出现或消失的临界条件, 即

$ {{\lambda }_{\rm{cr}}}=\left[{{\left( \frac{\partial {{C}_{\rm{m}}}}{\partial \dot{\theta }} \right)}_{0}}+{{C}_{\mu }}\left( 0, 0 \right) \right]/\left[1-{{\left( \frac{\partial {{C}_{\rm{m}}}}{\partial \ddot{\theta }} \right)}_{0}} \right]=0. $

飞行器自由飞行时, C_μ=0, 一般情况下, 2次动导数的量值远小于1, 于是有:

$ {{\lambda }_{\rm{cr}}}\approx {{\left( \frac{\partial {{C}_{\rm{m}}}}{\partial \dot{\theta }} \right)}_{0}}=0. $

(10)

从以上分析可看出, 飞行器再入时随Mach数下降, Hopf分叉又可分为两种情形:一种情形是λ由λ＜0经过λ=0变化至λ＞0时, 发生所谓的亚临界Hopf分叉, 此时, 奇点(配平攻角)由稳定的点吸引子演化为不稳定的点吸引子, 同时产生稳定的极限环吸引子; 另一种情形是λ由λ＞0经过λ=0变化至λ＜0时, 发生所谓的超临界Hopf分叉, 此时, 奇点(配平攻角)由不稳定的点吸引子演化为稳定的点吸引子, 同时稳定的极限环吸引子消失.

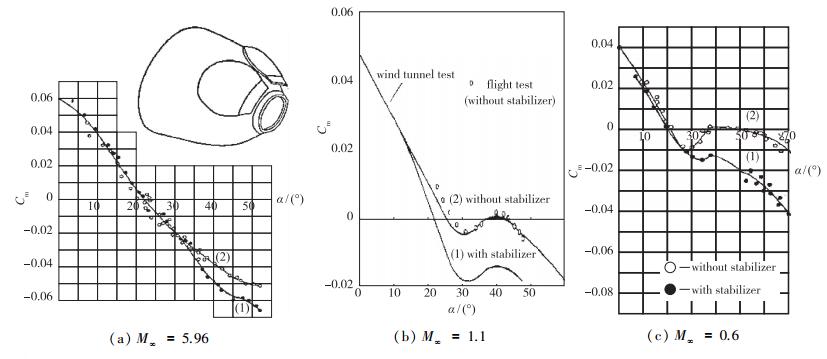
1.3 随参数变化相平面上的奇点数目改变时的分叉分析(情形2)

这是较为特殊的情形, 即飞行器再入大气层时, 随弹道下降Mach数降低, 在不同Mach数下, 配平攻角的大小和数量都发生改变(这是布局气动设计不期望出现的情形).此时, 随参数Mach数变化, 在相平面上奇点(即配平攻角)数目和性态都可能发生改变.图 7给出了不同M_∞下“联盟号”飞船返回舱C_m随α变化的曲线^{[2, 4]}.可以看出, 如果飞船返回舱倒锥背风面上增装2片稳定翼, 则飞船返回舱的力矩和攻角的特性将如图 7(a)，(b)，(c)中曲线(1) 所示.此时, 从高超声速到M_∞=0.6, 均只有1个C_m=0的配平攻角; 当2个稳定翼不存在时, 高Mach数下, 仍只有1个平衡点; 但M_∞=1.1(约数), 力矩特性的曲线将出现2个平衡点α₁和α′₂; M_∞=0.6时, 出现3个平衡攻角α₁，α₂和α₃, 见图 7(a)，(b)，(c)中曲线(2).这种情况表明, 在分析飞船返回舱俯仰动态特性时, 应当区别存在1个平衡点和2个3个平衡点的情况.

在多个奇点的情形下, 奇点周围轨线的形状, 不唯一由奇点的性态决定, 同时还要受到其他奇点的干扰(奇点吸引域).这是与单一奇点情形的主要不同, 再入时随Mach数变化, 奇点(配平攻角)失稳的机制也有所不同(即分叉类型不同).

设Mach数由高降低到某临界值M′_cr时(第1临界M), 力矩曲线由1个平衡点变为具有α₁, α′₂两个平衡点, 即当M_∞＜M′_cr的3个平衡点的α₂和α₃合并成1个α′₂, 力矩曲线在此点与α轴相切(见图 7(b)曲线(2)).这种临界情况可以证明^[10-11], 方程(8) 的线性部分的矩阵特征值λ_{1, 2}有1个(例如λ₁), 具有如下性质:

(1) 实部Reλ₁=0;

(2) 虚部lmλ₁=0;

(3) 随M_∞趋于M′_cr, λ₁沿实轴正负皆趋近0.

动力系统(8) 将发生鞍结点分叉.

下面分析发生鞍结点分叉后的轨线形状, 方法还是根据奇点处静动导数的符号来判别奇点落入p-q相平面的何区域.

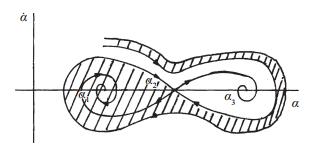
根据上面的分析(从图 7也易见), 当C_μ=0时, 方程(8) 在平衡点α₁, α₂, α₃处, 因分别有(∂C_m/∂θ)₀＜0, ＞0和＜0, 所以α₁, α₃处分别为结点, α₂处为鞍点.其中α和${\dot{\alpha }} $的相图性状依$ {{\left( \partial {{C}_{\rm{m}}}/\partial \dot{\theta } \right)}_{0}}$的不同而定.例如, 当α₁处$ {{\left( \partial {{C}_{\rm{m}}}/\partial \dot{\theta } \right)}_{0}}$＜0或Δ＜0和α₃处${{\left( \partial {{C}_{\rm{m}}}/\partial \dot{\theta } \right)}_{0}} $＜0或Δ＜0时, α₁, α₃处分别为稳定的结点(这里结点是广义的, 包括螺旋点临界结点退化结点和结点, 图中只画了螺旋点的情况), 相图如图 8所示.

图 8表明, 存在2个点吸引子α₁和α₃时(分别对应2个吸引盆或吸引域).对于α₁, 只在扰动偏离α₁很小时, 才能回复到α₁；一旦扰动变大, 有可能被吸引到α₃, 这是不希望发生的情况.

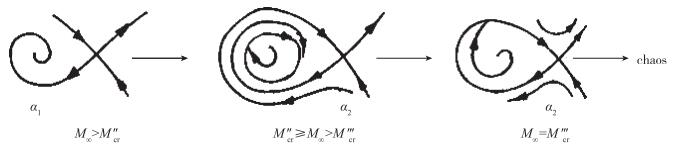
在α₁处, 若Mach数进一步改变, 在又一个临界Mach数M″_cr下(第2临界M), 此处的λ(M″_cr)=0(即λ发生变号), α₁处由稳定螺旋点演化为不稳定螺旋点, 发生Hopf分叉, 其附近就可能出现极限环, 降低M_∞, 极限环增大.当Mach数进一步改变, 达到第3临界Mach数M_∞=M"_cr时, 极限环通过α₂点, 发生同宿分叉, 将通过同宿轨道演变为混沌状态(见图 9).同样, 在α₃处, 也可能存在如图 10所示的情况.

2 数值模拟验证

针对上述2种情形(随参数M变化, 奇点数目唯一和奇点数目变化)下的3种分叉失稳形态(亚临界Hopf分叉超临界Hopf分叉鞍结点分叉), 选择3种航天飞行器构型进行了数值模拟验证.

对于每个外形, 需要求解3类流场:首先, 计算定态绕流流场, 以获取平衡攻角, 并为后续的非定常计算提供初场; 然后, 数值模拟强迫俯仰振荡过程, 通过参数辨识, 获取平衡攻角处的静动导数^{[6, 12]}, 给出分叉参数随Mach数的变化曲线; 最后, 计算自激俯仰振荡过程, 验证分叉理论分析结论.

2.1 OREX飞船再入失稳数值模拟验证(情形1，亚临界Hopf分叉)

日本的轨道再入实验飞船OREX(Orbital Re-entry Experiment Vehicle)^[13]是一个球冠加大倒锥外形的旋成体, 计算网格和外形见图 11.质心在体轴上, 再入时只存在一个大头朝前的平衡攻角α₀=0°, 对应于情形1.

风洞实验和飞行试验均表明, 该返回舱在再入经过跨超声速阶段时, 会发生俯仰方向的动态失稳现象, 出现绕平衡攻角的准极限环振荡.这里选取的Mach数M变化范围为1.5~6.0, Reynolds数均取Re=1.0×10⁵, 以单独考察俯仰动态特性随Mach数的演化规律.强迫俯仰运动给定为简谐振动, 即

$ \alpha ={{\alpha }_{0}}+{{\alpha }_{\rm{m}}}\sin \left( 2kt \right)={{\alpha }_{0}}+\theta \left( t \right). $

(11)

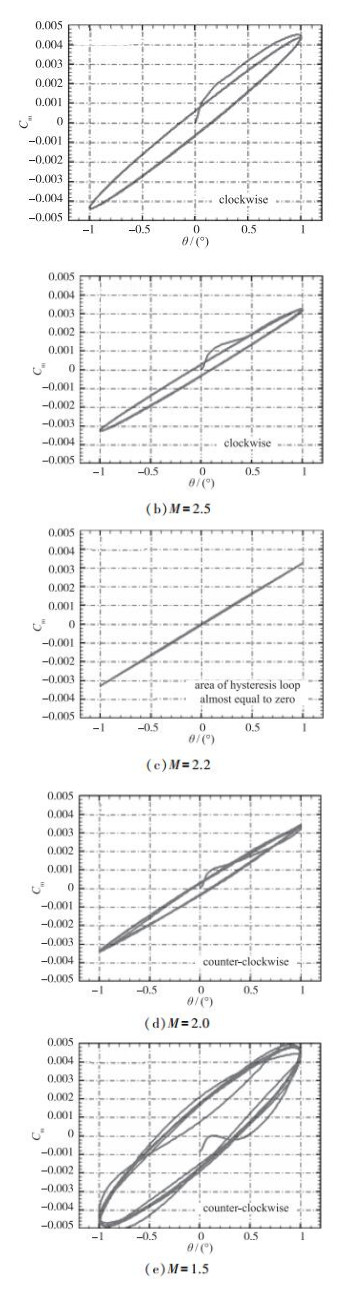
这里, 平衡攻角α₀=0°, 振幅α_m=1°, 无量纲的减缩频率k=0.2. 图 12给出了不同Mach数时俯仰运动绕平衡攻角的迟滞环.可以看到, 随着Mach数降低, 迟滞环由顺时针旋转演化至逆时针旋转, 包围的面积先减小, 后增大, 转化的临界Mach数约为2.2.

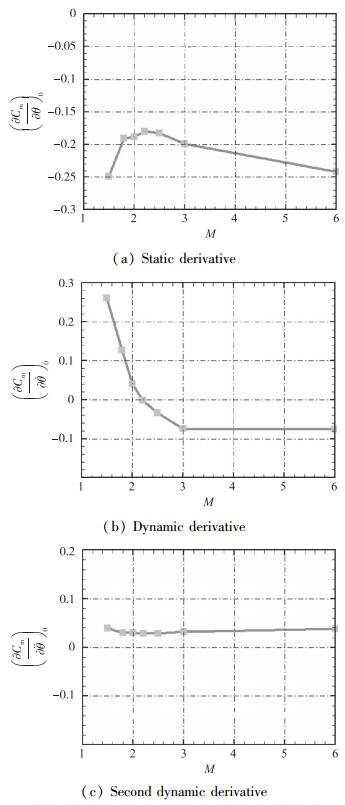
基于上述迟滞环, 采用最小二乘法即可辨识出平衡攻角处的静导数动导数和2阶动导数, 辨识结果随Mach数的变化曲线见图 13.在所有Mach数下, 静导数都小于0, 即静稳定.随Mach数降低, 动导数由小于0演化大于0, 发生变号的临界Mach数约为2.2. 2阶动导数量值很小, 基本可忽略不计.

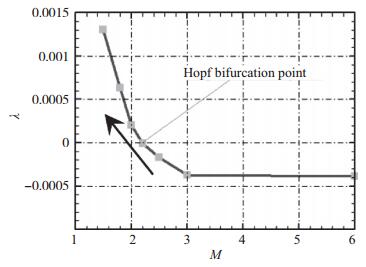
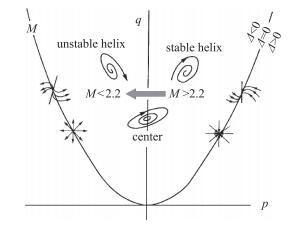
由静导数动导数和2阶动导数可计算出相平面上的特征参数p，q和Δ, 进而得到分叉参数λ(M)随Mach数的变化曲线, 其结果见图 14. 图 15还给出了随Mach数降低, 平衡攻角附近的俯仰动态特性在p-q平面上的性态变化示意图.

根据第1节情形1的Hopf分叉理论分析, 可以预测, 对于OREX飞船返回舱, 随着Mach数降低, λ由λ＜0经λ=0变为λ＞0, 其俯仰运动将发生亚临界Hopf分叉失稳, 平衡攻角将由稳定的点吸引子演化不稳定的点吸引子, 同时出现极限环吸引子, 分叉临界Mach数约为2.2.这个结论正确与否即可验证第1节的Hopf分叉理论, 下面通过数值模拟自激俯仰振荡的过程来进行验证.

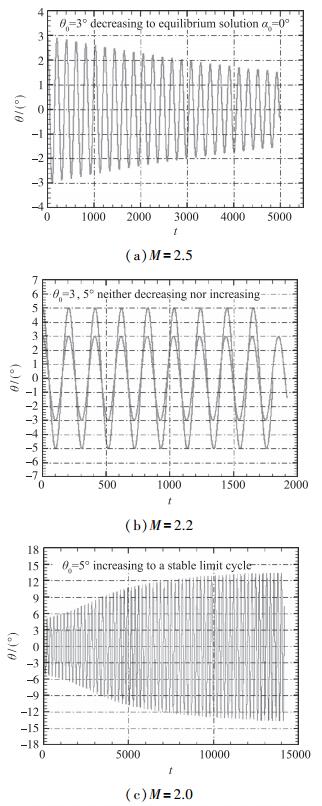
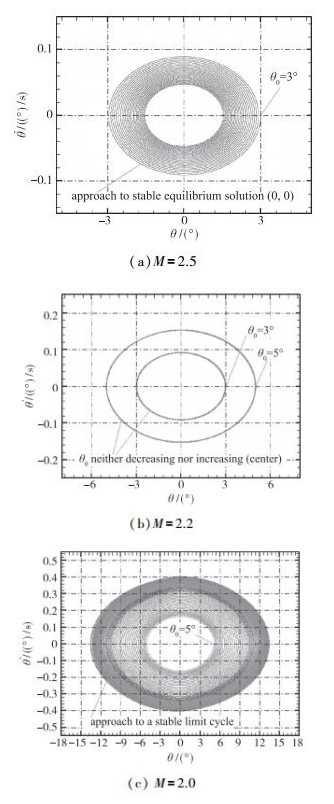
自激振荡的起始攻角为3或5°, 计算Mach数为2.5，2.2和2.0, 通过耦合求解方程(1)~(3), 数值模拟自激俯仰振荡的时间历程, 图 16给出了不同Mach数时俯仰角的时间历程曲线, 图 17给出了不同Mach数时俯仰角速度-俯仰角相图.可以看到, Mach数为2.5时, 返回舱从3°攻角释放后, 振幅逐渐减小; Mach数为2.2时, 从3和5°攻角释放后, 振幅几乎不增加也不减小; 而Mach数为2.0时, 俯仰振动的振幅不断增大, 最后发展为极限环振荡.即随着Mach数降低, 平衡攻角由稳定的点吸引子状态演化为极限环周期吸引子状态, 从而验证了本文动态失稳的Hopf分叉理论.

2.2 细长体再入失稳数值模拟验证(情形1，超临界Hopf分叉)

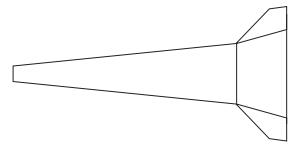
飞船返回舱是典型的大钝体再入飞行器, 另一类再入飞行器为细长体, 这里选用一种平头双锥细长体外形PNSB(plane nose slender body)^[14], 图 18为平头双锥外形示意图.

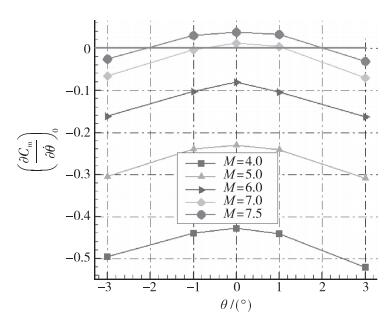
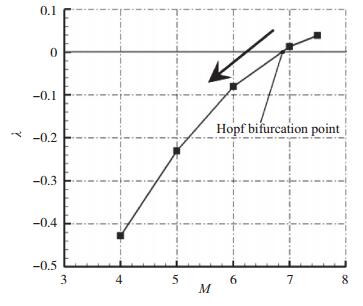
外形呈轴对称, 重心在体轴上, 因此, 在不同Mach数下, 平衡攻角均为0°, 属于奇点数目随Mach数降低不发生改变的情形1.计算Mach数分别取7.5，7.0，6.0，5.0，4.0, 计算方法过程与2.1节相同, 这里只给出典型的计算结果. 图 19给出了动导数随Mach数和俯仰角的变化曲线. 图 20给出了Hopf分叉参数随Mach数的变化规律, 变号临界Mach数约为6.8.

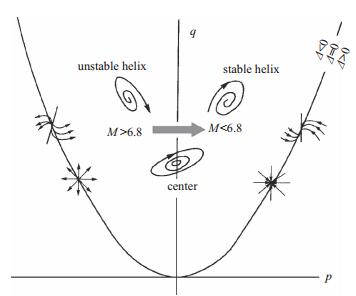
图 21给出了随Mach数降低, 平衡攻角在p-q平面上的性态变化示意图, 同理根据第1节情形1的Hopf分叉理论分析, 对于该细长体, 随着Mach数降低, λ由λ＞0经λ=0变为λ＜0, 其俯仰运动将发生超临界Hopf分叉失稳, 平衡攻角将由极限环周期吸引子演化为稳定的点吸引子, 分叉的临界Mach数M=6.8.

同理, 对于平头双锥细长体构型, 其俯仰运动随Mach数降低发生超临界Hopf分叉失稳的理论预测, 也可采用数值模拟自激俯仰振荡的过程来进行验证.

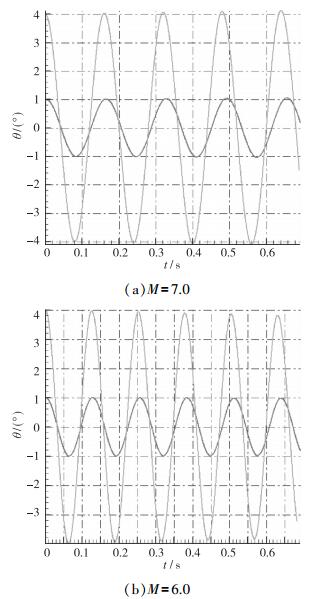
初始姿态角分别为1和3°, 俯仰角速度为1°/s. 图 22给出了Mach数分别为7.0和6.0的时间历程曲线.结合图 20可以看到，当M＞6.8时, 俯仰姿态角是发散的; 随Mach数降低, 当M＜6.8时, 俯仰姿态角是收敛的, 进一步验证了关于飞行器再入时动态失稳的超临界Hopf分叉理论.

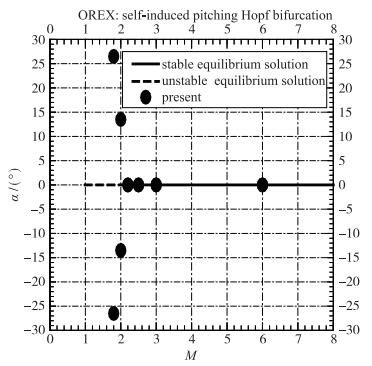
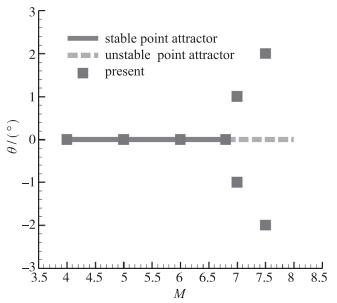
图 23和图 24给出了钝体OREX亚临界Hopf分叉图与细长体PNSB超临界Hopf分叉图的比较, 可见, 航天飞行器再入大气层时, 随Mach数降低, 发生亚临界Hopf分叉失稳比发生超临界Hopf分叉失稳的危害要严重得多.

2.3 类“联盟号”飞船(光体)再入失稳数值模拟验证(情形2，鞍结点分叉) 2.3.1 计算条件

类“联盟号”返回舱(光体)是一个球冠加大倒锥外形的旋成体^[15-16](见图 25), 其质心不在体轴上, 因而0°不是配平攻角, 不属于情形1.计算网格规模为100 × 50 × 41.计算条件见表 1, 其中k为无量纲的减缩频率.

这里不同Mach数下Reynolds数取为相同, 一方面是高度数据缺乏, 无法给出不同Mach数下的Reynolds数; 另一方面也是为了排除Reynolds数的影响, 只研究Mach数对静动态气动特性的影响.

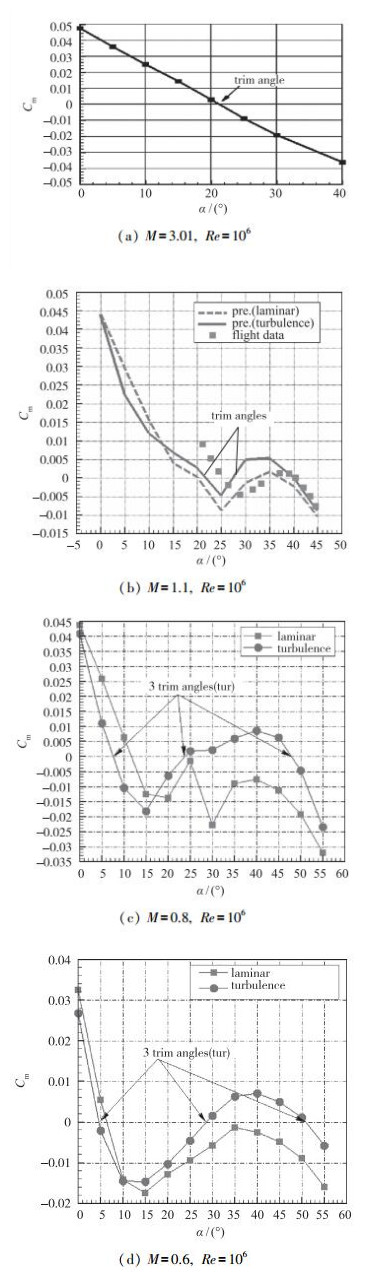
2.3.2 定态绕流计算

定态绕流计算除了M_∞=3.01是采用层流模型外, 其他3个Mach数采用了BL湍流模型. 图 26给出不同Mach数下对质心的俯仰力矩系数随攻角的变化曲线.从图中可以看到, 随Mach数降低, 配平攻角由1个演化至3个, 具体量值见表 2.需要注意的是，表中的量值根据计算结果，采用3次样条插值得到，因此都是近似值.

需要说明的是, 湍流模型对这种大钝体跨声速高Reynolds数较大攻角的绕流是至关重要的. 图 7给出文献中“联盟号”的试验结果, 可看到数值解在定性上与试验结果一致, 但在定量上有差别, 考虑原因有3个方面:一是计算的类“联盟号”返回舱模型与“联盟号”在外形和质心位置上有差别; 二是Re效应, 不同Mach数下高度和来流速度不一样, Re应有较大差别, 本文计算由于缺乏不同Mach数下的高度数据, Re统一取成10⁶, 这可能对结果有影响; 再一个原因可能是湍流模型, BL模型一般认为不适合于计算有大尺度分离的尾流.

2.3.3 强迫俯仰振荡绕流计算

表 3给出4个Mach数下配平攻角处的静动态气动特性, 表 4给出根据静动导数计算的配平攻角在相平面上的特征量.根据本文的定性理论分析结论以及表 3和表 4给出的计算结果, 可以预测类“联盟号”飞船返回舱(光体)再入时随Mach数降低可能发生的动态失稳分叉行为.

表 4中, p, q, Δ的定义见本文第1节根据它们的符号可以判断配平攻角(相平面上的奇点)在相平面上的类型, 从而分析奇点附近轨线的形态.

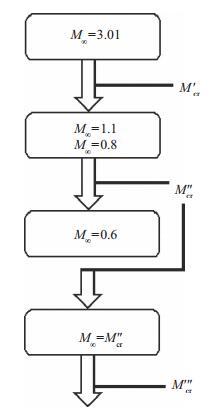
图 27给出了类“联盟号”返回舱(光体)再入时随Mach数降低可能发生的动态失稳分叉行为预测.首先，在Mach数为3.01和1.1之间存在临界Mach数M′_cr(第1临界Mach数), 在M′_cr处, 该返回舱的俯仰运动发生鞍结点分叉, 在相平面上的奇点演化特征为:一个稳定的结点→稳定的结点+鞍点→稳定的结点+鞍点+稳定结点.其次，在Mach数为0.8和0.6之间存在临界Mach数M″_cr(第2临界Mach数), 在M″_cr处, 该返回舱的第1个配平攻角发生Hopf分叉, 产生极限环, 在相平面上该奇点由:稳定的结点→不稳定的结点.最后，在M_∞=M″_cr以下存在临界Mach数M"_cr(第3临界Mach数), 在M"_cr处, 第1个配平攻角邻域的极限环与鞍点相交, 成为鞍点的分界线(即同宿轨线), 当Mach数大于或小于M"_cr时, 同宿轨线都不存在, 称M"_cr处发生同宿分叉.

2.3.4 自激俯仰运动数值仿真

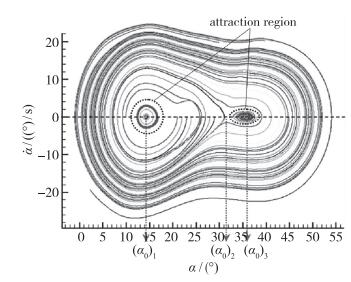
采用不同的初始俯仰角和俯仰角速度, 反映扰动的不同激励, 然后耦合求解非定常N-S方程和俯仰运动方程, 获取了100条俯仰运动的演化特征轨线图, 见图 28.

图 28的自激俯仰运动仿真结果表明, Mach数为0.8情况下, 飞船返回舱存在2个稳定的点吸引子, 即相平面上的稳定结点, 迎角分别约为14和36°, 在14和36°之间, 约30°处, 为不稳定鞍点, 与表 4给出的理论预测一致, 验证了定性理论分析结论.

但仿真结果还表明, 14和36°这两个稳定的点吸引子的吸引域都不大, 14°吸引子的吸引域大于36°吸引子的吸引域, 表明14°配平迎角(吸引子或稳定结点)应该是主要的飞行姿态, 如果遭遇较大扰动, 使得俯仰角有较大偏离, 进入14°吸引子的吸引域之外, 则俯仰运动的演化就可能进一步偏离14°配平迎角, 出项较危险的俯仰振荡情况. 表 4的预测没有反映这个信息, 表明静动导数的概念是局部稳定性的表征参数, 基于局部稳定性理论的定性分析方法不能研究吸引域的形态, 有必要开展全局稳定性分析研究.

3 结论

针对航天飞行器再入时的俯仰动态失稳问题, 基于Etkin假设, 建立了描述单自由度俯仰运动的平面自治动力系统数学模型, 引入分叉理论分析俯仰运动动态特性随Mach数变化的演化规律, 预示了亚临界Hopf分叉超临界Hopf分叉鞍结点分叉同宿分叉等失稳机制, 并给出了2类3种典型航天飞行器(钝体和细长体)再入俯仰运动失稳的非定常数值仿真验证结果.主要结论如下:

(1) 发展了再入飞行器动态失稳的分叉理论分析方法, 结合静动导数计算, 即可预测动态失稳现象临界参数和失稳后的轨线运动形态.

(2) 如果航天飞行器再入大气层时不同Mach数下均仅有1个配平攻角, 那么随Mach数降低, 可能存在1个临界Mach数, 俯仰运动失稳的机制为Hopf分叉, 并存在亚临界Hopf分叉和超临界Hopf分叉2种形态, 且亚临界Hopf分叉的危害远远大于超临界Hopf分叉.如果飞行器再入时发生超临界Hopf分叉失稳, 一般不影响飞行任务; 如果飞行器再入时发生亚临界Hopf分叉失稳, 则往往带来风险, 可能导致飞行任务失败.

(3) 如果航天飞行器再入大气层时随Mach数下降, 配平攻角的数目增加(一般是由1个演化至3个), 那么随Mach数降低, 俯仰运动失稳的机制更为复杂, 可能存在3个临界Mach数, 依次发生鞍结点分叉Hopf分叉和同宿分叉, 其危害更大, 在气动设计时应予以避免.