2. 北京空天技术研究所,北京 100074
2. Beijing Aerospace Technology Institute, Beijing 100074, China
为了满足现代军事作战隐身性能、机动性以及发射平台适应性的要求, 折叠翼舵导弹逐渐成为一种新的设计趋势[1].采用折叠翼舵还能有效缩小储运空间、便于运输, 从而提高武器系统的战术技术性能, 目前已在现代飞行器上获得广泛应用[2].折叠翼舵能否顺利展开, 是飞行器飞行成败的决定因素, 而折叠翼面的气动力特性又直接影响了翼面的顺利展开, 所以有必要对折叠翼舵展开过程中的气动载荷特性进行专门研究.
折叠翼舵的展开过程是一个动态过程[3-4].目前技术条件下要进行动态测力还存在一定困难, 因此本文在综合考虑计算精度和计算效率的前提下, 采用定常和非定常数值模拟两种不同方法, 进行翼面折叠展开过程气动载荷计算分析, 获得了典型工况下翼面折叠展开过程的载荷情况, 对比分析了非定常效应对气动载荷的影响, 结合实际使用需求, 给出了两种方法的优劣以及适用性.
1 研究对象简述本文研究对象简述如下:
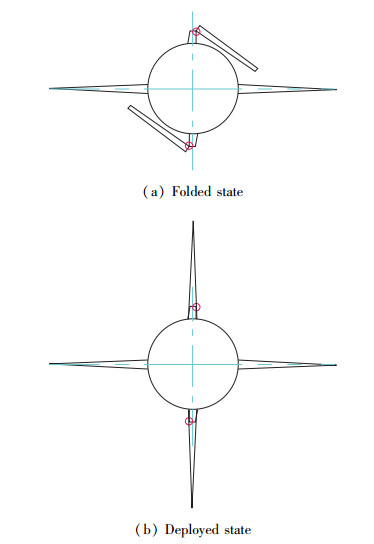
该飞行器采用十字形翼面布局, 在使用过程中, 左右翼面处于展开到位状态, 上下翼面处于折叠状态, 在高速飞行状态下(M=0.8左右)快速展开, 翼面折叠方式为顺航向、顺时针折叠, 折叠角120°, 投放后按照指令展开到位锁定, 折叠翼面主要由内翼组件、外翼组件和折叠展开机构组成, 翼面折叠及展开到位外形如图 1所示.
|
| 图 1 翼面示意图 Fig.1 Schematic of wings |
翼舵类部件折叠展开是一个比较复杂的动态过程, 须模拟整个运动过程[5-6], 这对于网格划分以及运动姿态控制要求较高, 且计算周期较长, 因此定常数值计算方法成为一种广泛使用的方法.这种方法的前提是忽略翼面转动带来的附加影响, 将整个展开过程离散成若干个指定折叠角状态, 把每个状态的力和力矩光滑连接起来, 得到展开全过程范围内作用在折叠翼面上的气动力的变化, 为设计展开机构提供依据.
数值求解采用Fluent软件来求解流场, 控制方程为定常三维N-S方程, 空气状态方程按理想气体考虑, 空气黏性系数采用Sutherland公式修正, 湍流模型为标准k-ε模型, 壁面速度分布采用壁面函数修正, 计算时选用基于密度的隐式格式求解.来流边界给定远场压力条件, 固定壁面给定无滑移、无渗透边界条件, 温度按绝热壁面处理.计算模型网格量为2×106左右, 计算域满足亚声速飞行器计算要求.
2.2 定常计算算例这种方法经地面实验验证, 计算精度较高, 结果可信.在典型状态M=0.5, α=-6°下, 对比风洞实验与数值模拟两种不同方法下的展开力矩结果, 见表 1.
| 下载CSV 表 1 数值计算结果与风洞实验结果对比 Tab.1 Comparisons of numerical to wind tunnel test results |
从表 1对比可知, 相同状态下, 数值计算结果与风洞实验结果误差在5%以内.主要原因在于数值计算模型须做一些简化处理, 如作动筒外表面采用光滑表面, 没有考虑尾翼根部的整流罩以及安定面与舵面之间的缝隙.但经对比可知, 误差在可接受范围内, 可以确认数值计算模型及方法是可信的.
本文将整个过程离散为展开角0(折叠状态), 30, 60, 90和120°(完全展开到位)5个状态, 开展相应状态下的定常气动载荷计算, 插值获得整个过程载荷变化, 其中离散角度越密, 则越便于曲线拟合.
本次算例状态如下:
M=0.75, H=9 km, 攻角α=2, -2°, 侧滑角β=0, 2, 4°.
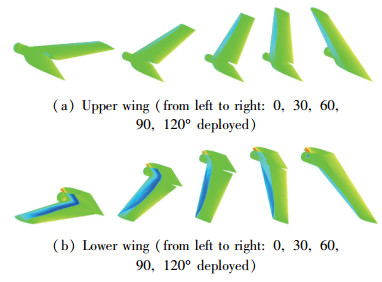
以M=0.75, H=9 km, α=2°, β=4°为例, 折叠翼面在展开过程中的气动载荷变化如图 2所示.
|
| 图 2 典型工况翼面展开过程气动载荷压力分布云图 Fig.2 Pressure distributions on wing in typical cases |
从压力分布云图可知, 翼面折叠状态下, 其内侧有很强的激波, 导致内侧总压力低于外侧总压力, 相对下翼面而言, 该激波基本伴随了整个展开过程, 导致对应的力和力矩呈现阻碍趋势; 而对于上翼面而言, 由于折叠翼面内侧处于迎风面, 在展开一定角度(大约60°)后该激波几乎消失.
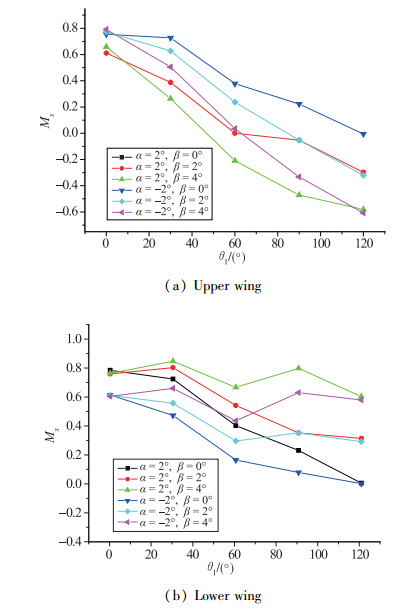
以折叠轴中心线取距, 阻碍展开的力矩为正, 计算结果如图 3所示.图中纵坐标Mx为绕折叠轴的展开力矩, 而横坐标θ1为翼面展开角度.
|
| 图 3 折叠部分展开力矩随展开角度变化(无量纲化) Fig.3 Non-dimensional aerodynamic moments of wing during deploying process |
分析数据可知, 翼面折叠状态下, 侧滑角对气动载荷影响很小, 但攻角不同, 气动载荷明显不同; 翼面展开到位后, 攻角对气动载荷影响很小, 而侧滑角影响较大, 这和折叠翼面为上下翼面相关, 符合流动特性.
翼面整个展开过程中, 初始时刻均为阻碍展开力矩, 该力矩基本随着展开角增大呈现减小趋势, 对于上翼面而言, 展开角大于60°后, 侧滑角的存在对于翼面来说是一个有利展开的力矩, 导致总载荷有利于翼面展开; 对于下翼面, 正好相反, 因此总载荷一直是阻碍展开的, 这和压力分布是相符的.
3 非定常数值计算 3.1 非定常计算方法本文研究对象展开速度较快, 为了获得翼面快速转动带来的非定常效应, 模拟翼面整个展开过程, 考虑真实角速度变化, 采用动网格开展非定常数值模拟计算, 以求获得非定常展开载荷.
同样采用Fluent软件求解流场[7-9], 基本参数设置同定常方法, 但非定常载荷计算还须设置非定常时间计算、动网格和指定翼面运动的用户定义函数(user-defined function, UDF). Fluent动网格模型可以用来模拟流场形状由于边界运动而随时间改变的问题.边界的运动形式可以是预先定义的, 即可以在计算前指定其速度或角速度(如匀速展开); 也可以是预先未做定义的, 即边界的运动要由前一步的计算结果决定(如作动筒瞬间作动), 本文采用的是前一种边界运动形式.
动网格计算中网格的动态变化过程可以用3种模型计算, 即弹簧近似光滑模型(spring-based smoothing)、动态分层模型(dynamic layering)和局部重划模型(local remeshing).本文采用局部重划模型, 这种方法要求网格为三角形(二维)或四面体(三维), 这对于适应复杂外形是有好处的, 局部网格重划法只会对运动边界附近区域的网格起作用[10-11].
3.2 非定常计算算例这种非定常计算方法在翼型NACA0012的典型Euler方程非定常气动力算例计算中得到验证, 计算的模型升力系数和力矩系数随攻角变化与实验结果比较接近, 因此这种非定常Euler方程的计算是可靠的, 具有较高的精度.
本文非定常计算典型状态为:
| $ M = 0.75, H = 9\;{\rm{km, }}\alpha = {1.36^ \circ }, \beta = {1.31^ \circ }. $ |
通过测量系统测得的展开过程中部分时刻点的角位移, 插值计算得到展开过程中角速度变化情况, 见表 2.表中, θ2为角位移, ω为角速度.从表中可知, 飞行器翼面实际展开过程角速度不恒定, 整个过程中上下翼面展开所用时间也不同, 但均在0.1 s左右.
| 下载CSV 表 2 上下翼面展开过程角速度 Tab.2 Angular velocity of upper and lower wing during deploying process |
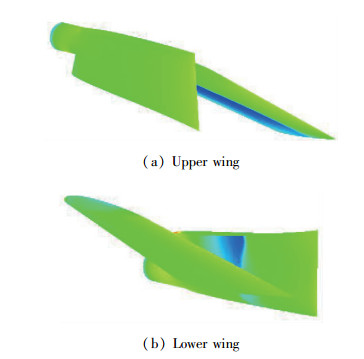
根据上述翼面展开过程进行非定常计算, 展开初始时刻翼面压力分布云图如图 4所示.展开到位时刻翼面压力分布云图如图 5所示.整个展开过程中, 上下翼面展开载荷变化如图 6所示, 图中纵坐标Mx, FN分别为阻碍翼面的力矩和垂直翼面的力, 方向均为阻碍展开为正, 横坐标t为展开时间.
|
| 图 4 翼面展开初始时刻压力分布 Fig.4 Pressure distributions on wing at beginning of deploying process |
|
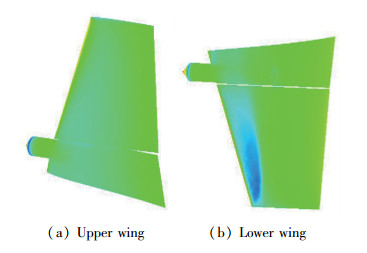
| 图 5 翼面展开到位时刻压力分布 Fig.5 Pressure distributions on wing when fully deployed |
|
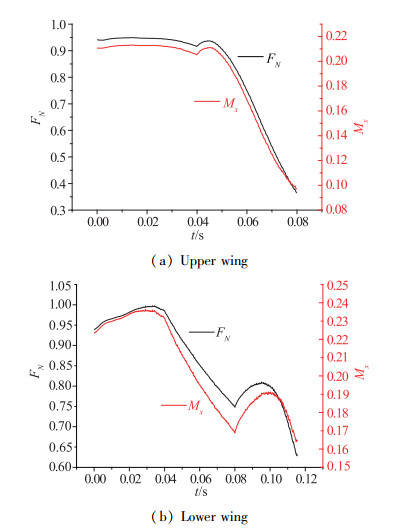
| 图 6 翼面法向力与力矩随展开时间变化(无量纲化) Fig.6 Non-dimensional aerodynamic loads on wing during deploying process |
由于飞行实测视频每一帧时间间隔为0.04 s, 数据有限, 因此每隔0.04 s数据有一个突变, 这是由于角速度突变造成的.从压力分布云图上可知, 翼面折叠状态下, 折叠内侧有很强的激波, 导致内侧总压力低于外侧总压力, 该激波基本伴随了前半个展开过程, 对应的力和力矩呈现阻碍趋势.
整个展开过程中, 由于飞行器正攻角飞行, 下翼面处于迎风面, 因此相对而言下翼面所受展开载荷较大, 但考虑角速度后, 上下翼面均附加一定的阻碍展开气动载荷影响, 在整个展开过程中展开力矩和法向力一直是阻碍展开的.
采用上述相同状态参数, 进行展开角度为0, 30, 60, 90和120°的定常气动载荷计算, 展开力矩对比见图 7, 相关无量纲数据对比见表 3.
|
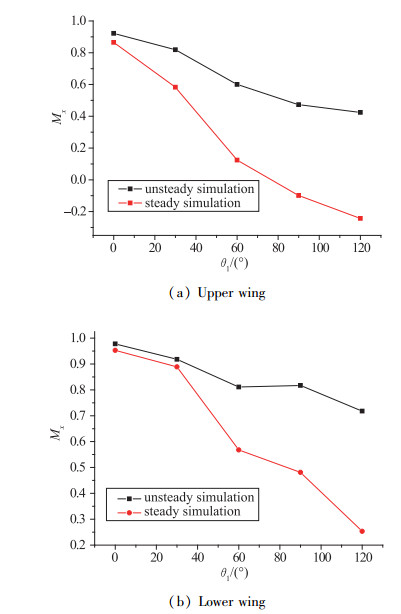
| 图 7 非定常与定常计算展开力矩对比(无量纲化) Fig.7 Comparisons of non-dimensional aerodynamic loads on wing between steady and unsteady numerical simulation |
| 下载CSV 表 3 非定常与定常计算展开力矩对比(无量纲化) Tab.3 Comparisons of non-dimensional aerodynamic loads on wing between steady and unsteady numerical simulation |
对比结果表明, 初始时刻由于展开角速度基本为零, 因此两者基本相当, 但随着展开角度增大, 展开角速度对翼面局部流场的影响作用增大, 导致两者载荷差异增大.定常计算仅考虑了来流对翼面的影响, 而非定常计算不仅考虑来流的影响, 同时也考虑了由于翼面展开角速度带来的当地流场改变的影响.以上翼面t=0.08 s时刻为例, 来流速度为227 m/s, 展开角速度为78.54 rad/s, 翼尖处的线速度为31.4 m/s, 即翼面展开速度为来流速度的13.8%左右.由此可知, 翼面展开过程的非定常效应对翼面展开载荷影响较大.
对于上翼面而言, 随着翼面展开角度越转越大, 来流对上翼面的影响由阻碍展开变为有利于展开, 而非定常计算中气动载荷一直是阻碍展开的.而下翼面虽然气动载荷一直是阻碍其展开的, 但定常计算载荷下降趋势明显大于非定常计算.总之, 两种方法计算结果趋势一致, 但由于翼面展开角速度的影响, 非定常效应给翼面增加了阻碍展开的载荷, 所以考虑非定常效应后阻碍展开的力/力矩增大, 这是符合物理规律变化的.
4 结论本文同时采用了定常和非定常数值计算两种数值模拟方法进行了气动载荷特性研究, 得出如下结论:
(1) 定常计算方法适用于翼面展开速度远小于来流速度, 在忽略运动带来的附加影响的情况下, 可以确保计算效率和计算结果精度;
(2) 非定常计算方法考虑运动带来的附加影响, 尤其是在展开速度与来流速度相当或差异不大的情况下, 可以模拟实际翼面运动轨迹, 考虑非定常效应, 计算结果更为真实可信;
(3) 本文非定常计算结果很好地展示了非定常效应影响, 但由于各种原因, 翼面整个展开运动过程模拟与实际会存在一定出入, 且计算模型模拟精度会低于定常计算所用模型, 因此也存在一定的局限性.
(4) 定常和非定常分析方法都存在各自的优劣性, 在具体使用过程中, 须结合具体问题选取合适的方法, 才能既保证计算精度, 又提高计算效率.
| [1] |
秦永明, 蔡琛芳, 董金刚. 机载导弹折叠舵展开气动特性试验研究[J]. 航空兵器, 2013(5): 3-6. Qin Y M, Cai C F, Dong J G. Experimental study on aerodynamics of airborne missile folding rudder[J]. Aero Weaponry, 2013(5): 3-6. (in Chinese) |
| [2] |
刘庆楣. 飞航导弹结构设计[M]. 北京: 宇航出版社, 1995. Liu Q M. Structure design of winged missile[M]. Beijing: China Astronautic Publishing House, 1995. (in Chinese) |
| [3] |
李东, 李斌, 刘仙名. 空空导弹折叠舵展开过程气动载荷分析[J]. 弹箭与制导学报, 2014, 34(3): 154-156. Li D, Li B, Liu X M. Analysis on aerodynamic loads during deployment of folded tails of an air-to-air missile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2014, 34(3): 154-156. (in Chinese) |
| [4] |
张伟, 郭晓光, 曹东兴. 一种折叠翼飞行器动态仿真分析与实验设计[J]. 科技导报, 2011, 29(20): 18-22. Zhang W, Guo X G, Cao D X. Investigation of a folding wing aircraft using dynamic analysis simulation and experimental method[J]. Sciense & Techndogy Review, 2011, 29(20): 18-22. DOI:10.3981/j.issn.1000-7857.2011.20.001 (in Chinese) |
| [5] |
郭秋亭, 张来平, 常兴华, 等. 变形飞机动态气动特性数值模拟研究[J]. 空气动力学学报, 2011, 29(6): 744-750. Guo Q T, Zhang L P, Chang X H, et al. Numerical simulation of dynamic aerodynamic characteristics of a Morphing Aircraft[J]. Acta Aerodynamica Sinica, 2011, 29(6): 744-750. (in Chinese) |
| [6] |
Sahu J. Advanced coupled CFD/RBD calculations of free-flight-projectile aerodynamics[C]. Proceedings of the Users Group Conference, 2005. http://dl.acm.org/citation.cfm?id=1114280.1114420
|
| [7] |
Oktay Baysalo. A CFD study of complex missile and store configurations in relative motion[R]. NASA-CR-197912, 1995. http://core.ac.uk/display/42782355
|
| [8] |
Newman J C, Oktay Baysalo. Transonic solutions of a wing/pylon/finned store using hybrid domain decompsition[R]. AIAA 1992-4571, 1992. http://www.researchgate.net/publication/23826416_Transonic_solutions_of_a_wingpylonfinned_store_using_hybrid_domain_decomposition
|
| [9] |
Yen G W, Oktay Baysalo. Computing high-speed flows past an oscillating cylinder near a vertical wall[R]. AIAA 1992-4653, 1992. http://www.researchgate.net/publication/23591041_Computing_high-speed_flows_past_an_oscillating_cylinder_near_a_vertical_wall
|
| [10] |
Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [11] |
Jones W T, Samareh-Abolhassani J. A Grid generation system for multi-disciplinary design optimization[R]. AIAA 1995-1689, 1995. http://www.researchgate.net/publication/2292156_A_Grid_Generation_System_For_Multi-Disciplinary_Design_Optimization
|
| [12] |
Robinson B A, Batina J T, Yang H T Y. Aeroelastic analysis of wings using the euler equations with a deforming Mesh[J]. Journal of Aircraft, 1991, 28(11): 781-788. DOI:10.2514/3.46096 |
| [13] |
李莉, 任茶仙, 张铎. 折叠翼机构展开动力学仿真及优化[J]. 强度与环境, 2007, 34(1): 17-21. Li L, Ren C X, Zhang D. Dynamic simulation and optimization design of deployment of folding-wing[J]. Structure & Environment Engineering, 2007, 34(1): 17-21. (in Chinese) |
| [14] |
余旭东, 赵伟, 马彩霞, 等. 战术导弹折叠翼结构动态响应分析[J]. 西北工业大学学报, 12(3), 1994, 12(3): 462-466. Yu X D, Zhao W, Ma C X, et al. Determination of time for complete opening of foldable wings of tactical missile[J]. Journal of northwest polytechnical university, 1994, 12(3): 462-466. (in Chinese) |
| [15] |
迟圣威. 折叠翼颤振理论分析和计算方法[D]. 南京: 南京航空航天大学, 2011. Chi S W. Theoretical and computational flutter study for folding wing configuration[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1011291761.htm |



