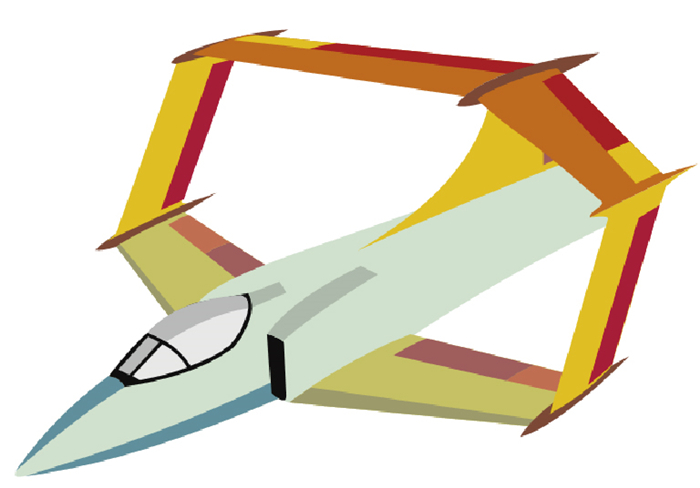
美国NASA的环境责任航空计划(environmen-tally responsible aviation, ERA)对新一代飞行器提出了减少70%污染排放量和50%燃油消耗的高要求.洛克希德·马丁公司针对该计划的报告中表明盒式翼布局可达到任务指标[1].盒式翼布局由前后两对翼构成, 前翼后掠, 后翼前掠, 并在翼尖处通过端板相连形成盒状外形, 如图 1所示[2].该布局翼尖连接的结构可以提高机翼结构刚度, 减小飞机结构质量[3].在同一展长和升力下, 可以最大程度地减小诱导阻力, 增大机翼有效展弦比, 提高飞行器气动性能, 减少燃油消耗[4].同时, 盒式翼平滑的升力分布有利于减小跨声速激波阻力[2].然而, 跨声速盒式翼布局飞行器提出至今, 尚未投入商业运营[5].其中, 双翼之间的跨声速气动干扰问题是该气动布局设计成功的一个关键因素。
传统布局通过增大翼展来减小机翼的诱导阻力, 但机翼结构和折叠机翼的复杂性等限制了常规单翼机的翼展长度, 而盒式翼的两对机翼很好地解决了这一问题[6].国内外针对盒式翼的气动性能、结构效率和操纵性能进行了多项研究. 1924年, Prandtl[4]提出在同一展长和升力条件下, 盒式翼布局可以最大程度地减小诱导阻力, 是“最好的翼系统”. 1974年, Miranda[2]在专利中提到, 除了减小诱导阻力, 盒式翼布局飞行器还追求近距作战操纵性、结构效率、跨超声速减阻等.盒式翼两个翼面上可以布置多个操纵舵面, 进行多操纵面的组合控制, 完成无需力矩配平的直接升力和直接侧力控制.同时闭合结构形式使翼尖处的扭转刚度增大, 减轻气弹问题, 提高结构刚度, 使其能承受更大的翼载荷. Bagwil等[7]指出通过翼尖连接的结构, 理论上可以达到双翼较强的支撑效应, 减小机翼质量.刘杰等[8]指出由于前翼先失速、后翼延迟失速, 使得失速时升力系数下降比较缓慢, 盒式翼具有较常规高升阻比长航时飞机布局更理想的失速特性.陈迎春等[9]和吴光辉等[10]对纵向飞行品质的研究指出:盒式翼布局飞机具有较大的后翼面积, 会引起较大的低头力矩, 使飞机的静稳定性过大, 产生特殊的操稳问题; 因此前翼面积应适当增大, 并使后翼前移.为减小前翼对后翼的干扰, 将后翼连接到垂尾上, 但会增加垂尾的结构质量.综上所述, 盒式翼布局可以减小诱导阻力, 提高机翼结构刚度, 减轻飞机质量, 有较好的跨声速升力分布和较高的操纵性能[11].
Lange等[12]提出盒式翼布局相对平滑的升力分布有利于减小跨声速激波阻力, 因而可将该布局应用于跨声速运输机.但跨声速飞行时, 由于不利激波和分离区的出现[13], 气动干扰会使得总阻力增大, 从而对飞行器的气动性能产生不利的影响.为了达到最佳的气动效率, 减小双翼之间的干扰, 须合理选择双翼的纵向距离和垂向间距[2].约定前翼在上、后翼在下为正交错布局; 前翼在下、后翼在上为负交错布局. Rhodes等[14]对于亚声速双翼干扰的研究表明, 双翼之间的交错和翼间隔会对机翼的气动性能产生较大的影响. Selberg等[15]发现不同弦长的双翼性能可以优于相同弦长的双翼, 且负交错和正翼差角会使双翼机的气动性能下降. Bagwil等[7]关于M=0.5的研究指出正交错布局为最佳气动布局. Barcala等[16-17]对几种不同后掠角和纵向距离的负交错布局做了详细研究, 表明前翼后掠、后翼前掠可达到最好的气动性能.张晓等[18]对150 km/h联翼的正负交错布局进行的数值研究表明正交错布局具有延迟失速、提高最大升力系数、更好的俯仰稳定性等优势.尹钧等[19]的研究表明垂直高度差不宜太大或太小, 否则均会导致气动性能的降低.郭亚军等[6]指出随着前后翼垂向间距的增大, 盒式翼升力和升阻比均增大; 增大前后翼的纵向距离, 盒式翼升力增加.上述研究多基于亚声速条件, 对于跨声速双翼干扰对布局气动性能的影响机理和参数研究比较缺乏.而跨声速的流动现象和干扰机理复杂, 需要进一步研究.
文章拟对跨声速盒式翼布局中双翼几何参数对布局升阻特性的影响进行数值分析, 旨在研究如何减弱双翼之间的干扰, 提升布局升阻特性.采用第1节介绍的名为ACANS的程序进行全部的数值计算, 并通过与实验数据的对比验证了程序的准确性.第2节介绍了计算模型.第3、4节分析了正负交错布局各参数对升阻特性的影响.结果表明, 无论是正交错还是负交错, 增大双翼的纵向距离, 都可以减弱干扰, 提高升阻比.但相对正交错布局, 负交错布局在双翼纵向距离为1.5倍上翼弦长即可达到无干扰升阻比, 对升阻特性的提升更明显.负交错时双翼的垂向间距对布局升阻比影响不大, 减小翼差角和前翼弦长有利于提高升阻比.
1 数值方法 1.1 控制方程采用有限差分程序ACANS(aerodynamic combustion and aerothermodynamic numerical simulation)进行数值计算.文献[20-22]通过对高速流动湍流边界层的数值计算与实验的对比, 验证了ACANS程序的可靠性. ACANS程序通过求解Favré-averaged Navier-Stokes方程[23]模拟求解可压缩湍流流动, 选择Spalart-Allmaras单方程湍流模型[24], 时间离散采用隐式格式.
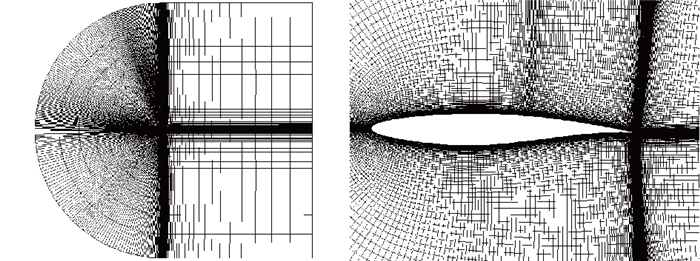
1.2 数值验证基于Cook等[25]的跨声速翼型绕流实验对ACANS程序应用于跨声速流场计算的可行性进行数值验证.文献[26]给出实验工况的修正值: M=0.73, 基于翼型弦长Reynolds数Re=6.5×106, α=2.79°.计算网格采用C型拓扑, 如图 2所示.为保证计算精度, 准确捕捉激波位置, 在前缘、后缘和激波处分别加密, 得到不同疏密程度(375×89, 430×108)的网格.翼型上下及来流上游取30倍弦长、翼型下游取40倍弦长作为计算域.为了准确模拟边界层流动, 翼面法向第1层网格高度取2×10-6, 满足y+ < 1.
|
| 图 2 网格拓扑 Fig.2 Grids topology |
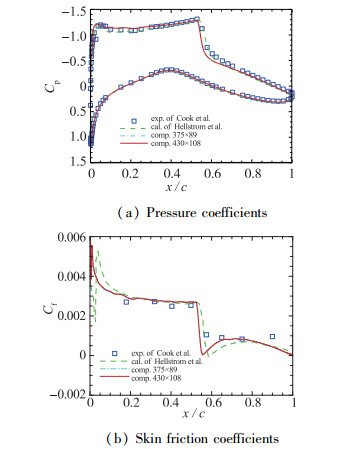
图 3给出了不同网格计算所得的翼型表面压力系数和摩擦阻力系数分布曲线, 并与Hellstrom等[27]的计算结果和实验值进行了比较.不同网格计算所得的数值接近, 且与实验值吻合较好, 激波位置捕捉准确.
|
| 图 3 不同网格数值模拟结果与实验值对比 Fig.3 Comparisons between experimental and numerical results on different grids |
表 1给出了不同网格计算所得的升力系数和阻力系数与Yu等[28]的计算结果及实验值的比较, 其中, 网格2升力系数、阻力系数与实验值误差均小于1%, 认为翼型沿流向的加密程度满足跨声速流场的计算要求.
| 下载CSV 表 1 升力系数和阻力系数, 不同网格数值模拟结果与实验值对比 Tab.1 Lift and drag coefficients, comparisons between experimental and numerical results on different grids |
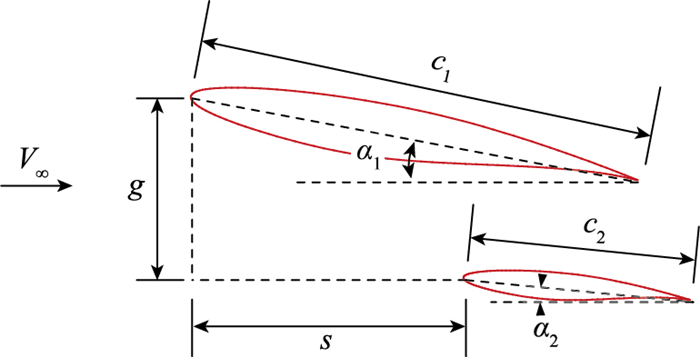
由于考虑正、负交错两种布局, 为了避免混淆, 下文对双翼采用上下翼叫法.研究的几何参数包括交错、翼间隔、翼差角和弦长比.以翼前缘为参考点, 各参数定义如图 4所示.交错s为平行于来流的纵向距离, 以下翼在上翼下游为正; 翼间隔g为垂直于来流的间距, s,g为对上翼弦长的无量纲参数; 翼差角δ表示上翼攻角α1和下翼攻角α2的差值: α1-α2; 弦长比r表示下翼相对上翼的弦长比: c2/c1.不同交错布局的网格如图 5所示.
|
| 图 4 参数定义 Fig.4 Parameter definition |

|
| 图 5 不同交错布局双翼网格 Fig.5 Grids for different staggered layouts |
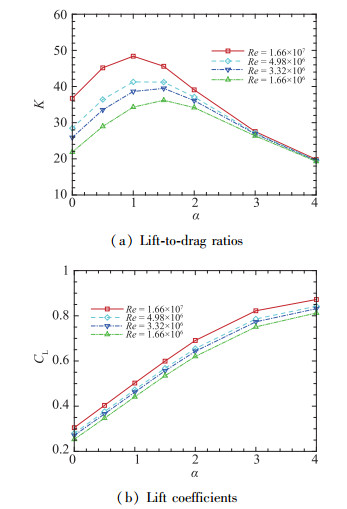
图 6给出了超临界翼型RAE2822在来流Mach数M=0.75, 不同Reynolds数下升阻比和升力系数随攻角变化曲线.该翼型升力系数在Reynolds数为1.66×107, 攻角为1°时达到0.5, 可作为巡航攻角.因此, 选用RAE2822翼型作为双翼的翼型, 以上翼攻角等于1°为基础, 通过比较双翼整体升阻比与无干扰升阻比研究各几何参数对布局升阻特性的影响.其中, 整体升阻比(Kwhole)是当双翼耦合时整体升力与整体阻力的比值.无干扰升阻比定义如下:
| $ {{K}_{\rm{noninterference}}}=\frac{{{L}_{1}}+{{L}_{2}}}{{{D}_{1}}+{{D}_{2}}} $ |
|
| 图 6 RAE2822翼型升阻比和升力系数随攻角变化 Fig.6 Variations of lift-to-drag ratio and lift coefficient with angle of attack of RAE2822 airfoil |
式中, L1, D1为基于上翼弦长Reynolds数下单个翼型的升力和阻力; L2, D2为基于下翼弦长Reynolds数下单个翼型的升力和阻力.因此无干扰升力系数取CL1+r×CL2, 无干扰阻力系数取CD1+r×CD2.
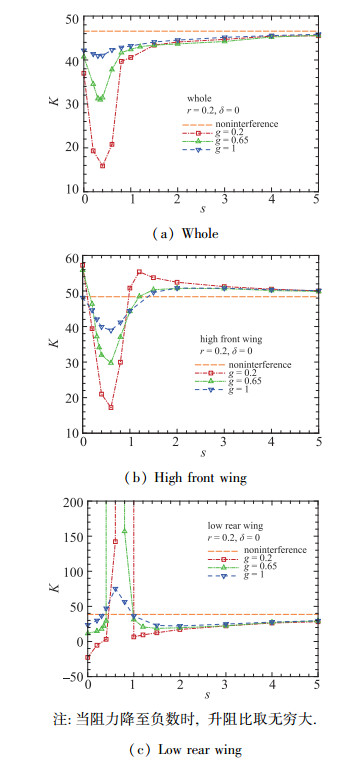
3 正交错布局研究正交错布局中各几何参数对双翼升阻特性的影响.选择r=0.2作初步分析.由于机身直径的限制, 翼间隔g一般小于1.不同翼间隔下升阻比随交错变化如图 7所示.可以看出, 整体升阻比均小于无干扰升阻比.不同翼间隔时升阻比的变化幅值不同, 翼间隔越小, 升阻比的变化幅值越大, 但总体趋势相同. s=0~1时, 整体升阻比下降幅值较大, 随交错呈Ⅴ型分布.上翼升阻比先减小后增大, 下翼升阻比与之相反, 当双翼几何中心在同一垂直平面时, 整体升阻比下降至最低.其中, g=1时相对无干扰升阻比下降12%, g=0.65时下降34%, g=0.2时下降66%;当下翼移向上翼前缘与后缘时, 升阻比相对有所增大. s > 1时, 上下翼升阻比都趋向于无干扰大小, 整体升阻比逐渐增大至接近无干扰升阻比, 但增长速度较慢, s=5时与无干扰升阻比相差2%左右.
|
| 图 7 正交错布局中升阻比随交错变化 Fig.7 Variations of the lift-to-drag ratio with stagger in positive staggered layout |
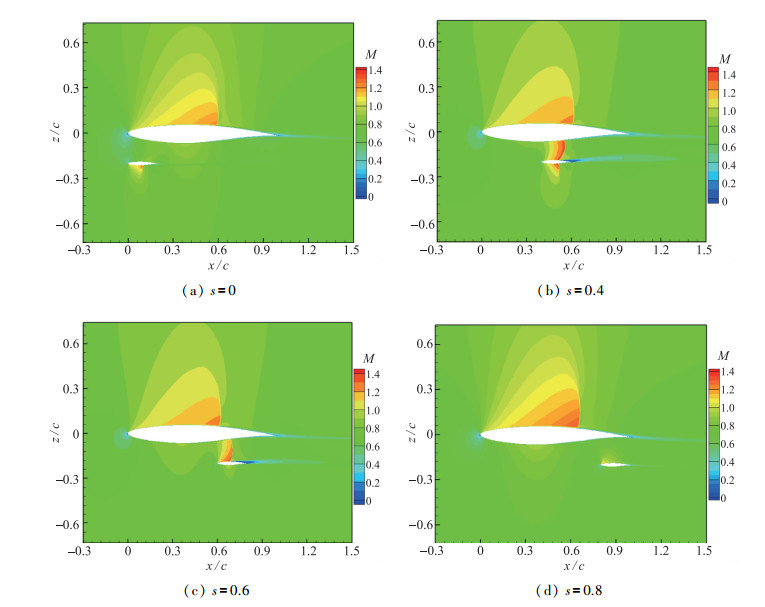
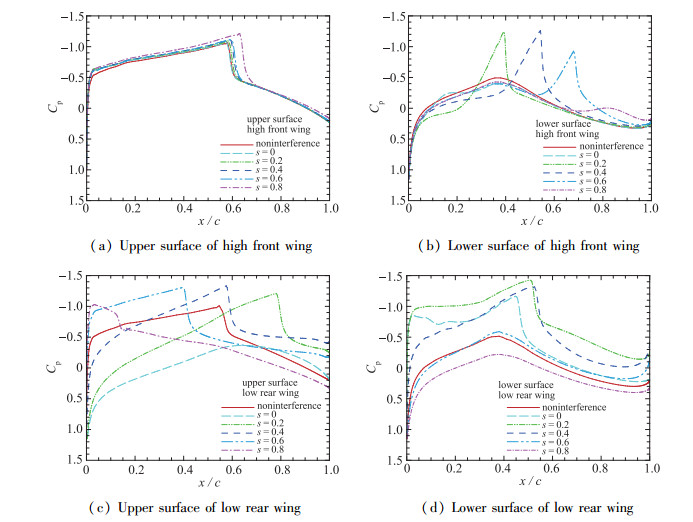
由图 7可知, 小交错s=0~1范围内气动参数变化剧烈, 图 8和图 9分别给出了该范围内双翼的Mach数云图和压力系数分布.上翼下翼面和下翼上翼面形成一个通道, 当下翼位于上翼正下方时, 通道内气流压缩形成一道强激波; 当下翼移至上翼前缘和后缘时, 通道内激波逐渐减弱并消失.由压力分布可知, 下翼的压力分布变化较大; 上翼除了s=0.8时上翼面激波后移10%, 下翼对上翼上翼面激波位置和强度的影响不大, 主要改变下翼面的压力分布.
|
| 图 8 双翼Mach数云图, g=0.2, r=0.2, δ=0 Fig.8 Mach number contours of dual wing, g=0.2, r=0.2, δ=0 |
|
| 图 9 双翼表面压力系数分布, g=0.2, r=0.2, δ=0 Fig.9 Pressure coefficient distributions of dual wing, g=0.2, r=0.2, δ=0 |
下翼位于上翼前半部分, 如s=0.2, 双翼之间形成收缩通道, 在下翼后缘和上翼下翼面迎风面之间形成激波.对上翼而言, 驻点下移使得上翼面超声速区负压增大, 强激波导致的下翼面低压区对升力的不利影响可由通道前和波后高压区抵消, 但额外的激波阻力使得阻力增大, 升阻比下降19%.对下翼而言, 上翼面激波移至后缘, 边界层有小分离, 且下翼驻点上移使得下翼面逆压梯度增大, 形成强激波, 升力减小167%, 上下两道激波使下翼阻力增大382%, 整体升阻比下降59%.当下翼往上翼前缘移动至s=0处, 上述效应逐渐减弱, 通道内不起激波, 上翼表面压力分布接近于无干扰时分布.
下翼位于上翼后半部分时, 双翼间形成扩张通道, 上下翼驻点均下移.如s=0.6, 尽管下翼上翼面边界层出现小分离, 但激波前移至迎风面且强度增大, 驻点下移使下翼面无强逆压梯度而不起激波, 因此压差升力增大, 同时压差阻力变为压差推力, 下翼总阻力减小68%, 升阻比相对无干扰时单翼升阻比增大267%.对上翼而言, 通道内激波打到下翼面背风区, 其背风面压力减小, 阻力增大151%, 升阻比下降64%.由于上翼对整体升阻比的影响大于下翼, 因此整体升阻比下降55%.当下翼往上翼后缘移动至s=0.8时, 上述作用逐渐减弱, 上翼激波后移, 通道内激波减弱直至消失, 下翼上下翼面均无激波产生.
当下翼和上翼的几何中心位于同一垂直平面即s=0.4时, 上翼下翼面和下翼上翼面的间隔最小, 通道内激波最强, 同时下翼驻点上移, 下翼面出现几乎等强度激波, 强逆压梯度使得下翼上下翼面波后边界层均出现大分离.通道内激波位于上翼背风面, 使上翼波阻增大同时升力减小.双翼升阻比相对单翼升阻比均有大幅度下降, 总阻力增大161%, 整体升阻比下降66%.
s=0~1时升阻比相对无干扰时下降幅度较大, g=0.2时下降15%~66%; g=0.65时下降11%~34%; g=1时下降8%~12%.可知, 小交错时升阻比随翼间隔增大而增大, 但翼间隔受机身直径的限制, 不能过大, 因此通过增大翼间隔减小升阻损失的效果有限.
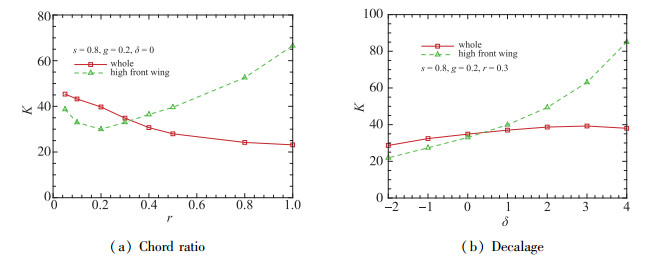
图 10给出了升阻比随弦长比和翼差角的变化规律.升阻比随翼差角增大先增大后减小, 但总体变化值不大.弦长比越小, 双翼干扰越小, 整体升阻比越大.但考虑到结构效率, 弦长不能太小.因此, 小交错时, 改变几何参数对升阻比的提升不大.
|
| 图 10 升阻比随弦长比和翼差角的变化 Fig.10 Variations of lift-to-drag ratio with chord ratio and decalage |
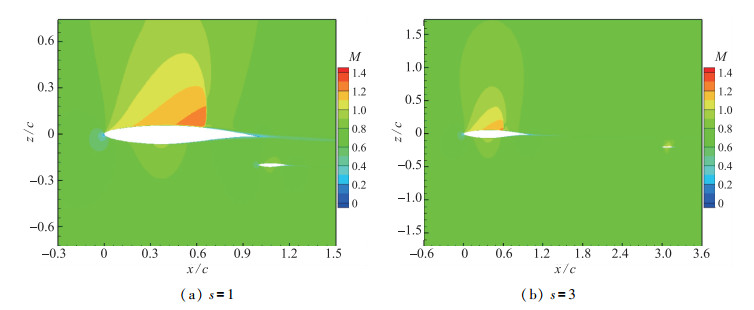
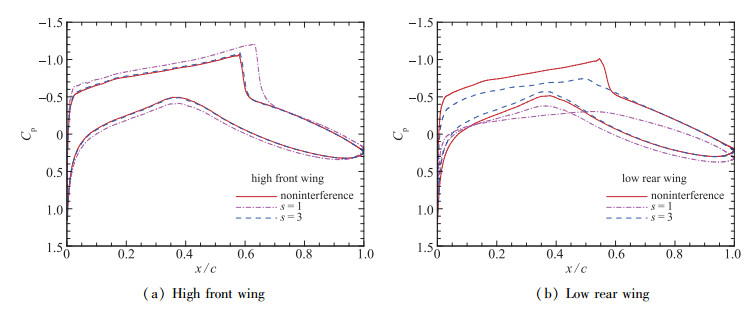
图 11和图 12给出了大交错s > 1时双翼的Mach数云图和压力分布, 可以看出此时下翼位于上翼的下洗区内, 其上翼面激波被消去, 上下压差减小, 升力减小, 升阻比下降.对上翼而言, 下翼前缘的驻点高压区使其后缘的压力增大, 阻力减小, 上下翼面压差增大, 升力增大, 升阻比提高.上翼对下翼的负作用和下翼对上翼的正作用使得整体升阻比下降幅值较小, s > 3后整体升阻比相对无干扰时幅值下降在5%以内.随着交错距离增大, 两种作用都减弱, 整体升阻比逐渐增大, 但增长速度缓慢.
|
| 图 11 双翼Mach数云图, g=0.2, r=0.2, δ=0 Fig.11 Mach number contours of dual wing, g=0.2, r=0.2, δ=0 |
|
| 图 12 双翼表面压力系数分布, g=0.2, r=0.2, δ=0 Fig.12 Pressure coefficient distributions of dual wing, g=0.2, r=0.2, δ=0 |
取s=4并增大下翼弦长, 观察发现上翼对下翼的下洗作用依然明显, 下翼激波被削弱.随着弦长比由0.1增大到1, 升阻比下降幅值的从1%增大到8%.因此, 正交错布局要达到与无干扰时接近的升阻比, 双翼纵向距离须达到5倍弦长及以上, 虽然可以提高升阻比, 但是过大的纵向距离会影响飞机俯仰力矩的变化, 使飞机产生静稳定性过大的问题[9].
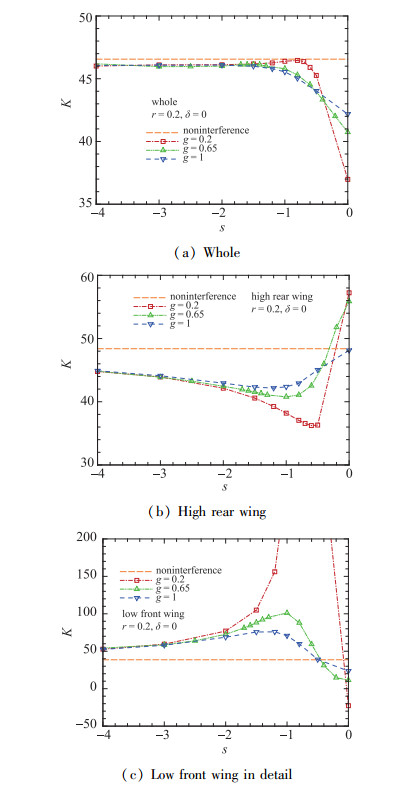
4 负交错布局上述分析表明增大双翼的纵向距离可减弱干扰, 提高升阻比.由图 7可知, 当交错减小时, 升阻比也逐渐增大, 因此继续减小交错值.考虑负交错布局, 整体及双翼升阻比随交错的变化如图 13所示.随着交错距离(绝对值)的增大, 上翼升阻比先减小后增大, 下翼升阻比先增大后减小, 不同翼间隔极值点不同.整体升阻比以相对正交错布局较快的增长速度趋近无干扰升阻比, 且翼间隔越小, 增长速度越快.
|
| 图 13 负交错布局升阻比随交错变化 注: g=0.2, s=-0.7~-0.5时, 下翼的阻力减小为负值, 为更好地观察变化趋势, 该部分升阻比取无穷大值. Fig.13 Variations of lift-to-drag ratio with stagger in negative staggered layout |
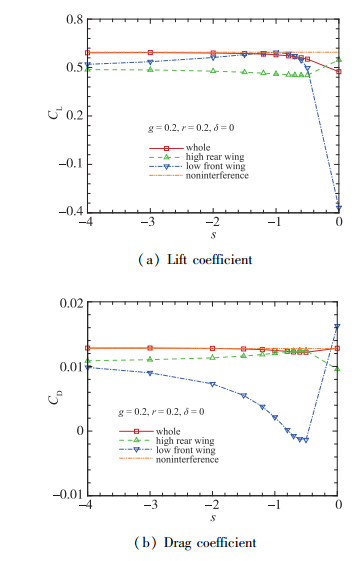
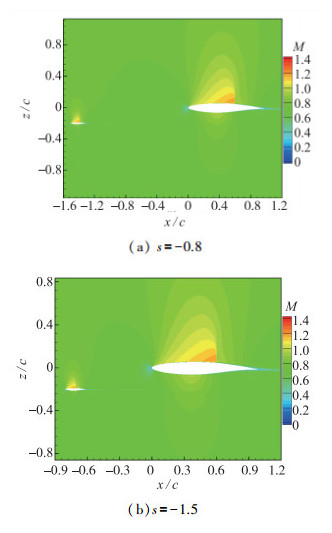
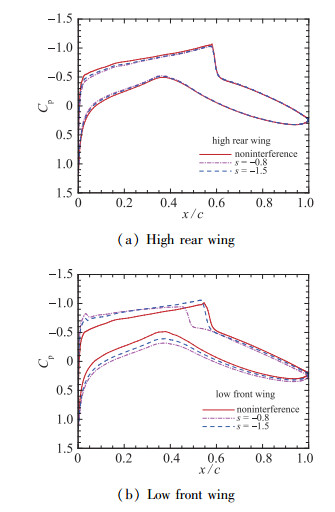
g=0.2时升阻比的增长速度最快, 在s=-1左右达到最大值后略有减小.双翼的升阻力系数变化如图 14所示.上翼的升阻力系数变化小, 下翼的升阻力系数变化大.这是因为, 气流经过下翼后产生了一定的下洗速度, 使上翼前半部分上下翼面压差减小, 升力减小, 阻力增大, 升阻比下降.由于上翼并不完全位于下翼的下洗区内且下翼弦长较小, 其对上翼的下洗作用不明显.对下翼而言, 上翼前缘的驻点高压区使其后缘的压力增大, 压差阻力下降, 分析气动力分量可知, 相对压差阻力, 黏性阻力的变化可忽略不计, 因此下翼阻力减小, 升阻比提高.上翼对下翼的正作用和下翼对上翼的负作用共同作用使得整体升阻比相对无干扰时只是略有下降, 且交错距离越大, 正负两种作用都越弱.从图 15的双翼Mach数云图和图 16的翼型表面压力分布也可看出, 虽然下翼的尾迹剪切层对上翼下方的流场有所影响, 但双翼之间的干扰已经很弱, 双翼激波强度和位置都与无干扰时接近.
|
| 图 14 升力和阻力系数随交错变化 Fig.14 Variations of lift coefficient and drag coefficient with stagger |
|
| 图 15 双翼Mach数云图, g=0.2, r=0.2, δ=0 Fig.15 Mach number contours of dual wing, g=0.2, r=0.2, δ=0 |
|
| 图 16 双翼表面压力系数分布, g=0.2, r=0.2, δ=0 Fig.16 Pressure coefficient distributions of dual wing, g=0.2, r=0.2, δ=0 |
表 2表明交错s=-1.5时, r=0.2, 不同翼间隔升阻比和无干扰升阻比的差值都已小于1.25%, 这是由于上翼对下翼的正作用和下翼对上翼的负作用共同使得双翼在纵向错开很短的距离时即可达到无干扰升阻比.而纵向距离较小使得负交错布局在提升升阻特性的同时也有利于提高机翼的结构刚度和操纵性能.
| 下载CSV 表 2 s=-1.5时不同翼间隔的升阻比 Tab.2 Lift-to-drag ratio at different gaps, s=-1.5 |
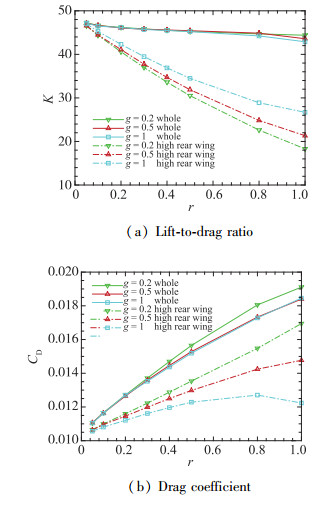
上述研究均基于r=0.2, 图 17给出s=-1.5, 不同翼间隔升阻比和总阻力系数随弦长比的变化曲线.弦长比越小, 双翼干扰越小, 总阻力越小, 整体升阻比越大.由图 6可知, 同一Mach数和攻角, 弦长增大, 翼型升阻比增大.因此, 随着弦长比r的增大, 下翼的升阻比增大, 但对上翼的干扰也增大, 使上翼升阻比呈几近线性下降趋势, 总阻力增大, 整体升阻比随之下降.双翼弦长相同时, 升阻比下降幅值最大, 相对无干扰下降8%~11%.因此, 为了提升升阻比, 可在保证结构刚度的前提下尽可能减小下翼的弦长.
|
| 图 17 升阻比和阻力系数随弦长比变化, δ=0 Fig.17 Variations of lift-to-drag ratio and drag coefficient with chord ratio, δ=0 |
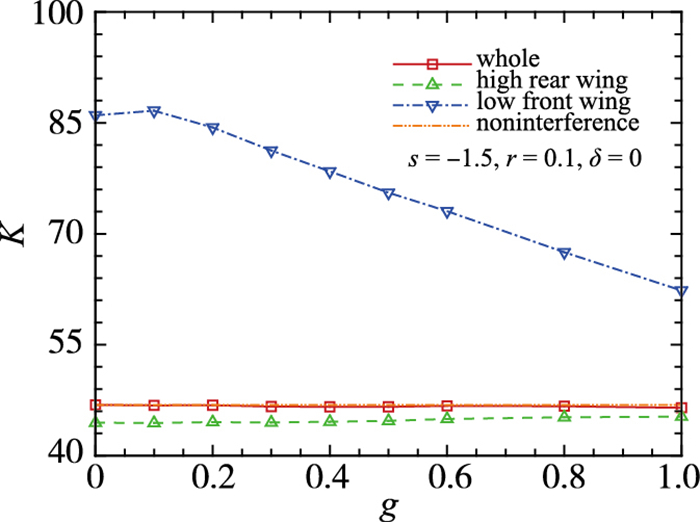
选择弦长比较小时的r=0.1分析, 升阻比随翼间隔的变化曲线如图 18所示.随着翼间隔的增大, 整体升阻比变化不大, 与无干扰时相比波动值在0.5%以下.上节分析不同弦长比对升阻比的干扰时, 选择了翼间隔为0.2, 0.5和1, 结果显示, 弦长比小于0.8时, 不同翼间隔整体升阻比相差值在1%以内.因此, 当下翼位于上翼前缘1.5倍距离时, 翼间隔对整体升阻比的影响几乎可以忽略不计.
|
| 图 18 升阻比随翼间隔变化 Fig.18 Variations of lift-to-drag ratio with gap |
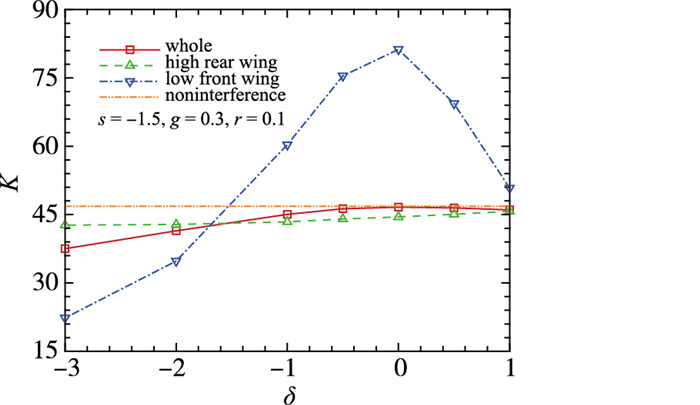
上述研究是基于双翼的攻角都等于1°的无翼差角情况, 图 19给出上翼攻角不变时, 升阻比随翼差角δ的变化曲线.随着δ的减小即下翼攻角增大, 整体升阻比先增大后减小, δ=0时达到最大.下翼升阻比先增大后减小, 与无干扰时翼型升阻比的变化趋势相同.由于下翼的下洗效应较弱, 上翼升阻比的变化幅值较小, 此时下翼是影响整体升阻比变化的主导因素.因此, s=-1.5时, 选择使下翼攻角升阻比最大的攻角可使整体升阻比达到最大.
|
| 图 19 升阻比随翼差角的变化 Fig.19 Variations of lift-to-drag ratio with decalage |
文章对盒式翼布局正负交错两种情况下的双翼气动干扰进行了数值研究.结果表明, 正交错布局中为提升布局升阻特性, 使整体升阻比接近无干扰升阻比, 双翼纵向距离须达到5倍上翼弦长及以上.此时下翼对焦点的力臂增大, 低头力矩增大, 可能产生静稳定性过大问题; 负交错布局中, 双翼纵向距离为1.5倍上翼弦长左右即可达到无干扰升阻比.无翼差角, 小弦长比时升阻比大, 翼间隔对升阻比的影响不大.因此, 双翼配置可采用1.5倍负交错和无翼差角, 并适当减小弦长, 调整翼间隔来提升布局升阻特性.
| [1] |
徐德康. 美国透露新一代民用飞机计划进展[J]. 国际航空, 2012(2): 45-47. Xu D K. The United States discloses progress of new generation civil aircraft program[J]. International Aviation, 2012(2): 45-47. (in Chinese) |
| [2] |
Miranda L R. Boxplane wing and aircraft: United States, 3834654[P]. 1974-09-10.
|
| [3] |
Wolkovitch J. The joined wing-an overview[J]. Journal of Aircraft, 1986, 23(3): 161-178. DOI:10.2514/3.45285 |
| [4] |
Prandtl L. Induced drag of multiplanes[R]. NACA-TN-182, 1924: 309-315.
|
| [5] |
Gagnon H, Zingg D W. Aerodynamic optimization trade study of a box-wing aircraft configuration[J]. Journal of Aircraft, 2016, 53(4): 971-981. DOI:10.2514/1.C033592 |
| [6] |
郭亚军, 高超, 肖虹, 等. 盒式机翼布局气动特性研究[J]. 航空计算技术, 2012, 42(2): 39-41. Guo Y J, Gao C, Xiao H, et al. Research on aerodynamic characteristics of a box-wing configuration[J]. Aeronau-tical Computing Technique, 2012, 42(2): 39-41. (in Chinese) |
| [7] |
Bagwil T L, Selberg B P. Aerodynamic investigation of joined wing configurations for transport aircraft[C]. 14th Applied Aerodynamics Conference, New Orleans: AIAA, 1996.
|
| [8] |
刘杰, 张曙光. 连接翼布局纵向控制特性[J]. 航空学报, 2008, 29(S1): 91-96. Liu J, Zhang S G. Longitudinal control features of joined-wing configuration[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(S1): 91-96. (in Chinese) |
| [9] |
陈迎春, 王立新, 王明丰, 等. 盒式布局飞机的纵向飞行品质研究[J]. 飞行力学, 2006, 24(3): 5-8. Chen Y C, Wang L X, Wang M F, et al. Longitudinal flight qualities of aircraft with joined-wing configuration[J]. Flight Dynamics, 2006, 24(3): 5-8. (in Chinese) |
| [10] |
吴光辉, 王妙香, 张健. 盒式布局飞机的纵向气动参数优化研究[J]. 飞行力学, 2007, 25(4): 5-7, 12. Wu G H, Wang M X, Zhang J. Research on longitudinal aerodynamic parameter optimize of a joined-wing configuration aircraft[J]. Flight Dynamics, 2007, 25(4): 5-7, 12. (in Chinese) |
| [11] |
Lange R H. Review of unconventional aircraft design concepts[J]. Journal of Aircraft, 1988, 25(5): 385-392. DOI:10.2514/3.45592 |
| [12] |
Lange R H, Cahill J F, Bradley E S, et al. Feasibility study of the transonic biplane concept for transport aircraft application[R]. NASA CR-132462, 1974. http://www.researchgate.net/publication/265026146_FEASIBILITY_STUDY_OF_THE_TRANSONIC_BIPLANE_CONCEPT_FOR_TRANSPORT_AIRCRAFT_APPLICATION_LG74ER0077
|
| [13] |
Gern F H, Ko A, Sulaeman E, et al. Multidisciplinary design optimization of a transonic commercial transport with strut-braced wing[J]. Journal of Aircraft, 2001, 38(6): 1006-1014. DOI:10.2514/2.2887 |
| [14] |
Rhodes M D, Selberg B P. Benefits of dual wings over single wings for high-performance business airplanes[J]. Journal of Aircraft, 1984, 21(2): 116-127. DOI:10.2514/3.48234 |
| [15] |
Selberg B P, Vincent G D. Investigation of chord ratio, stagger, decalage angle, and flap angle for dual wing configurations[C]. 24th Aerospace Sciences Meeting, Reno: AIAA, 1986. http://www.researchgate.net/publication/23866705_Investigation_of_chord_ratio_stagger_decalage_angle_and_flap_angle_for_dual_wing_configurations
|
| [16] |
Barcala-Montejano M Á, Rodríguez-Sevillano Á A, Rodríguez-Rojo M E, et al. A wind tunnel Two-Dimensional parametric investigation of biplane configurations[J]. Journal of Mechanics Engineering and Automation, 2014, 4(5): 412-421. |
| [17] |
Barcala-Montejano M Á, Cuerno-Rajado C, del Guidice S, et al. Experimental investigation on Box-Wing configuration for UAS[C]. 26th Bristol International Unmanned Air Vehicle Systems Conference, 2011. http://core.ac.uk/display/20051762
|
| [18] |
张晓, 胡冶, 张鹏, 等. 联翼布局飞机"正、负交错"构型对全机气动特性影响研究[C]. 2015年第二届中国航空科学技术大会论文集, 北京: 中国航空学会, 2015. Zhang X, Hu Y, Zhang P, et al. Study of the influence of positive/negative staggered planes on the aerodynamic characteristics of the whole aircraft[C]. China Aviation Science and Technology Conference, Beijing: CSAA, 2015(in Chinese). http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGHU201509001022.htm |
| [19] |
尹钧, 曹义华, 许正宇. 联结翼飞机主要布局参数对全机升阻特性影响研究[J]. 航空科学技术, 2015, 26(2): 14-18. Yin J, Cao Y H, Xu Z Y. Impacts study of joined wing aircraft main conifguration parameter on lift-drag characteristic[J]. Aeronautical Science and Technology, 2015, 26(2): 14-18. (in Chinese) |
| [20] |
Gao Z X, Jiang C W, Lee C H. A new wall function boundary condition including heat release effect for supersonic combustion flows[J]. Applied Thermal Engineer-ing, 2016, 92: 62-70. DOI:10.1016/j.applthermaleng.2015.09.089 |
| [21] |
Gao Z X, Jiang C W, Lee C H. Improvement and application of wall function boundary condition for high-speed compressible flows[J]. Science China Technological Sciences, 2013, 56(10): 2501-2515. DOI:10.1007/s11431-013-5349-4 |
| [22] |
Gao Z X, Jiang C W, Pan S W, et al. Combustion heat-release effects on supersonic compressible turbulent boundary layers[J]. AIAA Journal, 2015, 53(7): 1949-1968. DOI:10.2514/1.J053585 |
| [23] |
Wilcox D C. Turbulence modeling for CFD[M]. 3rd ed. California: DCW Industries, 2006, 243-261.
|
| [24] |
Spalart P R, Allmaras S R. A one-equation turbulence model for aerodynamic flows[C]. 30th Aerospace Sciences Meeting and Exhibit, Reno: AIAA, 1992. https://arc.aiaa.org/doi/abs/10.2514/6.1992-439
|
| [25] |
Cook P H, McDonald M A, Firmin M C P. Aerofoil RAE 2822-pressure distributions, and boundary layer and wake measurements[R]. Agard-AR-138, 1979.
|
| [26] |
Haase W, Brandsma F, Elsholz E, et al. EUROVAL-an European initiative on validation of CFD codes[M]. Wiesbaden: Vieweg, 1993.
|
| [27] |
Hellstrom T, Davidson L, Sweden G, et al. Reynolds stress transport modelling of transonic flow around the RAE2822 airfoil[C]. 32nd Aerospace Sciences Meeting and Exhibit, Reno: AIAA, 1994. http://www.researchgate.net/publication/247408616_Reynolds_stress_transport_modeling_of_transonic_flow_around_the_RAE2822_airfoil
|
| [28] |
Yu T, Wang J J, Zhang P F. Numerical simulation of gurney flap on RAE-2822 supercritical airfoil[J]. Journal of Aircraft, 2011, 48(5): 1565-1575. DOI:10.2514/1.C031285 |
| [29] |
Kang H, Genco N, Altman A. Gap and stagger effects on biplanes with end plates: part Ⅰ[C]. 47th AIAA Aero-space Sciences Meeting, Orlando: AIAA, 2009. http://www.researchgate.net/publication/269062106_Gap_and_Stagger_Effects_on_Biplanes_with_End_Plates_Part_I
|
| [30] |
Kang H, Genco N, Altman A. Gap and stagger effects on biplanes with end plates: part Ⅱ[C]. 47th AIAA Aerospace Sciences Meeting, Orlando: AIAA, 2009. http://www.researchgate.net/publication/269062106_Gap_and_Stagger_Effects_on_Biplanes_with_End_Plates_Part_I
|