2. 中国空气动力研究与发展中心计算空气动力研究所, 四川绵阳 621000;
3. 中国空气动力研究与发展中心低速空气动力研究所, 四川绵阳 621000
2. Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang, 621000, China;
3. Low Speed Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China
进入21世纪第二个十年以来, 随着互联网的发展和普及, 和以云计算、物联网、大数据等为代表的新一代信息技术的应用, 现代工业正在全方位地朝着以智能化为基本特征的“工业革命4.0”发展.作为航空航天工业设计过程中的一个环节, 计算流体力学(computational fluid dynamics, CFD)乘着计算机硬件飞速发展的东风, 在飞行器设计过程中扮演着越来越重要的角色. CFD技术从20世纪五六十年代开始起步, 经过几十年的发展,CFD计算方法和应用软件在20世纪末、21世纪初得到日新月异的发展, 时至今日, CFD已经成为飞行器设计过程中不可或缺的一个关键技术.
张涵信院士经过长期的研究, 将CFD的研究内容概括为5个M和1个A[1]. 5个M分别是:machine, mesh, method, mechanisms和mapping. machine, 即大型并行计算机, 它是CFD研究与应用的硬件基础; mesh, 即计算网格, 网格生成是整个数值计算的基础和前提, 已成为CFD的重要研究领域; method, 即计算方法, 流体力学控制方程的求解方法是CFD中最为活跃的领域, 目前已经发展了各种各样的求解方法, 比如有限差分法、有限体积法、有限元法等; mechanism, 即流动机理, 是CFD研究与应用的目的之一; mapping, 即流动显示, 将计算结果以静、动态的图形展示出来, 更加方便分析流动机理, 揭示流动规律. 1个A指application, 即应用, CFD研究的目的是为了在以航空航天为代表的众多工业领域得到良好的应用, 解决航空航天飞行器研制中的众多关键气动问题.自CFD诞生以来, 始终围绕着这5个M发展,并在实际工程中得到越来越广泛的应用(A).
由此可见, 网格生成技术(mesh generation techniques)是CFD的5个M的重要组成部分.在CFD工程应用中, 网格生成往往要占据整个计算周期人力时间的60%左右[2], 而且网格质量的好坏直接关系到计算结果的精度, 尤其是随着高精度、高分辨率格式的提出, 计算格式对网格质量的要求越来越高.
网格生成技术研究和网格生成软件研制在20世纪90年代得到蓬勃发展, 先后发展了拼接、搭接和重叠等多块结构网格技术, 并从计算固体力学中逐步引入了非结构网格技术, 考虑贴体的结构网格在边界层的模拟方面具有突出的优势, 耦合结构和非结构网格技术的混合网格技术随之出现[3].与此同时, 网格生成软件的市场化更是推动了技术的发展, 大幅提升了离散复杂外形的网格生成能力.而对于日益关注的机动飞行、多体分离等复杂动边界问题, 先后发展了多种多样的动态网格技术, 主要包括网格变形技术、网格重构技术、动态重叠网格技术和滑移网格技术等, 并在实际工程中得到成功应用[4].
然而进入21世纪以来, 作为CFD重要支柱的网格生成新方法却发展缓慢, 网格生成技术的发展基本处于停滞状态.现今广泛使用的网格生成技术和软件几乎与十年前的技术在本质上一样[5].
随着CFD在航空航天飞行器研制中的应用日益广泛, 国内在网格生成技术的应用方面取得了较大的进步.目前, 利用各种商业网格生成软件, 可以生成非常复杂的飞行器外形的结构或非结构计算网格.但是, 国内对网格生成技术本身的研究较少.在结构网格生成技术方面, 研究重点集中于如何处理多块重叠网格、多块拼接网格插值关系,而不是网格生成技术本身.在气动预研基金等项目的支持下, 中国空气动力研究与发展中心开展了交互式结构网格生成软件的初步研制, 目前已初步开发出基于GUI界面、有一定CAD数模构建和操作功能的多块结构网格生成软件“东方之蛛”1.0版本.在非结构网格和混合网格生成技术方面, 中国空气动力研究与发展中心[6~9]、浙江大学[10]、南京航空航天大学和北京大学等单位开展了相对较多的研究, 特别是浙江大学在并行化的非结构网格生成技术方面研究比较深入[11].尽管国内在某些网格生成方法上有所进展, 但是网格生成软件还远不能满足复杂外形计算网格快速生成的需求, 尤其是在自动化生成方面仍有很大的差距.
对于含运动边界的非定常数值模拟, 动态网格生成是其中一项关键技术.在这方面, 国内的发展现状与国际先进水平差距相对较小[4].国内相关单位发展了多种各具特色的动态网格生成技术, 如动态重叠结构和非结构网格技术、动态混合网格技术等, 这些技术在以多体分离、气动弹性为代表的复杂工程应用中发挥了重要作用, 并取得了较大成功.但是, 对于复杂构型的动边界问题, 仍需要开展并行化的动态网格生成技术研究, 大规模动态网格生成的鲁棒性和效率仍需要持续提高.
作为国内较早从事网格生成技术研究的团队之一, 在张涵信院士的指导下, 我们在静动态混合网格生成技术及相应的计算方法方面开展了持续的研究.近年来, 我们在该领域取得了一些可喜的进展.在张涵信院士80华诞之际, 我们对近年来的工作进行了简要的综述, 分别介绍了静动态混合网格生成、定常/非定常计算方法、网格技术的应用等方面的进展情况.最后, 结合网格生成技术目前还存在的问题, 展望了未来的发展方向.我们期待在未来的工作中能够取得更大的进展和突破, 以回馈张涵信院士长期的指导、关怀与帮助.
1 静态混合网格生成技术依照网格的拓扑结构, 计算网格可分为结构网格和非结构网格.结构网格的优点是数据结构简单, 存储方便, 计算简单快捷, 计算结果精度高; 其缺点是难以适应复杂外形, 对一些外形上的奇点需要进行特殊处理.非结构网格最早来源于固体力学中的有限元计算, 主要指二维的三角形和三维的四面体网格, 其优点是易于处理复杂外形, 数据结构的随机性使其易于进行网格自适应; 缺点是存储量大, 计算效率低.非结构网格的缺点在高Reynolds数计算时表现得尤为突出:高Reynolds数边界层模拟要求在物面法向有足够的网格分辨率, 这一点使得非结构网格数量急剧增长.为了在一定程度上减少网格量, 可以使用法向高度压缩的“各向异性”四面体单元.然而, 法向相邻两个各向异性四面体单元的中心连线和物面法向的偏离使得计算在某些情况下(如利用格心型有限体积法求解单元内的物理量梯度时)不够精确.因此, 生成高质量的边界层网格是网格生成技术中最关键的技术之一.本节我们首先简要介绍早先发展的基于层推进、阵面推进等的三棱柱/四面体/Cartesian混合网格生成方法[9], 然后介绍近年来发展的基于各向异性四面体网格聚合的混合网格生成方法[12, 13]和基于求解双曲型方程的三棱柱网格生成方法.
1.1 三棱柱/四面体/Cartesian混合网格生成方法Cartesian网格(实际上也是一种非结构网格), 尤其是规则的等距Cartesian结构网格, 在CFD计算中最早使用.它是一种最易生成的网格, 然而在流场中存在曲面边界时, 需对与曲面边界相交的单元进行特殊处理.为了提高绕流问题的网格离散效率, 一般需要在物面附近采用较密的网格, 而在远场采用较稀的网格, 由此发展了多层次的Cartesian网格技术或自适应Cartesian网格技术, 即在原始的均匀笛卡尔网格基础上, 根据几何外形特点或流场特点在流场局部区域内不断进行网格细化, 得到分布合理的非均匀Cartesian网格, 达到准确模拟复杂外形和捕捉流场特征等目的.相比于结构网格和非结构网格, 自适应Cartesian网格具有生成过程简单、效率高、自动化程度高、易于网格自适应等优点.然而Cartesian网格亦存在固有的不足. “纯粹”的Cartesian网格无法模拟曲面边界, 因为它在曲面边界附近会出现台阶效应(staircasing effects)[6].为了消除台阶效应, 可以对曲面边界切割的Cartesian网格单元进行特殊处理.一种方法是保留切割后的网格单元形状, 即切割出形状各异的多边形(2D)或多面体(3D)单元; 另一种方法是采用投影, 将物面附近的网格节点按照一定规则投影到物面上, 得到改进的Cartesian网格[14, 15]; 还有一种方法是将切割后的多边形/多面体划分为三角形/四面体, 形成所谓的Cartesian/非结构混合网格[6~9].以上方法仅适应于无黏流的数值模拟, 对于黏性流的模拟, 必须在边界层内生成合适的各向异性贴体网格.
基于结构网格、非结构网格(包括Cartesian网格)发展起来的混合网格技术结合了二者的优势:边界层内的网格一般采用半结构的三棱柱单元(在物面法向是结构的, 而在贴体方向是非结构的, 由几何层推进法生成[9]), 边界层以外单元是各向同性的四面体网格或Cartesian网格.与结构网格相比, 生成复杂外形的混合网格更加容易; 和纯非结构网格相比, 边界层法向上有很高的网格分辨率和很好的网格正交性, 极大地减少了网格量(边界层内比纯非结构网格减少大约2/3).这无疑对提高复杂外形的数值模拟精度和效率非常有利.
基于这一思想, 我们在20世纪90年代中后期发展了三棱柱/四面体/Cartesian混合网格生成技术, 详见文献[6~9]. 图 1给出了利用该方法生成的运输机、航天飞机外形无黏流计算网格, 在物面附近采用阵面推进法生成四面体网格, 可以改进直接投影法生成非结构网格的质量; 图 2显示了鱼体、双椭球外形黏性流计算的混合网格.上述混合网格方案, 既能实现流场大梯度区域的细节捕捉, 又能提高网格的自动化程度, 因而可以同时兼顾精度和效率.

|
| 图 1 三维构型无黏流计算混合网格 Fig.1 Hybrid grids over 3D configurations for inviscid flow simulations |

|
| 图 2 三维黏性流计算混合网格实例 Fig.2 Hybrid grids over 3D configurations for viscous flow simulations |
对于实际的复杂外形(如带弹战斗机和大型运输机), 要生成结构网格是非常困难的, 即使对于有着丰富经验的网格生成技术人员, 也需要花费较长的时间.混合网格因为只需要在边界层内保持结构/半结构性质, 而在外场用非结构网格填充, 相比结构网格而言, 大大降低了难度.但是, 生成复杂外形的混合网格也绝非易事, 往往需要人为地在空间中添加很多辅助线/面, 在生成过程中还可能遇到网格相交的情况, 极大地降低了生成混合网格的自动化程度.
众所周知, 生成非结构网格自动化程度高, 对复杂外形适应性强.最初的非结构网格是各向同性的四面体网格, 主要用于无黏流计算.随着CFD的发展, 为满足黏流计算的需要, 一些学者提出在黏性层内采用各向异性的非结构网格填充, 而在外场采用各向同性的非结构网格.在生成各向异性四面体网格时, 通常采用层推进法; 而采用阵面推进法、Delaunay方法及二者的结合生成各向同性四面体网格.这些方法在一些商业网格生成软件(如Gridgen)中已发展得非常成熟.通过观察层推进法和阵面推进法的算法可以发现, 二者在生成非结构网格时, 实际上是尽量在黏性层内生成各向异性的棱柱, 在棱柱生成不下去的时候, 层推进过程自动转换为阵面推进过程.为此, 作者利用生成非结构网格自动化程度高的特点, 在充分研究各向异性四面体生成方法的基础上, 发展了一种自动化程度较高的混合网格生成方法.为了叙述方便, 后文简称为聚合法[12, 13].
聚合法的基本思想是:在整个计算域填充了各向异性四面体网格和各向同性的四面体网格后, 将黏性层内的各向异性四面体网格聚合为三棱柱网格, 而外场的各向同性四面体网格保持不变.聚合法生成混合网格主要包括3个方面:聚合四面体单元、聚合面以及边界条件处理.聚合过程如图 3所示, 主要步骤包括:

|
| 图 3 各向异性四面体单元聚合过程 Fig.3 Procedure of agglomeration of anisotropy tetrahedral cells |
step1:判断四面体网格的拉伸属性, 即是各向同性还是各向异性.一般采用面积比、拉伸率等准则.聚合过程只针对各向异性四面体单元.
step2:对于各向异性四面体单元, 从特征面(一般是物面)开始, 沿法向, 每3个单元聚合为一个粗网格.
step3:将聚合得到的粗网格的侧面两两聚合为一个四边形.
图 4是采用聚合法生成的人体外形、带弹战斗机、运输机外形的混合网格.可见, 利用聚合法生成的混合网格对复杂外形具有良好的适应性, 而且网格过渡光滑, 质量较好.

|
| 图 4 聚合法生成三维混合网格实例 Fig.4 Hybrid grids generated by the agglomeration method |
归纳而言, 聚合法具有以下优点:
(1) 自动化程度高.空间网格可以实现自动化生成, 无需人为干预.
(2) 边界层网格质量好.传统的方法生成三棱柱网格时, 为了避免网格相交, 通常需要在生成棱柱网格时进行推进方向的优化, 导致推进方向和物面法向产生偏离.而聚合法生成网格时, 可以保证边界层内的绝大部分三棱柱网格的侧面和物面垂直, 从而尽可能适应物理特征的需求.
(3) 网格过渡光滑.通过控制参数, 使得在三棱柱网格和各向同性四面体网格之间填充各向异性四面体, 从而实现光滑过渡.
1.3 求解双曲型方程的三棱柱网格生成方法生成黏性层网格的另一个方法是通过数值方法生成网格, 即通过求解偏微分方程组(partial differential equations,PDE)的方式生成网格.其基本思想是:将网格的几何特征, 如正交性、单元体积等用偏导数的方式表示出来, 而这些偏导数根据一定的几何含义可以构造出一组偏微分方程组, 将计算域内的网格点看做是偏微分方程的解, 计算域的边界即是微分方程组的边界条件, 通过求解偏微分方程组的方式求得网格点在空间中的坐标, 从而达到生成网格的目的.
在利用数值方法生成网格时, 根据几何特征的描述不同可以构造出三类控制方程:椭圆型方程、抛物型方程和双曲型方程.椭圆型方程和抛物型方程适用于已知所有边界条件的情况下生成计算域网格, 而求解双曲型方程是在物面边界条件已知的基础上生成网格.黏性层网格的生成是由物面出发逐层生成网格, 这和双曲型方程生成网格的特性相符合, 因此可用求解双曲型方程的方法来生成黏性层的网格.
1980年, Steger等[16, 17]首次提出了通过求解双曲型方程的方法生成网格, 此法其后在Tai[18],Chan[19]等的推动下得到迅速发展. Matsuno[20]等随后将之推广到生成黏性层的三棱柱网格.
根据网格的正交控制和网格单元的体积控制的要求, 可以得到二维情况下的控制方程:
| $\begin{align} & {{\mathit{x}}_{\xi }}{{x}_{\eta }}+{{y}_{\xi }}{{y}_{\eta }}=0, \\ & {{x}_{\xi }}{{y}_{\eta }}-{{y}_{\xi }}{{y}_{\eta }}=1/\left| \mathit{\boldsymbol{J}} \right|=V. \\ \end{align}$ | (1) |
其中, J表示Jacobi矩阵∂(ξ, η)/∂(x, y), V表示单元的面积(二维)或体积(三维).式(1) 的第1式由网格的正交性控制得到, 第2式由网格的体积控制得到.考虑二维情况下从物理平面(x, y)到计算平面(ξ, η)的一一映射, ξ是贴体方向, η是和ξ垂直的推进方向.由于双曲型方程只需要一个初始边界条件, 所以首先在物体表面给定网格点分布以作为方程的边界条件(即η=0时的x, y值), 然后沿着η方向推进以生成网格.物理平面和计算平面的对应关系如图 5所示.

|
| 图 5 中文标题网格生成控制方程的物理域、计算域对应关系 Fig.5 Relationship between physical and computational domains for hyperbolic PDE-based method |
式(1) 一般在空间上采用迎风型格式离散, 时间上采用隐式离散以保证稳定性.通过迎风格式引入适当的数值耗散, 可以避免网格推进过程中出现“激波”, 即网格相交的情况.在此可以直接借用CFD中的一些成熟的算法.在每一层上用上一层的网格点坐标作为初始条件求解方程, 逐层求出每一层的网格点坐标, 上述方法是一个由物面开始逐渐向计算域更新的过程, 和几何层推进法有类似之处.
图 6是为了考核数值方法的鲁棒性而特意构造的一些有较多凸凹角的外形.和层推进法生成的黏性层网格相比, 数值方法对复杂几何生成的网格质量更高, 即使在几何特征变化剧烈的地方, 生成出来的网格正交性也很好. 图 7是利用求解双曲型方程的方法生成的三维导弹外形三棱柱网格.在边界层网格生成之后, 就可以利用前述的方法生成外层的其他网格, 最终得到高质量的混合网格.

|
| 图 6 求解双曲型方程生成的二维凹凸外形贴体网格 Fig.6 Body-fitted grids for 2D configurations generated by hyperbolic PDE-based method |

|
| 图 7 采用求解双曲型方程方法生成的导弹外形三棱柱网格 Fig.7 Prismatic grids over a missile generated by hyperbolic PDE-based method |
对于含运动边界的问题, 如多体分离、变体飞机、机动飞行、气动弹性等, 均需要发展合适的高效高质量动态网格生成技术.由于前述混合网格技术的优势, 因此动态混合网格生成技术是当前的主要发展趋势.
对于混合网格, 常见的网格变形方法有弹簧松弛法、求解PDE的方法和插值方法等.弹簧松弛法最早由Batina[21]提出, 之后由一些学者进行了改进, 是一种非常成熟并且使用广泛的网格变形方法.求解PDE的方法一般通过求解椭圆形方程来得到网格的位移场, 详见Lehner等[22],Jasak等[23]的工作.弹簧松弛法、求解PDE的方法在大规模动
网格生成时的效率较差, 且网格变形能力一般.插值方法中代表性的工作有Liu等的Delaunay背景网格映射方法[24], Rendall等的基于径向基函数(radial basis function,RBF)的插值方法[25, 26]. Delaunay背景网格映射法需要首先建立稀疏的背景网格, 然后通过背景网格和计算网格之间的映射关系实现计算网格的运动, 具有相当高的动态网格生成效率; 基于RBF的动网格方法是通过已知物面点的位移场插值得到整个空间点的位移场, 具有优越的网格变形能力, 但是当物面网格点较多时效率会急剧下降.
在21世纪初前后, 作者发展了一种将弹簧松弛法和局部网格重构法相结合的动态混合网格生成技术[27, 28].随后结合Delaunay背景网格映射法, 进一步改进了该动态网格生成技术[29, 30].在最近的研究及工程应用中[31, 32], 我们通过C++面向对象的程序设计思想, 进一步对动态混合网格的生成策略进行了改进, 并集成了RBF网格变形方法, 使动态混合网格的生成方式更为灵活, 以应对各种复杂工程应用的需要.
2.1 动态网格生成分区策略各种网格变形方法具有不同的优缺点[4], 为了发挥各种网格变形技术的特点, 方法本身的耦合是一种途径, 例如弹簧松弛法和Delaunay背景网格法的耦合, RBF和Delaunay背景网格法的耦合等.另一种途径则是各种方法在不同空间区域上的耦合, 即在不同的网格区域上采用不同的网格变形方法.
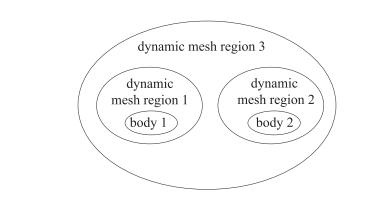
基于上述思想, 我们提出了基于网格分区的动网格生成策略.网格分区的基本原则是将计算区域按照实际计算需求分成若干个独立的子区域, 每个子区域采用一种最合适的动态网格技术进行网格变形.一般情况下, 网格的分区示意图如图 8所示:对于每个物体, 其周围的区域设置为随体区域, 而随体区域内各设置了一个主动变形区和一个被动变形区, 其中主动变形区通过解析的公式或者直接从数据库读取; 而被动变形区的网格则通过网格变形方法得到; 此外, 每个物体和远场边界之间的区域设置为主变形区域, 可以采用不同的动网格方法进行网格的变形.
|
| 图 8 动网格分区策略示意图 Fig.8 Strategy of domain decomposition for moving grid generation |
这种基于分区策略的动态混合网格生成技术有如下优点:
(1) 针对每个区域的特点, 可以采用最合适的网格变形方法, 以实现网格变形能力的最大化.
(2) 每个区域内网格的运动通过各自独立的参数进行控制.如舵偏角、6自由度参数等(生物仿生流体力学问题中各种控制变形的参数更为复杂).这种动态网格生成思路通过结合C++面向对象的软件设计方法, 特别适合于大型计算流体力学软件的设计和开发, 较易实现各种功能的耦合.
(3) 可以适用于多种复杂的工程实际问题, 例如带舵面偏转控制的多体分离问题、飞机机动运动过程中的气动弹性问题、生物外流仿生流体力学中的多自由度耦合运动问题等.
(4) 这种动态混合网格生成策略为各种网格变形技术的集成、耦合提供了非常便利的条件.例如针对舵面偏转的问题, 可以在局部区域内采用重叠网格技术或滑移网格技术, 可极大降低动态网格生成的难度.
2.2 基于RBF的动态混合网格生成方法RBF是一类关于距离的函数, 常用于数据插值.采用RBF生成动网格的思路是将网格点的位移场表示为到参考点距离的函数, 因此根据参考点的位移可以确定出空间每一点的位移.最近若干年基于RBF的动态网格技术发展迅速, 和传统的弹簧松弛法、求解PDE方程的方法相比, 它具有如下主要的优势:
(1) 具有优越的网格变形能力, 在相同的物面变形及位移条件下, 通过RBF方法得到的网格质量远高于传统的动网格技术.
(2) 网格的变形不依赖网格点的链接关系, 因此极大地简化了数据结构, 并有助于采用并行计算技术实现动态网格的生成.
(3) 只需要在计算开始之前进行一次矩阵求逆操作, 通过选择合适规模的物面参考点, 该动网格技术具有非常高的生成效率.
网格点位移场的函数表示为
| $\mathit{f}\left( r \right) = \sum\limits_{i = 1}^N {{\alpha _i}} \phi \left( {\left\| {r - {r_i}} \right\|} \right).$ |
其中, r为网格点的位置, ri表示为参考点的位置, αi为加权系数, 表示基函数.几种常见的基函数见表 1.以x方向为例, 加权系数通过物面参考点的已知位移求解:
| $\left( {\begin{array}{*{20}{c}} {\Delta {x_{{S_1}}}}\\ \vdots \\ {\Delta {x_{{S_N}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\phi _{{S_1}{S_1}}}}& \cdots &{{\phi _{{S_1}{S_N}}}}\\ \vdots & \ddots & \vdots \\ {{\phi _{{S_N}{S_1}}}}& \cdots &{{\phi _{{S_N}{S_N}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\alpha _{{S_1}}}}\\ \vdots \\ {{\alpha _{{S_N}}}} \end{array}} \right).$ |
其中, Si表示边界点集, SN为边界点数量.加权系数确定之后, 内点的位移可以表示为
| $\left( {\begin{array}{*{20}{c}} {\Delta {x_{{V_1}}}}\\ \vdots \\ {\Delta {x_{{V_N}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\phi _{{V_1}{S_1}}}}& \cdots &{{\phi _{{V_1}{S_N}}}}\\ \vdots & \ddots & \vdots \\ {{\phi _{{S_V}{S_1}}}}& \cdots &{{\phi _{{V_N}{S_N}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\alpha _{{S_1}}}}\\ \vdots \\ {{\alpha _{{S_N}}}} \end{array}} \right).$ |
其中, Vi表示内点, VN为内点数量.
| 下载CSV 表 1 几种常用于RBF方法的基函数 Tab.1 Some common base functions for RBF method |
图 9为针对NACA0012翼型剧烈柔性变形所做的测试, 动态网格的质量维持较好, 验证了RBF优越的网格变形能力.然而, 由于RBF方法需要在计算过程中对矩阵求逆, 当参考点数目较多时会导致计算效率急剧下降, 因此在实际工程应用中需要采用合适的算法, 选择较少的参考点数目, 在减少计算量的同时, 保证物面变形的保真. Rendall等[26]发展了一种基于贪婪算法的物面点选取算法, 具有不错的工程应用价值, 我们将该算法进行了集成. 图 10所示为针对鸽子外形进行的测试, 物面网格点数为40000, 经过筛选最终确定的参考点数目仅为500个, 因此极大地提升了动态网格的生成效率.

|
| 图 9 RBF方法动网格测试算例:NACA0012翼型柔性变形 Fig.9 Dynamic grids over a morphing NACA0012 airfoil by RBF method |

|
| 图 10 通过贪婪算法选择的物面参考点 Fig.10 Reference point set selected by the greedy method |
网格变形技术的好坏决定了网格的变形能力.然而, 对于工程实际中常遇到的剧烈柔性变形、多体相对运动、大位移运动等情况, 再好的网格变形技术也无法避免网格质量下降甚至网格交错等情况的发生.当网格无法满足计算要求时, 常用的办法是重新生成计算网格, 将旧网格上的流场变量插值到新网格上来.然而流场插值本身会比较耗时, 而且会引入插值误差.为减少插值误差的影响, 我们建立了局部网格重构技术.所谓局部重构, 就是将不满足计算要求的单元删除, 然后在局部重新生成满足要求的网格.由于局部重构保证了大部分网格单元的拓扑结构, 仅在重构区域内进行流场插值, 因此和全局重构相比,具有更好的计算效率和计算精度.局部网格重构的过程如下:
(1) 通过质量检测, 选出体积为负的“坏单元”和不满足质量要求的单元, 并进行标记.
(2) 删除需要重构的单元, 形成单连通的重构区域.
(3) 用Delaunay方法或阵面推进法在重构区域内生成新的四面体单元.
动网格生成及重构过程中, 必须建立一套网格质量判则, 以此对网格质量进行监控.对四面体网格而言, 文献[33]提出了系列质量判据:
判据1:四面体外接球半径/内切球半径, 最佳值为3.0;
判据2:四面体最大边长/内切球半径, 最佳值为4.899;
判据3:四面体外接球半径/最大边长, 最佳值为0.6125;
判据4:四面体最大边长/最小边长, 最佳值为1.0;
判据5:(四面体平均长度)3/四面体体积, 最佳值为8.4797;
判据6:(四面体体积)4/(4个面面积和)4, 最佳值为4.585×10-4.
本文依据网格变形过程的特点, 选择判据1和判据4来判断网格的质量.具体方法是, 将判据1的公式改为
| ${\mathit{Q}_{\rm{1}}}{\rm{ = }}{\mathit{Q}_{\rm{1}}}{\rm{/3 = }}\mathit{R}{\rm{/3}}\mathit{r}{\rm{.}}$ | (2) |
按式(2) 求得Q1, 按照判据4求得Q2, 取Q1和Q2中较小者为本单元的网格质量.通过实时监测网格单元的质量, 就可以根据实际计算要求来选择重构区域.一般情况下, 网格是否重构的判则为:(1) 出现“坏单元”; (2) 质量参数小于QC的单元比例大于C, 其中QC和C人为给定.选取较小的QC和较大的C可以减少网格重构的次数; 但如果具体计算状态对网格质量要求较高, 则可以选取较大的QC以及较小的C.在实际的动网格生成过程中, 单纯地依赖QC和C两个参数有时候并不能很好地反映出操作者的意愿, 此时需要通过图像显示人工判断网格质量的好坏, 当所关心的区域内网格质量不满足要求时, 则进行重构.重构区域的选取非常关键且带有一定的经验性.首先需要保证重构区域边界的完整性, 以便新四面体单元的顺利生成, 其次重构区域的大小要合适, 太大会引入较大的插值误差, 太小则对网格质量的改善不理想.
2.4 动态混合网格生成实例本节展示了上述动态混合网格技术在复杂问题中的应用实例.第1个算例为3条鱼的摆动过程(见图 11).模型采用了简化的金枪鱼外形, 计算网格采用三棱柱+四面体+六面体形式的混合网格.首先将网格分成了若干区域, 其中每个鱼体周围为单独的网格变形区域.在鱼体摆动过程中计算网格始终维持了较好的质量, 因此不需要进行网格重构.第2个算例为鸽子的扑翼过程(见图 12), 采用了弹簧松弛和Delaunay背景网格映射相结合的方法.第3个算例为机翼外挂物的分离过程(见图 13), 初始网格采用了三棱柱+四面体的混合网格.由于两体间存在剧烈的相对运动, 分离过程中计算网格的质量下降明显, 因此必须结合网格局部重构技术.为了维持计算网格的质量, 在整个分离过程中共进行了5次网格局部重构.

|
| 图 11 鱼类游动过程的动态混合网格 Fig.11 Dynamic hybrid grids over three fish schooling |

|
| 图 12 鸽子扑翼过程中的动态混合网格 Fig.12 Dynamic hybrid grids over the flapping wings of a pigeon |

|
| 图 13 机翼外挂物分离过程的动态混合网格 Fig.13 Dynamic hybrid grids during the store/wing separation |
基于上述静动态混合网格, 我们建立了求解RANS方程的有限体积定常/非定常算法.为提高计算效率, 发展了BLU-SGS隐式计算方法和分区并行计算技术; 针对运动网格非定常计算问题, 发展了满足几何守恒律的非定常算法.针对工程应用中常见的气动/运动/控制多学科耦合问题, 进一步发展了动力学方程、RANS方程、控制律以及动态混合网格生成的耦合求解方法.以下进行简要介绍.
3.1 空间和时间离散方法基于静态网格的定常/非定常算法都可以看作运动网格下非定常算法的特例, 因此本节仅针对运动网格下的非定常算法开展讨论.
运动网格下, N-S方程可以写成如下的积分形式:
| $\frac{{\rm{d}}}{{{\rm{d}}t}}\int\limits_\mathit{\Omega } \mathit{\boldsymbol{Q}} {\rm{d}}V + \oint\limits_{\partial \mathit{\Omega }} {\left( {\mathit{\boldsymbol{F}} - \mathit{\boldsymbol{Qk}}} \right)} \cdot \mathit{\boldsymbol{n}}{\rm{d}}\mathit{S}{\rm{ = }}\oint\limits_{\partial \mathit{\Omega }} {{\mathit{\boldsymbol{H}}_{{\rm{vis}}}}} {\rm{d}}S.$ | (3) |
其中, Ω为控制体, ∂Ω为控制体边界, k表示控制体外边界的运动速度, n为控制体边界的外法向, F表示静态网格的无黏通量, Hvis表示黏性通量.导数符号d表示跟随控制体的随体导数, 而不是跟随流体的物质导数.物理量Q以及无黏通量H=F-Qk·n写成向量形式为
| $\mathit{\boldsymbol{Q = }}\left[ \begin{array}{l} \rho \\ \rho u\\ \rho v\\ \rho w\\ \rho E \end{array} \right],\mathit{\boldsymbol{H = }}\left[ \begin{array}{l} \rho \left( {{v_n} - vgn} \right)\\ \rho u\left( {{v_n} - vgn} \right) + p{n_x}\\ \rho u\left( {{v_n} - vgn} \right) + p{n_y}\\ \rho w\left( {{v_n} - vgn} \right) + p{n_z}\\ \rho E\left( {{v_n} - vgn} \right) + p{n_n} \end{array} \right].$ |
其中, vn,vgn分别表示流体速度以及网格边界运动速度在单元边界外法向上的投影.
空间离散采用格心型的有限体积格式, 单元内物理量的梯度可以采用Gauss积分或者最小二乘法求得.对于混合网格, 如何选择重构物理量梯度所需的模版是一个关键问题, 一般采取两种方式:一是选择和本单元共享边界面的单元作为模版; 二是选择和本单元共享节点的单元作为模版.为了抑制激波前后的震荡, 采用了较为成熟的Barth或Vankatakrishnan限制器, 数值通量则采用了van Leer,Roe等较为成熟的计算格式.以Roe格式为例, 无黏通量可以表示为
| $\mathit{\boldsymbol{H}}{\rm{ = }}\frac{{\rm{1}}}{2}\left[ {{\mathit{\boldsymbol{H}}_{\rm{L}}}{\rm{ + }}{\mathit{\boldsymbol{H}}_{\rm{R}}} - \left| {{\rm{\tilde A}}} \right|{\rm{(}}{\mathit{Q}_{\rm{R}}} - {\mathit{Q}_{\rm{L}}}{\rm{)}}} \right]{\rm{.}}$ |
其中, Ã为无黏对流通量的Jacobi矩阵, 在求解该Jacobi矩阵过程中, 控制面上的物理量取左右变量的Roe平均.具体方法请参见文献[9, 13].
为了适应DES方法的计算, 尽可能在LES区域采用低耗散的数值格式, 我们借鉴Bui[34]和Travin等[35]的方法, 发展了改进的Roe格式, 即对流项的空间离散采用基于Roe格式的2阶迎风通量格式与2阶中心格式加权混合:
| $\mathit{\boldsymbol{F}} = \frac{1}{2}\left( {{\mathit{\boldsymbol{F}}_{\rm{L}}} + {\mathit{\boldsymbol{F}}_{\rm{R}}}} \right) + \sigma \left[ {\frac{1}{2}\left| {\mathit{\boldsymbol{\tilde A}}} \right|\left( {{\mathit{\boldsymbol{U}}_{\rm{R}}} - {\mathit{\boldsymbol{U}}_{\rm{L}}}} \right)} \right].$ |
而其中的σ为耗散调节系数, 即混合权函数, 采用文献[35]中的方法求解. σ=0对应2阶中心格式, σ=1对应2阶迎风格式.考虑计算稳定性, 对其最小值进行限制, 即σ=min(1, max(σ, σmin)), 取σmin=0.03, 则对于DES计算中的LES区域, 格式耗散与Bui[34]的建议较为一致.
对于某非结构网格单元, 半离散化之后的控制方程为
| $\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\mathit{\boldsymbol{Q}}\mathit{V}} \right){\rm{ = }}\mathit{\boldsymbol{Res}}{\rm{.}}$ |
其中, Res为空间离散之后的通量.对于定常问题, 可以直接采用BLU-SGS等隐式计算方法[36]; 对于非定常问题, 时间离散采用双时间步方法[37], 以2阶隐式Euler方法为例, 时间离散形式为
| $\begin{array}{l} \frac{{{\mathit{\boldsymbol{Q}}^{\mathit{m}{\rm{ + 1}}}}{\mathit{V}^{\mathit{n}{\rm{ + 1}}}} - {\mathit{\boldsymbol{Q}}^\mathit{m}}{\mathit{V}^{\mathit{n + }{\rm{1}}}}}}{{\Delta \tau }} + \\ \frac{{3{\mathit{\boldsymbol{Q}}^{\mathit{n}{\rm{ + 1}}}}{\mathit{V}^{\mathit{n}{\rm{ + 1}}}} - 4{\mathit{\boldsymbol{Q}}^n}{\mathit{V}^n} + {\mathit{\boldsymbol{Q}}^{\mathit{n}{\rm{ - 1}}}}{\mathit{V}^{\mathit{n - }{\rm{1}}}}}}{{2\Delta t}} = \mathit{\boldsymbol{Re}}{\mathit{\boldsymbol{s}}^{m + 1}}. \end{array}$ |
其中, m表示内迭代指标.将Resm+1线化处理, 则最终的离散形式为
| $\begin{array}{l} \left( {\frac{{{V^{n + 1}}}}{{\Delta \tau }} + \frac{{3{V^{n + 1}}}}{{2\Delta T}} + \frac{{\partial \mathit{\boldsymbol{Res}}}}{{\partial {\mathit{\boldsymbol{Q}}_i}}}} \right)\Delta \mathit{\boldsymbol{Q}}_i^m + \sum\limits_{j = 1}^{nf} {\frac{{\partial \mathit{\boldsymbol{Res}}}}{{\partial {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{j}}}}}} \Delta \mathit{\boldsymbol{Q}}_i^m = \\ - \frac{{3{\mathit{\boldsymbol{Q}}^m}{V^{n + 1}} - 4{\mathit{\boldsymbol{Q}}^n}{V^n} + {\mathit{\boldsymbol{Q}}^{n - 1}}{V^{n - 1}}}}{{2\Delta t}} + \mathit{\boldsymbol{Re}}{\mathit{\boldsymbol{s}}^m}. \end{array}$ | (4) |
式(4) 可以采用各种迭代方法求解, BLU-SGS在原始的LU-SGS方法基础上保留了特征矩阵的完整形式, 因此具有更为优越的收敛效率.具体方法参见文献[28, 30].
3.2 动网格下的几何守恒律几何守恒律(geometric conservation law, GCL)包含面积封闭和体积守恒两个概念, 其中体积守恒是运动网格下的非定常计算必须首先解决的一个问题.对于控制方程式(3), 假设流场均匀, 则可得到GCL方程如下:
| $\frac{{{\rm{d}}\mathit{V}}}{{{\rm{d}}\mathit{t}}} = \oint\limits_{\partial \mathit{\Omega }} \mathit{\boldsymbol{k}} .\mathit{\boldsymbol{n}}{\rm{d}}\mathit{S}\mathit{.}$ | (5) |
式(5) 表示控制体单元的体积变化率等于边界面法向运动速度的面积分, 在微分意义下是恒成立的, 而计算所采用的离散格式也需要使式(5) 得到满足, 才不至于在流场内引入额外的误差.
满足式(5) 的数值格式很多, 详见Lesoinne等[38],Ahn等[39],Liu等[40],Wang等[41]等的工作.这里我们采用了Wang提出的较为便捷的方法:直接对边界面的法向速度进行约束.对于1阶Euler隐式方法, 式(5) 的离散形式为
| $\frac{{\Delta {V^n}}}{{\Delta t}} = \sum\limits_{j = 1}^{nf} {vgn_{_j}^{n + 1}} S_j^{n + 1}.$ | (6) |
对于单元的每一个离散的边界面, 限定其法向速度的求解方法:
| $vgn_{_j}^{n + 1} = \frac{{\Delta V_j^n}}{{S_j^{n + 1}\Delta t}}.$ | (7) |
其中ΔVjn表示单元第j个面扫过的面积.式(7) 是满足式(6) 的充分条件.
进一步, 我们将其推广应用于2阶Euler隐式格式, 其法向速度求解方法为
| $vgn_{_j}^{n + 1} = \frac{{1.5\Delta V_j^n - 0.5\Delta V_j^{n + 1}}}{{S_j^{n + 1}\Delta t}}.$ |
在随后的研究中, 我们进一步从误差分析的角度对各种动网格几何守恒算法进行了理论分析, 发现可以将现有的几何守恒算法归为两类, 即限制整体积分误差的体积限制方法和限制每个边界面数值误差的表面限制方法, 并可以针对不同的时间格式写成统一的形式.进一步的研究发现, 对于不同的时间离散格式, 需要选用相适应的几何守恒算法, 否则无法达到预期时间精度.尽管各种几何守恒算法的计算结果大体一致, 但是我们发展的几何守恒算法在三维情况下更为简便.具体的理论分析详见文献[42].
3.3 气动/运动/控制耦合计算策略数值虚拟飞行是CFD面向工程应用的一个重要挑战之一, 其核心是多学科的非线性耦合, 包括飞行力学、流体力学、飞行控制等.关于数值虚拟飞行的国内外研究进展, 作者前期进行了比较详细的综述[43], 本节仅对其中的耦合求解策略进行简要介绍.
3.3.1 动力学方程/N-S方程的耦合刚体的运动分为平动、转动两部分.平动部分的动力学和运动学控制方程如下:
| $\left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}\mathit{\boldsymbol{v}}}}{{{\rm{d}}t}} = \frac{\mathit{\boldsymbol{F}}}{m}}\\ {\frac{{{\rm{d}}\mathit{\boldsymbol{r}}}}{{{\rm{d}}t}} = \mathit{\boldsymbol{v}}} \end{array}} \right..$ | (8) |
其中, v为刚体运动速度, r为刚体质心位置, F为刚体受力, m为刚体质量.
转动部分的动力学及运动控制方程如下:
| $\left\{ \begin{array}{l} \frac{{{\rm{d}}{\omega _x}}}{{{\rm{d}}\mathit{t}}} = \frac{{\left[ {{M_x} + \left( {{I_{yy}} - {I_{zz}}} \right){\omega _y}{\omega _z}} \right]}}{{{I_{xx}}}}\\ \frac{{{\rm{d}}{\omega _y}}}{{{\rm{d}}\mathit{t}}} = \frac{{\left[ {{M_y} + \left( {{I_{zz}} - {I_{xx}}} \right){\omega _x}{\omega _z}} \right]}}{{{I_{yy}}}}\\ \frac{{{\rm{d}}{\omega _z}}}{{{\rm{d}}\mathit{t}}} = \frac{{\left[ {{M_z} + \left( {{I_{xx}} - {I_{yy}}} \right){\omega _y}{\omega _x}} \right]}}{{{I_{zz}}}} \end{array} \right.,$ | (9) |
| $\left\{ \begin{array}{*{35}{l}} \frac{\rm{d}\alpha }{\rm{d}\mathit{t}}={{\omega }_{y}}\sin \gamma +{{\omega }_{z}}\cos \gamma \\ \frac{\rm{d}\beta }{\rm{d}\mathit{t}}=\frac{{{\omega }_{y}}\cos \gamma -{{\omega }_{z}}\sin \gamma }{\cos \alpha } \\ \frac{\rm{d}\gamma }{\rm{d}\mathit{t}}={{\omega }_{x}}-\frac{\left( {{\omega }_{y}}\cos \gamma -{{\omega }_{z}}\sin \gamma \right)}{\cos \alpha }\sin \alpha \\ \end{array}. \right.$ | (10) |
其中, ωx, ωy, ωz为刚体的转动角速度(体轴系); Mx, My, Mz为刚体所受俯仰力矩; I为转动惯量; α, β, γ分别为俯仰角、偏航角、滚转角, 其定义详见文献[30].
式(8)~(10) 可以写成统一的形式:
| $\frac{{{\rm{d}}\mathit{\boldsymbol{q}}}}{{{\rm{d}}\mathit{t}}} = \mathit{\boldsymbol{R}}\left( {q,t,\mathit{\boldsymbol{F,M}}} \right).$ | (11) |
其中, q表示刚体动力学的12个变量.刚体所受的气动力F及气动力矩M通过求解N-S方程得到.由于动力学和运动学方程与N-S方程的性质不同, 采用直接方法求解相当困难, 常用的方法是将N-S方程、动力学/运动学方程解耦求解.
式(11) 有多种时间推进格式, 利用线性多步法, 可将其写成统一的离散形式:
| ${\rm{a}}{\mathit{\boldsymbol{q}}^{{\rm{n + 1}}}}{\rm{ + b}}{\mathit{\boldsymbol{q}}^{\rm{n}}}{\rm{ + c}}{\mathit{\boldsymbol{q}}^{{\rm{n - 1}}}}{\rm{ = }}\Delta t\left( {{\rm{d}}{\mathit{\boldsymbol{R}}^{n + 1}} + e{\mathit{\boldsymbol{R}}^n} + f{\mathit{\boldsymbol{R}}^{n + 1}}} \right).$ | (1) |
其中几种常用的格式如表 2所示.
| 下载CSV 表 2 耦合计算中几种常用的时间推进格式 Tab.2 Some common temporal schemes in coupling simulations |
Adams-Bashforth格式为显式格式, 在求解过程中只需要历史的气动力数据, 因此可以与N-S方程采用松耦合的方式求解, 两者只需在时间推进的过程中进行一次信息交互即可; implicit Euler以及Adams-Moulton格式为隐式格式, 因此其时间推进过程要与N-S方程的时间推进过程相耦合. N-S方程的时间推进采用双时间步策略, 每一个真实时间步推进过程中采用若干个子迭代使流场逐渐收敛到n+1时刻.若动力学/运动学方程的求解采用隐式格式, 则需要在N-S方程子迭代的过程中适时与其交互, 即在每一个子迭代过程中更新计算网格、气动力, 这就是紧耦合策略.
以implicit Euler (1st order)为例, 式(12) 变为如下形式:
| ${\mathit{\boldsymbol{q}}^{\mathit{n}{\rm{ + 1}}}}{\rm{ - }}{\mathit{\boldsymbol{q}}^\mathit{n}}{\rm{ = }}{\mathit{\boldsymbol{R}}^{\mathit{n}{\rm{ + 1}}}}{\rm{\Delta }}t.$ |
其内迭代公式为
| ${\mathit{\boldsymbol{q}}^{\mathit{m}{\rm{ + 1}}}}{\rm{ = }}{\mathit{\boldsymbol{q}}^\mathit{n}}{\rm{ + }}{\mathit{\boldsymbol{R}}^\mathit{m}}{\rm{\Delta }}t.$ | (13) |
其中, m为内迭代指标.内迭代第1步(m=0), R采用n时刻的值, 因此第1步子迭代也可以称为预估步, 之后的子迭代则称为校正步.
实际计算过程中, 采用式(13) 有可能会导致子迭代的发散, 因此引入松弛因子ω, 得到如下子迭代公式:
| ${\mathit{\boldsymbol{q}}^{\mathit{m}{\rm{ + 1}}}}{\rm{ = }}\left( {1 - \omega } \right){\mathit{\boldsymbol{q}}^m}{\rm{ + }}\omega \left( {{\mathit{\boldsymbol{q}}^n} + {\mathit{\boldsymbol{R}}^n}\Delta t} \right).$ |
其中, ω要依据实际问题确定, 如果物理时间步长较大, 则需要相对较小的ω.
我们进一步对松耦合和紧耦合算法的稳定性进行了理论分析[44], 研究表明:当物体的密度与流体密度接近时, 显式的松耦合方法稳定性降低甚至发散, 而紧耦合方法在较大的时间步长时仍能给出收敛结果.因此需要根据具体问题, 选取合适的耦合算法.
3.3.2 控制律的耦合控制律作为飞行器控制过程的核心模块, 是飞行器设计过程中非常重要的一个环节.每一种飞行器会根据其自身的气动外形特点及机动飞行要求设计专门的控制系统.控制过程可分为开环控制和闭环控制两类, 开环控制没有引入反馈机制, 舵偏角按照预先设计的规律进行偏转, 因此会导致控制系统出现较大的稳态误差; 闭环控制则引入了反馈机制, 使控制过程更为精准.
飞行器的控制系统是一个复杂的多学科多物理系统, 为简化模拟过程, 舵机模块的响应在此处不予考虑, 此外, 流体力学控制方程、动力学方程的耦合求解仅作为整个控制回路的一个环节.鉴于控制系统的这些特点, 一体化数值模拟过程中控制律模块并不和流体力学控制方程、动力学方程进行实时耦合求解, 而是当到达一定的物理时间之后, 再调用控制律模块, 确定出舵偏等控制量的大小.考虑闭环控制的一体化算法的示意图如图 14所示:流体力学控制方程、动力学方程、动态混合网格生成作为一个多学科耦合系统, 可以采用松耦合或者紧耦合方式进行时间推进; 控制系统作为一个相对独立的模块, 在达到调用条件时执行.

|
| 图 14 耦合计算流程图 Fig.14 Flow chart of coupling approach |
在上述静/动态混合网格生成技术和计算方法研究的基础上, 我们研制了一款面向工程应用的通用CFD软件平台HyperFLOW[45, 46].该软件采用面向对象的设计理念和软件技术研发, 具有良好的通用性和可扩展性.针对HyperFLOW, 我们开展了系列的验证与确认研究工作, 同时广泛应用于复杂飞行器气动特性的数值模拟和复杂非定常流动问题的机理研究.如连续参加了国内的“航空CFD可信度研讨”活动, 对DLR-F6和高升力机翼等构型进行了网格收敛性研究; 进行了复杂战斗机外形的大攻角特性数值模拟; 开展了基于混合网格2阶精度FV格式的三角翼DES数值模拟; 进行了鸟类扑翼、鱼类巡游等生物仿生流体力学的数值模拟研究; 在复杂飞行器气动特性模拟方面, 对新型战斗机、多型战略战术导弹、捆绑火箭、新型临近空间飞行器等的定常和非定常气动特性进行了数值模拟, 给出了快速俯仰运动、舵面偏转动态响应对气动特性的影响规律; 在复杂飞行器多体分离方面, 对多种型号飞行器的整流罩分离、助推器分离、级间分离等开展了大量的数值模拟应用, 并在国内率先对高速、大动压条件下的热分离过程进行了数值模拟; 在耦合控制律的一体化数值模拟方面, 对某型机动导弹的姿态控制、过载控制、变Mach数机动过程等进行了数值模拟, 获得了与飞行仿真和靶试测量非常一致的计算结果.由于涉密原因, 下面仅对其中的部分工作进行简要介绍.
4.1 DLR-F6翼身组合体跨声速流数值模拟DLR-F6翼身组合体是国内第二届航空可信度研讨活动采用的跨声速算例, 来自第二届AIAA阻力预测研讨会(DPW-II)标准算例[47].该外形进行了精确细致的实验和系统的实验数据分析, 可以认为是真实世界的表征.来流条件是:M∞= 0.75, Re=3.0×106.
该外形复杂程度适中, 如果用整体外推的方式生成黏性层的棱柱网格, 只能推出一二十层, 若要满足高Reynolds数计算的需求, 必须人为地在空间添加辅助面, 以分块的方式推出黏性层网格.利用前述的聚合法可以很方便地、自动地生成混合网格. 图 15是该外形的物面/空间网格.在生成表面网格时, 为了更好地捕捉流场细节, 在外形曲率变化剧烈的地方加密了网格, 比如头部、机翼前缘等.为了在生成高质量的贴体网格的同时减少网格量, 在机翼前、后缘展向分布了各向异性的三角形网格.为了生成混合网格, 首先生成了该外形的空间非结构网格, 包括边界层内的各向异性四面体网格和边界层以外的各向同性四面体网格.在初始四面体的基础上进行网格聚合以生成混合网格.从图中可以看到, 空间网格从物面附近光滑过渡到远场(三棱柱和各向同性四面体网格之间用各向异性四面体过渡), 黏性层棱柱网格正交性较好.黏性层的三棱柱网格推出了40多层, 能很好地满足边界层模拟的需要.为了考核网格收敛性, 生成了粗、中、密3套网格, 网格量信息见表 3.

|
| 图 15 聚合法生成的DLR-F6混合网格 Fig.15 Hybrid grids over DLR-F6 configuration generated by the agglomeration method |
| 下载CSV 表 3 DLR-F6翼身组合体计算网格单元数 Tab.3 Grid information for DLR-F6 configuration |
计算中选用了SST两方程湍流模型. 图 16是气动力曲线与实验值、其他软件计算值的对比.我们的计算结果表现出很好的网格收敛性.对于极曲线, 放大后可见, 细网格和实验值符合得更好.和DPW-II中其他结果一样, HyperFLOW计算的升力均偏高, 俯仰力矩系数差异较大.该算例数值模拟结果的升力、阻力系数得到验证和确认, 具有可接受的可信度, 而俯仰力矩系数可信度稍差, 仍需改进.

|
| 图 16 DLR-F6翼身组合体气动力系数曲线 Fig.16 Aerodynamic coefficients for DLR-F6 configuration |
TrapWing高升力外形是第一届AIAA CFD High Lift Workshop的标模问题[48]. NASA高升力TrapWing模型是专门用来验证CFD软件计算高升力失速特性模拟能力的标准气动模型.该外形比较复杂, 是航空飞行器起降阶段的代表模型, 尤其是存在背风区大分离、局部分离等复杂流动现象, 使得精确预测难度较大, 失速攻角、最大升力系数预测也难度很大, 对计算软件和网格质量均有较高的要求.计算来流Mach数为0.2, 基于平均气动弦长(34.634in)的Reynolds数4.3×106.
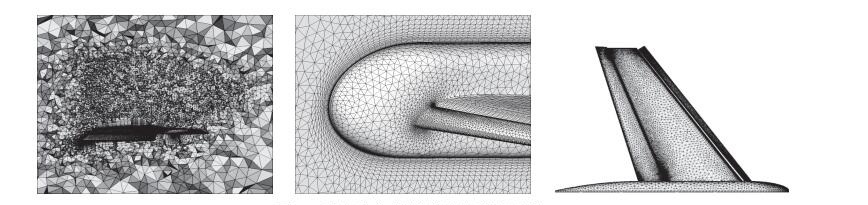
算例的计算模型验证采用网格收敛性研究方法, 即分别在粗、中、细网格上计算, 首先生成中等规模网格, 然后将物面网格维度按照1.5~2倍关系稀疏或加密, 生成粗网格和细网格, 表 4为3套网格的基本信息. 图 17为生成的三棱柱/四面体/金字塔混合网格(粗网格).为了捕捉机翼背风区的大范围分离, 在机翼上部空间进行了局部加密; 为了提高空间分辨率、降低网格量, 在机翼的前缘及后缘均使用了展向拉伸的各向异性三角形网格; 为了提高网格均匀过渡性, 采用各向异性四面体网格来过渡物面附近的三棱柱和外场的各向同性四面体网格.计算中选用SA-方程湍流模型. 图 18为气动力系数曲线与实验值、国外知名软件参考值[49]的比较, 两套网格的线性段均模拟较好, 在失速攻角附近, 多条曲线间存在差异.气动力曲线都表现了很好的网格收敛性, 且与实验值、参考值有相当的吻合度, 说明计算结果可信.
| 下载CSV 表 4 高升力外形计算网格单元数 Tab.4 Grid information for TrapWing configuration |
|
| 图 17 聚合法生成的高升力外形混合网格 Fig.17 Hybrid grids over TrapWing configuration generated by the agglomeration method |

|
| 图 18 TrapWing高升力外形气动力曲线 Fig.18 Aerodynamic coefficients for TrapWing configuration |
本节给出一个基于混合网格2阶精度有限体积算法的DES模拟结果.计算模型为65°后掠、尖前缘三角翼, 模型详细情况可参考文献[50].计算模拟的状态为来流攻角α=23°,Mach数M=0.4,基于平均气动弦长的Reynolds数Remac= 6×106.计算所用时间步长为0.001cr/U∞(cr为气动根弦长, U∞为来流速度), 网格单元总数约5.27×106, 物面附近采用结构网格, 其余区域采用非结构网格, 单元类型包括六面体、金字塔、四面体(见图 19).

|
| 图 19 三角翼DES模拟混合网格 Fig.19 Hybrid grids over a delta-wing |
图 20为对应Q涡量等值面.采用标准Roe格式模拟出的涡破裂形态主要为泡状破裂(见图 20(a)), 破裂点位置比较固定.采用Hybrid格式则模拟出了更为丰富的涡破裂形态, 主要表现为泡状破裂(见图 20(b))和双螺旋破裂(见图 20(c)), 不同破裂形态之间交替出现, 破裂点随之上下移动, 破裂点整体位置与Roe格式计算值相比在更下游.

|
| 图 20 Q等值面 Fig.20 Iso-surface of Q criterion |
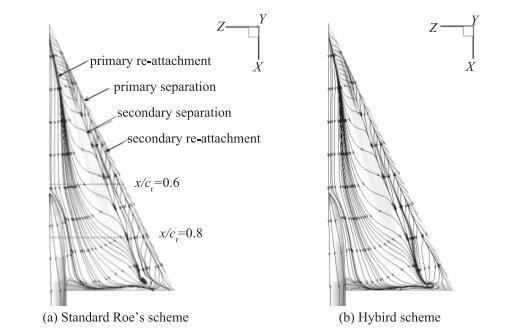
图 21为表面极限流线和物面压力分布.两种算法的表面极限流线基本都反映出了三角翼背风区的流动分离特性, 相互之间差异也较小, 但在x/cr = 0.6站位附近涡核区压力分布明显不同, Roe格式对应计算压力开始迅速恢复, 而Hybrid格式对应计算压力恢复则要滞后一些.
|
| 图 21 表面极限流线和压力分布 Fig.21 Surface streamlines and pressure contours |
图 22为x/cr = 0.6,0.8两个站位处的对应物面平均压力系数分布与试验的对比.在x/cr = 0.6站位, Roe格式计算的吸力峰值突然减小、涡核区变宽, 说明涡核开始破裂, 而Hybrid格式计算结果与试验值符合更好, 吸力峰依然比较陡峭, 破裂点在此站位下游, 这与从瞬时涡量等值面观察到的现象是一致的.在x/cr = 0.8站位, Hybrid格式开始出现涡破裂, 而试验观测的涡破裂也从此站位附近开始, 但两者的平均压力系数有较大差异, 计算的涡破裂位置可能在试验观测值的上游, 这有待于今后进一步改进.

|
| 图 22 表面压力系数分布与试验对比 Fig.22 Pressure coefficient distributions compared with experimental data |
本文分别从静态混合网格生成、动态混合网格生成、定常/非定常计算方法、网格技术的应用几方面简要介绍了作者及团队近年来在网格生成技术方面所取得的进展.总的来说, 目前已经基本建立了一套针对真实工程复杂外形的静/动态混合网格生成方法, 能基本实现自动化地生成高质量的空间静/动态混合网格, 发展了与之适应的数值求解方法, 开发了非定常计算/六自由度运动/动网格生成的一体化耦合计算平台, 初步具备了复杂外形DES模拟和数值虚拟飞行的模拟能力.秉承张涵信院士倡导的“创新是灵魂、应用是归宿”的治学理念, 上述网格生成技术及计算方法一直处于边发展、边应用之中, 在新型飞行器气动特性分析中发挥了较好的作用.
当前CFD技术正朝着分辨率更高、计算速度更快、数据生成更自动化的方向发展.对于处在工业革命4.0浪潮中的CFD技术来说, 自动化、智能化无疑是其未来发展的趋势.计算方法作为CFD的核心, 已经能实现大规模、自动化地并行计算; 然而, 作为CFD的另一个核心, 计算网格的生成却还未能实现完全的自动化.网格生成技术已成为未来CFD自动化、智能化发展的关键问题之一.
随着E级计算时代的来临, CFD数值模拟软件必须紧跟计算机技术的发展步伐, 实现与超级计算机的深度融合.但是现有的网格生成技术还在很大程度上制约着CFD的发展.综合分析未来的发展趋势, 作者认为未来的网格生成技术应在以下几个方面开展持续研究:
(1) 发展网格生成新方法.进入21世纪以来, CFD计算方法获得了极大的发展, 而作为CFD重要支柱的网格生成新方法却发展缓慢, 网格生成技术的发展基本处于停滞状态.现今广泛使用的网格生成技术和软件几乎与十年前的技术在本质上一样, 迫切需要在网格生成技术方面获得进一步的突破.
(2) 自动化的网格生成技术.需要结合CAD数模的自动检测与修补、基于外形特征的自动分辨技术、物面和空间网格的自动化生成与优化等技术, 发展自动化、智能化的网格生成技术.
(3) 并行化的网格生成技术.需要基于区域分解或并行化网格生成算法, 发展大规模并行网格生成技术, 突破上百亿超大规模网格生成的技术难题, 并实现快速的超大规模网格分区预处理.
(4) 网格自适应技术.应重点发展各向异性自适应网格技术、基于伴随办法的网格自适应技术、动态网格自适应技术等, 以提高网格的离散效率.
(5) 动态网格技术.需要重点提高动网格技术的鲁棒性、大规模网格的并行化生成效率等问题, 满足如伴随物体变形(如气动弹性变形、主动气动外形变形、控制舵面的偏转、旋翼的挥舞等)、多个物体的分离(如外挂物投放、火箭级间分离等)等复杂非定常问题模拟的需要, 为未来的数值虚拟飞行奠定基础.
(6) 高精度网格生成技术.针对高阶精度计算格式(尤其是基于非结构、混合网格的高精度格式)的需求, 发展高精度的物面描述方法及边界层内的高精度高质量网格生成方法.
致谢: 衷心感谢张涵信院士25年来的培养、关怀和帮助, 在他80华诞之际, 作者谨以此文对他表示崇高的敬意, 并致以深深的祝福.在研究过程中, 高树椿研究员等诸多老师给予了长期的指导, 作者亦得到邓小刚、王志坚、叶友达、沈清、刘君、刘伟、黎作武、贺国宏、陈坚强、毛枚良等众多学长的帮助, 呙超、杨永健、王振亚等同学先后参与相关工作, 段旭鹏、郭秋亭、刘伟、李明、孙杭义、马戎、何先耀、何磊、李泽禹等学生也对本文的工作做出了贡献, 中国空气动力研究与发展中心计算空气动力研究所的领导和同事们给予了大力支持和帮助, 在此一并表示诚挚的感谢!| [1] |
张涵信, 沈孟育.计算流体力学——差分方法的原理和应用[M].北京:国防工业出版社, 2003:1~472
Zhang H X, Shen M Y. Computational fluid dynamics—fundamentals and applications of finite difference methods[M]. Beijing: National Defence Industry Press, 2003: 1~472(in Chinese) |
| [2] | Baker T J. Mesh generation : art or science[J]. Progress in Aerospace Science, 2005, 41(1): 29-63.DOI:10.1016/j.paerosci.2005.02.002 |
| [3] | Thompson J F, Soni B K, Weatherill N P. Handbook of grid generation[M]. Boca Raton: CRC Press, 1998: 1~1136 |
| [4] |
张来平, 邓小刚, 张涵信. 动网格生成技术及非定常计算方法进展综述[J].
力学进展, 2010, 40(4): 424-447. Zhang L P, Deng X G, Zhang H X. Reviews of moving grid generation techniques and numerical methods for unsteady flow[J]. Advances in Mechanics, 2010, 40(4): 424-447.DOI:10.6052/1000-0992-2010-4-J2009-123 |
| [5] | Lohner R. Recent advances in parallel advancing front grid generation[J]. Archives of Computational Methods in Engineering, 2014, 21(2): 1-14. |
| [6] |
张来平. 非结构网格、矩形/非结构混合网格复杂无黏流场的数值模拟[D]. 绵阳: 中国空气动力研究与发展中心, 1996
Zhang L P. Numerical simulation for complex inviscid flow fields on unstructured grids and Cartesian/unstructured hybrid grids[D]. Mianyang: China Aerodynamics Research and Development Center, 1996(in Chinese) http: //www. doc88. com/p-2098284798832. html |
| [7] |
张来平, 张涵信. 复杂无黏流场数值模拟的矩形/三角形混合网格技术[J].
力学学报, 1998, 30(1): 104-108. Zhang L P, Zhang H X. A Cartesian/triangular hybrid grid solver for complex inviscid flow fields[J]. Acta Mechanica Sinica, 1998, 30(1): 104-108. |
| [8] |
张来平, 张涵信, 高树椿. 矩形/非结构混合网格技术及在二维/三维复杂无黏流场数值模拟中的应用[J].
空气动力学学报, 1998, 16(1): 79-88. Zhang L P, Zhang H X, Gao S C. A Cartesian/unstructured hybrid grid solver and its applications to 2D/3D complex inviscid flow fields[J]. Acta Aerodynamica Sinica, 1998, 16(1): 79-88. |
| [9] | Zhang L P, Zhang H X. Numerical simulations of 3D inviscid/viscous flow fields on Cartesian/unstructured/prismatic hybrid grids[A]. // The 4th Asian Computational Fluid Dynamics Conference[C]. Mianyang, 2000 https://es.scribd.com/doc/315973354/Ship-and-Offshore-Structures-Congress-pdf |
| [10] |
陈建军, 曹建, 徐彦, 等. 适应复杂外形的三维黏性混合网格生成算法[J].
计算力学学报, 2014, 31(3): 363-370. Chen J J, Cao J, Xu Y, et al. Hybrid mesh generation algorithm for viscous computations of complex aerodynamics configurations[J]. Chinese Journal of Computational Mechanics, 2014, 31(3): 363-370.DOI:10.7511/jslx201403014 |
| [11] |
陈建军. 非结构化网格生成及其并行化的若干问题研究[D]. 杭州: 浙江大学, 2006
Chen J J. Unstructured mesh generation and its parallelization[D]. Hangzhou: College of Computer Science, Zhejiang University, 2006(in Chinese) http: //www. cnki. com. cn/Article/CJFDTotal-ZDZC200804003. htm |
| [12] |
赵钟, 张来平, 赫新. 基于各向异性四面体网格聚合的复杂外形混合网格生成方法[J].
空气动力学学报, 2013, 31(1): 34-39. Zhao Z, Zhang L P, He X. Hybrid grid generation technique for complex geometries based on agglomeration of anisotropic tetrahedrons[J]. Acta Aerodynamica Sinica, 2013, 31(1): 34-39. |
| [13] | Zhang L P, Zhao Z, Chang X H, et al. A 3D hybrid grid generation technique and multigrid/parallel algorithm based on anisotropic agglomeration approach[J]. Chinese Journal of Aeronautics, 2013, 26(1): 47-62.DOI:10.1016/j.cja.2012.12.002 |
| [14] |
肖涵山. 自适应笛卡尔网格在三维复杂外形流场及机弹分离数值模拟中的应用[D]. 绵阳: 中国空气动力研究与发展中心, 2003
Xiao H S. Application of adaptive Cartesian grid algorithm for the numerical simulation of arbitrary geometries and store separation[D]. Mianyang: China Aerodynamics Research and Development Center, 2003(in Chinese) http: //edu. wanfangdata. com. cn/Periodical/Detail/jsjfz201102011 |
| [15] | Aftosmis M J, Berger M J, Melton J E. Adaptive Cartesian mesh generation[A]. //Handbook of Grid Generation[M]. Boca Raton: CRC Press, 1998: 600~625. http://dl.acm.org/citation.cfm?id=941507 |
| [16] | Steger J L, Chaussee D S. Generation of body fitted coordinates using hyperbolic partial differential equations[J]. SIAM Journal on Scientific & Statistical Computing, 1980, 1(4): 431-437. |
| [17] | Steger J L, Rizk Y M. Generation of three-dimensional body-fitted coordinates using hyperbolic partial differential equations[R]. NASA RM 86753, 1985 https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19850023574.pdf |
| [18] | Tai C H, Yin S L, Soong C Y. A novel hyperbolic grid generation procedure with inherent adaptive dissipation[J]. Journal of Computational Physics., 1995, 116: 173-179.DOI:10.1006/jcph.1995.1015 |
| [19] | Chan W M, Steger J L. A generalized scheme for three-dimensional hyperbolic grid generation[R]. AIAA 1991-1588, 1991 https://www.researchgate.net/publication/23867601_A_generalized_scheme_for_three-dimensional_hyperbolic_grid_generation |
| [20] | Matsuno K. Hyperbolic upwind method for prismatic grid generation[R]. AIAA 2000-1003, 2000 https://www.researchgate.net/publication/223532732_High-order_upwind_method_for_hyperbolic_grid_generation |
| [21] | Batina J T. Unsteady Euler airfoil solutions using unstructured dynamic meshes[J]. AIAA Journal, 2012, 28(8): 1381-1388. |
| [22] | LÖehner R, Yang C. Improved ALE mesh velocities for moving bodies[J]. Communications in Numerical Methods in Engineering, 1996, 12(10): 599-608.DOI:10.1002/(SICI)1099-0887(199610)12:10 |
| [23] | Jasak H, Tukovic Z. Automatic mesh motion for the unstructured finite volume method[J]. Transactions of FAMENA, 2007, 30(2): 1-20. |
| [24] | Liu X Q, Qin N, Xia H. Fast dynamic grid deformation based on Delaunay graph mapping[J]. Journal of Computational Physics, 2006, 211(2): 405-423.DOI:10.1016/j.jcp.2005.05.025 |
| [25] | Rendall T C, Allen C B. Efficient mesh motion using radial basis functions with data reduction algorithms[J]. Journal of Computational Physics, 2009, 228(17): 6231-6249.DOI:10.1016/j.jcp.2009.05.013 |
| [26] | Rendall T C, Allen C B. Reduced surface point selection options for efficient mesh deformation using radial basis functions[J]. Journal of Computational Physics, 2010, 229(8): 2810-2820.DOI:10.1016/j.jcp.2009.12.006 |
| [27] |
张来平, 王振亚, 杨永健. 复杂外形的动态混合网格生成方法[J].
空气动力学学报, 2004, 22(2): 231-236. Zhang L P, Wang Z Y, Yang Y J. Dynamic hybrid grid generation for complex geometries[J]. Acta Aerodynamica Sinica, 2004, 22(2): 231-236. |
| [28] | Zhang L P, Wang Z J. A block LU-SGS implicit dual time-stepping algorithm for hybrid dynamic meshes[J]. Computers & Fluids, 2004, 33(7): 891-916. |
| [29] |
张来平, 段旭鹏, 常兴华, 等. 基于Delaunay背景网格插值方法和局部网格重构的变形体动态混合网格生成技术[J].
空气动力学学报, 2009, 27(1): 32-40. Zhang L P, Duan X P, Chang X H, et al. A hybrid dynamic grid generation technique for morphing bodies based on Delaunay graph and local remeshing[J]. Acta Aerodynamica Sinica, 2009, 27(1): 32-40. |
| [30] | Zhang L P, Chang X H, Duan X P, et al. A block LU-SGS implicit dual time-stepping algorithm on hybrid dynamic meshes for bio-fluid simulations[J]. Computers & Fluids, 2009, 38: 290-308. |
| [31] | Zhang L P, Chang X H, Duan X P, et al. Applications of dynamic hybrid grid method for three-dimensional moving/deforming boundary problems[J]. Computers & Fluids, 2012, 62(12): 45-63. |
| [32] | Chang X H, Zhang L P, He X. Numerical study of the thunniform mode of fish swimming with different caudal fin shapes[J]. Computers & Fluids, 2012, 68: 54-70. |
| [33] | Blazek J. Computational fluid dynamics : principles and applications[J]. Computational Fluid Dynamics principles & Applications, 2001, 14(1): 134-143. |
| [34] | Bui T T. A parallel, finite-volume algorithm for large-eddy simulation of turbulent flows[J]. Computers & Fluids, 2000, 29(8): 877-915. |
| [35] | Travin A, Shur M, Strelets M, et al. Physical and numerical upgrades in the detached-eddy simulation of complex turbulent flows[A]. //412 EUROMECH Colloquium on LES of Complex Transitional and Turbulent flows[C]. Munich, 2000 http://link.springer.com/article/10.1023/B%3AAPPL.0000004937.34078.71 |
| [36] | Chen R F, Wang Z J. Fast, block lower-upper symmetric Gauss Seidel scheme for arbitrary grids[J]. AIAA Journal, 2000, 38(12): 2238-2245.DOI:10.2514/2.914 |
| [37] | Jameson A. Time dependent calculations using multigrid, with applications to unsteady flows past airfoils and wings[R]. AIAA 1991-1596, 1991 https://www.researchgate.net/publication/267982395_Time_dependent_calculations_using_multigrid_with_applications_to_unsteady_flows_past_airfoils_and_wings |
| [38] | Lesoinne M, Farhat C. Geometric conservation laws for flow problems with moving boundaries and deformable meshes, and their impact on aeroelastic computations[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 134: 71-90.DOI:10.1016/0045-7825(96)01028-6 |
| [39] | Ahn H T, Kallinderis Y. Strongly coupled flow/structure interactions with a geometrically conservative ALE scheme on general hybrid meshes[J]. Journal of Computational Physics, 2006, 219(2): 671-696.DOI:10.1016/j.jcp.2006.04.011 |
| [40] |
刘君, 白晓征, 张涵信, 等. 关于变形网格"几何守恒律"概念的讨论[J].
航空计算技术, 2009, 39(4): 1-5. Liu J, Bai X Z, Zhang H X, et al. Discussion about GCL for deforming grids[J]. Aeronautical Computing Technique, 2009, 39(4): 1-5. |
| [41] | Wang Z J, Yang H Q. Unsteady flow simulation using a zonal multi-grid approach with moving boundaries[R]. AIAA 1994-0057, 1994 http://www.academia.edu/3049652/Advance_in_Overset_Grid_Schemes_From_Chimera_to_DRAGON_Grids |
| [42] | Chang X H, Ma R, Zhang L P, et al. Further study on the geometric conservation law for finite volume method on dynamic unstructured mesh[J]. Computers & Fluids, 2015, 120: 98-110. |
| [43] |
张来平, 马戎, 常兴华, 等. 虚拟飞行中气动、运动和控制耦合的数值模拟技术[J].
力学进展, 2014, 44: 201410 Zhang L P, Ma R, Chang X H, et al. Review of aerodynamics/kinematics/flight-control coupling methods in virtual flight simulations[J]. Advances in Mechanics, 2014, 44: 201410DOI:10.6052/1000-0992-14-027 |
| [44] | Chang X H, Ma R, Zhang L P, et al. Fully implicit approach for flow/kinetic coupled problems based on dynamic hybrid mesh[A]. //The 8th International Conference on Computational Fluid Dynamics[C].Chengdu, 2014 |
| [45] |
赫新, 张来平, 赵钟, 等. 大型通用CFD软件体系结构与数据结构研究[J].
空气动力学学报, 2012, 30(5): 557-565. He X, Zhang L P, Zhao Z, et al. Research of general large scale CFD software architecture and data structure[J]. Acta Aerodynamica Sinica, 2012, 30(5): 557-565. |
| [46] | He X, Zhang L P, Zhao Z, et al. Research and development of structured/unstructured hybrid CFD software[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2013, 30 |
| [47] | 2nd AIAA CFD Drag Prediction Workshop[EB/OL]. http://aaac.larc.nasa.gov/ts-ab/cfdlarc-dpw/, 2003 |
| [48] | 1st AIAA CFD High Lift Prediction Workshop[EB/OL]. http://hiliftpw. larc.nasa.gov/ |
| [49] | Rumsey C L, Slotnick J P, Long M, et al. Summary of the first AIAA CFD High-Lift Prediction Workshop[J]. Journal of Aircraft, 2011, 48(6): 2068-2079.DOI:10.2514/1.C031447 |
| [50] | Chu J, Luckring J M. Experimental surface pressure data obtained on 65° delta wing across Reynolds number and Mach number ranges[R]. NASA TM 4645, 1996 http://cfd.mace.manchester.ac.uk/twiki/pub/ATAAC/TestCase008DeltaWing/ST08_Delta_wing_with_sharp_leading_edge.doc |
| [51] | Hall L H, Parthasarathy V. Validation of an automated Chimera/6-DOF methodology for multiple moving body problems[R].AIAA 1998-0767, 1998 http://www.oalib.com/paper/4591908 |



