气泡与壁面的相互作用问题广泛存在于化工、石油、制药等多相流系统中.气泡与壁面作用时反弹、黏附、破碎等动力学行为会对化学反应效率、壁面力学特性、系统传热传质等过程有着重要的影响.分析气泡与壁面作用时的液膜排液动力学过程和气泡受力是理解气泡吸附、破碎机制的关键.研究气泡碰撞动力学过程可以为量化凝结、聚集、黏附和破碎等过程提供参考, 同时为复杂多相流动系统提供子模型.
气泡上升及与壁面碰撞是一个基础的问题, 在实验和理论上都受到了极大的关注. Tsao等[1]最早用高速相机捕捉到了高Reynolds数下气泡与壁面作用下的反弹轨迹, 实验中气泡以终端速度撞击壁面会反弹多次直至黏性耗散掉气泡的动能.实验还发现气泡碰撞壁面反弹回来气泡的形状会恢复球形. Klaseboer等[2]对不同尺寸的水中甲烷液滴与壁面的碰撞过程进行了实验, 发现液滴会与气泡碰壁一样发生反弹. Kisior等[3-4]对表面催化物质以及壁面属性对气泡碰撞行为的影响进行了实验研究. Legendre等[5]、Zenit等[6]从能量的角度分析了实验中的气泡, 发现气泡撞击壁面的过程中气泡的动能会部分转化为气泡的表面能, 其余部分被耗散, 当气泡反弹时, 表面能可以转化为动能.以上的实验虽然观察到了气泡反弹过程的轨迹, 但未能给出其他重要的信息, 如气泡靠近壁面界面变形、气泡受力等.随后Hendrix等[7]采用同步相机和光学干涉方法对毫米级气泡与壁面的碰撞过程进行了实验, 实验过程中通过光学干涉法得到了气泡与壁面间的薄膜变化. Zhang等[8-9]和Liu等[10]利用集成薄膜测力仪对气泡碰撞过程的受力进行了实验测量, 这为一系列模型的验证提供了重要数据.
对气泡或液滴碰撞过程形成的薄膜排水动力学过程的模型描述吸引了众多学者. Klaseboer等[2]采用薄膜排水模型和壁面诱导力模型对甲烷液滴与壁面撞击的薄膜排水和反弹过程进行了理论计算, 但薄膜分布的准确性未得到验证. Podvin等[11]将Klaseboer的模型扩展到二维来描述气泡与倾斜壁面的碰撞问题. Hendrix等[7]和Klaseboer等[12]利用薄膜润滑理论对实验中的气泡进行了计算, 结果表明, 采用实验得到速度曲线作为边界条件时, 得到的薄膜演化规律与实验结果吻合得极其良好. Chan等[13]详细地总结了气泡和液滴的薄膜排水及聚合问题的发展历程, 文中表明Stokes-Reynolds-Young-Laplace模型最能精确地描述气泡碰撞过程中形成的薄膜演化.随后Manica等[14-15]对气泡/液滴碰撞过程中的薄膜排水过程以及受力进行了详细研究, 提出的气泡受力模型可以较好地预测不同尺度下的气泡反弹轨迹, 同时捕捉到的液膜变形与实验吻合良好.
综上可知, 对于气泡碰撞的动力学问题, 国外大量学者进行了研究, 实验从智能测量宏观上的气泡轨迹到可以测的微观尺度上的薄膜厚度演化, 直至在某些情形下可以测的气泡与壁面相互作用的受力.基于薄膜润滑理论的SRYL方程可以较好地描述气泡碰撞过程中的液膜剖面变化, 与实验结果吻合良好.限于实验条件, 对于上升气泡的研究仅针对部分尺寸气泡, 对于不同控制参数下的气泡反弹规律并不明确.鉴于SRYL方程和气泡受力模型的准确性, 本文利用这些模型对不同控制参数下的气泡碰壁反弹过程中的动力学行为做出了详细的研究, 并最终得到了气泡界面变形和反弹的规律.
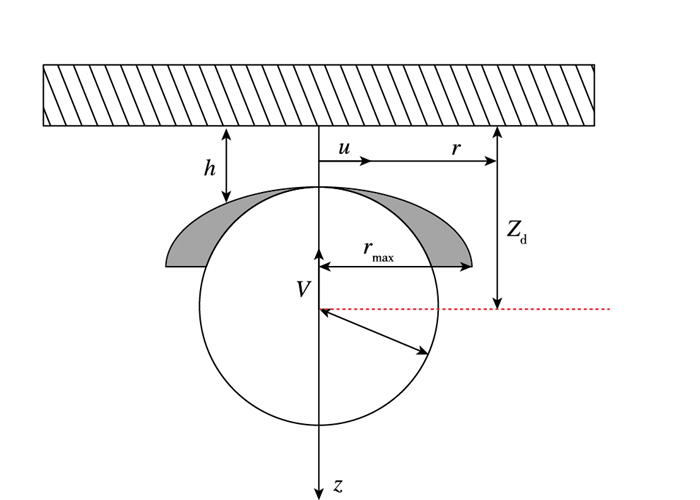
1 数学模型 1.1 气泡受力模型考虑如图 1所示的问题, 初始半径为R的气泡或液滴以速度V(t)垂直撞击壁面, 考虑这为轴对称问题, 气泡表面与壁面之间形成薄膜分布h(r, t), 气泡质心距壁面距离为Zd, 气泡表面与壁面间形成速度径向分布u, 薄膜内与气泡内部形成压差分布p(r, t), 薄膜径向分布的最大位置为rmax.将气泡的运动简化为质点运动, 可以得到气泡的受力方程
| $ \frac{4}{3}{\rm{ \mathsf{ π} }}{R^3}{\rho _{\rm{d}}}\frac{{{\rm{d}}V}}{{{\rm{d}}t}} = \sum F = {F_{\rm{B}}} + {F_{\rm{D}}} + {F_{\rm{A}}} + {F_{\rm{F}}} $ | (1) |
|
| 图 1 气泡碰撞壁面系统示意图 Fig.1 Sketch of the bubble-wall collision system |
其中, FB为气泡受到的浮力, FD为气泡受到的阻力或拽力, FA为附加质量力, FF为气泡撞击壁面界面变形引起的薄膜内润滑压力, 又称为薄膜诱导力, R为气泡半径, ρd为气泡密度, d代表离散相,即气泡本身,V为气泡质心速度.
由于重力的存在气泡上升过程中受到浮力的作用, 浮力大小与气泡体积和流体密度有关
| $ {F_{\rm{B}}} = - \frac{4}{3}{\rm{ \mathsf{ π} }}{R^3}\left( {{\rho _{\rm{d}}} - {\rho _{\rm{c}}}} \right)g $ | (2) |
式中, ρc为液体密度, c代表连续相,即气泡周围流体,g为重力加速度.
气泡运动过程中由于黏性的存在会受到阻力的作用, 阻力具有以下的形式[20]
| $ {F_{\rm{D}}} = {C_{\rm{D}}}\mathit{Re}\frac{{\rm{ \mathsf{ π} }}}{4}{\mu _{\rm{c}}}RV $ | (3) |
式中Re=2Rρc|V|/μc为气泡运动的瞬时Reynolds数, μc为液体的动力黏性系数.阻力系数CD通过对椭圆形气泡运动的分析计算得到, 并经实验验证具有很高的准确性[16].
| $ {C_{\rm{D}}} = \frac{{48}}{{Re}}G(\chi )\left( {1 + \frac{{H(\chi )}}{{\sqrt {Re} }}} \right) $ | (4) |
式中, χ为气泡的横纵比, 通过实验数据可以得到. G(χ)和H(χ)为通过理论分析计算得到的关于纵横比χ的函数.
| $ G(\chi ) = \frac{{{\chi ^{\frac{4}{3}}}}}{3}{\left( {{\chi ^2} - 1} \right)^{\frac{3}{2}}}\frac{{\sqrt {{\chi ^2} - 1} - \left( { - {\chi ^2} + 2} \right){{\cos }^{ - 1}}{\chi ^{ - 1}}}}{{{{\left( { - \sqrt {{\chi ^2} - 1} + {\chi ^2}{{\cos }^{ - 1}}{\chi ^{ - 1}}} \right)}^2}}} $ | (5) |
| $ \begin{array}{l} H(\chi ) = 0.019\;5{\chi ^4} - 0.213\;4{\chi ^3} + 1.702\;6{\chi ^2} - \\ \;\;\;\;\;\;\;\;\;\;\;\;2.146\;1\chi - 1.573\;2 \end{array} $ | (6) |
式(4)~(6)对应的阻力规律适用于流动界面条件下的上升气泡.当上升气泡处于稳定运动状态时, 阻力和浮力平衡, 此时气泡的运动速度成为终端速度VT.
对于不同大小的气泡, 其稳定运动时的变形横纵比和气泡的Weber数We有如下关系[16]
| $ \begin{array}{*{20}{c}} {We(\chi ) = 4{\chi ^{ - \frac{4}{3}}}\left( {{\chi ^3} + \chi - 2} \right)\left[ {{X^2}{{\sec }^{ - 1}}\chi - } \right.}\\ {{{\left( {{\chi ^2} - 1} \right)}^{\frac{1}{2}}}{]^2}{{\left( {{\chi ^2} - 1} \right)}^{ - 3}}} \end{array} $ | (7) |
而对于纯净的水中气泡, 根据实验拟合结果, 气泡变形横纵比与气泡半径有如下关系[15]
| $ {\chi ^{ - 1}} = \frac{{0.74 + 0.45\lambda }}{{1 - 1.17\lambda + 2.74{\lambda ^2}}} $ | (8) |
式中, λ=R/R0, 当0.3 mm < R < 1 mm时取R0=1 mm.当R < 0.3 mm时, 气泡的变形可以忽略, 可认为气泡为球形.当R > ~1 mm时, 气泡的运动轨迹开始向齿轮线转化而不再是直线型, 因此不再处于研究范围之内.
气泡从静止加速或与壁面碰撞变速的过程中, 由于周围流体的加速或减速会对气泡产生附加质量力.附加质量力由下式给出
| $ {F_{\rm{A}}} = \rho \frac{4}{3}{\rm{ \mathsf{ π} }}{R^3}{C_{\rm{m}}}\frac{{{\rm{d}}V}}{{{\rm{d}}t}} - \frac{1}{2}\rho \frac{4}{3}{\rm{ \mathsf{ π} }}{R^3}\frac{{{\rm{d}}{C_{\rm{m}}}}}{{{\rm{d}}H}}{V^2} $ | (9) |
式中, Cm为虚拟质量力系数, H为气泡与壁面的分离距离.右边第1项为经典的附加质量力表达式, 第2项的出现是因为附加质量力系数在气泡撞击壁面的过程中会发生变化.其中, 第2项的值与V2成正比, 因此始终指向远离壁面的方向.这意味着这一项不会对系统的阻尼起作用.
对于近似球形的气泡靠近壁面时的附加质量力系数有如下关系[17]
| $ \begin{array}{*{20}{c}} {{C_{\rm{m}}} = \frac{1}{2} + 0.192\;22{\zeta ^{ - 3.019}} + 0.062\;14{\zeta ^{ - 8.331}} + }\\ {0.034\;8{\zeta ^{ - 24.65}} + 0.013\;9{\zeta ^{ - 120.7}}} \end{array} $ | (10) |
其中,ζ=(H+R)/R. H为气泡界面与壁面的分离距离.对于椭圆形气泡, 在碰壁过程中的虚拟质量力系数随气泡与壁面距离的关系并不明确, 因此, 对于变形较大的椭圆形气泡假设认为碰撞过程中虚拟质量力系数保持不变, 并采用下式计算, 且不考虑壁面对附加质量力的影响.
| $ {C_{\rm{m}}} = 0.62\chi - 0.12,1 < \chi < 2.5 $ | (11) |
气泡撞击壁面的模型中最重要部分是气泡和固体表面之间的润滑膜以及控制气泡在该区域变形的表面张力, 这种黏性润滑和气泡变形之间的平衡将引起膜内积聚的压力, 其大小在特定条件下足以引起气泡反弹.将薄膜内的压力作面积积分可以得到薄膜排水力, 又叫壁面诱导力或附加薄膜压力.考虑轴对称薄膜, 可得
| $ {F_{\rm{F}}} = \int\limits_0^{{r_{\max }}} {2{\rm{ \mathsf{ π} }}rp{\rm{d}}r} $ | (12) |
式中rmax为薄膜分布的最大径向位置, rmax的选取与气泡的变形有关, p为薄膜内的液体压力,求解气泡的质心受力方程可以得到气泡质心速度变化V, 对速度V积分即可得到气泡的质心位置变化Zd.
1.2 Stokes-Reynolds-Young-Laplace模型采用合适的模型描述气泡撞击壁面时形成的薄膜演化和膜内压力变化是理解气泡碰撞动力学行为的关键.根据薄膜润滑理论, 薄膜厚度演化规律可由Stokes-Reynolds方程描述[14]
| $ \frac{{\partial h}}{{\partial t}} = \frac{1}{{M{\mu _{\rm{c}}}r}}\frac{\partial }{{\partial r}}\left( {r{h^3}\frac{{\partial p}}{{\partial r}}} \right) $ | (13) |
式中, M=12对应上述详细讨论的非流动界面边界条件, M=3对应流动界面边界条件.
上述中由于薄膜排水引起的水动力学压力p满足Young-Laplace方程[14]
| $ p=\frac{2 \sigma}{R}-\frac{\sigma}{r} \frac{\partial}{\partial r}\left(r \frac{\partial h}{\partial r}\right) $ | (14) |
当气泡远离壁面时, 式(14)中的水动力学压力p为0, 因此初始条件的选取须保证薄膜内的压力分布为0, 采用抛物型初始薄膜分布可以满足这一条件, 这一分布是半径为R的球形气泡表面的局部近似.因此t=0时的初始条件为
| $ h(r, 0)=H_{0}+\frac{r^{2}}{2 R} $ | (15) |
| $ Z_{\mathrm{d}}=h\left(r_{\max }, 0\right)+R-\frac{r_{\mathrm{max}}^{2}}{2 R} $ | (16) |
式中, H0为t=0时刻r=0位置处的薄膜厚度, 选取为气泡受壁面影响可以忽略的初始位置, 一般取H0=5R.
对于方程(13)和(14)构成的偏微分方程系统, 需要4个边界条件.在r=0处, 由于是轴对称模型, 采用对称边界
| $ \left.\frac{\partial h}{\partial r}\right|_{r=0}=0 $ | (17) |
| $ \left.\frac{\partial p}{\partial r}\right|_{r=0}=0 $ | (18) |
在薄膜的最外端, 此处薄膜近似认为未变形, 同时近似有薄膜厚度的变化速度与气泡质心的速度相等, 同时对于远场边界条件可假设压强径向衰减与1/r4成正比[18], 因此在r=rmax处有边界条件
| $ \left.\frac{\partial h}{\partial t}\right|_{r=\max }=V $ | (19) |
| $ r \frac{\partial p}{\partial r}+4 p=0 $ | (20) |
方程(1),(13),(14)及初始条件和边界条件(15)~(20)构成了描述气泡与壁面碰撞过程的动力学模型.将式(14)代入式(13)中可以得到关于薄膜厚度分布变化的4阶非线性偏微分方程.这一方程没有解析, 因此只能采用数值方法求解.该方程系统的求解采用直线法[19], 将偏微分方程组化为常微分方程组求解.首先将方程右端的空间倒数在[0, rmax]进行2阶中心差分离散, 得到以下耦合的差分方程组
| $ {\dot h_k} = f\left( {k\Delta r,t} \right),k = 0, \cdots ,N,\Delta r = {r_{\max }}/N $ | (21) |
对式(12)中的薄膜诱导力FF采用Simpson法则进行数值积分, 则最终的常微分方程组为
| $ \left( {\begin{array}{*{20}{c}} 1&0& \cdots &0&0\\ 0&1&0& \cdots &0\\ {}&{}& \vdots &{}&{}\\ 0&0& \cdots &1&0\\ 0&0& \cdots &0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\dot h}_0}}\\ {{{\dot h}_1}}\\ \vdots \\ {{{\dot h}_N}}\\ {\frac{{{\rm{d}}V}}{{{\rm{d}}t}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{f_0}}\\ {{f_1}}\\ \vdots \\ V\\ {\sum F } \end{array}} \right) $ | (22) |
这一常微分方程组可以使用MATLAB的ode15s算法求解.
2 结果分析计算选取Morton数Mo范围为10-8~10-12, 对应为低黏性流体, 计算选用的各种流体的物性参数和Morton数大小如表 1所示.计算涉及的气泡半径R0大小为0.1~1 mm, Reynolds数Re范围为5~750, Weber数We范围为0.005~3.5, 气泡与壁面发生正面碰撞, 气泡变形为球形或椭球型.气泡以终端速度与壁面发生正面碰撞.
| 下载CSV 表 1 计算流体属性 Tab.1 Fluid properties |
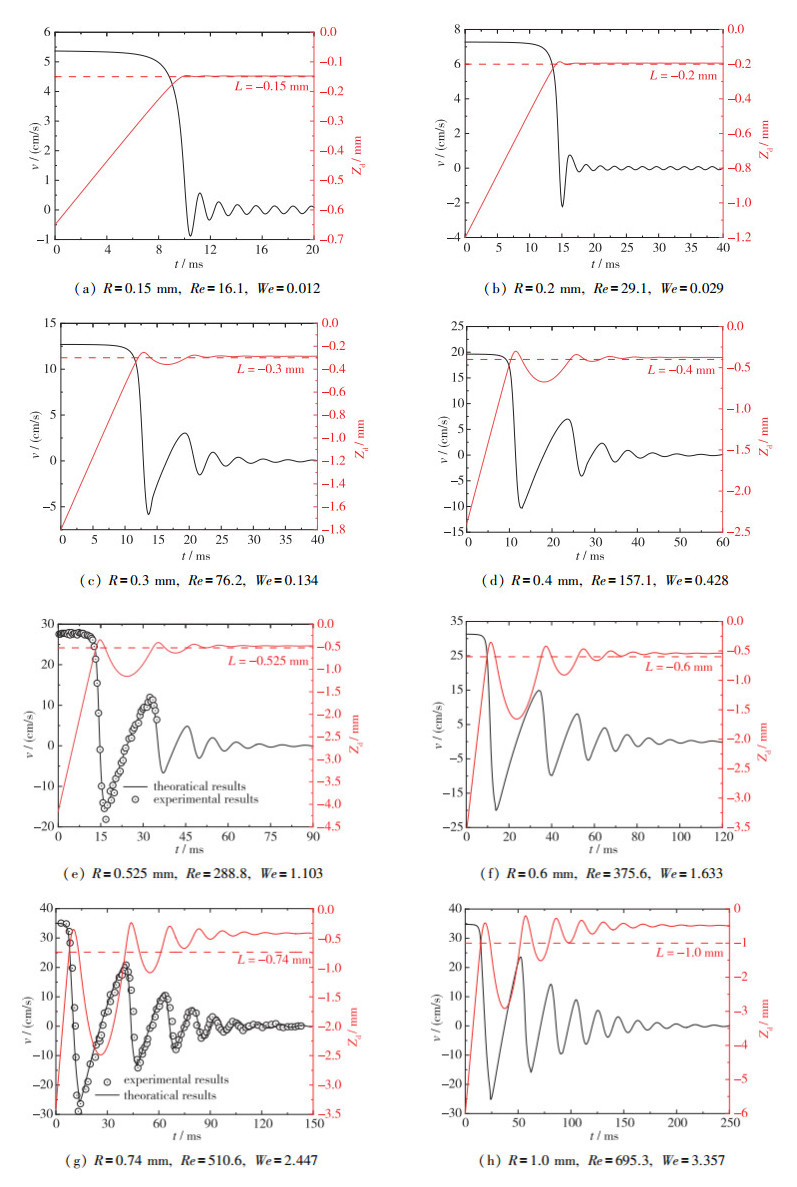
图 2显示了去离子水条件下(流体状态5)不同Reynolds数下气泡碰撞壁面过程中的速度变化和质心轨迹变化.计算过程中气泡的变形由式(7)计算.对于变形较小的气泡, 计算域rmax取0.9R, 随着气泡变形的增大, rmax的取值会相应增大.同时变形大的气泡在第1次与壁面碰撞的过程中会由椭球形恢复为球形[1].因此对于变形大的气泡, 计算过程中在气泡第1次与壁面撞击速度衰减为0开始, 阻力系数模型中的气泡横纵比设为χ=1.01;在气泡第1次反弹运动至速度为0的时刻开始, 改变计算域尺寸变为rmax=0.9R.从图中可以看出气泡在与壁面第1次碰撞之后速度迅速衰减, 速度衰减为0后反向增大, 气泡撞击壁面Reynolds数越大, 达到的反向速度越大, 气泡质心位置反向运动的幅度也越大.规定当气泡质心反向运动幅度(离壁面最近的位置到紧接着的最远位置的距离)超过气泡半径的1/10时, 气泡发生反弹现象, 否则认为气泡不发生反弹.则工况(a)的气泡未发生反弹, 工况(b)和(c)的气泡发生1次反弹, 工况(d)~(h)的气泡依次发生2~6次反弹, 气泡与壁面发生1到多次反弹直到气泡的动能被耗散掉.气泡在每一次撞击壁面时, 质心位置与壁面的最近距离会远小于气泡的半径.同时通过对比不同Reynolds数下的气泡质心轨迹可以发现, 随着Reynolds数的进一步升高, 气泡最终悬停在壁面附近时质心位置与壁面的距离会进一步小于气泡半径, 特别是工况(g)和(h)特别明显.在工况(e)和(g)中, 理论计算结果与Fujasová-Zedníková等[20]和Kosior等[21]的实验结果进行了对比, 可以看出理论计算结果与实验计算结果吻合良好, 这说明基于薄膜润滑理论的薄膜诱导力模型可以很好地预测气泡与壁面碰撞过程中的多次碰撞反弹动力学过程.同时可以看出, 在每一次碰撞和反弹过程中气泡的最大运动速度在变小, 而且气泡从接近壁面速度最大到远离壁面速度最大的运动阶段速度变化更快, 此时薄膜诱导力FF对气泡的运动起主导作用, FF在气泡与壁面碰撞的过程中会迅速增加和减小.再观察发生多次反弹时的气泡轨迹, 可以发现其衰减类似于阻尼振荡器, 但实际上的能量耗散小于采用黏性阻尼振荡器来分析这一系统时的能量耗散, 气泡反弹的幅度也大于采用黏性阻尼振荡器来分析得到的反弹幅度.这是由于气泡变形的存在, 使得能量转化为气泡表面能, 表面能可以再转化为气泡的动能, 这使得实际的黏性耗散小于黏性阻尼振荡器的耗散.
|
| 图 2 气泡碰壁质心速度和轨迹变化曲线图 Fig.2 Velocities and trajectories of bubble collision with rigid wall |
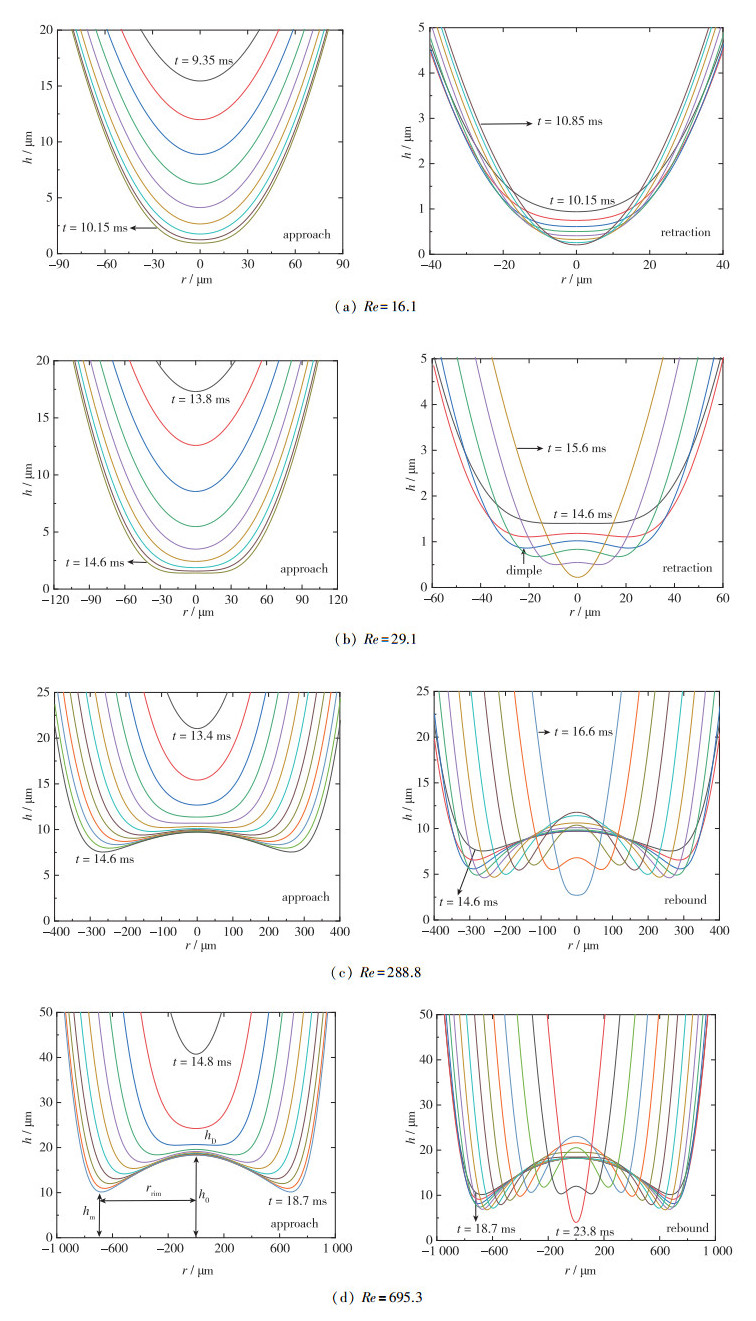
气泡在与壁面碰撞的过程中靠近壁面的界面会发生变形, 气泡的变形能够储存能量, 当气泡反弹时, 气泡储存的能量会恢复为气泡的动能.在不同的条件下, 气泡界面会出现丰富的变形, 例如酒窝状、丘疹状、涟漪状和皱纹状.以撞击壁面气泡质心速度为0的时刻作为分界点, 将薄膜演化分为接近阶段和缩回(反弹)阶段. 图 3显示了典型Reynolds数下气泡与壁面碰撞过程中的薄膜剖面变化.可以看出气泡在接近壁面的过程中会逐渐发生变形, Re=16.1时, 气泡界面变形较小, 而当Re=29.1时, 气泡界面已经变得非常平坦, 当Re=288.8时, 气泡在接近壁面的过程中气泡界面会先变平坦后界面曲率反向发展出酒窝状的变形, 当Re=695.3时酒窝状变形会变得更加明显; 在缩回阶段, Re=16.1时, 未观察到酒窝状变形, 而Re=29.1时, 酒窝状变形出现, 当Reynolds数进一步增大时, 酒窝状变形会变得更加明显.同时可以看出, 在缩回或反弹阶段, 虽然气泡质心在远离壁面, 但气泡界面仍然朝着液膜中心位置靠近, 酒窝状变形边缘凸起所在的径向位置会朝着液膜中心位置发展, 气泡界面也朝着中心位置移动, 当液膜中心位置发展至离壁面最近时, 酒窝状消失, 随后气泡界面开始与壁面分离, 气泡迅速反弹.对于其他Reynolds数的气泡与壁面碰撞过程中的薄膜剖面变化与以上典型Reynolds数气泡的薄膜剖面变化规律相同, 只是在酒窝状变形的程度和位置有相应差别, 这里不再赘述, 后面将会分析酒窝状变形出现的规律.
|
| 图 3 典型Reynolds数下气泡第1次碰壁过程中薄膜厚度变化示意图 Fig.3 Film thickness profiles during the first bubble-wall collision at typical Reynolds numbers |
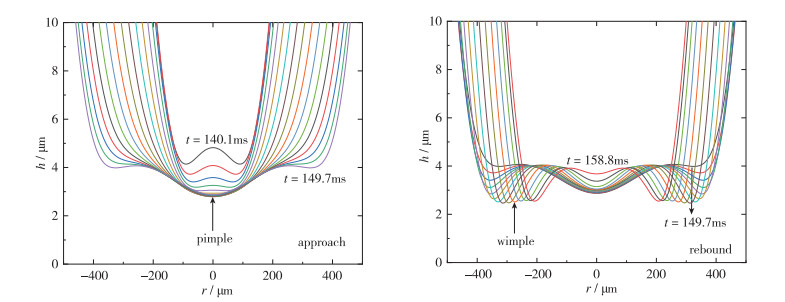
气泡多次反弹时后续反弹过程中的液膜剖面变化规律与第1次相同, 均会出现酒窝状的变形, 酒窝状变形的位置与变形程度会有所差异, 这里不再赘述.实际上酒窝状的变形在气泡碰壁过程中最容易形成, 而当气泡半径和Reynolds数均较大时, 在后续的碰撞过程中会出现其他的液膜形状. 图 4显示了Re=695.3的气泡第6次碰壁反弹过程中薄膜剖面的变化.在计算时间从140.1到149.7 ms时, 酒窝状变形逐渐变弱, 随后扁平, 并在液膜中心位置发展出鼓包, 而气泡界面向外扩张, 在径向外围形成第2个变形位置, 丘疹状变形出现, 此时气泡界面曲率在除r=0处均大于0, 但界面曲率的一次导数在除r=0外存在两个零点.在t=149.7~158.8 ms时, 丘疹状外围变形位置继续向壁面靠近, 逐渐形成向下凸起, 液膜中心位置朝远离壁面的位置发展, 形成向下凸起, 而两个向下凸起之间形成1个向上凸起, 丘疹状发展为涟漪状.涟漪状出现时, 界面曲率在除r=0外存在两个零点.在这两个零点位置之间界面曲率为负.
|
| 图 4 Re=695.3的气泡第6次碰撞反弹过程中薄膜剖面变化 Fig.4 Film profiles during the sixth bubble collision and rebound at Re=695.3 |
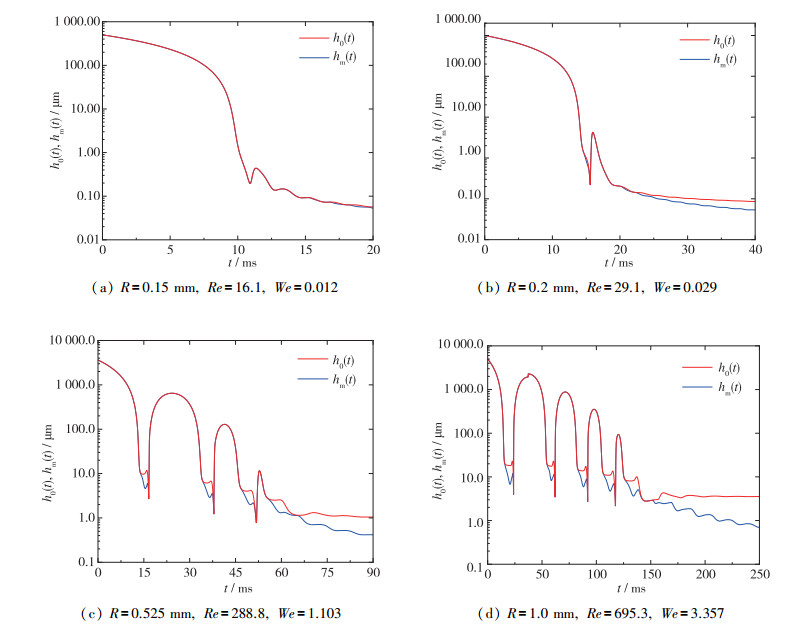
如图 3(d)所示, 液膜中心位置处薄膜厚度为h0, 酒窝状凸起位置处的薄膜厚度为hm, 可以看出当酒窝状凸起出现时有hm < h0. 图 5显示了典型工况下液膜中心位置和酒窝状凸起位置液膜厚度变化曲线.从图中可以看出, Re=16.1时, 气泡在与壁面碰撞的过程中未形成酒窝状, 在Re=29.1时, 形成了微弱的酒窝状, 随着Reynolds数的进一步增大, 酒窝状会变得越来越明显.当气泡与壁面发生多次碰撞反弹时, 每一次碰撞过程中都会形成酒窝状.当气泡最终悬停在壁面附近时, 气泡界面会以酒窝状的变形存在, 液膜中心位置薄膜厚度保持不变, 而酒窝状变形位置的液膜厚度会缓慢下降.当液膜出现破碎时, 破碎位置会首先出现在酒窝状变形凸起处, 此位置距离壁面最近, 会最先与壁面微纳结构发生作用, 引起薄膜破碎.同时我们可以观察到, 在前几次碰撞过程中, 气泡的动能大, 与壁面碰撞时, 中心位置液膜会随着气泡质心位置的回弹而一起大幅远离壁面, 而在后面的碰撞反弹过程中, 气泡的质心会发生较大幅度的回弹, 而液膜中心位置和酒窝状变形位置的液膜厚度基本不再发生变化, 此时, 靠近壁面的气泡界面会粘连在壁面附近发生进一步变形, 而气泡界面其余位置会随气泡质心位置一起振荡.
|
| 图 5 气泡碰壁过程中液膜中心位置和酒窝状凸起位置液膜厚度变化曲线 Fig.5 Film thickness at film center and barrier rim in the process of bubble-wall collision |
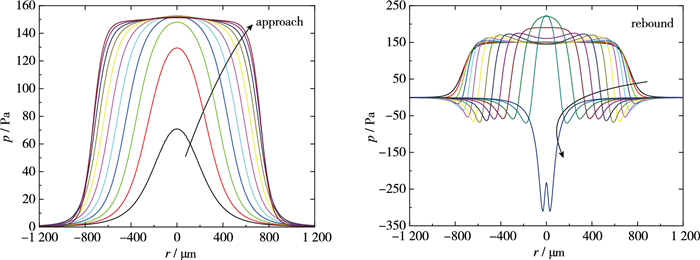
不同Reynolds数的气泡与壁面碰撞的过程中压强的变化规律基本相同, 只是压强的量级和具体变化位置有所不同, 这里以Re=695.3的气泡为例分析气泡碰壁过程中的压强变化规律.实际上, 压强变化与气泡界面变形息息相关, 界面出现不同的变形时, 压强会出现不同的径向剖面分布. 图 6显示了Re=695.3的气泡第1次与壁面相互作用时膜内压强变化规律.在气泡接近壁面过程中, 气泡初始压强分布为0, 随着气泡的变形, 中心位置压强迅速上升随后保持不变, 压强沿径向递减.其中最大压强接近150 Pa, 此气泡的Laplace压强2σ/R=144 Pa, 最大压强会大于球形气泡所具有的Laplace压强, 压强的差异由气泡撞击壁面时的局部变形引起.在气泡远离壁面反弹的过程中, 最大压强数值有所增加, 压强随径向加速衰减的位置向薄膜中心发展, 同时, 在酒窝状出现的位置及其外部会出现局部的负压区, 负压区位置随酒窝状的位置向薄膜中心发展.当酒窝状完全发展至中心处时, 会形成完全的负压区.负压区的存在会对气泡界面产生“吸力效应”, 因此气泡在反弹阶段, 界面会仍然朝壁面靠近.负压区的存在也会使壁面诱导力在部分时刻反向.当气泡反弹恢复至近似初始形状时, 压力分布衰减为0.
|
| 图 6 Re=695.3的气泡第1次碰壁反弹过程中膜内压强变化曲线 Fig.6 Pressure profiles during the first bubble collision and rebound at Re=695.3 |
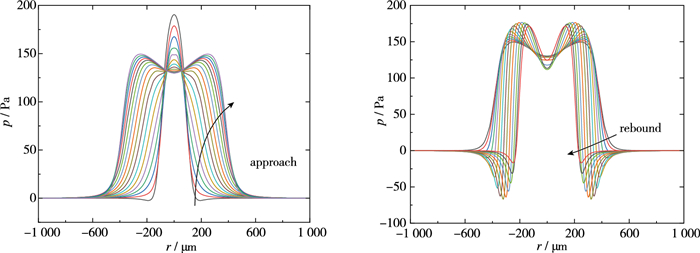
气泡在后续多次碰撞反弹过程中压强变化规律与第1次碰撞反弹时基本相同, 只是压强分布位置会随着酒窝状变形位置的变化而变化, 而当酒窝状变形发展为丘疹状和涟漪状时, 压强剖面分布才会相应发生变化, 图 7显示了Re=695.3的气泡第6次与壁面碰撞反弹过程中膜内压强分布变化.从图中可以看出, 在酒窝状存在时, 压强最大值位于液膜中心, 压强沿径向迅速衰减, 在酒窝状凸起位置存在局部负压区, 随着酒窝状的消失, 中心位置压强最大值下降, 负压区消失, 当丘疹状开始形成时, 压强最大值会出现在丘疹状变形的边缘处, 压强从此位置向液膜中心减小, 液膜中心周围部分位置的压强小于Laplace压强2σ/R=144 Pa.在酒窝状向涟漪状发展的过程中, 液膜中心位置的压强进一步下降, 而压强最大值的位置会逐步发展至界面向上凸起的位置.在界面朝外发展的向下凸起位置又形成了局部增大的负压区.
|
| 图 7 Re=695.3气泡碰壁第6次碰撞反弹过程中压强剖面变化 Fig.7 Pressure profiles during the sixth bubble collision and rebound at Re=695.3 |
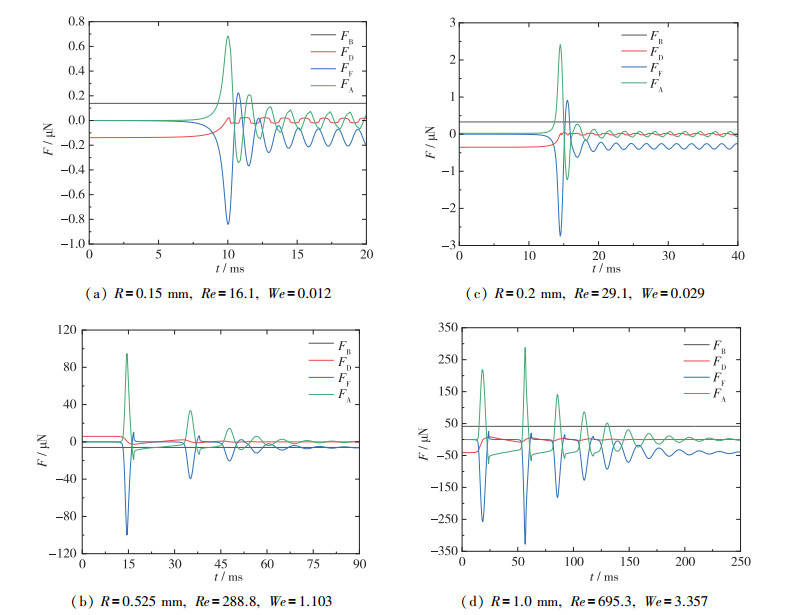
图 8显示了典型Reynolds数下气泡运动过程中的受力变化.气泡运动过程中受4个力的作用, 即升力FB, 阻力FD, 附加质量力FA和薄膜诱导力FF.在初始阶段气泡以终端速度运动, 浮力和阻力平衡, 气泡远离壁面受到的薄膜诱导力和附加质量力为0;在气泡撞击壁面的过程中, 薄膜诱导力和附加质量力急剧增大, 此时气泡的运动主要由薄膜诱导力和附加质量力主导; 薄膜诱导力达到最大时会急剧下降并出现局部的反向变化, 这是由于此时薄膜内部在中心位置附近出现局部的负压区, 在气泡运动趋于稳定时, 计算仍得到了周期性小幅度变化的薄膜诱导力和附加质量力, 此时气泡主要由浮力和薄膜诱导力平衡.同时从图 8中可以看出, 气泡在撞击壁面的过程中Reynolds数越大, 气泡受到的最大薄膜诱导力和附加质量力越大.在Re=16.1和29.1时, 气泡在第1次与壁面碰撞的过程中薄膜诱导力和附加质量力达到最大, 随后会衰减到与浮力大小相当; Re=288.8的气泡在每一次与壁面碰撞的过程中薄膜诱导力和附加质量力最大值逐渐变小, 当气泡不再发生明显的反弹时, 薄膜诱导力大小变得与浮力相当; Re=695.3时, 气泡第2次碰壁过程中的薄膜诱导力最大值会超过第1碰壁过程中的薄膜诱导力最大值, 在随后的碰撞过程中会逐渐衰减, 直到与浮力大小相当.
|
| 图 8 典型Reynolds数下气泡受力变化曲线图 Fig.8 Evolution of forces exerted on bubble at typical Reynolds numbers |
如图 3(d)所示, 气泡与壁面碰撞过程中第1次形成酒窝状时的薄膜厚度为hD. 考虑气泡界面为非流动界面时, 对于以恒定速度撞击壁面的气泡, 这一厚度可以通过理论分析得到[22], 其表达式为
| $ {h_{\rm{D}}} = cR\sqrt {2Ca} $ | (23) |
式中,Ca为气泡的毛细数.常数c的范围为0.4~0.7.对于本文计算考虑的气泡均为流动界面, 这一关系式也成立, 但是c的取值会与非流动界面情形下的c的值不同, 大概为4倍的关系, 即为
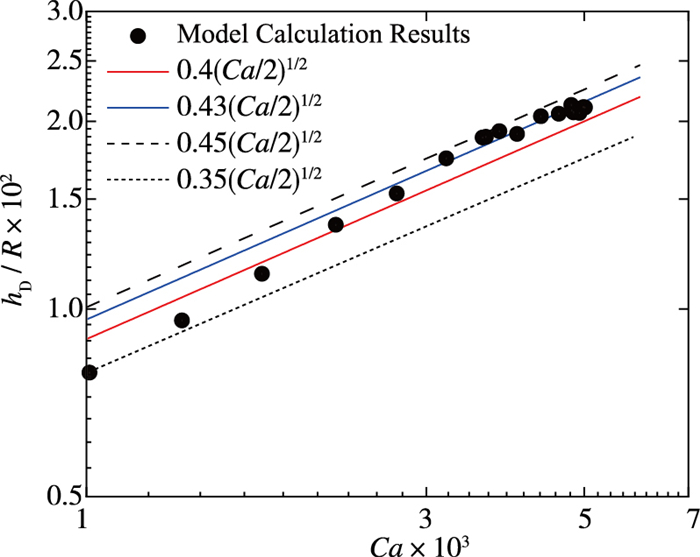
|
| 图 9 酒窝状变形形成时的液膜厚度随Ca变化曲线图 Fig.9 Evolution of the film thickness with capillary number during dimple formation |
从上面的计算结果可以看出, 气泡在撞击壁面的过程中在一定的条件下会发生反弹, 气泡会反弹1次到多次直至气泡的动能被完全耗散.同时随着Reynolds数的增加, 气泡碰撞壁面过程中反弹的次数和第1次反弹的最大幅度在增加.为了证实气泡反弹与Reynolds数的关系, 本文选取了表 1中6种Mo数下的气泡进行了计算. 图 10显示了在不同(We, Re)控制下的气泡反弹次数的机制.对于每一种Mo数, 气泡的控制参数均保证气泡的运动轨迹位于气泡轨迹机制图的稳定区域, 对于本文计算的部分Reynolds数很高的气泡, 控制参数可能位于气泡轨迹稳定的临界区域, 但在采用超纯净流体的实验中可以实现气泡的稳定上升.气泡的变形位于变形机制图中的球形和椭球型变形区域, 气泡的最大变形比为2.16, We最大为3.35.这些控制参数均保证式(7)的关系能够在误差允许的范围内成立.气泡反弹与否的标准与2.1节中的定义一致, 即气泡碰撞壁面后质心反向运动的最大幅度超过气泡半径的1/10,即认为气泡发生反弹. 图 10中通过红色虚线划分出了不同的反弹区域.从图 10中可以看出, 气泡碰壁反弹的次数与气泡的Reynolds数有着直接的关系, 与Weber数的关系不大, 在Re > ~29时, 气泡会发生反弹, 反之气泡不发生反弹, 此时Weber数越小, 发生反弹需要的Reynolds数会轻微地增大.当Re > ~90时, 气泡反弹次数增加为两次; 当Re > ~190时, 气泡反弹次数增加为3次; 当Re > ~310时, 气泡的反弹次数增加至4次; 当Re > ~430时, 气泡的反弹次数增加至5次; 当Re > ~586时, 气泡反弹次数增加至6次, 在现有的计算中考虑到垂直碰撞壁面, 气泡出现的最大反弹次数为6次.在达到最大反弹次数后, 气泡的质心位置还会有轻微的振荡变化, 但变化幅度小于气泡半径的1/10, 因此不认为气泡发生反弹.事实上, 通过观察液膜中心位置和酒窝状凸起位置的液膜厚度可以看出, 在此时这两个位置的厚度已经不再像之前碰撞反弹过程中一样发生大幅的变化, 这说明气泡已经黏附在壁面上, 不与壁面发生分离, 因此此时气泡质心位置的变化是由气泡界面的变形振荡引起的.从图 10中我们还可以观察到, 随着Reynolds数的增大, 反弹次数对We的依赖已经消失, 只与Reynolds数有关.
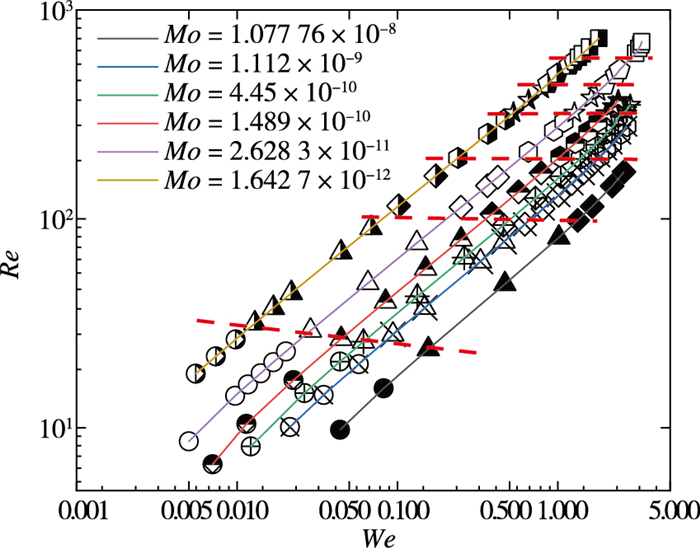
|
| 图 10 不同Mo数下气泡反弹规律:圆形对应气泡未反弹, 三角形反弹1次, 菱形反弹2次, 六边形反弹3次, 五角星反弹4次, 五边形反弹5次, 正方形反弹6次 Fig.10 Bubble rebound law at different Mo numbers: circles represent bubbles do not rebound, triangles represent bubbles rebound once, rhombuses represent bubbles rebound twice, hex- agons represent bubbles rebound three times, pentagram repre- sent bubbles rebound four times, pentagons represent bubbles rebound five times, squares represent bubbles rebound six times |
本文采用壁面诱导力模型和SRYL模型对不同Mo数和Reynolds数下气泡与壁面碰撞的问题进行了理论求解和分析.可以看出随着Reynolds数的增大, 气泡质心轨迹会经历从不反弹到反弹一次, 随后反弹多次的过程, 气泡的动能在多次反弹过程中会逐渐被耗散掉, 气泡反弹次数与Reynolds数有着直接的关系, 在不同的Mo数下, 气泡均在相同Reynolds数附近发生反弹次数的改变.随着Reynolds数的进一步增大, 气泡最终悬停在壁面附近时质心位置与壁面的距离会进一步小于气泡半径.采用本文模型计算得到的气泡速度变化与实验结果吻合良好, 说明本文的模型可以很好地预测气泡与壁面碰撞过程的轨迹变化.气泡在与壁面碰撞的过程中会出现丰富的薄膜动力学行为, 气泡界面会逐步形成酒窝状的变形, 酒窝状的变形程度随Reynolds数的增大而增大, 气泡在多次碰壁反弹过程中均会形成酒窝状变形, 酒窝状变形的演变规律与第1次碰壁反弹过程相同.气泡碰壁时, 膜内流体压强会逐渐上升, 在酒窝状变形形成时, 最大压强大于气泡Laplace压强, 在气泡反弹过程中, 会在酒窝状变形附近形成局部负压区, 负压区的位置会随着酒窝状变形凸起的位置发生变化.同时, 对于大变形和高Reynolds数气泡, 计算捕捉到了丘疹状和涟漪状的变形.气泡在与壁面碰撞过程中的运动主要由薄膜诱导力和附加质量力主导, 随着Reynolds数的增加, 薄膜诱导力的最大量级会逐渐增大, 薄膜诱导力和附加质量力会逐渐衰减, 最终气泡悬停在壁面上时气泡由浮力和薄膜诱导力平衡.计算得到的气泡在第1次与壁面碰撞过程中酒窝状形成时的液膜厚度hD与分析表达式
| [1] |
Tsao H K, Koch D L. Observations of high Reynolds number bubbles interacting with a rigid wall[J]. Physics of Fluids, 1997, 9(1): 44-56. |
| [2] |
Klaseboer E, Chevaillier J P, Maté A, et al. Model and experiments of a drop impinging on an immersed wall[J]. Physics of Fluids, 2001, 13(1): 45-57. |
| [3] |
Kosior D, Zawala J, Niecikowska A, et al. Influence of non-ionic and ionic surfactants on kinetics of the bubble attachment to hydrophilic and hydrophobic solids[J]. Colloids and Surfaces A:Physicochemical and Enginee-ring Aspects, 2015, 470: 333-341. |
| [4] |
Kosior D, Kowalczuk P B, Zawala J. Surface roughness in bubble attachment and flotation of highly hydrophobic solids in presence of frother-experiment and simulations[J]. Physicochemical Problems of Mineral Processing, 2018, 54(1): 63-72. |
| [5] |
Legendre D, Daniel C, Guiraud P. Experimental study of a drop bouncing on a wall in a liquid[J]. Physics of Fluids, 2005, 17(9): 097105. DOI:10.1063/1.2010527 |
| [6] |
Zenit R, Legendre D. The coefficient of restitution for air bubbles colliding against solid walls in viscous liquids[J]. Physics of Fluids, 2009, 21(8): 083306. DOI:10.1063/1.3210764 |
| [7] |
Hendrix M H W, Manica R, Klaseboer E, et al. Spatiotemporal evolution of thin liquid films during impact of water bubbles on glass on a micrometer to nanometer scale[J]. Physical Review Letters, 2012, 108(24): 247803. DOI:10.1103/PhysRevLett.108.247803 |
| [8] |
Zhang X R, Tchoukov P, Manica R, et al. Simultaneous measurement of dynamic force and spatial thin film thickness between deformable and solid surfaces by integrated thin liquid film force apparatus[J]. Soft Matter, 2016, 12(44): 9105-9114. DOI:10.1039/C6SM02067D |
| [9] |
Zhang X R, Manica R, Tang Y C, et al. Probing boundary conditions at hydrophobic solid-water interfaces by dynamic film drainage measurement[J]. Langmuir, 2018, 34(40): 12025-12035. DOI:10.1021/acs.langmuir.8b02492 |
| [10] |
Liu B, Manica R, Zhang X R, et al. Dynamic interaction between a millimeter-sized bubble and surface microbubbles in water[J]. Langmuir, 2018, 34(39): 11667-11675. DOI:10.1021/acs.langmuir.8b01202 |
| [11] |
Podvin B, Khoja S, Moraga F, et al. Model and experimental visualizations of the interaction of a bubble with an inclined wall[J]. Chemical Engineering Science, 2008, 63(7): 1914-1928. DOI:10.1016/j.ces.2007.12.023 |
| [12] |
Klaseboer E, Manica R, Hendrix M H, et al. A force balance model for the motion, impact, and bounce of bubbles[J]. Physics of Fluids, 2014, 26(9): 092101. DOI:10.1063/1.4894067 |
| [13] |
Chan D Y C, Klaseboer E, Manica R. Film drainage and coalescence between deformable drops and bubbles[J]. Soft Matter, 2011, 7(6): 2235-2264. DOI:10.1039/C0SM00812E |
| [14] |
Manica R, Klaseboer E, Chan D Y. The hydrody-namics of bubble rise and impact with solid surfaces[J]. Advances in Colloid and Interface Science, 2016, 235: 214-232. DOI:10.1016/j.cis.2016.06.010 |
| [15] |
Manica R, Klaseboer E, Chan D Y. Force balance model for bubble rise, impact, and bounce from solid surfaces[J]. Langmuir, 2015, 31(24): 6763-6772. DOI:10.1021/acs.langmuir.5b01451 |
| [16] |
Moore D W. The velocity of rise of distorted gas bubbles in a liquid of small viscosity[J]. Journal of Fluid Mechanics, 1965, 23(4): 749-766. DOI:10.1017/S0022112065001660 |
| [17] |
Kharlamov A A, Chára Z, Vlasák P. Hydraulic formulae for the added masses of an impermeable sphere moving near a plane wall[J]. Journal of Engineering Mathema-tics, 2008, 62(2): 161-172. |
| [18] |
Yiantsios S G, Davis R H. On the buoyancy-driven motion of a drop towards a rigid surface or a deformable interface[J]. Journal of Fluid Mechanics, 1990, 217: 547-573. DOI:10.1017/S0022112090000842 |
| [19] |
Chan D Y, Klaseboer E, Manica R. Theory of non-equilibrium force measurements involving deformable drops and bubbles[J]. Advances in Colloid and Interface Science, 2011, 165(2): 70-90. DOI:10.1016/j.cis.2010.12.001 |
| [20] |
Fujasová-Zedníková M, Vobecká L, Vejrazka J. Effect of solid material and surfactant presence on interactions of bubbles with horizontal solid surface[J]. The Canadian Journal of Chemical Engineering, 2010, 88(4): 473-481. |
| [21] |
Kosior D, Zawala J, Malysa K. Influence of n-octanol on the bubble impact velocity, bouncing and the three phase contact formation at hydrophobic solid surfaces[J]. Colloids and Surfaces A:Physicochemical and Enginee-ring Aspects, 2014, 441: 788-795. |
| [22] |
Klaseboer E, Manica R, Chan D Y. Universal behavior of the initial stage of drop impact[J]. Physical Review Letters, 2014, 113(19): 194501. DOI:10.1103/PhysRevLett.113.194501 |



