全球范围内稠油资源蕴藏丰富, 随着陆地上大幅度常规原油的开采, 人们把更多的目光投向了稠油, 投向了海洋.稠油黏度过大, 油品和管壁之间的剪切应力过大, 难以输送.选用低黏度流体以环状流形式包裹油相(形成环状流)进行油液输送, 将大幅降低稠油输送能耗, 是稠油管道运输的有效模式之一.众多学者对稠油-水核-环状流态黏度效应, 环状流型及环状流表面张力不稳定的理论进行了研究和探讨[1-3].李家元等[4]通过管道局部畸变、管壁亲水化以及管道内壁的凝胶吸附层研究了水环的稳定性.刘玉泉[5]讨论了横流下的管道中轴向环状流流动稳定性问题.以上主要讨论了直管内的流动. Sharma等[6]、Jiang等[7-8]研究了180°弯管内高黏度油水环状流动和基于Euler模型的柔性弯管油水环状流动数值模拟. Picardo等[9]研究了弯曲环形通道内的环状两相流的截面速度分布.壳牌石油公司和胜利油田清河采油区也采用了油水环状流技术[10].世界各地建立了3条短距离的水环稠油输送线, 取得了较好的节能效果[11].
目前学者很少探讨流道结构变化对环状流的影响, 江帆等[12-13]初步研究了阀门不同开度下的油水环状流变化情况, 在较小的阀门开度下, 环状流会遭到破坏, 并讨论了射流导致的漩涡对油水环状流的影响.但是海底管道可能受到来自外界的猛烈撞击导致管道变形引起流道结构变形, 杨政龙等[14]做了深海管道在冲击载荷作用下的局部屈曲特性研究, 本文主要探讨在冲击载荷作用下管道变形对油水环状流的影响及变形程度导致的相界面之间的压力关系.为后续的油水环状流在复杂结构下的稳定性研究提供参考.
1 流动控制方程两相流体均遵守质量守恒定律和动量守恒定律, 湍流模型选择标准k-ε模型, 油水之间的相互作用采用连续表面力CSF模型.其中连续性方程为
| $ \begin{aligned} &\frac{\partial \rho}{\partial t}+\nabla \cdot(\boldsymbol{v} \rho)=0\\ &\rho=\alpha_{\rm o} \rho_{\rm o}+\left(1-\alpha_{\rm o}\right) \rho_{\rm w} \end{aligned} $ |
式中, ρ为流体密度, t为时间, $\nabla$为散度符号, v为流体速度, ρo为油相密度, αo为油相体积分数, ρw为水相的密度.
动量守恒方程为
| $ \frac{\partial }{{\partial t}}(\rho \mathit{\boldsymbol{v}}) + \nabla \cdot (\rho \mathit{\boldsymbol{vv}}) = - \nabla \mathit{\boldsymbol{p}} + \nabla \mathit{\boldsymbol{\tau }} + \rho \mathit{\boldsymbol{g}} + \mathit{\boldsymbol{F}} $ | (1) |
| $ \mathit{\boldsymbol{\tau }} = \mu \left[ {\left( {\nabla \mathit{\boldsymbol{v}} + \nabla {\mathit{\boldsymbol{v}}^{\rm{T}}}} \right) - \frac{2}{3}\nabla \cdot (\mathit{\boldsymbol{vI}})} \right] $ |
式中, p为压力, τ为剪应力张量, $\nabla$为散度符号, g为重力加速度, F为外部体积力, μ为流体黏度, I为单位张量.
标准k-ε模型为
| $ \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k\mathit{\boldsymbol{v}})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon $ |
| $ \begin{aligned} \frac{\partial(\rho \varepsilon)}{\partial t}+\frac{\partial(\rho \varepsilon {\boldsymbol{v}})}{\partial x_{i}}=& \frac{\partial}{\partial x_{j}}+\left[\left(\mu+\frac{\mu_{\rm t}}{\sigma_{\varepsilon}}\right) \frac{\partial \varepsilon}{\partial x_{j}}\right] C_{1 \varepsilon} \frac{\varepsilon}{k} G_{k}-\\ & C_{2 \varepsilon} \rho \frac{\varepsilon^{2}}{k} \\ & \mu_{\rm t}=\rho C_{\mu} \frac{k^{2}}{\varepsilon} \end{aligned} $ |
式中, k为湍动能; ε为耗散率; Gk为平均速度梯度引起的湍动能产生项; C1ε, C2ε, Cμ均为常数, 其值分别为1.44, 1.92, 0.09; σk为湍动能k的湍流Prandtl数, 其值为1.0; σε为耗散率ε的湍流Prandtl数, 其值为1.3; xi为第i个坐标方向; xj为第j个坐标方向; μt为湍流黏度.
CSF表面张力模型为
| $ \begin{array}{c} \boldsymbol{F}_{\sigma}=\sigma_{\mathrm{ow}} \frac{\alpha_{\mathrm{o}} {\rho}_{\mathrm{o}} {\kappa} \nabla \alpha_{\mathrm{w}}+\alpha_{\mathrm{w}} {\rho}_{\mathrm{w}} {\kappa} \nabla \alpha_{\mathrm{o}}}{0.5\left({\rho}_{\mathrm{o}}+{\rho}_{\mathrm{w}}\right)} \\ {\kappa}=\nabla \cdot\left(\frac{\boldsymbol{n}}{|\boldsymbol{n}|}\right) \\ \boldsymbol{n}=\nabla \alpha_{\mathrm{o}} \end{array} $ |
式中, Fσ为油水界面张力, 可以作为外部体积力代入式(1); σow为油水界面张力系数; ρo, ρw分别为油相、水相密度; αo,αw分别为油相、水相体积分数; κ为界面曲率; n为油相体积分数的单位法向.
2 计算模型由于与柔性管道发生碰撞的物体不一定规则, 最先与管道碰撞的部位也有可能是不规则的, 因此在碰撞过程中将碰撞物体分别简化为球体、立方体以及不同圆锥角的锥体, 以研究不规则的物体与管道发生碰撞的情况[15], 管道变形主要产生棱角和光滑两种凹陷面, 因此选用球体和圆锥体作为碰撞模型, 利用SolidWorks软件创建柔性管结构变形的三维模型, 柔性管的流道直径为12 mm, 水平管道长300 mm, 如图 1所示.根据柔性管三维模型创建的流动区域模型, 整个模型由入口管道、柔性管变形管道、出口管道组成.考虑主要研究柔性管受到物体水平方向撞击, 探讨水平方向结构变形产生的湍动能、压力场对漩涡的影响及其流型的演变, 流体通过柔性管道的时间很短, 受重力因素产生的影响远远小于结构变形的影响, 为减少计算时间, 综合考虑可采用二维模型进行模拟.利用ANSYS Workbench中的Mesh模块对模型进行划分, 探讨撞击之后流道结构变形影响.如图 2(a)所示, 检查网格在柔性管管壁凹陷15%时, 节点数为24 763, 网格数量为24 102, 最大扭曲度为0.52;如图 2(b)所示, 节点数为24 807, 网格数量为24 143, 最大扭曲度为0.47.检查网格最大扭曲度为0.52和最小正交质量0.78, 符合数值模拟计算要求.

|
| 图 1 柔性管流动区域模型 Fig.1 Flow area model of flexible pipe |

|
| 图 2 网格模型 Fig.2 Mesh model |
为了了解环状流在柔性管道内的流动结构, 采用外环为水相, 内环为油相的两相Newton流体形成环状流, 两相流的流体物性参数如表 1所示.管道最大凹陷深度与管道内径之比定义为凹陷程度, 模拟柔性管受到猛烈撞击分别5%, 10%, 15%, 20%, 25%和30%这6种凹陷程度; 同时对最大变形程度进行不同流速的仿真.设定边界条件:入口为速度入口, 分析采用流体流速[16]分别为V1, V2, V3,如表 2所示.出口采用压力出口, 其余均为壁面.由于Reynolds数超过临界值, 流动区域产生湍流, 采用标准k-ε湍流模型.流动方程采用SIMPLE算法, 方程中各项的离散格式全部选择2阶迎风格式, 双精度求解.
| 下载CSV 表 1 各种流体的物性参数 Tab.1 Physical properties of various fluids |
| 下载CSV 表 2 入口速度参数 Tab.2 Inlet velocity parameters |
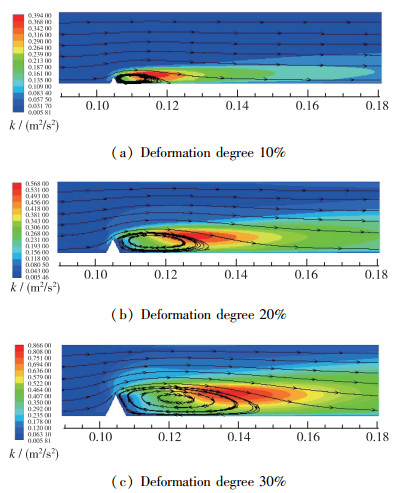
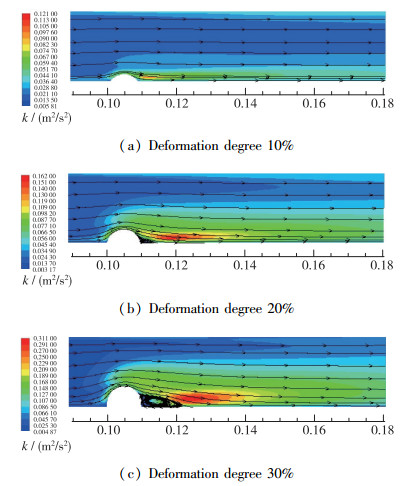
设定流体的入流速度为V2, 分析不同流道结构的凹陷及不同凹陷程度对漩涡结构的影响, 图 3和图 4分别为不同程度的V形和○形结构流道变形的湍动能云图及流线图.
|
| 图 3 不同程度的V形变形湍动能云图 Fig.3 Turbulent kinetic energy contours of V-shaped deformation with different degrees |
|
| 图 4 不同程度的○形变形湍动能云图 Fig.4 Turbulent kinetic energy contours of ○-shaped deformation with different degrees |
对比图 3(a), (b), (c)可以判断柔性管道受到锥形物体猛烈撞击时, 水平方向观察管道结构会发生V形凹陷, 随着凹陷程度的增加湍动能越来越大, 湍动能的变化区域范围也越来越大, 通过观察可以发现湍动能的最大值和最大凹陷深度点一直保持在同一水平线上, 但距离最大凹陷深度点的距离也越来越远, 湍动能的中心区域也随之增加.根据Bernoulli原理, 柔性管凹陷程度变大, 管道流动区域变窄, 此时经过这段变形区域时, 流体的流速会增加, 经过变形区域后, 流道管径突然变大, 此时容易产生湍流和涡旋, 因此变形程度越大, 湍动能也就越大, 中心凹陷点以下是管径的扩张区域, 湍流中心和最大凹陷深度点在同一水平线, 根据流线图判断漩涡在最大凹陷深度点到湍动能最大值中间, 漩涡的最外层流线在结构变形的右侧和湍动能最大值区域的中间位置, 漩涡的面积也随着凹陷程度的增加而变大.说明漩涡的区域范围及能量大小和湍动能有一定的关系.
对比图 4(a), (b), (c)可以判断在柔性管道受到球形物体猛烈撞击时, 水平方向观察管道结构会发生○形凹陷, 随着凹陷程度的增加湍动能越来越大, 湍动能的变化区域范围也越来越大, 湍动能的中心位置距离结构变形区域的位置也越来越远, 但是湍动能较大区域在凹陷中线点的水平线位置与管壁中间.观察流线图可以发现在凹陷程度较小时, 没有漩涡产生, 在凹陷程度达到20%时, 产生了一点漩涡, 随着凹陷程度增加, 漩涡面积及强度也随着增加.对比图 3可知, 同等程度的凹陷情况下, V形凹陷产生漩涡区域都大于○形凹陷产生的漩涡.漩涡的位置分布主要在变区域的右侧底部, 漩涡的最外层流线在结构变形的右侧底部和靠近湍动能最大值区域位置.产生这种现象主要是凹陷的结构变形有一定的弧度, 在流体流经最窄区域时流速增加, 经过最窄区域之后流道宽度没有快速增加, 而是有一定弧度的缓慢增加, 这样对流体的突变产生了一定的缓冲作用.
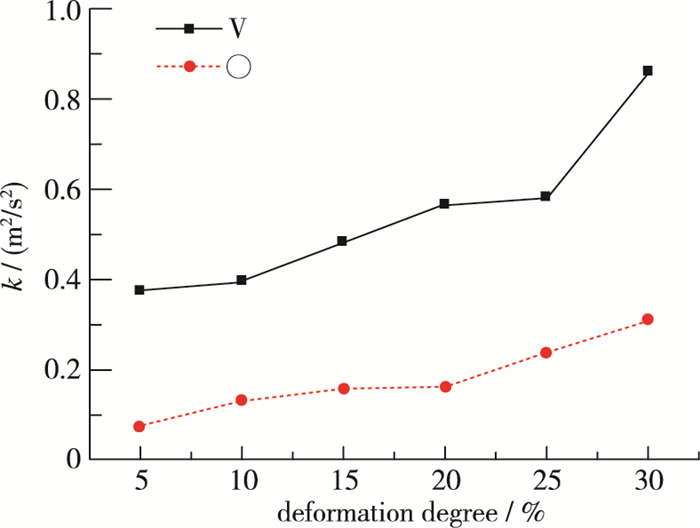
对比图 3和图 4可以得出在同等程度的凹陷情况下, V形凹陷产生的湍动能强度, 湍动能区域面积及湍动能中心点到最大凹陷深度点距离均大于○形凹陷产生的影响. V形凹陷产生漩涡强度及面积也均大于○形凹陷产生的影响.主要原因是V形的凹陷最大深度点是一个驻点, 经过这个点之后流体不能产生附壁作用, 流体离开了壁面, 流道扩宽区域呈线性增长, 此时流道的变化速率较快, 易产生较大的湍动能和漩涡; ○形最大凹陷深度点的斜率为0, 流体经过中心点后仍然会吸附在管道的壁面上, 此时流体会产生斜向下的流动方向, 因此湍动能的中心会低于V形产生的湍动能中心点.如图 5所示, V形产生的最大湍动能是○形产生的最大湍动能的3倍左右, 因此在实际操作中应避免产生V形变形, 如产生该结构变形也应当把驻点结构变成为有一定弧度的结构, 减少由于结构差异引起的漩涡影响.
|
| 图 5 不同凹陷结构中湍动能与凹陷程度的关系 Fig.5 Relationship between turbulent kinetic energy and deformation degree in different deformed structures |
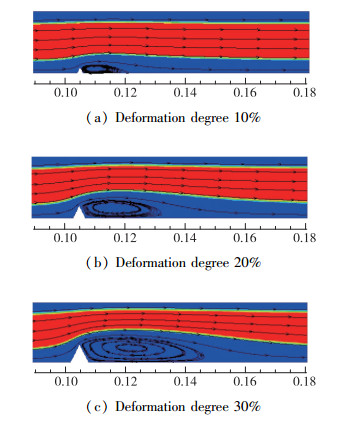
图 6为不同程度的V形结构流道变形的总压力云图.对比图 6(a), (b), (c),观察到管道结构发生V形凹陷, 随着凹陷程度的增加, 油相会被压缩得越小, 压缩的最小区域在最大凹陷深度点的右侧, 根据漩涡流线图判断大概在漩涡中心点的上方; 如图 6(a)所示, 漩涡中心距离最深凹陷点大概6 mm, 整个漩涡的长度大约为13 mm, 宽度为4 mm; 如图 6(b)所示, 漩涡中心距离最深凹陷点大概13 mm, 整个漩涡的长度大约为25 mm, 宽度为7 mm; 如图 6(c)所示, 漩涡中心距离最深凹陷点大概18 mm, 整个漩涡的长度大约为40 mm, 宽度为9 mm; 产生这种情况的主要原因是, 流体进入变形区域, 经过最大凹陷深度点时, 该点为一个驻点, 流体会失去附壁作用, 会产生一个斜向上的流速, 此时水相会挤压油相, 油相压缩到最小值时, 此刻垂直方向的速率最小, 水平方向速率最大, 因此油相压缩极值点会在变形区域右侧, 漩涡中心点的正上方.油相压缩得越小, 漩涡的强度及面积也就越大, 但是环状流的流型并没有发生破坏, 漩涡区域仍然为水相不含有油相, 在经过压缩区间后, 油相的流经宽度再次变大以至于可以恢复到柔性管入口时的环状流形态.
|
| 图 6 不同程度的V形变形流场图 Fig.6 Flow field of V-shaped deformation with different degrees |
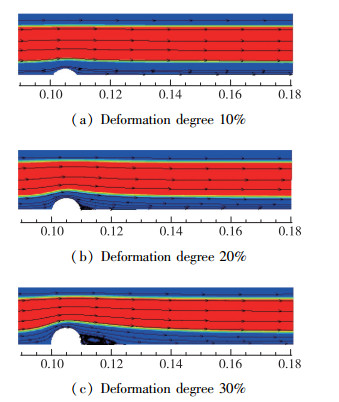
图 7为不同程度的O形结构流道变形的总压方图.对比图 7(a), (b), (c), 观察到管道结构发生○形凹陷, 随着凹陷程度的增加, 油相会被压缩得越小, 压缩的最小区域在最大凹陷深度点的正上方.根据漩涡流线图判断, 漩涡区域全部为水相, 不含油相, 且漩涡区域与油相区域相距较远, 如图 7(a)所示, 几乎没有漩涡产生; 如图 7(b)所示, 漩涡很小, 集中于漩涡中心距离最深凹陷点水平距离大概7 mm, 整个漩涡的长度大约为4 mm, 宽度为1.5 mm; 如图 7(c)所示, 漩涡中心距离最深凹陷点水平距离大概10 mm, 整个漩涡的长度大约为10 mm, 宽度为3 mm.对比图 6和图 7, 观察发现相同凹陷程度, V形的油相压缩区域比○形的油相压缩区域小, 主要产生原因是○形的结构变形, 流体可以附壁作用在管壁, 不会产生斜向上的流速, 经过该点的水平速率最大, 垂直方向速率最小, 因此压缩区域就在变形区域的正上方, 油相受到的挤压也就较小, 油相占用的区域较大, 环状流保持着稳定状态, 并能快速恢复到入口时的环状流形态.
|
| 图 7 不同程度的○形变形流场图 Fig.7 Flow field of ○-shaped deformation with different degrees |
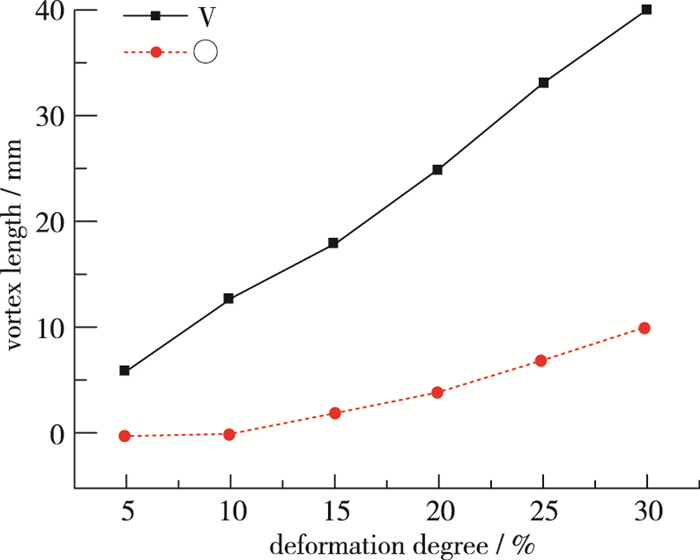
综合图 6和图 7, 在相同程度的结构变形中, V形产生的漩涡长度大于○形漩涡产生的长度, 如图 8所示, 漩涡长度与结构凹陷程度大致呈现一种线性关系, 且V形结构产生的漩涡长度增长率大于○形结构漩涡长度增长率.
|
| 图 8 不同凹陷结构中漩涡长度与凹陷程度的关系 Fig.8 Relationship between the length of vortex and the degree of deformation in different deformation structures |
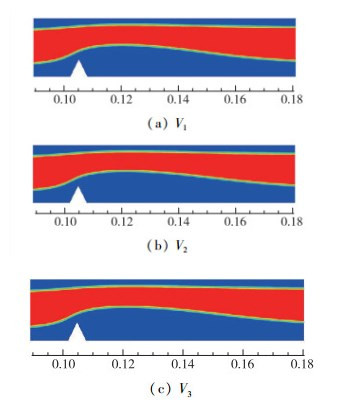
对比图 6和图 7可以得出凹陷程度相同情况下, V形变形比○形变形对环状流的影响更大, 此刻在V形凹陷程度达到30%时, 改变入口速率, 设定入口速度分别为V1, V2, V3.判断环状流流型是否仍然保持稳定.如图 9所示, 随着入口速度的增加, 环状流流型几乎没有发生改变, 初步可以判断在柔性管的水平段, 发生流道结构变形时, 速度差异对环状流的影响远小于流道结构变化对环状流产生的影响.
|
| 图 9 不同流速的V形变形流场图 Fig.9 Flow field of V-shaped deformation with different velocities |
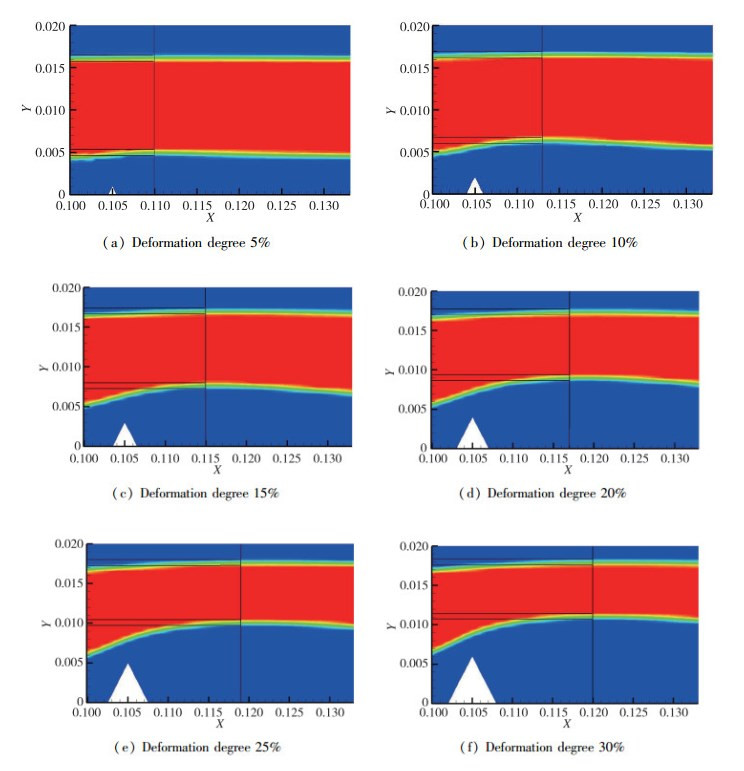
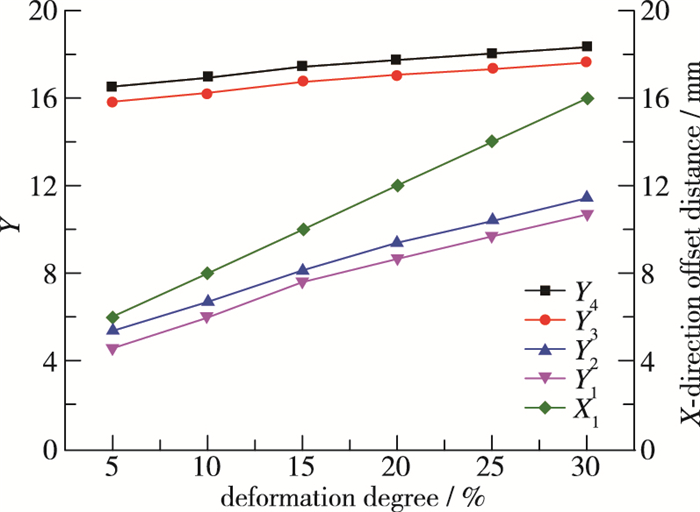
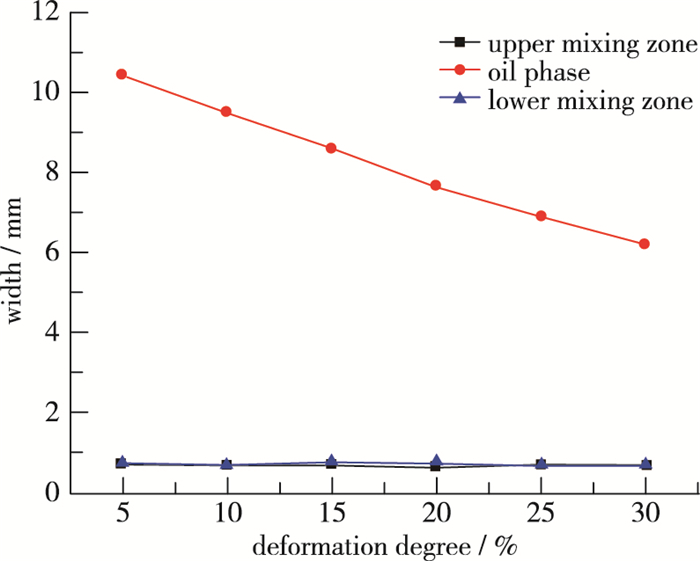
对比图 10(a)~(f),观察到管道结构发生V形凹陷, 随着凹陷程度的增加, 下层油水混合界面发生明显的上移, 油相区域明显受到挤压, 油相受到最大压缩区域也随之右移.由图 11(Y1为下层油水混合下边界, Y2为下层油水混合上边界, Y3为上层油水混合下边界, Y4为上层油水混合上边界 X1为最大凹陷深度点到油相最大压缩点的水平距离)具体的折线图可以发现, 随着凹陷程度的增加, 上层油水混合边界发生上移, 油环状流的上层水环受到挤压, 下层油水混合边界也同样发生上移, 但是下层混合边界上移距离明显大于上层边界移动距离, 这之间的差值就是油相流动界面被压缩的差额.如图 12所示, 随着凹陷程度的增加, 上下油水混合区域宽度几乎没有任何变化, 但油相的流动宽度发生明显改变, 凹陷程度小于20%时, 油相界面宽度呈线性关系减小, 凹陷程度大于20%时, 油水界面宽度的减少程度有所放缓.综合图 11和12, 可以得出在凹陷程度增加5%时(管径为20 mm, 5%即为1 mm), 下层油水混合边界上升不止1 mm.主要是因为凹陷程度增加, 流体斜向上的流速增加, 垂直于轴线方向上的流速会对流体进行挤压, 所以油水边界上升大于1 mm, 同样在挤压之后, 压强会增加, 增加相同程度的凹陷, 边界的移动距离将不断减小, 且仍大于增加的凹陷量.
|
| 图 10 不同凹陷程度的相图 Fig.10 Phase diagrams of different deformation degrees |
|
| 图 11 各相界面位置与凹陷程度的关系 Fig.11 Relationship between the interface position of each phase and the degree of deformation |
|
| 图 12 油相宽度与凹陷程度的关系 Fig.12 Relationship between oil phase width and deformation degree |
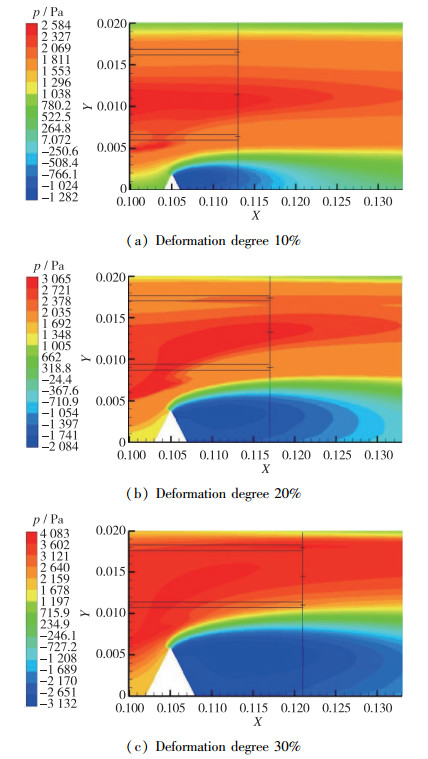
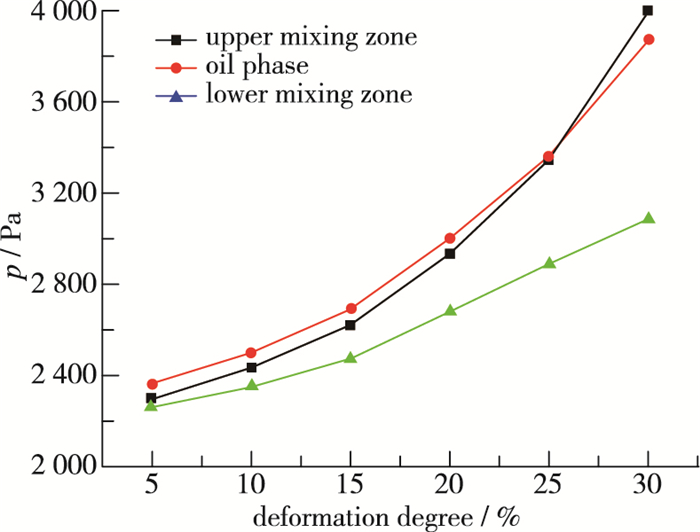
对比图 13(a), (b), (c),观察到管道结构发生V形凹陷, 随着凹陷程度的增加, 上层混合区, 油相, 下层混合区的压强也随之增加.压强集中区域首先出现在油相中间, 其次是上层混合区, 然后才是下层混合区.由图 14可以判断, 凹陷程度增加, 压强也随之增加, 且增加的强度越来越大, 对比上下层油水混合区, 上层的压强增长速度大于下层增长速度, 在凹陷程度大于25%之后, 上层油水混合区域的压强大于油相压强.综合图 11和图 14, 可以发现凹陷程度较大时, 油水混合区域能被压缩的范围已经很小了, 但是压强出现了较大的增幅.同时凹陷区域右侧出现较强的负压强, 在正负压差较大的情况下, 极易产生较大的漩涡和湍流, 因此在管道流体流动时要避免产生漩涡和湍流, 就须控制流道变形的程度及结构.
|
| 图 13 不同凹陷程度的压强云图 Fig.13 Pressure contours of different deformation degrees |
|
| 图 14 不同凹陷程度与压强之间的关系 Fig.14 Relationship between deformation degree and pressure |
(1) 探讨了湍动能和漩涡结构之间的关系, 漩涡产生于结构变形和湍动能中心点之间.凹陷程度越大, 产生湍动能越大, 导致的漩涡强度及面积也就越大.在同种凹陷程度下, 有棱角的V形凹陷产生影响远大于没有棱角的○形凹陷, 撞击引起的结构变形应当避免应力集中.
(2) V形结构变形产生的漩涡影响大于○形, 但是对于油水环状流的影响并不大, 流体通过结构变形区域之后仍能恢复油水环状流的稳定形态.
(3) 探讨油水界面的压强与凹陷程度的关系, 凹陷程度越大, 界面压强越大, 压强大小顺序依次是油相, 上层混合区, 下层混合区.
| [1] |
Cavicchio C A, Biazussi J L, De Castro M S, et al. Experimental study of viscosity effects on heavy crude oil-water core-annular flow pattern[J]. Experimental Thermal and Fluid Science, 2017, 92: 270-285. |
| [2] |
Vempati B, Panchagnula M V, Öztekin A, et al. Combined buoyancy and viscous effects in liquid-liquid flows in a vertical pipe[J]. Acta Mechanica, 2010, 210(1/2): 1-12. |
| [3] |
Dipin S P, Dinesh B, Sundararajan T, et al. A viscous potential flow model for core-annular flow[J]. Applied Mathematical Modelling, 2016, 40(7/8): 5044-5062. |
| [4] |
李家元, 梁长青, 张东敏, 等. 粘稠油水环输送的稳定性[J]. 油气储运, 1988, 7(6): 22-29. Li J Y, Liang C Q, Zhang D M, et al. The stability of transporting viscous oil in water ring[J]. Oil & Gas Storage and Transportation, 1988, 7(6): 22-29. (in Chinese) |
| [5] |
刘玉泉.剪切稀化流体二维流动的稳定性研究[D].北京: 清华大学, 2013. Liu Y Q. A study on the stability of two-dimensional flows of shear-thinning fluids[D]. Beijing: Tsinghua Univer-sity, 2013(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10003-1015007153.htm |
| [6] |
Sharma M, Ravi P, Ghosh S, et al. Studies on low viscous oil-water flow through return bends[J]. Experimental Thermal and Fluid Science, 2011, 35(3): 455-469. |
| [7] |
Jiang F, Wang Y J, Ou J J, et al. Numerical simulation on oil-water annular flow through the Π bend[J]. Indu-strial & Engineering Chemistry Research, 2014, 53(19): 8235-8244. |
| [8] |
Jiang F, Ke W, Skote M, et al. Simulation of non-Newtonian oil-water core annular flow through return bends[J]. Heat and Mass Transfer, 2018, 54(1): 37-48. |
| [9] |
Picardo J R, Pushpavanam S. Core-annular two-phase flow in a gently curved circular channel[J]. AIChE Journal, 2013, 59(12): 4871-4886. |
| [10] |
赵红艳, 敬加强. 探析环状流研究现状与进展[J]. 石化技术, 2015(2): 124-126. Zhao H Y, Jing J Q. Research and development of annular flow[J]. Petrochemical Industry Technology, 2015(2): 124-126. (in Chinese) |
| [11] |
于欢, 姜亚杰, 吴玉国. 稠油管道输送技术概述[J]. 当代化工, 2016, 45(1): 102-104, 108. Yu H, Jiang Y J, Wu Y G. Overview of heavy oil pipeline transportation technology[J]. Contemporary Che-mical Industry, 2016, 45(1): 102-104, 108. (in Chinese) |
| [12] |
江帆. 阀门开度对环状流结构的影响研究[J]. 流体机械, 2016, 44(11): 25-29. Jiang F. Study on the influence of opening angle on the core annular flow structure[J]. Fluid Machinery, 2016, 44(11): 25-29. (in Chinese) |
| [13] |
江帆, 岳鹏飞, 黎斯杰, 等. 高黏石油管道球阀内油水环状流数值模拟[J]. 油气储运, 2017, 36(7): 800-804, 815. Jiang F, Yue P F, Li S J, et al. Numerical simulation of oil-water annular flow inside the ball valve in high-pour-point oil pipeline[J]. Oil and Gas Storage and Transportation, 2017, 36(7): 800-804, 815. (in Chinese) |
| [14] |
杨政龙, 余建星, 陈海成, 等. 深海管道在冲击载荷作用下的局部屈曲特性研究[J]. 天津大学学报(自然科学与工程技术版), 2019, 52(3): 255-261. Yang Z L, Yu J X, Chen H C, et al. Local buckling characteristics of deep-sea pipelines under impact loading[J]. Journal of Tianjin University (Science and Technology), 2019, 52(3): 255-261. (in Chinese) |
| [15] |
杨秀娟, 闫涛, 修宗祥, 等. 海底管道受坠物撞击时的弹塑性有限元分析[J]. 工程力学, 2011, 28(6): 189-194. Yang X J, Yan T, Xiu Z X, et al. Elastic-plastic finite element analysis of submarine pipeline impacted by falling objects[J]. Engineering Mechanics, 2011, 28(6): 189-194. (in Chinese) |
| [16] |
岳鹏飞.阀门开度对油水环状流的影响研究[D].广州: 广州大学, 2016. Yue P F. Study on influence of valve opening on oil-water annular flow[D]. Guangzhou: Guangzhou University, 2016(in Chinese). |



