有限差分法(finite difference method, FDM)经典理论建立在Descartes直角坐标系下, 构建差分格式时考虑一维空间的模型方程.然而, 实际工程问题几乎都是三维的, 而且绝大多数流场构型复杂, 采用直角网格难以准确描述物理空间和满足计算边界条件, 应用中通常采用数学方法变换到与物体形状相吻合的贴体坐标系(body-fitted coordin-ates, BFC)后再进行有限差分格式离散.例如, Descartes坐标系(t, x, y, z)下的三维守恒型Euler方程为
| $ \frac{\partial U}{\partial t}+\frac{\partial F}{\partial x}+\frac{\partial G}{\partial y}+\frac{\partial H}{\partial z}=0 $ | (1) |
应用到复杂构型流场后通过坐标变换把不规则的曲线映射成计算空间(τ, ξ, η, ζ)上的直线, 实际格式离散方程为
| $ \frac{\partial \hat{U}}{\partial \tau }+\frac{\partial \hat{F}}{\partial \xi }+\frac{\partial \hat{G}}{\partial \eta }+\frac{\partial \hat{H}}{\partial \zeta }=0 $ | (2) |
以上是计算流体力学教科书中关于BFC的经典论述.本文对坐标变换推导过程分析以后发现, 在空间离散条件下两个方程不等价, 目前CFD采用方程(2)作为方程(1)在BFC下的等价形式进行编程存在模型误差, 在此认识基础上, 推导出方程(1)的等价控制方程形式及其离散相容性要求, 最后给出一种算法.
本文对普遍应用的CFD经典理论提出争议, 调研了国内相关航空航天院校采用的教材和经典教科书[1-4], 还没有看到类似的观点.
1 贴体坐标系的离散近似方程和离散等价方程由于本文是对现有结论的争议, 为便于理解和表达, 首先采用空间二维标量模型进行细致推导. Descartes坐标系(t, x, y)下的模型方程为
| $ \frac{\partial u}{\partial t}+\frac{\partial f}{\partial x}+\frac{\partial g}{\partial y}=0 $ | (3) |
其中,u为守恒变量, f和g为对流通量.采用如下坐标变换函数及其反函数
| $ \left\{ \begin{array}{l} t = t\left( {\tau ,\xi ,\eta } \right)\\ x = x\left( {\tau ,\xi ,\eta } \right)\\ y = y\left( {\tau ,\xi ,\eta } \right) \end{array} \right.,\left\{ \begin{array}{l} \tau = \tau \left( {t,x,y} \right)\\ \xi = \xi \left( {t,x,y} \right)\\ \eta = \eta \left( {t,x,y} \right) \end{array} \right. $ |
可得
| $ \begin{align} &\frac{\partial u}{\partial \tau }+{{\xi }_{t}}\frac{\partial u}{\partial \xi }+{{\eta }_{t}}\frac{\partial u}{\partial \eta }+{{\xi }_{x}}\frac{\partial f}{\partial \xi }+{{\eta }_{x}}\frac{\partial f}{\partial \eta }+{{\xi }_{y}}\frac{\partial g}{\partial \xi }+ \\ &\ \ \ {{\eta }_{y}}\frac{\partial g}{\partial \eta }=0 \\ \end{align} $ | (4) |
这是原始方程(3)在计算坐标系(τ, ξ, η)下的非守恒形式, 后面有算例可以验证, 以此为基础离散对流通量会产生非物理解, 须将上式转化为守恒形式.方程乘以Jacobi行列式J-1=|∂(x, y)/∂(ξ, η)|, 利用如下偏导数关系式(实际用到6个, 仅给出1个)
| $ \left( \frac{{{\xi }_{x}}}{J} \right)\frac{\partial f}{\partial \xi }=\frac{\partial }{\partial \xi }\left( \frac{{{\xi }_{x}}f}{J} \right)-f\frac{\partial }{\partial \xi }\left( \frac{{{\xi }_{x}}}{J} \right) $ | (5) |
则方程(4)变为
| $ \begin{align} &\frac{\partial }{\partial \tau }\left( {{J}^{-1}}u \right)+\frac{\partial }{\partial \xi }\left( {{J}^{-1}}u{{\xi }_{t}}+{{J}^{-1}}f{{\xi }_{x}}+{{J}^{-1}}g{{\xi }_{y}} \right)+ \\ &\quad \quad \quad \quad \quad \frac{\partial }{\partial \eta }\left( {{J}^{-1}}u{{\eta }_{t}}+{{J}^{-1}}f{{\eta }_{x}}+{{J}^{-1}}g{{\eta }_{y}} \right)=u\frac{\partial {{J}^{-1}}}{\partial \tau }+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ u\frac{\partial }{\partial \xi }\left( {{J}^{-1}}{{\xi }_{t}} \right)+u\frac{\partial }{\partial \eta }\left( {{J}^{-1}}{{\eta }_{t}} \right)+\ f\frac{\partial }{\partial \xi }\left( {{J}^{-1}}{{\xi }_{x}} \right)+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ g\frac{\partial }{\partial \xi }\left( {{J}^{-1}}{{\xi }_{y}} \right)+\ f\frac{\partial }{\partial \eta }\left( {{J}^{-1}}{{\eta }_{x}} \right)+g\frac{\partial }{\partial \eta }\left( {{J}^{-1}}{{\eta }_{y}} \right) \\ \end{align} $ |
如下中间变量称为BFC中的守恒变量和对流通量
| $ \left\{ \begin{align} &\hat{u}={{J}^{-1}}u \\ &\hat{f}={{J}^{-1}}u{{\xi }_{t}}+{{J}^{-1}}f{{\xi }_{x}}+{{J}^{-1}}g{{\xi }_{y}} \\ &\hat{g}={{J}^{-1}}u{{\eta }_{t}}+{{J}^{-1}}f{{\eta }_{x}}+{{J}^{-1}}g{{\eta }_{y}} \\ \end{align} \right. $ |
整理后得到
| $ \frac{\partial \hat{u}}{\partial \tau }+\frac{\partial \hat{f}}{\partial \xi }+\frac{\partial \hat{g}}{\partial \eta }=\left( u{{I}_{t}}+f{{I}_{x}}+g{{I}_{y}} \right) $ | (6) |
这是控制方程在计算坐标系(τ, ξ, η)下守恒型的完整形式, 与原始方程相比变成非齐次方程, 为便于讨论, 将源项记为S=uIt+fIx+gIy, 其中
| $ \begin{align} &{{I}_{t}}=\frac{\partial }{\partial \tau }\left( \frac{\text{1}}{J} \right)+\frac{\partial }{\partial \xi }\left( \frac{{{\xi }_{t}}}{{{J}^{{}}}} \right)+\frac{\partial }{\partial \eta }\left( \frac{{{\eta }_{t}}}{{{J}^{{}}}} \right) \\ &\ \ \, \, =\frac{\partial }{\partial \tau }\left( \frac{\text{1}}{J} \right)+\frac{\partial }{\partial \xi }\left( {{{\hat{\xi }}}_{t}} \right)+\frac{\partial }{\partial \eta }\left( {{{\hat{\eta }}}_{t}} \right) \\ &{{I}_{x}}=\frac{\partial }{\partial \xi }\left( \frac{{{\xi }_{x}}}{J} \right)+\frac{\partial }{\partial \eta }\left( \frac{{{\eta }_{x}}}{J} \right)\, =\frac{\partial }{\partial \xi }\left( {{{\hat{\xi }}}_{x}} \right)+\frac{\partial }{\partial \eta }\left( {{{\hat{\eta }}}_{x}} \right) \\ &{{I}_{y}}=\frac{\partial }{\partial \xi }\left( \frac{{{\xi }_{y}}}{J} \right)+\frac{\partial }{\partial \eta }\left( \frac{{{\eta }_{y}}}{J} \right)\, =\frac{\partial }{\partial \xi }\left( {{{\hat{\xi }}}_{y}} \right)+\frac{\partial }{\partial \eta }\left( {{{\hat{\eta }}}_{y}} \right) \\ \end{align} $ | (7) |
作为初步研究, 下面仅讨论静止网格(It=0)中的定常流动.如果坐标变换函数空间导数连续, 那么Ix=0, Iy=0恒成立, 源项S=0, 因此得到目前CFD领域在BFC中作为编程基础的方程形式
| $ \frac{\partial \hat{u}}{\partial \tau }+\frac{\partial \hat{f}}{\partial \xi }+\frac{\partial \hat{g}}{\partial \eta }=0 $ | (8) |
如果坐标变换函数已知, 方程(8)中用到的坐标变换系数和Jacobi行列式J计算如下
| $ \begin{array}{l} \left\{ \begin{array}{l} {{\hat \xi }_x} = {J^{ - 1}}{\xi _x} = {y_\eta }\\ {{\hat \xi }_y} = {J^{ - 1}}{\xi _y} = - {x_\eta } \end{array} \right.\quad \left\{ \begin{array}{l} {{\hat \eta }_x} = {J^{ - 1}}{\eta _x} = - {y_\xi }\\ {{\hat \eta }_y} = {J^{ - 1}}{\eta _y} = {x_\xi } \end{array} \right.\quad \\ J = \left| {\frac{{\partial (x,y)}}{{\partial (\xi ,\eta )}}} \right| = \left( {{x_\xi }{y_\eta } - {x_\eta }{y_\xi }} \right) \end{array} $ |
但是, BFC的网格常采用软件生成, 给出包含相邻关系信息的空间离散点集来描述两个坐标系之间的映射关系,
由于S≠0是坐标离散以后出现的, 后面把含有源项的方程称为离散等价方程, CFD领域常用的齐次方程称为离散近似方程.
2 离散空间的源项及其对流场的影响基于分辨S中Ix和Iy影响的考虑, 取如下坐标变换函数, 这样在整个计算区域内有
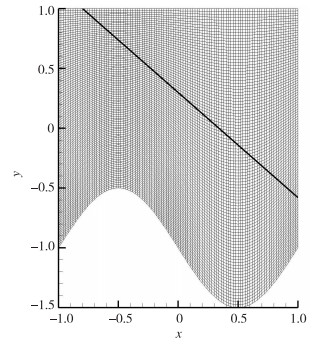
|
| 图 1 计算区域及网格点坐标 Fig.1 Computational grids |
| $ \left\{ \begin{align} &x(\xi , \eta )=-1+0.02\xi , \\ &y(\xi , \eta )=-1+0.005(100-\eta )\sin (0.02\text{ }\!\!\pi\!\!\text{ }\xi )+0.02\eta \\ &0\le \xi \le 100, \ 0\le \eta \le 100 \\ \end{align} \right. $ |
为便于表述, 以上ξx等系数的离散计算称为差商, 空间导数∂/∂ξ和∂/∂η的离散计算称为格式.
首先, 根据已知网格点坐标值, 分别采用3点2阶中心差分和5点4阶中心差分计算差商, 以ηx为例, 数值解记为ηx(2)和ηx(4), 理论解记为ηx(T).为消除边界影响并保证算法的统一性, 选择离开边界4排网格点的区域进行数据分析, 绝对误差的最大值σmax和平均值σave如表 1所示, 4阶差商精度更高, 符合理论预期.其他系数也是同样规律, 在此不再具体给出.
| 下载CSV 表 1 不同差商计算的ηx与解析值的比较 Tab.1 Errors of ηx in various difference quotients compared with theory results |
除Ix和Iy, S还受对流通量F和G的影响, 构建如下流场模型:平行于x轴、Ma∞=2的超声速来流中在x=-0.8, y=1.0位置有入射角β=41°的斜激波, 激波理论位置见图 1中斜线, 激波前无量纲参数为(ρ, u, v, p)=(1,
对于二维Euler方程, S的形式和式(6)类似, 不过有4个元素(S1,S2,S3,S4).在以下计算中F和G直接代入理论值, 采用3种格式离散Ix,Iy中的空间导数∂/∂ξ和∂/∂η, 数据分析时同样选择离开边界4排网格点的区域以便消除边界影响.导数和差商组合后共9种情况, 因为微分形式下的S为0, 所以此时计算得到的S本身就是离散误差, 其平均值如表 2所示.
| 下载CSV 表 2 不同计算格式的源项比较 Tab.2 Source values of different schemes |
可看出4个元素的变化规律一致.选择第1个元素S1=ρuIx+ρvIy进行分析, S1流场空间分布如图 2所示, 可以看出除激波附近, S1沿纵向基本没有变化, 这和所设计的网格有关.对图 1所示网格, Iy为0, 因此只须分析Ix则可确定原因.其中当差商采用2阶中心计算, 格式也采用2阶中心计算时, Ix的计算公式为
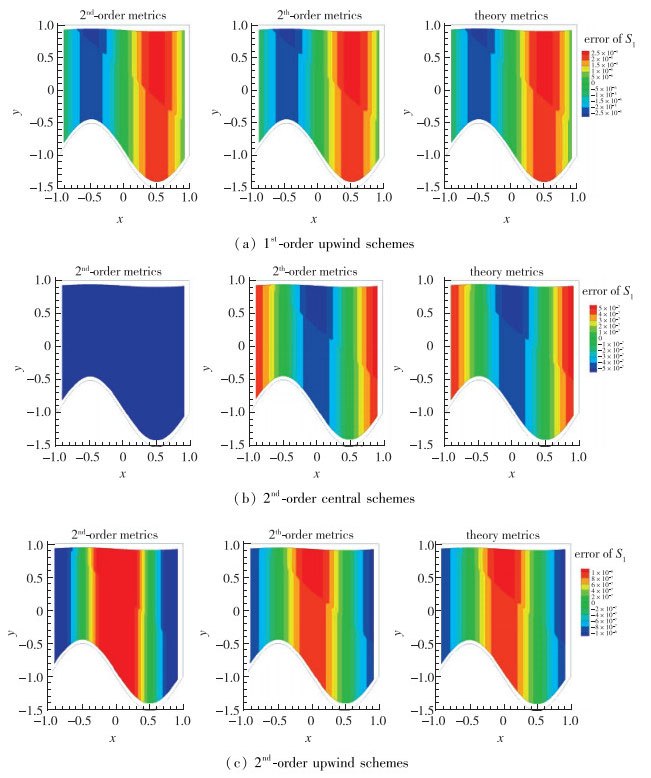
|
| 图 2 无量纲S1分布云图 Fig.2 Value distributions of the dimensionless S1 |
| $ \begin{align} &{{I}_{x}}=\frac{\partial }{\partial \xi }\left( {{{\hat{\xi }}}_{x}} \right)+\frac{\partial }{\partial \eta }\left( {{{\hat{\eta }}}_{x}} \right)=\frac{{{\left( {{{\hat{\xi }}}_{x}} \right)}_{i+1}}-{{\left( {{{\hat{\xi }}}_{x}} \right)}_{i-1}}}{2\Delta \xi }+\frac{{{\left( {{{\hat{\eta }}}_{x}} \right)}_{j+1}}-{{\left( {{{\hat{\eta }}}_{x}} \right)}_{j-1}}}{2\Delta \eta }= \\ &\frac{{{\left( {{y}_{\eta }} \right)}_{i+1}}-{{\left( {{y}_{\eta }} \right)}_{i-1}}}{2\Delta \xi }+ \frac{{{\left( -{{y}_{\xi }} \right)}_{j+1}}-{{\left( -{{y}_{\xi }} \right)}_{j-1}}}{2\Delta \eta }=\frac{{{y}_{i+1, j+1}}-{{y}_{i+1, j-1}}}{4\Delta \xi \Delta \eta }\\ &-\frac{{{y}_{i-1, j+1}}-{{y}_{i-1, j-1}}}{4\Delta \xi \Delta \eta }- \quad \quad \frac{{{y}_{i+1, j+1}}-{{y}_{i-1, j+1}}}{4\Delta \xi \Delta \eta }+\frac{{{y}_{i+1, j-1}}-{{y}_{i-1, j-1}}}{4\Delta \xi \Delta \eta }=0 \\ \end{align} $ | (9) |
可以看出, 这是系数差商和导数格式组合产生S=0的特殊情况, 除此之外, 即使差商采用理论值, 离散Ix时也会出现误差, 符合理论分析.
表 2和图 2表明, 格式和差商对S的影响如下: (1)格式影响比差商大, 随着格式精度增加误差减小, 其中中心型格式的误差又比迎风型格式误差小; (2)相同格式不同差商的S在同一量级, 差商离散对S无明显规律性; (3)除了过激波跳跃外, 沿y方向参数变化很小.
2.2 源项对数值解的影响除了特殊组合, 在离散空间上S≠0, 离散近似方程没有考虑这种情况, 以上推导过程已经证明S是离散近似方程相对于原始方程产生的误差, 下面来考察S≠0对流场的影响.
基于以下理由选择1阶迎风格式:
(1) 干净, 其他能稳定捕捉激波的高阶格式均须使用限制器或调整模板, 难以写出具体网格点上的计算格式, 不便于后续分析.
(2) 稳定, 没有更稳定的空间格式, 其他格式不可能消除这一格式出现的数值异常现象.
(3) 误差, 这是截断误差最大的格式, 如果它不能掩盖源项影响, 其他格式更明显.
(4) 区别, 目前国内外消除几何离散引入误差的几何守恒律研究是针对高精度格式, 本文反其道而行之, 选择精度最低的格式以示不同.
通量分裂采用Van Leer格式, 离散等价方程和离散近似方程的左端对流项采用1阶迎风格式
| $ \begin{align} &\hat{U}_{i, j}^{n+1}=\hat{U}_{i, j}^{n}-\Delta \tau \left[ \left( \hat{F}_{i, j}^{+}-\hat{F}_{i-1, j}^{+} \right)+\left( \hat{F}_{i+1, j}^{-}-\hat{F}_{i, j}^{-} \right) \right.+ \\ &\left. \quad \quad \left( \hat{G}_{i, j}^{+}-\hat{G}_{i, j-1}^{+} \right)+\left( \hat{G}_{i, j+1}^{-}-\hat{G}_{i, j}^{-} \right) \right]+\alpha \Delta \tau S \\ \end{align} $ | (10) |
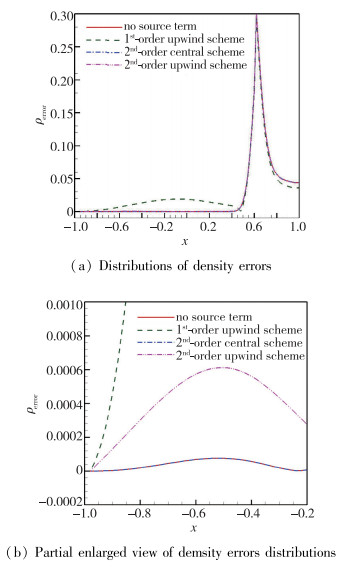
离散近似方程没有源项, α=0, 计算中系数采用不同差商得到的数值解记为U0(2), U0(4)和U0(T), 离散等价方程α=1, 源项有9种组合, 得到数值解记为Ui(2), Ui(4)和Ui(T)(i=1, 2, 3), 共计12个流场.由于激波前后参数变化剧烈, 所有工况流场参数看不出明显差异.将数值解与理论值相减得到误差, 以2阶差商为例, 没有源项的U0(2)对应的密度误差分布如图 3(a)所示, 有源项的以U1(2)为例, 对应的密度误差分布如图 3(b)所示, 两者差别并不大, 结合表 2量级比较, 两个方程数值解的差异完全淹没在格式捕捉激波过程中出现的误差之中.
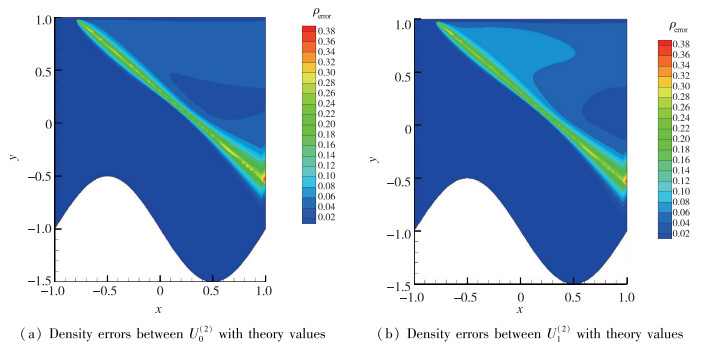
|
| 图 3 S=0和S≠0时流场密度误差云图 Fig.3 Distributions of density errors |
考虑到本文关注的是S≠0引起的数值解差异, 采用直接比较办法, 以目前CFD编程出发的离散近似方程为参考, 选择密度差|ρin-ρ0n |进行考察, 云图分布如图 4所示, 可以明显看出S≠0对流场的影响.对照前面S大小的信息, 有相似的规律: (1)格式精度增加差异减小, 其中采用2阶中心格式计算得到的差异最小; (2)相同格式不同差商差异变化不明显.但是, S大小分布规律和它对流场的影响有明显的差异: (1)有流场以后沿y向有明显变化; (2)S最大区域不在激波过渡区.
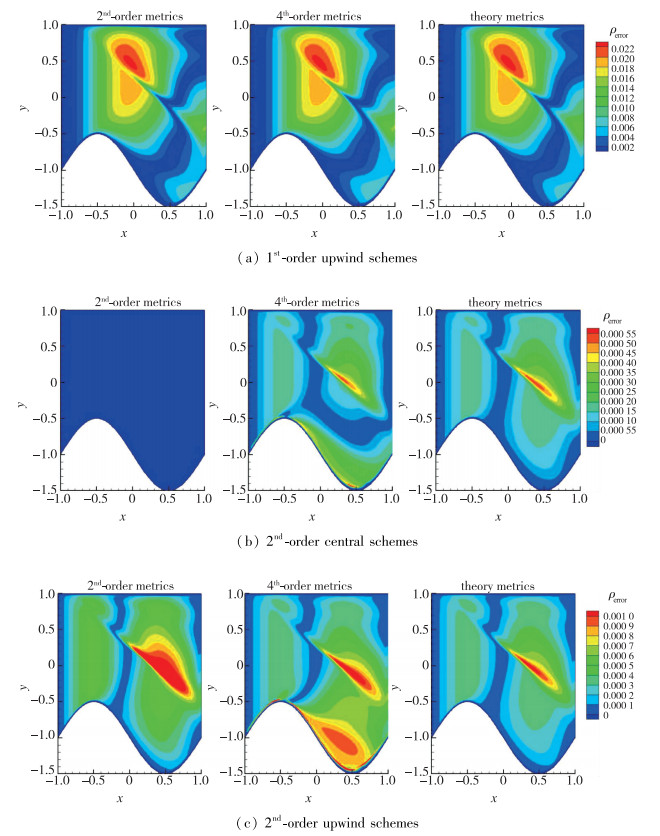
|
| 图 4 密度差的分布云图 Fig.4 Error distributions of density |
由上节数值实验可得出如下结论:在BFC离散空间中大部分情况下S≠0, 这时引起数值解的变化远大于离散格式的精度误差, 但是无法说明离散等价方程和离散近似方程数值解的精度.进一步选择U0(2)及其对应的3种格式, 从(-1, 0)点发出的横向网格线上, 计算值与理论值的误差及其在激波前的局部放大如图 5所示.令人意外的是, 尽管S=0两个算例没有差异, 但在均匀流区域误差也不为0.在程序中追踪误差来源, 发现有两个原因: (1)根据超声速流动迎风特性x方向只有
|
| 图 5 横向网格线上数值解与理论值的误差 Fig.5 Density errors on the line of J=50 |
回顾之前所述的坐标变换, 源项是在方程由非守恒型式到守恒型式变换过程中才出现的, 其中使用了偏导数恒等式(5).上面实际计算中源项中的∂(
按照相容性原则, 离散等价方程的1阶迎风格式应该写成如下形式
| $ \begin{align} &\hat{U}_{i, j}^{n+1}=\hat{U}_{i, j}^{n}-\Delta \tau \left[ \left( \hat{F}_{i, j}^{+}-\hat{F}_{i-1, j}^{+} \right)+\left( \hat{F}_{i+1, j}^{-}-\hat{F}_{i, j}^{-} \right) \right.+ \\ &\quad \quad \quad \quad \quad \quad \quad \left. \left( \hat{G}_{i, j}^{+}-\hat{G}_{i, j-1}^{+} \right)+\left( \hat{G}_{i, j+1}^{-}-\hat{G}_{i, j}^{-} \right) \right]+ \\ &\quad \quad \quad \quad \Delta \tau F_{ij}^{+}\left[ \left( {{\left. {{{\hat{\xi }}}_{x}} \right|}_{i, j}}-{{\left. {{{\hat{\xi }}}_{x}} \right|}_{i-1, j}} \right)+\left( {{\left. {{{\hat{\eta }}}_{y}} \right|}_{i, j}}-{{\left. {{{\hat{\eta }}}_{y}} \right|}_{i, j-1}} \right) \right]+ \\ &\quad \quad \quad \quad \Delta \tau F_{ij}^{-}\left[ \left( {{\left. {{{\hat{\xi }}}_{x}} \right|}_{i+1, j}}-{{\left. {{{\hat{\xi }}}_{x}} \right|}_{i, j}} \right)+\left( {{\left. {{{\hat{\eta }}}_{x}} \right|}_{i, j+1}}-{{\left. {{{\hat{\eta }}}_{x}} \right|}_{i, j}} \right) \right]+ \\ &\quad \quad \quad \quad \Delta \tau G_{ij}^{+}\left[ \left( {{\left. {{{\hat{\xi }}}_{y}} \right|}_{i, j}}-{{\left. {{{\hat{\xi }}}_{y}} \right|}_{i-1, j}} \right)+\left( {{\left. {{{\hat{\eta }}}_{x}} \right|}_{i, j}}-{{\left. {{{\hat{\eta }}}_{x}} \right|}_{i, j-1}} \right) \right]+ \\ &\quad \quad \quad \quad \Delta \tau G_{ij}^{-}\left[ \left( {{\left. {{{\hat{\xi }}}_{y}} \right|}_{i+1, j}}-{{\left. {{{\hat{\xi }}}_{y}} \right|}_{i, j}} \right)+\left( {{\left. {{{\hat{\eta }}}_{y}} \right|}_{i, j+1}}-{{\left. {{{\hat{\eta }}}_{y}} \right|}_{i, j}} \right) \right] \\ \end{align} $ | (11) |
原则上匹配以后, 对于图 1所示网格
| $ \left( \hat{F}_{i, j}^{+}-\hat{F}_{i-1, j}^{+} \right)=F_{i, j}^{+}\left( {{\left. {{{\hat{\xi }}}_{x}} \right|}_{i, j}}-{{\left. {{{\hat{\xi }}}_{x}} \right|}_{i-1, j}} \right) $ |
由于Van Leer通量分裂格式同时受流场参数和坐标变换系数影响, 实际计算中发现通量和坐标变换系数的比值不是源项中的流动参数, 即
| $ \frac{\left( \hat{F}_{i, j}^{+}-\hat{F}_{i-1, j}^{+} \right)}{\left( {{\left. {{{\hat{\xi }}}_{x}} \right|}_{i, j}}-{{\left. {{{\hat{\xi }}}_{x}} \right|}_{i-1, j}} \right)}=\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{F}_{i, j}^{+}\ne F_{i, j}^{+} $ |
显然按照以上计算出
引入符号
| $ \hat{F}=\left[ F, G \right]\cdot {{\left[ {{{\hat{\xi }}}_{x}}, {{{\hat{\xi }}}_{y}} \right]}^{\text{T}}}=\mathit{\Phi }\cdot {{\mathit{\Gamma }}^{\text{T}}}\hat{G}=\mathit{\Phi }\cdot {{\mathit{\Pi }}^{\text{T}}} $ | (12) |
源项表示为
| $ S=F{{I}_{x}}+G{{I}_{y}}=\mathit{\Phi }\cdot {{\left( \frac{\partial \mathit{\Gamma }}{\partial \xi } \right)}^{\text{T}}}+\mathit{\Phi }\cdot {{\left( \frac{\partial \mathit{\Pi }}{\partial \eta } \right)}^{\text{T}}} $ | (13) |
在连续空间求导数, 得到如下关系式
| $ \begin{align} &\frac{\partial \hat{F}}{\partial \xi }=\mathit{\Phi }\cdot {{\left( \frac{\partial \mathit{\Gamma }}{\partial \xi } \right)}^{\text{T}}}+\frac{\partial \mathit{\Phi }}{\partial \xi }\cdot {{\mathit{\Gamma }}^{\text{T}}} \\ &\frac{\partial \hat{G}}{\partial \eta }=\mathit{\Phi }\cdot {{\left( \frac{\partial \mathit{\Pi }}{\partial \eta } \right)}^{\text{T}}}+\frac{\partial \mathit{\Phi }}{\partial \eta }\cdot {{\mathit{\Pi }}^{\text{T}}} \\ \end{align} $ |
如果采用相同格式离散上式和源项式(13)中导数, 采用离散算子δ1表示为
| $ \begin{align} &{{\delta }^{1}}\hat{F}=\mathit{\Phi }\cdot {{\left( {{\delta }^{1}}\mathit{\Gamma } \right)}^{\text{T}}}+\left( {{\delta }^{1}}\mathit{\Phi } \right)\cdot {{\mathit{\Gamma }}^{\text{T}}} \\ &{{\delta }^{1}}\hat{G}=\mathit{\Phi }\cdot {{\left( {{\delta }^{1}}\mathit{\Pi } \right)}^{\text{T}}}+\left( {{\delta }^{1}}\mathit{\Phi } \right)\cdot {{\mathit{\Pi }}^{\text{T}}} \\ &S=\mathit{\Phi }\cdot {{\left( {{\delta }^{1}}\mathit{\Gamma } \right)}^{\text{T}}}+\Phi \cdot {{\left( {{\delta }^{1}}\mathit{\Pi } \right)}^{\text{T}}} \\ \end{align} $ |
代入得到考虑空间离散的半离散形式
| $ \frac{\partial \hat{U}}{\partial \tau }+\left( {{\delta }^{1}}\mathit{\Phi } \right)\cdot {{\mathit{\Gamma }}^{\text{T}}}+\left( {{\delta }^{1}}\mathit{\Phi } \right)\cdot {{\mathit{\Pi }}^{\text{T}}}=0 $ | (14) |
这样一来, 虽然是从离散等价方程出发, 但是
| $ \frac{\partial \hat{U}}{\partial \tau }+{{\delta }^{1}}\left( \mathit{\Phi }\cdot \mathit{\Gamma }_{i, j}^{\text{T}} \right)+{{\delta }^{1}}\left( \mathit{\Phi }\cdot \mathit{\Pi }_{i, j}^{\text{T}} \right)=0 $ |
引入符号
| $ \begin{align} &\hat{U}_{i, j}^{n+1}=\hat{U}_{i, j}^{n}-\Delta \tau \left[ \left( \hat{F}_{i, j}^{+}-\tilde{F}_{i-1, j}^{+} \right)+\left( \tilde{F}_{i+1, j}^{-}-\hat{F}_{i, j}^{-} \right) \right.+ \\ &\left. \ \ \ \ \ \ \ \ \ \ \left( \hat{G}_{i, j}^{+}-\tilde{G}_{i, j-1}^{+} \right)+\left( \tilde{G}_{i, j+1}^{-}-\hat{G}_{i, j}^{-} \right) \right] \\ \end{align} $ | (15) |
和式(10)相比, 式(15)的形式等价于在“冻结”系数Γn, mT=ΓijT+O(Δx, Δy)以后, α=0的齐次离散近似方程, 按照目前CFD教科书观点,不论δ1空间精度多少, 总精度只有1阶, 但从推导过程可知它是从α≠0离散等价方程出发, 通过符号
守恒型方程计算经常须采用通量分裂格式, 系数Γ和Π在分裂格式中不一定满足以上线性关系式(12), 如前面算例的
尽管算子δ1可以对应任意格式, 但是本文基于下述理由没有选择高精度格式: (1)前面推导和算例表明高精度格式不能保证S=0, 即依靠格式不能把离散近似方程改变成离散等价方程; (2)在S≠0情况下误差最大的1阶精度无法掩盖其影响, 高精度格式更是不可能消除; (3)高精度格式的模板调整和限制器选择与流场有关, 在激波等参数剧烈变化的区域无法区分出BFC的影响.
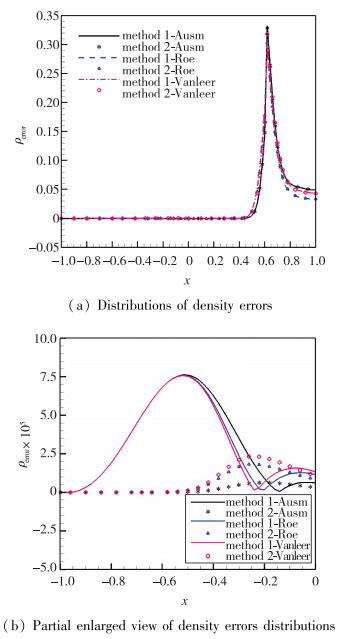
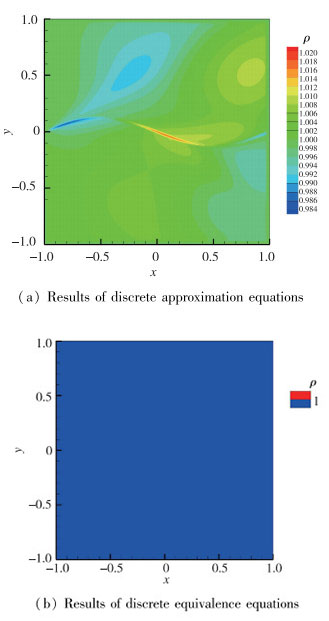
系数选择2阶差商, 离散近似方程采用式(10)计算, 记为方法1;离散等价方程采用式(15)计算, 记为方法2.给出从(-1, 0)点发出的横向网格线上数值解与理论值的误差分布及其局部放大如图 6所示, 查看数据发现在x < -0.5区域采用离散等价方程计算得到的误差远小于采用离散近似方程计算得到的误差, 由此看来, 离散等价方程在捕捉激波方面没有改善, 但在激波影响区域以外明显提高了精度.对于没有激波的均匀流场, 选取来流Mach数Ma∞=2.0, 分别采用离散近似方程及离散等价方程进行数值模拟, 计算网格如图 7所示, 其y方向中心线是一条振幅为0.125的正弦曲线, 网格数100×100, 空间离散采用1阶迎风格式, 时间离散采用1阶显示推进, 对流通量分裂采用Roe格式, 输出时间T=5.0, 图 8是数值模拟密度分布云图.由图 8可以看出, 采用离散近似方程得到的结果是均匀流场不再保持均匀性, 其误差主要集中在网格变化最大的正弦曲线附近, 而离散等价方程则完全能消除BFC引起的误差, 保持流场不变.
|
| 图 6 横向网格线上的密度误差曲线 Fig.6 Density errors on the line of J=50 |
|
| 图 7 均匀流场计算网格 Fig.7 Computational grids for uniform flow |
|
| 图 8 均匀流场的数值模拟密度分布云图 Fig.8 Density distributions of uniform flow |
如何在BFC中保持均匀流场的均匀特性是几何守恒律(geometric conservation law, GCL)关注的研究内容.早在1961年, Trulio等[6]就在其报告中提出了一维问题中的“体积守恒(conservation of volume)”概念. 1978年, Steger[7-8]和Pulliam等[9]在采用守恒型控制方程计算任意几何外形流动时发现并提出了几何守恒律问题.随后, Thomas等[10-11]在Steger和Pulliam的研究基础上提出了守恒型的坐标变换系数计算方法, 并正式提出了“GCL”这一概念, 被后来者广泛引用.随着高阶精度格式的发展与应用, Gaitonde等[12]和Visbal等[13]将Thomas等的方法推广到了紧致格式(compact schemes,CS)中. Nonomura等[14]又推广到加权紧致非线性格式(weighted compact nonlinear schemes,WCNS)[15]格式中并对有限差分格式中运动网格的GCL进行了研究[16-17].此外, Nonomura等[14]还对有限差分格式框架下的WENO格式[18]进行了研究, 发现WENO格式难以满足几何守恒律, 为适应复杂流场的数值模拟, 须对WENO格式进行改造. 2011年, Deng等给出并证明了满足GCL的充分条件—CMM(conservative metric method)[19]条件, 并于2013年提出了坐标变换系数计算结果唯一的对称守恒算法(symmetrical conservative metric method, SCMM)[20-21].近些年来, 国内外学者对GCL的研究主要集中在WENO格式, 朱志斌等[22]及Nonomura等[23]将WENO格式分解为中心差分部分及数值耗散部分, 中心差分部分采用守恒形式计算并将耗散部分的网格坐标变换系数固化为当地半节点值, 建立了满足GCL的WENO格式. Zhu等[24]通过适当的离散坐标变换系数来补偿因GCL产生的误差进而保持WENO格式的均匀流特性.
通过和以上有关有限差分格式的几何守恒律研究文献比较, 本文的差异主要体现在如下几点:
(1) 出发方程:几何守恒律的出发方程依然是离散近似方程, 不涉及源项.本文建立的线性算法尽管没有显示源项, 但是它是基于离散等价方程推导出来的, 冻结坐标变换系数不是线化近似而是体现源项的影响.
(2) 算法机理:几何守恒律耦合考虑坐标变换系数差商和对流项导数格式来建立算法, 原则上,格式不同对应的差商不同, 因此, 目前研究成果主要集中在紧致类格式, 对目前广泛使用的如TVD,NND,ENO,WENO等包含限制器的格式还较为困难.本文的线性算法解耦差商和格式, 推导中导数离散采用算子表示, 原则上适合于任意格式.
(3) 格式精度:理论上格式采用高精度以后, 差商计算也须提高精度, 才能在BFC中达到格式的精度, 这也是近年来兴起几何守恒律研究的原因, 对于应用了几十年的2阶精度格式很少提及.本文的理论和算例都表明即使1阶精度格式也难以掩盖两个方程引起的差异.
(4) 空间维数:以上看到文献的几何守恒律针对三维空间条件下坐标变换系数差商计算的相容性, 其问题本质是四边形面积和六面体体积的计算方法不唯一, 在二维空间中有些问题不存在, 所建立的算法中不再需要.
5.2 方程形式本文耦合算法的半离散形式(14)本质上就是前面推导中非守恒型方程的离散形式, 但是从非守恒型方程出发建立程序会出现非物理解, 由于篇幅关系这里仅提供本文作者经历过的算例来说明.
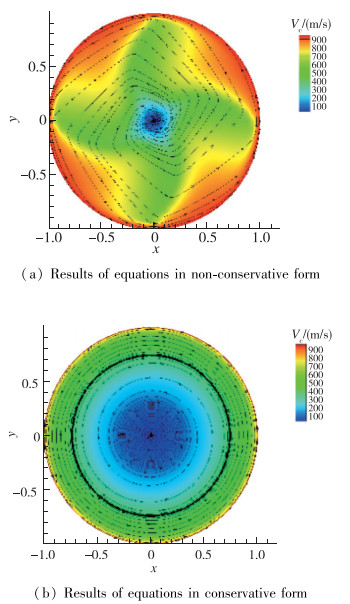
采用如图 9所示的规则网格模拟刚体旋转运动, Van Leer分裂格式直接处理方程(1)中直角坐标系的通量F和G, 再乘以当地点的BFC系数得到相应的通量
|
| 图 9 计算网格 Fig.9 Computational grids |
|
| 图 10 周向速度分布 Fig.10 Distributions of circumferential velocity |
通过理论分析和数值验证, 得到如下结论:
(1) 理论推导表明, 离散条件下坐标变换恒等式不再成立, 从带有源项的离散等价方程出发建立有限差分格式可以消除贴体坐标系变换过程中引入的误差.
(2) 分析曲线贴体坐标系变换过程, 提出离散等价方程的差分格式需要满足的准则, 并且给出满足准则的差分格式的算子形式.原则上算子可以适用于所有格式, 考虑限制器等因素, 仅给出1阶迎风格式的验证算例, 高精度格式效果还须验证.
(3) 对于均匀流场, 本文可以消除坐标变换引入的误差, 对于存在斜激波的流场, 减少激波上游误差能够有效提高下游的精度.
| [1] |
ANDERSON J D.计算流体力学基础及其应用[M].吴颂平, 刘赵淼, 译.北京: 机械工业出版社, 2007: 116-148. Anderson J D. Computational fluid dynamics[M]. Wu S P, Liu Z M, translated. Beijing: China Machine Press, 2007: 116-148(in Chinese). |
| [2] |
阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006: 18-25. Yan C. Computational fluid mechanics and its application[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2006: 18-25. (in Chinese) |
| [3] |
任玉新, 陈海昕. 计算流体力学基础[M]. 北京: 清华大学出版社, 2006: 97-102. Ren Y X, Chen H X. Computational fluid dynamics[M]. Beijing: Tsinghua University Press, 2006: 97-102. (in Chinese) |
| [4] |
刘巍, 张理论, 王勇献, 等. 计算空气动力学并行编程基础[M]. 北京: 国防工业出版社, 2013: 18-28. Liu W, Zhang L L, Wang Y X, et al. Foundations of computational aerodynamics parallel programming[M]. Beijing: National Defend Industry Press, 2013: 18-28. (in Chinese) |
| [5] |
刘君, 韩芳, 夏冰. 有限差分法中几何守恒律的机理及算法[J]. 空气动力学学报, 2018, 36(6): 917-926. Liu J, Han F, Xia B. Mechanism and algorithm for geometric conservation law in finite difference method[J]. Acta Aerodynamica Sinica, 2018, 36(6): 917-926. DOI:10.7638/kqdlxxb-2018.0034 (in Chinese) |
| [6] |
Trulio J G, Trigger K R. Numerical solution of the one-dimensional Lagrangian hydrodynamic equations[R]. California University, Livermore, CA(United States). Lawrence Radiation Laboratory, 1961.
|
| [7] |
Steger J L. Implicit finite difference simulation of flow about arbitrary geometrics with application to airfoils[C]. Albuquerque: 10th Fluid and Plasmadynamics Conference, 1977: 665. https://history.arc.nasa.gov/hist_pdfs/awards/hjaa_1987.pdf
|
| [8] |
Steger J L. Implicit finite difference simulation of flow about arbitrary two-dimensional geometrics with applica-tion to airfoils[J]. American Instkute of Aeronautics and Astronautics Joumal, 1978, 16(7): 679-686. DOI:10.2514/3.7377 |
| [9] |
Pulliam T H, Steger J L. On implicit finite-difference simulations of three-dimensional flow[C]. 16th Aerospace Sciences Meeting, Huntsville: 1978: 10. https://www.researchgate.net/publication/24149994_On_implicit_finite-difference_simulations_of_three-dimensional_flow
|
| [10] |
Thomas P D, Lombard C K. The geometric conservation law-a link between finite-difference and finite-volume methods of flow computation on moving grids[R]. AIAA 1978-1208, 1978. http://adsabs.harvard.edu/abs/1978fpdy.confT....T
|
| [11] |
Thomas P D, Lombard C K. Geometric conservation law and its application to flow computations on moving grids[J]. American Instkute of Aeronautics and Astronautics Joumal, 1979, 17(10): 1030-1037. DOI:10.2514/3.61273 |
| [12] |
Gaitonde D V, Visbal M R. Further development of a Navier-Stokes solution procedure based on higher-order formulas[C]. 37th Aerospace Sciences Meeting and Exhibit. 1999: 557. https://arc.aiaa.org/doi/abs/10.2514/6.1999-557
|
| [13] |
Visbal M R, Gaitonde D V. On the use of higher-order finite-difference schemes on curvilinear and deforming meshes[J]. Journal of Computational Physics, 2002, 181: 155-185. DOI:10.1006/jcph.2002.7117 |
| [14] |
Nonomura T, Iizuka N, Fujji K. Free-stream and vortex preservation properties of high-order WENO and WCNS on curvilinear grids[J]. Computers & Fluids, 2010, 39: 197-214. |
| [15] |
Deng X G, Zhang H. Developing high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2000, 165(1): 22-44. DOI:10.1006/jcph.2000.6594 |
| [16] |
Abe Y, Iizuka N, Nonomura T, et al. Conservative metric evaluation for high-order finite difference schemes with the GCL identities on moving and deforming grids[J]. Journal of Computational Physics, 2013, 232(1): 14-21. DOI:10.1016/j.jcp.2012.08.031 |
| [17] |
Abe Y, Iizuka N, Nonomura T, et al. Geometric interpretations and spatial symmetry property of metrics in the conservative form for high-order finite-difference sche-mes on moving and deforming grids[J]. Journal of Computational Physics, 2014, 260: 163-203. DOI:10.1016/j.jcp.2013.12.019 |
| [18] |
Liu X D, Osher S, Chan T. Weighted essentially non-oscillatory schemes[J]. Journal of Computational Physics, 1994, 115(1): 200-212. DOI:10.1006/jcph.1994.1187 |
| [19] |
Deng X G, Mao M L, Tu G H, et al. Geometric conservation law and applications to high-order finite difference schemes with stationary grids[J]. Journal of Computa-tional Physics, 2011, 230: 1100-1115. DOI:10.1016/j.jcp.2010.10.028 |
| [20] |
Deng X G, Min Y B, Mao M L, et al. Further studies on geometric conservation law and applications to high-order finite difference schemes with stationary grids[J]. Journal of Computational Physics, 2013, 239: 90-111. DOI:10.1016/j.jcp.2012.12.002 |
| [21] |
闵耀兵.高阶精度有限差分方法几何守恒律研究[D].中国空气动力研究与发展中心, 2015. Min Y B. The studies on geometric conservation law for high order finite difference method[D]. China Aerodynamics Research and Development Center, 2015(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90113-1016066178.htm |
| [22] |
朱志斌, 杨武兵, 禹旻. 满足几何守恒律的WENO格式及其应用[J]. 计算力学学报, 2017, 34(6): 779-784. Zhu Z B, Yang W B, Yu M. A WENO scheme with geometric conservation law and its application[J]. Chinese Journal of Computational Mechanics, 2017, 34(6): 779-784. (in Chinese) |
| [23] |
Nonomura T, Terakado D, Abe Y, et al. A new technique for freestream preservation of finite-difference WENO on curvilinear grid[J]. Computers & Fluids, 2015, 107: 242-255. |
| [24] |
Zhu Y J, Sun Z S, Ren Y X, et al. A numerical strategy for freestream preservation of the high order weighted essentially non-oscillatory schemes on stationary curvilinear grids[J]. Journal of Scientific Computing, 2017, 72(3): 1021-1048. DOI:10.1007/s10915-017-0387-x |




