高超声速巡航飞行器(HCV)具有飞行速度快、高度适中、机动能力强、航程远等特点, 具有很强的战略性和带动性.高超声速飞行器技术的突破与应用, 将会引发航空航天技术的跨越式变革, 对国家综合实力产生深远影响.先进气动布局是影响高超声速飞行器设计水平的核心因素[1], 但在高超声速飞行器中提高升阻比较为困难, 随着飞行Mach数增加存在“升阻比屏障”. Nonweiler[2]于1959年首次提出了“乘波”的设计思路并设计了第一个乘波体, 起初乘波体由于其容积率低, 不具备工程实用价值, 未得到广大设计人员的认可.直到20世纪80年代, 美国马里兰大学的Rasmussen等[3-4]由圆锥绕流流场生成乘波构型, 该方法生成的乘波构型具有圆锥形激波面, 即锥导乘波体设计方法, 乘波体的设计才再次引起广泛关注.乘波构型设计是突破高超声速飞行器“升阻比屏障”的一种有效尝试, 核心思想是高超声速飞行器升力产生机理不同于低速绕流压力分布特征, 其波后上下表面压力差是升力获取的核心机理, 飞行器边缘是下表面高压和上表面低压的激波分界面, 隔离下表面高压和上表面低压, 获取最大升力.根据现有高超飞行器相关研究进展, 乘波构型已成为高超声速飞行器布局设计的主要选择方案之一, 文献[5]研究了一种高超声速试验飞行器(HEXAFLY), 文中指出, 在高超声速飞行器研究面临的6大主要技术中总体和气动布局设计依然是高超声速飞行器面临的主要关键技术.李世斌等[6]提出了“串联”和“并联”的飞行器设计理论设计高超声速巡航飞行器, 使其兼顾低Mach数和高Mach数的飞行性能, 有效提升飞行器的总体性能. Cui等[7]提出了一种采用双乘波面组合设计前体的高超声速飞行器, 结果表明该设计可以使飞行器具有较好的发动机工作状态并且能够获得相对较高的升阻比.叶友达[8]通过CFD技术给出了典型高速高升阻比飞行器气动布局优化设计的初步进展.刘晓斌等[9]采用双向飞翼设计了一种新的空天飞行器, 能够同时满足亚声速和高超声速气动性能, 通过仿真分析说明了该类飞行器在未来宽速域空天往返飞行器中巨大的潜在应用能力.虽然国内外大量学者对乘波体构型的设计进行了系统而相对全面的研究, 但是基于乘波体的高超声速飞行器设计方法较为单一, 主要集中在单个乘波体和多级乘波体设计, 对于参数可变的高超声速巡航飞行器的研究较少.因此本文提出了一种基于乘波思想又不完全追求全乘波的灵活布局设计方法, 实现了飞行器边缘乘波效应、中心体根据需求设计的具有乘波特性的高超声速巡航飞行器.该方法可有效保持乘波飞行器的优秀气动性能, 又可以协调多种几何与气动约束, 使得各部件得到有效解耦, 实现了高超声速飞行器的参数化调整和模块化设计.本文方法一定程度上能够提升高超声速巡航飞行器的升阻比和实用价值, 为未来高超声速巡航飞行器气动布局设计提供重要参考.
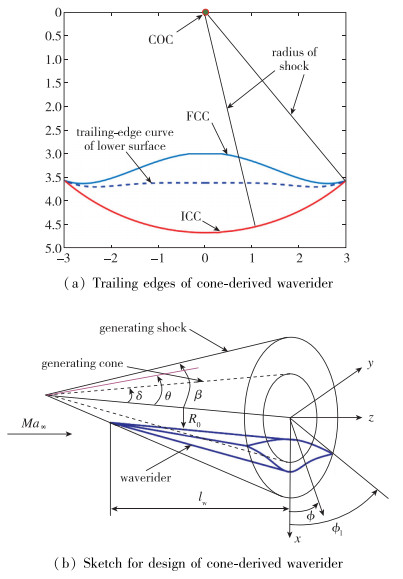
1 锥导乘波体设计以零攻角圆锥流场为基本流场, 通过给定乘波体后缘上表面曲线FCC, 然后逆向追踪与激波面相交得到前缘点, 然后利用流线追踪技术得到下表面流线, 通过放样从而可以得到乘波体构型.如图 1所示, 图 1(a)给出了FCC曲线和乘波体出口截面的轮廓图,图 1(b)展示了基于锥型流的锥导乘波体设计过程.
|
| 图 1 锥导乘波体设计示意图 Fig.1 Schematic illustration of cone-derived waverider |
圆锥流场控制方程
| $ \frac{\gamma-1}{2}\left[v_{\max }^{2}-v_{\mathrm{r}}^{2}-\left(\frac{\mathrm{d} v_{\mathrm{r}}}{\mathrm{d} \theta}\right)^{2}\right]\left(2 v_{\mathrm{r}}+\frac{\mathrm{d} v_{\mathrm{r}}}{\mathrm{d} \theta} \cot \theta+\frac{\mathrm{d}^{2} v_{\mathrm{r}}}{\mathrm{d} \theta^{2}}\right)-\\ \frac{\mathrm{d} v_{\mathrm{r}}}{\mathrm{d} \theta}\left(v_{\mathrm{r}} \frac{\mathrm{d} v_{\mathrm{r}}}{\mathrm{d} \theta}+\frac{\mathrm{d} v_{\mathrm{r}}}{\mathrm{d} \theta} \frac{\mathrm{d}^{2} v_{\mathrm{r}}}{\mathrm{d} \theta^{2}}\right)=0 $ |
采用临界声速无量纲化后的表达式如下
| $ \left\{\begin{array}{l}{\frac{\mathrm{d} v_{\mathrm{r}}^{*}}{\mathrm{d} \theta}=v_{\theta}^{*}} \\ {\frac{\mathrm{d} v_{\theta}^{*}}{\mathrm{d} \theta}+v_{\mathrm{r}}^{*}=\frac{\left(c / c^{*}\right)^{2}\left(v_{\mathrm{r}}^{*}+v_{\theta}^{*} \cot \theta\right)}{v_{\theta}^{* 2}-\left(c / c^{*}\right)^{2}}}\end{array}\right. $ |
锥导乘波体上表面后缘曲线采用常用的4次曲线线型
| $ y(z)=a z^{4}+b z^{2}+R_{0} $ |
已知乘波体上表面后缘曲线节点为(xbu, ybu, zbu), 激波角为β, 圆锥半顶角为δ, 则前缘节点坐标为
| $ \left\{\begin{array}{l}{x_{1}=x_{\mathrm{bu}}} \\ {y_{1}=y_{\mathrm{bu}}} \\ {z_{1}=\sqrt{x_{1}^{2}+y_{1}^{2}} \cot \beta}\end{array}\right. $ |
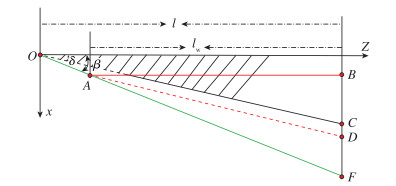
为了便于本文组合布局设计, 本文采用近似乘波体设计方法, 如图 2所示, 假设流线通过激波后直接与锥体表面平行, 已知乘波体长度为lw, 可得到下表面后缘曲线节点坐标为
|
| 图 2 近似乘波体设计示意图 Fig.2 Schematic illustration of simplified cone-derived waverider |
| $ \left\{\begin{array}{l}{x_{\mathrm{bl}}=x_{\mathrm{bu}}+\left(l-z_{1}\right) \tan \delta \cos \phi} \\ {y_{\mathrm{bl}}=y_{\mathrm{bu}}+\left(l-z_{1}\right) \tan \delta \sin \phi} \\ {z_{\mathrm{bl}}=z_{\mathrm{bu}}}\end{array}\right. $ |
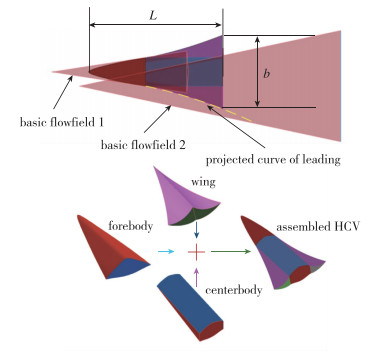
组合布局飞行器采用乘波前体、乘波机翼和中心体组合设计, 纵向分两段, 乘波前体是第1段, 机翼和中心体是第2段.前体采用确定乘波体后缘曲线设计, 如图 3所示, 乘波机翼采用确定前缘曲线, 同时满足与乘波前体的光滑过渡和机翼后掠角的要求.中心体初步设计时采用乘波后缘沿着前体流线方向直接追踪到与机翼底部, 平齐形成中心体下表面, 上表面选择自由流面.该方法设计的中心体与乘波机翼可以达到无缝对接, 同时也可以尽可能地保持前体下表面的高压气流.由于该飞行器并不是严格按照整个飞行器都是乘波体的设计方法设计出来的, 本文设计的高超声速巡航飞行器被定义为具有“乘波特性”的高超声速飞行器, 但是该方法突破了传统乘波体对于飞行器尺寸、激波角、一体化等的设计约束, 实现了工程应用中变参数变工况的灵活设计要求.
|
| 图 3 组合布局高超飞行器设计图 Fig.3 Design diagram of combined hypersonic vehicles |
设计思路:将飞行器沿纵向分为多级单独设计, 横向采用中心体与乘波机翼进行组合设计.
提高升阻比的原理:确保前体乘波与乘波机翼都具有乘波体的基本性能, 通过改变中心体的设计参数提高升阻比, 其中前体与机翼的乘波体设计未来可采用不同Mach数的组合, 从而为设计宽速域飞行器提供参考.
3 计算方法与验证 3.1 计算方法本文以ANSYS FLUENT为计算平台, 采用非结构网格的有限体积方法求解, 通过AUSM格式构造无黏通量, 空间离散采用2阶迎风格式.入口采用压力远场边界条件, 出口采用压力出口边界条件, 壁面选择绝热无滑移壁面边界条件.
3.2 空天飞机算例验证 3.2.1 算例说明为了验证数值方法的可信性, 本文选择空天飞机[10]作为数值方法的验证算例, 由于空天飞机模型复杂, 机翼后部存在分离, 流场比较复杂, 能够验证算法对复杂构型的适用性.该模型在FD-07风洞, FD-20脉冲风洞, FD-14A激波风洞, JF4B炮风洞等风洞进行了多Mach数和多攻角的气动力和气动热实验.具有丰富的实验数据和高超声速飞行器的典型外形.
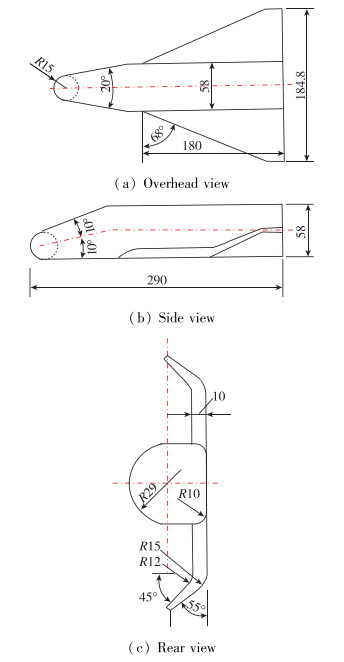
空天飞机基本模型由机头、机身与机翼3个主要部件组成.机头是由钝头圆锥修型得到, 机身是半圆柱(上半部)与半方柱(下半部)的组合体, 机翼为大后掠三角翼, 前缘后掠角为68°, 双翼翼尖具有上反的特点, 全机无立尾布局.模型全长290 mm, 展向为184.8 mm, 最大高度58 mm.空天飞机模型尺寸见图 4,5.风洞条件如表 1所示.
|
| 图 4 空天飞机模型三视图及主要尺寸 Fig.4 Principal dimension of space shuttle model |

|
| 图 5 空天飞机模型 Fig.5 Space shuttle models for wind tunnel and numerical simulation |
| 下载CSV 表 1 空天飞机实验边界条件 Tab.1 Boundary conditions for space shuttle tests |
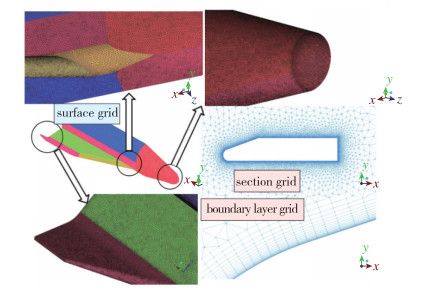
全机网格采用非结构混合网格构型, 采用半模型计算减少计算量.在飞机表面划分三棱柱网格, 其他计算域为四面体网格, 第1层网格厚度为0.01 mm, 保证基于单位长度Reynolds数的y+在5以下, 总网格量为5.26×106.
|
| 图 6 空天飞机网格 Fig.6 Grids for space shuttle |
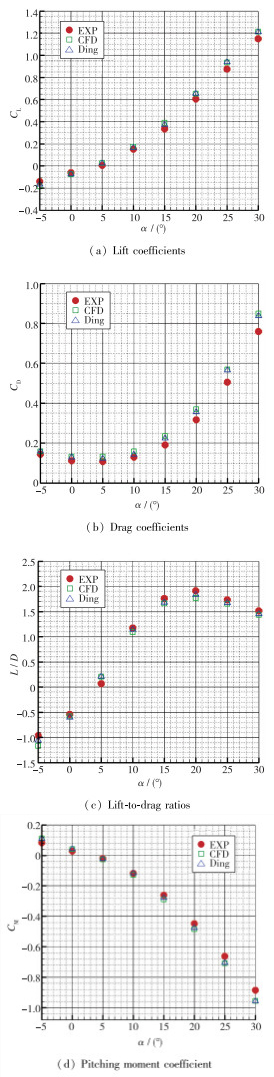
丁峰[11]采用结构网格、非结构网格对空天飞机进行了详细的数值模拟, 结果表明结构网格和非结构网格都能较好地得到气动数据, 且与实验数据接近, 但是结构网格捕捉到的激波分辨率更高.由于本文的计算网格为非结构混合网格, 这里将计算结果分别与实验数据和丁峰采用结构网格的计算结果进行对比, 见图 7,8.文献[10]给出的是轴向力和法向力参数.升力系数和阻力系数可通过以下关系式求得

|
| 图 7 空天飞机纹影图(密度云图)与试验纹影图对比 Fig.7 Comparisons of schlieren image(density contour) between numerical and experimental results for space shuttle |
|
| 图 8 气动参数对比 Fig.8 Comparisons of aerodynamic parameters between numerical computation and experimental data |
| $ \begin{aligned} C_{\mathrm{L}} &=C_{\mathrm{N}} \cos \alpha-C_{\mathrm{A}} \sin \alpha \\ C_{\mathrm{D}} &=C_{\mathrm{N}} \sin \alpha+C_{\mathrm{A}} \cos \alpha \end{aligned} $ |
本文计算结果能够与实验数据和丁峰的数值计算结果基本吻合, 证明了本文计算方法的可行性以及采用非结构混合网格处理高超声速计算的合理性.
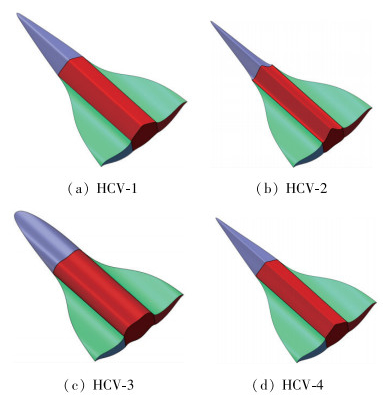
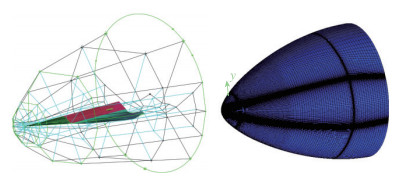
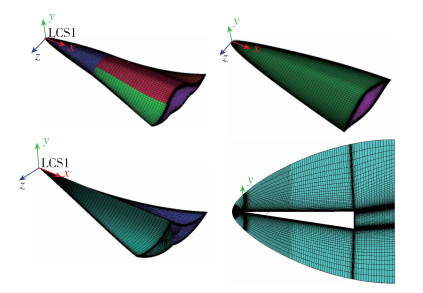
4 数值分析 4.1 组合布局构型设计为了研究不同参数对飞行器气动性能的影响, 本文选择中心体长度L, 机翼展长b和机身厚度h这3种参数进行对比分析. 图 9给出了本文设计方法设计的不同高超飞行器构型, 图中飞行器的机翼保持一致, 前体变化导致中心体构型的改变, 可以看出本文设计方法具有很大的灵活性.本文以HCV-1为研究对象来研究不同参数的影响.利用无黏数值计算, 采用ICEM划分结构网格, 共划分71个块区域.第1层网格厚度为1×10-4 m, 基于机身长度的Reynolds数为2.7×107. 图 10给出了本文计算采用的结构网格拓扑以及计算域大小. 图 11展示了不同部件的表面网格.本文气动参数以底部面积为参考面积, 在阻力计算中考虑了底部阻力的影响.
|
| 图 9 组合布局高超飞行器构型 Fig.9 Configurations of combined hypersonic vehicles |
|
| 图 10 拓扑分块与结构网格 Fig.10 Topology and structured grids |
|
| 图 11 不同构型的表面网格与截面网格 Fig.11 Surface and section grids of different configurations |
为了研究网格尺度对计算结果的影响, 本文以无黏流场为计算对象进行了网格收敛性分析. 表 2给出不同网格规模下的计算结果, 可以看出, 网格对计算结果的影响较小, 随着网格数量增加, 升力系数和阻力系数趋于稳定, 为了保证一定的计算精度, 同时为了提高效率.本文计算选择中等规模网格进行分析.
| 下载CSV 表 2 网格收敛性分析 Tab.2 Grid independency |
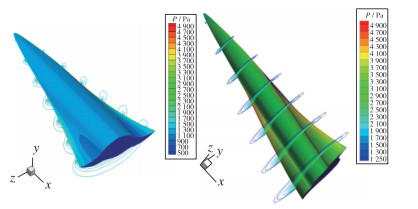
图 12给出了飞行器无黏条件下的表面压力云图和不同截面压力分布.可以看出, 由于飞行器上表面与来流平行, 因此上表面压力较小, 属于低压区.下表面是激波压缩面对应较高的压力, 同时也可以看出中心体也保持了较高的压力, 与本文预期设计基本一致.从而保证了整个飞行器具有较高的升阻比.通过不同截面压力分布来看, 飞行器边缘有少量的压力泄露, 这是由于本文乘波体是基于近似假设设计导致的.但是总体上依然可以保证较好的乘波性能.
|
| 图 12 压力云图分布 Fig.12 Pressure contour distributions |
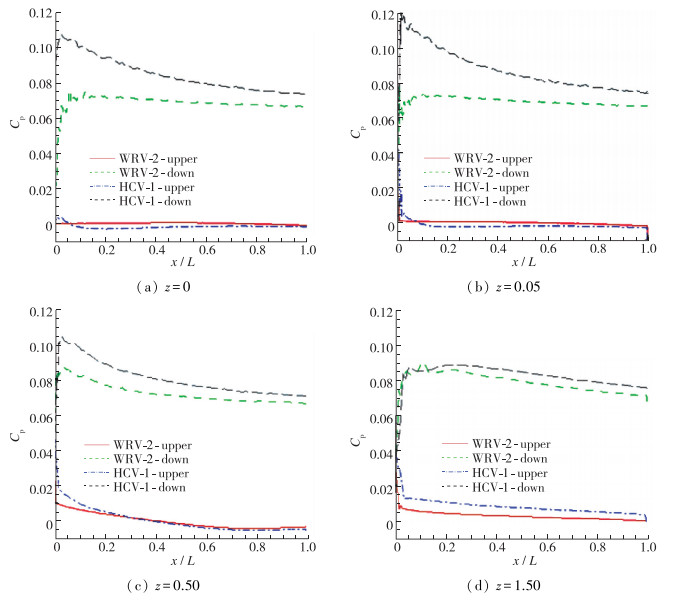
图 13给出了单独乘波机翼和组合体在不同翼展截面处的上下表面无量纲压力系数对比.由于整个飞行器的上表面都是与自由来流平行, 在设计工况下的压力系数接近0, 两种飞行器相差不大.但是下表面压力表现出了明显的差异, 整体上来看, HCV-1的下表面压力系数普遍高于WRV-2, 说明前体和中心体的压缩程度较机翼更强.随着沿流向距离增加, 两种飞行器的压力系数逐渐接近, 随着展向距离增加, HCV-1和WRV-2的压力系数分布变化不大, 说明采用本文方法设计的飞行器压力分布比较均匀, 具有较好的流场特征.
|
| 图 13 组合体与乘波体截面压力系数对比 Fig.13 Comparisons of pressure coefficients between combined vehicle and waverider |
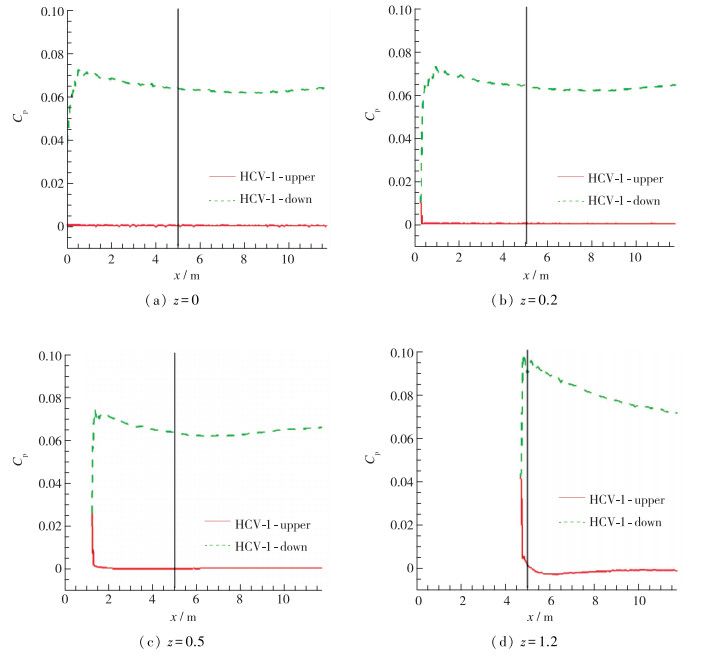
为了研究中心体的气动性能特征, 本文沿展向提取了剖面处的上下表面压力系数, 如图 14所示, 图中竖直线表示的是前体和中心体的衔接处.可以看出, 中心体下表面的压力基本上维持了前体下表面后缘处的压力值, 使得高压较好地保持在飞行器下表面, 从而保证了整个飞行器具有较好的气动性能.
|
| 图 14 中心体压力系数分布 Fig.14 Pressure coefficient distributions at different slices of centerbody |
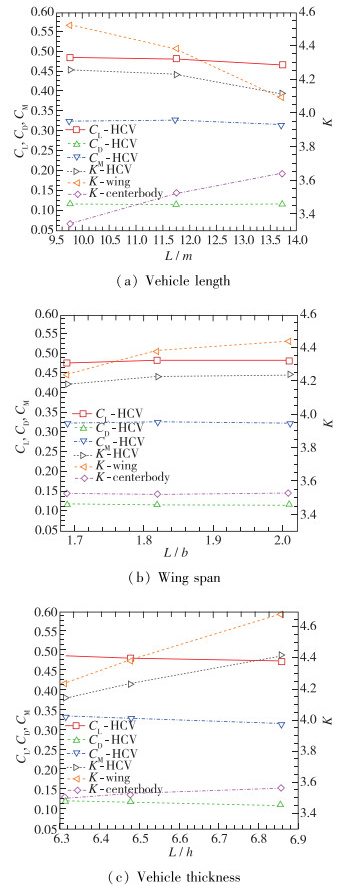
图 15展示了不同设计参数对组合布局飞行器气动性能的影响研究, 其中K为升阻比.从图 15(a)可以看出, 随着中心体长度的增加, 飞行器的升力系数稍有下降, 阻力系数和力矩系数基本维持不变.机翼的升阻比出现了明显的下降, 但是中心体的升阻比有所增加, 全机的升阻比有一定程度下降. 图 15(b)显示随着机翼翼展增加, 机翼和全机的升阻比稍有增加. 图 15(c)给出了飞行器厚度对气动性能的影响.可以看出, 随着长厚比增加, 升力系数和阻力系数有所下降.机翼、中心体和全机的升阻比都出现了明显的增加.由于飞行器厚度与激波压缩程度紧密相关, 减小飞行器的厚度使得容积率下降, 有利于升阻比的改善.
|
| 图 15 不同设计参数对飞行器气动性能的影响 Fig.15 Effects on aerodynamic performance of different design parameters |
在飞行器气动优化过程中, 采用FFD[12]技术可以实现局部扰动的参数变化而不是外形本身整体的参数化来减少设计变量, 设计参数就是各个FFD控制点的位移.韩忠华等[13], 陈立立等[14], 陈颂等[15]分别采用FFD方法进行了机翼和翼型的气动优化分析, 结果表明FFD方法可以显著地实现优化减阻, 证明了FFD方法在气动优化设计中的可行性和实用性.但是很少看到文献应用FFD方法进行高超声速布局优化, 本文将FFD方法引入到高超声速气动布局的优化设计中.
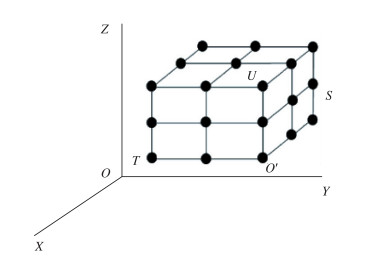
FFD方法采用Bernstein基函数来定义位移求解模式.首先构造ASD控制体对待变形物体进行包围, 并构造局部坐标系O′-STU如图 16所示, 其中,O′是局部坐标系的原点, S, T, U是轴矢量. Descartes坐标系O-XYZ中任意一点X在局部坐标系中具有坐标(s, t, u), X=X0+sS+tT+uU.式中, X0为局部坐标系的原点.
|
| 图 16 局部坐标系 Fig.16 Local coordinates |
| $ \begin{array}{*{20}{c}} {s = \frac{{\mathit{\boldsymbol{T}} \times \mathit{\boldsymbol{U}} \cdot \left( {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}_0}} \right)}}{{\mathit{\boldsymbol{T}} \times \mathit{\boldsymbol{U}} \cdot \mathit{\boldsymbol{S}}}}, }\\ {t = \frac{{\mathit{\boldsymbol{S}} \times \mathit{\boldsymbol{U}} \cdot \left( {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}_0}} \right)}}{{\mathit{\boldsymbol{S}} \times \mathit{\boldsymbol{U}} \cdot \mathit{\boldsymbol{T}}}}, u = \frac{{\mathit{\boldsymbol{S}} \times \mathit{\boldsymbol{T}} \cdot \left( {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}_0}} \right)}}{{\mathit{\boldsymbol{S}} \times \mathit{\boldsymbol{T}} \cdot \mathit{\boldsymbol{U}}}}} \end{array} $ |
待变形的几何外形上每一个点在FFD控制体中的局部坐标为
| $ \begin{array}{c}{x(s, t, u)=\sum\limits_{i=0}^{l} \sum\limits_{j=0}^{m} \sum\limits_{k=0}^{n} P_{i, j, k} B_{l}^{i}(s) B_{m}^{j}(t) B_{n}^{k}(u)} \\ {P_{i, j, k}=O^{\prime}+\frac{i}{l} S+\frac{j}{m} T+\frac{k}{n} U}\end{array} $ |
其中, l, m, n分别表示FFD控制体3个方向上的阶数, Bli(s), Bmj(t), Bnk(u)分别是l, m, n阶次的Bernstein基函数.
| $ B_{l}^{i}(s)=\frac{l !}{i !(l-i) !} s^{i}(1-s)^{l-i} $ |
Bmj(t), Bnk(u)与Bli(s)类同, 不再赘述.
当控制点Pi, j, k变形到P′i, j, k, 变形后几何外形上每一个点的位置为
| $ x^{\prime}(s, t, u)=\sum\limits_{i=0}^{l} \sum\limits_{j=0}^{m} \sum\limits_{k=0}^{n} P_{i, j, k}^{\prime} B_{1}^{i}(s) B_{m}^{j}(t) B_{n}^{k}(u) $ |
通过对控制体内的控制点进行变换就可以得到变形后的飞行器几何构型.如图 17所示为采用FFD方法对高超声速飞行器机翼厚度进行变形, 包括压缩和拉伸.

|
| 图 17 基于FFD自由变形技术的HCV-1变形示意图 Fig.17 Deformation diagram of HCV-1 by FFD method |
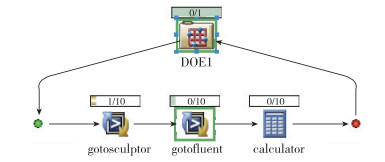
本文优化设计流程如图 18所示, 首先编写HCV-1.def脚本文件, 然后通过批处理文件run_sculptor.bat运行实现网格的变形, 输出变形后的cas/dat文件.编写HCV-1_sculptor.jou的fluent可执行脚本文件, 通过run_fluent.bat批处理文件运行变形后的cas/dat文件, 并输出cl.dat和cd.dat数据文件, 通过calculator计算升阻比, 从而实现整个DOE实验设计的运行流程.
|
| 图 18 优化流程图 Fig.18 Framework of optimization process |
图 19给出了本文的优化结果, 根据结果来看, 通过对机翼后缘厚度的控制可以实现飞行器升阻比的明显变化.优化后0°攻角下的高超声速飞行器最大升阻比稍大于优化前的结果, 说明采用FFD优化技术可以实现飞行器性能的提升, 证明了本文优化方法的可行性.
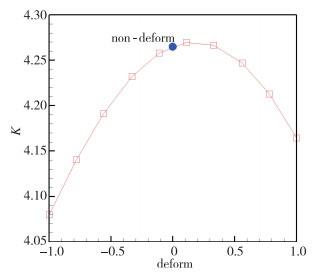
|
| 图 19 升阻比优化结果 Fig.19 Optimized result of lift-to-drag ratio |
采用组合式高超声速飞行器布局设计可以较好地保持传统乘波体的乘波特性, 可以将高压限制在飞行器下表面.该种布局保持了飞行器边缘乘波特性, 前体和机翼的激波角可以参数化调整, 中心体可根据设计需求进行容积调整, 实现了高超声速巡航飞行器的参数化设计.计算结果表明本文设计的飞行器具有较高的升阻比和容积特性, 在前体不变的前提下, 飞行器的长度和宽度对飞行器总体气动性能影响较小.飞行器的厚度对气动性能的影响较为显著. FFD自由变形技术可以实现对高超声速飞行器的气动优化, 使得飞行器的升阻比得到一定提升.因此可以看出, 本文提出的设计方法不但保持了较好的升阻特性, 而且实现了高超声速飞行器的多部件多参数设计和优化, 具有更好的灵活性和实际工程应用价值,可作为未来变形飞行器的技术参考.
| [1] |
王若冰, 谷良贤. 高超声速飞行器气动外形与内部布局一体化优化设计[J]. 飞行力学, 2015, 33(4): 344-348. Wang R B, Gu L X. Aerodynamic and layout integration optimization design for hypersonic vehicle[J]. Flight Dynamics, 2015, 33(4): 344-348. (in Chinese) |
| [2] |
Nonweiler T R. Aerodynamic problems of manned space vehicles[J]. The Aeronautical Journal, 1959, 63(585): 521-528. |
| [3] |
Rasmussen M P. Waverider configurations derived from inclined circular and elliptic cones[J]. Journal of Spacecraft and Rockets, 1980, 17(6): 537-545. DOI:10.2514/3.57771 |
| [4] |
Rasmussen M L, Jischke M C, Daniel D C. Experimental forces and moments on cone-derived waveriders for M∞=3 to 5[J]. Journal of Spacecraft and Rockets, 1982, 19(6): 592-598. DOI:10.2514/3.62306 |
| [5] |
Pezzella G, Marini M, Cicala M, et al. Aerodynamic characterization of HEXAFLY scramjet propelled hypersonic vehicle[R]. AIAA 2014-2844, 2014.
|
| [6] |
李世斌, 罗世彬, 黄伟, 等. 新型高超声速飞行器气动构型设计[J]. 弹箭与制导学报, 2012, 32(4): 155-157, 164. Li S B, Luo S B, Huang W, et al. The design of aerodynamic configuration for a novel hypersonic vehicle[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(4): 155-157. DOI:10.3969/j.issn.1673-9728.2012.04.042 (in Chinese) |
| [7] |
Cui K, Hu S C, Li G L, et al. A conceptual design of next generation hypersonic air-breathing airplanes with dual waveriders forebody[R]. AIAA 2015-3646, 2015.
|
| [8] |
叶友达. 近空间高速飞行器气动特性研究与布局设计优化[J]. 力学进展, 2009, 39(6): 683-694. Ye Y D. Study on aerodynamic characteristics and design optimization for high speed near space vehicles[J]. Advances In Mechanics, 2009, 39(6): 683-694. DOI:10.3321/j.issn:1000-0992.2009.06.009 (in Chinese) |
| [9] |
刘晓斌, 徐柯哲, 朱国祥. 双向飞翼空天飞行器概念外形研究[J]. 空气动力学学报, 2017, 35(3): 415-420, 443. Liu X B, Xu K Z, Zhu G X. Research on bi-directional flying wing space shuttle configuration[J]. Acta Aerodynamica Sinica, 2017, 35(3): 415-420, 443. DOI:10.7638/kqdlxxb-2017.0021 (in Chinese) |
| [10] |
李素循. 典型外形高超声速流动特性[M]. 北京: 国防工业出版社, 2007. Li S X. The flow characteristics for the typical model in hypersonic flows[M]. Beijing: National Defense Industry Press, 2007. (in Chinese) |
| [11] |
丁峰.吸气式高超声速飞行器内外流一体化"全乘波"气动设计理论和方法研究[D].长沙: 国防科学技术大学, 2016. Ding F. Research of a novel airframe/inlet integrated full-waverider aerodynamic design methodology for air-breat-hing hypersonic vehicles[D]. Changsha: National University of Defense Technology, 2016(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90002-1018996814.htm |
| [12] |
Sóbester A, Forrester A I. Aircraft aerodynamic design:geometry and optimization[J]. United Kingdom:John Wiley & Sons, Ltd, 2014. |
| [13] |
韩忠华, 张瑜, 许晨舟, 等. 基于代理模型的大型民机机翼气动优化设计[J]. 航空学报, 2019, 40(1): 522398. Han Z H, Zhang Y, Xu C Z, et al. Aerodynamic optimization design of large civil aircraft wings using surrogate-based model[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(1): 522398. (in Chinese) |
| [14] |
陈立立, 郭正, 侯中喜. 自由变形技术在RAE2822翼型优化设计中的应用[J]. 国防科技大学学报, 2018, 40(5): 45-53. Chen L L, Guo Z, Hou Z G. Application of free-form deformation technique for RAE2822 airfoil optimization design[J]. Journal of National University of Defense Technology, 2018, 40(5): 45-53. (in Chinese) |
| [15] |
陈颂, 白俊强, 孙智伟, 等. 基于DFFD技术的翼型气动优化设计[J]. 航空学报, 2014, 35(3): 695-705. Chen S, Bai J Q, Sun Z W, et al. Aerodynamic optimization design of airfoil using DFFD technique[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 695-705. (in Chinese) |



