在现代先进战机的空战中, 高机动性和高敏捷性占有越来越突出的地位.这些性能往往通过大攻角的飞行才能显现出来.当这样的先进战机进行大攻角飞行时, 各种非指令运动经常会伴随而来, 其中非指令摇滚运动最为常见.为了保证这些先进战机和驾驶员的安全性, 所有这类非指令运动必须在战机的初步设计阶段全部消除掉.这样, 就极大地促进了人们深入研究战机在大攻角飞行中的复杂流动现象和机理, 从而在最近几十年内使大攻角下的非线性流动现象和机理的研究有了极大的进展, 人们的认识得到了极大的提高.
在20世纪80年代Hunt等的总结和研究[1~4]表明:一个简单的旋成体模型, 在大攻角下的绕流中显现出十分复杂的现象, 研究该流动的困难是相同模型、其风洞实验结果却无法重复, 包括和别人的结果比较, 甚至连自己的实验结果也不一致.为了解决风洞实验数据的重复性问题, 人们曾进行过大量的研究.例如, 尽量提高模型加工的精度和表面光洁度[4], 以提高风洞实验数据的重复性; 考虑到大攻角下, 模型易于振动, 专门设计了支撑模型的防振支架[4, 5]; 为了认识湍流度对实验结果重复性的影响, 又在不同湍流度的风洞中进行了实验研究[4].尽管进行了如此多的研究, 但影响实验数据重复性的主控因素仍未找到.最后, 在Keener等的实验研究[6, 7]启发下, 人们才发现模型头部的不规则扰动是主控实验数据重复性的关键因素.这些头部不规则扰动主要来自模型的机械加工, 我们将这类扰动称为自然扰动.无论将加工公差定得多小, 这样的不规则性总是存在的.由于加工中这类不规则性沿周向是随机的, 所以对应的前体非对称涡的响应也是随机的. Hunt将这类非对称涡流形变化的现象称为滚转角效应[1], 并在文献[1, 2, 4]中详细讨论了这一效应.
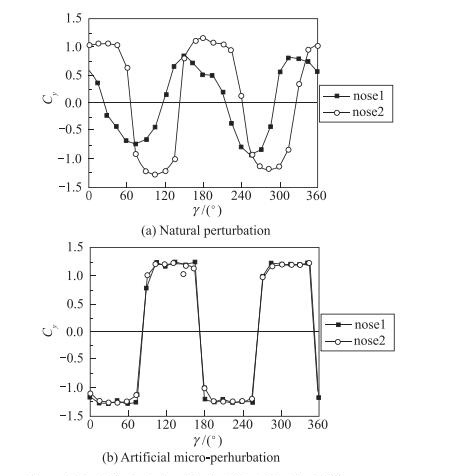
显然, 对于无法重复实验的研究是十分困难的, 那么如何才能避免这种非对称涡在流形上的不确定性和相应实验数据的不重复性?邓学蓥课题组针对自然扰动的随机性分布, 提出在模型头部粘贴较自然扰动更大的确定的人工微扰动[8, 9], 这时, 前体非对称涡的响应仅针对确定的人工微扰动了, 而自然扰动的响应则都被淹没在其中.这一结论得到了风洞实验的证明:若在模型头尖部粘贴人工微扰动, 那么由自然扰动触发的前体非对称涡响应的不确定性将完全消失, 仅留下对人工微扰动的响应, 即由图 1(a)演化为图 1(b)所示的前体非对称涡流形.图中侧向力系数Cy用来表征前体非对称流动的程序,Cy中的下标y表示侧向力方向,γ表示模型头尖部扰动的周向角.
|
| 图 1 在自然扰动和人工扰动下模型的侧向力分布(α=50°) Fig.1 Side force on ogive cylinder model under conditions of natural perturbation and artificial micro-perturbation (α=50°) |
基于人工扰动的风洞实验技术, 邓学蓥课题组进行了旋成体机身和小后掠机翼翼身组合体模型摇滚运动与控制的实验研究[10~12].进一步发展了旋转模型头部扰动的控制技术, 以抑制飞行器自由摇滚运动.
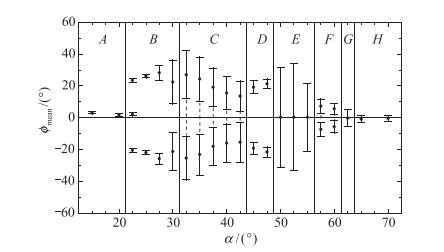
近期邓学蓥课题组又研究了非常规翼身组合体模型的大攻角非指令摇滚运动[13, 14], 却发现其摇滚运动形态在自然扰动状态下始终是确定的, 它的风洞实验数据具有很好的重复性, 如图 2所示. 图 2给出了非常规布局模型在不同攻角下摇滚运动的平衡位置及其振幅.图中φmean虽然该模型与前一个图 3所示的实验模型都能诱发非指令摇滚运动, 但是这两个模型诱发相同运动方式的流动形态和机理究竟有何差别?这是本文的研究重点之一.这样, 在清晰两类流形和流动机理的基础上, 就很容易提出抑制这两类实验模型非指令摇滚运动的流动控制技术.
|
| 图 2 非常规翼身组合体摇滚运动随攻角的变化曲线 Fig.2 Evolutions of free-to-roll motion with αover the chined forebody/wing configuration |
|
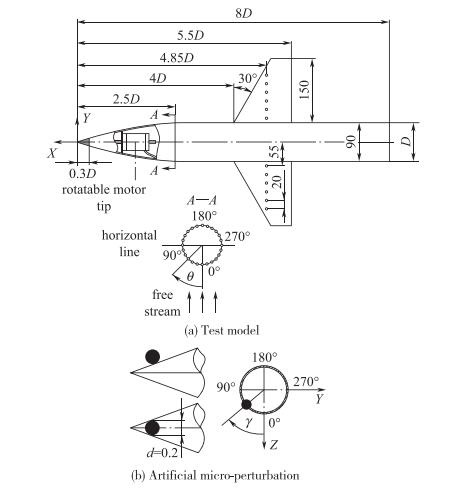
| 图 3 风洞的实验模型和模型头部人工微扰动 Fig.3 Experimental model and artificial tip micro-perturbation |
图 3给出了本课题组进行风洞实验研究的组合体模型, 其前机身为尖拱旋成体, 长细比λ前体=3.0, 后机身为等直段的圆柱体(直径D=90mm), λ后体=5.0.其机翼的前缘后掠角为30°, 根弦前缘顶点位于机身的x/D=-4.0. 图 3(b)为该模型头尖部人工扰动位置参数的示意图.由于旋成体机身的非对称涡流动对ReD的大小较为敏感[13~17], 所以我们在研究中将使ReD保持在亚临界Reynolds数范围内, 即绕流边界层始终处于层流的范围内.
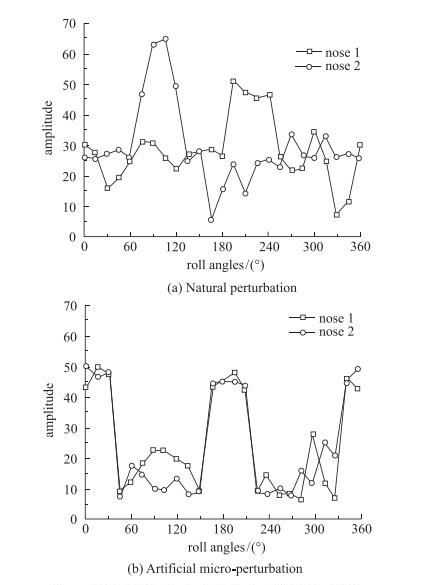
1.1 实验模型摇滚运动形态的不确定性我们发现在摇滚运动的风洞实验中, 模型的运动形态是不确定的, 它的实验数据不仅无法重复, 且具有随机性.如图 4(a)所示, 该模型通过加工两个形状完全一致的头部, 并都在风洞中进行了摇滚运动实验, 图中两条曲线表示的是带有这两个头部的模型在做摇滚运动时的最大振幅随模型滚转角变化的状况.从中可以看到两条曲线是不重复的.为什么会发生这种运动情况呢?该模型要形成摇滚运动必须要有作用在机翼上的滚转力矩来驱动, 模型上的滚转力矩实际上是由模型两侧的非对称流动形成的, 旋成体在攻角较小时(例如α=20°时), 机身前体涡是对称的, 随着攻角的增加该对称涡流动会变得不稳定, 这种不稳定流动对模型头部周向不规则性表现得特别敏感, 风洞实验表明, 模型头尖部机械加工公差内的这种扰动能将前体不稳定的对称涡流动触发为非对称涡流动.由于自然扰动沿模型头尖部的周向分布是随机的, 所以前体非对称涡的响应也是随机的, 因此, 不仅前体非对称涡流动的流形具有不确定性, 而且由前体非对称涡诱发的摇滚运动形态也具有不确定性,从而使摇滚运动的实验数据不具重复性,如图 4(a)所示.如果将自然扰动改变为人工扰动,那么不仅非对称涡流动具有确定性,它所诱导的摇滚运动形态也呈现为确定的,如图 4(b)所示.
|
| 图 4 模型头部为自然扰动和人工微扰动下的摇滚曲线(α=50°) Fig.4 Wing rock motions under conditions of natural perturbation and artificial micro-perturbation (α=50°) |
为了更好地理解上述“扰动”“触发”“确定性”“重复性”等一些专有名词, 下面对它们进行深入浅出的解释.首先, 旋成细长体绕流的非对称涡是如何形成的?当细长旋成体的攻角不断增加时, 其对称涡流动进入不稳定流动区[17], 在头尖部扰动的触发下, 形成非对称涡, 其非对称涡的方位, 依赖于头尖部扰动的周向位置.同时, 实验结果还表明, 在前体非对称涡绕流条件下, 通过模型头尖部扰动的触发, 还可形成与该扰动周向位置对应的非对称涡状态, 这就是Hunt[1]所称的前体非对称涡的滚转角效应.这里, 我们用的是触发而不是相互作用或干扰.扰动是指其边界条件相对所要触发的流动的边界条件是极小的, 似乎可以忽略.但是扰动对流动的演化作用却是很大的,扰动的这种作用称为触发.流动的相互作用或干扰是指形成两者的边界条件都是较大的, 其结果流动将依赖于这两个边界条件所对应的流动.确定性通常是就运动形态或流形形态而言的.而重复性通常是指风洞实验数据的重复程度, 它既可以是运动数据也可以是气动数据.
1.2 人工微扰动与摇滚运动的确定性既然模型在自然扰动下, 其风洞实验中的前体非对称涡流形和相应的摇滚运动的形态都具有不确定性, 那么如何才能使前体非对称涡流形和相应的摇滚运动形态变成确定的?最简便的一个做法是在旋成体机身的头尖部粘贴确定的微三角块或微球形颗粒[8, 9, 18, 19]作为人工微扰动.实验结果表明, 不仅前体非对称涡的流形是确定的, 而且风洞实验数据也是重复的, 如图 1(b)所示.由于早期头尖部粘贴的微三角块是自制的, 难以保证每次制作和粘贴的重复性, 所以实验数据中有时会出现一些跳点, 为了避免这一现象, 在后期的研究中统一采用0.02mm的商用塑料球形颗粒, 以避免实验中的跳点现象, 提高实验的重复性精度[19].
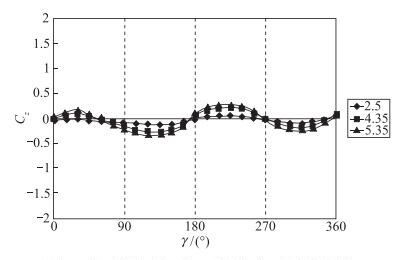
1.3 在一定攻角下前体非对称涡流形随扰动滚转角的演化规律由模型头尖部扰动触发, 非对称涡随滚转角的演化规律不仅受攻角的影响, 而且还会受模型布局的影响.在图 3所示布局模型的前体扰动周向位置的变化会对前体非对称涡的方位有演化作用.当攻角较小时(例如α=30°), 其非对称涡在机身上诱导的截面侧向力随滚转角一周的变化规律呈类正弦双周期连续态分布, 如图 5所示; 当攻角较大时(例如α=50°), 其非对称涡在机身上诱导的截面侧向力随滚转角一周的变化规律呈现为双周期、双稳态分布的特性, 如图 1(b)所示.所谓双稳态是指攻角大到一定程度时, 其非对称涡的涡量不再随攻角而增加, 趋于饱和, 称其为稳态.由于当滚转角变化时, 非对称涡会演化到其镜像位置, 它所诱导的截面侧向力也与原先的符号相反, 故而形成非对称涡的两个稳态, 称其为双稳态.
|
| 图 5 非对称涡在机身上诱导的截面侧向力分布 Fig.5 Side force on the forebody induced by the asymmetric vortices |
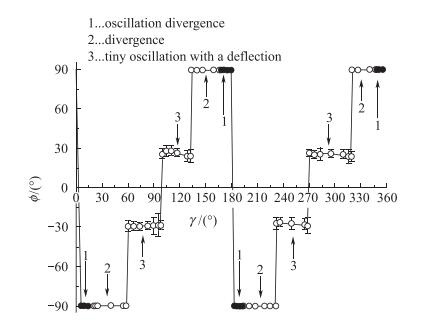
图 6给出了模型的攻角α=40°时, 摇滚运动随扰动位的变化曲线, 其中实验点是运动的平衡位置, 图中实验点的滚转角φ为90°时, 则表示为滚转发散.实验中的现象[10]表明, 当扰动位于0°或180°时, 其摇滚运动为振荡发散; 若扰动位偏离0°或180°时, 其摇滚运动为直接发散; 当扰动位于其他位置时, 其摇滚运动为偏向一侧的微振.
|
| 图 6 不同扰动位置的摇滚运动类型 Fig.6 Motion types of different perturbation circumferential locations |
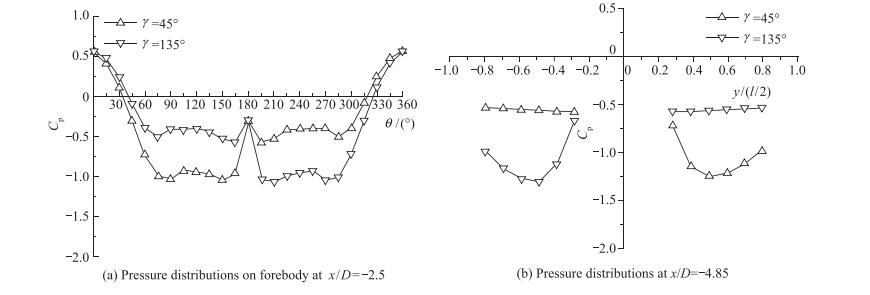
图 6清晰地显示了模型的自由摇滚运动(含发散), 然而, 模型要形成摇滚运动只有旋成体机身和前体非对称涡流动是不够的, 必须要有机翼的存在.那么本模型中的机翼是如何形成并获取模型摇滚运动所需的滚转力矩呢?模型中机翼的前缘后掠角只有30°(见图 3(a)), 当攻角α=40°时, 单独机翼流动呈对称的完全分离流, 然而在前体非对称涡的诱导下, 仅在机翼的一侧(与前体非对称高位涡相同一侧)会诱导出机翼涡, 从而形成机翼上的非对称流动, 如图 7所示.当前体扰动位于γ=45°时,对应的前体非对称涡是左低右高(前体涡未显示), 这样在位于右侧机翼上诱导出机翼涡, 如图 7(a)所示.当头尖部扰动位于γ=135°时, 前体非对称涡是左高右低, 结果在左侧机翼上诱导出机翼涡, 如图 7(b)所示.此外, 还通过风洞测压实验, 进一步验证了上述结论(见图 8). 图 8(a)为在机身上截面x/D=-2.5处的压力分布, 其中的两条压力分布曲线, 分别对应的前体微扰动位为γ=45°和γ=135°.而图 8(b)为在机翼上截面x/D=-4.85处相应的两条压力分布曲线, 就这样在机翼上形成了随扰动位变化的滚转力矩.

|
| 图 7 机翼涡随前体扰动位置的变化 Fig.7 Variations of wing vortex with artificial perturbation |
|
| 图 8 在两个扰动位下的机身和机翼上的压力分布 Fig.8 Pressure distributions over forebody and wing with two different artificial perturbations |
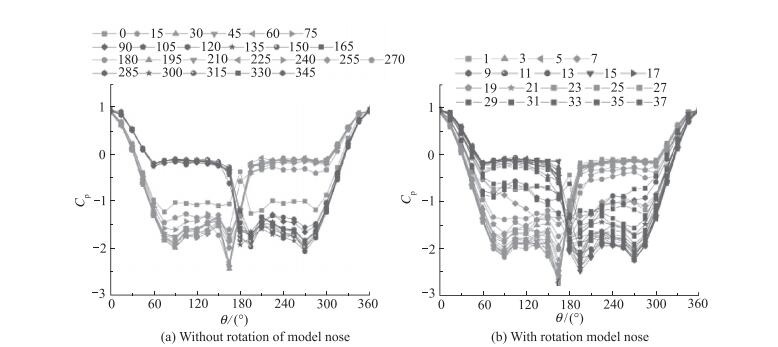
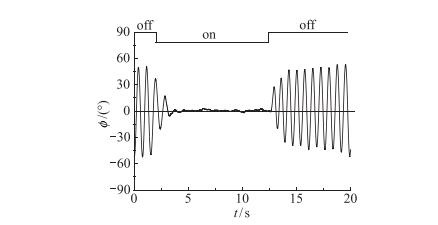
由上一节的研究可以看到, 机翼上的机翼涡完全由前体非对称涡诱导的, 而前体非对称涡的方位又是由扰动的周向位置决定的.这就是说, 前体的微扰动周向位置对模型的摇滚运动具有主控作用.众所周知, 模型的摇滚运动不仅取决于作用在模型上滚转力矩的大小, 而且还取决于该力矩作用的时间.如果前体头尖部的扰动可以旋转, 那么滚转力矩作用的时间也可由旋转的频率f扰动来确定, 即f扰动越大, 则其作用时间越短.当然, 这是假设前体非对称涡存在的情况.为此, 应首先证明在头部扰动旋转的条件下, 前体非对称涡是否存在?为此, 专门设计、加工了一个如图 3所示的前体头部可旋转的模型, 并可在截面x/D=-2.5处进行测压, 其实验结果如图 9所示.其中图 9(a)表示头部扰动不旋转, 只是静态地改变它的周向位置. 图 9(b)则是头部扰动旋转时的结果.实验表明, 当头部扰动旋转时, 前体非对称涡始终存在, 只是非对称涡方位的变换随着头部旋转频率的提高而加快, 即触发非对称涡的扰动在固定方位下的时间缩短, 以至使所诱发的滚转力矩来不及让模型做摇滚运动.从而该控制技术得到了实验的完全证明.利用该技术, 图 3(a)所示模型在大攻角下的非指令摇滚运动可以得到很好的抑制, 如图 10所示.实验中模型自由摇滚的频率为1.375Hz, 而头部扰动的旋转频率为6Hz.
|
| 图 9 模型头部旋转或不旋转时的风洞实验压力分布(x/D=-2.5) Fig.9 Pressure distributions at x/D=-2.5 when rotating tip of the model or not |
|
| 图 10 旋转头部来抑制模型自由摇滚的风洞实验 Fig.10 Suppression of wing rock by rotating tip |
为了更好地降低RCS(radar cross-section)的信号, 非常规机身的组合体布局是现代先进战机能适应这一要求,它往往是现代先进战机采用的一种布局形式. 图 11中的简图为本研究所用的非常规机身组合体模型.所谓非常规机身是指其侧缘为尖缘的机身, 如图 11所示.

|
| 图 11 非常规机身组合体布局的实验模型示意图 Fig.11 Sketch of the chined forebody/wing configuration model |
在摇滚运动的实验中发现, 该模型的摇滚运动不再是不确定的, 如图 2所示, 运动的实验数据具有很好的重复性.那么, 为什么该非常规模型的大攻角非指令摇滚运动特牲与旋成体机身和小后掠机翼的组合体模型的摇滚运动特性存在那么大的差别?
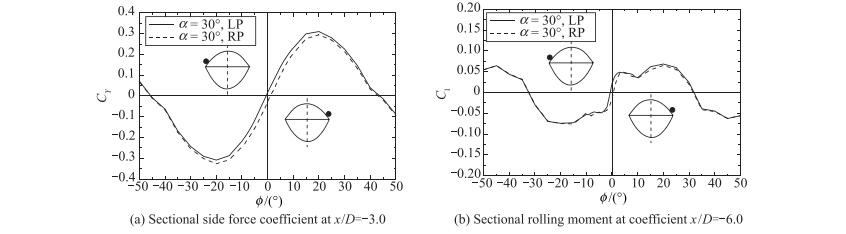
2.1 绕不同组合体模型的两类非对称流动图 3(a)和图 11给出的是本研究中两类不同的组合体模型, 其最为核心的区别是前者的机身是旋成身,机翼的前缘占掠角仅为30°; 而后者的机身侧缘为尖缘,其机翼的前缘占掠角达48°.当这两个模型的机身滚转一定的角度后, 前者机身的边界条件没有任何变化, 改变的仅是前体上的扰动周向位置; 然而, 后者除了机身前体的扰动状况有变化外, 其机身的绕流边界条件也发生了变化. 图 12给出了α=30°非常规组合体模型在各个滚转角φ下x/D=-3.0截面的侧向力曲线和x/D=-6.0截面的滚转力矩曲线.该图中应注意, 模型头尖部左右两侧分别粘贴了人工微扰动, 它们在滚转角φ=0°时左右扰动触发的侧向力、滚转力矩分别为一正一负, 实线代表左侧微扰动触发的, 而虚线曲线则表示右侧微扰动触发的.在图中看到这两条曲线仅在φ=0°的邻近范围内有差异, 其外, 该两组曲线几乎是重合的.以此表明头尖部扰动的影响仅限于φ=0°的邻近, 其外, 模型的滚转力矩系数Cl主要由边界条件(这里就是滚转角φ)主控的.上述分析结果说明, 非常规组合体模型的非对称绕流诱发的自由摇滚运动是由边界条件主控的, 如图 12所示.尽管自然扰动仍然是随机的、不确定的, 但它并不主控该摇滚运动.
|
| 图 12 非常规组合体模型在两个极端扰动位下的侧向力和滚转力矩随滚转角的变化曲线 Fig.12 Variations of side force and rolling moment of the chined forebody/wing configuration under two extreme artificial perturbations |
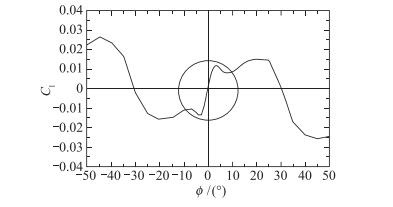
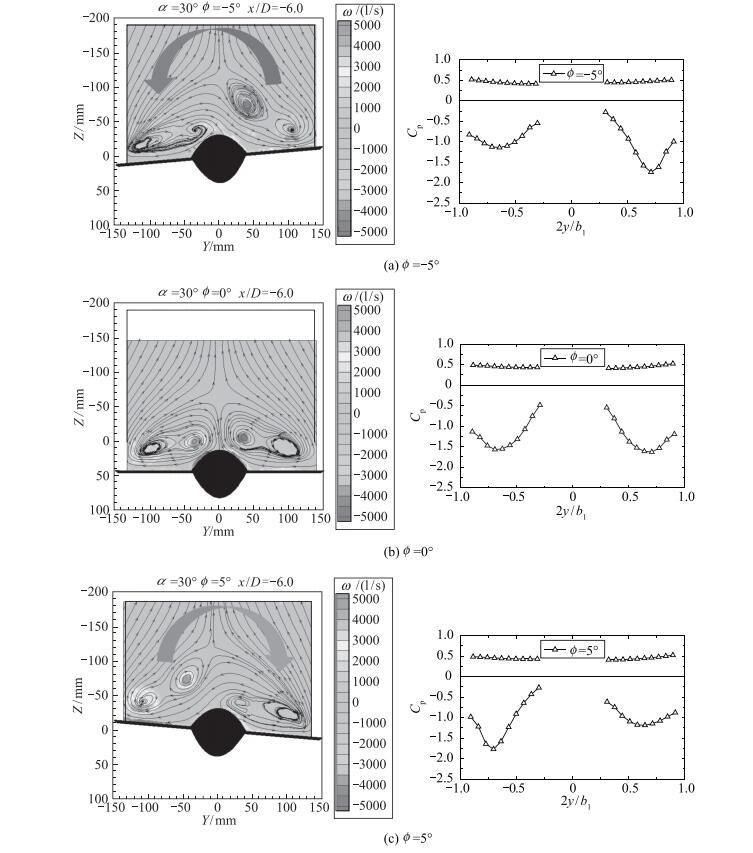
从图 13可以清晰地看到, 当模型的滚转角φ=0°时, 其摇滚运动是不稳定的, 所以, φ=0°是无法成为运动的平衡滚转角的.若模型起始位于φ=0°位置上, 由一个极小滚转力矩的触发而偏到两侧φ > 0°和φ < 0°的稳定位置上, 以它们为平衡位置才能做摇滚运动, 形成侧偏摇滚运动.那么是什么样的流动才能诱发φ=0°时, 模型摇滚运动的不稳定性呢?从图 14中看到, 在φ=0°时导致模型摇滚运动不稳定性是由两侧机翼上不对称的机翼涡涡强诱发的:图中左侧为截面x/D=-6.0背风翼面上的PIV(particle image velocimetry)结果, 其右侧为该截面迎、风面处的压力分布.从图中看到, 当φ=-5°, 其滚转力矩企图往更负的方向发展, 如左图中箭头所示(见图 14(a)).反之亦然(见图 14(c)).从而在φ=0°处显示出运动不稳定性.
|
| 图 13 模型的滚转力矩随滚转角变化的曲线 Fig.13 Variations of rolling moment with roll angle |
|
| 图 14 机翼涡诱发了模型在φ=0°摇滚运动的不稳定性 Fig.14 Instability of rolling motion of the model at φ=0° induced by wing vortex |
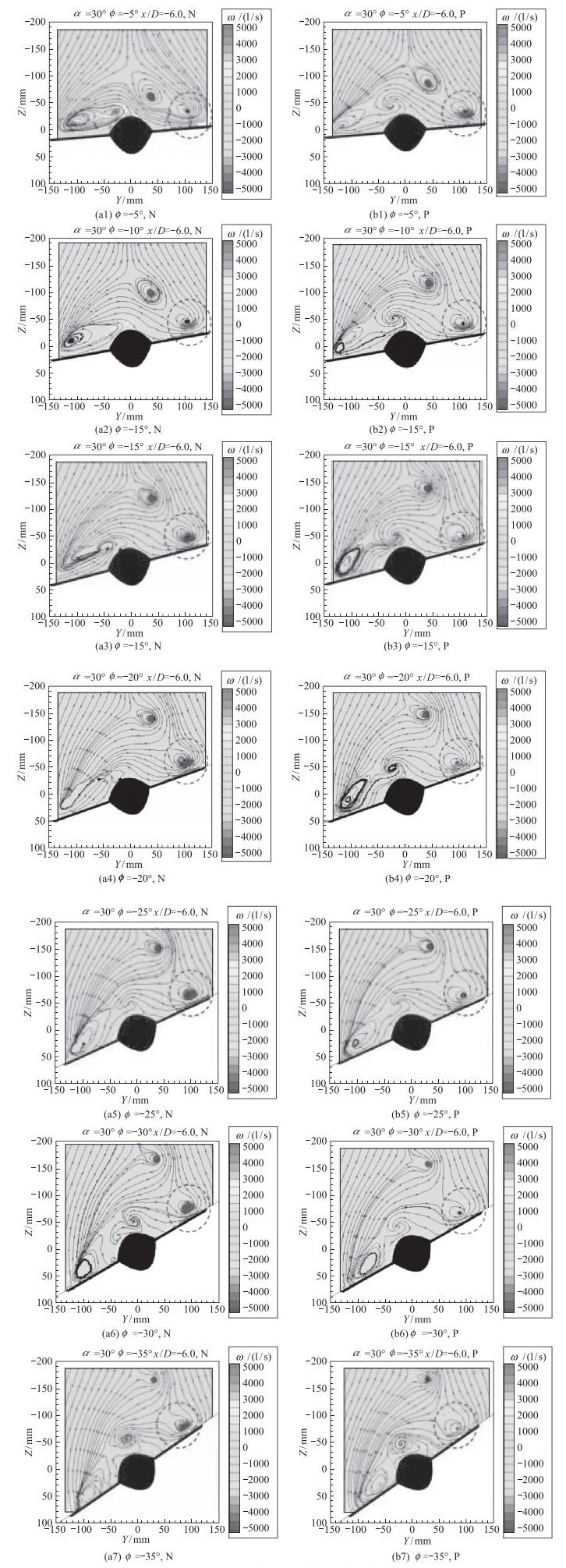
大量的实验证明, 非常规组合体模型的摇滚运动主要源于非对称机翼涡的涡强变化, 如图 15所示.图中模型攻角α=30°, 微颗粒扰动置于前体的右侧.所以, 模型首先向φ < 0°方向偏侧, 以滚转角约为φ=-20°的平衡位置做摇滚运动, 其时间历程曲线如图 16所示.在图 15中, 左侧的PIV是向φ的负向
|
| 图 15 非对称机翼涡流动诱发的模型摇滚运动 Fig.15 Rolling motion induced by the wing asymmetric vortices |
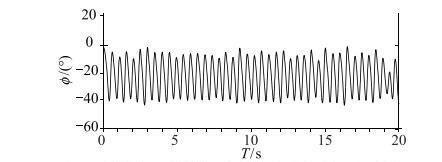
|
| 图 16 非常规组合体模型侧偏自由摇滚时间历程曲线 Fig.16 Time history of side free wing rock of chined body configuration model |
摇滚(如图中N所示), 右侧是向正向摇滚(如图中P所示).先看左侧:随着负向滚转角的增加, 其右涡涡强变大, 直到φ=30°达到最大.其后又开始变小, 直到φ=-38°左右达到最小值, 摇滚切换到正向, 其右翼的涡强从φ=-30°又开始增加,直至φ=-5°.就这样, 周而复始地实现自由摇滚运动.而且可以看到该摇滚运动是由机翼涡主控的.那么该机翼涡是如何形成的?本实验研究进一步证实了非常规组合体模型的机翼涡是由前体非对称涡诱导形成的, 在前体非对称涡高位涡一侧的机翼上形成了机翼涡[20].
2.4 非常规组合体模型非指令摇滚运动的控制上文详细讨论了两类组合体模型的非指令自由摇滚运动的流动机理:旋成体机身/小后掠机翼
的组合体模型的自由摇滚运动是由前体非对称涡主控的, 可用旋转前体头部来抑制非指令摇滚运动.然而, 非常规组合体模型的摇滚运动是由模型的边界条件主控的, 这时不能再用旋转头部的控制技术来抑制非指令摇滚运动, 而应该用改变边界条件的方法来抑制.例如:在模型上设计某种装置, 来破坏前体非对称涡流动(使其破裂), 从而使模型摇滚的机翼涡不再能形成; 或者利用模型布局中的某些装置来直接破坏机翼涡流动(使其破裂), 达到抑制非常规模型自由摇滚运动的目的.
3 结论本文对两类模型的自由摇滚运动进行了研究, 探索其流动机理, 提出抑制摇滚的流动控制方法.得出研究结论如下:
(1) 旋成体组合体模型大攻角下的前体非对称涡流动是不确定的, 其自由摇滚运动也是不确定的, 为了得到确定的前体非对称涡流形和确定的摇滚形态, 必须在模型头尖部适当的周向位置上粘贴人工微扰动.
(2) 为了抑制旋成体组合体模型在大攻角下的非指令摇滚运动, 可采用快速旋转模型头部扰动的流动控制技术来实现.
(3) 非常规组合体模型在大攻角下的前体非对称涡流动仅在φ=0°时是不确定的, 在其他滚转角下都是确定的, 其非指令摇滚运动也是如此, 它是另一类由模型边界条件主控的非对称涡流动和相应的非指令摇滚运动.
(4) 非常规组合体模型在大攻角下的一些运动特性都是由前体非对称涡诱导的机翼涡流动主控的.
(5) 非常规组合体模型在大攻角下的非指令摇滚运动已无法由旋转模型头部扰动的控制方法来抑制, 必须通过改变模型的边界条件来实现.
| [1] | Hunt B L. Asymmetric vortex forces and wakes on slender bodies[R]. AIAA 1982-1336, 1982 https://link.springer.com/article/10.1007/s13272-012-0051-y |
| [2] | Hunt B L, Dexter P C. Pressure on a slender body at high angle of attack in a very low turbulence level airstream[R]. AGARD-CP-247, 1978 http://link.springer.com/article/10.1007%2FBF02485860 |
| [3] | Lamont P J, Hunt B L. Pressure and force distributions on a sharp-nosed circular cylinder at large angles of inclination to a uniform subsonic stream[J]. Journal of Fluid Mechanics, 1976, 76(3): 519-599.DOI:10.1017/S0022112076000773 |
| [4] | Dexter P C, Hunt B L. The effects of roll angle on the flow over a slender body of revolution at high angles of attack[R]. AIAA 1981-0358, 1981 https://link.springer.com/article/10.1007/s11431-009-0120-6 |
| [5] | Zilliac G G, Degani D, Tobak M. Asymmetric vortices on slender body of revolution[J]. AIAA Journal, 1991, 29(5): 667-675.DOI:10.2514/3.59934 |
| [6] | Keener E R, Chapman G T, Cohen L, et al. Side forces on a tangent-ogive forebody with a fineness ratio of 3.5 at high angles of attack and Mach numbers from 0.1 to 0.7[R]. NASA TM X-3437, 1977 |
| [7] | Keener E R, Chapman G T, Cohen L, et al. Side forces on forebodys at high angles of attack and Mach numbers from 0.1 to 0.7 two tangent ogives, paraboloid and cone[R]. NASA TM X-3438, 1977 |
| [8] | Chen X R, Deng X Y, Wang Y K, et al. Influence of nose perturbations on behavior of asymmetric vortices over slender body[J]. Acta Mechanica Sinica, 2002, 18(6): 581-593.DOI:10.1007/BF02487960 |
| [9] | Deng X Y, Wang G, Chen X R, et al. A physical model of asymmetric vortex flow structure in regular state over slender body at high angle of attack[J]. Science in China Series E: Technological Sciences, 2003, 46(6): 561-573.DOI:10.1007/BF02984534 |
| [10] |
徐思文. 快速拉起时前体涡诱导机翼摇滚及其控制[D]. 北京: 北京航空航天大学, 2015
Xu S W. Forebody vortices induced wing rock and its suppression[D]. Beijing: BUAA, 2015(in chinese) http://industry.wanfangdata.com.cn/hk/Magazine?magazineId=bjhkhtdxxb&yearIssue=2015_11 |
| [11] | Wang B, Deng X Y, Ma B F, et al. Effect of tip perturbation and wing locations on rolling oscillation induced by forebody vortices[J]. Acta Mechanica Sinica, 2010, 26: 787-791. |
| [12] |
马宝峰. 前体涡诱导机翼摇滚的实验研究[R]. 博士后研究工作报告, 北京航空航天大学, 2007
Ma B F. Experimental investigation of roll oscillation induced by forebody vortex[R]. A dissertation for Post BUAA, 2007(in Chinese) http://industry.wanfangdata.com.cn/hk/Magazine?magazineId=kqdlxxb&yearIssue=2010_5 |
| [13] | Deng X Y, Shi W, Wang Y K. The investigation of uncommanded motion and its flow mechanism of chined forebody/wing model[A]. //8th Asian-Pacific Conference on Aerospace Technology and Science[C]. Jeju Island, 2015 |
| [14] | Mange R L, Roos F W. The aerodynamics of a chined forebody[R]. AIAA 1998-2903, 1998 https://link.springer.com/article/10.1007/s11431-010-3141-2 |
| [15] | Lamont P J. Pressures around an inclined ogive cylinder with laminar, transitional, or turbulent separation[J]. AIAA Journal, 1982, 20(10): 1492-1499. |
| [16] |
柏楠. 前体非对称涡绕流流场结构的Re数效应研究[D]. 北京: 北京航空航天大学, 2008
Bo N. The study on Reynolds number effect of asymmetric vortices flow structure over forebody[D]. Beijing: BUAA, 2008(in Chinese) http://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU200708008013.htm |
| [17] | Keener E R, Chapman G T. Similarity in vortex asymmetries over slender bodies and wings[J]. AIAA Journal, 1977, 15(9): 1370-1372.DOI:10.2514/3.60795 |
| [18] |
陈学锐. 细长体非对称涡的扰动效应及其主动控制研究[D]. 北京: 北京航空航天大学, 2003
Chen X R. Perturbation effect and active control on behaviors of asymmetric vortices over slender body[D]. Beijing: BUAA, 2003 (in Chinese) http://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU201211007191.htm |
| [19] |
田伟. 细长旋成体及融合体型机身大迎角背涡流动特性研究[D]. 北京: 北京航空航天大学, 2010
Tian W. Study on behaviors of leeward vortices over slender body and chined fuselage at high angle attack[D]. Beijing: BUAA, 2010(in Chinese) http://www.doc88.com/p-6465221148320.html |
| [20] |
石伟. 非常规组合体模型的横向非指令运动及流动机理研究[D]. 北京: 北京航空航天大学, (待发表)
Shi W. Study on uncommanded lateral motions and flow mechanisms of a chined fuselage configuration[D].Beijing: BUAA (in preparation)(in Chinese) |



