飞行器空气动力系统是非线性很强的动力学系统, 如何精确、高效刻画其系统的空气动力数学模型一直是困扰气动界的难题, 也是飞行器设计计算、仿真系统研制和飞行特性分析不可或缺的关键环节[1], 是空气动力学专业最重要的研究方向. 早期Bryan[2]研究了飞机的气动力线性数学模型, Maple等[3]研究了导弹气动力模型的数学形式并给出了一般推导和性质. Zipfel[4]进一步阐述了导弹的气动对称性. Klein[5]研究了飞机大攻角气动力多项式和样条的非线性代数模型. Oh[6]研究了导弹三维气动数学模型的两种具体表达形式, 对模型预测结果进行了试验结果确认. 傅建明[7]研究了喷流姿控战术导弹三维气动力数学模型, 给出了一般推导. 何开锋等[8]根据风洞试验结果建立了有尾翼导弹数学模型. 很明显, 近年来因Taylor-Fourier混合级数气动力数学模型所需样本点少、精度高、适应性广而备受关注和应用推广, 前景灿烂[8]. 但是, 面对飞行试验的气动力辨识和气动力模型修正, 多种风洞试验结果、多次飞行试验结果、多种CFD软件计算结果这三者的不同不确定度的多源数据融合问题, 面对飞行试验连续时序的非模型样本节点融合问题, 状态参数Φ, δP, δY, δR四元解析函数的Taylor-Fourier混合级数业已难以适从, 有待建立空气动力状态参数Ma∞, αΦ, Φ, δP, δY, δR的六元解析函数的新气动模型. 鉴于Taylor-Fourier混合级数气动力数学模型的优点以及Chebyshev多项式具有最大限度地降低Runge现象和对于连续函数最佳一致逼近的特点[9], 用Chebyshev级数建立关于Ma∞, αΦ的二元模型函数, 复合Φ, δP, δY, δR的四元Taylor-Fourier混合级数, 形成Ma∞, αΦ, Φ, δP, δY, δR的六元Chebyshev-Taylor-Fourier混合级数模型函数.
飞行试验气动辨识是利用飞行器遥测和外测(雷测、光测)的过载、角速度、姿态、速度、位置等数据建立描述飞行器基本特性的数学模型的应用性学科, 极大似然准则和最小方差准则是常用的辨识准则[10-12]. 对于给定的候选数学模型集, 根据辨识准则建立辨识方程组后, 系统辨识问题就转化成了一个极值优化计算问题[13]. 目前对应极大似然准则的气动辨识方法有应用最广泛的极大似然法(maximum likelihood estimation,MLE), 它具有完备的理论体系和许多诸如有效性、渐进一致性、渐进正态性等良好的性质[14-15]; 对应最小方差准则的气动辨识方法有原理简练且数值技术有效的最小二乘法[16-17]. 对于假定模型函数形式确定未知参数的线性系统, 最小二乘参数估计方法已有有效实用的软件包.
风洞试验、CFD计算和飞行试验是空气动力数据获取的三大手段. 工程中飞行器风洞试验数据常遇到来源于不同风洞设备的数据, CFD计算数据会遇到来源于不同CFD软件、不同网格形式和数量的数据, 飞行试验数据也面临不同飞行序列的数据, 这些不同来源的数据可能有不同精度和不同不确定度, 如何高效可靠地融合这些参差不齐的数据是型号气动工作者面临的十分棘手的问题. 吉凤贤等[18]基于二次多项式,针对给定的Mach数和攻角状态, 尝试了气动载荷CFD计算与风洞试验数据的融合, 王文正等[19]基于四元解析函数,针对给定的Mach数和攻角状态, 尝试了CFD计算与风洞试验数据的融合, 但这些方法都难以适应飞行试验类宽Mach数和攻角区间的数据融合. 此外,获取气动力数据的三大途径中误差源复杂各异, 且往往不知气动力真值, 难以建立误差传递模型, 需要分析之间复相关性来平衡各数据源间的精度和不确定度.
针对上述需求和问题, 本文发展了一种基于加权最小二乘原理的气动力多源数据融合和气动力辨识方法, 该方法采用二元Chebyshev级数、Taylor级数和Fourier级数技术建立飞行器气动模型函数, 采用权函数技术平衡各数据源间不同精度和不确定度, 采用最小二乘法原理确定超定方程组解, 从而获得Chebyshev-Taylor-Fourier混合级数模型函数的各项参数值, 最终确定多源数据融合的飞行器气动力(力矩)系数模型函数数学表达式. 文中应用实例展示出该方法具有良好的工程应用价值.
1 Chebyshev-Taylor-Fourier混合级数模型函数对于常规的飞行器外形, 定常部分气动力(力矩)可以以来流Mach数Ma∞, 来流合成攻角αΦ, 气流滚转角Φ, 俯仰通道舵偏角δP, 偏航通道舵偏角δY和滚转通道舵偏角δR为自变量建立函数关系. 气流滚转角Φ为自变量的模型函数采用Fourier级数形式逼近, 俯仰通道舵偏角δP, 偏航通道舵偏角δY和滚转通道舵偏角δR三个自变量的模型函数采用Taylor级数形式逼近, 来流Mach数Ma∞, 来流合成攻角αΦ两个自变量的模型函数采用Chebyshev级数形式逼近, 最终飞行器定常部分总气动力(力矩)数学模型由Chebyshev, Taylor和Fourier级数复合, 构成Chebyshev-Taylor-Fourier混合级数模型函数.
1.1 基本概念和定义定义当量舵概念[7]. 假设俯仰、偏航、滚转通道舵偏为δP, δY, δR, 定义
| $ \left\{ {\begin{array}{*{20}{l}} {{\delta _{\rm{P}}} = \delta \cos {\varphi _\delta }}\\ {{\delta _{\rm{Y}}} = \delta \sin {\varphi _\delta }}\\ {{\delta _{\rm{R}}} = {\delta _{\rm{a}}}} \end{array}} \right. $ | (1) |
式中, δ为当量舵偏角, φδ为当量舵滚转角, δa为平均舵偏角.
1.2 混合级数模型函数n角对称指当飞行器连续绕纵轴x轴从一个位置旋转角度ϕ=2π/n至另一位置, 几何外形能完全重叠, 则称为n角对称, 其中n为自然数[7]. 由于气动力随Φ和φδ呈周期性变化, 因而可根据二元Fourier级数展开原理, 将气动力(力矩)表示为
| $ \begin{array}{*{20}{l}} {F\left( {M{a_\infty },{\alpha _\varPhi },\varPhi ,\delta ,{\varphi _\delta },{\delta _{\rm{a}}}} \right) = }\\ {\sum\limits_{p,q = 1}^\infty {\left[ {{a_{p,q}}\sin \left( {p\varPhi + q{\varphi _\delta }} \right) + {b_{p,q}}\cos \left( {p\varPhi + q{\varphi _\delta }} \right)} \right]} } \end{array} $ | (2) |
式中, ap, q, bp, q为关于Ma∞, αΦ, δ和δa的函数.
根据飞行器n角对称性, 旋转角度ϕ=2π/n后要保证气动力不变, 即
| $ \begin{array}{*{20}{l}} {F\left( {M{a_\infty },{\alpha _\varPhi },\varPhi ,\delta ,{\varphi _\delta },{\delta _{\rm{a}}}} \right) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} F\left( {M{a_\infty },{\alpha _\varPhi },\varPhi + \phi ,\delta ,{\varphi _\delta } + \phi ,{\delta _{\rm{a}}}} \right)} \end{array} $ | (3) |
鉴于Φ, δ, φδ, δa的任意性, 必须有
| $ p + q = mn,m = 0, \pm 1, \pm 2, \cdots $ | (4) |
根据飞行器镜面对称性, 纵向分量系数应满足
| $ \begin{array}{l} {F_1}\left( {M{a_\infty },{\alpha _\varPhi },\varPhi ,\delta ,{\varphi _\delta },{\delta _{\rm{a}}}} \right) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {F_1}\left( {M{a_\infty },{\alpha _\varPhi }, - \varPhi ,\delta , - {\varphi _\delta }, - {\delta _{\rm{a}}}} \right) \end{array} $ | (5) |
鉴于Φ, δ, φδ, δa的任意性, 必须有
| $ \left\{ {\begin{array}{*{20}{l}} {{a_{p,q}}\left( {{\delta _{\rm{a}}}} \right) = - {a_{p,q}}\left( { - {\delta _{\rm{a}}}} \right)}\\ {{b_{p,q}}\left( {{\delta _{\rm{a}}}} \right) = {b_{p,q}}\left( { - {\delta _{\rm{a}}}} \right)} \end{array}} \right. $ | (6) |
根据二元Taylor级数展开原理及式(2),(4),(6), ap,q, bp, q分别关于δ和δa的Taylor级数展开, 飞行器纵向分量系数可表示为
| $ \begin{array}{*{20}{c}} {{F_1}\left( {M{a_\infty },{\alpha _\varPhi },\varPhi ,\delta ,{\varphi _\delta },{\delta _{\rm{a}}}} \right) = \sum\limits_{i,j,k,l}^\infty {\left\{ {{a_{i,j,k,l}}\delta _{\rm{a}}^{2l - 1}{\delta ^k}\sin [(ni - } \right.} }\\ {\left. {\left. {j)\varPhi + j{\varphi _\delta }} \right] + {b_{i,j,k,l}}\delta _{\rm{a}}^{2l}{\delta ^k}\cos \left[ {(ni - j)\varPhi + j{\varphi _\delta }} \right]} \right\}} \end{array} $ | (7) |
式中, ai, j, k, l, bi, j, k, l为关于Ma∞, αΦ的函数; i=0, ±1, ±2, …; j=0, 1, 2, …; k=0, 1, 2, …; l=0, 1, 2, ….
根据飞行器镜面对称性, 横侧向分量系数应满足
| $ \begin{array}{l} {F_2}(\left. {M{a_\infty },{\alpha _\varPhi },\varPhi ,\delta ,{\varphi _\delta },{\delta _{\rm{a}}}} \right) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {F_2}\left( {M{a_\infty },{\alpha _\varPhi }, - \varPhi ,\delta , - {\varphi _\delta }, - {\delta _{\rm{a}}}} \right) \end{array} $ | (8) |
鉴于Φ, δ, φδ, δa的任意性, 必须有
| $ \left\{ {\begin{array}{*{20}{l}} {{a_{p,q}}\left( {{\delta _{\rm{a}}}} \right) = {a_{p,q}}\left( { - {\delta _{\rm{a}}}} \right)}\\ {{b_{p,q}}\left( {{\delta _{\rm{a}}}} \right) = - {b_{p,q}}\left( { - {\delta _{\rm{a}}}} \right)} \end{array}} \right. $ | (9) |
根据二元Taylor级数展开原理及式(2),(4),(9), ap, q和bp, q分别关于δ和δa的Taylor级数展开, 飞行器横侧向分量系数可表示为
| $ \begin{array}{*{20}{r}} {{F_2}\left( {M{a_\infty },{\alpha _\varPhi },\varPhi ,\delta ,{\varphi _\delta },{\delta _{\rm{a}}}} \right) = \sum\limits_{i,j,k,l}^\infty {\left\{ {{c_{i,j,k,l}}\delta _{\rm{a}}^{2l}{\delta ^k}\sin [(ni - } \right.} }\\ {\left. {\left. {j)\varPhi + j{\varphi _\delta }} \right] + {d_{i,j,k,l}}\delta _{\rm{a}}^{2l - 1}{\delta ^k}\cos \left[ {(ni - j)\varPhi + j{\varphi _\delta }} \right]} \right\}} \end{array} $ | (10) |
式中, ci, j, k, l, di, j, k, l为关于Ma∞, αΦ的函数; i=0, ±1, ±2, …; j=0, 1, 2, …; k=0, 1, 2, …; l=0, 1, 2, ….
根据二元Chebyshev级数展开原理, ai, j, k, l和bi, j, k, l分别关于Ma∞和αΦ的Chebyshev级数展开后可得:
飞行器纵向分量系数为
| $ \begin{array}{*{20}{l}} {{F_1}\left( {M{a_\infty },{\alpha _\varPhi },\varPhi ,\delta ,{\varphi _\delta },{\delta _{\rm{a}}}} \right) = \sum\limits_{i,j,k,l,r,s}^\infty {\left\{ {{a_{i,j,k,l,r,s}}{T_r}(x) \cdot } \right.} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_s}(y)\delta _{\rm{a}}^{2l - 1}{\delta ^k}\sin \left[ {(ni - j)\varPhi + j{\varphi _\delta }} \right] + {b_{i,j,k,l,r,s}} \cdot }\\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_r}(x){T_s}(y)\delta _{\rm{a}}^{2l}{\delta ^k}\cos \left[ {(ni - j)\varPhi + j{\varphi _\delta }} \right]} \right\}} \end{array} $ | (11) |
飞行器横侧向分量系数为
| $ \begin{array}{l} {F_2}\left( {M{a_\infty },{\alpha _\varPhi },\varPhi ,\delta ,{\varphi _\delta },{\delta _{\rm{a}}}} \right) = \sum\limits_{i,j,k,l,r,s}^\infty {\left\{ {{c_{i,j,k,l,r,s}}{T_r}(x) \cdot } \right.} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_s}(y)\delta _{\rm{a}}^{2l}{\delta ^k}\sin \left[ {(ni - j)\varPhi + j{\varphi _\delta }} \right] + {d_{i,j,k,l,r,s}} \cdot \\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_r}(x){T_s}(y)\delta _{\rm{a}}^{2l - 1}{\delta ^k}\cos \left[ {(ni - j)\varPhi + j{\varphi _\delta }} \right]} \right\} \end{array} $ | (12) |
式中,ai, j, k, l, r, s,bi, j, k, l, r, s,ci, j, k, l, r, s,di, j, k, l, r, s是常系数, Tr和Ts分别是关于Ma∞和αΦ的Chebyshev多项式
| $ \begin{array}{*{20}{c}} {{T_r}(x) = \cos \left( {r{{\cos }^{ - 1}}(x)} \right)}\\ {{T_s}(y) = \cos \left( {s{{\cos }^{ - 1}}(y)} \right)}\\ {x = \frac{{2M{a_\infty } - M{a_{\infty \max }} - M{a_{\infty \min }}}}{{M{a_{ \propto \max }} - M{a_{\infty \min }}}}}\\ {y = \frac{{2{\alpha _\varPhi } - {\alpha _{\varPhi \max }} - {\alpha _{\varPhi \min }}}}{{{\alpha _{\varPhi \max }} - {\alpha _{\varPhi \min }}}}} \end{array} $ | (13) |
式中, r=1, 2, …;s=1, 2, ….
根据飞行器控制舵面的物理意义合理选择k, j的取值, 并应用式(1)和三角函数的倍角公式可将函数F1和F2转换成以Ma∞, αΦ, Φ, δP, δY, δR为自变量的函数形式
| $ \begin{array}{*{20}{l}} {{F_1}\left( {M{a_\infty },{\alpha _\varPhi },\varPhi ,{\delta _{\rm{P}}},{\delta _{\rm{Y}}},{\delta _{\rm{R}}}} \right) = \sum\limits_{i,j,k,l,r,s}^\infty {\left\{ {{a_{i,j,k,l,r,s}}{T_r}(x) \cdot } \right.} }\\ \begin{array}{l} \ \ \ \ \ \ \ \ {T_s}(y)\delta _{\rm{R}}^{2l - 1}\delta _{\rm{P}}^j\delta _{\rm{Y}}^k\sin (i\varPhi ) + {b_{i,j,k,l,r,s}}{T_r}(x) \cdot \\ \ \ \ \ \ \ \ \ \left. {{T_s}(y)\delta _{\rm{R}}^{2l}\delta _{\rm{P}}^j\delta _{\rm{Y}}^k\cos (i\varPhi )} \right\} \end{array} \end{array} $ | (14) |
| $ \begin{array}{*{20}{l}} {{F_2}\left( {M{a_\infty },{\alpha _\varPhi },\varPhi ,{\delta _{\rm{P}}},{\delta _{\rm{Y}}},{\delta _{\rm{R}}}} \right) = \sum\limits_{i,j,k,l,r,s}^\infty {\left\{ {{c_{i,j,k,l,r,s}}{T_r}(x) \cdot } \right.} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_s}(y)\delta _{\rm{R}}^{2l}\delta _{\rm{p}}^j\delta _{\rm{Y}}^k\sin (i\varPhi ) + {d_{i,j,k,l,r,s}}{T_r}(x) \cdot }\\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_s}(y)\delta _{\rm{R}}^{2l - 1}\delta _{\rm{P}}^j\delta _{\rm{Y}}^k\cos (i\varPhi )} \right\}} \end{array} $ | (15) |
利用Taylor级数中幂函数的可导性以及Fourier级数和Chebyshev级数中三角函数系的正交性, 对δP, δY, δR这3个变量求导和对Ma∞, αΦ, Φ这3个变量积分可求取Chebyshev-Taylor-Fourier混合级数中的系数值
| $ \begin{array}{l} {a_{i,j,k,l,r,s}} = \frac{4}{{{{\rm{ \mathsf{ π} }}^{\rm{3}}}}}\int_{ - 1}^1 {\int_{ - 1}^1 {\int_{ - {\rm{ \mathsf{ π} }}}^{\rm{ \mathsf{ π} }} {\frac{{{\partial ^{(j + k + 2l - 1)}} \ \ {F_1}\left( {x,y,\varPhi ,{\delta _{\rm{P}}},{\delta _{\rm{Y}}},{\delta _{\rm{R}}}} \right)}}{{\partial \delta _{\rm{P}}^j\partial \delta _{\rm{Y}}^k\partial \delta _{\rm{R}}^{2l - 1}}}} } } \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{T_r}(x){T_s}(y)}}{{\sqrt {1 - {x^2}} \sqrt {1 - {y^2}} }}\sin (i\varPhi ){\rm{d}}x{\rm{d}}y{\rm{d}}\varPhi \end{array} $ | (16) |
| $ \begin{array}{l} {b_{i,j,k,l,r,s}} = \frac{{4\lambda }}{{{{\rm{ \mathsf{ π} }}^{\rm{3}}}}}\int_{ - 1}^1 {\int_{ - 1}^1 {\int_{ - {\rm{ \mathsf{ π} }}}^{\rm{ \mathsf{ π} }} {\frac{{{\partial ^{(j + k + 2l)}} \ \ {F_1}\left( {x,y,\varPhi ,{\delta _{\rm{P}}},{\delta _{\rm{Y}}},{\delta _{\rm{R}}}} \right)}}{{\partial \delta _{\rm{P}}^j\partial \delta _{\rm{Y}}^k\partial \delta _{\rm{R}}^{2l}}} \cdot } } } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{T_r}(x){T_s}(y)}}{{\sqrt {1 - {x^2}} \sqrt {1 - {y^2}} }}\cos (i\varPhi ){\rm{d}}x{\rm{d}}y{\rm{d}}\varPhi \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} {\lambda = \frac{1}{2},}&{i = 0}\\ {\lambda = 1,}&{i \ne 0} \end{array}} \right. \end{array} $ | (17) |
| $ \begin{array}{l} {c_{i,j,k,l,r,s}} = \frac{4}{{{{\rm{ \mathsf{ π} }}^{\rm{3}}}}}\int_{ - 1}^1 {\int_{ - 1}^1 {\int_{ - {\rm{ \mathsf{ π} }}}^{\rm{ \mathsf{ π} }} {\frac{{{\partial ^{(j + k + 2l)}} \ \ {F_2}\left( {x,y,\varPhi ,{\delta _{\rm{P}}},{\delta _{\rm{Y}}},{\delta _{\rm{R}}}} \right)}}{{\partial \delta _{\rm{P}}^j\partial \delta _{\rm{Y}}^k\partial \delta _{\rm{R}}^{2l}}} \cdot } } } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{T_r}(x){T_s}(y)}}{{\sqrt {1 - {x^2}} \sqrt {1 - {y^2}} }}\sin (i\varPhi ){\rm{d}}x{\rm{d}}y{\rm{d}}\varPhi \end{array} $ | (18) |
| $ \begin{array}{l} {d_{i,j,k,l,r,s}} = \frac{{4\lambda }}{{{{\rm{ \mathsf{ π} }}^{\rm{3}}}}}\int_{ - 1}^1 {\int_{ - 1}^1 {\int_{ - {\rm{ \mathsf{ π} }}}^{\rm{ \mathsf{ π} }} {\frac{{{\partial ^{(j + k + 2l - 1)}} \ \ {F_2}\left( {x,y,\varPhi ,{\delta _{\rm{P}}},{\delta _{\rm{Y}}},{\delta _{\rm{R}}}} \right)}}{{\partial \delta _{\rm{P}}^j\partial \delta _{\rm{Y}}^k\partial \delta _{\rm{R}}^{2l - 1}}} \cdot } } } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{T_r}(x){T_s}(y)}}{{\sqrt {1 - {x^2}} \sqrt {1 - {y^2}} }}\cos (i\varPhi ){\rm{d}}x{\rm{d}}y{\rm{d}}\varPhi \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} {\lambda = \frac{1}{2},}&{i = 0}\\ {\lambda = 1,}&{i \ne 0} \end{array}} \right. \end{array} $ | (19) |
至此飞行器的非线性气动力建模就成为某些未知参数通过多种实验设计来确定的参数估计问题.
工程中往往根据气动力(力矩)的波动情况选定截断阶次逼近, 显然式(14),(15)关于未知系数是线性的, 确定这些系数的方法有两种: 一种是通过公式(16)~(19)数值求导和数值积分计算得到, 这种方法需要足量的数据保证精度; 另一种是通过最小二乘法进行参数估计, 既可适度减少样本点而不失精度, 又能很容易通过加权方法实现多源数据融合, 但是这种方法需要精心选择样本点或设计试验条件来保证数据相容性.
2 加权最小二乘多源数据融合方法众所周知, 最小二乘法是处理超定问题的有效方法. 假定通过不同的观测方法得到若干对观测数据yi及其实验条件(Ma∞, αΦ, Φ, δP, δY, δR)i, 数据拟合的目的就是要利用最小二乘法, 将基于模型函数的计算值与观测量之间的残差平方和最小化, 相应的优化模型如下所示
| $ \begin{array}{l} \min \left\{ {{\chi ^2}} \right\} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_i {{w_i}} {\left[ {{y_i} - F\left( {M{a_{\infty i}},{\alpha _{\varPhi i}},{\varPhi _i},{\delta _{{\rm{P}}i}},{\delta _{{\rm{Y}}i}},{\delta _{{\rm{R}}i}}} \right)} \right]^2} \end{array} $ |
式中, wi为权值, 反映相应观测量的可靠性. 观测量的不确定度越大, 其所分配到的权值就应越小. 然而在很多情况下观测量的可靠性是无法预先获得的, 还需要根据实验条件、实验方法等具体因素对权值进行估计.
2.1 加权线性最小化问题的处理方法选取Chebyshev-Taylor-Fourier混合级数模型函数M项基函数{fi(Ma∞, αΦ, Φ, δP, δY, δR)}线性组合逼近, 即
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {{f_1}\left( {{\mathit{\boldsymbol{x}}_1}} \right)}&{{f_2}\left( {{\mathit{\boldsymbol{x}}_1}} \right)}& \cdots &{{f_M}\left( {{\mathit{\boldsymbol{x}}_1}} \right)}\\ {{f_1}\left( {{\mathit{\boldsymbol{x}}_2}} \right)}&{{f_2}\left( {{\mathit{\boldsymbol{x}}_2}} \right)}& \cdots &{{f_M}\left( {{\mathit{\boldsymbol{x}}_2}} \right)}\\ \vdots & \vdots &{}& \vdots \\ {{f_1}\left( {{\mathit{\boldsymbol{x}}_N}} \right)}&{{f_2}\left( {{\mathit{\boldsymbol{x}}_N}} \right)}& \cdots &{{f_M}\left( {{\mathit{\boldsymbol{x}}_N}} \right)} \end{array}} \right] $ |
引入N×N阶加权矩阵, 如下所示
| $ \mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} {{w_1}}&0&0& \cdots &0\\ 0&{{w_2}}&0& \cdots &0\\ 0&0& \ddots & \cdots &0\\ \vdots & \vdots & \vdots & \ddots &0\\ 0&0& \cdots &0&{{w_N}} \end{array}} \right] $ |
于是多源数据融合问题就转化成求解线性方程组WJa=Wy的问题. 采用广义逆法可得模型参数最小二乘解a=[a1, a2, …aM]T
| $ \mathit{\boldsymbol{a}} = {\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{WJ}}} \right)^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{Wy}} $ |
实际上取矩阵
| $ \mathit{\boldsymbol{ \boldsymbol{\varSigma} }} = \left[ {\begin{array}{*{20}{c}} {\sqrt {{w_1}} }&0&0& \cdots &0\\ 0&{\sqrt {{w_2}} }&0& \cdots &0\\ 0&0& \ddots & \cdots &0\\ \vdots & \vdots & \vdots & \ddots &0\\ 0&0& \cdots &0&{\sqrt {{w_N}} } \end{array}} \right] $ |
方程组ΣJa=Σy的最小二乘解a=(JTΣTΣJ)-1JTΣTΣy=(JTWJ)-1JTWy, 因此可以沿用常规最小二乘法求解ΣJa=Σy, 获取多源数据融合中遇到的加权问题.
2.2 加权矩阵的权值选取策略权值是反映各个观测量对确定模型参数的重要性或可靠性, 加权的基本思想为: 如果观测量yk的不确定度高于yl的不确定度, 那么为其分配的权值wk就应小于wl. 权值取零相当于异常观测值的剔除功能.
理论上, 最优加权值应与单次观测量值无关, 而与观测量的不确定度有关, 即
| $ {w_i} = \frac{1}{{\sigma _i^2}} $ |
式中,σi为观测量中误差的标准不确定度, 该不确定度表示在试验条件下观测量与其真实值之间的偏差, 严格来说它表示误差的标准差.
风洞试验、CFD计算和飞行试验是飞行器气动数据获取的3大手段, 其观测量的可靠度通常与实验条件、实验方法和实验人员等诸多因数相关. 风洞试验观测量的可靠度与尺度模拟、风洞品质、天平精度等因数相关, 其不确定度可以从风洞试验报告中获得标准差σi; CFD计算观测量的可靠度与CFD软件品质、使用人员的经验、网格数量和网格品质等因数相关, 无法直接获得σi, 也没有关于观测量概率分布的先验知识; 飞行试验观测量的可靠度与遥测时滞、加速度计精度、角速度计精度、飞行参数精度和大气参数精度等因数相关, 严格来说也无法直接获得σi, 不过目前普遍对飞行试验的飞行器过载特性、动态响应特性和速度特性给予高度肯定.
3 应用实例和分析为了不失一般性, 选择目前工业部门更为关注的导弹末速精度、过载能力和机动响应特性问题开展应用分析研究. 本文针对某头部Karman曲线和“×”形尾舵布局的无翼尾舵正常式气动布局轴对称战术导弹, 以轴向力、法向力系数以及俯仰力矩系数风洞试验和飞行试验结果为多源数据实例, 选择14×17×25项Chebyshev-Taylor-Fourier混合级数模型函数表达式进行数据融合应用验证.
3.1 纵向气动力分量建模轴对称导弹轴向力系数CA(不含摩擦阻力和底部阻力部分)、法向力系数CN和俯仰力矩系数mz(参考点为弹体头部尖点)的表达式可写为下列统一的函数形式
| $ \begin{array}{l} f = {a_1} + {a_2}\cos (4\varPhi ) + {a_3}\cos (8\varPhi ) + {a_4}\left( {{\delta _{\rm{P}}}\cos \varPhi + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\delta _{\rm{Y}}}\sin \varPhi } \right) + {a_5}\left( {\delta _{\rm{P}}^2 + \delta _{\rm{Y}}^2} \right) + {a_6}\left( {\delta _{\rm{P}}^2 - \delta _{\rm{Y}}^2} \right)\cos (2\varPhi ) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {a_7}\left( {\delta _{\rm{P}}^3\cos \varPhi + \delta _{\rm{Y}}^3\sin \varPhi } \right) + \cdots + {a_{22}}\delta _{\rm{R}}^2{\delta _{\rm{p}}}{\delta _{\rm{Y}}}\left( {{\delta _{\rm{P}}}\sin \varPhi + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\delta _{\rm{Y}}}\cos \varPhi } \right)/\left( {\delta _{\rm{P}}^2 + \delta _{\rm{Y}}^2} \right) + {a_{23}}\delta _{\rm{R}}^2\delta _{\rm{P}}^2\delta _{\rm{Y}}^2/\left( {\delta _{\rm{P}}^2 + \delta _{\rm{Y}}^2} \right) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {a_{24}}\delta _{\rm{R}}^2{\delta _{\rm{p}}}{\delta _{\rm{Y}}}\sin \varPhi + {a_{25}}{\delta _{\rm{R}}}{\delta _{\rm{P}}}{\delta _{\rm{Y}}}\left( {{\delta _{\rm{P}}}\cos \varPhi - } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\delta _{\rm{Y}}}\sin \varPhi } \right)/\left( {\delta _{\rm{P}}^2 + \delta _{\rm{Y}}^2} \right) \end{array} $ | (20) |
式中, ai为Chebyshev多项式
| $ {a_i} = \sum\limits_{r = 1}^{14} {\sum\limits_{s = 1}^{17} {{c_{rs}}} } {T_r}(x){T_s}(y) $ |
x, y定义见(13)式.
为有效降低函数模型插值中的Runge现象, 式(20)中舵偏组合的各舵偏角幂次和最大选择不超过3. 同时为解决矩阵求逆稳健性问题, 式(20)中各舵偏组合的舵偏角统一采用某一最大舵偏角进行条件缩放, 以保持舵偏的条件数值在区间[-1, 1]以内.
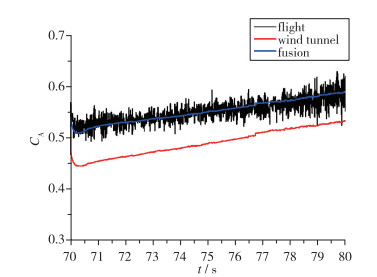
3.2 融合结果分析飞行试验前通过样本点风洞试验设计, 获得25组不同δP, δY, δR, Φ组合, 14个Ma∞和17个αΦ的轴向力系数(不含摩擦阻力和底部阻力部分)、法向力系数和俯仰力矩系数(参考点为弹体头部尖点), 构成方程个数等于未知量个数的方程组, 采用Gauss消元等方法可获得其风洞试验解. 通过对飞行试验的飞行参数、加速度计、角速度计等遥测数据处理分析、补充更多状态的相容气动数据, 选取合理的加权矩阵(本文应用实例认为风洞试验和飞行试验可靠度相当,选为单位矩阵), 构建方程个数多于未知量个数的超定方程组, 采用线性最小二乘广义逆法获得其风洞试验和飞行试验两源数据融合解. 图 1,2, 3分别给出了轴向力系数、法向力系数和俯仰力矩系数的风洞试验结果、飞行试验结果和气动辨识后的两源数据融合结果, 比较表明融合后的模型函数结果与飞行试验结果吻合度很高, 具有良好的工程应用价值.
|
| 图 1 轴向力系数比较 Fig.1 Comparison of axial force coefficients |
|
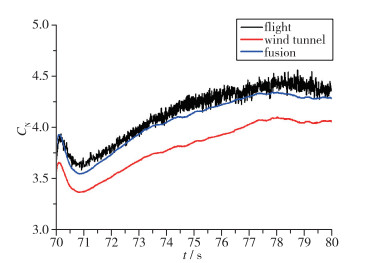
| 图 2 法向力系数比较 Fig.2 Comparison of normal force coefficients |
|
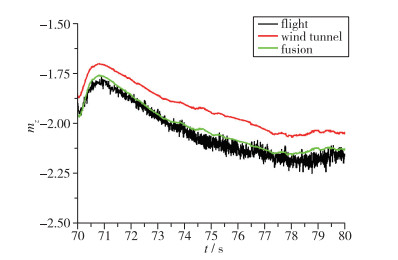
| 图 3 俯仰力矩系数比较 Fig.3 Comparison of pitching moment coefficients |
本文提出了一种基于Chebyshev-Taylor-Fourier混合级数模型函数的多源数据融合方法. 该方法既适用于飞行试验的气动力辨识和气动力模型修正, 也适用于多种风洞试验结果、多次飞行试验结果、多种CFD软件计算结果以及风洞试验结果、CFD计算结果和飞行试验结果的多源数据融合建模. 某轴对称导弹应用实例表明, 该方法融合后的模型函数结果与飞行试验结果吻合度很高, 具有良好的工程应用价值.
| [1] |
刘勇, 阳贵兵. 作战仿真系统可信度评估研究[J]. 空天防御, 2019, 2(2): 49-52. Liu Y, Yang G B. Research on warfare simulation system credibility evaluation[J]. Air & Space Defense, 2019, 2(2): 49-52. (in Chinese) |
| [2] |
Bryan G H. Stability in aviation[M]. London: McMillan and Co., 1911.
|
| [3] |
Maple C G, Synge J L. Aerodynamic symmetry of projectiles[J]. Quarterly of Applied Mathematics, 1949, 6(4): 345-366. DOI:10.1090/qam/28170 |
| [4] |
Zipfel P H. Aerodynamic symmetry of aircraft and guided missiles[J]. Journal of Aircraft, 1976, 13(7): 470-475. DOI:10.2514/3.44536 |
| [5] |
Klein V, Batterson J G. Determination of airplane model structure from flight data using splines and stepwise regression[R]. NASA TP-2126, 1983.
|
| [6] |
Oh Y H. Three dimensional interpolation method for missile aerodynamics[C]. 27th Aerospace Sciences Meeting. Reno, NV: AIAA, 1989.
|
| [7] |
傅建明. 喷流姿控战术导弹三维气动力数学模型[J]. 上海航天, 2005, 22(4): 13-18. Fu J M. Three dimensional aerodynamic mathematical model for tactical missiles with jet steering[J]. Aerospace Shanghai, 2005, 22(4): 13-18. DOI:10.3969/j.issn.1006-1630.2005.04.004 (in Chinese) |
| [8] |
何开锋, 王文正, 钱炜祺. 根据风洞试验结果建立有尾翼导弹数学模型[J]. 流体力学实验与测量, 2004, 18(4): 62-66. He K F, Wang W Z, Qian W Q. Mathematic modeling for the missile aerodynamics with tail-wing according to wind-tunnel test results[J]. Experiments and Measurements in Fluid Mechanics, 2004, 18(4): 62-66. DOI:10.3969/j.issn.1672-9897.2004.04.014 (in Chinese) |
| [9] |
Mason J C, Handscomb D C. Chebyshev polynomials[M]. Boca Raton: Chapman &Hall/CRC Press LLC, 2003.
|
| [10] |
Jategaonkar R V. Flight vehicle system identifica-tion[M]. 2nd ed. Reston: American Institute of Aeronautics and Astronautics, Inc., 2015.
|
| [11] |
Klein V, Morelli E A. Aircraft system identification[M]. Reston: American Institute of Aeronautics and Astronautics, Inc., 2006.
|
| [12] |
Tischer M B, Remple R K. Aircraft and rotorcraft system identification[M]. Reston: American Institute of Aeronautics and Astronautics, Inc., 2006.
|
| [13] |
蔡金狮, 汪清, 王文正, 等. 飞行器系统辨识学[M]. 北京: 国防工业出版社, 2003. Cai J S, Wang Q, Wang W Z, et al. Identification of the aerocraft system[M]. Beijing: National Defence Industry Press, 2003. (in Chinese) |
| [14] |
赵亚男, 钱杏芳. 反坦克导弹气动参数辨识的最大似然法[J]. 兵工学报: 弹箭分册, 1991(4): 13-21. Zhao Y N, Qian X F. A maxinum likelihood method for aerodynamic parameters identification of antitank missile[J]. Journal of China Ordance, 1991(4): 13-21. (in Chinese) |
| [15] |
张天姣, 钱炜祺, 何开锋, 等. 基于最大似然法的风洞自由飞试验气动力参数辨识技术研究[J]. 实验流体力学, 2015, 29(5): 8-14. Zhang T J, Qian W Q, He K F, et al. Research on aerodynamic parameter identification technology in wind tunnel free-flight test based on maximum likelihood estimation[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(5): 8-14. (in Chinese) |
| [16] |
王惠文. 偏最小二乘回归方法及其应用[M]. 北京: 国防工业出版社, 1999. Wang H W. Partial least-squares regression-method and applications[M]. Beijing: National Defense Industry Press, 1999. (in Chinese) |
| [17] |
Tilo S. Data Fitting and Uncertainty[M]. Germany: Vieweg+Teubner Verlag, 2011.
|
| [18] |
吉凤贤, 姚卫星, 何义. 面向MDO的试验结果和数值分析结果的融合方法[J]. 南京航空航天大学学报, 2008, 40(4): 530-533. Ji F X, Yao W X, He Y. Data fusion of experimental and numerical simulation results for MDO[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2008, 40(4): 530-533. DOI:10.3969/j.issn.1005-2615.2008.04.023 (in Chinese) |
| [19] |
王文正, 桂业伟, 何开锋, 等. 基于数学模型的气动力数据融合研究[J]. 空气动力学学报, 2009, 27(5): 524-528. Wang W Z, Gui Y W, He K F, et al. Aerodynamic data fusion technique exploration[J]. ACTA Aerodynamica Sinica, 2009, 27(5): 524-528. DOI:10.3969/j.issn.0258-1825.2009.05.004 (in Chinese) |



