2. 卡拉布里亚大学物理系, 意大利科森扎 87036;
3. 特拉华大学物理与天文系, 美国特拉华州纽瓦克 19716;
4. 北京大学, 北京 100871
2. Dipartimento di Fisica, Università della Calabria, I-87036 Cosenza, Italy;
3. Department of Physics and Astronomy, University of Delaware, Newark DE 19716, USA;
4. Peking University, Beijing 100871, China
湍流普遍存在于空间等离子体中, 如太阳日冕不断向外膨胀从而形成的等离子体流——太阳风, 就呈现出湍流特征[1-4]. 等离子体湍流的高度非线性, 使其包含多尺度(含能尺度区、惯性尺度区、耗散尺度区、离子尺度、电子尺度、Debye长度等)及多过程相互作用. 尺度间的能量级串是湍流研究中一个十分重要的概念, 能量从大尺度逐级向小尺度传递, 直至达到某一足够小的尺度, 能量通过黏性、电阻作用耗散成热. 基于以上物理图像, 学者们提出利用能量级串建立太阳风加热与太阳风湍流发展之间的关系[5]. 卫星观测发现太阳风从日冕向行星际空间膨胀的过程不是绝热膨胀冷却的过程[6], 高温太阳风加热机制是空间物理学的关键前沿课题之一. 此外, 恒星际、星系际间存在有超高能的粒子(宇宙线), 而关于粒子如何加速至高能是长期未得到解决的问题之一. 等离子体湍流耗散作为一种引起粒子加热加速的机制, 具有重要作用. 显然, 对等离子体湍流能量传输和耗散过程的研究有助于理解空间中的许多物理现象.
通过尺度l的能流率是能量传输过程中最基本的量, 能量在无穷大Reynolds数下的惯性区的传输是守恒的, 这意味着能流是常数. 值得注意的是, 这里的能流率指的是净能量传递, 即全场平均, 但局部的能量传输很有可能是间歇过程, 那么局部的能量传输可能与平均值有很大偏离. 为了给出局部的能量传输率, 采用滤波的方法[7]可以得到通过尺度l的亚格子能流Πl(x). 在中性流体湍流中, 局部亚格子能流的空间分布具有间歇性[8-9], 并且可正可负, 可以理解为从局部来看能量可能从大尺度传向小尺度, 亦可从小尺度传向大尺度. 对于等离子体湍流局部的亚格子能流的研究, 在近几年才引起关注, 如Yang等[10-12]采用可压缩磁流体动力学(magnetohydrodynamic, MHD)湍流数值模拟以及全粒子(particle-in-cell, PIC)模拟讨论局部亚格子能流的间歇性, Camporeale等[13]的研究表明, Hall磁流体(Hall magnetohydrodynmic, HMHD)湍流中, 大的局部亚格子能流倾向于在流场的相干结构处发生.
级串的能量被耗散成热最直接的方式是通过磁流体湍流的黏性耗散和电阻耗散, 然而在空间环境中, 带电粒子的平均自由程往往远大于研究对象的特征尺度, 于是一般认为空间等离子体是无碰撞的. 对于无碰撞等离子体湍流, 能量的耗散不能简单地由磁流体湍流模型的黏性、电阻耗散实现, 耗散区如何把扰动的能量传给无碰撞等离子体, 一直是学术界的争论焦点. 基于太阳风湍流的波动性, 太阳风加热所需的能量可能来自波动-粒子相互作用的波动能量[14-16], 如离子回旋波或动理学Alfvén波(kinetic Alfvén wave, KAW)的回旋共振耗散或Landau阻尼耗散. 此外, 数值模拟和卫星观测数据表明, 能量耗散主要在局部发生, 对应有相干结构(如电流片)[17-19]或磁重联[20-21]. 对于无碰撞等离子体能量耗散而言, 哪种机制起主要作用, 甚至哪种波动和粒子的相互作用起主要作用, 仍然是研究的热点.
依据不同的能量耗散机制, 可以给出能量耗散率(粒子加热率). Wan等[22-23]提出将电场对等离子体所做的功j·E作为无碰撞等离子体能量耗散的近似, 其中电流密度j和电场E可直接由卫星观测数据得到, 因此这一结果被广泛应用[24-26]. 电场做功, 代表了电磁能的损失, 但无法确定最终多少能量分别转化为电子、离子的热能. Yang等[11-12]分析压强张量做功(压强张量与速度梯度张量的相互作用,
本文主要从上述3方面: 局部亚格子能流Πl(x), 电场做功j·E, 压强张量做功
对无碰撞等离子体, 可采用Vlasov方程进行统计描述,
| $ \frac{{\partial {f_\alpha }}}{{\partial t}} + \mathit{\boldsymbol{v}} \cdot \frac{{\partial {f_\alpha }}}{{\partial \mathit{\boldsymbol{x}}}} + (\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{v}} \times \mathit{\boldsymbol{B}}) \cdot \frac{{\partial {f_\alpha }}}{{\partial \mathit{\boldsymbol{v}}}} = 0 $ |
式中, fα(x, v, t)为α粒子在相空间(x, v, t)的分布函数, α=i表示离子, α=e表示电子. 位置空间中的宏观量, 如密度、速度、压强、热流等, 可以通过分布函数的矩得到, 以量γ(v)为例, 速度空间积分后得到
| $ \varGamma (\mathit{\boldsymbol{x}},t) = \int \gamma (\mathit{\boldsymbol{v}}){f_\alpha }(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{v}},t){\rm{d}}\mathit{\boldsymbol{v}} $ |
如果把γ(v)取为α粒子的质量mα, 动量mαv, 能量mαv2, Vlasov方程的矩分别对应质量、动量和能量方程
| $ {\frac{{\partial {\rho _\alpha }}}{{\partial t}} + \boldsymbol \nabla \cdot \left( {{\rho _\alpha }{\mathit{\boldsymbol{u}}_\alpha }} \right) = 0} $ | (1) |
| $ \begin{array}{l} {\frac{{\partial \left( {{\rho _\alpha }{\mathit{\boldsymbol{u}}_\alpha }} \right)}}{{\partial t}} + \boldsymbol \nabla \cdot \left( {{\rho _\alpha }{\mathit{\boldsymbol{u}}_\alpha }{\mathit{\boldsymbol{u}}_\alpha }} \right) = }\\ \ \ \ \ { - \boldsymbol \nabla \cdot {\mathit{\boldsymbol{P}}_\alpha } + {q_\alpha }{n_\alpha }\left( {E + {\mathit{\boldsymbol{u}}_\alpha } \times \mathit{\boldsymbol{B}}} \right)}\\ \frac{{\partial {W_\alpha }}}{{\partial t}} + \boldsymbol \nabla \cdot \left( {{W_\alpha }{\mathit{\boldsymbol{u}}_\alpha } + {\mathit{\boldsymbol{P}}_\alpha } \cdot {\mathit{\boldsymbol{u}}_\alpha } + {\mathit{\boldsymbol{h}}_\alpha }} \right) = {q_\alpha }{n_\alpha }{\mathit{\boldsymbol{u}}_\alpha } \cdot \mathit{\boldsymbol{E}} \end{array} $ | (2) |
式中, qα为α粒子电荷量, ρα=mαnα为α粒子质量密度, nα为α粒子数密度, uα为α粒子的流体速度, Pα为压强张量, hα为热流矢量.
| $ {{n_\alpha } = \int {{f_\alpha }} (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{v}},t){\rm{d}}\mathit{\boldsymbol{v}}} $ |
| $ {{\mathit{\boldsymbol{u}}_\alpha } = \frac{1}{{{n_\alpha }}}\int \mathit{\boldsymbol{v}} {f_\alpha }(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{v}},t){\rm{d}}\mathit{\boldsymbol{v}}} $ |
| $ {{\mathit{\boldsymbol{P}}_\alpha } = {m_\alpha }\int {\left( {\mathit{\boldsymbol{v}} - {\mathit{\boldsymbol{u}}_\alpha }} \right)} \left( {\mathit{\boldsymbol{v}} - {\mathit{\boldsymbol{u}}_\alpha }} \right){f_\alpha }(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{v}},t){\rm{d}}\mathit{\boldsymbol{v}}} $ |
| $ {{\mathit{\boldsymbol{h}}_\alpha } = \frac{1}{2}{m_\alpha }\int {{{\left( {\mathit{\boldsymbol{v}} - {\mathit{\boldsymbol{u}}_\alpha }} \right)}^2}} \left( {\mathit{\boldsymbol{v}} - {\mathit{\boldsymbol{u}}_\alpha }} \right){f_\alpha }(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{v}},t){\rm{d}}\mathit{\boldsymbol{v}}} $ |
上述能量Wα可进一步分解为平均部分(流体动能Eαf=ραuα2/2)和随机热运动部分(内能EαI=mα∫(v-uα)2fα(x, v, t)dv/2). 电磁能(Em=(B2+E2)/2)方程可以由Maxwell方程得到.
| $ \begin{array}{*{20}{c}} {\frac{{\partial E_\alpha ^{\rm{f}}}}{{\partial t}} + \boldsymbol \nabla \cdot \left( {E_\alpha ^{\rm{f}}{\mathit{\boldsymbol{u}}_\alpha } + {\mathit{\boldsymbol{P}}_\alpha } \cdot {\mathit{\boldsymbol{u}}_\alpha }} \right) = }\\ {\left( {{\mathit{\boldsymbol{P}}_\alpha } \cdot \boldsymbol \nabla } \right) \cdot {\mathit{\boldsymbol{u}}_\alpha } + {\mathit{\boldsymbol{j}}_\alpha } \cdot \mathit{\boldsymbol{E}}} \end{array} $ | (3) |
| $ {\frac{{\partial E_\alpha ^{\rm{I}}}}{{\partial t}} + \boldsymbol \nabla \cdot \left( {E_\alpha ^{\rm{I}}{\mathit{\boldsymbol{u}}_\alpha } + {\mathit{\boldsymbol{h}}_\alpha }} \right) = - \left( {{\mathit{\boldsymbol{P}}_\alpha } \cdot \boldsymbol \nabla } \right) \cdot {\mathit{\boldsymbol{u}}_\alpha }} $ | (4) |
| $ {\frac{{\partial {E^{\rm{m}}}}}{{\partial t}} + \boldsymbol \nabla \cdot (\mathit{\boldsymbol{E}} \times \mathit{\boldsymbol{B}}) = - \mathit{\boldsymbol{j}} \cdot \mathit{\boldsymbol{E}}} $ | (5) |
式中,
为了研究各尺度间的能量传输, 可采用物理空间滤波器[30]. 低通过滤后的量可记为
| $ {\bar a_l}(\mathit{\boldsymbol{x}}) = \int {{G_l}} (\mathit{\boldsymbol{r}})a(\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{r}}){\rm{d}}\mathit{\boldsymbol{r}} $ |
式中, l为过滤尺度, Gl(r)为滤波函数. 本文采用的是盒式滤波器. 密度加权滤波(Favre滤波)
将质量方程(1)和动量方程(2)作过滤, 可得到α粒子过滤后流体动能
| $ \frac{{\partial \tilde E_\alpha ^{\rm{f}}}}{{\partial t}} + \boldsymbol \nabla \cdot \mathit{\boldsymbol{J}}_\alpha ^u = - \varPi _\alpha ^{uu} - \varPhi _\alpha ^{uT} - \varLambda _\alpha ^{ub} $ | (6) |
式中,
综上所述, 能量传输的主要过程可以用3个量衡量: 代表电磁能与流体动能之间传输的电场做功j·E, 代表流体动能和内能之间传输的压强张量做功
混合Vlasov-Maxwell (hybrid Vlasov-Maxwell, HVM)模拟[31]是将等离子体系统看成由动理离子和流体电子组成, 本文中采用的是冷电子模型. 求解的方程包括3部分:
(1) Vlasov方程用以求离子分布函数fi(x, v, t)
| $ \frac{{\partial {f_{\rm{i}}}}}{{\partial t}} + \mathit{\boldsymbol{v}} \cdot \frac{{\partial {f_{\rm{i}}}}}{{\partial \mathit{\boldsymbol{x}}}} + (\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{v}} \times \mathit{\boldsymbol{B}}) \cdot \frac{{\partial {f_{\rm{i}}}}}{{\partial \mathit{\boldsymbol{v}}}} = 0 $ |
(2) Ohm定律用以求电场E(x, t)
| $ \mathit{\boldsymbol{E}} - d_{\rm{e}}^2{\boldsymbol \nabla ^2}\mathit{\boldsymbol{E}} = - {\mathit{\boldsymbol{u}}_{\rm{i}}} \times \mathit{\boldsymbol{B}} + \frac{{\mathit{\boldsymbol{j}} \times \mathit{\boldsymbol{B}}}}{{{n_{\rm{i}}}}} $ |
(3) Maxwell方程用以求磁场B(x, t)
| $ {\frac{{\partial \mathit{\boldsymbol{B}}}}{{\partial t}} = - \boldsymbol \nabla \times \mathit{\boldsymbol{E}}} $ |
| $ {\boldsymbol \nabla \times \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{j}}} $ |
式中采用离子质量mi, 离子回旋频率的倒数Ωi-1=mic/(eB0)(c为光速, e为离子电荷, B0为背景磁场), Alfvén速度
对于上述Vlasov方程的数值求解, 采用时间分裂法(time splitting method), 在坐标空间x及速度空间v依次进行时间推进. 电磁场的数值求解采用的电流推进方法(current advance method), 算法的细节可参见文献[31]. 本文中的算例是在2.5D-3V相空间进行的模拟, 即坐标空间的矢量有3个方向的分量, 但只依赖于2维的坐标位置(x, y), 速度空间是3维的. 坐标空间的计算域大小为Lx=Ly=L=2π×25di, x, y方向均采用周期边条件, 均匀网格, 网格数为10242, 空间步长约0.15di. 速度空间的计算域
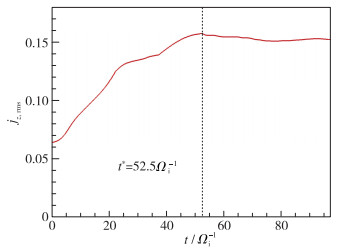
图 1给出了z方向电流密度均方根jz, rms=
|
|
图 1 z方向电流密度均方根 |
|
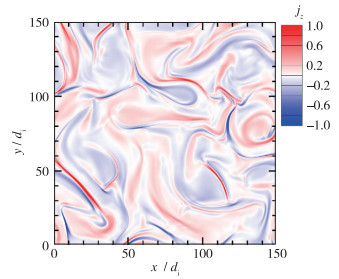
| 图 2 t=t*=52.5Ωi-1时刻, z方向电流密度jz的云图 Fig.2 Contour map of jz at t=t*=52.5Ωi-1 |
|
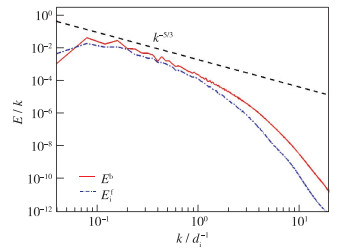
| 图 3 t=t*=52.5Ωi-1时刻, 磁能Eb和离子流体动能Eif的能谱 Fig.3 Energy spectra of magnetic fluctuations Eb and ion bulk flow Eif at t=t*=52.5Ωi-1 |
等离子体湍流包含多种形式的能量, 如流体动能、内能、电磁能, 同时包含多个尺度, 尤其对于宇宙空间中无碰撞或弱碰撞的等离子体, 往往是非平衡的过程, 需要考虑电子、离子的动理学效应. 因此除了磁流体尺度(如含能尺度、惯性尺度、耗散尺度), 还需要考虑更小的动理学尺度行为. 对等离子体湍流的能量传输过程的研究, 可以采用不同的量对其进行表征, 本文将从尺度相关性以及空间相关性研究它们之间的区别与联系.
3.1 能量转换1.1节中方程(3)~(5)给出了电场做功j·E和压强张量做功
将方程(3)作全场平均, 并对时间t进行积分, 可得到离子流体动能随时间的变化方程
| $ \Delta E_{\rm{i}}^{\rm{f}}(t) = \int\limits_0^t {\left\langle {\left( {{\mathit{\boldsymbol{P}}_{\rm{i}}} \cdot \boldsymbol \nabla } \right) \cdot {\mathit{\boldsymbol{u}}_{\rm{i}}}} \right\rangle } {\rm{d}}t + \int\limits_0^t {\left\langle {{\mathit{\boldsymbol{j}}_{\rm{i}}} \cdot \mathit{\boldsymbol{E}}} \right\rangle } {\rm{d}}t $ | (11) |
式中,
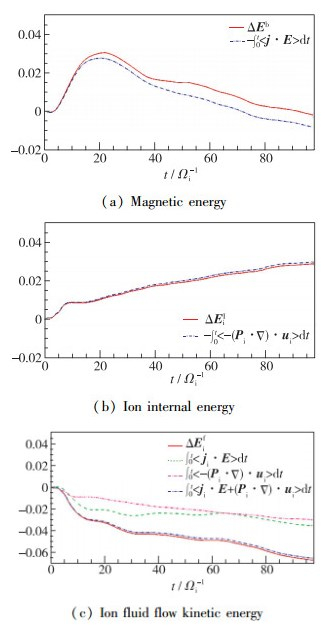
图 4给出了磁能、离子内能、离子流体动能随时间的变化及电场做功和压强张量做功的时间积分. 图 4(a)中磁能的变化与电场做功趋势一致, 它们之间的差异可能是由数值模拟的精度以及时间积分的精度所致. 图 4(b)中离子内能的变化和压强张量做功几乎重合, 而图 4(c)中离子流体动能的变化和电场做功(离子部分)及压强张量做功之和基本重合. 图 4证实了电场做功表示磁能的损失, 其连接了磁能和流体动能, 而压强张量做功表示内能的增加, 其连接了流体动能和内能.
|
| 图 4 全场平均的磁能、离子内能和离子流体动能随时间的变化 Fig.4 Temporal evolution of magnetic energy, ion internal energy and ion fluid flow kinetic energy |
通过滤波, 可以分析不同尺度各能量传输通道的作用. 方程(6)给出了滤波后亚格子应力引起的尺度间的离子动能传输Πiuu,过滤后的离子压强张量做功
|
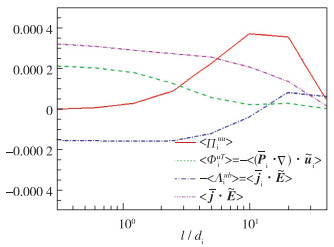
| 图 5 全场平均的离子亚格子能流, 过滤后的离子压强张量做功, 离子部分电场做功,总电场做功, 随过滤尺度l的变化 Fig.5 Volume integrated cross-scale energy transfer flux for ions, filtered pressure tensor work for ions, electric field work on ions and total electric field work, as a function of filtering length l |
整体来看, 亚格子能流〈Πiuu〉为正, 动能从大尺度向小尺度传输. 能量级串理论中, 能量以恒定能流从大尺度向小尺度传输, 该假设在可压缩流体湍流中也得到证实[9, 38], 对于磁流体湍流, 已有的研究[39]表明, 尽管动能在无黏性、无电阻情况下不是守恒量, 但在惯性区动能从大尺度向小尺度传输的能流可以近似认为是恒定的. 图 5中的〈Πiuu〉并没有呈现较长的平台, 这可能是因为本算例的惯性区不够长, Reynolds数不够高. 从图 5中可以看到当l~10di时, 亚格子能流〈Πiuu〉最大, 可以认为其主要作用区域在10di附近.
压强张量做功引起的离子动能和内能之间传输的能流
电场做功引起的动能和磁能之间传输的能流
从以上分析可得到, 亚格子能流Πiuu, 压强张量做功
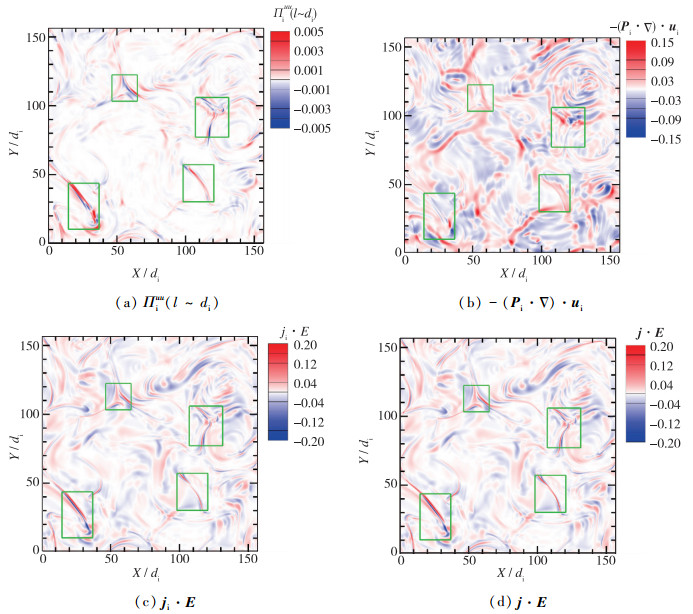
前一节分析了各能量传输项的全场平均的性质, 为了研究它们的空间分布特性, 图 6画出了各能量传输通道的云图. 亚格子能流, 尽管全场来看, 〈Πiuu〉>0, 但局部的亚格子能流可正可负, 意味着局部来看能量可能从大尺度传向小尺度, 或从小尺度传向大尺度. 同样局部的压强张量做功、电场做功也可正可负.
|
| 图 6 离子亚格子能流, 离子压强张量做功, 离子部分电场做功, 总电场做功的云图 Fig.6 Contour maps of cross-scale energy transfer flux for ions, pressure tensor work for ions, electric field work on ions and total electric field work |
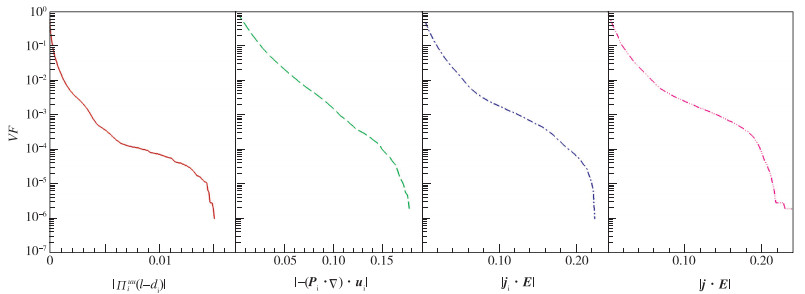
从图 6可以看到, 各能量传输通道的空间分布是极不均匀的, 具有较强的间歇性, 强的能量传输集中在较小区域, 可通过各能量传输通道在空间点取值来说明, 例如对量f(x), 可定义f>f0的体积(或面积)分数VF(f|f0)为整个计算域中满足f>f0的区域与计算域的比. 图 7给出了各能量通道绝对值所占的体积(或面积)分数, 可以看到随着能量传输的增强, 即各能量传输通道的绝对值增大, 其在整个计算域所占的体积(或面积)减小. 如果以能量传输通道的全场最大值的1/5为界, 记为fmax/5, 亚格子能流|Πiuu|>|Πiuu|max/5所占的区域约为计算域的0.2%, 同样的方法可以得到压强张量做功
|
| 图 7 离子亚格子能流, 离子压强张量做功, 离子部分电场做功, 总电场做功绝对值所占的空间体积(或面积)分数 Fig.7 Filling fraction of volume (or area) occupied by absolute values of cross-scale energy transfer flux for ions, pressure tensor work for ions, electric field work on ions and total electric field work |
另一方面, 对比图 6中不同能量传输通道的空间分布, 可发现它们的整体形态是非常相似的, 比如图 6中绿色框标示的部分. 将图 6与图 2对比, 可看到各能量传输通道与电流密度的空间分布也存在一定相似性, 强相干结构处对应着强能量传输, 这与最近研究的结果[22-23, 36, 40-41]是一致的. 为了定量描述它们空间分布的相关性, 可采用不同量之间的统计相关函数, 例如两个量f, g之间的2阶空间相关函数可记作
| $ R(f,g,|\mathit{\boldsymbol{r}}|) = \frac{{\langle (f(\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{r}}) - \langle f\rangle )(g(\mathit{\boldsymbol{x}}) - \langle g\rangle )\rangle }}{{\langle (f(\mathit{\boldsymbol{x}}) - \langle f\rangle )(g(\mathit{\boldsymbol{x}}) - \langle g\rangle )\rangle }} $ |
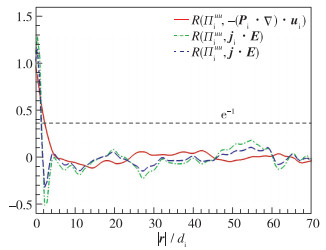
图 8给出了不同间距下各能量传输通道的相关函数, 可看出各能量传输通道的相关函数随着间距|r|的增大而快速减小. 如果利用R(f, g, rc)=e-1(其中e=2.71828…为自然常数)定义相关长度rc, 则可以得到各能量传输通道之间的相关长度大约为2di, 因此各能量传输通道对应的强能量传输的空间位置, 尽管可能不是完全重合, 但距离很近.
|
| 图 8 离子亚格子能流, 离子压强张量做功, 离子部分电场做功, 总电场做功之间的2阶空间相关函数 Fig.8 Second-order spatial correlation functions of cross-scale energy transfer flux for ions, pressure tensor work for ions, electric field work on ions and total electric field work |
从Vlasov-Maxwell方程出发, 可推导出电场做功、压强张量做功、亚格子能流等能量传输通道. 本文通过物理空间滤波, 研究了各能量传输通道的尺度依赖性, 混合Vlasov-Maxwell模拟的结果表明, 电场做功主要集中在较大尺度, 而压强张量做功集中在小尺度, 其间伴随有尺度间的能量传输. 各能量传输通道的空间分布非常相似, 具有强间歇性, 并且与强相干结构相关, 即强能量传输倾向于发生在强相干结构处.
基于以上结果, 并结合近年数值模拟和卫星观测的结果, 可以大致概括等离子体湍流从磁流体尺度到动理学尺度的能量传输主要过程: (1)经典的能量级串概念[42-43]中, 能量从含能尺度输入, 在惯性区级串, 在能量级串的过程中电磁场与流场的间歇性出现, 不断形成多尺度的相干结构; (2)已有的研究表明, 电场做功集中在强电流片处[22-23], 本文结果表明电场做功实现了电磁能与流体动能之间的转化; (3)已有的研究表明, 速度梯度张量会导致压强张量各向异性的产生[37], 于是压强张量做功集中在强变形拉伸(涡结构)处[12, 29, 37], 本文结果验证了压强张量做功能实现流体动能和内能之间的转化, 该过程主要发生在小尺度.
致谢 第一作者感谢南方科技大学校长卓越博士后基金及国家自然科学基金(11902138)的资助. 第二作者感谢国家自然科学基金(91752201, 11672123)的资助. 本研究工作得到南方科技大学科学与工程计算中心支持.| [1] |
Coleman Jr P J. Turbulence, viscosity, and dissipation in the solar-wind plasma[J]. The Astrophysical Journal, 1968, 153: 371-388. DOI:10.1086/149674 |
| [2] |
Goldstein M L, Roberts D A, Matthaeus W H. Magnetohydrodynamic turbulence in the solar wind[J]. Annual Review of Astronomy and Astrophysics, 1995, 33(1): 283-325. DOI:10.1146/annurev.aa.33.090195.001435 |
| [3] |
Tu C Y, Marsch E. MHD structures, waves and turbulence in the solar wind: observations and theories[J]. Space Science Reviews, 1995, 73(1/2): 1-210. DOI:10.1007/BF00748891 |
| [4] |
Bruno R, Carbone V. The solar wind as a turbulence laboratory[J]. Living Reviews in Solar Physics, 2005, 2(1): 4. DOI:10.12942/lrsp-2005-4 |
| [5] |
Tu C Y. The damping of interplanetary Alfvénic fluctuations and the heating of the solar wind[J]. Journal of Geophysical Research: Space Physics, 1988, 93(A1): 7-20. DOI:10.1029/JA093iA01p00007 |
| [6] |
Richardson J D, Paularena K I, Lazarus A J, et al. Radial evolution of the solar wind from IMP 8 to Voyager 2[J]. Geophysical Research Letters, 1995, 22(4): 325-328. DOI:10.1029/94GL03273 |
| [7] |
Germano M. Turbulence: the filtering approach[J]. Journal of Fluid Mechanics, 1992, 238: 325-336. DOI:10.1017/S0022112092001733 |
| [8] |
Chen Q N, Chen S Y, Eyink G L, et al. Intermittency in the joint cascade of energy and helicity[J]. Physical Review Letters, 2003, 90(21): 214503. DOI:10.1103/PhysRevLett.90.214503 |
| [9] |
Wang J C, Yang Y T, Shi Y P, et al. Cascade of kinetic energy in three-dimensional compressible turbulence[J]. Physical Review Letters, 2013, 110(21): 214505. DOI:10.1103/PhysRevLett.110.214505 |
| [10] |
Yang Y, Matthaeus W H, Shi Y P, et al. Compressibility effect on coherent structures, energy transfer, and scaling in magnetohydrodynamic turbulence[J]. Physics of Fluids, 2017, 29(3): 035105. DOI:10.1063/1.4979068 |
| [11] |
Yang Y, Matthaeus W H, Parashar T N, et al. Energy transfer channels and turbulence cascade in Vlasov-Maxwell turbulence[J]. Physical Review E, 2017, 95(6): 061201. DOI:10.1103/PhysRevE.95.061201 |
| [12] |
Yang Y, Matthaeus W H, Parashar T N, et al. Energy transfer, pressure tensor, and heating of kinetic plasma[J]. Physics of Plasmas, 2017, 24(7): 072306. DOI:10.1063/1.4990421 |
| [13] |
Camporeale E, Sorriso-Valvo L, Califano F, et al. Coherent structures and spectral energy transfer in turbulent plasma: a space-filter approach[J]. Physical Review Letters, 2018, 120(12): 125101. DOI:10.1103/PhysRevLett.120.125101 |
| [14] |
Gary S P, Saito S. Particle-in-cell simulations of Alfvén-cyclotron wave scattering: Proton velocity distributions[J]. Journal of Geophysical Research: Space Physics, 2003, 108(A5): 1194. |
| [15] |
He J S, Wang L H, Tu C Y, et al. Evidence of Landau and cyclotron resonance between protons and kinetic waves in solar wind turbulence[J]. The Astrophysical Journal Letters, 2015, 800(2): L31. DOI:10.1088/2041-8205/800/2/L31 |
| [16] |
Hollweg J V, Isenberg P A. Generation of the fast solar wind: A review with emphasis on the resonant cyclotron interaction[J]. Journal of Geophysical Research: Space Physics, 2002, 107(A7): SSH 12-SSh 12137. |
| [17] |
Dmitruk P, Matthaeus W H, Seenu N. Test particle energization by current sheets and nonuniform fields in magnetohydrodynamic turbulence[J]. The Astrophysical Journal, 2004, 617(1): 667-679. DOI:10.1086/425301 |
| [18] |
TenBarge J M, Howes G G. Current sheets and collisionless damping in kinetic plasma turbulence[J]. The Astrophysical Journal Letters, 2013, 771(2): L27. DOI:10.1088/2041-8205/771/2/L27 |
| [19] |
Perri S, Goldstein M L, Dorelli J C, et al. Detection of small-scale structures in the dissipation regime of solar-wind turbulence[J]. Physical Review Letters, 2012, 109(19): 191101. DOI:10.1103/PhysRevLett.109.191101 |
| [20] |
Retinò A, Sundkvist D, Vaivads A, et al. In situ evidence of magnetic reconnection in turbulent plasma[J]. Nature Physics, 2007, 3(4): 235-238. DOI:10.1038/nphys574 |
| [21] |
Sundkvist D, Retinò A, Vaivads A, et al. Dissipation in turbulent plasma due to reconnection in thin current sheets[J]. Physical Review Letters, 2007, 99(2): 025004. DOI:10.1103/PhysRevLett.99.025004 |
| [22] |
Wan M P, Matthaeus W H, Karimabadi H, et al. Intermittent dissipation at kinetic scales in collisionless plasma turbulence[J]. Physical Review Letters, 2012, 109(19): 195001. DOI:10.1103/PhysRevLett.109.195001 |
| [23] |
Wan M P, Matthaeus W H, Roytershteyn V, et al. Intermittent dissipation and heating in 3D kinetic plasma turbulence[J]. Physical Review Letters, 2015, 114(17): 175002. DOI:10.1103/PhysRevLett.114.175002 |
| [24] |
Chasapis A, Matthaeus W H, Parashar T N, et al. In situ observation of intermittent dissipation at kinetic scales in the Earth's magnetosheath[J]. The Astrophy-sical Journal Letters, 2018, 856(1): L19. DOI:10.3847/1538-4357/aaafd1 |
| [25] |
Ergun R E, Goodrich K A, Wilder F D, et al. Magnetic reconnection, turbulence, and particle acceleration: observations in the Earth's magnetotail[J]. Geophysical Research Letters, 2018, 45(8): 3338-3347. DOI:10.1002/2018GL076993 |
| [26] |
Yao Z H, Rae I J, Guo R L, et al. A direct examination of the dynamics of dipolarization fronts using MMS[J]. Journal of Geophysical Research: Space Physics, 2017, 122(4): 4335-4347. DOI:10.1002/2016JA023401 |
| [27] |
Sitnov M I, Merkin V G, Roytershteyn V, et al. Kinetic dissipation around a dipolarization front[J]. Geophysical Research Letters, 2018, 45(10): 4639-4647. DOI:10.1029/2018GL077874 |
| [28] |
Pezzi O, Yang Y, Valentini F, et al. Energy conversion in turbulent weakly-collisional plasmas: Eulerian Hybrid Vlasov-Maxwell simulations[J]. Physics of Plasmas, 2019, 26(7): 072301. DOI:10.1063/1.5100125 |
| [29] |
Chasapis A, Yang Y, Matthaeus W H, et al. Energy conversion and collisionless plasma dissipation channels in the turbulent magnetosheath observed by the magnetospheric multiscale mission[J]. The Astrophysical Journal, 2018, 862(1): 32. DOI:10.3847/1538-4357/aac775 |
| [30] |
Germano A. Turbulence: the filtering approach[J]. Journal of Fluid Mechanics, 1992, 238: 325-336. DOI:10.1017/S0022112092001733 |
| [31] |
Valentini F, Trávníček P, Califano F, et al. A hybrid-Vlasov model based on the current advance method for the simulation of collisionless magnetized plasma[J]. Journal of Computational Physics, 2007, 225: 753-770. DOI:10.1016/j.jcp.2007.01.001 |
| [32] |
Perrone D, Passot T, Laveder D, et al. Fluid simulation of plasma turbulence at ion scales: comparison with Vlasov-Maxwell simulations[J]. Physics of Plasmas, 2018, 25(5): 052302. DOI:10.1063/1.5026656 |
| [33] |
Greco A, Valentini F, Servidio S, et al. Inhomogeneous kinetic effects related to intermittent magnetic discon-tinuities[J]. Physical Review E, 2012, 86(6): 066405. DOI:10.1103/PhysRevE.86.066405 |
| [34] |
Servidio S, Valentini F, Califano F, et al. Local kinetic effects in two-dimensional plasma turbulence[J]. Physical Review Letters, 2012, 108(4): 045001. DOI:10.1103/PhysRevLett.108.045001 |
| [35] |
Servidio S, Valentini F, Perrone D, et al. A kinetic model of plasma turbulence[J]. Journal of Plasma Physics, 2015, 81(1): 325810107. DOI:10.1017/S0022377814000841 |
| [36] |
Parashar T N, Matthaeus W H. Propinquity of current and vortex structures: effects on collisionless plasma hea-ting[J]. The Astrophysical Journal, 2016, 832(1): 57. DOI:10.3847/0004-637X/832/1/57 |
| [37] |
Del Sarto D, Pegoraro F. Shear-induced pressure aniso-tropization and correlation with fluid vorticity in a low collisionality plasma[J]. Monthly Notices of the Royal Astronomical Society, 2018, 475(1): 181-192. DOI:10.1093/mnras/stx3083 |
| [38] |
Aluie H. Compressible turbulence: the cascade and its locality[J]. Physical Review Letters, 2011, 106(17): 174502. DOI:10.1103/PhysRevLett.106.174502 |
| [39] |
Yang Y, Shi Y P, Wan M P, et al. Energy cascade and its locality in compressible magnetohydrodynamic turbule-nce[J]. Physical Review E, 2016, 93(6): 061102. DOI:10.1103/PhysRevE.93.061102 |
| [40] |
Yang Y, Wan M P, Matthaeus W H, et al. Scale dependence of energy transfer in turbulent plasma[J]. Monthly Notices of the Royal Astronomical Society, 2019, 482(4): 4933-4940. DOI:10.1093/mnras/sty2977 |
| [41] |
Sorriso-Valvo L, Perrone D, Pezzi O, et al. Local energy transfer rate and kinetic processes: the fate of turbulent energy in two-dimensional Hybrid Vlasov-Maxwell numerical simulations[J]. Journal of Plasma Physics, 2018, 84(2): 725840201. DOI:10.1017/S0022377818000302 |
| [42] |
Richardson L F. Weather prediction by numerical process[M]. Cambridge: Cambridge University Press, 1922.
|
| [43] |
Frisch U. Turbulence: the legacy of A. N. Kolmogorov[M]. Cambridge: Cambridge University Press, 1995.
|




