当飞机亚声速穿越低温云层时, 空气中的过冷水滴、冰晶等可能会撞击到飞机迎风面的某些部件而结冰, 其中过冷水滴对飞机的性能和安全性影响最大[1].美国NASA飞行事故统计和原因调查报告数据显示, 因结冰造成的事故占所有飞行事故的9%左右[2].所以在各类飞行器设计研制中, 都须考虑结冰防护的问题.目前为止, 热防冰一直是飞机结冰防护的主要方法, 包括热气防冰和电热防冰两类.相关学者通过冰风洞实验[3-4]和仿真计算[5-6]对热气防冰开展了大量研究工作, 并研制出仿真计算软件FENSAP-ICE和LEWICE.近年来学者们对热气防冰内外流场耦合传热方面开展了深入研究, 得到了不少研究结果, 并且有机翼热气防冰系统风洞实验结果的报道[7], 其中热气防冰中最常见的是传热效率较高的笛形管冲击射流防冰, 也是本文主要关注的一种热气防冰方式.
热气防冰是在机翼前缘内部安装笛形管, 从笛形管射流孔喷出热气到前缘金属蒙皮上来实现热传递, 达到防冰目的[8].目前大型客机机翼采用的多是热气防冰, 但从发动机引气有限, 有时能量不足以达到干防冰的效果, 部分水溢流到防冰区外冻结, 形成展向冰脊.冰脊一旦形成, 对飞行安全的威胁程度不亚于前缘积冰, 机翼上冰脊形成之后, 冰脊后的气流严重分离, 将导致飞机升阻比的减小, 带来一系列不利影响.尽管一般的飞机都是对称的, 但是冰脊在机翼上形成的位置和形状一般不对称, 因此会产生一个较大的滚转力矩.若冰脊的形状、位置和大小处于敏感位置, 则会导致飞机滚转失控; 冰脊还会导致副翼流场严重改变, 使得副翼铰链力矩发生严重变化, 极易导致飞行事故[9].所以对热气防冰及冰脊形成的相关研究有其必要性.
本文基于流固耦合传热的思想, 通过求解内外空气流场、水滴撞击特性、结冰与溢流水计算得出相应的数值模拟结果.并根据数值模拟结果, 验证使用方法的合理性、可行性与有效性, 加以定量或定性分析来得出一些有价值的结论, 为今后相关研究提供参考与借鉴.
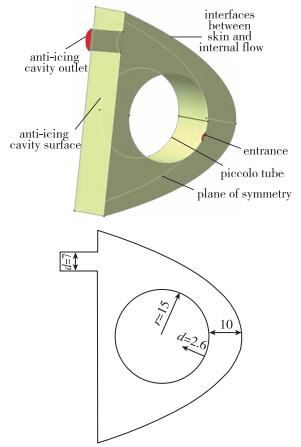
1 数值模拟方法 1.1 防冰系统及数值模拟策略针对热气防冰, 将整个计算域分为3个部分:外流场计算域、防冰腔流场计算域及蒙皮热传导计算域. 图 1为本文模拟热气防冰所采用的防冰腔模型示意图及几何尺寸说明, 模型沿展向厚度为20 mm.因为设计防冰腔须对多个相关参数进行优化来提高其热转化效率[10], 所以本文的模型并不是最优, 但也具有一定的代表性.防冰腔流场计算域由发动机引气, 通过控制引气管道的压强来控制防冰腔的质量流量.文中计算给定防冰腔入口的压力.温度和速度、出口的压力还有交接面温度等边界条件, 进行防冰腔内流动数值模拟.并在此基础上通过蒙皮传热来与外流场耦合, 实现热气防冰.
|
| 图 1 防冰腔模型视图及几何尺寸(mm) Fig.1 Anti-icing cavity model and its geometric size(mm) |
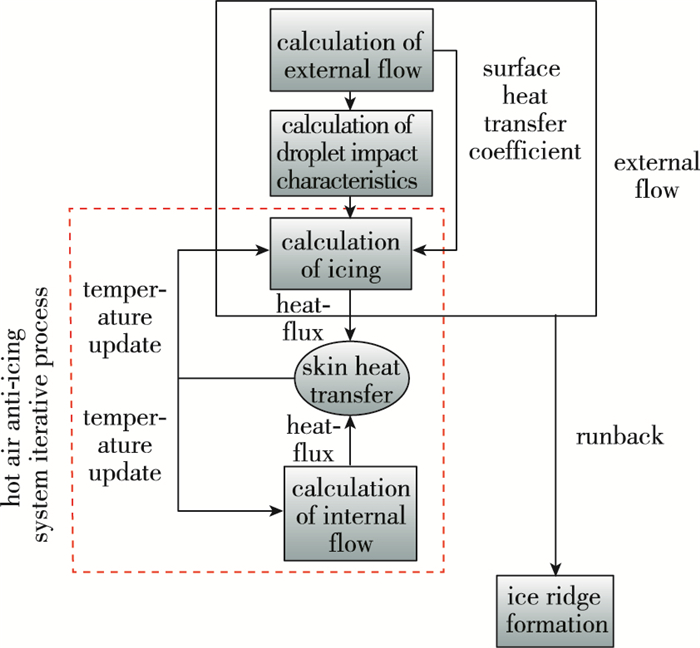
图 2为数值模拟流程图, 首先分别进行内外流场的计算, 计算稳定后, 将其计算结果利用蒙皮与内外流场交接, 进行热传递来实现内外流场耦合传热.计算时先给定蒙皮表面的初始温度, 作为交接面的初值, 内外流场交接面温度不断迭代直至蒙皮表面温度不变.
|
| 图 2 数值模拟流程图 Fig.2 Flowchart of numerical simulation |
空气流场是对质量、动量、能量的偏微分方程求解, 采用经典的Galerkin有限元方法进行空间离散, 采用流线迎风格式, 横向耗散为1×10-9, 迎风方向为2阶精度, 以此来保证数值计算精度, 并消除N-S方程离散项的不稳定性.求解Spalart-Allmaras湍流模型.
对于可压缩流动的质量守恒, 流体的密度与压力和速度不是线性函数, 可以写成如下方程
| $ \frac{{\partial {\rho _{\rm{a}}}}}{{\partial t}} + \nabla \cdot \left( {{\rho _{\rm{a}}}{\mathit{\boldsymbol{V}}_{\rm{a}}}} \right) = 0 $ |
其中, ρa是空气密度, Va是空气速度.对于Newton流体来说, Newton第二运动定律表明作用在流体粒子上的总力等于其动量的时间变化率.在三维流场中的N-S方程如下
| $ \frac{{\partial {\rho _{\rm{a}}}{\mathit{\boldsymbol{V}}_{\rm{a}}}}}{{\partial t}} + \nabla \cdot \left( {{\rho _{\rm{a}}}{\mathit{\boldsymbol{V}}_{\rm{a}}}{\mathit{\boldsymbol{V}}_{\rm{a}}}} \right) = \nabla \cdot {\sigma ^{ij}} + {\rho _{\rm{a}}}\mathit{\boldsymbol{g}} $ |
| $ \begin{array}{l} {\sigma ^{ij}} = - {\delta ^{ij}}{p_{\rm{a}}} + {\mu _{\rm{a}}}\left[ {{\delta ^{jk}}{\nabla _k}{\nu ^i} + {\delta ^{ik}}{\nabla _k}{\nu ^j} - \frac{2}{3}{\delta ^{ij}}{\nabla _k}{\nu ^k}} \right]\\ \;\;\;\;\; = - {\delta ^{ij}}{p_{\rm{a}}} + {\tau ^{ij}} \end{array} $ |
| $ {\tau ^{ij}} = {\mu _{\rm{a}}}\left[ {{\delta ^{jk}}{\nabla _k}{\nu ^i} + {\delta ^{ik}}{\nabla _k}{\nu ^j} - \frac{2}{3}{\delta ^{ij}}{\nabla _k}{\nu ^k}} \right] $ |
其中, pa是静压, μa是动力黏性系数, 由Sutherland经验公式确定.
能量方程
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {{\rho _a}{E_a}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\rho _{\rm{a}}}{V_{\rm{a}}}{H_{\rm{a}}}} \right) = }\\ {\nabla \cdot \left( {{\kappa _{\rm{a}}}\left( {\nabla {T_{\rm{a}}}} \right) + {\nu _i}{\tau _{ij}}} \right) + {\rho _{\rm{a}}}\mathit{\boldsymbol{g}} \cdot {\mathit{\boldsymbol{V}}_{\rm{a}}}} \end{array} $ |
其中, Ea和Ha分别是总内能和焓, κa是热传导率, Ta是空气静温.
1.3 水滴撞击特性计算采用Euler法进行水滴撞击特性计算[11], 把水滴看成连续相, 在流场中, 空气与水滴分别具有各自连续的速度、温度与体积分数分布, 建立水滴控制方程时引入如下假设[9, 12]:
(1) 水滴均匀分布, 以球形存在, 不破裂, 不凝聚, 不发生热交换, 物理参数不变.
(2) 作用于水滴的外力只有空气阻力, 忽略空气浮力、重力以及空气的湍流脉动对水滴运动的影响.
(3) 只考虑空气对水滴的影响, 不考虑水滴对空气的影响.
根据以上假设可以建立水滴的控制方程如下
| $ \begin{array}{*{20}{c}} {\frac{{\partial \alpha }}{{\partial t}} + \nabla \cdot \left( {\alpha {\mathit{\boldsymbol{V}}_{\rm{d}}}} \right) = 0}\\ {\frac{{\partial \left( {\alpha {\mathit{\boldsymbol{V}}_{\rm{d}}}} \right)}}{{\partial t}} + \nabla \left[ {\alpha {\mathit{\boldsymbol{V}}_{\rm{d}}} \otimes {\mathit{\boldsymbol{V}}_{\rm{d}}}} \right] = }\\ {\frac{{{C_{\rm{d}}}R{e_{\rm{d}}}}}{{24K}}\alpha \left( {{\mathit{\boldsymbol{V}}_{\rm{a}}} - {\mathit{\boldsymbol{V}}_{\rm{d}}}} \right) + \alpha \left( {1 - \frac{{{\rho _{\rm{a}}}}}{{{\rho _{\rm{d}}}}}} \right)\frac{1}{{F{r^2}}}} \end{array} $ |
其中, α和Vd分别为水滴的含量和速度.动量方程右侧第1项为施加在水滴平均直径的阻力, 其正比于相对速度, 水滴Reynolds数Red见下式, 其中d为水滴直径
| $ R{e_{\rm{d}}} = \frac{{{\rho _{\rm{a}}}{\rm{d}}{V_{{\rm{a}},\infty }}\left\| {{V_{\rm{a}}} - {V_{\rm{d}}}} \right\|}}{{{\mu _{\rm{a}}}}} $ |
其中, K为惯性参数, K=ρdd2Va, ∞/(18L∞μa), L∞为特征长度.
水滴阻力系数Cd为
| $ {C_{\rm{d}}} = \left\{ {\begin{array}{*{20}{l}} {\left( {24/R{e_{\rm{d}}}} \right)\left( {1 + 0.15Re_{\rm{d}}^{{\rm{0}}.687}} \right)\left( {R{e_{\rm{d}}} \le 1300} \right)}\\ {0.4\left( {R{e_{\rm{d}}} > 1300} \right)} \end{array}} \right. $ |
方程右侧第2项表示浮力与重力, 正比于局部Froude数.
| $ Fr = \frac{{\left\| {{V_{{\rm{a}},\infty }}} \right\|}}{{\sqrt {{L_\infty }g} }} $ |
在获得水滴的流场信息之后, 计算当地水滴收集系数β.
| $ \beta = - \alpha {\mathit{\boldsymbol{V}}_{\rm{d}}} \cdot \mathit{\boldsymbol{n}} $ |
因此, 壁面上水滴撞击质量可以表示为下式, 其中LWC为液态水含量, V∞为自由来流速度.
| $ {{\dot m}_{\rm{w}}} = \beta {\rm{LWC}}{{\rm{V}}_\infty } $ |
采用经典的Galerkin有限元方法求解离散方程, 水滴求解是时间推进的, 对于1个单元, 当地时间步的选择基于显式Euler中心有限差分格式的稳定性分析, 这种格式将会提供一个最大理论时间步Δtstab, 采用这个时间步推进, 直到计算达到一个稳态.每一个时间步, 只须一次Newton迭代即可使其线性化.计算停止的条件为:控制方程的总残差收敛水平达到1×10-8.
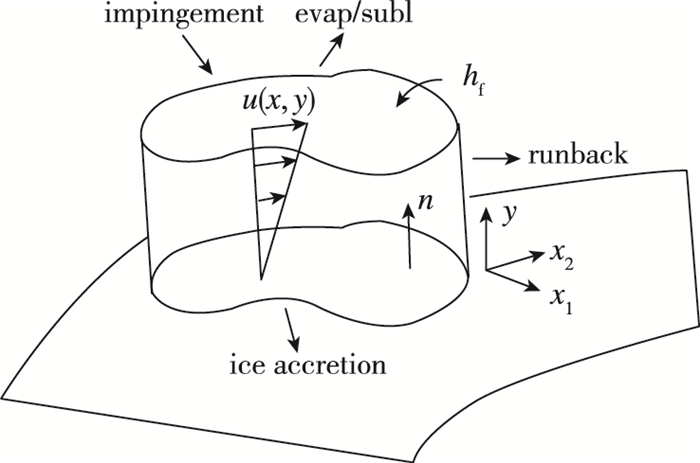
1.4 结冰与溢流水计算图 3为结冰与溢流传热传质现象的模型[13], 在固体表面由于水滴撞击形成水膜, 水膜在气流剪切力作用下向后流动, 基于表面热力学条件, 部分水膜可能结冰、蒸发或升华.
|
| 图 3 结冰与溢流模型 Fig.3 Icing and runback model |
水膜的速度是表面坐标x=(x1, x2)和表面的法线y的函数.通过引入垂直于墙壁的水膜速度(x, y), 在壁面速度为0, 简化了这个问题.
| $ {\mathit{\boldsymbol{V}}_{\rm{f}}}(\mathit{\boldsymbol{x}},y) = \frac{y}{{{\mu _{\rm{f}}}}}{\mathit{\boldsymbol{\tau }}_{{\rm{a}},{\rm{wall}}}}(\mathit{\boldsymbol{x}}) $ |
其中, 空气的剪切应力τa, wall是水膜的主要驱动力, 这种假设适合水膜很薄条件下使用, 在结冰和防冰数值模拟中水膜厚度很少大于10 μm, 所以适合使用这种假设, 通过在水膜厚度上平均水膜速度, 水膜平均速度可以推导出来
| $ {\mathit{\boldsymbol{V}}_{\rm{f}}}(\mathit{\boldsymbol{x}},y) = \frac{1}{{{h_{\rm{f}}}}}\int_0^{{h_{\rm{f}}}} {{\mathit{\boldsymbol{V}}_{\rm{f}}}(\mathit{\boldsymbol{x}},y){\rm{d}}y} = \frac{{{h_{\rm{f}}}}}{{2{\mu _{\rm{f}}}}}{\mathit{\boldsymbol{\tau }}_{{\rm{a}},{\rm{ wall }}}}(\mathit{\boldsymbol{x}}) $ |
结冰计算假设水膜是连续的, 在所有壁面上求解质量和能量两个偏微分方程:
质量守恒
| $ {\rho _{\rm{f}}}\left[ {\frac{{\partial {h_{\rm{f}}}}}{{\partial t}} + \nabla \cdot \left( {{\mathit{\boldsymbol{V}}_{\rm{f}}}{h_{\rm{f}}}} \right)} \right] = {V_\infty }{\rm{LWC}}\beta - {{\dot m}_{{\rm{evap}}}} - {{\dot m}_{{\rm{ice}}}} $ |
右边3项分别是:水滴撞击收集的质量, 蒸发的质量, 结冰的质量.
能量守恒
| $ \begin{array}{l} {\rho _{\rm{f}}}\left[ {\frac{{\partial {h_{\rm{f}}}{c_{\rm{f}}}{T_{\rm{f}}}}}{{\partial t}} + \nabla \cdot \left( {{\mathit{\boldsymbol{V}}_{\rm{f}}}{h_{\rm{f}}}{c_{\rm{f}}}{T_{\rm{f}}}} \right)} \right] = \\ \;\;\;\;\left[ {{c_{\rm{f}}}\left( {{T_\infty } - {T_{\rm{f}}}} \right) + \frac{{{{\left\| {{{\mathit{\boldsymbol{\overline V}} }_{\rm{d}}}} \right\|}^2}}}{2}} \right]{V_\infty }{\rm{LWC}}\beta - {L_{{\rm{evap }}}}{{\dot m}_{{\rm{evap}}}} + \\ \;\;\;\;\left( {{L_{{\rm{fusion }}}} - {c_{\rm{s}}}T} \right){{\dot m}_{{\rm{ice}}}} + \sigma \varepsilon \left( {T_\alpha ^4| - T_{\rm{f}}^4} \right) - {c_{\rm{h}}}\left( {{T_{\rm{f}}} - } \right.\\ \;\;\;\;\left. {{T_{{\rm{ice}},{\rm{ rec }}}}} \right) + {Q_{\rm{h}}} \end{array} $ |
右边的前3项是水滴撞击、蒸发、结冰产生的热传递, 后边3项是辐射、对流、一维热通量, ρf, cf分别为水膜的密度和比热, cs为冰的比热, σ为Boltzmann常数, ε为发射率, Lfusion为融化潜热, Levap为蒸发潜热. V∞, T∞, LWC是给定条件.剪切应力τa, wall, 对流热通量Qh, 由空气流场求解出.水滴撞击求解出水滴收集系数β, 水滴撞击速度Vd, 3个未知参数需要去求解:水膜厚度hf, 平衡温度Tf, 结冰的瞬时质量增加mice.考虑他们之间的关系来闭合方程组
| $ \left\{ {\begin{array}{*{20}{l}} {{h_{\rm{f}}} \le 0}\\ {{{\dot m}_{{\rm{ice}}}} \ge 0}\\ {{h_{\rm{f}}}{T_{\rm{f}}} \ge 0}\\ {{{\dot m}_{{\rm{ice}}}}{T_{\rm{f}}} \le 0} \end{array}} \right. $ |
这些不等式保证在平衡温度低于273.15 K时没有液态水, 水膜温度高于273.15 K没有冰生成.
2 算例分析 2.1 热气防冰分析计算模型如图 1所示, 采用ICEM对计算域进行网格划分, 图 4为内流场、外流场及蒙皮计算网格图.物面第1层网格Y+值均小于1, 为了更加准确地模拟复杂防冰腔内流动, 对防冰腔流场计算域的网格同样进行了加密, 并且在笛形管射流口处进行了局部加密, 网格量总数约为1.14×106.为了提高机翼前缘水滴撞击特性和结冰时溢流水的计算准确性, 首先对机翼前缘进行网格加密, 外流场网格数约为5.5×105.其次, 前缘加热区蒙皮的网格数约为8×104, 蒙皮厚度为1 mm.参考热气防冰相关文献[14-17]给出本文所选用的计算条件如表 1所示.

|
| 图 4 热气防冰计算网格图 Fig.4 Computational grids of hot air anti-icing |
| 下载CSV 表 1 热气防冰计算条件参数 Tab.1 Calculation parameters of hot air anti-icing |
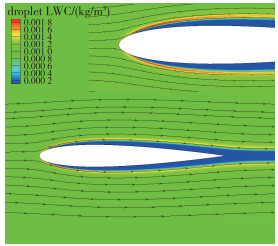
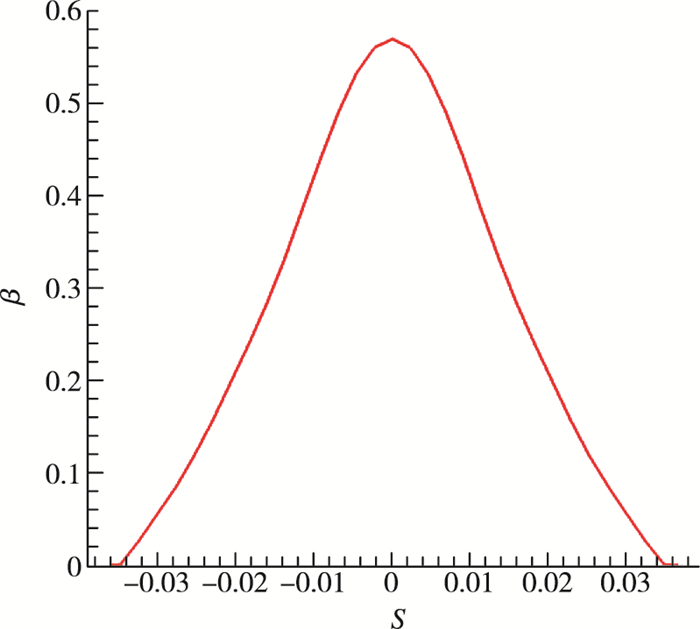
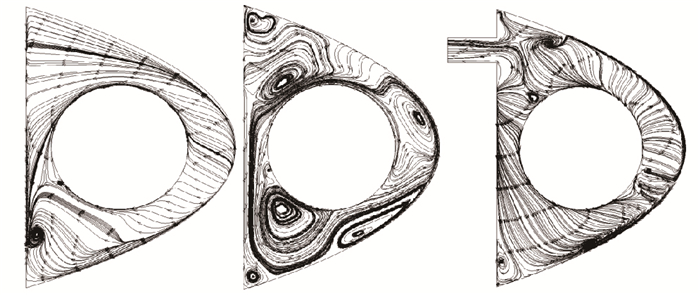
图 5为液态水含量与水滴运动轨迹数值模拟结果图, 因为水滴的平均直径为20 μm, 为小水滴, 忽略了水滴的重力、浮力、湍流脉动对水滴运动的影响, 所以水滴的运动轨迹与来流空气的运动轨迹基本一致, 因此遮蔽区边界比较明显, 遮蔽区里的液态水含量为零. 图 6为水滴收集系数, 纵坐标为水滴收集系数β, 横坐标S为距前缘点的弧长, 可以看出驻点处水滴收集系数最大, 约为0.58, 沿驻点向后递减至0.在参考文献[10]中也得到相似的计算结果, 验证了该方法对于水滴撞击计算的准确性. 图 7为防冰腔空间流线图, 从图 7可以看出, 由于射流的高速撞击和防冰腔的复杂结构, 腔内流动对比外流场显得十分复杂, 特别是在射流入口区域, 流线急剧弯曲, 在绕过笛形管从防冰腔出口流出, 腔内复杂的流动在一定程度上提高了热气利用率. 图 8为防冰腔不同截面流线图, 也可以看出不同截面流动差别很大, 体现腔内三维流动效应明显.因此, 为了提高热气利用率, 在今后防冰系统设计过程中应当合理设计防冰腔内流动形态, 争取可以最大限度利用热气携带的热量.
|
| 图 5 液态水含量与水滴运动轨迹 Fig.5 Liquid water content and water droplet track |
|
| 图 6 水滴收集系数 Fig.6 Droplet collection efficiency |

|
| 图 7 防冰腔空间流线图 Fig.7 Streamlines of internal flow |
|
| 图 8 防冰腔截面流线图 Fig.8 Streamlines of different sections of internal flow |
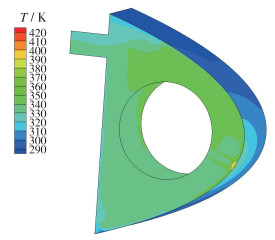
图 9为外流场表面剪切应力云图, 因为壁面剪切应力是水膜运动的主要驱动力, 可以从图中看出剪切应力从前缘向两侧先增加再减小, 与来流空气流向速度特性相符. 图 10为内外流场耦合后防冰腔表面温度分布, 腔内温度大多集中在350 K左右, 射流孔对应的防冰腔前缘处温度最高可达420 K, 温度向周围扩散逐渐减小, 与参考文献[16]中壁面温度分布规律相符, 验证了方法的合理性.

|
| 图 9 外流场表面剪切应力云图 Fig.9 Shear stress contour of external flow |
|
| 图 10 防冰腔表面温度分布 Fig.10 Temperature distribution of antiicing cavity surface |
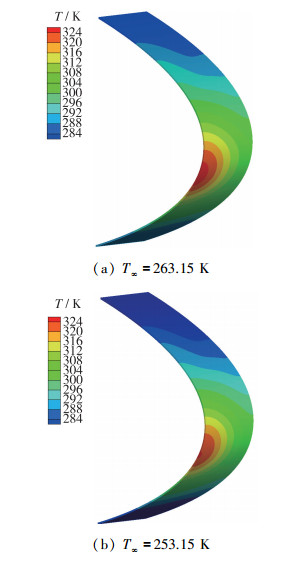
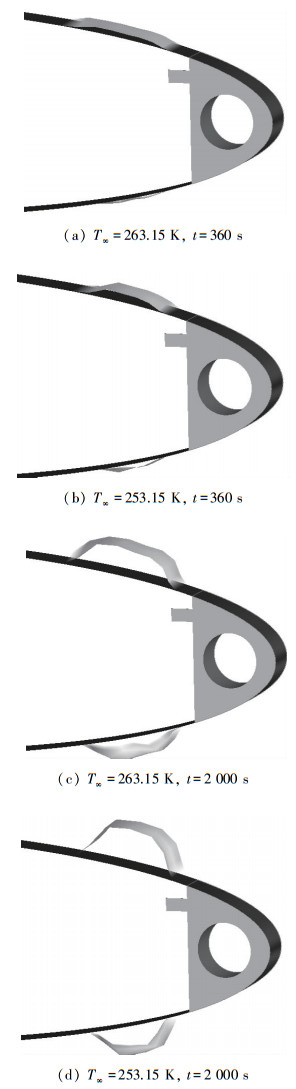
图 11为机翼表面蒙皮温度分布, 从图中可以看出前缘加热区温度均高于273.15 K, 可以保证前缘防冰区没有积冰.但是因为防冰腔热量供给不足, 达不到干防冰的要求, 表面形成水膜会溢流到防冰区外形成冰脊[16].如图 12所示, 冰脊的严重程度与积冰时间和环境温度有关, 所以本文对积冰时间与环境温度形成冰脊对气动特性的影响进行了分析.
|
| 图 11 机翼表面蒙皮温度分布 Fig.11 Temperature distributions of wing skin surface |
|
| 图 12 不同条件下冰脊形成图 Fig.12 Ice ridge formation under different conditions |
从表 2中对比看到, 热气防冰系统开启后形成冰脊会对整个绕流流场的气动特性有很大影响, 当积冰时间相同的时候, 环境温度降低升力减小, 阻力增加更明显; 当环境温度相同的时候, 积冰时间越长升力减小, 阻力增加越明显.
| 下载CSV 表 2 冰脊形成对气动特性的影响 Tab.2 Influence of ice ridge formation on aerodynamic characteristics |
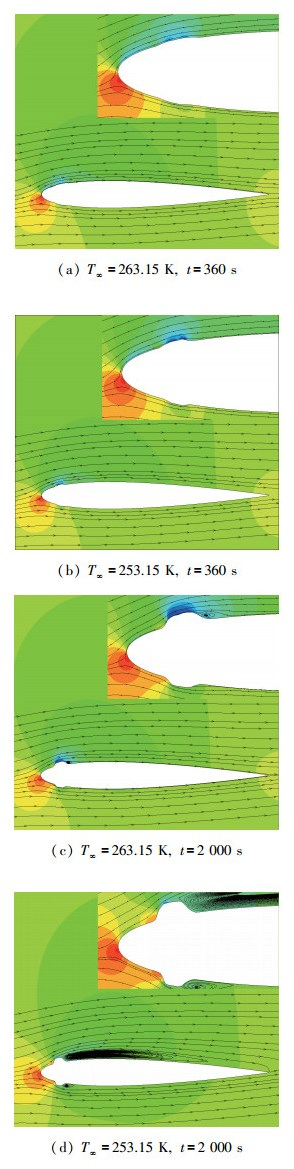
从图 13中对比看到, 环境温度T=253.15 K, 积冰时间t=2 000 s的时候形成的冰脊对原流场的破坏较大, 导致来流流过冰脊后在上表面形成了一个较长的分离泡, 非定常特性明显, 可能导致飞机失稳, 加大飞机操纵难度, 增加飞行危险性.
|
| 图 13 冰脊形成后绕流流场变化图 Fig.13 Influence of ice ridge formation on flow |
本文将热气防冰与冰脊形成数值模拟紧密地结合在一起, 得到的结论有:
(1) 实现热气防冰动态流动的数值模拟, 并对数值模拟结果的合理性进行分析, 证实该方法的可行性和有效性.在后续的工作中会对比、验证现有公开的文献和实验数据, 来确定方法的准确性.
(2) 防冰腔内部流场相对复杂, 在设计的过程中应该充分利用热气携带的热量, 尽量避免流动死水区的形成, 保证热气与蒙皮更多的接触, 提高热气利用率.
(3) 在环境温度很低的情况下热气防冰的开启应当充分考虑到冰脊形成的问题, 因为环境温度低防冰需要更多的能量, 如果能量的供给不合适, 即便除掉了前缘积冰, 但是在防冰区外迅速形成展向冰脊, 其危害可能会比前缘积冰更加严重, 对飞行安全造成更大的威胁.
| [1] |
Bragg M B, Perkins W R, Sarter N B, et al. An interdisciplinary approach to inflight aircraft icing safety[R]. AIAA 1998-0095, 1998.
|
| [2] |
Jones S M, Reveley M S, Evans J K, et al. Subsonic aircraft safety icing study[R]. NASA/TM-2008-215107, 2008.
|
| [3] |
Papadakis M, Wong S H, Yeong H W, et al. Icing tunnel experiments with a hot air anti-icing system[R]. AIAA 2008-444, 2008.
|
| [4] |
Souder R H, Sheldon D W, Ide R F, et al. NASA Glenn icing research tunnel user manual[R]. NASA TM 2003-212004, 2003.
|
| [5] |
Planquart P, Vanden B G, Buchlin J M. Experimental and numerical optimization of a wing leading edge hot air anti-icing system[R]. AIAA 2005-1227, 2005.
|
| [6] |
Pellissier F, Habashi W, Pueyo A. Design optimization of hot-air anti-icing systems by FENSAP-ICE[R]. AIAA 2010-1238, 2010.
|
| [7] |
霍西恒, 王大伟, 李革萍, 等. 某型飞机机翼防冰系统性能验证研究[J]. 民用飞机设计与研究, 2013(4): 13-16, 45. Huo X H, Wang D W, Li G P, et al. Research of wing anti-ice system performance validation for civil aircraft[J]. Civil Aircraft Design & Research, 2013(4): 13-16, 45. DOI:10.3969/j.issn.1674-9804.2013.04.004 (in Chinese) |
| [8] |
Wong S H, Papadakis M, Wong J. CFD analysis of a wing with a bleed air ice protection system[R]. AIAA 2013-2935, 2013.
|
| [9] |
易贤.飞机积冰的数值计算与积冰试验相似准则研究[D].绵阳: 中国空气动力研究与发展中心, 2007. Yi X. Numerical computation of aircraft icing and study on icing test scaling law[D]. Mianyang: China Aerodynamics Research and Development Center, 2007(in Chinese). |
| [10] |
王昆, 白俊强, 夏露, 等. 飞机热气防冰系统与冰脊预测的数值模拟[J]. 航空动力学报, 2014, 29(11): 2695-2703. Wang K, Bai J Q, Xia L, et al. Numerical simulation of aircraft hot air anti-icing system and ice ridge predic-tion[J]. Journal of Aerospace Power, 2014, 29(11): 2695-2703. (in Chinese) |
| [11] |
Bourgault Y, Boutanios Z, Habashi W G. Three-dimensional Eulerian approach to droplet impingement simula-tion using FENSAP-ICE, Part 1:model, algorithm, and validation[J]. Journal of Aircraft, 2000, 37(1): 95-103. DOI:10.2514/2.2566 |
| [12] |
胡剑平, 刘振侠, 张丽芬. 霜状冰结冰数值模拟研究[J]. 航空计算技术, 2011, 41(6): 8-11. Hu J P, Liu Z X, Zhang L F. Numerical simulation of 3D rime ice[J]. Aeronautical Computing Technique, 2011, 41(6): 8-11. DOI:10.3969/j.issn.1671-654X.2011.06.003 (in Chinese) |
| [13] |
Bourgault Y, Beaugendre H, Habashi W. Development of a shallow-water icing model in FENSAP-ICE[J]. Journal of Aircraft, 2000, 37(4): 604-646. |
| [14] |
Saeed F, Paraschivoiu I. Optimization of a hot-air anti-icing system[R]. AIAA 2003-733, 2003.
|
| [15] |
Planquart P, Vanden B G, Buchlin J M. Experimental and numerical optimization of a wing leading edge hot air anti-icing system[R]. AIAA 2005-1277, 2005.
|
| [16] |
Papadakis M, Wong S H, Yeong H W, et al. Icing tunnel experiments with a hot air anti-icing system[R]. AIAA 2008-444, 2008.
|
| [17] |
De Santos L C, Domingos R H, Maria R B, et al. Sensitivity analysis of a bleed air anti-ice thermal model to geometrical and operational parameters[R]. AIAA 2008-0445, 2008.
|




