2. 中国科学院大学工程科学学院,北京 100049
2. College of Sciences and Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
有关Rayleigh-Bénard热对流的研究通常采用Boussinesq假设, 即假定流体的热物性参数均为常数, 只考虑体积力中流体密度随温度的变化, 且假定密度是温度的线性函数.基于Boussinesq假设得到的解即为通常所关注的常物性解(constant property solution, CPS).然而, Boussinesq假设仅适用于温度跨度比较小同时流体的热物性变化也比较小的流动和传热过程[1-2].对于物性变化较大的热对流, 采用Boussinesq假设对方程进行简化, 将得到误差较大甚至是错误的结果.
流体热物性随温度的变化增强了控制方程的非线性, 给数值研究和理论分析带来很大困难, 有关变物性影响的研究通常只关注部分物性变化对流动稳定性及传热性能的影响.有关流动稳定性的研究[3-4]表明:流体黏度随温度的变化对流动不稳定特性有显著影响.有关物性变化影响传热性能的研究[5-6], 通常采用partial Boussinesq假设, 即流体密度对温度的依赖性仍采用Boussinesq假设的处理方式, 与此同时, 考虑黏度、导热系数、比热容随温度的变化, 从而得到基于partial Boussinesq假设的PBA解.有关由水平方向上的温度梯度驱动的空腔内热对流的研究结果表明:与PBA解相比, CPS低估了传热性能, 流体热物性的变化对传热过程是有利的.
格子Boltzmann方法(lattice Boltzmannmethod, LBM)基于介观动理论, 在处理强非线性问题时具有独特优势[7]. Guo等[8]采用LBM模拟了多孔介质内的热对流, 分析了流体黏性随温度变化的影响, Zhang等[9]采用LBM模拟了由大温差驱动的热对流, 分析了两个输运参数随温度变化的影响.最近, 本文作者Cao[10]则提出了一种变物性格子Boltzmann通量求解器(VPLBFS), 消除了传统LBM[8-9]中流体密度不变的约束条件, 能有效捕捉流体全部物性变化的影响, 获得变物性解(variable property solution, VPS).通过定量地分析CPS以及PBA解偏离VPS的程度, 论证了考虑流体全部物性变化的必要性[11].在本文中, 作者采用VPLBFS模拟超临界CO2的Rayleigh-Bénard热对流, 分析不同温差条件下的non-Boussinesq效应.
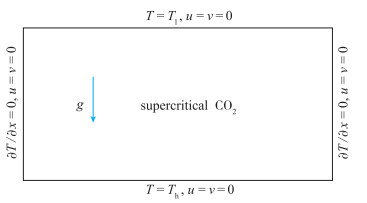
1 物理问题及控制方程本文研究超临界CO2的Rayleigh-Bénard热对流.鉴于目前对non-Boussinesq效应的理解很有限, 无法准确地给出non-Boussinesq条件下由热传导过渡到Rayleigh-Bénard热对流的扰动波长, 所以, 本文将研究水平方向是固壁边界而非无限大的Rayleigh-Bénard热对流. 图 1给出了物理问题的示意图, 竖直方向存在温度梯度, 上壁面是低温侧, 温度Tl恒为308 K, 下壁面是高温侧, 温度Th在不同算例中取不同值; 左右两侧均为绝热壁面.
|
| 图 1 物理问题的示意图 Fig.1 Schematic diagram of physical problem |
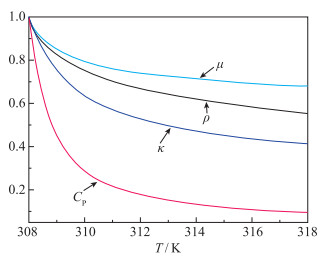
与传统流体相比, 超临界流体的独特之处在于其热物性参数对温度和压力的变化非常敏感, 尤其是在临界温度附近.这一物性特征使得超临界流体成为近几十年学术界和工程应用部门关注的焦点之一.在本文研究的3个算例中, 压力恒为8.0 MPa, 对应的伪临界温度是307.8 K, 上壁面温度Tl恒为308 K, 下壁面温度Th分别为310, 313和318 K.参考有关变物性影响的研究[3-5], 本文将上壁面温度Tl定义为参考温度Tref. 图 2给出了超临界CO2的热物性参数随温度的变化, 热物性参数均采用Tref处的参数值进行了无量纲化处理.虽然3个算例中的温差均比较小, 但流体的热物性随温度的变化非常剧烈, 必然会对动量输运和能量传输过程造成一定的影响.
|
| 图 2 超临界CO2的热物性变化, 压力为8.0 MPa Fig.2 Thermo-physical properties of supercritical CO2, pressure is 8.0 MPa |
对于低速流动, 可以忽略热耗散和压缩功的影响, 从而将控制方程写成以下形式:
| $ \frac{\partial \mathit{\rho }}{\partial \mathit{t}}\rm{+}\nabla \rm{ } \cdot \rm{ }\left( \mathit{\rho }\mathit{\boldsymbol{u}} \right)\rm{=0} $ | (1) |
| $ \begin{align} & {{\partial }_{\rm{t}}}\left( \mathit{\rho }\mathit{\boldsymbol{u}} \right)\rm{+}\nabla \rm{ } \cdot \rm{ }\left( \mathit{\rho }\mathit{\boldsymbol{uu}} \right)\rm{=-}\nabla \mathit{p}\rm{+}\nabla \rm{ } [ \rm{ }\mathit{\mu }\rm{(}\nabla \mathit{\boldsymbol{u}}\rm{+(}\nabla \mathit{\boldsymbol{u}}{{\rm{)}}^{\rm{T}}}\rm{) } ] \rm{ +}\mathit{\boldsymbol{F}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \mathit{\rho }{{\mathit{C}}_{\rm{p}}}\rm{(}{{\partial }_{\rm{t}}}\mathit{T}\rm{+}\mathit{\boldsymbol{u}}\rm{ }\ \cdot\rm{ }\nabla \mathit{T}\rm{)=}\nabla \rm{ } \cdot \rm{ (}\mathit{\kappa }\nabla \mathit{T}\rm{)} \\ \end{align} $ |
其中, F表示浮升力, F=g(ρ-ρref), 下标“ref”用于识别参考温度Tref上的热物性参数.初始时刻, 超临界CO2处于静止状态, 温度为Tl, 速度边界条件为无滑移条件, 热边界条件如图 1所示.
2 变物性格子Boltzmann通量求解器考虑流体热物性随温度变化的单相流动与气液两相流之间在某种程度上存在一定的相似性, 变物性格子Boltzmann通量求解器(VPLBFS)借鉴了传统格子Boltzmann方法(LBM)对气液两相流的处理方式[12], 引入压力分布函数取代密度分布函数, 将连续性方程(1)改写成以下形式:
| $ \left( {{\partial }_{\rm{t}}}\mathit{p+}\mathit{\boldsymbol{u}}\rm{ } \cdot \rm{ }\nabla \mathit{p} \right)+\mathit{\rho c}_{\rm{s}}^{2}\nabla \cdot \mathit{\boldsymbol{u}}\rm{=0} $ |
从而消除了传统不可压缩LBM[8-9]中流体密度不变的约束条件(p=ρcs2).
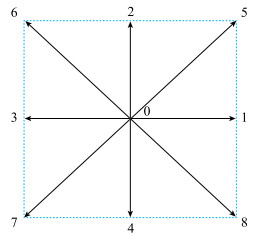
在本文中, 压力分布函数记作f(x, t), 温度分布函数记作g(x, t), 格子速度模型采用处理二维问题时最常用的D2Q9模型, 如图 3所示.
|
| 图 3 D2Q9格子速度模型 Fig.3 D2Q9 lattice velocity model |
各个方向的粒子速度eα, 以及平衡分布函数fαeq和gαeq, 具有以下形式:
| $ \begin{array}{l} \mathit{\boldsymbol{e}}_{\mathit{\alpha }}\left\{ \begin{array}{l} 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\alpha }{\rm{ = 0}}\\ \left( {{\rm{cos}}\left[{\frac{{\left( {\mathit{\alpha }-1} \right){\rm{ \mathit{ π} }}}}{2}} \right], {\rm{sin}}\left[{\frac{{\left( {\mathit{\alpha }-1} \right){\rm{ \mathit{ π} }}}}{2}} \right]} \right)\mathit{c}{\rm{, }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\alpha }{\rm{ = }}1, 2, 3, 4\\ \sqrt 2 \left( {{\rm{cos}}\left[{\frac{{\left( {\mathit{\alpha }-5} \right){\rm{ \mathit{ π} }}}}{2} + \frac{{\rm{ \mathit{ π} }}}{4}} \right], {\rm{sin}}\left[{\frac{{\left( {\mathit{\alpha }-5} \right){\rm{ \mathit{ π} }}}}{2} + \frac{{\rm{ \mathit{ π} }}}{4}} \right]} \right)\mathit{c, }\;\;\;\;\;\;\;\;\;\;\;\mathit{\alpha }{\rm{ = }}5, 6, 7, 8 \end{array} \right.\\ \mathit{f}_{^{_\mathit{\alpha }}}^{{\rm{eq}}}{\rm{(}}\mathit{\boldsymbol{x}}{\rm{, }}\mathit{t}{\rm{) = }}{\mathit{\omega }_\mathit{\alpha }}\left[{\mathit{p}{\rm{ + }}\mathit{\rho c}_{\rm{s}}^2\left( {\frac{{{\mathit{\boldsymbol{e}}_\mathit{\alpha }}{\rm{\cdot}}\mathit{\boldsymbol{u}}}}{{\mathit{c}_{\rm{s}}^2}}{\rm{ + }}\frac{{{{\left( {{\mathit{\boldsymbol{e}}_\mathit{\alpha }}{\rm{\cdot}}\mathit{\boldsymbol{u}}} \right)}^{\rm{2}}}{\rm{-}}{{\left( {{\mathit{c}_{\rm{s}}}{\rm{|}}\mathit{\boldsymbol{u}}{\rm{|}}} \right)}^{\rm{2}}}}}{{{\rm{2}}\mathit{c}_{\rm{s}}^4}}} \right){\rm{}}} \right]{\rm{, }}\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\alpha }{\rm{ = 0, 1, 2, }} \ldots {\rm{, 8}}\\ \mathit{g}_{^{_\mathit{\alpha }}}^{{\rm{eq}}}{\rm{(}}\mathit{\boldsymbol{x}}{\rm{, }}\mathit{t}{\rm{)}} = \left\{ \begin{array}{l} - \frac{3}{2}{\mathit{\omega }_\mathit{\alpha }}\mathit{T}\frac{{{{\left| \mathit{\boldsymbol{u}} \right|}^2}}}{{{\mathit{c}^2}}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\alpha }{\rm{ = 0}}\\ {\mathit{\omega }_\mathit{\alpha }}\mathit{T}\left( {\frac{3}{2}{\rm{ + }}\frac{3}{2}\frac{{{\mathit{\boldsymbol{e}}_\mathit{\alpha }}{\rm{\cdot}}\mathit{\boldsymbol{u}}}}{{{\mathit{c}^{\rm{2}}}}}{\rm{ + }}\frac{9}{2}\frac{{{{\left( {{\mathit{\boldsymbol{e}}_\mathit{\alpha }}{\rm{\cdot}}\mathit{\boldsymbol{u}}} \right)}^{\rm{2}}}}}{{{\mathit{c}^{\rm{4}}}}}{\rm{ - }}\frac{3}{2}\frac{{{{\left| \mathit{\boldsymbol{u}} \right|}^{\rm{2}}}}}{{{\mathit{c}^{\rm{2}}}}}} \right){\rm{, }}\;\;\;\;\;\;\;\;\mathit{\alpha }{\rm{ = 1, 2, 3, 4}}\\ {\mathit{{\omega }}_\mathit{{\alpha }}}\mathit{{T}}\left( {{\rm{3 + 6}}\frac{{{\mathit{\boldsymbol{e}}_\mathit{\alpha }}{\rm{\cdot}}\mathit{\boldsymbol{u}}}}{{{\mathit{c}^{\rm{2}}}}}{\rm{ + }}\frac{9}{2}\frac{{{{\left( {{\mathit{\boldsymbol{e}}_\mathit{\alpha }}{\rm{\cdot}}\mathit{\boldsymbol{u}}} \right)}^{\rm{2}}}}}{{{\mathit{c}^{\rm{4}}}}}{\rm{ - }}\frac{3}{2}\frac{{{{\left| \mathit{\boldsymbol{u}} \right|}^{\rm{2}}}}}{{{\mathit{c}^{\rm{2}}}}}} \right){\rm{, }}\;\;\;\;\;\;\;\mathit{\alpha }{\rm{ = 5, 6, 7, 8}} \end{array} \right. \end{array} $ |
其中, c=δx/δt, δt为粒子运动的时间步长, 其大小等于格子尺寸δx, 声速cs=c/
| $ \begin{array}{l} \mathit{p = }\sum\limits_{\mathit{\alpha }{\rm{ = 0}}}^8 {\mathit{f}_\mathit{\alpha }^{{\rm{eq}}}} = \sum\limits_{\mathit{\alpha }{\rm{ = 0}}}^8 {{\mathit{f}_\mathit{\alpha }}}, \mathit{p}\mathit{\boldsymbol{u}}\mathit{c}_{\rm{s}}^2 = \sum\limits_{\mathit{\alpha }{\rm{ = 0}}}^8 {{\mathit{\boldsymbol{e}}_\mathit{\alpha }}\mathit{f}_\mathit{\alpha }^{{\rm{eq}}}} = \sum\limits_{\mathit{\alpha }{\rm{ = 0}}}^8 {{\mathit{\boldsymbol{e}}_\mathit{\alpha }}{\mathit{f}_\mathit{\alpha }}} \\ \mathit{T = }\sum\limits_{\mathit{\alpha }{\rm{ = 0}}}^8 {\mathit{g}_\mathit{\alpha }^{{\rm{eq}}}} = \sum\limits_{\mathit{\alpha }{\rm{ = 0}}}^8 {{\mathit{g}_\mathit{\alpha }}}, \mathit{T}\mathit{\boldsymbol{u = }}\sum\limits_{\mathit{\alpha }{\rm{ = 0}}}^8 {{\mathit{\boldsymbol{e}}_\mathit{\alpha }}\mathit{g}_\mathit{\alpha }^{{\rm{eq}}}} = \sum\limits_{\mathit{\alpha }{\rm{ = 0}}}^8 {{\mathit{\boldsymbol{e}}_\mathit{\alpha }}{\mathit{g}_\mathit{\alpha }}} \end{array} $ |
对标准格子Boltzmann方程进行Chapman-Enskog多尺度分析, 同时将因物性变化引入的附加项以及体积力视为源项, 从而得到待求解的方程[10-11]:
| $ \frac{{\partial \mathit{p}}}{{\partial \mathit{t}}}{\rm{ + }}\nabla {\rm{\cdot}}\left( {\sum\limits_{\mathit{\alpha }{\rm{ = 0}}}^8 {{\mathit{\boldsymbol{e}}_\mathit{\alpha }}\mathit{f}_\mathit{\alpha }^{{\rm{eq}}}} } \right){\rm{ = - }}\mathit{\boldsymbol{u}} \cdot \nabla {\rm{(}}\mathit{p - \rho c}_{\rm{s}}^2{\rm{)}} $ | (2) |
| $ \frac{{\partial \mathit{p}\mathit{\boldsymbol{u}}\mathit{c}_{\rm{s}}^2}}{{\partial \mathit{t}}}{\rm{ + }}\nabla {\rm{\cdot}}\left( {\sum\limits_{\mathit{\alpha }{\rm{ = 0}}}^8 {{\mathit{\boldsymbol{e}}_\mathit{\alpha }}{\mathit{\boldsymbol{e}}_\mathit{\alpha }}} \left[{\mathit{f}_\mathit{\alpha }^{{\rm{eq}}}{\rm{ + }}\left( {{\rm{1-}}\frac{1}{{{\rm{2}}{\mathit{\tau }_\mathit{f}}}}} \right)\mathit{f}_\mathit{\alpha }^{{\rm{neq}}}} \right]{\rm{ - }}\mathit{\mu }{\mathit{\Pi }^{\rm{e}}}} \right){\rm{ = }}\mathit{Fc}_{\rm{s}}^2 $ | (3) |
| $ \frac{{\partial \mathit{T}}}{{\partial \mathit{t}}}+\nabla {\rm{\cdot}}\left[{\sum\limits_{\mathit{\alpha }{\rm{ = 0}}}^8 \left( {{\mathit{\boldsymbol{e}}_\mathit{\alpha }}\mathit{g}_\mathit{\alpha }^{{\rm{eq}}}{\rm{ + }}\left( {{\rm{1-}}\frac{1}{{{\rm{2}}{\mathit{\tau }_\mathit{g}}}}} \right){\mathit{\boldsymbol{e}}_\mathit{\alpha }}\mathit{g}_\mathit{\alpha }^{{\rm{neq}}}} \right)} \right]={\rm{ - }}\mathit{\kappa }\nabla \mathit{T}{\rm{\cdot}}\nabla \frac{\mathit{D}}{\mathit{\kappa }} $ | (4) |
其中,
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;{\mathit{\Pi }^{\rm{e}}}{\rm{ = }}\frac{1}{\mathit{\rho }}{\rm{[}}\mathit{\boldsymbol{u}}\nabla {\rm{ + (}}\mathit{\boldsymbol{u}}\nabla {{\rm{)}}^{\rm{T}}}{\rm{](}}\mathit{p - \rho c}_{\rm{s}}^2{\rm{)}}\\ \mathit{f}_\mathit{\alpha }^{{\rm{neq}}}{\rm{(}}\mathit{\boldsymbol{x}}{\rm{, }}\mathit{t}{\rm{) = - }}{\mathit{\tau }_\mathit{f}}{\rm{[}}\mathit{f}_\mathit{\alpha }^{{\rm{eq}}}{\rm{(}}\mathit{\boldsymbol{x}}{\rm{, }}\mathit{t}{\rm{)-}}\mathit{f}_\mathit{\alpha }^{{\rm{eq}}}{\rm{(}}\mathit{\boldsymbol{x}}{\rm{-}}{\mathit{\boldsymbol{e}}_\mathit{\alpha }}{\mathit{\delta }_{\rm{t}}}{\rm{, }}\mathit{t}{\rm{-}}{\mathit{\delta }_{\rm{t}}}{\rm{)]}}\\ \mathit{g}_\mathit{\alpha }^{{\rm{neq}}}{\rm{(}}\mathit{\boldsymbol{x}}{\rm{, }}\mathit{t}{\rm{) = - }}{\mathit{\tau }_\mathit{g}}{\rm{[}}\mathit{g}_\mathit{\alpha }^{{\rm{eq}}}{\rm{(}}\mathit{\boldsymbol{x}}{\rm{, }}\mathit{t}{\rm{)-}}\mathit{g}_\mathit{\alpha }^{{\rm{eq}}}{\rm{(}}\mathit{\boldsymbol{x}}{\rm{-}}{\mathit{\boldsymbol{e}}_\mathit{\alpha }}{\mathit{\delta }_{\rm{t}}}{\rm{, }}\mathit{t}{\rm{-}}{\mathit{\delta }_{\rm{t}}}{\rm{)]}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\mathit{ }\;\;\;\;\;{\mathit{\tau }_\mathit{f}}{\rm{ = }}\frac{\mathit{\mu }}{{\mathit{\rho c}_{\rm{s}}^2{\mathit{\delta }_{\rm{t}}}}}{\rm{ + 0}}{\rm{.5 }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\tau }_\mathit{g}}{\rm{ = }}\frac{{{\rm{3}}\mathit{\kappa }}}{{{\rm{2}}\mathit{\rho }{\mathit{C}_{\rm{p}}}{\mathit{c}^{\rm{2}}}{\mathit{\delta }_{\rm{t}}}}}{\rm{ + 0}}{\rm{.5}} \end{array} $ |
当采用Boussinesq假设或partial Boussinesq假设时, 密度不变的约束条件成立, 因此Πe=0.
在VPLBFS中, 采用Shu等[13-14]发展的格子Boltzmann通量求解器(LBFS)求解方程(2)~(4), 因此, VPLBFS具备LBFS的所有优势, 如:便于使用非均匀网格、可以在物理空间赋边界条件、存储量小, 与此同时, 保留了传统LBM的所有优点.详细的求解过程见文献[10-11].
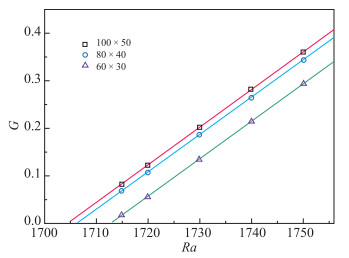
基于Boussinesq假设对VPLBFS进行简化, 采用其简化形式模拟了水平方向无限大的Rayleigh-Bénard热对流, 得到了通常关注的CPS, 图 4给出了不同Rayleigh数条件下的扰动增长率, 采用不同数量的非均匀网格得到的临界Rayleigh数与理论结果1 707.8[15]的差异均小于0.3%, 表明了算法和程序的可靠性.
|
| 图 4 采用不同网格数得到的扰动增长率G Fig.4 Growth rates of disturbances G obtained by using different meshes |
本文采用VPLBFS对超临界CO2的Rayleigh-Bénard热对流进行二维分析, 得到了基于Boussinesq假设的CPS, 基于partial Boussinesq假设的PBA解, 以及考虑流体全部物性变化的VPS, 分析了不同温差条件下的non-Boussinesq效应.考虑到VPLBFS在网格划分方面的优势, 本文使用了非均匀网格, 网格分布示意图见图 5.经网格独立性检验, 下文采用了100×50的网格.

|
| 图 5 非均匀网格示意图 Fig.5 Schematic diagram of non-uniform meshes |
Rayleigh数和Prandtl数定义为以下形式:
| $ \begin{array}{l} \mathit{Ra}{\rm{ = }}\frac{{\mathit{g}{\rm{\Delta }}\mathit{\rho }{\mathit{H}^{\rm{3}}}{\mathit{\rho }_{{\rm{ref}}}}{\mathit{C}_{{\rm{p, ref}}}}}}{{{\mathit{\mu }_{{\rm{ref}}}}{\mathit{\kappa }_{{\rm{ref}}}}}}\\ \;\mathit{Pr}{\rm{ = }}\frac{{{\mathit{\mu }_{{\rm{ref}}}}{\mathit{C}_{{\rm{p, ref}}}}}}{{{\mathit{\kappa }_{{\rm{ref}}}}}} \end{array} $ | (5) |
其中, H为上下壁面的间距, Δρ表示与温度差Th-Tl对应的密度差.式(5)中定义的Ra和Pr普遍适用于基于Boussinesq假设的情况, 考虑部分物性变化的情况以及考虑流体全部物性变化的情况.
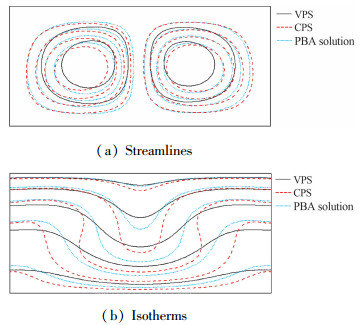
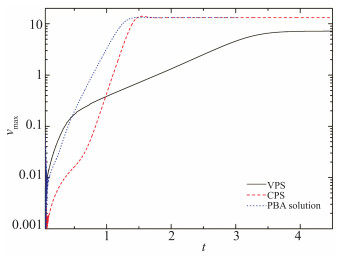
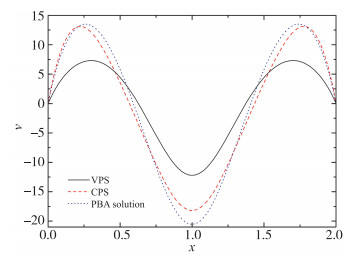
3.1 non-Boussinesq效应采用VPLBFS的两种简化形式和标准形式分别模拟了超临界CO2的Rayleigh-Bénard热对流, 下壁面温度Th=310 K, 利用式(5)计算得到的Ra和Pr分别为5×103和11.987.其中, 一种简化形式是基于Boussinesq假设, 由此得到CPS, 另一种简化形式是基于partial Boussinesq假设, 可以得到PBA解. 图 6给出了采用VPLBFS的标准形式得到的VPS与CPS和PBA解之间的比较, 包括稳态阶段的流线和等温线. 3种数值解之间存在明显差异, 流体热物性变化的影响不容忽视, non-Boussinesq效应对Rayleigh-Bénard热对流有显著的抑制作用.等温线的分布表明:与CPS相比, PBA解与VPS之间的差异小很多, 这是因为PBA解考虑了流体黏度、导热系数和比热容随温度的变化. 图 7给出了竖直速度分量最大值vmax的时间演化, 虽然起始阶段VPS中vmax的增幅最为明显, 但很快被CPS和PBA解中的vmax超越; 在稳态阶段, CPS中的vmax与PBA解中的vmax近乎相等, 明显大于VPS中的vmax. 图 8给出了水平中轴线上的竖直速度分量, CPS和PBA解均高估了Rayleigh-Bénard热对流的强度, 严重偏离VPS.换言之, 对于Rayleigh-Bénard热对流, non-Boussinesq效应是不利因素, 起到了明显的抑制作用.
|
| 图 6 流线和等温线的分布 Fig.6 Distributions of streamlines and isotherms at steady state |
|
| 图 7 不同时刻竖直速度分量最大值的比较 Th-Tl=2 K, Ra=5×103, Pr=11.987 Fig.7 Comparisons of the maximum vertical velocity at different moments between three numerical solutions Th-Tl=2 K, Ra=5×103, Pr=11.987 |
|
| 图 8 水平中轴线上的竖直速度分量 Th-Tl=2 K, Ra=5×103, Pr=11.987 Fig.8 Vertical velocity components in horizontal midline Th-Tl=2 K, Ra=5×103, Pr=11.987 |
首先, 将VPLBFS用于模拟Th=313 K, Tl=308 K的Rayleigh-Bénard热对流, Ra=104, Pr=11.987.如果仍将Rayleigh数设置为5×103, 在VPS中, 流体仍处于热传导状态, 并没有形成自然对流.这表明, 流体热物性变化幅度的增大加强了non-Boussi-nesq效应对热对流的抑制作用.
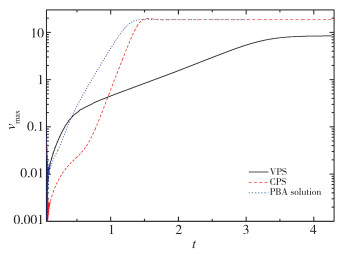
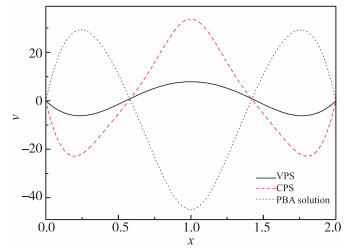
图 9给出了3种数值解中竖直速度最大值vmax的时间演化, vmax的变化趋势以及3种数值解之间定性的差异与图 7所示温差为2 K的结果一致. 图 10给出了水平中轴线上竖直速度分量的比较, VPS中流体运动速度明显小于CPS和PBA解中的情况, non-Boussinesq效应对Rayleigh-Bénard热对流有非常显著的影响.此外, PBA解中两个涡的运动方向与CPS中的情况恰好相反, 表明热传导状态失稳之后可能出现两个稳态解.
|
| 图 9 不同时刻竖直速度分量最大值的比较 Th-Tl=5 K, Ra=104, Pr=11.987 Fig.9 Comparisons of the maximum vertical velocities at different moments between three numerical solutions Th-Tl=5 K, Ra=104, Pr=11.987 |
|
| 图 10 水平中轴线上竖直速度分量的比较 Th-Tl=5 K, Ra=104, Pr=11.987 Fig.10 Comparisons of vertical velocities in horizontal midline between three numerical solutions Th-Tl=5 K, Ra=104, Pr=11.987 |
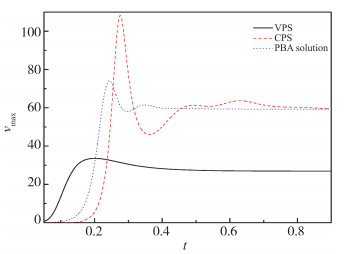
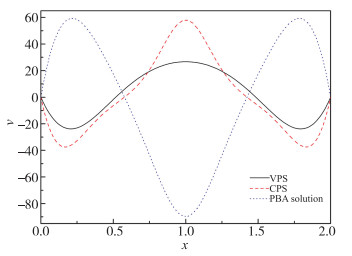
其次, 将VPLBFS用于模拟Th=318 K, Tl=308 K的Rayleigh-Bénard热对流, Pr=11.987.在该算例中, 将Ra设置为2×104, 因为当Ra=104时, 在VPS中超临界CO2仍处于热传导状态, 尚未形成热对流. 图 11给出了竖直速度分量最大值vmax的时间演化过程.与图 7和图 9中的结果类似, 在3个数值解中, VPS中的vmax首先增大, 其次是PBA解, 最后才是CPS, 表明物性变化对Rayleigh-Bénard热对流的影响不容忽视; 在热对流达到稳态阶段, PBA解中的vmax与CPS中的值近乎相等, VPS中的vmax还不及PBA解和CPS的一半. 图 12给出了水平中轴线上数值速度分量的比较, 3种数值解之间定性的差异与图 10中的结果完全一致.
|
| 图 11 不同时刻竖直速度分量最大值的比较 Th-Tl=10 K, Ra=2×104, Pr=11.987 Fig.11 Comparisons of the maximum vertical velocities at different moments between three numerical solutions Th-Tl=10 K, Ra=2×104, Pr=11.987 |
|
| 图 12 水平中轴线上竖直速度分量的比较 Th-Tl=10 K, Ra=2×104, Pr=11.987 Fig.12 Comparisons of vertical velocities in horizontal midline between three numerical solutions Th-Tl=10 K, Ra=2×104, Pr=11.987 |
本文采用变物性格子Boltzmann通量求解器(VPLBFS)模拟超临界CO2的Rayleigh-Bénard热对流, 得到了基于Boussinesq假设的CPS, 只考虑部分物性变化的基于partial Boussinesq假设的PBA解, 以及考虑流体全部物性变化的VPS.通过3种数值解之间的对比, 分析了non-Boussinesq效应对Rayleigh-Bénard热对流的重要影响, 进一步讨论了不同温差条件下的non-Boussinesq效应, 论证了在研究超临界流体的Rayleigh-Bénard热对流时考虑流体全部物性变化的必要性.初步的研究结果表明, non-Boussinesq效应对稳态的Rayleigh-Bénard热对流有非常显著的抑制作用.
| [1] |
Gray D D, Giorgini A. The validity of the Boussinesq approximation for liquids and gases[J]. International Journal of Heat and Mass Transfer, 1976, 19(5): 545-551. |
| [2] |
Zhong Z Y, Yang K T, Lloyd J R. Variable property effects in laminar natural convection in a square enclosure[J]. Journal of Heat Transfer, 1985, 107(1): 133-138. |
| [3] |
Wall D P, Wilson S K. The linear stability of channel flow of fluid with temperature-dependent viscosity[J]. Journal of Fluid Mechanics, 1996, 323: 107-132. |
| [4] |
Chen Y M, Pearlstein A J. Stability of free-convection flows of variable-viscosity fluids in vertical and inclined slots[J]. Journal of Fluid Mechanics, 1989, 198: 513-541. |
| [5] |
Leal M A, Machado H A, Cotta R M. Integral transform solutions of transient natural convection in enclosures with variable fluid properties[J]. International Journal of Heat and Mass Transfer, 2000, 43(21): 3977-3990. |
| [6] |
曹玉会. 基于变物性的格子玻尔兹曼通量求解器[J]. 工程热物理学报, 2017. Cao Y H. A variable property-based lattice Boltzmann flux solver[J]. Journal of Engineering Thermophysics, 2017. (in Chinese) |
| [7] |
Chen S, Doolen G. Lattice Boltzmann method for fluid flows[J]. Annual Review of Fluid Mechanics, 1998, 30: 329-364. |
| [8] |
Guo Z L, Zhao T S. Lattice Boltzmann simulation ofnatural convection with temperature-dependent viscosity in a porous cavity[J]. Progress in Computational Fluid Dynamics, 2004, 5(1/2): 110-117. |
| [9] |
Zhang X R, Cao Y H. A lattice Boltzmann model fornatural convection with a large temperature difference[J]. Progress in Computational Fluid Dynamics, 2011, 11(5): 269-278. |
| [10] |
Cao Y H. Variable property-based lattice Boltzmann flux solver for thermal flows in the low Mach number limit[J]. International Journal of Heat and Mass Transfer, 2016, 103: 254-264. |
| [11] |
Cao Y H, Zhang Y. Investigation on the natural convectionin horizontal concentric annulus using the variable property-based lattice Boltzmann flux solver[J]. International Journal of Heat and Mass Transfer, 2017, 111: 1260-1271. |
| [12] |
He X Y, Chen S Y, Zhang R Y. A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability[J]. Journal of Computational Physics, 1999, 152(2): 642-663. |
| [13] |
Shu C, Wang Y, Teo C J, et al. Development of lattice Boltzmann flux solver for simulation of incompressible flows[J]. Advances in Applied Mathematics and Mechanics, 2014, 6(4): 436-460. |
| [14] |
Shu C, Wang Y, Yang L M, et al. Lattice Boltzmann flux solver:an efficient approach for numerical simulation of fluid flows[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2014, 31(1): 1-15. |
| [15] |
Drazin P G, Reid W H. Hydrodynamic stability[M]. Cambridge University Press, 2004, 52.
|



