2. 美国俄亥俄州立大学工程学院, 哥伦布 43210
2. School of Engineering, the Ohio State University, Columbus 43210, USA
具有壳核结构的微胶囊在科学研究以及工程技术等方面都有广泛的应用前景, 比如药物靶向运输与缓释新药剂型研制食品添加剂包封农药利用度增强细胞三维培养等.制备这种微胶囊有许多不同的方法, 如乳化[1-2]软刻蚀[3]喷雾干燥[4]外部流[5-6]等.其中, 利用外部流的毛细流动[7]是一种非常有效的方法, 它能够平稳地将不同流体射流的界面拉伸到微米量级或更小, 射流最后因不稳定性破碎成单分散性的小液滴或颗粒.
流动聚焦(flow focusing, FF)是一种毛细流动现象, 它利用外部高速流动气体的驱动以及小孔的聚焦作用使得毛细管中以一定流量流动的液体在毛细管口形成锥形, 并于锥形顶端发出微射流, 即典型的锥-射流结构, 射流最后因不稳定性在一定长度处破碎成单分散性的液滴.流动聚焦技术是由西班牙Gañán-Calvo课题组在1998年第1次提出[5], 在微纳米颗粒和液滴的制备方面有着突出优点, 比如颗粒大小可控性强以及药物包裹率高等[8-9].因此开展相关的研究对于探讨其物理机理改进制备工艺等都具有重要的意义.
单一流动聚焦的研究已经取得了较大进展[10].其中, Gañán-Calvo课题组[11-13]和本课题组[14-16]都开展了相关的不稳定性研究.近年来, 基于流动聚焦原理, 一些新型的包裹技术比如同轴流动聚焦(co-flow focusing, CFF)被提出, 并显示了极强的应用价值[8].虽然CFF比FF有着更为广阔的应用前景, 在微纳米胶囊微纳米管道等的制备方面具有一定优势, 但由于涉及内外两层界面, 其过程控制和物理机理比FF更为复杂, 且相关的研究也极少.
在同轴射流不稳定性研究方面, Chauhan等开展了线性时间不稳定性分析, 分析了长波数(k→0) 内外层射流半径比a=R2/R1→1以及a→∞等极限情况下射流界面扰动的发展和演化情况[17]. Herrada等对同轴射流开展了时空不稳定性分析, 研究了射流的绝对-对流不稳定性, 得到了它们之间的转换曲线, 并对其转换规律进行了分析[18].但是, 两文均忽略了驱动流体的密度和黏性, 且采用的是均匀速度型进行理论分析, 因此不能全面揭示界面扰动的发展规律.
本文从液体驱动的同轴流动聚焦实验出发, 建立了有黏复合射流的物理模型.模型中考虑了驱动流体对同轴射流的动力学影响, 并基于管流和误差函数构造了同轴射流和驱动流体的基本速度型, 便于更清楚地揭示同轴流动聚焦的物理机制, 加强实验过程控制以及改进制作工艺, 促进实际应用.
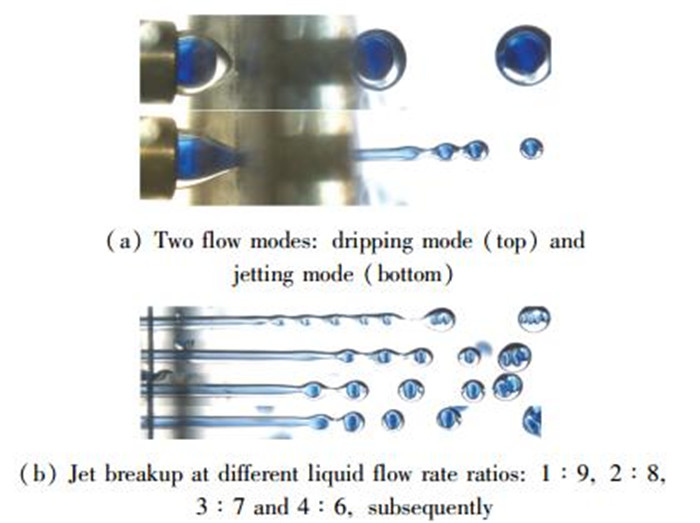
1 理论模型 1.1 物理模型和基本假设为了得到合理的物理模型, 开展了初步的液驱同轴流动聚焦实验, 获得了复合射流的运动形态.实验中内层流体为水和蓝墨水的混合物(体积比8:1), 外层流体为40黏度的二甲基硅油, 驱动流体为水. 图 1(a)给出了内流量Q1=30 ml/h, 外流量Q2=70 ml/h时, 在不同驱动流量Q3(上: 700 ml/h, 下: 1200 ml/h)下的两种流动模式(滴模式和射流模式); 图 1(b)则给出了不同内外液体流量比下复合射流破碎过程, 以及内外层液滴不同包裹形态的典型图片(驱动流量Q3=1400 ml/h, 而Q1+Q2=100 ml/h).
|
| 图 1 液体驱动下同轴流动聚焦中锥形和射流微观形貌 Fig.1 Microscopic morphology of cone and jet in liquid-driven coaxial flow focusing |
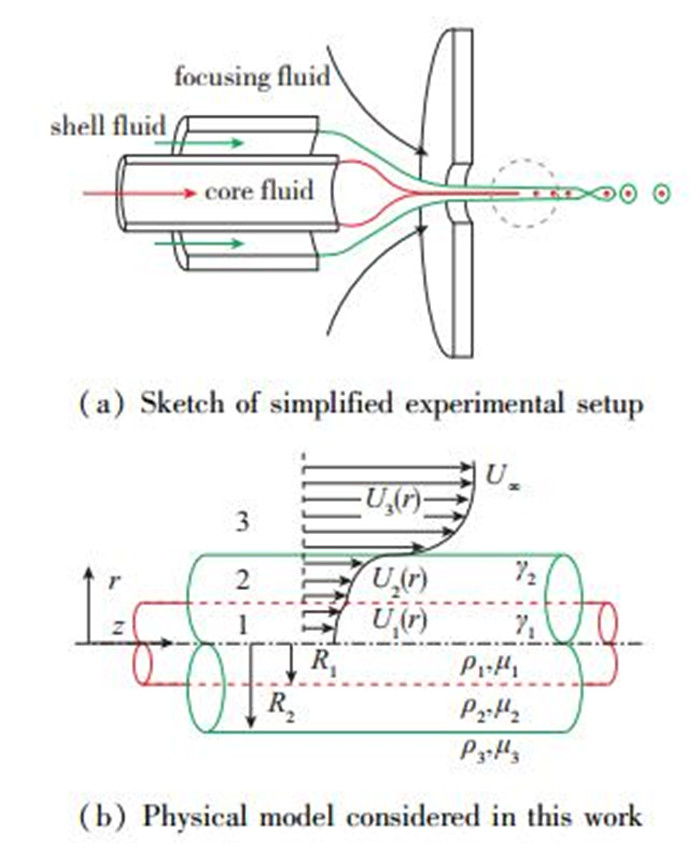
图 2(a)给出了典型同轴流动聚焦的实验装置简图.本文主要关注扰动在同轴射流上的发展演化情况(图 2(a)中虚线圆圈所示部分), 因此需要对同轴射流以及其周围的流场进行简化.在忽略射流直径的变化[5]以及驱动流体在外边界的剪切层影响[11]后, 射流的理论模型可以简化到如图 2(b)所示.为便于理论分析, 类似于单轴流动聚焦的理论研究[14-15], 本模型给出如下合理假设: (1) 液体都是黏性不可压缩的Newton流体; (2) 忽略重力温度的影响, 交界面为物质面, 界面两边的物质在界面上不发生蒸发凝结渗透和互相融解等现象; (3) 扰动前射流的直径为常数, 三相流体的物理属性均不变.
|
| 图 2 简化实验装置以及简化物理模型示意图 Fig.2 Sketch of simplified experimental setup and physical model considered in this work |
本文的同轴射流模型涉及的物理参数主要有:内外层液体和驱动流体的密度ρ1, 2, 3, 动力学黏性系数μ1, 2, 3, 基本速度型U1, 2, 3(r), 液体流量速度Q1, 2, 3, 内外层界面张力系数γ1, 2, 以及内外层射流的半径R1, 2等(其中下标1, 2, 3分别代表内层外层及驱动流体).为了便于分析并得到普适的结论, 须对各方程进行无量纲化, 取R2, U2=Q2/π(R22-R12), R2/U2, ρ2U22, ρ2, μ2以及γ2为特征尺度, 相应的无量纲参数有: Weber数We=ρ2U22R2/γ2; Reynolds数Re=ρ2U2R2/μ2; 密度比S=ρ1/ρ2, Q=ρ3/ρ2; 黏性比N=μ1/μ2, M=μ3/μ2, 射流内外层半径比κ=R1/R2以及内外界面张力系数比τ=γ1/γ2等.
1.2 基本速度型在稳定性分析以前, 须给出同轴射流以及驱动流体在未扰动状态下的基本速度型.但在同轴流动聚焦中流场非常复杂且是空间演化的, 很难直接求解出其速度分布, 因此需要对速度型进行简化.文献中使用过多种形式的基本速度型, 如无黏模型中采用的均匀速度型[19]有黏模型中通过边界层数值求解得到单轴流动聚焦中的基本速度型[11]等.在实际的稳定性分析中, 一些近似的函数常被用来构造流动的基本速度型并取得了一定的成功, 如误差函数双曲正切函数[15-16, 20].本文采用管流+误差函数的形式构造同轴流动聚焦中的基本速度型.
假定同轴射流的直径在研究范围内不变, 通过流体控制方程中心轴处速度对称以及内界面处的速度连续和剪切力平衡条件, 可以得出内外层液体射流的速度分布与Hagen-Poiseuille管流类似, 即
| $ {U_1}\left( r \right) = \frac{{1 - {U_1}}}{{N + \left( {1 - N} \right){\kappa ^2}}}\left( {2{r^2} - {\kappa ^2}} \right) + {U_1} $ |
| $ {U_2}\left( r \right) = \frac{{N\left( {1 - {U_1}} \right)}}{{N + \left( {1 - N} \right){\kappa ^2}}}\left[{2{r^2}-\left( {1 + {\kappa ^2}} \right)} \right] + 1 $ |
其中, U1=(Q1/πR12)/U2.
对于驱动流体, 采用误差函数, 即
| $ {U_3}\left( r \right) = a \cdot {\rm{erf}}\left[{b\left( {r-1} \right)} \right] + c $ |
的形式来构造其基本速度型, 其中a, b, c是待定系数.由外界面处速度连续以及剪切力平衡条件并在无穷远处给定速度U∞, 可以得到U3(r)的最终形式:
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{U_3}\left( r \right) = c + }\\ {\left( {{U_\infty } - c} \right) \cdot {\rm{erf}}\left\{ {\frac{{2\sqrt {\rm{\pi }} N\left( {1 - {U_1}} \right)\left( {r - 1} \right)}}{{M\left[ {N + \left( {1 - N} \right){\kappa ^2}} \right]\left( {{U_\infty } - c} \right)}}} \right\}} \end{array} $ |
其中,
| $ c = 1 + \frac{{N\left( {1 - {U_1}} \right)}}{{N + \left( {1 - N} \right){\kappa ^2}}}\left( {1 - {\kappa ^2}} \right) $ |
和单轴FF理论分析类似[15-16], 为了得到小扰动的控制方程, 可将各物理量分解为基本量和扰动量的叠加, 即ψ=Ψ+
| $ \nabla \cdot {{\mathit{\boldsymbol{\tilde u}}}_i} = 0, i = 1, 2, 3 $ | (1) |
| $ \frac{{\partial {{\mathit{\boldsymbol{\tilde u}}}_i}}}{{\partial t}} + {\mathit{\boldsymbol{\tilde u}}_i} \cdot \nabla {U_i} + {U_i} \cdot \nabla {\mathit{\boldsymbol{\tilde u}}_i} = - \frac{1}{{{\rho _i}}}\nabla {\tilde p_i} + \frac{{{\mu _i}}}{{{\rho _i}}}{\nabla ^2}{\mathit{\boldsymbol{\tilde u}}_i} $ | (2) |
其中Ui=Ui(r)ez.而在柱坐标系(r, θ, z)下, 扰动速度有
由于扰动的存在, 内外界面均会偏离其初始位置.对于无限小的扰动来说, 界面的位置函数可以表示为rsj=Rj+ηj, j=1, 2的形式, 其中ηj为扰动引起的界面位移偏量.涉及的边界条件有:
(1) 对称轴(r=0) 处的相容关系
| $ \mathop {\lim }\limits_{r \to 0} \frac{{\partial {{{\bf{\tilde u}}}_{}}}}{{\partial \theta }} = 0,\mathop {\lim }\limits_{r \to 0} \frac{{\partial \tilde p}}{{\partial \theta }} = 0 $ |
(2) 内外界面(rsj=Rj+ηj, j=1, 2) 处
① 速度连续条件
| $ {\mathit{\boldsymbol{u}}_j} = {\mathit{\boldsymbol{u}}_{j + 1}} $ |
② 运动学边界条件
| $ {{\tilde v}_j} = \left( {\frac{\partial }{{\partial t}} + {U_j}\frac{\partial }{{\partial \mathcal{z}}}} \right){\eta _j} $ |
③ 动力学边界条件
| $ \left( {{\mathit{\boldsymbol{T}}_{j + 1}} - {\mathit{\boldsymbol{T}}_j}} \right) \cdot {\mathit{\boldsymbol{n}}_j} = {\gamma _j}\left( {\nabla \cdot {\mathit{\boldsymbol{n}}_j}} \right){\mathit{\boldsymbol{n}}_j} $ |
其中,nj(j=1, 2) 分别为内外界面上的法向单位向量,
(3) 无穷远(r→∞)处扰动衰减为0条件
| $ \mathop {\lim }\limits_{r \to \infty } \mathit{\boldsymbol{\tilde u}} = 0, \mathop {\lim }\limits_{r \to \infty } \tilde p = 0 $ |
为了推导该问题的色散关系, 采用正则模法将扰动量展开成Fourier级数的形式, 即(注:正体i为虚数单位):
| $ \begin{array}{l} {\mathit{\boldsymbol{u}}_i} = Ui\left( r \right){\mathit{\boldsymbol{e}}_z} + \left( {{{\hat v}_i}\left( r \right), {{\hat w}_i}\left( r \right), {{\hat u}_i}\left( r \right)} \right){{\rm{e}}^{{\rm{i}}\left( {kz + n\theta - wt} \right)}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_i} = {p_{0i}} + {{\hat p}_i}\left( r \right){{\rm{e}}^{{\rm{i}}\left( {kz + n\theta - wt} \right)}} \end{array} $ | (3) |
| $ {\eta _j} = {{\hat \eta }_j}{{\rm{e}}^{{\rm{i}}\left( {kz + n\theta - wt} \right)}}, i = 1, 2, 3, j = 1, 2 $ |
其中,k为轴向波数, n为周向波数, ω为时间频率.在时间不稳定性分析中, k是实数, ω=ωr+iωi是复数, ωi和ωr分别代表扰动的时间增长率和相速度; 下标i代表虚部,r代表实部;而在时空不稳定性分析中, k, ω均为复数, 即k=kr+iki, ω=ωr+iωi.
将小扰动的形式(3) 代入流体的控制方程(1) 和(2), 去掉
| $ \frac{{{\rm{d}}{{\hat v}_i}}}{{{\rm{d}}r}} + \frac{{{{\hat v}_i}}}{r} + \frac{{{\rm{i}}n{{\hat w}_i}}}{r} + {\rm{i}}\alpha {{\hat u}_i} = 0 $ | (4) |
| $ \frac{1}{{R{e_i}}}\left[{\frac{{{{\rm{d}}^2}{{\hat v}_i}}}{{{\rm{d}}{r^2}}} + \frac{1}{r}\frac{{{\rm{d}}{{\hat v}_i}}}{{{\rm{d}}r}}-\left( {{\alpha ^2} + \frac{{{n^2} + 1}}{{{r^2}}} + {\rm{i}}\alpha R{e_i}{U_i}} \right){{\hat v}_i}} \right] - \frac{1}{{R{e_i}}}\frac{{2{\rm{i}}n}}{{{r^2}}}{{\hat w}_i} - {\left( {\frac{1}{S}} \right)^{{\delta _{i1}}}}{\left( {\frac{1}{Q}} \right)^{\delta i3}}\frac{{{\rm{d}}{{\hat p}_i}}}{{{\rm{d}}r}} = - {\rm{i}}\beta {{\hat v}_i} $ | (5) |
| $ \frac{1}{{R{e_i}}}\left[ {\frac{{{{\rm{d}}^2}{{\hat w}_i}}}{{{\rm{d}}{r^2}}} + \frac{1}{r}\frac{{{\rm{d}}{{\hat w}_i}}}{{{\rm{d}}r}} - \left( {{\alpha ^2} + \frac{{{n^2} + 1}}{{{r^2}}} + {\rm{i}}\alpha R{e_i}{U_i}} \right){{\hat w}_i}} \right] + \frac{1}{{R{e_i}}}\frac{{2{\rm{i}}n}}{{{r^2}}}{{\hat v}_i} - {\left( {\frac{1}{S}} \right)^{{\delta _{i1}}}}{\left( {\frac{1}{Q}} \right)^{{\delta _{i3}}}}\frac{{{\rm{i}}n}}{r}{{\hat p}_i} = - {\rm{i}}\beta {{\hat w}_i} $ | (6) |
| $ \frac{1}{{R{e_i}}}\left[ {\frac{{{{\rm{d}}^2}{{\hat u}_i}}}{{{\rm{d}}{r^2}}} + \frac{1}{r}\frac{{{\rm{d}}{{\hat u}_i}}}{{{\rm{d}}r}} - \left( {{\alpha ^2} + \frac{{{n^2}}}{{{r^2}}} + {\rm{i}}\alpha R{e_i}{U_i}} \right){{\hat u}_i}} \right] - \frac{{{\rm{d}}{U_i}}}{{{\rm{d}}r}}{{\hat v}_i} - {\left( {\frac{1}{S}} \right)^{{\delta _{i1}}}}{\left( {\frac{1}{Q}} \right)^{{\delta _{i3}}}}{\rm{i}}\alpha {{\hat p}_i} = - {\rm{i}}\beta {{\hat u}_i} $ | (7) |
其中, δ为Kronecker函数, 而
| $ \alpha = {R_2}k, \beta = w{R_2}/{U_2} $ |
| $ R{e_1} = Re \cdot S/N, R{e_2} = Re, R{e_3} = Re \cdot Q/M $ |
相应的边界条件为:
(1) 在对称轴r=0处
| $ \begin{array}{l} {{\hat v}_i} = {{\hat w}_1} = \frac{{{\rm{d}}{{\hat u}_1}}}{{{\rm{d}}r}} = \frac{{{\rm{d}}{{\hat p}_1}}}{{{\rm{d}}r}} = 0\left( {n = 0} \right)\\ \;\;\;\;\;{{\hat u}_1} = {{\hat p}_1} = 0, {{\hat v}_1} + {\rm{i}}{{\hat w}_1} = 0\\ \;\;\;\;\;2\frac{{{\rm{d}}{{\hat v}_1}}}{{{\rm{d}}r}} + {\rm{i}}\frac{{{\rm{d}}{{\hat w}_1}}}{{{\rm{d}}r}} = 0\left( {n = 1} \right)\\ \;{{\hat u}_1}{\rm{ = }}{{\hat v}_1}{\rm{ = }}{{\hat w}_1}{\rm{ = }}{{\hat p}_1}{\rm{ = }}0\left( { \ge 2} \right) \end{array} $ | (8) |
(2) 界面
① 速度连续条件
| $ \begin{array}{l} \;\;\;\;\;\;\;{{\hat v}_j} = {{\hat v}_{j + 1}}, {{\hat w}_j} = {{\hat w}_{j + 1}}\\ {{{\rm{\hat u}}}_j} + \frac{{{\rm{d}}{U_j}}}{{{\rm{d}}r}}{{\hat \eta }_j} = {{{\rm{\hat u}}}_{j + 1}} + \frac{{{\rm{d}}{U_{j + 1}}}}{{{\rm{d}}r}}{{\hat \eta }_j} \end{array} $ | (9) |
② 运动学边界条件
| $ - {\rm{i}}\beta {{\hat \eta }_j} = {{\hat v}_j} - {\rm{i}}\alpha {U_{sj}}{{\hat \eta }_j} $ | (10) |
③ 动力学边界条件
| $ {{\hat p}_{j + 1}} - \frac{{2{M^{{\delta _{j2}}}}}}{{Re}}\frac{{{\rm{d}}{{\hat v}_{j + 1}}}}{{{\rm{d}}r}} - {{\hat p}_j} + \frac{{2{N^{{\delta _{j1}}}}}}{{Re}}\frac{{{\rm{d}}{{\hat v}_j}}}{{{\rm{d}}r}} = \frac{{{\tau^{{\delta _{j1}}}}}}{{We}}\left( {\frac{{1 - {n^2}}}{{{\kappa ^{2{\delta _{j1}}}}}} - {\alpha ^2}} \right){{\hat \eta }_j}$ | (11) |
| $ {N^{{\delta _{j1}}}}\left( {{\rm{i}}n{{\hat v}_j} - {{\hat w}_j} + {\kappa ^{{\delta _{j1}}}}\frac{{{\rm{d}}{{\hat w}_j}}}{{{\rm{d}}r}}} \right) = {M^{{\delta _{j2}}}}\left( {{\rm{i}}n{{\hat v}_{j + 1}} - {{\hat w}_{j + 1}} + {\kappa ^{{\delta _{j1}}}}\frac{{{\rm{d}}{{\hat w}_{j + 1}}}}{{{\rm{d}}r}}} \right) $ | (12) |
| $ {N^{{\delta _{j1}}}}\left( {\frac{{{{\rm{d}}^2}{U_j}}}{{{\rm{d}}{r^2}}}{{\hat \eta }_j} + \frac{{{\rm{d}}{{{\rm{\hat u}}}_j}}}{{{\rm{d}}r}} + {\rm{i}}\alpha {{\hat v}_j}} \right) = {M^{{\delta _{j2}}}}\left( {\frac{{{{\rm{d}}^2}{U_{j + 1}}}}{{{\rm{d}}{r^2}}}{{\hat \eta }_j} + \frac{{{\rm{d}}{{{\rm{\hat u}}}_{j + 1}}}}{{{\rm{d}}r}} + {\rm{i}}\alpha {{\hat v}_{j + 1}}} \right) $ | (13) |
(3) 在外边界r→∞处
| $ {\hat v_3} = {\hat w_3} = {\hat u_3} = {\hat p_3} = 0 $ | (14) |
满足边界条件(8)~(14) 的控制方程(4)~(7) 不能得到解析解, 本文采用的处理方法是将其离散化, 并通过Chebyshev谱配置方法[14, 20]构造广义特征值问题进行数值求解.求解方法和单轴FF类似[15-16].实际计算中, 无穷远处设定为外部射流半径的7倍, 即r =7R2处, 选取的配置点从内到外依次为20, 20,60, 数值计算结果符合收敛性要求.参考状态选取水-硅油-水液体驱动的同轴流动聚焦实验状态, 相应的无量纲参数具体如下: Re=2, We=1.7, U1=0.938, U∞=1.405, S=1.031, Q=1.031, N=0.025, M=0.025, κ=0.56, τ=1.
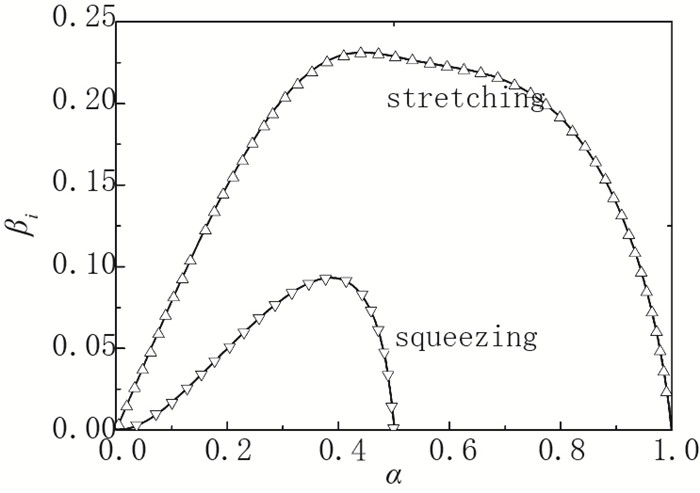
3.1 程序验证在给出稳定性分析的结果之前, 首先需要验证程序的准确性.由于文献中尚未报道过非均匀速度型下同轴射流的黏性稳定性分析, 本文通过将同轴射流模型进行简化, 进一步和前人的研究工作相比较.忽略驱动流体的黏性和密度(ρ3=0, μ3=0), 并假定未扰动状态下射流和驱动流体均静止(即U1(r)=U2(r)=U3(r)=0), 此时同轴射流模型与Chauhan等于2000年开展的研究模型一致[17].在无量纲参数为n=0, S=1, N=1, κ=0.5, τ=0.5, We=1, Re=63.25时, 两个不稳定模的时间增长率随轴向波数的变化曲线如图 3所示, 可见计算结果与文献中完全一致.
|
| 图 3 数值结果验证(实线代表本文的计算结果, 符号表示Chauhan等得到的结果[17]) Fig.3 Numerical validations (solid lines show the results of present model and symbols denote the results of Chauhan et al) |
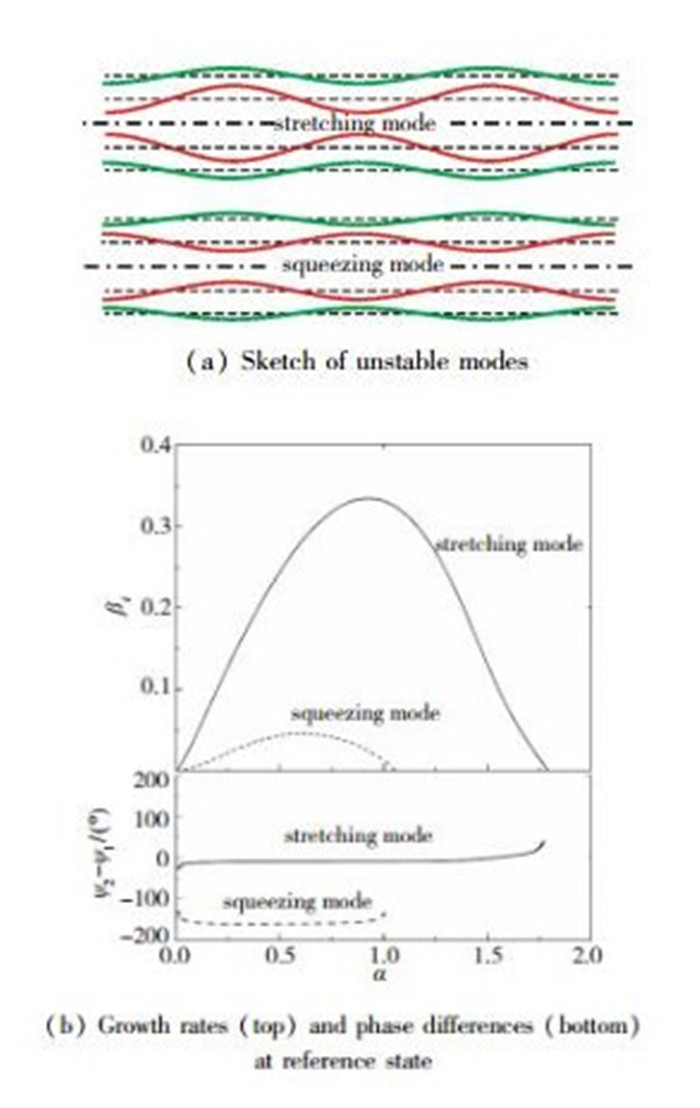
在同轴射流的稳定性分析中, 给定一个轴向波数α, 一般存在两个大于0的扰动增长率βi, 对应两个不同的不稳定模态, 通常称为stretching模和squeezing模[17-18].其中stretching模对应的内外界面扰动几乎是同相位发展的, 而squeezing模对应的内外界面扰动发展几乎是反相的(见图 4(a)).
|
| 图 4 内外界面上的不稳定模示意图及参考模态下两种不稳定模态的扰动增长率曲线和内外界面相位差 Fig.4 Sketch of unstable modes and growth rates and phase differences at reference state |
图 4(b)给出了参考状态下两种不稳定模态的扰动增长率曲线, 可以看出stretching模对应的扰动增长率远远大于squeezing模对应的扰动增长率, 在射流不稳定过程中起主导作用, 这与实验观测到的内外界面扰动总是同相的现象吻合, 因此在下文主要讨论stretching模的发展和演化.同时需要注意, 在当前研究的参数范围内, 轴对称扰动(n=0) 的增长率比非轴对称扰动(n≥1) 的增长率大很多, 因此下文只讨论轴对称扰动(n=0) 的发展演化情况.
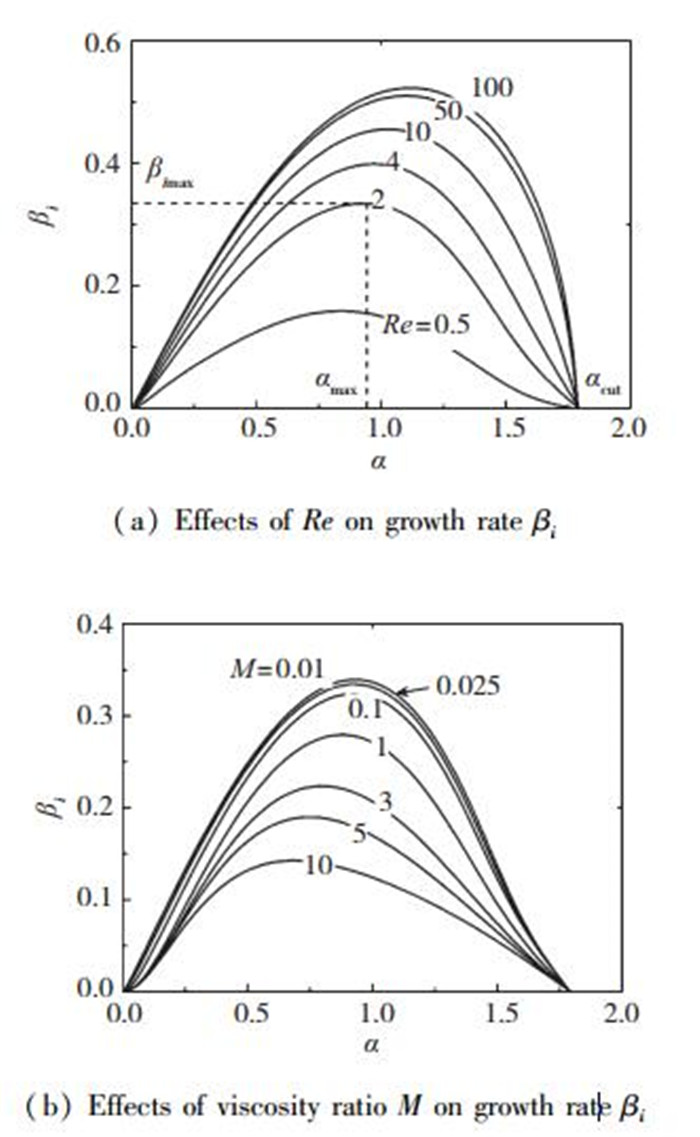
3.3 黏性和表面张力的影响首先指出, 在求解时间稳定性的色散关系β=β(α)时, 给定参数下, 每条曲线存在一个最大的扰动增长率βimax及其对应的轴向波数αmax以及右临界波数αcut, 具体定义见图 5(a).由于最大增长率βimax对应的扰动增长比其他波数下的扰动增长要快, 认为其对扰动增长起决定性作用, 并最终主宰射流的破碎, 此时对应的波数αmax就决定了射流破碎后形成液滴的大小.当αmax较小时形成的液滴较大, 对应长波不稳定性; 而当αmax较大时形成的液滴较小, 对应短波不稳定性. αcut的大小则决定了不稳定区域的大小.
|
| 图 5 Reynolds数和黏性比M对扰动增长率βi的影响 Fig.5 Effects of Re and viscosity ratio M on growth rate βi |
Reynolds数Re和黏性比M对扰动增长率βi的影响见图 5.随着Re的减小(M的增大), stretching模对应的最不稳定扰动增长率βimax均减小.进一步计算表明黏性比N对扰动增长率的影响与M类似, 这表明增大流体的黏性能抑制同轴射流的失稳, 原因主要在于增加流体的黏性将增大黏滞阻力以及增强黏性耗散效应, 使得扰动衰减更快.此外, 随着流体黏性的增加(Re减小或M增大), stretching模对应的αmax均有减小的趋势, 此时射流破碎后形成的液滴尺寸变大.可见, 增大流体的黏性虽然可以促进同轴射流的稳定, 但也会增大制备液滴的粒径.
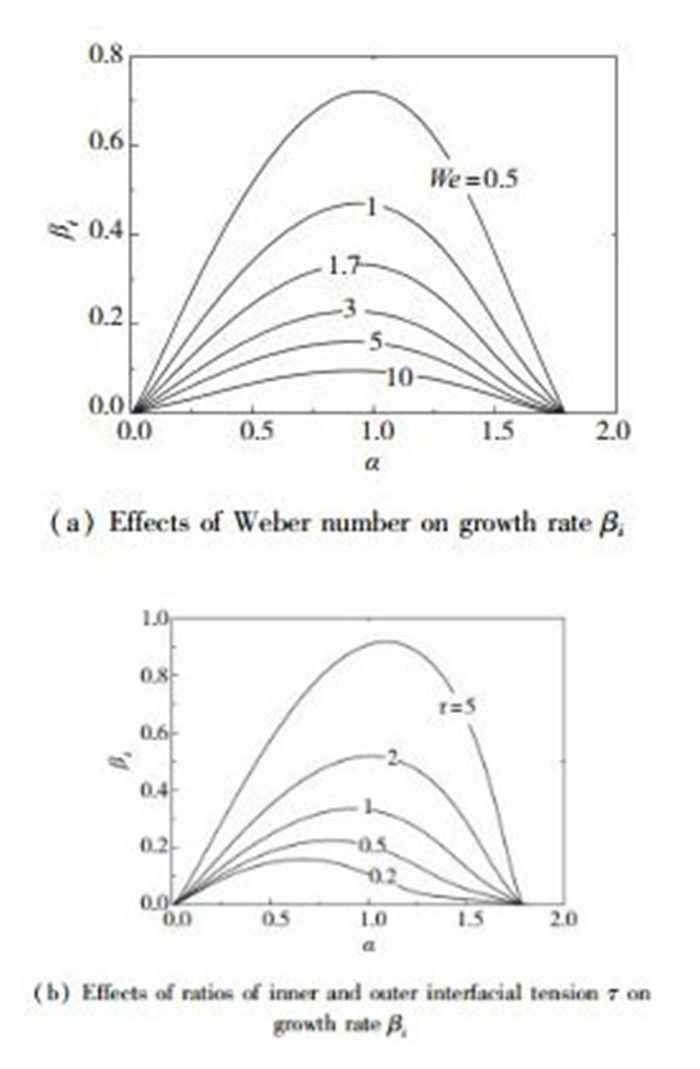
图 6给出了扰动增长率βi随Weber数以及内外界面张力系数比τ的变化情况.随着We减小或τ增大, stretching模对应的最不稳定扰动增长率βimax均增大, 可见增加内外层界面的界面张力均有利于同轴射流的破碎.这主要是因为在研究的参数范围内, 增长的扰动均处于长波区域(α≤1/κ), 而界面张力在长波区域会促进轴对称扰动的增长[14-15].另外, 虽然改变Weber数时stretching模对应的αmax变化不大, 但随着τ增加, αmax有着较为明显的增大, 可见增加内层界面的界面张力有利于减小射流破碎后形成液滴的尺寸.
|
| 图 6 Weber数和内外界面张力系数比τ对扰动增长率βi的影响 Fig.6 Effects of Weber number and ratios of inner and outer interfacial tension τ on growth rate βi |
此外还研究了内层流体和驱动流体的密度对同轴射流稳定性的影响.随着密度比S和Q的增大, 扰动增长率βi逐渐减小, 内层流体和驱动流体的密度均对同轴射流的稳定起促进作用; 比较S和Q对βi的影响还发现, βi对S的变化更为敏感.密度对同轴射流稳定性的影响主要源于射流惯性的改变:当增大S时, 同轴射流的惯性提高, 但此时射流受到的界面张力和黏性剪切力均保持不变, 因此扰动的增长速率将会变慢.
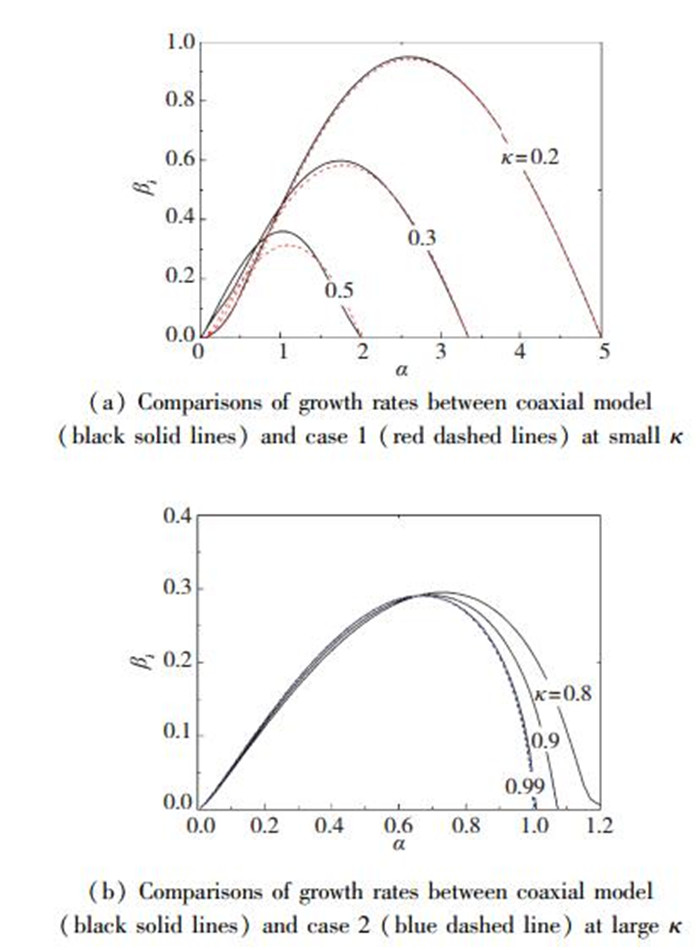
3.4 内外层界面间的耦合关系本小节重点讨论同轴射流中内外层界面间的耦合关系.建立两种极端情况下的分析模型, case 1:对应较小的κ, 此时内外界面相隔很远, 忽略外层界面以及驱动流体对内部射流的影响, 研究内部射流在外层流体作用下的稳定性; case 2:对应κ → 1的情况, 此时内外界面非常接近, 将内外界面合并为一个界面(Q2 → 0, 内界面无限靠近外界面, 外层流体消失), 其界面张力系数γ=γ1+γ2, 研究此单轴射流在驱动流体作用下的稳定性. 图 7给出了不同半径比κ下case 1, case 2以及同轴模型计算得到的扰动增长率曲线, 其中case 1的结果用红色虚线表示, case 2的结果用蓝色虚线表示, 同轴模型的结果用黑色实线表示. 3个模型比较时须保持无量纲化的特征尺度一致, 基本速度型对应: case 1中采用的速度型U1(r)和U2(r),case 2中采用的速度型为κ=1时的U1(r)和U3(r).
|
| 图 7 不同半径比κ下3种模型的扰动增长率曲线 Fig.7 Temporal growth rate curves of three models under different κ |
比较case 1和同轴模型发现:当κ≤0.2时, 两个模型对应的扰动增长率曲线基本一致, 可见此时内外层界面间基本没用相互作用, 是解耦的, 同轴射流可拆分为两个单轴射流来分析; 当κ≥0.3以后, 随着κ的增大, 两个模型对应的扰动增长率曲线差别越来越明显, 界面间相互作用越来越强,且相比于case 1, 同轴模型对应着更大的βimax以及更小的αmax, 这说明外层界面会促进内层界面上扰动的发展并对内层界面有轴向拉伸作用.
比较case 2和同轴模型发现:当κ=0.99时, case 2和同轴模型得到的结果基本相同; 随着κ的减小, case 2对应的扰动增长率曲线保持不变, 而同轴模型对应的βimax降低αmax增大, κ越小, case 2越偏离实际情况; 相比于case 2, 同轴模型有着更小的βimax以及更大的αmax, 说明内层界面会减弱外层界面上的扰动增长(外界面将一部分的扰动能量传递给内界面)并使外界面在轴向上压缩.
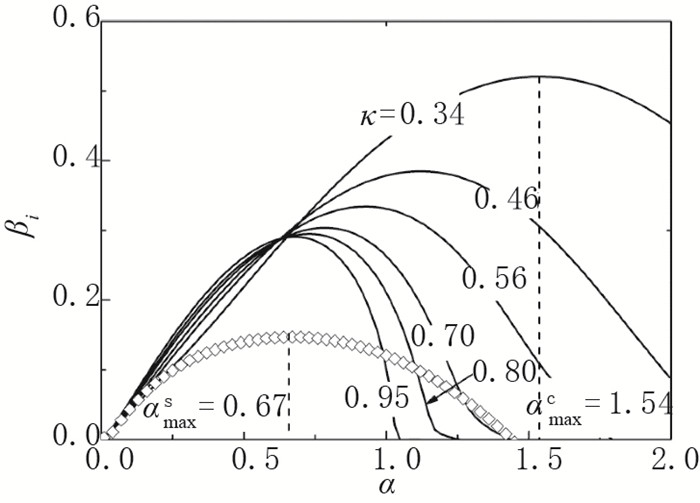
从图 1可看出同轴射流破碎后内外层液滴的包裹情况与内外层流量比Qr =Q1/Q2息息相关, 下面给出定性的理论解释.当Qr较大(κ较大)时, 由上文的分析可知内外界面是耦合在一块的, 内外层射流将同步破碎, 最后形成一包一结构的复合液滴.当Qr较小(κ较小)时, 内层射流一般会先于外层射流破碎, 简单起见, 这里我们假定内层射流破碎形成的液滴对外层射流界面的扰动增长影响不大, 内层射流破碎后可将外层射流当做单轴射流处理.因此, 内部射流在其破碎点附近的扰动波长由同轴模型给出, λi=2πR2/αmaxc, 其中αmaxc是同轴模型对应的最不稳定波数;而外部射流在其破碎点附近的扰动波长接近于单轴射流的情况, λo=2πR2/αmaxs, 其中αmaxs是单轴模型对应的最不稳定波数.由图 8可以看出, 当κ较小时, αmaxc要远远大于αmaxs, 因此λo比λi大很多, 从而形成一包多结构的复合液滴.
|
| 图 8 不同半径比κ下的扰动增长率曲线 Fig.8 Temporal growth rate curves under different κ |
绝对和对流不稳定性是时空模式下的两种性质不同的不稳定性, 当增长的扰动仅向扰动源位置的下游或上游一个方向传播, 使得在充分长的时间后扰动“逸”出了所研究的流动区域, 流场最后恢复到未扰动的状态, 则称流动是对流不稳定的; 如果增长的扰动既向下游传播又向上游传播, 在充分长的时间后扰动“污染”了整个流场, 使之无法恢复到未扰动的状态, 则称流动是绝对不稳定的.两种不稳定性的转换边界可由零群速度鞍点(α0, β0)决定, 本文选用鞍点图法来求解零群速度鞍点, 并采用Briggs-Bers碰撞准则[21]来判定其是否为物理鞍点, 具体可见参考文献[22].绝对和对流不稳定性的研究已经被广泛用于解释实验中观察到的滴模式和射流模式之间的转换[15, 18, 23], 其中, 绝对不稳定性对应滴模式, 而对流不稳定性则对应射流模式.
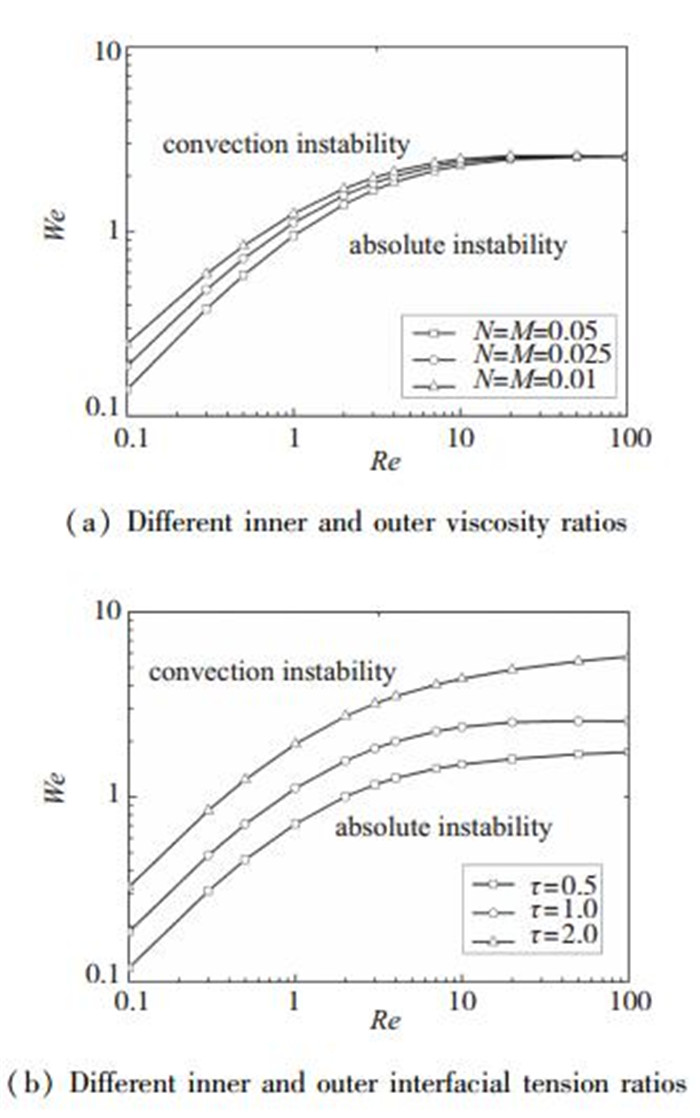
图 9(a)和(b)分别给出了不同黏性比以及不同内外界面张力比下同轴射流在Re-We平面上绝对和对流不稳定性的转换曲线, 其中曲线的下部分为绝对不稳定性, 反之为对流不稳定性.随着Re的增加, 转换曲线的临界We随之变大, 且临界We随着内层流体和驱动流动的黏性增加而减小, 随着内界面张力的增大而增大; 由此可知流体的黏性越大界面张力越小, 同轴射流越容易进入射流模式区域.同时还可以看出, 当Re较小时, 转换曲线的临界We变化较大, 其随Re的增大迅速增加; 当Re较大时, 临界We的变化很小.比较图 6(a)和(b)还发现内外界面张力的改变对临界We影响更大, 而且在不同的内层和驱动流体黏性下, 其临界We随着Re的增加逐步靠近, 最终当Re≥10时, 临界We趋于一致.
|
| 图 9 同轴射流在Re-We平面上的“绝对-对流”不稳定性转换曲线 Fig.9 Transition curves of absolute-convective instability in Re-We plane for coaxial jet |
本文根据液体驱动下的同轴流动聚焦实验建立了同轴射流的物理模型, 并基于管流和误差函数建立了基本速度型, 同时采用正则模方法得到了线化的小扰动控制方程及其相应的边界条件; 利用数值计算获得了扰动在时间域内的不稳定模态, 分析了主要控制参数对不稳定模态的影响规律; 同时初步展开了时空稳定性分析, 得到了Re-We平面上的绝对-对流不稳定性转换曲线.结果表明:一般情况下, stretching模在射流的不稳定过程中起主导作用, 内外界面的扰动发展是同相位的; 液体的黏性对同轴射流的稳定性均有着促进作用, 并且越大的黏性对应着越大的射流破碎波长; 增加内外层界面的界面张力均有利于射流的破碎, 并且较大的内界面张力有利于减小形成液滴的尺寸; 内外层界面间的耦合作用以及复合液滴的包裹情况均与内外射流的半径比息息相关:内外界面非常接近时, 界面间耦合很强, 此时容易形成一包一结构复合液滴, 内外界面相隔较远时, 界面间耦合很弱, 此时容易得到一包多结构复合液滴; 绝对-对流不稳定性转换的临界Weber数随Reynolds数内层界面张力的增大而增大, 随内层和驱动流体的黏性增大而减小.这些结果将有助于提高同轴流动聚焦的过程控制, 为实际应用提供理论指导.
下一步将系统开展相应的同轴流动聚焦实验, 并与理论分析对比, 同时更加深入地分析内外层界面间的耦合关系以及绝对-对流不稳定性的转换问题.
| [1] | Zambaux M F, Bonneaux F, Gref R, et al. Influence of experimental parameters on the characteristics of poly(lactic acid) nanoparticles prepared by a double emulsion method[J]. Control Release, 1998, 50(1/3): 31-40. |
| [2] | Rosca I D, Watari F, Uo M. Microbubble formation and its mechanism in single and double emulsion solvent e-vaporation[J]. Control Release, 2004, 99(2): 271-280.DOI:10.1016/j.jconrel.2004.07.007 |
| [3] | Guan J, Ferrell N, Lee L J, et al. Fabrication of polymeric microparticles for drug delivery by soft lithography[J]. Biomaterials, 2006, 27(21): 4034-4041.DOI:10.1016/j.biomaterials.2006.03.011 |
| [4] | He P, Davis S S, Illum L. Chitosan microspheres prepared by spray drying[J]. International Journal of Pharmaceutics, 1999, 187(1): 53-65.DOI:10.1016/S0378-5173(99)00125-8 |
| [5] | Gañán-Calvo A M. Generation of steady liquid microthreads and micron-sized monodisperse sprays in gas streams[J]. Physical Review Letters, 1998, 80(2): 285DOI:10.1103/PhysRevLett.80.285 |
| [6] | Cohen I, Li H, Hougland J L, et al. Using selective withdrawal to coat microparticles[J]. Science, 2001, 292: 265-267.DOI:10.1126/science.1059175 |
| [7] | Barrero A, Loscertales I G. Micro -and nanoparticles via capillary flows[J]. Annual Review of Fluid Mechanics, 2007, 39(1): 89-106.DOI:10.1146/annurev.fluid.39.050905.110245 |
| [8] | Gañán-Calvo A M, Montanero J M, Martín-Banderas L, et al. Building functional materials for health care and pharmacy from microfluidic principles and flow focusing[J]. Advanced Drug Delivery Reviews, 2013, 65(11/12): 1447-1469. |
| [9] | Martín-Banderas L, Flores-Mosquera M, Riesco-Chueca P, et al. Flow focusing: a versatile technology to produce size-controlled and specific morphology microparticles[J]. Small, 2005, 1: 688DOI:10.1002/(ISSN)1613-6829 |
| [10] |
司廷, 尹协振. 流动聚焦研究进展及其应用[J].
科学通报, 2011, 56(8): 537-546. Si T, Yin X Z. Progress and application of flow focusing[J]. Chinese Science Bulletin, 2011, 56(8): 537-546. |
| [11] | Gordillo J M, Pérez-Saborid M, Gañán-Calvo A M. Linear stability of co-flowing liquid-gas jets[J]. Journal of Fluid Mechanics, 2001, 448: 23-51. |
| [12] | Montanero J M, Rebollo-Muñoz N, Herrada M A, et al. Global stability of the focusing effect of fluid jet flows[J]. Physical Review E, 2011, 83(3 Pt 2): 036309 |
| [13] | Gañán-Calvo A M, Ferrera C, Montanero J M. Universal size and shape of viscous capillary jets: application to gas-focused microjets[J]. Journal of Fluid Mechanics, 2011, 670: 427-438.DOI:10.1017/S0022112010006476 |
| [14] |
司廷. 流动聚焦的实验和理论研究[D]. 合肥: 中国科学技术大学, 2009.
Si T. Experimental and theoretical investigation on flow focusing[D]. Hefei: University of Science and Technology of China, 2009(in Chinese). |
| [15] | Si T, Li F, Yin X Z, et al. Modes in flow focusing and instability of coaxial liquid-gas jets[J]. Journal of Fluid Mechanics, 2009, 629: 1-23.DOI:10.1017/S0022112009006211 |
| [16] | Si T, Li F, Yin X Z, et al. Spatial instability of coflowing liquid-gas jets in capillary flow focusing[J]. Physics of Fluids, 2010, 22(11): 112105DOI:10.1063/1.3490066 |
| [17] | Chauhan A, Maldarelli C, Papageorgiou D T, et al. Temporal instability of compound threads and jets[J]. Journal of Fluid Mechanics, 2000, 420: 1-25.DOI:10.1017/S0022112000001282 |
| [18] | Herrada M A, Montanero J M, Ferrera C, et al. Analysis of the dripping-jetting transition in compound capillary jets[J]. Journal of Fluid Mechanics, 2010, 649: 523-536.DOI:10.1017/S0022112010000443 |
| [19] | Li F, Yin X Y, Yin X Z. Instability analysis of a coaxial jet under a radial electric field in the nonequipotential case[J]. Physics of Fluids, 2006, 18: 037101DOI:10.1063/1.2181604 |
| [20] | Khorrami M R, Malik M R, Ash R L. Applications of spectral collocations techniques to the stability of swirling flows[J]. Journal of Computational Physics, 1989, 81(1): 206-229.DOI:10.1016/0021-9991(89)90071-5 |
| [21] | Briggs R J. Electron-stream interaction with plasmas[M]. Cambridge: MIT Press, 1964. |
| [22] |
尹协远, 孙德军.旋涡流动的稳定性[M].北京:国防工业出版社, 2003: 25-43.
Yin X Y, Sun D J. Vortex stability[M]. Beijing: National Defence Industry Press, 2003: 25-43(in Chinese). |
| [23] | Gañán-Calvo A M, Riesco-Chueca P. Jetting-dripping transition of a liquid jet in a lower viscosity co-flowing immiscible liquid: the minimum flow rate in flow focusing[J]. Journal of Fluid Mechanics, 2006, 553: 75-84.DOI:10.1017/S0022112006009013 |



