计算流体力学(CFD)是气动设计工作的核心[1], 采用先进的CFD方法, 可以大大减少设计工作的研制周期.传统的CFD方法主要通过数值计算方法, 将连续流场离散化, 对流体力学的控制方程(如Euler方程或Navier-Stokes方程)进行求解[2], 从而预测流场的流动.对于复杂的计算目标外型或工况条件, 传统的CFD方法计算周期长, 结果难以收敛, 在一定程度上限制了该方法在处理复杂问题的应用.
随着机器学习理论的不断发展, 有研究者尝试将其应用到CFD领域[3-8], 通过建立人工神经网络, 在给定的目标和工况条件下, 计算流场流动的复杂结构.通过训练和优化, 人工神经网络能够准确预测输入和输出之间的映射关系, 处理复杂的非线性问题.将人工神经网络应用到CFD计算领域中, 可以依赖已有的数据[9], 在类似工况条件下进行未知流场的预测.区别于传统的CFD方法, 人工神经网络不依赖于对控制方程的求解, 而是建立一个黑盒模型, 基于训练样本的输入和输出关系, 通过网络模型里神经元的信息传递和处理, 建立一个映射关系.在训练好神经网络之后, 可以通过改变输入参数(翼型参数), 直接预测出相应的输出参数(流场信息).同时, 人工神经网络也可以作为以流场信息为输入, 翼型参数为输出的函数逼近模型, 在翼型反设计的初级阶段进行迅速的优化处理.
本文实现人工神经网络在翼型计算领域中应用的方法如下:首先通过PARSEC参数化方法, 围绕基准翼型构造了一定翼型空间范围的翼型库, 利用XFOIL进行数值模拟, 搭建和翼型库具有一一映射关系的流场信息库.通过训练和优化神经网络, 实现基于此模型的快速、高可信度的翼型气动力预测, 以及新型的翼型优化设计方法.
通过自动化编程实现样本库的批量生成, 实现了不同翼型空间的样本量下, 神经网络的训练和优化过程.实验结果表明, 在机器学习领域中, 基于神经网络的翼型反设计模型的精确性高度依赖于训练样本量的大小和覆盖范围.
在给定设计工况条件下, 基于训练和优化后的人工神经网络模型, 可以通过改变翼型表面压力分布, 反设计出翼型几何形状, 并与设计要求具有良好的一致性.与国外文献中给定压力分布的人工神经网络计算模型相比, 本文方法给出反设计结果准确度明显更为优越.
1 神经网络的优化 1.1 样本库的建立研究表明, 作为机器学习科学的重要分支, 人工神经网络的预测能力强烈地依赖于训练样本量的大小和覆盖范围.因此, 本文的首要工作在于建立具有一一映射关系的翼型库和流场信息库, 并以此为样本库(涵盖输入和输出内容), 进行后续人工神经网络的训练和优化.具体而言, 翼型库的建立将通过PARSEC参数法进行翼型描述, 围绕基准翼型生成一定范围的翼型族.
PARSEC是翼型参数化方式之一, 主要用于亚声速和跨声速翼型的外型重塑, 具有较为精确的翼型外型控制能力.依赖于11个重要的翼型几何参数, PARSEC参数化方法得以在极坐标中描述翼型的外型. PARSEC参数化方法不须依赖于任何翼型基线, 基于一定的翼型几何约束条件, 通过11个控制参数, 研究者就可以生成大范围的翼型外型.
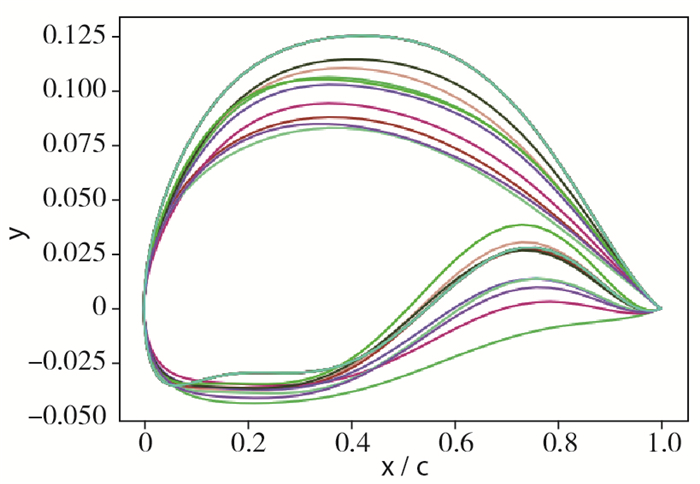
本例中, 以翼型NACA2412作为基线, 给予PA-RSEC控制参数一定范围的扰动, 随机生成10 000组翼型数据, 并选取其中20组翼型外型作图, 见图 1.
|
| 图 1 基于PARSEC参数化生成的部分翼型库范围 Fig.1 Partial airfoil library ranges based on PARSEC parameterization |
基于此, PARSEC参数化方法快速地在基准翼型附近生成一定范围的翼型族, 提供了可供神经网络进行样本学习的翼型几何信息库.
在综合考虑空间、时间效率以及计算精确性等因素后, 对于现有的流体力学计算软件, 决定采用XFOIL对翼型库中的翼型进行流场计算和记录.在剔除不符合实际的翼型外型和对应的不收敛的气动计算结果后, 翼型库和流场信息库将形成一个具有一一映射关系的样本库.
XFOIL软件采用基于势流计算的面源法, 利用流动边界层的积分函数, 以位于边界层位移厚度内流和外流的边界条件作为迭代收敛的标志, 以此计算翼型扰流附近的流场情况. XFOIL可以快速预测低Reynolds数下的翼型性能, 计算黏性压力分布和捕获后缘分离和层流分离气泡. XFOIL采用近似的eN包迹法来计算转捩点, 并假设扰动的总振幅达到经验值时, 翼型上的给定点发生转捩现象. XFOIL作为快速的流体力学计算软件, 可以应用于翼型设计初步阶段的气动性能分析[8].
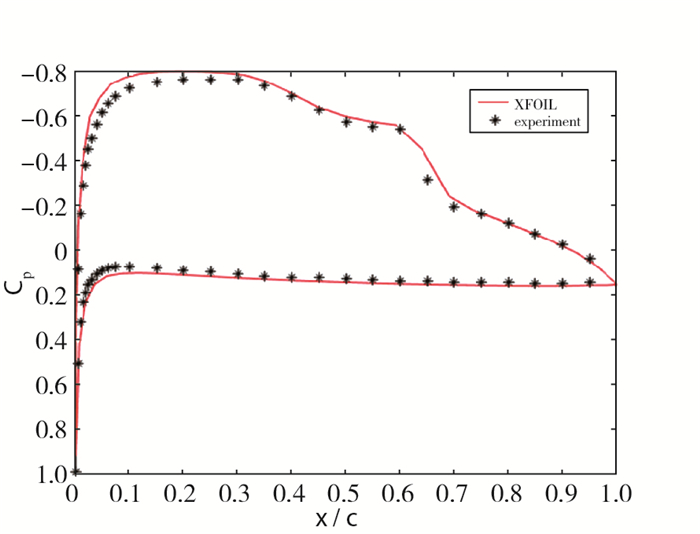
研究表明, XFOIL在计算翼型扰流问题中, 对于小迎角、低Reynolds数的工况条件, 其计算更容易收敛, 且结果具有较高的准确性.故采用E387翼型, 在Reynolds数为300 000, Mach数为0.2, 迎角为2°的工况条件下进行翼型绕流计算, 所得的计算结果和实验结果的对比如下.如图 2可知, 在低Reynolds数和小迎角工况条件下, XFOIL的翼型扰流计算结果较为准确, 与实验数据的拟合程度较高.
|
| 图 2 XFOIL计算结果和实验结果对比 Fig.2 Comparisons between XFOIL calculation and experiment result |
对于已生成的翼型库中翼型, 采用XFOIL进行升力系数、阻力系数和压力系数分布的计算, 得到可供神经网络进行样本学习的流场信息库.其中, 计算工况如表 1所示.
| 下载CSV 表 1 翼型气动力计算工况 Tab.1 Working conditions over the calculation of airfoil aerodynamic parameters |
误差逆向传播(back-propagation,BP)神经网络, 是一种单向传播的多层前向网络. BP网络的主要结构包括有输入层、中间层(隐层)和输出层, 上下层之间各个神经元全连接, 通过传递函数对输入响应进行处理, 从而具备较强的非线性问题处理能力.其误差的修正, 从输出层经过各个中间层逐层修正各连接层的权值和阈值, 最终回到输入层, 故称为“误差逆向传播算法”.
对于该3层神经网络, 其样本库共有m个样本, 第k个样本以下标k表示.每个样本的输入为n维向量, 输出为q维向量.由于输入层的神经元个数应等于输入向量的维数, 故输入层共有n个神经元.对于中间层, 我们可以自定义其神经元个数, 一般约等于2倍的输入维数, 此处假设其为p个神经元.对于输出层, 其神经元个数等于输出向量的维数, 因此有q个神经元.神经网络上下层之间通过权值连接, 且每个神经元都有一个介于(-1, 1)的阈值, 通过每次训练和学习, 神经网络更新这些参数, 使得输入模式响应的正确率不断上升.
对于神经网络的学习训练过程, 其步骤主要为:
(1) 初始化, 为神经网络所有的权值和阈值生成介于(-1, 1)的随机数.
(2) 随机选取一组具有对应关系的输入样本Pk和目标样本, Tk, 其中k为样本在训练样本集中的索引.
(3) 通过神经元对响应的传递和传递函数的非线性化处理, 计算输出层的输出向量Ck; 常用的传递函数有Sigmoid型的对数、正切函数等.
(4) 利用目标输出向量Tk和网络实际输出向量Ck, 计算输出层的各神经元的一般化误差.
(5) 计算中间层各神经元的一般化误差.
(6) 利用输出层各神经元的一般化误差与中间层的输出Bk来修正连接权值和阈值.
(7) 利用中间层各神经元的一般化误差与输入层的输入向量Pk来修正连接权值和阈值.
(8) 随机选取下一个学习样本向量提供给网络, 返回到步骤(3), 直到m个训练样本训练完毕.
(9) 检验样本库中选取一组输入和目标样本, 返回步骤(3), 若网络全局误差E小于预先设定的一个极小值, 则网络收敛.
BP神经网络的优化可以通过调节其控制参数, 改变其网络结构来实现.本例以升阻系数的预测作为研究问题, 建立以翼型外型(翼型坐标)为输入, 升力系数为输出和以翼型外型为输入, 阻力系数为输出的神经网络, 分别从训练样本数, 训练次数, 隐藏层神经元个数, 传递函数进行优化训练.神经网络结构见表 2.
| 下载CSV 表 2 神经网络结构 Tab.2 BP neural network structure |
对于该问题的计算复杂度, 查阅文献后可知, 计算样本量大多置于(100, 1 000)这个区间范围.选取4 000个翼型作为最大的样本量进行优化设计.同时, 选取400组样本作为验证样本集, 用以分析该神经网络的误差变化并检验其预测能力.
(1) 训练样本数
当网络的体系结构是固定时, 训练集的大小是决定神经网络的泛化能力的关键因素.如何选取适度的训练样本大小, 一直是一个持续公开的研究领域.
对于该问题, 随着训练样本量的增加, 其误差绝对值并没有显著的下降.经过反复调试后知, 在训练样本量等于500时, 误差绝对值第1次达到最小值, 随着训练样本量的增加, 部分样本重复了该问题的特征点, 使得神经网络对于这部分样本的拟合无效, 此时随着训练样本量的增加, 其误差变化不明显, 预测能力停滞不前, 消耗了无用功的训练时间.
(2) 训练次数
在反复训练的过程中, 全局逼近神经网络通过修正神经元的权值和阀值, 实现对输出函数的逼近.随着训练次数的增加, BP神经网络的学习将会逐渐覆盖到训练集合的独特性, 从而忽略普遍性, 这将有可能导致过拟合现象训练样本数.
防止过拟合可以通过及早停止、扩大训练数据、加入正则约束或者随机丢弃等方法来实现, 本例中, 通过调整神经网络的训练次数来控制其输出结果的拟合准确度.
(3) 隐藏层神经元个数
通过选取合适的隐藏层神经元个数, 加之以传递函数的处理, 可以实现从输入到输出的非线性映射.一般认为, 隐藏层神经元个数与求解模型的复杂度、输入和输出向量维度有着密切的关系.过多的隐藏层单元会导致神经网络的计算效率降低, 而过少的单元个数则会降低神经网络的容错性.迄今为止, 尚未存在明确的隐藏层神经元个数的表达式, 往往须针对不同问题进行实验后才能获得最优解.
对于该问题的复杂度, 以隐藏层神经元个数作为自变量, 该神经网络的预测能力在(10, 40)区间随着神经元个数的递增而增强, 当神经元个数超过40后, 其预测能力开始大幅下降, 后又慢慢增强.从其绝对值误差最小值的位置看, 隐藏层神经元个数取40时, 系统达到最优.
(4) 传递函数
基于传递函数(又称之为非线性激活函数), BP神经网络得以实现对非线性问题的处理.传递函数的普遍应用形式是logistic函数, 本例中主要使用logsig和tansig函数进行处理, 并在输出层中设置purelin线性函数进行优化.传递函数的作用是对输入响应进行非线性处理, 若没有该函数作用, 则无论神经元的阈值和权值经多少次学习和修正, 该神经网络对于输入响应始终是线性化处理, 这对于非线性问题的逼近是无效的.
对于传递函数讨论的结果如表 3所示.
| 下载CSV 表 3 不同训练和传递函数的计算结果 Tab.3 Results based on different training and activation functions |
通过给定翼型表面的压力分布, 计算求得对应的翼型, 这在工程领域上称之为翼型的反设计.在翼型设计初期, 快速、实时、准确的翼型设计方法可以缩小工程周期, 并为后期精确设计打下坚实的基础.本单元将基于BP神经网络对翼型反设计方法进行研究, 以XFOIL计算求得的压力系数分布作为训练样本的输入参数, 并通过PARSEC参数法降低输出参数(翼型坐标)的维度.此时的设计工况与表 1计算压力分布系数的工况相同.
在对BP神经网络进行调试后发现, 若一次性预测所有的PARSEC控制参数, 网络难以捕捉所有参数的非线性映射关系, 使得部分参数的预测结果误差过大, 不满足工程要求.因此将11个控制参数分成3组, 分别构造3个BP神经网络对该问题进行预测, 并对这3个神经网络进行各自的参数调优.
此时, 基于一组已知翼型计算求得压力分布系数(该翼型不在训练样本集中), 以该压力分布系数作为输入, 通过本例中训练好的神经网络模型预测翼型PARSEC参数, 并利用PARSEC表达法描述出翼型外型.将其与基准的已知翼型对比, 见表 4.
| 下载CSV 表 4 翼型反设计的输出误差分布 Tab.4 Output error distributions of airfoil inverse design |
基于该神经网络, 在某个工况下, 利用给定的翼型表面压力分布, 可以准确地求解对应的翼型.误差范围严格控制在工程误差范围内, 绘制的预测翼型和给定翼型基本重合.
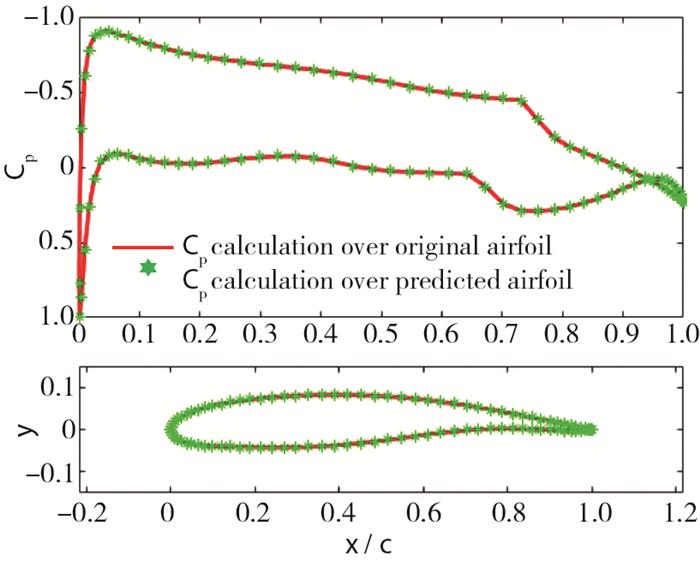
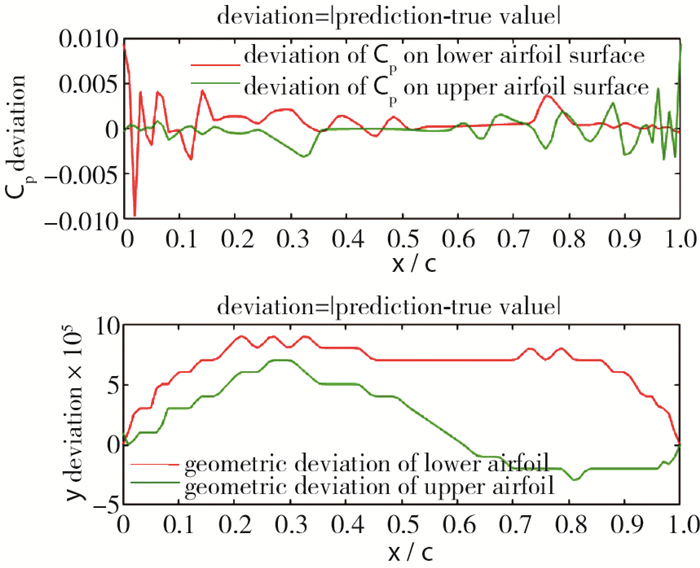
同时, 以下将考虑这些微小的误差(预测翼型和给定翼型之间的位移偏差)是否会造成压力分布曲线(关心量)的较大偏差.做如下操作, 利用XFOIL对预测翼型进行气动力求解, 获得新的压力分布曲线图, 并将其与给定的压力分布曲线图进行对比, 见图 3和图 4.
|
| 图 3 原翼型的压力分布和预测翼型的计算压力分布对比图 Fig.3 Comparisons of Cp distributions between the original airfoil and the predicted airfoil |
|
| 图 4 针对压力分布系数和翼型几何坐标, 原翼型和预测翼型的偏移大小 Fig.4 Deviation of Cp distribution and airfoil geometry |
此处采用偏移量作为该神经网络进行翼型反设计能力的衡量标准, 由图可知, 该神经网络预测翼型的准确性高, 且由预测翼型计算得来的压力系数分布与基准压力系数分布重合度高, 即PARSEC参数法的气动性能鲁棒性较好.所谓鲁棒性, 就是指在给予一个小扰动后, 其性能是否会产生较大的偏差, 如果不会, 则鲁棒性较好, 反之亦然.
在2015 11th International Conference on Natural Computation (ICNC)会议上, 研究者Waqas S等[15]提出了一篇基于蚁群优化和遗传算法的论文, 其中采用了BP神经网络和RBF神经网络, 通过给定的翼型表面压力分布系数求得对应的翼型.
在该文中“Results of neural network”部分, 研究者分析和说明了其神经网络的训练结果.通过设置“known”和“unknown”两组, 建立了神经网络训练样本集和神经网络训练样本集外的结果测试.其检验的方式和本文一致, 也是基于通过真实翼型的计算压力系数分布曲线而输出预测翼型, 并利用预测翼型和真实翼型之间的偏差量作为误差的衡量标准和预测能力的优劣性分析.为了将本文的实验结果和实验结果作比较, 以输出的11个PAESEC参数做MSE误差分析, 并以“known”和“unknown”两组作为实验对象, 进行结果分析比较.
| 下载CSV 表 5 本文和Waqas组的计算结果对照 Tab.5 Comparisons of the results with Waqas results |
此处, 设置已知组为2 000个翼型、未知组为200个翼型.在本例中, 对于已知组, 均方误差小于1×10-5的预测翼型占比98.4%;对于未知组, 均方误差小于1×10-5的预测翼型占比95.5%.和ICNC会议上, 研究者Waqas论文相比, 本文的实验结果更优, 精确度远远优于Waqas的实验结果(分别为54.6%和56.5%).
区别于研究者Waqas, 本文采用3个BP神经网络共同预测翼型的输出, 这使得本文得以更准确地逼近输出函数, 实现复杂非线性问题的拟合.另外一个重要因素在于训练样本量的大小——本文的训练样本量远远大于该文献的训练样本量.该实验结果也与神经网络预测能力极大地依赖于训练样本量这个已有结论相吻合.
3 结论传统的流场计算方法在工况复杂度高时, 时间成本和计算成本之间的矛盾往往不可协调.随着机器学习理论的发展, 基于数据驱动的模型引起了众多研究者的关注和兴趣.结合流体力学领域中已有的大量实验和仿真数据, 研究者可以通过建立神经网络模型实现流场计算和翼型优化设计.利用神经网络的学习和训练, 流场计算和翼型优化过程可以大大节约时间和空间成本, 得以在翼型设计初期实现实时、准确的计算和预测.
对于翼型反设计模型, 本文采用3个BP神经网络对该问题进行预测和逼近, 实验结果表明该方法具有极高的精确性.将其与已有文献中的类似实验结果进行讨论, 可知训练样本量的数量对于神经网络的预测能力有极大作用.同时,对于复杂问题的预测问题,采用多个神经网络共同训练,可以提高其准确率.
同时, 本文探索了各参数对于神经网络优化和训练的作用, 验证了神经网络在翼型气动力计算和翼型反设计中的可行性, 在大数据时代背景下为流体力学和机器学习的学科交叉融合进行基础研究座铺垫, 验证了其在翼型设计初期的工程实现价值.
| [1] |
Anderson J D Jr. Fundamentals of aerodynamics[J]. AIAA Journal, 2011, 48: 2983-2983. |
| [2] |
Zhang Z J, Duraisamy K. Machine learning methods for data-driven turbulence modeling[R]. AIAA 2015-2460, 2015. https://arc.aiaa.org/doi/abs/10.2514/6.2015-2460
|
| [3] |
Parish E J, Duraisamy K. A paradigm for data-driven predictive modeling using field inversion and machine learning[J]. Journal of Computational Physics, 2016, 305: 758-774. DOI:10.1016/j.jcp.2015.11.012 |
| [4] |
Müller S, Milano M, Koumoutsakos P. Application of ma-chine learning algorithms to flow modeling and optimi-zation[C]. Center for Turbulence Research Annual Research Briefs, Stanford University, Stanford, 1999: 169-178.
|
| [5] |
Gautier N, Aider J-L, Duriez T, et al. Closed-loop separation control using machine learning[J]. Journal of Fluid Mechanics, 2015, 770: 442-457. DOI:10.1017/jfm.2015.95 |
| [6] |
Guo X, Li W, Iorio F. Convolutional neural networks for steady flow approximation[C]. Proceedings of the 22nd ACMSIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, 2016: 481-490. https://www.kdd.org/kdd2016/papers/files/adp1175-guoA.pdf
|
| [7] |
Zuo Z, Shuai B, Wang G, et al. Convolutional recurrent neural networks: Learning spatial dependencies for image representation[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2015: 18-26. https://www.cv-foundation.org/openaccess/content_cvpr_workshops_2015/W03/papers/Zuo_Convolutional_Recurrent_Neural_2015_CVPR_paper.pdf
|
| [8] |
Drela M. XFOIL: an analysis and design system for low Reynolds number airfoils[C]. Conference on Low Rey-nolds Number Airfoil Aerodynamics, University of Notre Dame, Springer Berlin Heidelberg, 1989: 1-2. https://link.springer.com/chapter/10.1007%2F978-3-642-84010-4_1
|
| [9] |
Selig M S. UIUC airfoil data site[R]. Department of Aeronautical and Astronautical Engineering University of Illinois at Urbana-Champaign, 1996.
|
| [10] |
Widrow B, Lehr M A. 30 years of adaptive neural networks:perceptron, madaline, and backpropagation[J]. Proceedings of the IEEE, 1990, 78(9): 1415-1442. DOI:10.1109/5.58323 |
| [11] |
Lippmann R P. An introduction to computing with neural nets[J]. IEEE Acoustics, Speech and Signal Processing Magazine, 1988, 2(4): 4-22. |
| [12] |
Grossberg S, Mingolla E, Todovoric D. A neural network architecture for preattentive vision[J]. IEEE Transactions on Biomedical Engineering, 1989, 36: 65-83. DOI:10.1109/10.16450 |
| [13] |
Amari S I. Mathematical foundations of neurocom-puting[J]. Proceedings of the IEEE, 1990, 78(9): 1443-1463. DOI:10.1109/5.58324 |
| [14] |
Barnard E. Optimization for training neural nets[J]. IEEE Transactions on Neural Networks, 1992, 3(2): 232-240. DOI:10.1109/72.125864 |
| [15] |
Saleem W, Kharal A, Ahmad R, et al. Comparison of ACO and GA techniques to generate Neural Network based Bezier-PARSEC parameterized airfoil[C]. The 201511th International Conference on Natural Computation, IEEE, 2015. http://www.inase.org/library/2015/zakynthos/bypaper/MATH/MATH-20.pdf
|
| [16] |
Wickramasinghe U K, Carrese R, Li X. Designing airfoils using a reference point based evolutionary many-objective particle swarm optimization algorithm[C]. Evolutionary Computation, IEEE, 2010. https://ieeexplore.ieee.org/document/5586221?arnumber=5586221
|
| [17] |
Sun G, Sun Y, Wang S. Artificial neural network based inverse design:Airfoils and wings[J]. Aerospace Science and Technology, 2015, 42: 415-428. DOI:10.1016/j.ast.2015.01.030 |
| [18] |
Song W B, Keane A J. A study of shape parameterisation methods for airfoil optimisation[C]. American Institute of Aeronautics and Astronautics, 2004. https://www.researchgate.net/publication/242097385_A_Study_of_Shape_Parameterisation_Methods_for_Airfoil_Optimisation
|




