近年来, 近空间高超声速飞行器的研制受到航空航天领域的广泛关注[1-2]. 与传统的宇宙飞船、航天飞机等具有钝头外形的再入式飞行器不同, 近空间飞行器需要在大气层内做长时间的巡航和机动飞行, 这就需要其具有高升阻比的气动外形和控制结构. 而这种非流线型的构型在高速飞行时将不可避免地产生强烈的激波-边界层干扰(shock-wave/boundary-layer interactions, SWBLI), 并常常伴随着流动的分离和再附. 由SWBLI引起的再附点附近的热流峰值可以达到无干扰时的10~100倍, 甚至是驻点热流的数倍之多[3-4]. 因此, 在高速飞行时, 飞行器将处于严峻而复杂的气动热环境中, 准确地预测峰值热流对飞行器的热防护设计尤为重要.
现有预测SWBLI引起的峰值热流的方法仍有不足. 一方面, 实验很难同时满足实际飞行时的焓、Reynolds数等条件[5]. 另一方面, 尽管计算流体力学(CFD)已广泛用于飞行器设计, 但其对峰值热流的预测仍然存在非常大的不确定度[6-8]. 传统上工程主要依靠热流与压强的比拟关联式[9-11]间接预测峰值热流. 然而不同模型的关联式需要不同的拟合参数, 带有强烈的工程经验性质, 其物理本质也不明确. 因此, 对峰值热流的理论分析和有效预测显得很有必要.
在早期的研究中, 有两类理论方法可用于求解分离-再附流动的热流问题. 第一类是以Lees等[12]和Nielsen等[13]为代表的动量积分方法,它是Karman-Pohlhausen方法[14]的拓展和修正. Klineberg等[15]引入能量方程拓展了Lees的方法使其能够求解热流. Murphy[16]评估了上述几种方法, 发现这些方法只能预测弱激波干扰下的压强, 无法准确预测热流. 而且, 动量积分方法需要假设一个合理的速度剖面和温度剖面, 这是非常困难的. 另一类可求解分离-再附流动热流的方法是一种渐近展开方法, 即三层结构理论. Lighthill[17]最早提出两层结构的概念, 认为黏性只在边界层内靠近壁面的薄亚层起作用. 根据这一概念, Neiland[18]和Stewartson等[19]针对超声速分离流动,Messiter[20]针对不可压缩平板后缘附近流动,分别独立地给出了三层结构理论. 随后, Brown等[21]将三层结构理论拓展到高超声速, Rizzetta等[22-23]引入了能量方程, 讨论了超声速压缩拐角流动的热流, Daniels[24-25]将三层结构理论类比到再附点附近. 尽管三层结构理论在多方面都得到了成功应用, 但理论本身还存在一些局限性, 例如: 引入极高Reynolds数假设(Re>108), 使得理论在较低Reynolds数下存在不足, 而且理论的控制方程是隐式椭圆偏微分方程, 其求解难度不亚于一般的CFD求解程序, 当出现显著的回流区时, 解可能会出现不稳定性, 难以解决大尺度分离的问题[26].
然而, 工程上更关心的近空间高超声速飞行器面临的流动Reynolds数较低(104~105), 且更关注大尺度分离引发的气动加热问题. 最近, 李邦明[27]针对再附点局部区域, 首次引入斜驻点流动模化再附点附近干扰区无黏流动, 虽然其最终仍须借助热流比拟关联式[9]来计算峰值热流, 但验证了构造这类非渐近的模型理论的可行性和有效性.
为了解决中低Reynolds数下高超声速大分离流动中的再附区气动加热问题, 本文结合三层结构理论的思想,引入斜驻点流动模型, 用以模化再附点附近整个剪切层内部的流动, 构建了一个新的模型理论框架. 同时, 针对压缩拐角分离-再附流动模型, 本文给出了再附点区外缘以及斜驻点流动区参数的求解方案, 从而形成一套完整的求解压缩拐角流动峰值热流的方法. 本文仅考虑完全分离的定常二维层流流动, 并假设流体为量热完全气体.
1 模型理论的构建前人的研究指出, 由SWBLI引起的不同类型的分离-再附流动并没有本质的区别[26]. 无论是激波入射边界层, 还是压缩拐角流动, 或者是正激波诱导的分离和再附, 均是由边界层在分离点脱出形成自由剪切流, 并撞向壁面形成再附流动, 其压力和热流分布也相似. 李邦明[27]认为所有的再附流动是相似的, 可以用统一的理论来描述. 根据这个观点, 本文将压缩拐角分离-再附流动分成两个部分: 包含热流峰值点的再附点局部区域和外部无黏流动. 首先建立再附点局部区域的模型理论.
1.1 再附点局部区域的建模再附区流动的特征很大程度上取决于分离产生的自由剪切层的特性. 边界层在分离点脱出后形成的自由剪切层一般只受到惯性力和黏性力作用, 经过不断演化, 层内流动更接近于类Couette流. 这种剪切层携带均匀涡量, 撞击壁面形成再附流动, 非常符合斜驻点流动的特征, 即由驻点流(西门子流动)[28]加入均匀剪切分量得到.
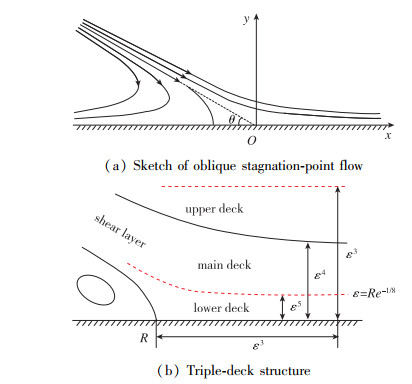
图 1(a)是斜驻点流动的示意图, 平板壁面处于Descartes坐标系y=0处, 流体处在y>0区域, θ为斜驻点的倾斜角, 即零流线与平板的夹角. 流动在远场的流函数可写为[29-31]
| $ {\psi _{\rm{e}}} = axy + \frac{1}{2}b{y^2} $ | (1) |
|
| 图 1 再附点附近的流动特征 Fig.1 Structure of reattachment flow |
即西门子流动和均匀剪切流的叠加. 易知
| $ \tan \theta = - {\left( {\frac{v}{u}} \right)_{{\psi _{\rm{e}}} = 0}} = \frac{{2a}}{b} $ | (2) |
其中, a表示x=0处的流向速度梯度, b表示涡量, a,b为常量. 由于均匀剪切流并非边界层型的流动, 斜驻点流动形成的边界层厚度可以用相应的西门子流动的边界层厚度表征, 即为
| $ {\delta _0} = \sqrt {\frac{{{\mu _{\rm{e}}}}}{{{\rho _{\rm{e}}}a}}} $ | (3) |
由经典斜驻点理论(1) 式看出, 斜驻点流动速度在远场趋于无穷. 在实际流动中, 远场应为均匀流. 因此, 该模型需要修正. 根据三层结构理论[19], 流动在分离点或再附点等奇性点附近具有三层结构, 即有黏有旋的下层、无黏有旋的主层和无黏无旋的上层, 见图 1(b). 这意味着, 附着后的剪切层的绝大部分可以当作无黏流来处理, 黏性只在剪切层靠近壁面的薄亚层起作用, 而剪切层的外部是无黏势流. 对于紧靠壁面的黏性层, 实际上是剪切层再附之后发展出来的新的边界层.
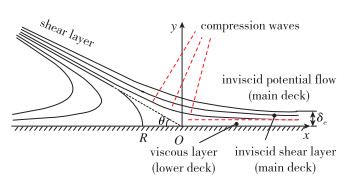
因此, 可以建立描述再附点下游局部区域的“斜驻点-三层结构”模型, 如图 2所示. 靠近壁面的下层是有黏有旋的斜驻点边界层, 简称为“黏性层”, 其厚度可设为cδδ0, 其中cδ为常数; 中间层是无黏有旋的斜驻点边界层外流, 可称之为“无黏剪切层”, 其厚度为δe; 上层是无黏无旋的势流, 决定了无黏剪切层外缘的流动参数, 如压强pe, 温度Te, 密度ρe, 速度ue等.
|
| 图 2 斜驻点-三层结构模型 Fig.2 Oblique-stagnation-point-triple-deck model |
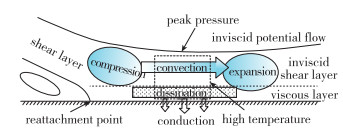
斜驻点-三层结构模型反映了再附点下游局部区域的流场特征, 同样也反映了其传热特征. 高速流动的能量方程[32]为
| $ (\rho \mathit{\boldsymbol{v}} \cdot \nabla )h = \mathit{\boldsymbol{v}} \cdot \nabla p + \varPhi + \nabla \cdot (k\nabla T) $ |
其中, ρ,T,p,v分别为流体的密度、温度、压强、速度, Φ为耗散函数, k为导热系数, 焓h=cpT, 其中cp为定压比热容. 再附点附近的剪切层是一个薄层, 类似于经典的平板边界层, 其法向速度远小于流向速度, 即v
|
| 图 3 剪切层传热示意图 Fig.3 Sketch of heat transfer in shear layer |
基于再附点下游局部区域流动物理特性, 建立了“斜驻点-三层结构”模型, 下面将给出模型中黏性层和无黏剪切层即斜驻点部分的数学描述.
黏性层的厚度相对于流向尺度而言是一个小量, 因此可仿照经典边界层的量级分析方法, 给出黏性层的控制方程
| $ \left\{ \begin{array}{l} \frac{{\partial (\rho u)}}{{\partial x}} + \frac{{\partial (\rho v)}}{{\partial y}} = 0\\ \rho u\frac{{\partial u}}{{\partial x}} + \rho v\frac{{\partial u}}{{\partial y}} = {\rho _{\rm{e}}}{u_{\rm{e}}}\frac{{\partial {u_{\rm{e}}}}}{{\partial x}} + {\rho _{\rm{e}}}{v_{\rm{e}}}\frac{{\partial {u_{\rm{e}}}}}{{\partial y}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial u}}{{\partial y}}} \right)\\ \rho \left( {u\frac{{\partial h}}{{\partial x}} + v\frac{{\partial h}}{{\partial y}}} \right) = \frac{\partial }{{\partial y}}\left( {k\frac{{\partial T}}{{\partial y}}} \right) + \mu {\left( {\frac{{\partial u}}{{\partial y}}} \right)^2} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} u\left( {{\rho _{\rm{e}}}{u_{\rm{e}}}\frac{{\partial {u_{\rm{e}}}}}{{\partial x}} + {\rho _{\rm{e}}}{v_{\rm{e}}}\frac{{\partial {u_{\rm{e}}}}}{{\partial y}}} \right) \end{array} \right. $ | (4) |
其中,下标e表示黏性层外缘即无黏剪切层中的物理量. 与经典的边界层方程不同的是, 斜驻点边界层的外流是带有涡量的无黏剪切流, 满足
| $ {\rho _{\rm{e}}}{u_{\rm{e}}}\frac{{\partial {u_{\rm{e}}}}}{{\partial x}} + {\rho _{\rm{e}}}{v_{\rm{e}}}\frac{{\partial {u_{\rm{e}}}}}{{\partial y}} = - \frac{{\partial {p_{\rm{e}}}}}{{\partial x}} $ |
对应动量和能量方程各增加一项.
鉴于斜驻点黏性流动方程(4) 与经典边界层方程类似, 下面将拓展自相似理论, 给出方程(4) 的数学求解方案. 第一, 类似Howarth-Dorodnitsyn变换[34-35], 引入坐标变换
| $ \left\{ {\begin{array}{*{20}{l}} {\xi = \int_0^x {\frac{a}{{b{\delta _0}}}} {\rm{d}}x}\\ {\eta = \int_0^y {\frac{1}{{{C_\rho }{\delta _0}}}} {\rm{d}}y} \end{array}} \right. $ | (5) |
并假设∂η/∂x=0, 其中Cρ=ρe/ρ. 由于再附点附近ρe, Te等均达到峰值, 其流向的变化可以忽略, 均看作常数, 因而δe也是常数. 第二, 参考Tooke等[36]的不可压缩斜驻点流动解法, 假设黏性层内流函数仍然具有与无黏剪切层类似的驻点分量加剪切分量的形式, 即
| $ \psi = \delta _0^2(\xi f(\eta ) + g(\eta )) $ |
则黏性层内的流动速度为
| $ \left\{ {\begin{array}{*{20}{l}} {u = \frac{{{\rho _{\rm{e}}}}}{\rho }\frac{{\partial \psi }}{{\partial y}} = \frac{1}{{{\delta _0}}}\frac{{\partial \psi }}{{\partial \eta }} = b{\delta _0}\left( {\xi {f^\prime } + {g^\prime }} \right)}\\ {v = - \frac{{{\rho _{\rm{e}}}}}{\rho }\frac{{\partial \psi }}{{\partial x}} = - \frac{{{\rho _{\rm{e}}}}}{\rho }\frac{a}{{b{\delta _0}}}\frac{{\partial \psi }}{{\partial \xi }} = - {C_\rho }a{\delta _0}f} \end{array}} \right. $ | (6) |
第三, 如上所述, 斜驻点边界层外缘并非均匀流, 再附点局部区域存在沿流向的温度梯度, 由速度沿流向线性分布可知, 能量方程的压缩项和耗散项沿流向呈二次函数分布, 因此对于壁温为Tw的等温壁面可假设温度分布也为二次函数分布, 即
| $ \frac{{T - {T_{\rm{w}}}}}{{{T_{{\rm{aw}}}} - {T_{\rm{e}}}}} = {\varTheta _0}(\eta ) + {\varTheta _1}(\eta )\xi + {\varTheta _2}(\eta ){\xi ^2} $ | (7) |
其中, Taw为恢复温度,
| $ {\psi _{\rm{e}}} = ax\left( {y - {c_\delta }{\delta _0}} \right) + \frac{1}{2}b{y^2} $ |
从而可得无黏剪切层的流动速度为
| $ \left\{ {\begin{array}{*{20}{l}} {{u_{\rm{e}}} = \frac{{\partial {\psi _{\rm{e}}}}}{{\partial y}} = ax + by}\\ {{v_{\rm{e}}} = \frac{{\partial {\psi _{\rm{e}}}}}{{\partial x}} = - a\left( {y - {c_\delta }{\delta _0}} \right)} \end{array}} \right. $ | (8) |
边界层位移厚度的参数cδ可类比于平板边界层中的参考温度法, 取为
| $ {c_\delta } = {c_1} + {c_2}\frac{{\gamma + 1}}{2}Ma_{\rm{e}}^2 + {c_3}\frac{{{T_{\rm{w}}}}}{{{T_{\rm{e}}}}} $ |
其中, c1=-1.27, c2=0.15, c3=1.57. 将(6)~(8) 式代入到方程(4) 中, 并按(5) 式进行坐标变换, 最终得到
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left( {C{f^{\prime \prime }}} \right)}^\prime } + f{f^{\prime \prime }} - {f^{\prime 2}} + {{\bar T}_0} + {c_\delta }{{\bar T}_1} = 0\quad {\rm{ (a) }}}\\ {{{\left( {C{g^{\prime \prime }}} \right)}^\prime } + f{g^{\prime \prime }} - {f^\prime }{g^\prime } + {c_\delta }{{\bar T}_0} = 0\quad {\rm{ (b) }}}\\ {{{\left( {\frac{C}{{Pr}}\varTheta _0^\prime } \right)}^\prime } + f\varTheta _0^\prime = {g^\prime }{\varTheta _1} + {P_0}\quad {\rm{ (c) }}}\\ {{{\left( {\frac{C}{{Pr}}\varTheta _1^\prime } \right)}^\prime } + f\varTheta _1^\prime - {f^\prime }{\varTheta _1} = 2{g^\prime }{\varTheta _2} + {P_1}\quad {\rm{ (d) }}}\\ {{{\left( {\frac{C}{{Pr}}\varTheta _2^\prime } \right)}^\prime } + f\varTheta _2^\prime - 2{f^\prime }{\varTheta _2} = {P_2}\quad {\rm{ (e) }}} \end{array}} \right. $ | (9) |
其中,
| $ {\left\{ \begin{array}{l} {P_0} = {H_{\rm{r}}}D_{\rm{r}}^2\left( {{c_\delta }{g^\prime }{{\bar T}_0} - C{g^{\prime \prime 2}}} \right)\\ {P_1} = {H_{\rm{r}}}D_{\rm{r}}^2\left( {\left( {{c_\delta }{f^\prime } + {g^\prime }} \right){{\bar T}_0} + {c_\delta }{g^\prime }{{\bar T}_1} - 2C{f^{\prime \prime }}{g^{\prime \prime }}} \right)\\ {P_2} = {H_{\rm{r}}}D_{\rm{r}}^2\left( {{f^\prime }{{\bar T}_0} + \left( {{c_\delta }{f^\prime } + {g^\prime }} \right){{\bar T}_1} + {c_\delta }{g^\prime }{{\bar T}_2} - C{f^{\prime \prime 2}}} \right) \end{array} \right.} $ |
| $ {\left\{ \begin{array}{l} {{\bar T}_0} = {T_{\rm{w}}}/{T_{\rm{e}}} + \left( {{T_{{\rm{aw}}}}/{T_{\rm{e}}} - 1} \right){\varTheta _0}\\ {{\bar T}_1} = \left( {{T_{{\rm{aw}}}}/{T_{\rm{e}}} - 1} \right){\varTheta _0}\\ {{\bar T}_2} = \left( {{T_{{\rm{aw}}}}/{T_{\rm{e}}} - 1} \right){\varTheta _0} \end{array} \right.} $ |
利用黏性层与无黏剪切层之间的匹配和壁面条件, 并假定ψ(ξ, 0)=0, 可得方程的边界条件为
| $ \begin{array}{*{20}{l}} {\left\{ {\begin{array}{*{20}{l}} {f(0) = 0,{f^\prime }(0) = 0,{f^\prime }\left( {{\eta _{\rm{e}}}} \right) = 1}\\ {g(0) = 0,{g^\prime }(0) = 0,{g^{\prime \prime }}\left( {{\eta _{\rm{e}}}} \right) = 1} \end{array}} \right.}\\ {\left\{ {\begin{array}{*{20}{l}} {{\varTheta _0}(0) = 0}\\ {{\varTheta _0}\left( {{\eta _{\rm{e}}}} \right) = \Delta {T_{\rm{r}}}} \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} {{\varTheta _1}(0) = 0}\\ {{\varTheta _1}\left( {{\eta _{\rm{e}}}} \right) = 0} \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} {{\varTheta _2}(0) = 0}\\ {{\varTheta _2}\left( {{\eta _{\rm{e}}}} \right) = 0} \end{array}} \right.} \right.} \right.} \end{array} $ | (10) |
其中,Hr=b2δe2(cp(Taw-Tw)), Dr=δe/δ0, ΔTr=(Te-Tw)/(Taw-Tw), C=(ρu)/(ρeue). ηe是经过坐标变换的黏性层的厚度.
假设在再附点局部区域C仅是坐标η的函数, 即C=C(η), 则方程(9) 和(10) 与ξ无关, 即流动在再附点局部是自相似的. 然而此处再附点的自相似与经典的边界层自相似又有所不同. 可以看到, 再附点附近流动的动量方程化成了两个常微分方程9(a) 和9(b), 说明再附点附近流动是两个自相似流动即西门子流动和均匀剪切流叠加而成. 而能量传输是3个自相似过程的叠加.
要定解方程(9) 和(10), 须给出黏性层外缘的流动条件, 从而确定方程中的无量纲参数Hr,Dr,ΔTr. 然而, 黏性层外缘为无黏剪切层, 其流动状态仍不易获得. 为了解决这个问题, 可以借鉴黏性激波层理论[37], 将控制方程描述的区域从黏性层扩展到整个剪切层. 再附点附近的剪切层一般由上游边界层分离脱出形成, 其厚度与上游边界层相当, 相对于流向尺度而言仍是一个小量. 因此, 方程(9) 和(10) 同样适用于整个剪切层. 而剪切层外缘的流动条件可以通过无黏理论给出, 较易获得, 具体过程将在下一节讨论. 此时有
| $ {\eta _{\rm{e}}} = \int_0^{{\delta _{\rm{e}}}} {\frac{1}{{{C_\rho }{\delta _0}}}} {\rm{d}}y $ |
最终, 对方程(9) 采用数值迭代法进行求解, 可给出无量纲壁面温度梯度Θ0′(0), 那么再附点后的峰值热流为
| $ {q_{\rm{w}}} \approx - \varTheta _0^\prime (0)\frac{{{k_{\rm{w}}}}}{{{\delta _0}}}\frac{{{\rho _{\rm{w}}}}}{{{\rho _{\rm{e}}}}}\left( {{T_{{\rm{aw}}}} - {T_{\rm{w}}}} \right) $ | (11) |
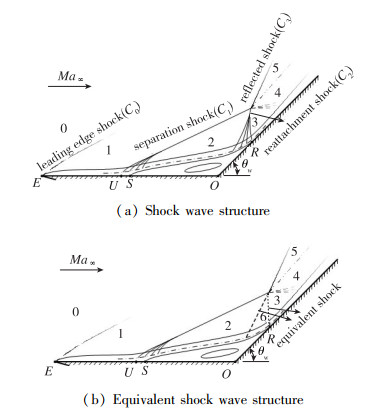
上节建立了斜驻点-三层结构模型的理论求解方案, 在求解高超声速分离-再附流动时, 仍须给出斜驻点流动外缘的无黏流动条件, 本节选取压缩拐角流动为例, 见图 4. 压缩拐角流动是一类典型的分离-再附流动, 图 4(a)给出了二维中等角度压缩拐角模型的激波结构示意图. 流动再附发生在3区上游, 热流峰值位于再附点压缩波系的根部. 需要注意的是, 3区可能很小, 以至于只有一个点. 为了应用前文给出的模型理论, 需要通过来流Mach数Ma∞, Reynolds数ReL, 温度T∞及壁温Tw, 拐角角度θw得到再附点附近的流动参数, 即由0区的参数求解3区的参数. 3区的流动参数可分为两类: 第一类是无黏剪切层外缘的压强pe, 温度Te, 密度ρe, 速度ue, 不妨称之为“外缘参数”; 第二类是无黏剪切层的厚度δe以及a, b, 不妨称之为“剪切层参数”. 下面将分别说明如何得到这两类参数.
|
| 图 4 压缩拐角流动 Fig.4 Ramp flow |
“外缘参数”可以通过无黏理论和黏性干扰理论得到. 1区的流动参数可由强/弱干扰理论[38]给出, 流动从1区到2区实际经过了分离激波-边界层干扰区, 假设分离点位置已知, 则可由自由干扰理论[39]给出2区流动参数; 2区到3区须经过再附激波-边界层干扰区, 目前没有相关理论可以描述. 若并不关心干扰区内的流动变化, 可以将2区到3区之间的压缩波系简化成两道斜激波, 如图 4(b)所示, 2区和3区之间形成6区, 设6区的气流角度为
| $ {\theta _6} = ({\theta _{\rm{w}}} - {\theta _2})\alpha + {\theta _2},0{\rm{ < }}\alpha {\rm{ < }}1 $ | (12) |
则α决定了压缩波系的强度, 而α由来流参数和几何参数决定. 本文所使用的计算和实验数据表明, 在较广的流动参数范围内, α对流动参数的变化不敏感, 且有α=0.8. 下文将显示两道斜激波简化计算是合理的. 综上所述, 1~ 6区的流动参数均可以通过无黏激波理论得到.
“剪切层参数”可以通过基本流动原理和近似得到. 具体地, 假设从流动分离到3区, 剪切层内的流量守恒, 近似有ρeueδe=ρuuuδu, 其中,下标u表示上游干扰起点U处的参数. 则3区剪切层的厚度δe为
| $ {\delta _{\rm{e}}} = \frac{{{\rho _u}{u_u}}}{{{\rho _{\rm{e}}}{u_{\rm{e}}}}}{\delta _u} $ | (13) |
由式(8), ue=ax+bδe, 对于图 4所示的压缩拐角流动, 剪切层撞向壁面的角度θ很小, 有a
| $ b = \frac{{{u_{\rm{e}}}}}{{{\delta _{\rm{e}}}}} $ | (14) |
由式(2)可知a的值, 其中倾斜角θ=θw-θ2. 至此, “剪切层参数”均可以得到.
2 结果与讨论 2.1 理论结果与数值结果和实验结果的对比验证为了验证前文的理论, 本文使用DSMC方法模拟了一系列的高超声速压缩拐角流动. DSMC方法在中低Reynolds数高超声速流动中是公认可靠的, 已在相当多的研究当中得到应用[40-43]. 计算采用Bird[44]开发的DS2V程序. 计算气体为空气(79%N2, 21%O2)且采用量热完全气体模型. 分子碰撞采用变径硬球模型, 壁面采用完全漫反射模型. 根据不同算例的来流参数, 所用的模拟分子数约为107~108. 计算终止条件为流场达到定常状态, 即计算结果不随时间变化. 达到定常时不同算例所对应的物理流动时间为20~30 ms, 约为30~50倍的流动特征时间. 流动参数为Ma∞=7~11, ReL=(1, 2)×104, θw=25°, T∞=60 K, Tw=300 K. 另外, 理论得到的峰值热流也与前人的CFD结果[45]、实验结果[46-48]进行了对比. 各算例的流动参数见表 1.
| 下载CSV 表 1 各算例的流动参数、峰值热流及其对应的理论结果 Tab.1 Flow parameters, peak heat flux coefficients and theoretical results |
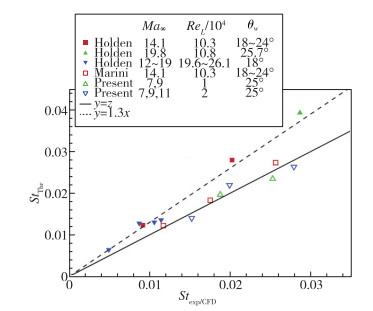
针对不同的实验条件和数值模拟条件, 利用本文的理论框架预测其峰值热流系数St=qw/(ρ∞u∞cp(T0-Tw)), 其中,T0为来流总温. 理论预测的结果与数值模拟、实验结果的对比情况如图 5所示, 具体数值见表 1. 图中横坐标为数值模拟或实验结果, 纵坐标为理论预测结果; 实心点表示实验条件, 空心点表示数值模拟条件. 从图中可以看出, 理论预测与数值结果符合得较好, 说明本文的理论在中低Reynolds数的条件下是定量合理的. 相对于实验结果, 理论预测偏高30% 左右. 这可能是由于实验中存在着真实气体效应和三维效应, 而理论中并未考虑这些因素的影响. 如Nompelis等[49]指出, 振动非平衡效应可以使热流降低约20%. 而三维效应显著减小分离区的大小[50-51], 这显然会导致热流的变化. 由下文的讨论可知, 减小分离区会降低峰值热流的大小.
|
| 图 5 理论预测与数值模拟、实验结果的对比 Fig.5 Comparison of theoretical prediction with the results from simulations and experiments |
由前文的理论分析知, 再附点附近的流动可以看作是驻点流和均匀剪切流的叠加, 且已验证在流动倾斜度较大(即θ较小)的压缩拐角再附流动中是合理的. 本节将讨论另一种极限情况, 即流动接近垂直于壁面, 即正驻点流动.
当再附流动接近驻点流时, 剪切分量为零, 流动不带有涡量, 有b=0, 则Hr=0. 此时, 方程(9)(c) 和(9)(d) 为齐次方程且具有齐次边界条件, 为零解. 方程(9) 可简化为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left( {C{f^{\prime \prime }}} \right)}^\prime } + f{f^{\prime \prime }} - {f^{\prime 2}} + {{\bar T}_0} = 0}\\ {{{\left( {\frac{C}{{Pr }}{\varTheta _0}^\prime } \right)}^\prime } + f{\varTheta _0}^\prime = 0} \end{array}} \right. $ |
这与经典的驻点边界层方程相同. 此时, 方程的数值解经拟合可得到Θ′0(0)=0.564Pr0.401. 由式(11) 并考虑到
| $ {q_{\rm{w}}} = - 0.564{Pr ^{ - 0.6}}{C_{\rm{w}}}\sqrt {{\rho _{\rm{e}}}{\mu _{\rm{e}}}} \sqrt {\frac{{{\rm{d}}{u_{\rm{e}}}}}{{{\rm{d}}x}}} \left( {{h_{{\rm{aw}}}} - {h_{\rm{w}}}} \right) $ |
这与驻点热流的结果[52]一致. 由此可见, 本文的模型理论可以退化到经典的驻点边界层理论, 因此, 在大倾斜度的再附流动中也应当具有一定的合理性.
2.3 分离区大小和边界层厚度对峰值热流的影响控制分离区的大小和边界层的厚度是流动控制中的重要手段[53], 因而探讨分离区的大小和边界层的厚度对峰值热流的影响规律很有必要. 分离区的大小或边界层厚度的改变将影响再附点区的外缘参数和剪切层参数, 从而改变热流. 在本文的理论中, 可以直接设置分离点的位置或干扰起点U处的边界层厚度, 来研究其对峰值热流的影响.
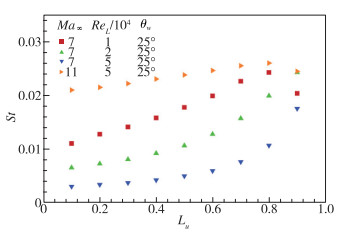
图 6为不同的Mach数和Reynolds数条件下压缩拐角流动的峰值热流随着分离区大小的变化曲线. 其中,横坐标Lu为无量纲的上游影响距离, 即图 4中O点到U点的距离与平板长度之比, 表征分离区的大小; 纵坐标是通过理论得到的峰值热流系数. 当分离区极大时(Lu>0.8), 由于分离点太靠近前缘, 分离激波边界层干扰与前缘激波边界层干扰相互影响, 前文的压缩拐角求解方案不适用, 因此不予讨论. 一般情况下(Lu < 0.8), 减小分离区的大小可以降低峰值热流, 且Mach数越低, 效果越显著.
|
| 图 6 分离区大小对峰值热流的影响 Fig.6 Influence of the separation length on the peaking heat flux |
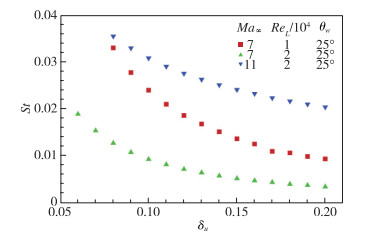
图 7为不同的Mach数和Reynolds数条件下压缩拐角流动的峰值热流随着边界层分离时的厚度变化曲线. 其中, 横坐标为干扰起点的边界层厚度, 纵坐标是通过理论得到的峰值热流系数. 在本文所使用的算例中, 分离时的实际边界层厚度为0.07~0.14. 从图中可以看出, 增大干扰起点的边界层厚度有利于降低峰值热流. 相对而言, 在较低Mach数和较低Reynolds数条件下, 效果更为显著.
|
| 图 7 干扰起点的边界层厚度对峰值热流的影响 Fig.7 Influence of the boundary layer thickness on the peaking heat flux |
本文提出了再附点附近流动的斜驻点-三层结构模型理论, 并据此给出了预测高超声速压缩拐角分离-再附流动的峰值热流的工程理论. 理论预测的压缩拐角再附热流峰值与DSMC计算结果大致相符, 验证了斜驻点流动模型理论在中低Reynolds数参数范围内的合理性和有效性. 并且, 理论可以退化至经典的驻点边界层理论, 表明模型理论具有可拓展性. 最后利用该理论探讨了压缩拐角流动中分离区的大小和干扰起点的边界层厚度对峰值热流的影响, 发现减小分离区的大小或增大干扰起点的边界层厚度均可以有效降低峰值热流, 尤其对于中低Reynolds数情况, 效果更为显著.
致谢 作者得到中国科学院大学余永亮教授和王智慧教授的热心帮助和指导, 在此表示衷心的感谢.| [1] |
McClinton C R. High speed/hypersonic aircraft propulsion technology development[C]. Proceedings of Advances on Propulsion Technology for High-Speed Aircraft, AVT-150 RTO AVT/VKI Lecture Series. Rhode St.Genese, 2007: 1-32.
|
| [2] |
Bertin J J, Cummings R M. Fifty years of hypersonics: where we've been, where we're going[J]. Progress in Aerospace Sciences, 2003, 39(6/7): 511-536. |
| [3] |
庄逢甘, 赵梦熊. 航天飞机的气动热——航天飞机的空气动力学问题之四[J]. 气动实验与测量控制, 1988, 2(3): 1-7. |
| [4] |
Dolling D S. Fifty years of shock-wave/boundary-layer interaction research: what next?[J]. AIAA Journal, 2001, 39(8): 1517-1531. DOI:10.2514/2.1476 |
| [5] |
Bose D, Brown J L, Prabhu D K, et al. Uncertainty assessment of hypersonic aerothermodynamics prediction capability[J]. Journal of Spacecraft and Rockets, 2013, 50(1): 12-18. DOI:10.2514/1.A32268 |
| [6] |
Gnoffo P A, Berry S A, van Norman J W. Uncertainty assessments of hypersonic shock wave-turbulent boun-dary-layer interactions at compression corners[J]. Journal of Spacecraft and Rockets, 2013, 50(1): 69-95. DOI:10.2514/1.A32250 |
| [7] |
Knight D, Longo J, Drikakis D, et al. Assessment of CFD capability for prediction of hypersonic shock interac-tions[J]. Progress in Aerospace Sciences, 2012, 48-49: 8-26. DOI:10.1016/j.paerosci.2011.10.001 |
| [8] |
贺立新. 间断Galerkin有限元方法及其与有限体积混合计算方法研究[D]. 绵阳: 中国空气动力研究与发展中心, 2008. He L X. Discontinuous Galerkin finite element method on hybrid grids and finite element/finite volume mixed method[D]. Mianyang: China Aerodynamics Research and Development Center, 2008(in Chinese). |
| [9] |
Simeonides G, Haase W, Manna M. Experimental, analytical, and computational methods applied to hypersonic compression ramp flows[J]. AIAA Journal, 1994, 32(2): 301-310. DOI:10.2514/3.11985 |
| [10] |
Hankey Jr W L, Holden M S. Two-dimensional shock wave-boundary layer interactions in high speed flows[R]. Advisory Group for Aerospace Research and Development (AGARD), 1975.
|
| [11] |
Neumann R D. Special topics in hypersonic flow, in aerodynamic problems of hypersonic vehicles[R]. AGARD Lecture Series 42, 1972.
|
| [12] |
Lees L, Reeves B L. Supersonic separated and reattaching laminar flows: I. General theory and applica-tion to adiabatic boundary-layer/shock-wave interaction[J]. AIAA Journal, 1964, 2(11): 1907-1920. DOI:10.2514/3.2700 |
| [13] |
Nielsen J N, Lynes L L, Goodwin F K. Calculation of laminar separation with free interaction by the method of integral relations. Part Ⅰ: Two-dimensional supersonic adiabatic flow[R]. Itek Corp Palo Alto Ca Vidya Div, 1965.
|
| [14] |
Pohlhausen K. Zur näherungsweisen integration der differentialgleichung der iaminaren grenzschicht[J]. ZAMM-Journal of Applied Mathematics and Mechanics, 1921, 1(4): 252-290. DOI:10.1002/zamm.19210010402 |
| [15] |
Klineberg J M, Lees L. Theory of laminar viscous-inviscid interactions in supersonic flow[J]. AIAA Journal, 1969, 7(12): 2211-2221. DOI:10.2514/3.5518 |
| [16] |
Murphy J D. A critical evaluation of analytic methods for predicting laminar boundary-layer, shock-wave interac-tion[R]. NASA TN D-7044, 1971.
|
| [17] |
Lighthill M J. On boundary layers and upstream influence. I. A comparison between subsonic and supersonic flows[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1953, 217(1130): 344-357. |
| [18] |
Neiland V Y. Theory of laminar boundary layer separation in supersonic flow[J]. Fluid Dynamics, 1969, 4(4): 33-35. DOI:10.1007/BF01094681 |
| [19] |
Stewartson K, Williams P G. Self-induced separation[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1969, 312(1509): 181-206. |
| [20] |
Messiter A F. Boundary-layer flow near the trailing edge of a flat plate[J]. SIAM Journal on Applied Mathema-tics, 1970, 18(1): 241-257. DOI:10.1137/0118020 |
| [21] |
Brown S N, Stewartson K, Williams P G. Hypersonic self-induced separation[J]. The Physics of Fluids, 1975, 18(6): 633-639. DOI:10.1063/1.861210 |
| [22] |
Rizzetta D P, Burggraf O R, Jenson R. Triple-deck solutions for viscous supersonic and hypersonic flow past corners[J]. Journal of Fluid Mechanics, 1978, 89(3): 535-552. DOI:10.1017/S0022112078002724 |
| [23] |
Rizzetta D P. Asymptotic solution for two-dimensional viscous supersonic and hypersonic flows past compression and expansion corners[D]. Columbus: Ohio State University, 1976.
|
| [24] |
Daniels P G. Laminar boundary-layer reattachment in supersonic flow. Part 2. Numerical solution[J]. Journal of Fluid Mechanics, 1980, 97(1): 129-144. DOI:10.1017/S0022112080002467 |
| [25] |
Daniels P G. Laminar boundary-layer reattachment in supersonic flow[J]. Journal of Fluid Mechanics, 1979, 90(2): 289-303. DOI:10.1017/S0022112079002214 |
| [26] |
Babinsky H, Harvey J K. Shock wave-boundary-layer interactions[M]. Cambridge: Cambridge University Press, 2011.
|
| [27] |
李邦明. 壁面流动分离-再附产生高气动热的广义物理模型及其理论和应用研究[D]. 北京: 中国科学院大学, 2013. Li B M. A general theoretical model for peak aeroheating in high-enthalpy reattaching flow[D]. Beijing: University of Chinese Academy of Sciences, 2013(in Chinese). |
| [28] |
Hiemenz K. Die Grenzschicht an einem in den gleichformigen Flussigkeitsstrom eingetauchten geraden Kreiszy-linder[J]. Dingler's Polytechnical Journal, 1911, 326: 321-324. |
| [29] |
Dorrepaal J M. An exact solution of the Navier-Stokes equation which describes non-orthogonal stagnation-point flow in two dimensions[J]. Journal of Fluid Mechanics, 1986, 163: 141-147. DOI:10.1017/S0022112086002240 |
| [30] |
Tamada K. Two-dimensional stagnation-point flow impinging obliquely on a plane wall[J]. Journal of the Physical Society of Japan, 1979, 46(1): 310-311. DOI:10.1143/JPSJ.46.310 |
| [31] |
Stuart J T. The viscous flow near a stagnation point when the external flow has uniform vorticity[J]. Journal of the Aerospace Sciences, 1959, 26(2): 124-125. DOI:10.2514/8.7963 |
| [32] |
庄礼贤, 尹协远, 马晖扬. 流体力学[M]. 2版. 合肥: 中国科学技术大学出版社, 2009. Zhuang L X, Yin X Y, Ma H Y. Fluid mechanics[M]. 2nd ed. Hefei: China University of Science and Techno-logy Press, 2009. (in Chinese) |
| [33] |
Holden M S. Experimental studies of separated flows at hypersonic speeds. Ⅱ-Two-dimensional wedge separated flow studies[J]. AIAA Journal, 1966, 4(5): 790-799. DOI:10.2514/3.3548 |
| [34] |
Howarth L. Concerning the effect of compressibility on lam inar boundary layers and their separation[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1948, 194(1036): 16-42. |
| [35] |
Dorodnitsyn A A. Boundary layer in a compressible gas[J]. Prikl. Mat. Mekh, 1942, 6(6): 449-486. |
| [36] |
Tooke R M, Blyth M G. A note on oblique stagnation-point flow[J]. Physics of Fluids, 2008, 20(3): 033101. DOI:10.1063/1.2876070 |
| [37] |
Davis R T. Numerical solution of the hypersonic viscous shock-layer equations[J]. Journal of Spacecraft and Rockets, 2003, 40(5): 787-795. DOI:10.2514/2.6905 |
| [38] |
Hayes W D, Probstein D F. Hypersonic flow theory[M]. New York: Academic Press, 1959.
|
| [39] |
Chapman D R, Kuehn D M, Larson H K. Investigation of separated flows in supersonic and subsonic streams with emphasis on the effect of transition[R]. National Advisory Committee for Aeronautics 1356, 1958.
|
| [40] |
Wang Z H, Yu Y L, Bao L. Heat transfer in nonequilibrium flows with homogeneous and heterogeneous recombination reactions[J]. AIAA Journal, 2018, 56(9): 3593-3599. DOI:10.2514/1.J056953 |
| [41] |
Chen X X, Wang Z H, Yu Y L. General Reynolds analogy for blunt-nosed bodies in hypersonic flows[J]. AIAA Journal, 2015, 53(8): 2410-2416. DOI:10.2514/1.J053962 |
| [42] |
Leite P H M, Santos W F. Computational analysis of the flow field structure of a non-reacting hypersonic flow over forward-facing steps[J]. Journal of Fluid Mechanics, 2015, 763: 460-499. DOI:10.1017/jfm.2014.677 |
| [43] |
Moss J N, Bird G A. Direct simulation Monte Carlo simulations of hypersonic flows with shock interactions[J]. AIAA Journal, 2005, 43(12): 2565-2573. DOI:10.2514/1.12532 |
| [44] |
Bird G A. Molecular gas dynamics and the direct simulation of gas flows[M]. Oxford: Clarendon Press, 1994.
|
| [45] |
Marini M. Analysis of hypersonic compression ramp laminar flows under sharp leading edge conditions[J]. Aerospace Science and Technology, 2001, 5(4): 257-271. DOI:10.1016/S1270-9638(01)01109-9 |
| [46] |
Holden M S, Moselle J R. Theoretical and experimental studies of the shock wave-boundary layer interaction on compression surfaces in hypersonic flow[R]. Aerospace Research Laboratories, Wright-Patterson AFB Technical Report ARL 70-0002, 1970.
|
| [47] |
Holden M S. Boundary-layer displacement and leading-edge bluntness effects on attached and separated laminar boundary layers in a compression corner. Ⅱ-experimental study[J]. AIAA Journal, 1971, 9(1): 84-93. DOI:10.2514/3.6127 |
| [48] |
Holden M S. A study of flow separation in regions of shock wave-boundary layer interaction in hypersonic flow[R]. AIAA 1978-1169, 1978.
|
| [49] |
Nompelis I, Candler G V, Holden M S. Effect of vibrational nonequilibrium on hypersonic double-cone experi-ments[J]. AIAA Journal, 2003, 41(11): 2162-2169. DOI:10.2514/2.6834 |
| [50] |
Rudy D H, Thomas J L, Kumar A, et al. Computation of laminar hypersonic compression-corner flows[J]. AIAA Journal, 1991, 29(7): 1108-1113. DOI:10.2514/3.10710 |
| [51] |
Komives J R, Nompelis I, Candler G V. Numerical investigation of unsteady heat transfer on a double wedge geometry in hypervelocity flows[R]. AIAA 2014-2354, 2014.
|
| [52] |
Van Driest E R. The problem of aerodynamic heating[J]. Aeronautical Engineering Review, 1956, 15(10): 26-41. |
| [53] |
Sriram R, Jagadeesh G. Correlation for length of impinging shock-induced large separation bubble at hypersonic speed[J]. AIAA Journal, 2015, 53(9): 2771-2776. DOI:10.2514/1.J053271 |




