“航天探索, 动力先行”. 与利用燃料氧化燃烧产生推力的化学推进相比, 电推进利用电离推进剂加速工质形成射流, 具有比冲高、推力小、控制精度高、使用寿命长等优点, 尤其适用于航天器位置保持、轨道转移、轨道维持、姿态控制和深空探测等太空任务[1]. 根据推进剂加速机制的不同, 可将电推进分为3类: 电热推进[2-4]、电磁推进[5-7]和静电推进[8]. 射频离子推力器基于感性耦合放电技术, 无放电电极, 不存在电子轰击式推力器的阴极寿命问题, 同时没有电子回旋共振式离子推力器需要外部静磁场和固定推进剂流量以达到电子回旋共振的限制, 具有结构简单、工作寿命长、推力动态范围大、性能调节响应灵敏[9]等特点, 是国际电推进领域的研究热点之一.
无论是高推力精度要求的太空任务(如欧洲航天局的Darwin,GAIA,LISA等), 还是协同运作的立方星星座任务(如SpaceX的StarLink), 都迫切需要微推进系统[10]. 微型射频离子推力器满足体积小、质量小、推力小、响应快速、控制精确的要求, 除此之外结构简单、工作寿命长, 是最具有发展潜力的推力器之一.
目前, 对微型射频离子推力器的研究主要集中在欧洲和美国, 典型样机有德国吉森大学的RIT-10[11-12],RIT-4[10, 13], 美国宾夕法尼亚州立大学的MRIT[14], 美国BUSEK公司的BIT-3. 其中RIT-10于2001年在ARTEMIS通信卫星上得到正式应用, 用于执行南北位置保持任务[15], BIT-3预计2020年之后将搭载太空发射系统升空[16]. 国内研制微型射频离子推力器起步较晚, 相关研究较少, 最早是由中国科学院空间科学技术中心对RIT-15采用氙作为工质进行性能实验测试[17]. 中科院力学所的μRIT-2.5已进行飞行验证[18].
射频离子推力器电离室内的感性耦合放电等离子体特性和推力器的性能密切相关. 感性耦合放电等离子体数值仿真可以提供比实验更加丰富的结果, 甚至可以揭示在实验中无法观察到的现象, 因此得到国内外的广泛关注. 针对射频离子推力器内部感性耦合等离子体的数值仿真模型主要有3种: 全局模型[19-20]、流体模型[21-22]、粒子模型[23-24]. 流体模型与全局模型相比可以得到等离子体特性参数的空间分布, 与粒子模型相比节省计算时间与空间消耗, 具有显著优势.
在射频离子推力器的工作过程中, 放电室内的物理场包括流场、等离子体浓度场、射频线圈施加的电磁场. 各个物理场之间呈现强耦合关系: 流场影响中性粒子及放电室气压的分布; 电磁场影响等离子体中的电离过程, 改变带电粒子的浓度分布; 等离子体通过Joule和非Joule加热效应, 影响流场分布. 微型射频离子推力器流体模型考虑了上述多物理场的耦合以获得等离子体特征参数分布, 并揭示放电过程中质量、动量和能量传递的机制.
文献中对大尺寸感性耦合放电有较多的流体模型研究[25-26], 本文对依据缩尺准则设计的放电室内径40 mm的微型射频离子推力器进行分析, 建立了低气压、小尺度下的感性耦合等离子体流体模型, 探究了等离子体放电特征参数随推进剂工质气压、放电吸收功率、射频频率以及线圈匝数等因素的变化规律. 结果表明, 推进剂工质气压、放电吸收功率是调节微型射频离子推力器性能的主要因素.
1 等离子体流体模型 1.1 流体条件验证流体模型将等离子体中各种粒子看作连续流体, 用质量、动量、能量方程描述等离子体行为. 在使用流体模型分析推力器放电过程之前, 首先须明确在所设计推力器工况下流体模型是否适用.
当工质气压在在13.3 Pa(100 mtorr)以上时, 等离子体内碰撞占据主导, 可以将带电粒子看作连续流体. 但微型射频离子推力器的工质气压一般为0.1~1 Pa, 故须预先分析流体模型在此情况下是否适用. Mikellides等[27]的研究表明, 当粒子的平均自由程远小于放电室的特征长度时, 碰撞会占据主导, 具体表述见下式
| $ Kn = \frac{{{\lambda _{{\rm{mfp}}}}}}{L} < 0.4 $ |
式中, Kn是粒子的Knudsen数, λmfp是粒子的平均自由程, L是放电室的特征长度. 射频离子推力器内部电子Knudsen数较大, 但电子由于会被鞘层反射, 碰撞机会增大, 故电子Knudsen数不具代表性. 考虑离子与中性粒子的碰撞, 其平均自由程如下式所示[22].
| $ {\lambda _{{\rm{mfp}}}} = \frac{1}{{{n_{\rm{n}}}{Q_{{\rm{in}}}}}} $ |
式中, nn是放电室内部中性粒子数密度, Qin是离子-中性粒子散射碰撞截面, 单位为m2[28].
| $ {Q_{{\rm{in}}}} = \frac{{8.280{\kern 1pt} {\kern 1pt} 72 \times {{10}^{ - 16}}}}{{{c_{\rm{r}}}}} $ |
式中, cr是由约化质量定义的单电荷离子与中性粒子的相对热运动速度.
| $ {c_{\rm{r}}} = \sqrt {\frac{{16{k_{\rm{B}}}{T_{\rm{i}}}}}{{{\rm{ \mathsf{ π} }}{m_{\rm{i}}}}}} $ |
式中, kB是Boltzman常数, Ti是离子温度, mi是离子质量. 中性粒子数密度通过中性流的Maxwell平均通量方程计算.
| $ \dot m = {m_{\rm{n}}}\left( {\frac{{{n_{\rm{n}}}{{\bar c}_{\rm{n}}}}}{4}{A_{{\rm{grid}}}}{\varPhi _{\rm{n}}}} \right) $ |
式中,
| $ {{\bar c}_{\rm{n}}} = \sqrt {\frac{{8{k_{\rm{B}}}{T_{\rm{i}}}}}{{{\rm{ \mathsf{ π} }}{m_{\rm{i}}}}}} $ |
由双栅系统近似公式可得到有效透明度为
| $ {\varPhi _{\rm{n}}} = \frac{1}{{\frac{1}{{{\varPhi _{{\rm{screen }}}}}} + \frac{1}{{{\varPhi _{{\rm{accel}}}}}} - 1}} $ |
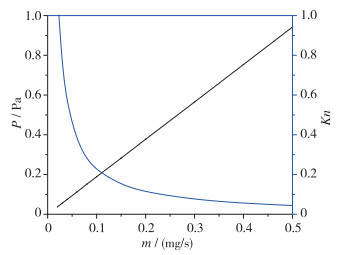
由上述公式, 可得所设计微型射频离子推力器放电室内离子Knudsen数随工质流量的变化规律. 同时, 根据理想气体状态方程可得放电室内部压强随工质流量的变化规律, 如图 1所示.
|
| 图 1 流体条件验证 Fig.1 Fluid condition verification |
由图 1可知, 在推力器工质气压为0.133 Pa时, 工质流量约为0.6 mg/s, 对应Kn为0.37, 小于0.4. 因此可以推断, 当工质气压在0.133 Pa以上时,采用流体模型是合理的.
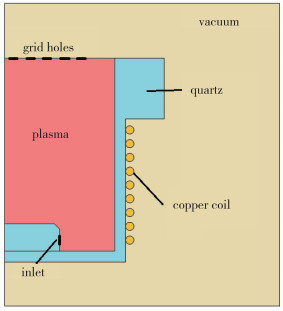
1.2 几何构建图 2为按照所设计微型射频离子推力器建立的二维轴对称简化模型的几何构造, 考虑了放电室入口与出口间工质流动. 轴对称处理会导致现实中的螺旋型线圈变为轴对称的环形, Tsay[22]用实验验证了采用两种不同构型线圈得到结果的最大误差不超过5%, 证明了二维轴对称模型的合理性.
|
| 图 2 二维轴对称模型 Fig.2 Two-dimensional axisymmetric model |
由图 2可知, 模型包括等离子体、石英放电室、铜线圈和真空4个部分, 物理性质见表 1, 其中等离子体的物理性质由等离子体模块计算得出.
| 下载CSV 表 1 各部分材料的物理性质 Tab.1 Physical properties of each part of the material |
中性粒子的数密度以及压强、速度分布对电离影响很大, 故须对氙气流场进行计算. 对于射频离子推力器, 电离度在10-3的量级, 离子对流场的影响可以忽略. 采用动量方程和连续性方程对氙气流场进行描述.
| $ \begin{array}{*{20}{c}} {\rho \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + \rho (\mathit{\boldsymbol{u}} \cdot \nabla )\mathit{\boldsymbol{u}} = \nabla \cdot [ - p\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{K}}] + \mathit{\boldsymbol{F}}}\\ {\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho \mathit{\boldsymbol{u}}) = 0} \end{array} $ |
式中, ρ是流体密度, t是时间, u是流体速度矢量, p是流体压强, I是单位矩阵, K是黏性应力张量, F是力矢量.
壁面边界条件为无滑移, 入口设置为流量边界条件, 出口设置为压力边界条件.
研究表明, 背景气体温度对等离子体特征参数影响不大[29]. 故微型射频离子推力器流体模型不考虑等离子体的加热效应, 背景气体温度设置为室温300 K.
1.4 等离子体等离子体模块通过导入碰撞截面数据, 在时域计算电子碰撞反应以及重物质反应, 最终得到等离子体特性参数分布. 选取化学反应体系见表 2, 其中,ΔΣ表示反应过程中的能量损耗,kf表示反应速率,1~5的反应速率由其碰撞截面数据计算. 碰撞截面数据来自文献[31].
| 下载CSV 表 2 模型中考虑的反应 Tab.2 Reactions considered in the model |
流体模型将粒子看作连续流体.电子浓度方程与能量方程为
| $ {\frac{{\partial {n_{\rm{e}}}}}{{\partial t}} + \nabla \cdot {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{\rm{e}}} = {R_{\rm{e}}} - (\mathit{\boldsymbol{u}} \cdot \nabla ){n_{\rm{e}}}} $ |
| $ {\frac{{\partial {n_\varepsilon }}}{{\partial t}} + \nabla \cdot {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\varepsilon } + \mathit{\boldsymbol{E}} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{\rm{e}}} = {S_{{\rm{en}}}} - (\mathit{\boldsymbol{u}} \cdot \nabla ){n_\varepsilon } + {P_{{\rm{ind}}}}} $ |
式中, ne是电子密度, Γe是电子通量, Re是电子源项, u是中性流体的速度矢量, nε是电子能量密度, Γε是电子能通量, E是电场矢量, Sen是反应与碰撞造成的能量损失, Pind是输入功率. 其中,
| $ {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{\rm{e}}} = - \left( {{\mu _{\rm{e}}} \cdot \mathit{\boldsymbol{E}}} \right){n_{\rm{e}}} - {D_{\rm{e}}} \cdot \nabla {n_{\rm{e}}}} $ |
| $ {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\varepsilon } = - \left( {{\mu _\varepsilon } \cdot \mathit{\boldsymbol{E}}} \right){n_\varepsilon } - {D_{{\rm{en}}}} \cdot \nabla {n_\varepsilon }} $ |
式中, μe是电子迁移率, De是电子扩散系数, με是电子能迁移率, Den是电子能扩散系数, 在电子能量分布函数满足Maxwell分布的情况下, 通过Einstein关系计算[31].
| $ {{\mu _{\rm{e}}} = \frac{e}{{{m_{\rm{e}}}{\nu _{\rm{m}}}}},{D_{\rm{e}}} = {\mu _{\rm{e}}}{T_{\rm{e}}}} $ |
| $ {{\mu _\varepsilon } = \frac{5}{3}{\mu _{\rm{e}}},{D_{{\rm{en}}}} = {\mu _\varepsilon }T} $ |
式中, νm是弹性碰撞频率. 用漂移-扩散方程计算重物质输运, 适用于除电子之外的所有粒子.
| $ \rho \frac{{\partial {\omega _k}}}{{\partial t}} + \rho (\mathit{\boldsymbol{u}} \cdot \nabla ){\omega _k} = \nabla \cdot {\mathit{\boldsymbol{j}}_k} + {R_k} $ |
式中, ωk是第k种物质的质量分数, jk是第k种物质的扩散通量矢量, Rk是第k种物质的产率系数. 采用Poisson方程计算等离子体的电势V.
| $ \nabla \cdot \mathit{\boldsymbol{D}} = {\rho _{\rm{q}}},\quad \mathit{\boldsymbol{E}} = - \nabla V $ |
式中, ρq是等离子体的体电荷密度. 边界条件设置参考对感性耦合等离子体放电的研究[29].初始电子密度设置为为1017 m-3, 初始平均电子能量为5 eV. 在壁面处不考虑二次电子发射, 壁面边界条件如下[29]
| $ { - \mathit{\boldsymbol{n}} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{\rm{e}}} = \frac{1}{4} \cdot {v_{{\rm{eth}}}} \cdot {n_{\rm{e}}}} $ |
| $ { - \mathit{\boldsymbol{n}} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\varepsilon } = \frac{5}{{12}} \cdot {v_{{\rm{eth}}}} \cdot {n_\varepsilon }} $ |
式中, n表示表面的法向量, veth是电子的热运动速度. 对静电边界条件, 工质入口与出口处设置为零电荷与绝缘, 壁面处设置为接地.
1.5 电磁场电磁场模块通过在频域求解Maxwell方程组, 得到磁场以及感应电场的变化规律.
| $ {\nabla \times \mathit{\boldsymbol{H}} = \mathit{\boldsymbol{J}}} $ |
| $ {\mathit{\boldsymbol{B}} = \nabla \times \mathit{\boldsymbol{A}}} $ |
| $ {\mathit{\boldsymbol{J}} = \sigma \mathit{\boldsymbol{E}} + {\rm{j}}\omega \mathit{\boldsymbol{D}} + \sigma \mathit{\boldsymbol{v}} \times \mathit{\boldsymbol{B}} + {\mathit{\boldsymbol{J}}_{\rm{e}}}} $ |
| $ {\mathit{\boldsymbol{E}} = - {\rm{j}}\omega \mathit{\boldsymbol{A}}} $ |
将上述4式化简合并后, 可以得到
| $ \left( {{\rm{j}}\omega \sigma - {\omega ^2}{\varepsilon _0}{\varepsilon _{\rm{r}}}} \right)A + \nabla \times \left( {\frac{1}{{{\mu _0}{\mu _{\rm{r}}}}}\nabla \times A} \right) = {J_{\rm{e}}} $ |
式中, j是虚数单位, ω是射频源的角频率, σ是等离子体电导率, ε0是真空介电常数, A是磁矢势, μ0是真空磁导率, Je是应用外部电流. 由上式求解磁矢势, 根据磁矢势计算出磁场与感应电场.
1.6 多物理场耦合等离子体模块与磁场模块通过等离子体电导与变压器模型形成耦合关系. 首先根据反应进度实时计算出等离子体的电导率
| $ {\sigma _{{\rm{plasma }}}} = \frac{{{q^2}{n_{\rm{e}}}}}{{{m_{\rm{e}}}\left( {{\nu _{\rm{e}}} + {\rm{j}}\omega } \right)}} $ |
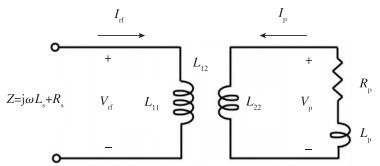
式中, q是元电荷, me是电子质量, νe是电子碰撞频率. 其次引入变压器模型, 该模型将线圈看作变压器的初级, 等离子体看作次级.[32]
| $ {{{\tilde V}_{{\rm{rf}}}} = {\rm{j}}\omega {L_{11}}{{\tilde I}_{{\rm{rf}}}} + {\rm{j}}\omega {L_{12}}{{\tilde I}_{\rm{p}}}} $ |
| $ {{{\tilde V}_{\rm{p}}} = {\rm{j}}\omega {L_{21}}{{\tilde I}_{{\rm{rf}}}} + {\rm{j}}\omega {L_{22}}{{\tilde I}_{\rm{p}}}} $ |
式中,
|
| 图 3 变压器模型 Fig.3 Transformer model |
通过等离子体内的感应电流密度以及感应电场来计算等离子体吸收的功率密度如下
| $ {Q_{{\rm{rh}}}} = \frac{1}{2} Re \left( {\mathit{\boldsymbol{J}} \cdot {\mathit{\boldsymbol{E}}^{\rm{T}}}} \right) $ |
式中, J是等离子体内的感应电流密度, E是等离子体内的感应电场强度.
2 结果与讨论 2.1 特定工况计算结果利用构建的微型射频离子推力器流体模型, 对工质流量为0.33 mg/s、放电室压强为0.8 Pa、吸收功率为20 W、线圈射频频率为2.5 MHz工况下的射频放电等离子体进行了数值仿真.
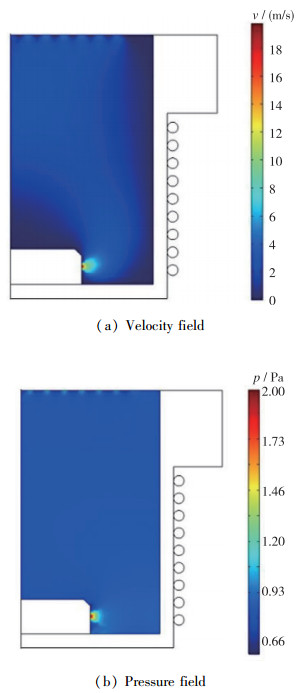
图 4为达到稳态时推力器内部流场. 由图可知, 速度与压强的最大值均发生在工质入口处, 这是因为入口处的流通面积很小, 氙气工质进入时产生堆积形成了较大的速度、压强峰值. 同理, 在工质出口可以看到类似的速度、压强极值. 由图 4(b)可知, 放电室内的工质气压均匀保持在0.8 Pa, 为等离子体的均匀分布提供了条件.
|
| 图 4 流场计算结果 Fig.4 Flow field calculation results |
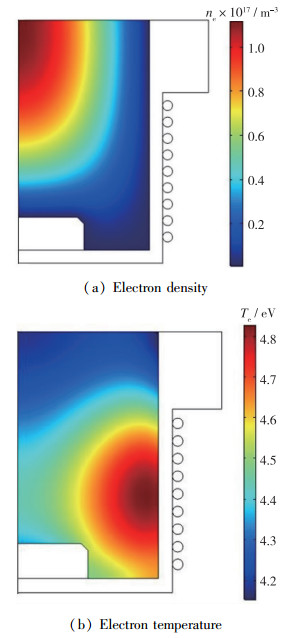
图 5为等离子体电子密度与电子温度分布. 由图 5(a)可知, 电子密度在轴线处有最大值, 在壁面处有最小值, 这是因为壁面处离子与电子通过表面反应再结合产生中性粒子, 造成离子电子损失. 由图 5(b)可知, 电子温度在线圈附近有最大值, 在轴线处有非零最小值, 这是因为趋肤效应导致功率大多沉积在线圈附近, 使电子温度较高.
|
| 图 5 等离子体特性参数分布 Fig.5 Distribution of plasma characteristic parameters |
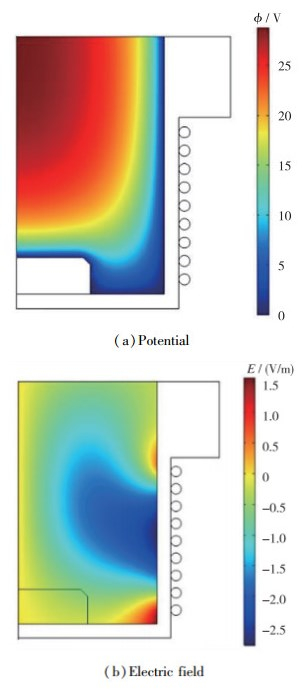
电势与感应电场的分布如图 6所示. 由图可知, 电势的峰值出现在轴线处; 而电场强度模在壁面处达到最大值, 向轴向逐渐减小, 在轴线处趋近于零.
|
| 图 6 电场分布 Fig.6 Distribution of electric field |
图 5与图 6中的等离子体特性参数以及电场分布与文献[21]结果有相同趋势, 证明结果合理性.
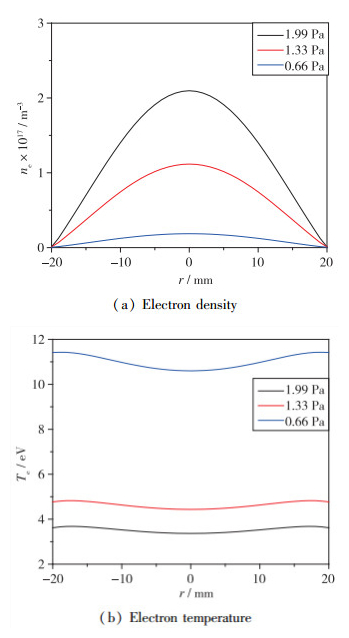
2.2 工质气压对等离子体特性参数影响在吸收功率为20 W, 射频频率为2.5 MHz的工况下, 工质气压对径向等离子体特征参数的影响如图 7所示. 由图 7(a)可知, 电子密度随工质气压的增大而增加. 这是因为随着工质气压增大, 中性粒子数密度会增加, 电子与中性粒子碰撞频率增加, 加快了电离反应的速率, 从而导致离子密度的上升, 由于等离子体的准中性, 电子密度也随之增加. 由图 7(b)可知, 电子温度随工质气压的减小而升高, 这是因为工质气压减小后, 高能电子与中性粒子以及离子之间的碰撞频率降低, 损失能量减少, 表现为电子温度上升.
|
| 图 7 工质气压对等离子体特性参数影响 Fig.7 Influence of propellent pressure on plasma characteristic parameters |
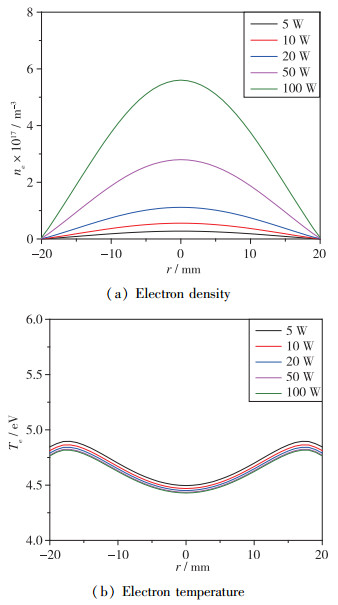
在工质气压为1.33 Pa, 射频频率为2.5 MHz的工况下, 吸收功率对径向等离子体特征参数的影响如图 8所示. 由图 8(a)可知, 电子密度随吸收功率的增大而增加, 这是因为有更多的电功率由于电离生成等离子体. 相比之下, 电子温度则表现出功率无关性, 几乎不随吸收功率的增大而改变, 如图 8(b)所示.
|
| 图 8 吸收功率对等离子体特性参数影响 Fig.8 Influence of absorption power on plasma characteristic parameters |
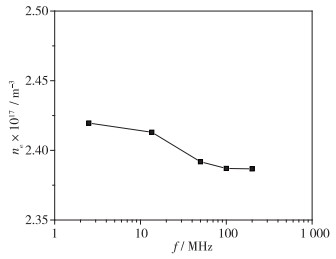
在吸收功率为20 W, 工质气压为1.33 Pa时, 选取2.5,13.56,50,100,200 MHz等5个常见频率, 探究射频频率对等离子体特征参数的影响, 结果如图 9所示. 可以看出电子密度随射频频率的增加略有下降, 与文献[23]中粒子模型计算结果趋势一致. 电子温度随频率增大几乎不变. 栅极附近的等离子体密度直接决定了栅极系统引出的束流大小, 进而影响推力器的推力, 为使栅极附近鞘层等离子体密度尽可能大, 设计时选择较小的射频频率. 由于射频频率对等离子体特性参数的影响很小, 且在推力器工作过程中改变其射频频率较为困难, 射频频率一般不作为调节推力性能的参数.
|
| 图 9 射频频率对等离子体特性参数影响 Fig.9 Influence of RF frequency on plasma characteristic parameters |
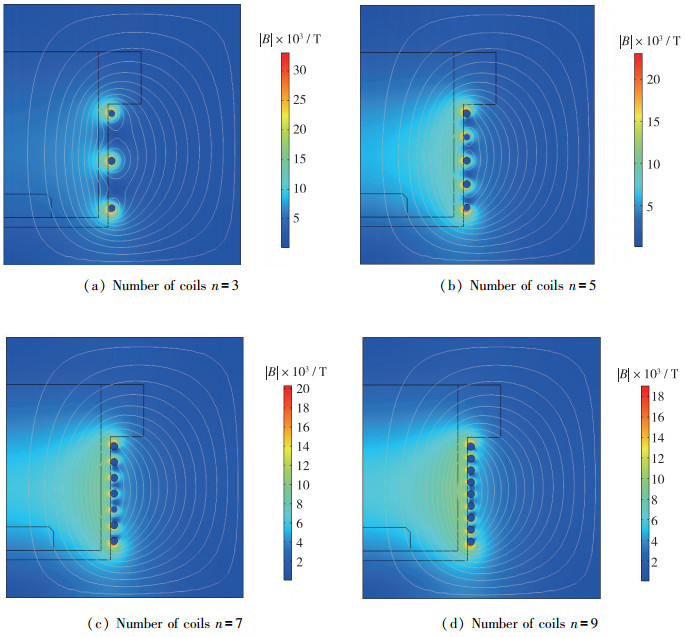
线圈匝数通过影响电磁场进而影响等离子体特征参数分布. 在吸收功率为20 W, 射频频率为2.5 MHz, 工质气压为1.33 Pa时, 选取线圈匝数为3, 5, 7, 9匝, 探究线圈匝数对等离子体特征参数的影响. 图 10为不同线圈匝数下磁场分布. 由图可知, 随着线圈匝数的增加, 磁通密度更加紧密地聚集在放电室内部靠近壁面的位置, 但放电室内磁场分布几乎不变. 表 3为不同匝数下等离子体特征参数, 其中,ne代表电子密度,Te代表电子温度. 结果表明, 线圈匝数对电离室内平均电子密度以及平均电子温度几乎没有影响.
|
| 图 10 线圈匝数对磁场影响 Fig.10 Influence of number of coils on the magnetic field |
| 下载CSV 表 3 线圈匝数对等离子体特性参数影响 Tab.3 Influence of number of coils on plasma characteristic parameters |
本文建立了微型射频离子推力器感性耦合放电等离子体流体模型, 对特定工况下的推力器等离子体特性参数分布进行了仿真研究, 探究了等离子体放电特征参数随推进剂工质气压、放电吸收功率、射频频率以及线圈匝数等因素的变化规律. 结论如下:
(1) 对于所设计内径为40 mm的微型射频离子推力器, 在工质气压为0.133 Pa以上时, 可以采用流体模型进行仿真分析.
(2) 在吸收功率、射频频率和线圈匝数保持不变时, 工质气压增大会使电子密度增加, 电子温度降低.
(3) 在工质气压、射频频率和线圈匝数保持不变时, 吸收功率增大会使电子密度增加, 电子温度几乎不变.
(4) 在其他参数相同时, 射频频率和线圈匝数对等离子体特征参数的影响可以忽略.
(5) 由上述结论可以看出, 推进剂工质气压、放电吸收功率是调节微型射频离子推力器性能的主要因素, 该研究为综合调控微型射频离子推力器的工作性能奠定了良好的基础.
致谢 本研究获得国家自然科学基金(51977110)、中央高校基本科研业务费(NT2020007)资助项目资助.| [1] |
张岩. 空间电推进技术应用现状与发展趋势[J]. 上海航天, 2019, 36(6): 24-34. Zhang Y. Application status and development trend of space electric propulsion technology[J]. Aerospace Shanghai, 2019, 36(6): 24-34. (in Chinese) |
| [2] |
Liebeskind J G, Hanson R K, Cappelli M A. Laser-induced fluorescence diagnostic for temperature and velocity measurements in a hydrogen Arcjet plume[J]. Applied Optics, 1993, 32(30): 6117-6127. DOI:10.1364/AO.32.006117 |
| [3] |
于达仁, 刘辉, 丁永杰, 等. 空间电推进原理[M]. 哈尔滨: 哈尔滨工业大学出版社, 2014. Yu D R, Liu H, Ding Y J, et al. Fundamentals of space electric propulsion[M]. Harbin: Harbin Institute of Technology Press, 2014. (in Chinese) |
| [4] |
Lawrence T J. Research into resistojet rockets for small satellite applications[D]. Guildford: University of Surrey, 1998.
|
| [5] |
康小录, 杭观荣, 朱智春. 霍尔电推进技术的发展与应用[J]. 火箭推进, 2017, 43(1): 8-17, 37. Kang X L, Hang G R, Zhu Z C. Development and application of Hall electric propulsion technology[J]. Journal of Rocket Propulsion, 2017, 43(1): 8-17, 37. (in Chinese) |
| [6] |
Raitses Y, Fisch N J. Parametric investigations of a nonconventional Hall thruster[J]. Physics of Plasmas, 2001, 8(5): 2579-2586. DOI:10.1063/1.1355318 |
| [7] |
Solbes A, Thomassen K, Vondra R J. Analysis of solid Teflon pulsed plasma thruster[J]. Journal of Spacecraft and Rockets, 1970, 7(12): 1402-1406. DOI:10.2514/3.30181 |
| [8] |
Mazouffre S. Electric propulsion for satellites and spacecraft: established technologies and novel approaches[J]. Plasma Sources Science and Technology, 2016, 25(3): 033002. DOI:10.1088/0963-0252/25/3/033002 |
| [9] |
Dobkevicius M. Modelling and design of inductively coupled radio frequency gridded ion thrusters with an application to Ion Beam Shepherd type space missions[D]. Southampton: University of Southampton, 2017.
|
| [10] |
Feili D, Loeb H W, Schartner K H, et al. Performance mapping of new μN-RITs at Giessen[C]. Proceedings of the 29thInternational Electric Propulsion Conference, Princeton: Princeton University, 2005: 252.
|
| [11] |
Walther R, Schaefer M, Freisinger J. Plasma diagnostics of the RF-ion thruster 'RIT-10'[C]. 9th International Electric Propulsion Conference, Bethesda, 1972: 472.
|
| [12] |
Groh K, Blum O, Rado H, et al. Inert gas radio-frequency thruster RIT 10[C]. 14th International Electric Propulsion Conference, Princeton, 1979: 2100.
|
| [13] |
Feili D, Di Cara D M, Leiter H J, et al. The μNRIT-4 Ion Engine: a first step towards a European mini-Ion Engine System development[C]. Proceedings of the 30th International Electric Propulsion Conference, Florence, 2007.
|
| [14] |
Trudel T A, Bilén S G, Micci M M. Design and performance testing of a 1-cm miniature radio-frequency ion thruster[C]. Proceedings of the 31st International Electric Propulsion Conference, Ann Arbor, 2009, 167: 20-24.
|
| [15] |
Loeb H W, Schartner K H, Meyer B K, et al. Forty years of Giessen EP-activities and the recent RIT-Microthruster development[C]. Proceedings of the 29th International Electric Propulsion Conference, Princeton: Princeton University, 2005: 31.
|
| [16] |
Tsay M, Frongillo J, Zwahlen J. Qualification model development of cubesat RF ion propulsion system BIT-3[C]. Proceedings of the 31st Int Symp Space Technol, Matsuyama, 2017.
|
| [17] |
酆惠芬. 15厘米射频离子推力器-RIT-15的实验研究[J]. 中国空间科学技术, 1986(3): 56-67. Feng H F. An experiment investigation of 'RIT-15' 15cm RF-thruster[J]. Chinese Space Science and Technology, 1986(3): 56-67. (in Chinese) |
| [18] |
贺建武, 马隆飞, 薛森文, 等. 射频离子微推力器的研究进展[C]. 第十二届中国电推进学术研讨会-01-72. 哈尔滨, 2016. He J W, Ma L F, Xue S W, et al. Research progress of RF ion micro thrusters[C]. Proceedings of the 12th China Electric Propulsion Seminar-01-72. Harbin, 2016(in Chinese). |
| [19] |
Piejak R B, Godyak V A, Alexandrovich B M. A simple analysis of an inductive RF discharge[J]. Plasma Sources Science and Technology, 1992, 1(3): 179-186. DOI:10.1088/0963-0252/1/3/006 |
| [20] |
Vahedi V, Lieberman M A, DiPeso G, et al. Analytic model of power deposition in inductively coupled plasma sources[J]. Journal of Applied Physics, 1995, 78(3): 1446-1458. DOI:10.1063/1.360723 |
| [21] |
吴辰宸, 孙新锋, 顾左, 等. 射频离子推力器放电与引出特性调节规律仿真与试验研究[J]. 推进技术, 2019, 40(1): 232-240. Wu C C, Sun X F, Gu Z, et al. Numerical and experimental research of optimal regulation with discharge and beam current extraction for RIT[J]. Journal of Propulsion Technology, 2019, 40(1): 232-240. (in Chinese) |
| [22] |
Tsay M M. Two-dimensional numerical modeling of radio-frequency ion engine discharge[D]. Cambridge: Massachusetts Institute of Technology, 2010.
|
| [23] |
Takao Y, Eriguchi K, Ono K. Two-dimensional particle-in-cell simulation of a micro RF ion thruster[C]. Proceedings of the 32nd International Electric Propulsion Conference, Wiesbaden, 2011.
|
| [24] |
Takao Y, Kusaba N, Eriguchi K, et al. Two-dimensional particle-in-cell Monte Carlo simulation of a miniature inductively coupled plasma source[J]. Journal of Applied Physics, 2010, 108(9): 093309. DOI:10.1063/1.3506536 |
| [25] |
Kim D G, Jeong Y D, Shon Y, et al. Modified fluid simulation of an inductively coupled plasma discharge[J]. Applied Science and Convergence Technology, 2019, 28(6): 221-225. DOI:10.5757/ASCT.2019.28.6.221 |
| [26] |
Lei F, Li X P, Liu Y M, et al. Simulation of a large size inductively coupled plasma generator and comparison with experimental data[J]. AIP Advances, 2018, 8(1): 015003. DOI:10.1063/1.5016354 |
| [27] |
Mikellides I G, Katz I, Goebel D M, et al. Hollow cathode theory and experiment. Ⅱ. A two-dimensional theoretical model of the emitter region[J]. Journal of Applied Physics, 2005, 98(11): 113303. DOI:10.1063/1.2135409 |
| [28] |
Szabo J J. Fully kinetic numerical modeling of a plasma thruster[D]. Cambridge: Massachusetts Institute of Technology, 2001.
|
| [29] |
Brezmes A O, Breitkopf C. Fast and reliable simulations of argon inductively coupled plasma using COMSOL[J]. Vacuum, 2015, 116: 65-72. DOI:10.1016/j.vacuum.2015.03.002 |
| [30] |
安秉健. 自持空心阴极关键尺寸影响与设计准则研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. An B J. Research of influence and design criteria of hollow cathode key dimensions[D]. Harbin: Harbin Institute of Technology, 2014(in Chinese). |
| [31] |
刘阳. 基于COMSOL软件的双腔室射频感性耦合氩等离子体源的二维流体力学模拟[D]. 大连: 大连理工大学, 2017. Liu Y. Two-dimensional fluid simulation of dual-chamber radio-frequency inductively coupled argon plasma source based on COMSOL software[D]. Dalian: Dalian Univer-sity of Technology, 2017(in Chinese). |
| [32] |
Lieberman M A, Lichtenberg A J. Principles of plasma discharges and materials processing[M]. 2nd ed. New York: John Wiley & Sons, 2005.
|




