2. 西北工业大学无人系统技术研究院,陕西西安 710072
2. Unmanned System Research Institute, Northwestern Polytechnical University, Xi'an 710072, China
随着战争态势和防空装备的发展, 对先进飞行器的气动和隐身提出了更高的要求, 提高飞行器的气动特性和隐身特性成为了目前飞行器设计的重要研究内容.计算机技术推动了基于计算流体力学与计算电磁学的数值模拟的快速进步, 使气动外形精细化设计向多目标、多学科耦合方向发展[1].
在兼顾气动隐身性能, 进行飞行器外形优化设计方面, 国内外进行了许多研究.何开锋等[2]采用Reynolds平均N-S方程、时域有限体积法结合Kriging模型对飞翼进行了气动隐身的一体化设计; 夏露等利用多学科优化设计和遗传算法, 开展了飞行器气动与隐身的协同优化设计, 取得了良好的设计结果[3], 采用分层交换差分粒子群算法对飞翼布局翼型进行气动隐身综合设计, 提高了翼型的综合性能[4]; 焦子涵等[5]基于Kriging代理模型, 通过直接全局优化算法对高超声速飞行器开展气动隐身多学科优化设计, 并与风洞试验结果进行了比较; 邓海强等[6]对翼身融合布局无人机进行了计入配平约束的多目标优化设计, 并分析了外形参数对隐身性能的影响; 王荣等[7]利用物理光学法和一致性几何绕射理论、气动黏性/无黏模型, 结合多目标优化算法对飞翼隐身无人机的平面外形进行优化, 指出了气动与隐身设计之间的权衡折中设计; Lee等[8-9]采用全速势方程、物理光学法作为性能评估方法, 通过多目标进化算法对飞行器进行气动隐身优化设计, 获得了无激波翼型以及超临界菱形机翼.综合国内外研究成果, 针对气动隐身优化设计问题, 大多应用代理模型等近似技术建模并采用进化类优化算法寻优, 或者直接进行多学科多目标进行类优化.虽然这些方法可以直接求解出Pareto前沿, 从而可以得到多目标问题的最优解集, 但是迭代收敛较慢, 而且优化效率随着设计变量增加而降低.
基于梯度的优化设计方法在处理大规模设计变量问题、提高寻优效率方面具有突出的效果[10], 但是需要将多目标问题转化为单目标子问题.引入数学规划思想, Zhang等[11]提出的一种基于分解技术的多目标进化算法(MOEA/D), 不同于经典的多目标进化算法NSAG-II等, MOEA/D算法可以实现子问题间信息互享、协同优化, 进而提高优化效率. MOEA/D最核心的是分解策略, 即将多目标优化问题分解成多个标量形式的单目标优化子问题, 然后同时求解这些具有相似解的相邻子问题.常见的分解方法[11]有线性加权和法, Tchebycheff法和边界交叉法, 其中Tchebycheff法对优化解的前沿形状不敏感, 计算简单[12].
因此, 本文提出一种基于Tchebycheff分解思想的飞行器气动/隐身多学科优化设计方法, 结合离散伴随方程与物理光学微分技术对飞行器外形进行优化.分解思路则是把多目标分解成多个单目标, 形成单目标支路, 对每个支路单独采用梯度优化算法进行求解.其中, 求解离散伴随方程能够高效地获得气动目标对设计变量的梯度, 物理光学微分则可得到雷达散射截面对设计变量的梯度.
1 多目标优化问题 1.1 Tchebycheff分解方法多目标优化问题可以表示为
| $ \begin{array}{*{20}{c}} {\min }~~~{\mathit{\boldsymbol{F}}(\mathit{\boldsymbol{x}}) = \left( {{f_1}(\mathit{\boldsymbol{x}}), {f_2}(\mathit{\boldsymbol{x}}), \cdots , {f_m}(\mathit{\boldsymbol{x}})} \right)}\\ {{\rm{ subject to }}}~~~{\mathit{\boldsymbol{x}} \in \mathit{\Omega }} \end{array} $ | (1) |
其中, x为设计变量, Ω为决策空间, F: Ω →Rm是一个包含了m个目标的实值目标函数, Rm称为目标区间.通过寻优, 得到一系列满足条件的可行解, 使得目标函数最小的解x*为Pareto非支配解, 所有非支配解构成的集合为Pareto最优解集.
经过Tchebycheff分解后的多目标优化问题如下
| $ \begin{array}{c}{\min } ~~~{g^{\mathrm{T} \operatorname{ch}}\left(F(\boldsymbol{x}) | \boldsymbol{\lambda}, \boldsymbol{z}^{*}\right)=\max\limits_{1 \leqslant i \leqslant m}\left\{\boldsymbol{\lambda}_{i}\left(f_{i}(\boldsymbol{x})-z_{i}^{*}\right)\right\}} \\ {\text { subject to }} ~~~{\boldsymbol{x} \in \mathit{\Omega }}\end{array} $ | (2) |
其中, λ=(λ1, λ2, …, λm), λi为子问题的优化权重系数,
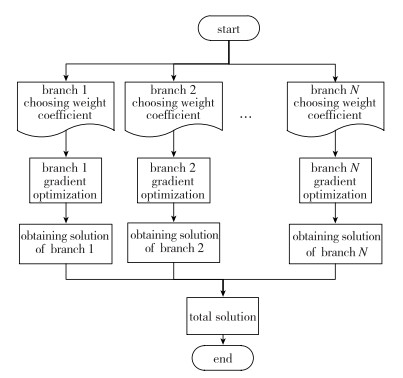
本文建立的多目标优化设计框架由两部分组成, 图 1为基于分解策略的总优化框架, 图 2为梯度优化框架.在总框架中, 首先根据分支个数以及子目标个数进行权重分配, 整合成单目标优化, 之后每一分支采用梯度优化方法进行单目标优化, 然后将各个分支获得的解集进行整合之后, 得到最终的总解集.
|
| 图 1 基于分解策略的优化流程 Fig.1 Flow chart of optimization based on decomposition |
|
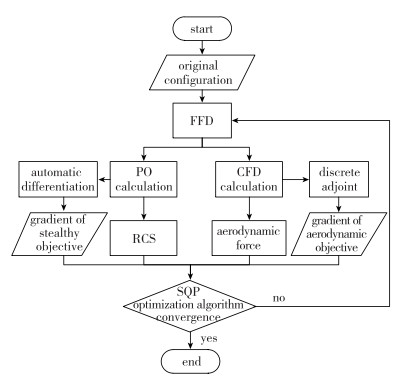
| 图 2 梯度优化流程 Fig.2 Flow chart of gradient optimization |
对于梯度优化设计框架, 主要由以下部分组成:基于非均匀有理B样条(non-uniform rational B-splines, NURBS)的自由变形(free form deformation, FFD)外形参数化, 基于径向基函数(radial basis function, RBF)的动网格方法, 基于物理光学法的RCS数值计算, 基于Reynolds平均N-S方程(RANS)的流场数值求解, 梯度求解以及序列二次规划优化算法.
2 物理光学法在计算电磁学领域, 物理光学法作为一种计算目标雷达散射截面的高频算法而被广泛应用.由Stratton-Chu散射场积分方程出发, 根据高频散射的局部性原理, 不考虑目标各部分之间的相互影响, 引入远场近似和切平面近似, 物理光学法通过对入射场在目标表面感应产生等效表面电流, 再对感应电流场进行近似积分从而求解出散射场[13].
根据物理光学法的假设条件, 入射场在目标表面形成的表面电流为
| $ {\mathit{\boldsymbol{J}}_{\rm{s}}} = 2\mathit{\boldsymbol{n}} \times {\mathit{\boldsymbol{H}}_{\rm{i}}} $ |
式中, n为表面法向量, Hi为入射磁场强度.将Js代入以下积分公式, 可以求得远区的散射电磁场[14]
| $ \boldsymbol{E}_{{\rm s}}=-2 \mathrm{j} k \sqrt{\frac{\mu_{0}}{\varepsilon_{0}}} \psi_{0} \iint\limits_{S} \boldsymbol{s} \times \boldsymbol{s} \times\left(\boldsymbol{n} \times J_{{\rm s}}\right) \mathrm{e}^{{\rm j} k \cdot(i-s)} \mathrm{d} S $ |
式中, j表示虚数, k为波数,μ0和ε0分别为自由空间磁导率和电导率, ψ0为远场Green函数. i和s为入射与散射方向的单位矢量.由雷达散射截面的表达式
| $ \sigma=\lim\limits_{R \rightarrow \infty} 4 {\rm{ \mathsf{ π}}} R^{2} \frac{\left|\boldsymbol{E}^{{\rm s}}\right|^{2}}{\left|\boldsymbol{E}^{\mathrm{i}}\right|^{2}} $ |
式中, Es表示散射电磁场矢量, Ei表示入射电磁场矢量, 即可得到目标的雷达散射截面(RCS).
3 梯度求解方法 3.1 离散伴随方程法气动优化目标函数为
| $ f_{\mathrm{a}}\left(\boldsymbol{X}_{\mathrm{a}}(\boldsymbol{x}), \boldsymbol{Q}(\boldsymbol{x})\right) $ | (3) |
式中,fa是飞行器的气动力系数,x为设计变量,Xa(x)为由设计变量所确定的CFD计算网格,R为流场残差,则有
| $ \boldsymbol{R}\left(\boldsymbol{X}_{\mathrm{a}}(\boldsymbol{x}), \boldsymbol{Q}(\boldsymbol{x})\right)=0 $ | (4) |
将式(3)和式(4)分别对x求全导数
| $ \frac{\mathrm{d} f_{\mathrm{a}}}{\mathrm{d} x}=\frac{\partial f_{\mathrm{a}}}{\partial \boldsymbol{X}_{\mathrm{a}}} \frac{\mathrm{d} \boldsymbol{X}_{\mathrm{a}}}{\mathrm{d} x}+\frac{\partial f_{\mathrm{a}}}{\partial \boldsymbol{Q}} \frac{\mathrm{d} \boldsymbol{Q}}{\mathrm{d} \boldsymbol{x}} $ | (5) |
| $ \frac{\partial \boldsymbol{R}}{\partial \boldsymbol{X}_{\mathrm{a}}} \frac{\mathrm{d} \boldsymbol{X}_{\mathrm{a}}}{\mathrm{d} \boldsymbol{x}}+\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{Q}} \frac{\mathrm{d} \boldsymbol{Q}}{\mathrm{d} \boldsymbol{x}}=0 $ | (6) |
将式(6)代入式(5)有
| $ \frac{\mathrm{d} f_{\mathrm{a}}}{\mathrm{d} \boldsymbol{x}}=\frac{\partial f_{\mathrm{a}}}{\partial \boldsymbol{X}_{\mathrm{a}}} \frac{\mathrm{d} \boldsymbol{X}_{\mathrm{a}}}{\mathrm{d} \boldsymbol{x}}-\frac{\partial f_{\mathrm{a}}}{\partial \boldsymbol{Q}}\left[\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{Q}}\right]^{-1}\left[\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{X}_{\mathrm{a}}} \frac{\mathrm{d} \boldsymbol{X}_{\mathrm{a}}}{\mathrm{d} \boldsymbol{x}}\right] $ | (7) |
式(7)涉及[∂R/∂Q]-1的求解,而对大规模矩阵的求逆运算代价非常大,因此构造伴随变量ψ使得
| $ \boldsymbol{\psi}^{\mathrm{T}}=\frac{\partial f_{\mathrm{a}}}{\partial \boldsymbol{Q}}\left[\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{Q}}\right]^{-1} $ | (8) |
由此将式(7)化为求解1个线性方程组的形式
| $ \left[\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{Q}}\right]^{\mathrm{T}} \boldsymbol{\psi}=\left[\frac{\partial f_{\mathrm{a}}}{\partial \boldsymbol{Q}}\right]^{\mathrm{T}} $ |
上式即为原始方程相对于目标函数的伴随方程,将原来求逆运算转换为求解线性方程组.将式(8)代入式(7)有
| $ \frac{\mathrm{d} f_{\mathrm{a}}}{\mathrm{d} \boldsymbol{x}}=\frac{\partial f_{\mathrm{a}}}{\partial \boldsymbol{X}_{\mathrm{a}}} \frac{\mathrm{d} \boldsymbol{X}_{\mathrm{a}}}{\mathrm{d} \boldsymbol{x}}-\boldsymbol{\psi}^{\mathrm{T}}\left[\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{X}_{\mathrm{a}}} \frac{\mathrm{d} \boldsymbol{X}_{\mathrm{a}}}{\mathrm{d} \boldsymbol{x}}\right] $ |
求解上式即可获得气动目标函数对设计变量的梯度dfa/dx.
3.2 隐身目标梯度求解本文运用开源自动微分工具TAPENADE[15]对物理光学法程序进行微分处理.隐身优化目标函数为
| $ f_{\mathrm{e}}\left(\boldsymbol{X}_{\mathrm{e}}(\boldsymbol{x}), \boldsymbol{J}(\boldsymbol{x})\right) $ |
通常选取一定角度范围内的RCS均值作为目标函数fe, 将上式对x求全导数
| $ \frac{\mathrm{d} f_{\mathrm{e}}}{\mathrm{d} \boldsymbol{x}}=\frac{\partial f_{\mathrm{e}}}{\partial \boldsymbol{X}_{\mathrm{e}}} \frac{\mathrm{d} \boldsymbol{X}_{\mathrm{e}}}{\mathrm{d} \boldsymbol{x}}+\frac{\partial f_{\mathrm{e}}}{\partial \boldsymbol{J}_{\mathrm{s}}} \frac{\mathrm{d} \boldsymbol{J}_{\mathrm{s}}}{\mathrm{d} \boldsymbol{x}} $ |
即可获得目标函数对设计变量的梯度dfe/dx.式中, Xe为物体表面网格坐标点坐标矢量, Js为目标表面电流.
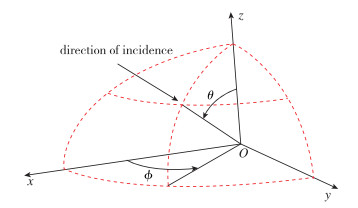
4 机翼优化设计算例 4.1 优化问题及优化模型本文选取跨声速机翼作为研究对象, 进行气动隐身综合优化设计, 图 3为RCS计算模型的坐标系定义, 其中包含了入射方向对应的方位角ϕ与俯仰角θ定义, RCS设计状态为:频率f=7.0 GHz, 垂直极化, 单站散射; 重点入射角范围为: 135°≤ϕ≤ 225°, 80°≤θ≤100°.
|
| 图 3 计算坐标系示意 Fig.3 Computational coordinate system |
机翼的几何外形参数为表 1中所列, 初始外形及优化过程的FFD控制体如图 4(a)所示, 其优化的气动设计状态为: Ma=0.785, 设计升力系数CL=0.2, Re=5.09×106.优化设计变量包括来流迎角α, FFD控制点(图 4(a)中的实心圆点)的Z向位移(共计55个设计变量), 优化目标为阻力系数CD最小、重点入射角范围内的雷达散射截面均值RCSave最小.
| 下载CSV 表 1 机翼几何外形参数 Tab.1 Geometrical shape parameters of the wing |

|
| 图 4 机翼FFD控制体及厚度约束 Fig.4 FFD control frame and thickness constraints of the wing |
从实际工程角度出发, 机翼需要满足一定的结构及容积要求, 因此对机翼施加厚度约束, 如图 4(b)中所示, 本文在沿展向均布的4个约束控制剖面上各采用了10个约束, 总共40个厚度约束, 保证每个约束处的相对厚度不小于初始值.本文多目标优化问题可以表示为
| $ \begin{array}{*{20}{l}} {\min }&{\left\{ {\begin{array}{*{20}{l}} {{C_{{\rm{D\_}}Ma0.785}}}\\ {{\rm{RC}}{{\rm{S}}_{{\rm{are}}}}} \end{array}} \right.}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}}&{\left\{ {\begin{array}{*{20}{l}} {{C_{\rm{L}}} = 0.2}\\ {{t_i} \ge {t_{{\rm{o}}i}}, i = 1, 2, \cdots , 40} \end{array}} \right.} \end{array} $ | (9) |
式中, ti为当前优化的翼型相对厚度, toi为初始翼型相对厚度.
将Tchebycheff分解策略应用于本文的优化问题, 则由式(9)与式(2)可以进一步将该问题表示为min gMDO=max{λ1(CD-z1*), λ2(RCSave-z2*)}其中, gMDO为气动隐身优化目标函数, (z1*, z2*)=(80.0count,-50.0)即理想目标函数解.优化中将权重系数λ1取值为0.2, 0.35, 0.5, 0.65, 0.8, 分别对应下文中的优化解Opt_1, Opt_2, Opt_3, Opt_4, Opt_5, 而λ2满足: λ2=1.0 -λ1.
4.2 优化设计结果不同权重系数下优化前后构型的气动性能与隐身性能对比如表 2所示, initial代表初始构型, 其余为优化构型.由表 2可以看出, 优化构型均满足了设计升力系数的约束, 从Opt_1到Opt_5, 气动性能对应的权重系数逐渐增大, 阻力系数CD逐渐减小, RCS均值则逐渐增大. 图 5所示为各分解支路的优化解分布, 图中右上角(黑色方框所示)为初始构型的性能, 采用不同的权重系数, 优化得到的结果不相同, 增加某一子目标的权重, 则该子目标值的减小量增多.与初始构型相比, 优化构型的最大减阻量对应Opt_5, 阻力系数减小了4.72%, 升阻比提高了4.91%;最大RCS均值减小量对应Opt_1, RCS均值减小了17.05 dBsm.
| 下载CSV 表 2 初始构型与优化构型性能参数对比 Tab.2 Comparison of initial and optimized performance parameters |

|
| 图 5 各支路优化解分布对比 Fig.5 Comparison of optimal solution distribution of each branch |
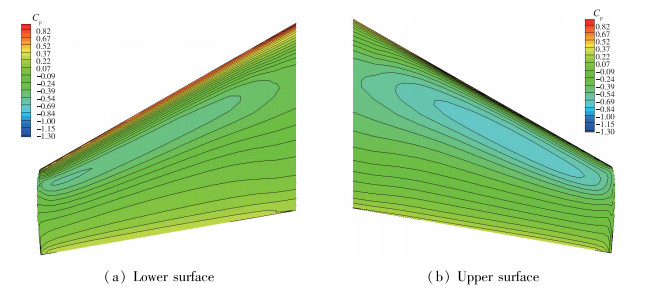
优化前后构型的机翼表面压力系数分布云图如图 6~11所示, 初始机翼上表面外翼段出现了等压线密集区, 压力梯度大, 该处有明显的激波, 经过优化设计, 激波得到抑制并基本消除, 同时下表面的前缘高压力区域得到扩大.

|
| 图 6 初始构型initial压力云图 Fig.6 Pressure contours of original configuration (initial) |

|
| 图 7 优化后构型Opt_1压力云图 Fig.7 Pressure contours of optimal configuration (Opt_1) |
|
| 图 8 优化后构型Opt_2压力云图 Fig.8 Pressure contours of optimal configuration (Opt_2) |

|
| 图 9 优化后构型Opt_3压力系数分布 Fig.9 Pressure contours of optimal configuration (Opt_3) |

|
| 图 10 优化后构型Opt_4压力云图 Fig.10 Pressure contours of optimal configuration (Opt_4) |

|
| 图 11 优化后构型Opt_5压力云图 Fig.11 Pressure contours of optimal configuration (Opt_5) |
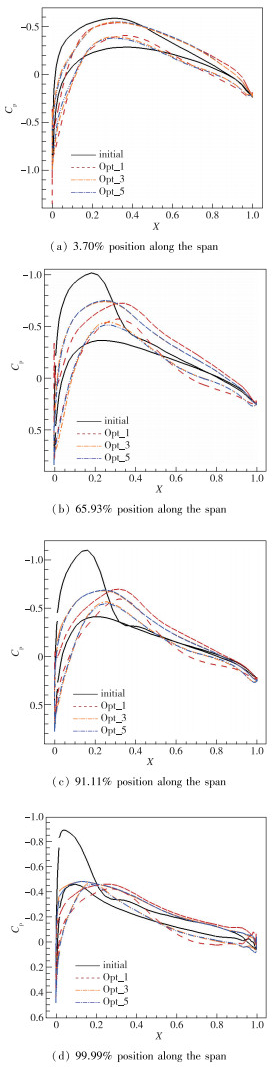
图 12为优化前后机翼的剖面压力系数分布对比, 综合前面的优化结果, 为便于对比与分析, 图中仅将Opt_1, Opt_3, Opt_5与初始构型进行对比.优化构型的压力分布形态大体一致, 优化使得激波区对应的剖面逆压梯度消失, 上表面负压值降低, 负压峰后移, 峰值点后的压力恢复区变长, 压力恢复变得缓和, 同时下表面的载荷增加, 并带有一定的前加载.从展向环量分布对比图 13中可以看出, 优化后的机翼环量分布更加贴合椭圆形环量分布, 即机翼内侧升力增加, 外侧升力减小, 气动性能的权重系数越大, 趋向效果越明显.
|
| 图 12 优化前后机翼剖面压力系数分布对比 Fig.12 Comparisons of pressure coefficient distributions of wing section between initial and optimized configurations |

|
| 图 13 优化前后机翼展向环量分布对比 Fig.13 Comparisons of circulation distributions along the span between initial and optimized configurations |
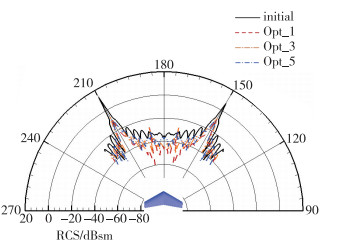
将图 12中对应各站位的优化前后机翼剖面翼型进行对比, 如图 14所示, 优化后的翼型满足厚度约束要求, 翼型前缘半径减小, 甚至会出现类“鹰嘴”的尖前缘外形(如图 14(a), (b)所示), 较小的前缘半径使重点方位的镜面反射波强度减弱, 机翼的前向RCS得到减缩.如图 15~17所示, 不同俯仰角下, 优化后机翼的前向RCS均有较大程度的减小, 机翼的隐身性能得以改善, 同时随着隐身性能权重系数的增大, 减小的趋势明显.
将图 12中对应各站位的优化前后机翼剖面翼型进行对比, 如图 14所示, 优化后的翼型满足厚度约束要求, 翼型前缘半径减小, 甚至会出现类“鹰嘴”的尖前缘外形(如图 14(a), (b)所示), 较小的前缘半径使重点方位的镜面反射波强度减弱, 机翼的前向RCS得到减缩.如图 15~17所示, 不同俯仰角下, 优化后机翼的前向RCS均有较大程度的减小, 机翼的隐身性能得以改善, 同时随着隐身性能权重系数的增大, 减小的趋势明显.

|
| 图 14 优化前后机翼剖面几何外形对比 Fig.14 Comparisons of wing section shapes between initial and optimized configurations |

|
| 图 15 θ=80°优化前后周向RCS分布对比 Fig.15 Comparisons of azimuthal RCS distributions at θ=80° between initial and optimized configurations |

|
| 图 16 θ=90°优化前后周向RCS分布对比 Fig.16 Comparisons of azimuthal RCS distributions at θ=90° between initial and optimized configurations |
|
| 图 17 θ=100°优化前后周向RCS分布对比 Fig.17 Comparisons of azimuthal RCS distributions at θ=100° between initial and optimized configurations |
优化后的内侧翼型剖面出现小幅度的扭转角增大, 外侧翼剖面则扭转角减小甚至出现负扭转, 使得优化后构型的展向环量分布更加接近椭圆形分布, 如图 13所示, 一定程度上又减小了诱导阻力.
5 结论本文基于多目标分解思想中的Tchebycheff分解方法, 将多学科多目标优化转化为多个单目标优化子问题, 建立了一套基于分解策略的气动隐身梯度优化设计系统.
在给定条件及约束下, 对某跨声速机翼进行气动隐身优化设计, 优化后机翼的气动性能与隐身性能得到综合提升.优化后机翼上表面激波基本消除, 因此阻力下降明显, 升阻比提高.优化后机翼的前缘半径减小, 甚至出现类“鹰嘴”的尖前缘, 降低了前缘处电磁波散射强度, 降低了RCS.研究表明本文的设计方法能够满足实际设计要求, 验证了该优化设计方法具有较好的实用性, 同时优化结果可以为气动隐身一体化工程设计提供参考.
| [1] |
Vinh H, Van Dam C P, Dwyer H A. Shape optimization for aerodynamic efficiency and low observability[R]. AIAA 1993-3115, 1993.
|
| [2] |
何开锋, 钱炜祺, 陈坚强, 等. 基于流体力学和电磁学方程数值求解的飞行器气动隐身一体化设计[J]. 空气动力学学报, 2009, 27(2): 180-185. He K F, Qian W Q, Chen J Q, et al. Integrated aircraft design of aerodynamic and stealthy performance with numerically solving fluid dynamics and electro-magnetics equations[J]. Acta Aerodynamica Sinica, 2009, 27(2): 180-185. DOI:10.3969/j.issn.0258-1825.2009.02.007 (in Chinese) |
| [3] |
夏露, 高正红, 李天. 飞行器外形多目标多学科综合优化设计方法研究[J]. 空气动力学学报, 2003, 21(3): 275-281. Xia L, Gao Z H, Li T. Investigation of integrated multi-disciplinary and multi-objective optimization of the aircraft configuration design method[J]. Acta Aerodynamica Sinica, 2003, 21(3): 275-281. DOI:10.3969/j.issn.0258-1825.2003.03.003 (in Chinese) |
| [4] |
夏露, 张欣, 杨梅花, 等. 飞翼布局翼型气动隐身综合设计[J]. 西北工业大学学报, 2017, 35(5): 821-826. Xia L, Zhang X, Yang M H, et al. Airfoil aerodynamic stealth integrated design for a flying wing configuration[J]. Journal of Northwestern Polytechnical University, 2017, 35(5): 821-826. DOI:10.3969/j.issn.1000-2758.2017.05.012 (in Chinese) |
| [5] |
焦子涵, 邓帆, 刘辉, 等. 高超声速飞行器气动/隐身优化设计方法[J]. 宇航学报, 2016, 37(9): 1031-1040. Jiao Z H, Deng F, Liu H, et al. Aerodynamic and stealthy optimization design method of hypersonic vehicle[J]. Journal of Astronautics, 2016, 37(9): 1031-1040. DOI:10.3873/j.issn.1000-1328.2016.09.001 (in Chinese) |
| [6] |
邓海强, 余雄庆. 亚声速翼身融合无人机概念外形参数优化[J]. 航空学报, 2014, 35(5): 1200-1208. Deng H Q, Yu X Q. Configuration optimization of subsonic blended wing body UAV conceptual design[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1200-1208. (in Chinese) |
| [7] |
王荣, 闫溟, 白鹏, 等. 飞翼无人机平面外形气动隐身优化设计[J]. 航空学报, 2017, 38(S1): 73-80. Wang R, Yan M, Bai P, et al. Optimization design of aerodynamics and stealth for a flying-wing UAV planform[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(S1): 73-80. (in Chinese) |
| [8] |
Lee D, Gonzalez L F, Srinivas K, et al. Aerodynamic/RCS shape optimisation of unmanned aerial vehicles using hierarchical asynchronous parallel evolutionary algo-rithms[R]. AIAA 2006-3331, 2006.
|
| [9] |
Lee D, Gonzalez L F, Srinivas K, et al. Multi-objective/multidisciplinary design optimisation of blended wing body UAV via advanced evolutionary algorithms[R]. AIAA 2007-36, 2007.
|
| [10] |
Kenway G K, Martins J. Aerodynamic shape optimization of the CRM configuration including buffet-onset condi-tions[R]. AIAA 2016-1294, 2016.
|
| [11] |
Zhang Q F, Li H. MOEA/D:a multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759 |
| [12] |
毕晓君, 王朝. 基于MOEA/D的船舶水动力性能优化[J]. 哈尔滨工程大学学报, 2018, 39(10): 1681-1687, 1694. Bi X J, Wang C. Ship hydrodynamic performance optimization based on MOEA/D[J]. Journal of Harbin Engineering University, 2018, 39(10): 1681-1687, 1694. (in Chinese) |
| [13] |
桑建华. 飞行器隐身技术[M]. 北京: 航空工业出版社, 2013: 48-52. Sang J H. Low-observable technologies of aircraft[M]. Beijing: Aviation Industry Press, 2013: 48-52. (in Chinese) |
| [14] |
Knott E F, Shaeffer J F, Tuley M T. Radar cross section[M]. 2nd Edition. Boston: SciTech Publishing, 2004: 44-46, 189-191.
|
| [15] |
Hascoët L. Tapenade:a tool for automatic differentiation of programs[J]. Anesthesiology, 2004, 53(6): 521-521. |



