2. 航天飞行器气动热防护实验室, 北京 100074
2. Laboratory of Aero-thermal Protection Techonology for Aerospace Vehicle, Beijing 100074, China
喷雾冷却作为一种高效的热控/散热技术, 能够实现高传热热流和高传热系数, 是当前的研究热点. 文献[1-4]报道了冷却性能的实验研究, 文献[5-9]报道了喷雾冷却性能的影响因素及其影响规律研究, 文献[10-11]报道了喷雾冷却性能的实验关联式研究, 文献[12-16]报道了喷雾冷却的强化传热研究. Liang等综述了喷雾冷却在单相模式、相变模式、临界状态中的机理认识与实验结论, 是当前该领域最全面的系统综述[17-18]. Pautsch等[19-20]研究了单相传热模式下的喷雾冷却性能, 探索了喷嘴阵列的冷却效果, 指出在多喷嘴喷雾中液膜流动状态对冷却性能影响很大. Zhou等[21]研究了水工质的两相喷雾冷却实验, 通过参数化规律研究指出喷雾流量是影响冷却性能的最关键因素. Mudawar等[22-24]针对单相、相变模式下的喷雾冷却过程开展了实验研究, 并提出了具有较广泛适用范围的传热实验关联式. 在众多研究工作中, 针对喷雾冷却性能的模拟计算方法鲜有报道. 当前, 喷雾冷却技术的设计与应用过程均依赖于实验关联式, 而实验关联式的预测适用范围受到实验数据获取条件的制约. 发展具有普适性的喷雾冷却模拟方法需要针对喷雾冷却过程中的传热机理进行模化.
喷雾冷却过程中的基本传热现象存在时间尺度小、长度尺度小等特征, 这给直接实验测量与物理机理研究带来了挑战. 近年来喷雾冷却的传热机理已经获得了一定的共识. 研究文献[17-18, 25]表明, 喷雾冷却主要有4种传热机制: (1)喷雾形成液膜的对流传热; (2)喷雾形成液膜中的池沸腾传热; (3)类比经典池内沸腾, 喷雾液滴撞击液膜产生了额外数量巨大的“二次沸腾气泡”, 这些气泡增大了发生相变过程的相界面, 提升了相变传热率; (4)液滴撞击液膜会击碎液膜中气泡, 缩短了气泡的生命周期, 提高了气泡的生长频率, 形成了二次气泡高频化的相变传热强化机制.
针对喷雾冷却传热机理开展模化的计算方法研究目前仍处于起步阶段. Tan[26]利用Monte Carlo方法描述粒径与速率呈均匀分布的喷雾液滴群撞击液膜形成二次气泡, 首次实现了对喷雾冷却性能的模拟计算, 虽然其采用的传热计算模型没有经过实验验证, 但其对喷雾液滴群的描述方法具有很高的参考价值. 在其基础上, Xie等[27]发展了利用Monte Carlo方法描述具有非均匀分布粒径与速率的喷雾液滴及其生成的二次气泡、利用液滴冲击传热关联式和气泡生长解析模型分别描述单相和相变传热的喷雾冷却模拟计算方法, 计算结果与实验具有较高的一致性. Tan[26]和Xie等[27]发展了可描述喷雾液滴群的计算方法, 但其在传热计算中没有针对性地对喷雾冷却4个传热机制开展模化, 限制了计算模型的准确性与适用范围.
本文基于Tan[26]和Xie等[27]对喷雾液滴群的描述方法, 基于针对喷雾冷却4个传热机制的模化, 发展了喷雾冷却相变传热模拟计算方法, 并通过所搭建的喷雾冷却实验台, 利用实验数据校核了计算方法.
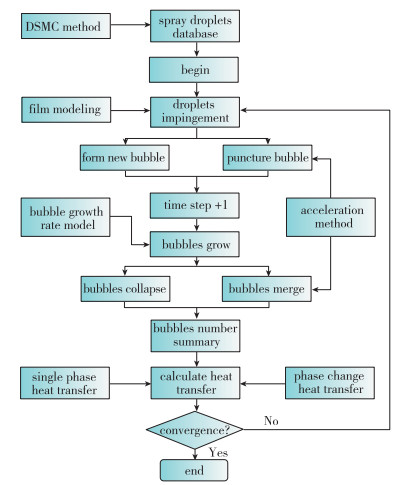
1 计算模型与方法计算流程中首先利用Monte Carlo算法生成数量足够的、符合实验测量分布规律的粒子数据库, 以此来模拟喷雾过程中的喷射液滴. 液滴撞击液膜后, 会生成二次气泡. 二次气泡会按照由热力学环境与液滴动力学参数共同决定的生长速率规律而逐渐变大. 气泡与液滴、气泡、液膜均会发生干涉, 液滴撞击气泡会击碎气泡, 气泡与气泡相接触会发生融合, 气泡生长至接触液膜表面时会发生破碎. 编写程序以时间为线索描述上述过程, 以气泡为主要关注对象来统计气泡的生成、生长、破碎、融合等行为, 并通过记录单位时间内气泡的破碎数量、气泡破碎时体积来获得相变传热率. 通过结合液膜单相对流传热计算与气泡相变传热计算, 实现喷雾冷却4个传热机制的同时模拟. 图 1给出了计算总流程图. 计算模型主要有以下几个模块构成: 液滴生成模块、气泡生成与生长模块、气泡干涉模块、传热计算模块、液膜计算模块、计算加速模块、可视化后处理模块.
|
| 图 1 计算流程图 Fig.1 Calculation procedures |
本文中, 喷雾液滴群的表征采用相变Doppler测试仪PDA得到的液滴直径、液滴流速、液滴数量密度的概率密度分布, 并以此作为输入条件提供给计算模型实现对喷雾液滴群的普适性与准确性模化. 利用Kreitzer等提出的Monte Carlo算法[28]生成液滴数据库, 使液滴群的直径、速率、数量密度概率分布吻合实验测量结果.
1.2 气泡生成与生长模块喷雾冷却过程中存在于液膜中的气泡有两类, 一是由壁面凹坑、瑕疵等微结构成核的沸腾气泡, 二是基于液滴撞击液膜形成的二次气泡. 沸腾气泡一般附着在二维的壁面上生长, 而二次气泡会分布在具有有限厚度的液膜三维区域. 喷雾冷却过程高速摄影实验表明, 二次气泡的数量密度远大于沸腾成核气泡[25], 因此, 采用忽略沸腾成核气泡、仅考虑二次气泡的假设是合理的. 喷雾液滴群撞击液膜会产生二次气泡, 因此, 二次气泡的成核位置随机分布在液滴直径边缘区域内.
成核后二次气泡在气泡表面不断吸热并发生汽化使气泡逐渐长大. 气泡的生长速率是喷雾相变冷却性能模拟的核心环节, 决定了相变过程的发生速率. 采用Mikic解析计算模型来描述气泡的生长过程[29], 可以将气泡半径写成时间的函数
| $ {R^ + } = \frac{2}{3}\left[ {{{\left( {{t^ + } + 1} \right)}^{3/2}} - {{\left( {{t^ + }} \right)}^{3/2}} - 1} \right] $ |
式中,
| $ {{R^ + } = RA/{B^2},{t^ + } = t{A^2}/{B^2}} $ |
| $ {A = {{\left[ {\frac{{2\left[ {{T_\infty } - {T_{{\rm{sat}}}}\left( {{P_\infty }} \right)} \right]{h_{{\rm{lv}}}}{\rho _{\rm{v}}}}}{{3{\rho _{\rm{l}}}{T_{{\rm{sat}}}}\left( {{P_\infty }} \right)}}} \right]}^{1/2}},B = {{\left( {\frac{{12{\alpha _1}}}{\pi }} \right)}^{1/2}}Ja} $ |
| $ {Ja = \frac{{{\rho _1}{c_{{\rm{p,l}}}}\left[ {{T_\infty } - {T_{{\rm{sat}}}}\left( {{P_\infty }} \right)} \right]}}{{{\rho _{\rm{v}}}{h_{{\rm{lv}}}}}}} $ |
其中, R+为无量纲气泡半径, t+为无量纲气泡生长时间, R为气泡半径, t为气泡生长时间, A,B为过程变量, T∞为液膜温度, P∞为液膜压力, Tsat(P∞)为液膜饱和温度, hlv为液膜工质的相变潜热, ρv为液膜蒸汽密度, ρl为液膜液体工质密度, αl为液膜液体工质的热扩散系数, Ja为Jacobi数, cp, l为液膜液态工质的定压比热.
1.3 液滴、液膜与气泡的干涉文献[25]报道的高速摄影结果表明, 液滴、液膜、气泡之间会发生运动干涉, 本文考虑了3种干涉情形: (1)液滴撞击气泡会击碎气泡; (2)气泡长大后与液膜表面干涉会使气泡破碎; (3)气泡长大过程中与相邻气泡接触会发生气泡间融合. 气泡的击碎以撞击液膜的液滴和液膜中气泡的几何尺寸关系作判据, 当液滴半径Rd与气泡半径Rb之和小于二者圆心距Lm时即认为会发生气泡的击碎. 气泡被击碎后, 该气泡消失, 气泡体积计入总相变气体体积以计算传热率. 气泡的破碎以液膜中气泡与液膜厚度的几何关系作判据, 当气泡直径Db大于液膜厚度hfilm时, 即认为发生气泡的破碎. 气泡破碎后, 该气泡消失, 气泡体积计入总相变气体体积. 气泡的融合以两个气泡的几何关系作判据, 当两个气泡半径之和Rb, 1+Rb, 2大于二者圆心距Lm时, 即认为发生气泡的融合. 气泡融合后, 两个原气泡消失, 在两个气泡的等效质心位置形成一个新气泡, 新气泡体积等于两个原气泡体积之和.
1.4 传热计算模块基于当前对喷雾冷却传热机制的认识, 喷雾冷却传热的计算方法主要考虑液膜单相对流传热与沸腾相变传热. 文献[25]利用高速摄影实验观测表明壁面缺陷等微结构成核的沸腾气泡数量密度远小于喷雾液滴撞击液膜成核形成的二次气泡数量密度, 因而在计算喷雾冷却传热过程时可以忽略壁面成核的沸腾传热, 仅仅考虑二次成核气泡的相变传热[27].
喷雾冷却中液膜对流传热过程可以采用Mudawar等的实验关联式[22]进行计算
| $ Nu = 4.70Re_{\rm{s}}^{0.61}Pr_{\rm{f}}^{0.32} $ |
喷雾冷却中二次成核气泡的相变过程可以通过统计大量气泡在时间轴上的生成、生长、消失行为来获得对宏观喷雾相变冷却过程的模拟计算. 同时, 利用对前述液滴与气泡间的干涉过程的考虑来模化二次成核气泡的高生长频率机制. 由此, 实现了对喷雾冷却4个传热机制的模化.
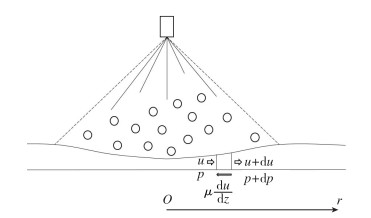
1.5 液膜流场计算喷雾冷却单相与沸腾相变传热计算过程中都需要液膜的厚度与流速信息作为输入, 因而需要对液膜流场进行模化计算. 液膜示意图见图 2. 假设稳定喷雾液滴在不断撞击液膜时, 液膜会吸收所有的液滴,液滴与液膜总质量守恒, 同时液膜的厚度与速度分布能够达到一个稳定状态, 又假设液滴撞击液膜时液滴的动量会转化为液膜中的压力[30].
|
| 图 2 喷雾冷却液膜示意图 Fig.2 Schematic diagram of spray film |
建立如图 2所示的中心对称柱坐标系, 以喷嘴正下方为坐标原点. 液膜厚度为hfilm(r), 液膜径向方向尺度为R. 液膜两个方向的动量守恒方程为
| $ {u\frac{{\partial u}}{{\partial r}} + w\frac{{\partial u}}{{\partial z}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial r}} + \nu \left[ {\frac{{{\partial ^2}u}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial u}}{{\partial r}} - \frac{u}{{{r^2}}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}}} \right] + {g_r}} $ |
| $ {u\frac{{\partial w}}{{\partial r}} + w\frac{{\partial w}}{{\partial z}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} + \nu \left( {\frac{{{\partial ^2}w}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial w}}{{\partial r}} + \frac{{{\partial ^2}w}}{{\partial {z^2}}}} \right) + {g_z}} $ |
通过数量级分析简化上述方程组, 并结合壁面上的无滑移边界条件与液膜表面上的自由表面边界条件, 最终可以得到液膜内流速型线与液膜厚度的表达式
| $ {u(r,z) = \frac{1}{\mu }\left( {\frac{{{\rm{d}}S}}{{{\rm{d}}r}} - \frac{{{\rm{d}}p}}{{{\rm{d}}r}}} \right)\left[ {{h_{{\rm{film}}}}(r)z - {z^2}} \right]} $ |
| $ {{h_{{\rm{film}}}}(r) = {{\left[ {Q(r)/\left( {\frac{{\rho {\rm{ \mathsf{ π} }}r}}{{3\mu }}\left( {\frac{{{\rm{d}}S}}{{{\rm{d}}r}} - \frac{{{\rm{d}}p}}{{{\rm{d}}r}}} \right)} \right)} \right]}^{1/3}}} $ |
式中,
利用上面两式, 可根据已知的喷雾流量及其分布来计算得到液膜的厚度、流速分布.
液膜流动时, 液膜中二次气泡会随之流动. 但计算结果表明, 二次气泡的生命周期很短(很容易被击碎或破碎), 在其生命周期内随液膜流动的位移相对于发热面长度尺度小1~2个数量级, 因而有理由认为可以忽略气泡的运动速率与位移.
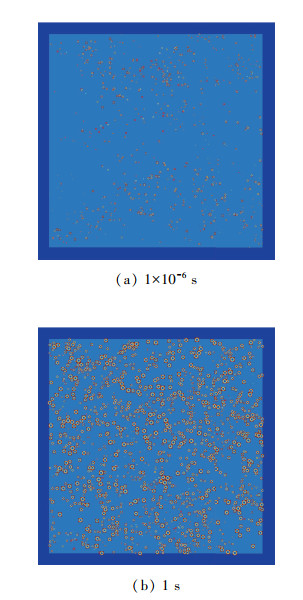
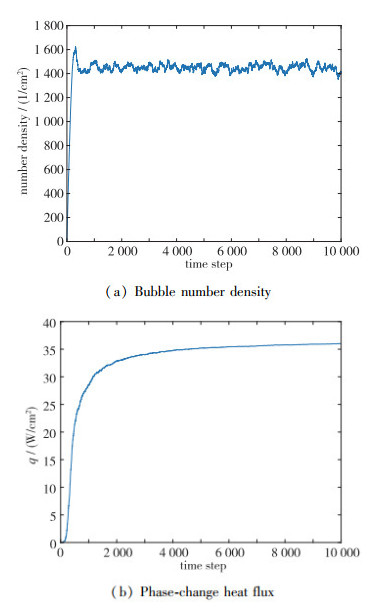
1.6 计算收敛的判断喷雾冷却计算过程中会以给定的流量规律持续不断地引入液滴粒子, 以模拟喷雾液滴持续碰壁、撞击液膜的过程, 同时液滴不断生成二次气泡, 二次气泡随时间与传热过程不断长大, 并根据干涉规则出现气泡的击碎、破碎与融合现象. 在计算过程初期, 计算域中气泡数量不断提高、气泡直径不断变大, 如图 3所示; 当计算达到收敛状态时, 液膜中气泡数量密度、二次气泡沸腾传热热流应趋于一个动态的稳定值, 可据此来判断计算过程是否收敛, 如图 4所示.
|
| 图 3 不同时刻液膜中的气泡分布 Fig.3 Bubble distributions in film at different times |
|
| 图 4 计算过程的收敛 Fig.4 Convergence of calculation |
设计并搭建了喷雾冷却实验台, 可开展相变模式下的喷雾冷却实验研究. 实验台具体细节可参见文献[31].
2.2 计算模型实验校核为了对比本文计算方法与本文喷雾冷却样机实验结果, 针对样机实验环境进行了计算.
本文实验条件: 室温21℃,室压1.0×105 Pa,冷却介质初始温度21℃, 喷雾喷射压力0.058 MPa. 控制表面温度为113.9℃时, 实现了传热热流211.93 W/cm2. 以本文方法计算, 在相同条件下, 控制表面温度为114℃时, 实现了传热热流166.75 W/cm2. 为进一步验证, 以Rybicki等报道的喷雾冷却传热关联式作参照[24]
| $ B{o^*} = 4.79 \times {10^{ - 3}}{\left( {\frac{{{c_{{\rm{p}},{\rm{f}}}}\left( {{T_{{\rm{surf}}}} - {T_{\rm{f}}}} \right)}}{{{h_{{\rm{fg}}}}}}} \right)^{5.75}} $ |
其中,式中无量纲数定义为
| $ B{o^*} = \left( {\frac{{q{d_{32}}}}{{{\mu _{\rm{f}}}{h_{{\rm{fg}}}}}}} \right){\left( {\frac{{{\rho _{\rm{f}}}}}{{{\rho _{\rm{g}}}}}} \right)^{ - 2.5}}{\left( {\frac{{{\rho _{\rm{f}}}{{\bar Q}^{\prime \prime 2}}{d_{32}}}}{\sigma }} \right)^{0.35}} $ |
式中,cp, f为比热,Tsurf为表面温度,Tf为液体工质温度,hfg为汽化潜热,d32为Sauter平均直径,q为热流,Q″2d32为单位面积的喷雾流量,μf为液体黏度,ρf为液体密度,ρg为气体密度,σ为表面张力系数.
Mudawar称该实验关联式相对其实验数据库的拟合平均绝对误差为22.7%.
利用上式计算相同实验条件下, 控制表面温度在113.9℃时, 传热热流为191.25 W/cm2, 平均绝对误差MAE=22.7%.
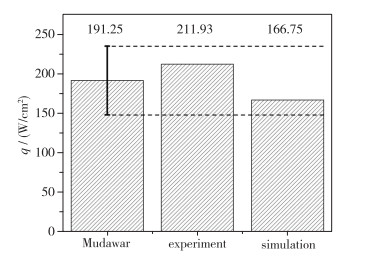
对比本文实验结果、计算结果与Mudawar结果, 如图 5所示. 图 5表明, 本文的计算结果与本文实验、Mudawar实验关联式均吻合较好.
|
| 图 5 计算模型校核 Fig.5 Comparisons between simulation and experiment |
图 5所示本模型计算结果与Mudawar实验值、本文实验值相比偏低, 其误差来源可能是3个方面: 第一是计算模型输入的喷雾液滴表征信息不够准确, 由于实验条件的限制, 本文无法直接测量喷雾液滴的粒径、速率及其概率密度分布等信息, 只能借用文献报道的相同型号喷嘴的类似实验数据; 第二是计算过程采用的气泡、液膜、液滴之间的干涉模型十分简单, 而真实物理世界中的相关现象是十分复杂的, 涉及分子间作用力以及相表面扰动波等多尺度物理过程, 而直接计算此类过程是很难实现的, 因而简化处理模型不可避免地引入了计算模型中的系统误差; 第三是气泡生长速率解析模型在推导过程中使用了一些均温、无扰动条件等简化假设, 会引起计算误差.
本文计算方法对相变传热的预测计算依赖于气泡生长速率的计算模型. 当喷雾冷却应用于过载、微重力等特殊环境时, 可通过推导并利用特殊环境下的气泡生长速率模型, 扩展本文计算方法的适用范围.
3 结论喷雾冷却是一种高效的热控技术. 为了探索形成完善的喷雾冷却技术设计流程, 本文开展了喷雾冷却传热过程的建模研究. 针对喷雾冷却传热过程的4个传热机制, 基于Monte Carlo方法描述了不同粒径与速率分布的液滴撞击液膜并生成二次气泡的过程, 通过液态介质中气泡生长速率的解析计算模型考虑了气泡的生长过程, 并结合模化气泡与气泡之间、液滴与气泡之间、气泡与液膜之间的干涉行为描述了气泡的演化过程, 通过统计稳态时气泡总体积的变化率来反求相变传热速率, 利用对流传热公式计算了液膜对流传热, 由此形成了喷雾冷却相变传热模拟计算方法. 基于喷雾冷却实验台开展了稳态喷雾冷却实验, 对计算结果进行了实验校核. 研究得到了以下结论:
(1) 本文发展的计算方法能够较好地模拟喷雾冷却相变传热性能.
(2) 影响本文方法计算精度的第一类因素为计算模型输入信息的准确性, 包括喷雾形成液滴的粒径、速率及其分布, 因此可通过提供准确性更高的输入信息来改进计算精度.
(3) 影响本文方法计算精度的第二类因素为气泡的干涉与生长模型. 气泡干涉模型包括气泡、液滴、液膜之间的干涉行为及其预测, 气泡生长模型为气泡生长速率的解析模型. 因而, 进一步发展预测精度更高的气泡干涉模型与气泡生长模型将有助于本文计算方法的改进与完善.
| [1] |
Liu X F, Liu J H, Xue R, et al. Heat transfer optimization of R134a phase change spray cooling in a closed loop system[J]. Experimental Thermal and Fluid Science, 2017, 92: 248-258. |
| [2] |
Zhang Z, Li J, Jiang P X. Experimental investigation of spray cooling on flat and enhanced surfaces[J]. Applied Thermal Engineering, 2013, 51(1/2): 102-111. |
| [3] |
Hou Y, Liu X F, Liu J H, et al. Experimental study on phase change spray cooling[J]. Experimental Thermal and Fluid Science, 2013, 46: 84-88. DOI:10.1016/j.expthermflusci.2012.11.023 |
| [4] |
Tao Y J, Huai X L, Wang L, et al. Experimental characterization of heat transfer in non-boiling spray cooling with two nozzles[J]. Applied Thermal Engineering, 2011, 31(10): 1790-1797. DOI:10.1016/j.applthermaleng.2011.02.025 |
| [5] |
Yan Z B, Toh K C, Duan F, et al. Experimental study of impingement spray cooling for high power devices[J]. Applied Thermal Engineering, 2010, 30(10): 1225-1230. DOI:10.1016/j.applthermaleng.2010.02.003 |
| [6] |
Chen R H, Chow L C, Navedo J E. Optimal spray characteristics in water spray cooling[J]. International Journal of Heat and Mass Transfer, 2004, 47(23): 5095-5099. DOI:10.1016/j.ijheatmasstransfer.2004.05.033 |
| [7] |
Wang Y Q, Liu M H, Liu D, et al. Experimental study on the effects of spray inclination on water spray cooling performance in non-boiling regime[J]. Experimental Thermal and Fluid Science, 2010, 34(7): 933-942. DOI:10.1016/j.expthermflusci.2010.02.010 |
| [8] |
Cheng W L, Zhang W W, Jiang L J, et al. Experimental investigation of large area spray cooling with compact chamber in the non-boiling regime[J]. Applied Thermal Engineering, 2015, 80: 160-167. DOI:10.1016/j.applthermaleng.2015.01.055 |
| [9] |
Liu J H, Xue R, Chen L, et al. Influence of chamber pressure on heat transfer characteristics of a closed loop R134-a spray cooling[J]. Experimental Thermal and Fluid Science, 2016, 75: 89-95. DOI:10.1016/j.expthermflusci.2016.01.011 |
| [10] |
Panão M R, Moreira A L. Heat transfer correlation for intermittent spray impingement: a dynamic approach[J]. International Journal of Thermal Sciences, 2009, 48(10): 1853-1862. DOI:10.1016/j.ijthermalsci.2009.02.018 |
| [11] |
Horacek B, Kiger K T, Kim J. Single nozzle spray cooling heat transfer mechanisms[J]. International Journal of Heat and Mass Transfer, 2005, 48(8): 1425-1438. DOI:10.1016/j.ijheatmasstransfer.2004.10.026 |
| [12] |
Bhatt N H, Lily R R, Varshney P, et al. Enhancement of heat transfer rate of high mass flux spray cooling by ethanol-water and ethanol-tween20-water solution at very high initial surface temperature[J]. International Journal of Heat and Mass Transfer, 2017, 110: 330-347. DOI:10.1016/j.ijheatmasstransfer.2017.02.094 |
| [13] |
Zhang Z, Jiang P X, Ouyang X L, et al. Experimental investigation of spray cooling on smooth and micro-structured surfaces[J]. International Journal of Heat and Mass Transfer, 2014, 76: 366-375. DOI:10.1016/j.ijheatmasstransfer.2014.04.010 |
| [14] |
Zhang W, Wang Z L. Heat transfer enhancement of spray cooling in straight-grooved surfaces in the non-boiling regime[J]. Experimental Thermal and Fluid Science, 2015, 69: 38-44. DOI:10.1016/j.expthermflusci.2015.08.001 |
| [15] |
Bostanci H, Rini D P, Kizito J P, et al. High heat flux spray cooling with ammonia: investigation of enhanced surfaces for HTC[J]. International Journal of Heat and Mass Transfer, 2014, 75: 718-725. DOI:10.1016/j.ijheatmasstransfer.2014.04.019 |
| [16] |
Bostanci H, Altalidi S S, Nasrazadani S. Two-phase spray cooling with HFC-134a and HFO-1234yf on practical enhanced surfaces[J]. Applied Thermal Engineering, 2018, 131: 150-158. DOI:10.1016/j.applthermaleng.2017.11.142 |
| [17] |
Liang G T, Mudawar I. Review of spray cooling-Part 1:Single-phase and nucleate boiling regimes, and critical heat flux[J]. International Journal of Heat and Mass Transfer, 2017, 115: 1174-1205. DOI:10.1016/j.ijheatmasstransfer.2017.06.029 |
| [18] |
Liang G T, Mudawar I. Review of spray cooling-Part 2:High temperature boiling regimes and quenching applica-tions[J]. International Journal of Heat and Mass Transfer, 2017, 115: 1206-1222. DOI:10.1016/j.ijheatmasstransfer.2017.06.022 |
| [19] |
Pautsch A G, Shedd T A. Spray impingement cooling with single- and multiple-nozzle arrays. Part Ⅰ: Heat transfer data using FC-72[J]. International Journal of Heat and Mass Transfer, 2005, 48(15): 3167-3175. DOI:10.1016/j.ijheatmasstransfer.2005.02.012 |
| [20] |
Shedd T A, Pautsch A G. Spray impingement cooling with single- and multiple-nozzle arrays. Part Ⅱ: visualization and empirical models[J]. International Journal of Heat and Mass Transfer, 2005, 48(15): 3176-3184. DOI:10.1016/j.ijheatmasstransfer.2005.02.013 |
| [21] |
Zhou N Y, Chen F J, Cao Y C, et al. Experimental investigation on the performance of a water spray cooling system[J]. Applied Thermal Engineering, 2017, 112: 1117-1128. DOI:10.1016/j.applthermaleng.2016.10.191 |
| [22] |
Mudawar I, Valentine W S. Determination of the local quench curve for spray-cooled metallic surfaces[J]. Journal of Heat Treating, 1989, 7(2): 107-121. DOI:10.1007/BF02833195 |
| [23] |
Estes K A, Mudawar I. Correlation of Sauter mean diameter and critical heat flux for spray cooling of small surfaces[J]. International Journal of Heat and Mass Transfer, 1995, 38(16): 2985-2996. DOI:10.1016/0017-9310(95)00046-C |
| [24] |
Rybicki J R, Mudawar I. Single-phase and two-phase cooling characteristics of upward-facing and downward-facing sprays[J]. International Journal of Heat and Mass Transfer, 2006, 49(1/2): 5-16. |
| [25] |
Rini D P, Chen R H, Chow L C. Bubble behavior and nucleate boiling heat transfer in saturated FC-72 spray cooling[J]. Journal of Heat Transfer, 2002, 124(1): 63-72. DOI:10.1115/1.1418365 |
| [26] |
Tan S W. Computer simulation of a spray cooling system with FC-72[D]. Orlando: University of Central Flori-da, 2001.
|
| [27] |
Xie J L, Wong T N, Duan F. Modelling on the dynamics of droplet impingement and bubble boiling in spray cooling[J]. International Journal of Thermal Sciences, 2016, 104: 469-479. DOI:10.1016/j.ijthermalsci.2016.02.016 |
| [28] |
Kreitzer P, Kuhlman J. Spray cooling droplet imping-ement model[R]. AIAA 2010-4500, 2010.
|
| [29] |
Carey V P. Liquid-vapor phase-change phenomena[M]. 2nd ed. London: CRC Press, 2008.
|
| [30] |
Xie J L, Zhao R, Duan F, et al. Thin liquid film flow and heat transfer under spray impingement[J]. Applied Thermal Engineering, 2012, 48: 342-348. DOI:10.1016/j.applthermaleng.2012.04.044 |
| [31] |
宋立业, 罗晓光, 马汉东, 等. 喷雾冷却过程的数值模拟方法探索[J]. 气体物理, 2020, 5(4): 56-63. Song L Y, Luo X G, Ma H D, et al. Exploration of numerical simulation method of spray cooling heat transfer[J]. Physics of Gases, 2020, 5(4): 56-63. (in Chinese) |



