层流到湍流的转捩一直是流体力学中最重要的前沿问题之一[1].层流时飞行器表面所受的阻力和传热能力与湍流时大不相同, 且流动分离位置也有很大差异[2].转捩位置对飞行器气动力特性, 尤其是阻力特性具有重大影响.因此, 研究飞行器绕流的转捩位置预测方法对于气动力分析与精细化设计具有十分重要的意义.
在计算机技术飞速发展的今天, 大涡模拟(LES)[3]和直接数值模拟(DNS)[4]方法已经可以实现对流动比较精准的转捩预测[5], 已被用于低Reynolds数平板和翼型的研究.但由于其计算量过大, 目前还不适合工程应用.目前工程上常用的转捩预测方法主要有基于Reynolds平均的湍流/转捩模式和基于线性稳定性理论的eN方法.前者中较为流行的是Menter等[6]提出的一种耦合SST k-ω湍流模型的γ-
尽管如此, 发展较早的基于线性稳定性理论的eN方法能通过层流小扰动增长放大理论更为合理地揭示转捩机理问题, 是目前工程中最常使用的转捩预测方法. Stock等[14]开展了将RANS方程与eN转捩判断方法耦合用于定常流动的研究, 取得了很大进展.德国宇航院(DLR)的Krumbein等[15]将eN转捩预测方法与基于非结构网格的复杂流场计算程序TAU耦合在一起进行流动的转捩判断.张坤等[16]将N-S方程、层流边界层方程以及线性稳定性方程求解与eN方法耦合实现了翼型/机翼的转捩自动判断.但由于线性稳定性理论引入了平行流假设, 使流动的横向速度和流向参数的弱增长被忽略.且该方法对N-S方程层流解精度要求较高, 复杂流场的适应性不好[17].
为了克服线性稳定性分析的缺点, 提出了解抛物化稳定性方程(parabolized stability equations, PSE)的方法[18-19]和全局稳定性分析方法[20], 模态分解方法也逐渐成为稳定性分析和流场特征结构分析的有力工具.其中, 本征正交分解[21](proper orthogonal decomposition, POD)方法以及动模态分解[22](dynamic mode decomposition, DMD)方法是当前比较流行的两种模态分解方法.不同于POD按能量对模态进行排序, Schmid[22]提出了按频率对系统模态进行排序的DMD方法, 随后成为众多研究者研究的热点[23-25].
DMD方法能直接从实验或数值模拟的流场中提取流动的动态信息, 通过动态系统的特征值估测流动的演化趋势并进行稳定性分析.刘方良[26]、韩莉[27]首先将DMD与eN方法结合, 提出了一套转捩预测新方法, 称为DMD/eN方法.该方法用于翼型转捩预测与其他转捩判断方法的主要区别是, 不需要求解稳定性或经验关系式方程, 而是从CFD数值模拟的结果中提取流动稳定性信息进行DMD分析.但当时作为初步研究, 并未对该方法的原理进行解释和探究, 且在实现方法上存在缺陷.此后, 韩忠华等[28]对该方法的原理及实现过程进一步研究, 逐步形成了一套较为完整的DMD/eN方法原理与算法体系.本文改进了其中DMD网格线生成方法和N值的积分策略, 使其更符合eN包络线思想, 且增加了该方法的适用范围.
1 DMD/eN方法 1.1 DMD网格线划分与翼型数据处理方法DMD的理论推导和算法验证详见文献[22].这里仅介绍改进的DMD网格线划分方法和对翼型流场数据的处理.
通过分析, 空间DMD更适用于本文研究的转捩预测方法.由于空间DMD要求快照的空间间隔是等距的, 故首先要将原翼型计算网格的流动数据插值到DMD分析的网格线上.
以NLF0416翼型4°攻角的绕流计算为例, 展示了上表面的DMD网格线划分.图 1(a)为改进前以原点为起点, 沿x轴等距划分的网格线.可见在翼型前缘处沿翼型表面网格线间有较大间隔, 无法保证DMD沿弧长推进求解对网格线等间距的要求, 该现象对于钝前缘翼型更加严重.其次, 对于有攻角的翼型绕流, 前缘驻点偏离原点, 会造成上下表面分析数据错位.针对以上缺陷, 图 1(b)为改进后的网格线, 以翼型前缘驻点为分界点, 将翼型分为上下表面, 分别生成垂直于翼型表面沿弧长等距划分的DMD网格线, 每条网格线上的数据相当于一个空间流场快照(两种方法均取了201快照用于展示).这样有效避免了上述问题, 使得DMD求解沿流向推进, 更符合eN方法原理.
其次, 提取流动信息, 构成流场快照矩阵:
| $ \mathit{\boldsymbol{V}}_1^N = \{ {\mathit{\boldsymbol{v}}_1}, {\rm{ }}{\mathit{\boldsymbol{v}}_2}, {\rm{ }}{\mathit{\boldsymbol{v}}_3}, \ldots, {\rm{ }}{\mathit{\boldsymbol{v}}_N}\} $ |
其中, vi表示第i个抽样数据的流场信息, 称为快照(snapshots); V1N是流场快照形成的矩阵, 下标和上标分别是起始和终止的流场快照编号.本文用于稳定性分析的流场状态量是速度信息, 即(u, v), 其中u, v分别是直角坐标系下x方向和y方向的速度.具体表示如下:
| $ \mathit{\boldsymbol{V}}_1^N = \left[ \begin{array}{l} u_1^1\;\;u_2^1\;\; \ldots \;\;u_N^1\\ v_1^1\;\;v_2^1\;\; \ldots \;\;v_N^1\\ \;\; \vdots \;\;\;\; \vdots \;\;\; \ddots \;\;\; \vdots \\ u_1^M\;u_2^M\; \ldots \;\;u_N^M\\ v_1^M\;\;v_2^M\;\; \ldots \;\;v_N^M \end{array} \right] $ |
其中, uij和vij表示翼型表面沿弧长第i站位处, 网格点序号为j时的速度.图 2以翼型上表面弧长方向等分为200份(N=201), 沿物面法向等分为100份(M=101) 为例, 展示了DMD计算所用的网格示意图(将图 1中的网格线展示为整体网格的形式).第i站位是从前缘驻点开始第i条网格线位置, 网格点序号j则是某一站位的外法向网格线上的网格点标号.图 2中的放大图以翼型上表面靠近前缘处第11~13站位为例给出了网格点序号, 为清晰起见, 物面法向网格取间隔为4进行展示.注意这里只对边界层内的流动进行DMD分析, 故网格线j方向长度只须包含边界层区域即可.

|
| 图 1 DMD网格线改进前与改进后对比示意图 Fig.1 Diagram of inproved DMD grid lines compared with initial generation |

|
| 图 2 翼型表面站位及DMD网格点序号示意图 Fig.2 Schematics of DMD grid point at different position of airfoil surface |
根据DMD理论, 空间速度场可由表征流场内在动力学机制的过渡矩阵A联系起来:
| $ \mathit{\boldsymbol{AV}}_{1}^{N-1}=\mathit{\boldsymbol{V}}_{2}^{N} $ |
采用文献[22]介绍的求解伴随矩阵
最后, 对DMD得到的特征值进行对数映射即可得到空间模式下的特征值:
| $ \lambda =\text{log}\left( \mu \right)/\Delta s={{\lambda }_{\text{r}}}+{{\lambda }_{\text{i}}}\text{i} $ |
其中, λr为指数放大率或衰减率, λi为空间波数.
1.2 eN包络线扰动放大N因子的积分策略参照线性稳定性理论与eN方法的结合方式和eN包络线思想, 本文改进后提出的DMD和eN方法的结合过程及N值积分策略如下所述:
(1) 以驻点为起点, 沿弧长s对上下表面的流场数据进行划分.将翼型表面分成m段, 根据理论分析和经验, 取m=10, 则0~0.1s/c为第1段, 0~0.2s/c为第2段, 以此类推(这里的c为无量纲化为1的翼型弦长).
(2) 沿翼型流向进行推进求解, 对翼型表面每一段的流场数据进行DMD计算, 得到该段的稳定性特征值.
(3) 确定有效特征值.本文采用两种快照数对某段流场进行DMD分析, 选择不稳定特征值(λi, λr)中重叠性最好的特征值分别作为各自流场快照数在本段的有效特征值, 对应的模态即是本段的特征模态.研究中发现数值噪声对DMD分析的结果影响较大, 选取重叠性最好的特征值是为了避免数值噪声干扰.由于不同快照的特征值中重叠最好的两个也存在微小差异(并不是完全重合), 故以流场快照数多的结果为准.
(4) 改进后的N因子计算方法如式(1) 所示.即对DMD分析得到的空间放大率乘以对应段的长度, 得到翼型表面每段对应的扰动放大因子Ni(下标i为段标号).
| $ {{N}_{i}}={{s}_{i}}\times {{\lambda }_{\text{r}i}} $ | (1) |
(5) 对比找出Ni超过转捩阀值Ncrit时对应的段标号, 记为s; 连接该段及以前每段末的的扰动放大因子N1, N2, ……, Ns, 得到一条类似包络线的N值增长曲线, 如图 3所示.在该曲线上线性插值得到转捩阀值对应的弧长位置s/c, 再通过比较翼型表面网格点弧长与弦长的对应关系, 插值得到对应的转捩点弦长位置x/c.

|
| 图 3 改进后的N因子积分示意图 Fig.3 Diagram of improved method of N factor integration |
以上为DMD/eN方法的实现步骤, 下面将该方法与RANS求解器进行耦合.图 4为绕翼型定常流动的转捩预测过程.首先, 采用RANS求解器对绕翼型的流动进行固定转捩数值模拟, 须保证较大层流范围且使流场充分收敛; 其次, 提取边界层内部的速度信息, 形成用于DMD分析的流场快照; 而后, 采用DMD/eN方法进行流动转捩预测; 最后, 将判断的转捩点位置回带到RANS求解器进行迭代, 直至得到收敛的结果.

|
| 图 4 RANS求解器与DMD/eN方法耦合转捩判断示意图 Fig.4 Diagram of transition prediction using RANS solver coupling with DMD/eN method |
文献[28]已经证明: DMD得到的某段经过对数映射后的特征值实部, 实际是该段特征扰动的平均放大率.
根据上述结论和1.2节中改进了的N值积分策略, 本文提出的转捩预测方法更类似于eN包络线方法.其原理为:从定常层流解中提取边界层速度信息, 逐步向后推进, 对每段进行DMD分析, 得到每段特征扰动的特征值.将该特征值对应的放大率乘以该段长度得出该段末的扰动放大因子N.推进到N值达到转捩阀值时结束, 连接每段结束后的N值形成一条局部平均的包络线(类似于LST/eN方法的包络线).通过阀值N与包络线N值增长的对比得到转捩点位置.
DMD进行稳定性分析后, 计算得到的不同段上的有效特征值, 对应的并不是同一个时间频率, 这与eN包络线法中包络线上对应的有时不是同一时间频率是类似的.一般来说, 该有效特征值对应的是LST/eN方法中包络线上平均放大率最大的扰动, 即DMD/eN方法计算的每段末的N值都为当前段增长最大的N值, 其对应的频率为当前增长最快的频率.这也与eN包络线思想是一致的.与LST/eN方法不同的是, DMD/eN方法不需要求解一系列圆频率下的扰动增长曲线, 只关心特征扰动的放大情况.
此外, 在一段流动区域内, LST/eN方法积分的是同一时间频率下的放大率, 而改进前的DMD/eN方法对流动区域进行分段求解, 不同段间叠加计算的放大率对应的很可能不是同一个时间频率, 所以原来的N值积分方法从理论上讲存在一定缺陷.而改进了N值积分策略后的DMD/eN方法采用[0, 0.1s/c], [0, 0.2s/c], [0, 0.3s/c]……推进求解的方法, 在达到阀值之前分析区间的长度不断增加, 并无间断.这样就保证了在一段流动区域内计算出的平均放大率对应的是同一个时间频率, 保证了N值积分的正确性.
2 DMD/eN方法的转捩预测算例 2.1 LSC72613跨声速自然层流翼型为了验证本文发展的N值积分方法的有效性, 选择LSC72613翼型[29]进行DMD分析和转捩预测.
LSC72613翼型是由西北工业大学翼型叶栅国家重点实验室自主研发的自然层流超临界翼型.计算状态为: M=0.72, Re=2×107, α=0.577 2°.采用RANS求解器, 湍流模型为Spalart-Allmaras(S-A).图 5给出了LSC72613的计算网格图, 网格单元数为640×256, 其中翼型上下表面共有512个网格单元, 第一层网格距物面高度是2×10-6c.其中, c为翼型弦长.

|
| 图 5 LSC72613翼型计算网格 Fig.5 Computational grids of LSC72613 airfoil |
本文采用课题组自主研发的二维流动求解程序PMNS2D对翼型进行固定转捩数值模拟, 上下表面的初始固定转捩点位置设在约70%弦长处, 以保证有足够的层流区用于DMD分析.改进的分段方法使得随着求解的推进, 每段的长度增加, 快照数逐渐增多, 为了降低后面段中数值误差的影响, 选取总快照数为100和200来进行DMD分析.
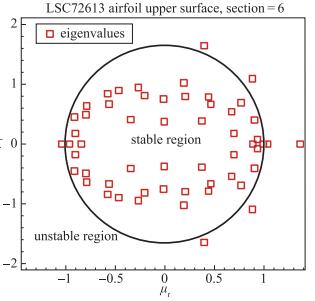
图 6展示了总快照数为100的第6段的动模态分解得到的特征值分布.黑色实线是一个单位圆, 代表中性稳定; 位于单位元内部的是稳定的特征值, 位于单位圆外部的是不稳定的特征值.
|
| 图 6 DMD特征值分布示意图[0, 0.6s/c] Fig.6 Diagram of eigenvalues computed by DMD |
图 7为第6段对数映射后的有效特征值选取示意图.横坐标为空间波数λi, 纵坐标为空间放大率λr.因特征值分布关于纵轴对称, 仅展示波数为正的结果.红色方框和蓝色三角分别为总快照数为100和200时对应的特征值.不同段快照数不同, 图 7所示为第6段, 故快照数分别是60和120.黑色方框选中的点为不稳定特征值中距离最小的点.其中距离计算方法如式(2) 所示:
| $ d=\sqrt{{{({{\lambda }_{\text{i},100\_6}}-{{\lambda }_{\text{i},200\_6}})}^{2}}+{{({{\lambda }_{\text{r},100\_6}}-{{\lambda }_{\text{r},200\_6}})}^{2}}} $ | (2) |

|
| 图 7 有效特征值选取示意图 Fig.7 Schematics of selecting effective eigenvalues |
根据1.2节中的有效特征值的选取规则, 选择快照数120对应的特征值为有效特征值, 60快照相当于标定作用.
采用1.2节叙述的方法, 分别对不同总快照数对应的每段有效特征值进行N值的计算, 得到翼型上下表面的N值增长, 如表 1和表 2所示.表中section表示段数, s/c和x/c分别表示每段末的弧长和对应的弦向坐标, N factor表示不同段末的扰动放大N因子.以总快照数多的(200快照)N值发展曲线作为转捩位置的判断依据.这里转捩阀值取9, 分别将超过转捩阀值的位置及对应的转捩阀值用红色加粗来表示.从表中右半部分200快照的对应列可看出上表面N值在约70%弧长处超过阀值, 下表面在约60%弧长处超过阀值.此后为湍流区, 按原理不必再进行DMD分析.
| 下载CSV 表 1 DMD计算的LSC72613翼型上表面N值增长 Tab.1 N factors calculated by DMD for upper surface of LSC72613 airfoil |
| 下载CSV 表 2 DMD计算的LSC72613翼型下表面N值增长 Tab.2 N factors calculated by DMD for lower surface of LSC72613 airfoil |
通过线性插值得到DMD/eN方法的转捩点位置.由于该翼型缺少实验值, 故本文分别采用FLUENT的γ-
| 下载CSV 表 3 不同求解器转捩点位置和升/阻力系数计算结果对比 Tab.3 Comparisons of transition locations and lift/drag coefficients between different solvers |
图 8为以上4种方法的压力分布对比图, 并在图中用不同颜色的直线标出对应方法的转捩点位置.可见压力分布几乎完全重合, 上表面转捩点位置差异很小, 下表面转捩点位置除FLUENT结果略微靠前外, 其余3种方法的结果都很接近.图 9为该翼型的压力云图和流线图, 与图 8上表面压力系数突增的位置对应, 大约在60%弦向处有一道激波.
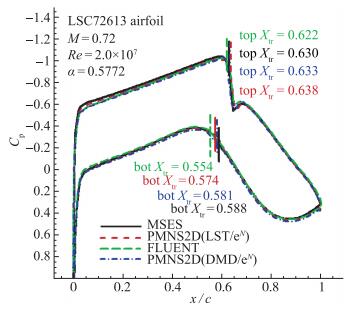
|
| 图 8 不同流动求解器计算的压力分布与转捩位置对比图 Fig.8 Comparisons of pressure distributions and transition location between different flow solvers |

|
| 图 9 LSC72613翼型自由转捩下的计算压力云图和流线图(DMD/eN方法) Fig.9 Pressure contours and streamlines computed by free-transition simulation for LSC72613 airfoil (DMD/eN method) |
分别将表 1和表 2中DMD/eN方法计算得到的总快照数为200的数据, 表示为N值随x/c变化的曲线, 并与LST/eN方法计算得到的N值发展曲线进行对比.上下表面的结果分别如图 10和图 11所示.实线为LST/eN方法得到的不同频率下的N因子增长曲线, 而黑色粗虚线为上述DMD/eN方法计算的N值增长曲线.从图中看出, DMD/eN方法的N值增长曲线很接近LST/eN方法的包络线.虽然个别站位处有些差异, 但大体的增长趋势是一致的, 转捩点位置误差在合理范围内.这也在一定程度上验证了本文发展积分策略的合理性, 是一种符合eN包络线思想的计算方法.

|
| 图 10 LSC72613翼型上表面DMD/eN与LST/eN方法的N值增长对比图 Fig.10 Comparisons of N growth between DMD/eN and LST/eN method on upper surface of LSC72613 airfoil |

|
| 图 11 LSC72613翼型下表面DMD/eN与LST/eN方法的N值增长对比图 Fig.11 Comparisons of N growth between DMD/eN and LST/eN method on lower surface of LSC72613 airfoil |
本文改进的DMD网格线生成方法和N值的积分策略适用于不同攻角的翼型绕流计算.为进一步验证方法的正确性, 选择了不同攻角下转捩位置实验值丰富的NLF0416翼型[30-31]进行数值模拟.计算状态是M=0.1, Re=4×106.转捩后的湍流区域采用SA湍流模型. NLF0416翼型计算网格如图 12所示, 计算网格量为640×240, 第1层网格高度2×10-6c.

|
| 图 12 NLF0416翼型计算网格 Fig.12 Computational grids of NFL0416 airfoil |
下面以攻角α=1°为例, 较为详细地展示计算结果.
与2.1节算例相同, 采用总快照数100和200对翼型表面进行DMD分析, 分别计算出上下表面的N值增长.将推进求解中N值达到阀值及之前段的N值表示为随x方向变化的曲线, 并与LST/eN方法的N值增长曲线进行对比, 如图 13和图 14所示.根据以往的经验, 在利用eN方法进行NLF0416翼型流动的转捩预测时, 阀值N取为6较为合适.由图可见, 上表面DMD/eN方法推进求解得到的N值增长曲线与LST/eN方法的包络线吻合很好, 而下表面DMD/eN方法的N值比LST/eN方法增长要早, 但总体趋势是可比的.
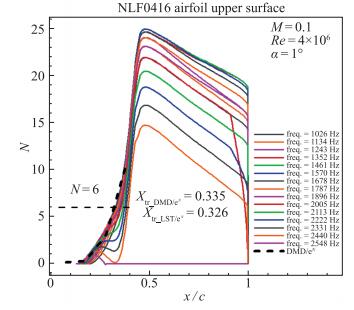
|
| 图 13 NLF0416翼型上表面DMD/eN与LST/eN方法的N值增长对比图(α=1°) Fig.13 Comparisons of N growth between DMD/eN and LST/eN method on upper surface of NLF0416 airfoil |

|
| 图 14 NLF0416翼型下表面DMD/eN与LST/eN方法的N值增长对比图(α=1°) Fig.14 Comparisons of N growth between DMD/eN and LST/eN method on lower surface of NLF0416 airfoil |
表 4为DMD/eN方法与LST/eN方法计算得到的上下表面转捩点位置与实验值的对比.实验测出了翼型表面层流与湍流区的位置, 转捩发生在两者之间.由表 4可知, 上表面DMD/eN方法计算的转捩点位置比LST/eN方法更接近实验值, 但两者都比实验值稍靠前.下表面两者均在层流点附近, 与实验值吻合良好.将DMD/eN方法计算得到的自由转捩的压力分布与全湍流和实验值进行对比, 如图 15所示.蓝色方框是1°攻角下的实验压力分布, 黑色实线和红色虚线分别是自由转捩和全湍流下的压力分布.两者都与实验值吻合较好, 但在翼型上表面前半部分, 由放大图能明显看出, 自由转捩的结果更加接近实验值.
| 下载CSV 表 4 NLF0416翼型上/下表面转捩点位置计算与实验值比较(α=1°) Tab.4 Comparisons of predicted transition location with experimental data on upper/lower surface of NLF0416 airfoil (α=1°) |
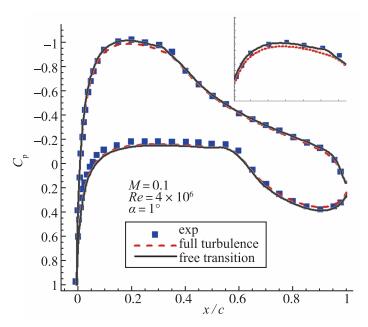
|
| 图 15 NLF0416翼型全湍流及自由转捩计算结果与实验压力分布比较 Fig.15 Comparisons of pressure distributions computed in state of full turbulence and free transition with experimental data for NLF0416 airfoil |
由于层流黏性系数远小于湍流黏性系数, 故这两种流态下翼型表面的摩擦阻力差异很大.图 16为NLF0416翼型全湍流和自由转捩状态下的物面摩擦力系数分布图.其中, 黑色虚线是全湍流模拟的摩阻系数, 蓝色虚线和红色实线是考虑转捩的分别采用LST/eN和DMD/eN方法计算得出的结果.可见, LST/eN和DMD/eN两种方法得到的摩阻系数分布吻合良好.翼型上下表面对应的摩阻系数分别在各自转捩点附近有一个突增, 对应位置在0.33和0.5左右.转捩点之前为层流, 全湍流模拟的Cf远大于自由转捩的结果, 而转捩点之后进入湍流, 两者Cf的值开始逐步接近.

|
| 图 16 NLF0416翼型全湍流与自由转捩表面摩擦力系数对比图 Fig.16 Comparisons of skin friction (Cf) for NLF0416 airfoil between full turbulence and free transition |
表 5中给出了本文方法计算得到的自由转捩的阻力系数和全湍流与实验值的对比.可见, 自由转捩计算的阻力系数比全湍流大幅接近实验值, 进一步说明了本文转捩预测方法对于提高阻力预测精度的意义.
| 下载CSV 表 5 NLF0416翼型计算阻力系数与实验值的比较(α=1°) Tab.5 Comparisons of calculated drag coefficient with experimental value for NLF0416 airfoil |
以上1°攻角的算例较详细地展示了DMD/eN方法对NLF0416翼型的转捩预测结果, 验证了本文方法的正确性.下面将对-6~6°中多个攻角状态的NLF0416翼型绕流进行转捩点预测, 并与实验值、文献[30]及LST/eN方法的计算结果进行对比.其中, 文献[30]采用了经验关系式方法耦合FLUENT求解器进行转捩预测.
表 6为若干攻角下的NLF0416翼型上下表面的转捩点计算结果对比.为了方便比较, 表中只列出了上表面中有转捩点实验值的攻角状态.同理, 表 7展示了下表面的结果.可见, 在大部分攻角下, DMD/eN的计算结果都与文献[30]较为接近, 且都在实验转捩范围内, 是合理的结果.个别攻角的计算结果与实验值略有偏差, 但误差也在合理范围内.
| 下载CSV 表 6 NLF0416翼型上表面不同攻角转捩位置计算结果与实验值的比较 Tab.6 Comparisons of calculated transition locations with experimental data on upper surface of NLF0416 airfoil for different angles of attack |
| 下载CSV 表 7 NLF0416翼型下表面不同攻角转捩位置计算结果与实验值的比较 Tab.7 Comparisons of calculated transition locations with experimental data on lower surface of NLF0416 airfoil for different angles of attack |
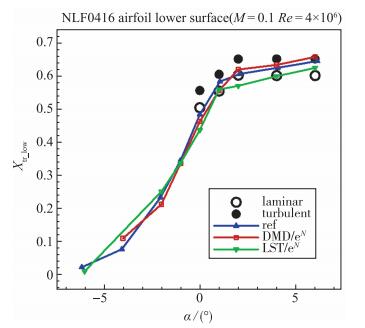
为了更清楚地表现转捩点位置, 分别做出了NLF0416翼型上下表面采用以上3种方法计算得到的转捩点随攻角的变化曲线, 如图 17, 18所示.其中, 黑色空心点和实心点分别为实验测得的层流区和湍流区位置; 蓝色、红色、绿色线分别代表文献[30]、DMD/eN方法和LST/eN方法计算得到的转捩点位置所连成的曲线; Xtr_up和Xtr_low分别代表翼型上下表面的转捩点位置.由图 17可见, 随着攻角的增大, 上表面转捩点逐步向翼型前缘移动. DMD/eN的计算结果基本位于层流和湍流点之间, 且和文献结果符合较好, 而LST/eN方法计算的结果比实验值略靠前.由图 18可知, 不同攻角下3种方法的转捩点计算结果均符合较好, 且变化趋势一致, 进一步验证了本文方法的正确性.可见随着攻角的增大, 下表面转捩点向翼型后缘移动.这是由于随着攻角的增加, 下表面作为压力面, 顺压梯度增加, 更易保持层流, 故转捩点后移.上表面的规律与之相反, 但原理是类似的.

|
| 图 17 NLF0416翼型上表面转捩点位置随攻角的变化 Fig.17 Variations of transition locations along with angles of attack on upper surface of NLF0416 airfoil |
|
| 图 18 NLF0416翼型下表面转捩点位置随攻角的变化 Fig.18 Variations of transition locations along with angles of attack on lower surface of NLF0416 airfoil |
综上, 通过LSC72613翼型和NLF0416翼型不同攻角下的转捩预测算例, 验证了本文改进的DMD/eN方法用于不同攻角下翼型定常绕流转捩预测的正确性; 同时, 将DMD/eN方法的N值增长曲线与LST/eN方法进行对比, 发现与其包络线吻合良好, 进一步说明了改进的N值积分策略的合理性和有效性.
3 结论本文在原有DMD/eN方法的基础上, 改进了DMD网格线生成方法和包络线扰动放大因子N的积分策略.将该方法用于翼型定常绕流的转捩计算, 研究结论如下:
(1) 改进的以驻点为起点沿弧长等距划分的DMD网格线生成方法, 能够满足空间DMD对网格等间距的要求.且以该网格线为基础进行后续的稳定性分析更符合eN方法原理.
(2) 对于新发展的DMD与eN方法结合的N值积分策略, 理论上符合eN包络线思想.算例中DMD/eN方法的N值发展曲线和LST/eN方法的包络线吻合较好, 进一步验证了改进的DMD/eN方法与包络线方法的可比性.
(3) 改进的DMD/eN方法采用从驻点开始, 沿流向推进求解的方式.该方法适用于不同攻角下翼型绕流的转捩点预测.
(4) 在保证DMD分析精度的情况下, 选取合适的快照数(不宜过多), 取两种快照数对应的不稳定特征值中重叠性最好的作为有效特征值, 是一种有效的特征值选取方式.
致谢: 感谢刘方良、韩莉等对该方法研究工作的贡献, 也感谢许建华老师在科研中给与的帮助.| [1] |
符松, 王亮. 湍流转捩模式研究进展[J].
力学进展, 2007, 37(3): 409-416. Fu S, Wang L. Progress in turbulence/transition model-ling[J]. Advances in Mechanics, 2007, 37(3): 409-416. DOI:10.6052/1000-0992-2007-3-J2006-159 |
| [2] |
周恒. 关于转捩和湍流的研究[C]. 2003空气动力学前沿研究论文集, 北京: 中国空气动力学会, 2003: 87-93.
Zhou H. Studies on transition and turbulence[C]. 2003 Advanced Research Papers on Aerodynamics, Beijing:Aerodynamic Society of China, 2003:87-93(in Chinese). |
| [3] | Brazell M J, Brazell M J, Stoellinger M K, et al. Using LES in a discontinuous Galerkin method with constant and dynamic SGS models[R]. AIAA 2015-0060, 2015. |
| [4] | Schlatter S, Örlü R. Assessment of direct numerical simulation data of turbulent boundary layers[J]. Journal of Fluid Mechanics, 2010, 659(4): 116-126. |
| [5] | Fasel H F, Meitz H L, Bachman C R. DNS and LES for investigating transition and transition control[R]. AIAA 1997-1820, 1997. |
| [6] | Menter F R, Langtry R B, Likki S R, et al. A correlation-based transition model using local variables-part Ⅰ:model formulation[J]. Journal of Turbomachinery, 2006, 128(3): 413-422. DOI:10.1115/1.2184352 |
| [7] |
陈奕, 高正红. Gamma-Theta转捩模型在绕翼型流动问题中的应用[J].
空气动力学学报, 2009, 27(4): 411-418. Chen Y, Gao Z H. Application of Gamma-Theta transition model to flows around airfoils[J]. Acta Aerodynamica Sinica, 2009, 27(4): 411-418. |
| [8] | Watanabe Y, Misaka T, Obayashi S, et al. Application of cross-flow transition criteria to local correlation-based transition model[R]. AIAA 2009-1145, 2009. |
| [9] | Seyfert C, Krumbein A. Correlation-based transition transport modeling for three-dimensional aerodynamic configurations[R]. AIAA 2012-0448, 2012. |
| [10] | Grabe C, Krumbein A. Extension of the γ-Reθt model for prediction of crossflow transition[R]. AIAA 2014-1269, 2014. |
| [11] |
徐家宽, 白俊强, 乔磊, 等. 横流不稳定性转捩预测模型[J].
航空学报, 2015, 36(6): 1814-1822. Xu J K, Bai J Q, Qiao L, et al. Transition model for predicting crossflow instabilities[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1814-1822. |
| [12] | Wang L, Fu S. Modelling flow transition in a hypersonic boundary layer with Reynolds-averaged Navier-Stokesapproach[J]. Science in China Series G:Physics, Mechanics and Astronomy, 2009, 52(5): 768-774. DOI:10.1007/s11433-009-0047-8 |
| [13] | Fu S, Wang L. RANS modeling of high-speed aerodynamic flow transition with consideration of stability theory[J]. Progress in Aerospace Sciences, 2013, 58: 36-59. DOI:10.1016/j.paerosci.2012.08.004 |
| [14] | Stock H W, Haase W. Navier-Stokes airfoil computations with eN transition prediction including transitional flow regions[J]. AIAA Journal, 2000, 38(11): 2059-2066. DOI:10.2514/2.893 |
| [15] | Krumbein A. Automatic transition prediction and application to 3D wing configurations[R]. AIAA 2006-914, 2006. |
| [16] |
张坤, 宋文萍. NS方程计算中耦合转捩自动判断的阻力精确计算方法初探[J].
空气动力学学报, 2009, 27(4): 400-404. Zhang K, Song W P. Accurate drag calculation by coupling automatic prediction of transition point to the Navier-Stokes method[J]. Acta Aerodynamica Sinica, 2009, 27(4): 400-404. |
| [17] |
张雯, 刘沛清, 郭昊, 等. 湍流转捩工程预报方法研究进展综述[J].
实验流体力学, 2014, 28(6): 1-12. Zhang W, Liu P Q, Guo H, et al. Review of transition prediction methods[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(6): 1-12. |
| [18] | Herbert T. Parabolized stability equations[J]. Annual Review of Fluid Mechanics, 1997, 29(1): 245-283. DOI:10.1146/annurev.fluid.29.1.245 |
| [19] | Bertolotti F P, Herbert T. Analysis of the linear stability of compressible boundary layers using the PSE[J]. Theoretical and Computational Fluid Dynamics, 1991, 3(2): 117-124. DOI:10.1007/BF00271620 |
| [20] | Noack B R, Morzynski M, Tadmor G. Reduced-order modelling for flow control[M]. Belin:Springer Science & Business Media, 2011:77-110. |
| [21] | Chatterjee A. An introduction to the proper orthogonal decomposition[J]. Current Science, 2000, 78(7): 808-817. |
| [22] | Schmid P J. Dynamic mode decomposition of numerical and experimental data[J]. Journal of Fluid Mechanics, 2010, 656: 5-28. DOI:10.1017/S0022112010001217 |
| [23] | Schmid P J, Li L, Juniper M P, et al. Applications of the dynamic mode decomposition[J]. Theoretical and Computational Fluid Dynamics, 2011, 25(1): 249-259. |
| [24] | Wan Z H, Zhou L, Wang B F, et al. Dynamic mode decomposition of forced spatially developed transitional jets[J]. European Journal of Mechanics B/Fluids, 2015, 51: 16-26. DOI:10.1016/j.euromechflu.2014.12.001 |
| [25] | Mohan A T, Visbal M R, Gaitonde D V. Model reduction and analysis of deep dynamic stall on a plunging airfoil using dynamic mode decomposition[R]. AIAA 2015-1058, 2015. |
| [26] |
刘方良. 低Reynolds数翼型流动转捩判断与优化设计方法[D]. 西安: 西北工业大学, 2014: 33-67.
Liu F L. Transition prediction and optimization design method for low-Reynolds-number airfoil[D]. Xi'an:Northwestern Polytechnical University, 2014:33-67(in Chinese). |
| [27] |
韩莉. 翼型非定常流动的转捩预测方法研究[D]. 西安: 西北工业大学, 2015: 21-64.
Han L. Transition prediction method in unsteady airfoil flows[D]. Xi'an:Northwestern Polytechnical University, 2015:21-64. (in Chinese) |
| [28] |
韩忠华, 王绍楠, 韩莉, 等. 一种基于动模态分解的翼型流动转捩预测新方法[J].
航空学报, 2017, 38(1): 30-46. Han Z H, Wang S N, Han L, et al. A novel method for automatic transition prediction of flows over airfoils based on dynamic mode decomposition[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 30-46. |
| [29] | Han Z H, Chen J, Zhu Z, et al. Aerodynamic design of transonic natural-laminar-flow(NLF) wing via surrogate-based global optimization[R]. AIAA 2016-2041, 2016. |
| [30] | Basha W. Accurate drag prediction for transitional external flow over airfoils[D]. Canada: Concordia University, 2006: 56-85. |
| [31] | Somers D M. Design and experimental results for a natural-laminar-flow airfoil for general aviation applications[R]. NASA-TP-1861, 1981. |



