2. 中国空气动力研究与发展中心计算空气动力研究所,四川绵阳 621000;
3. 中国空气动力研究与发展中心超高速空气动力研究所,四川绵阳 621000
2. Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China;
3. Hypervelocity Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China
在计算流体力学应用中经常会遇到包含运动边界的流动问题, 例如复杂多体分离、飞行器机动飞行、直升机旋翼运动、风力机叶片旋转、鸟类/昆虫/鱼类等生物体柔性运动等.针对此类问题开展数值模拟, 首先需要解决运动边界条件下的动态网格生成问题.此外, 由于此类包含运动边界的流动问题往往是一个多学科耦合问题, 因此还要发展和动态网格技术相匹配的非定常流动数值模拟方法以及多学科耦合求解算法, 以满足工程应用的需求.
常见的处理运动边界问题的方法有动态重叠网格技术[1]、变形网格技术[2]以及内置边界方法[3]等.重叠网格是由若干个子网格块组合形成覆盖整个计算域的网格, 子网格块之间通过网格装配技术建立插值关系.通过子网格块的刚性运动, 可以非常方便地模拟大位移、相对运动等问题.变形网格技术通过将边界网格的运动传递到内部网格点以生成每个时刻的动态网格, 其优点是可以保持网格拓扑结构的一致性, 且适用于柔性边界问题.内置边界方法通过在控制方程中引入模拟物理边界影响的源项, 降低了网格生成难度, 且物体运动过程中不需要对网格进行特殊处理, 但是其在模拟高Reynolds数可压缩流问题时精度仍有待提高.
随着CFD所模拟的工程问题越来越复杂, 多学科耦合、精细化数值模拟等都对数值计算方法尤其是网格生成技术提出了更高要求.为了更好地解决柔性变形、相对运动、大位移运动相互耦合的复杂工程问题, 重叠网格技术和变形网格技术的结合是一种较好的技术途径.此外, 为了满足工程应用对精细化数值模拟的要求, 往往需要采用较大规模的计算网格, 而串行的重叠网格装配技术以及变形网格技术显然难以满足工程应用对计算效率的要求, 需要发展并行化的动网格生成技术.
针对以上问题, 作者发展了一种并行环境下重叠和变形耦合的动态混合网格技术, 该技术采用了基于网格分区的分布式并行方案, 每一个网格分区根据其所依赖的物理边界运动信息进行变形, 然后通过并行化重叠网格隐式装配技术进行挖洞和宿主单元查找.其中网格变形采用了基于径向基函数(radial basis function, RBF)的插值方法, 为提高网格变形效率, 采取了并行化的参考点选择算法以及插值算法.在该动态混合网格技术的基础上, 发展了流动/运动/控制一体化数值模拟方法, 进一步改进了作者课题组之前发展的具有完全自主知识产权的多学科耦合数值模拟平台——HyperFLOW.本文将对这些工作进行简要介绍, 并展示一些典型的应用算例.
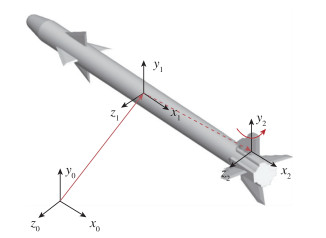
1 动态混合网格生成技术 1.1 并行环境下重叠/变形网格技术的整体思路一般而言, 物体的复杂运动可以分解为体轴系内的柔性变形和整体的刚性运动.对于某些附着在其他物体上的部件(如飞行器的尾舵), 除了自身的运动之外, 还要随着飞行器进行牵连运动, 因此可采用3组6自由度参数定义其刚性运动, 即:部件自身的自由度, 部件所附着的物体的自由度, 部件在其所附着的物体中安装的自由度. 图 1给出了物体刚性运动定义的示意图, 其中x0/y0/z0为惯性坐标系(简称C0), x1/y1/z1为飞行器质心坐标系(简称C1), x2/y2/z2为尾舵安装位置的坐标系(简称C2), 则尾舵的运动由其旋转角度、C2相对于C1的6自由度参数、C1相对于C0的6自由度参数共同决定.
|
| 图 1 坐标系以及物体刚体运动的定义 Fig.1 Definition of the reference frame and the rigid movement of body |
分别采用网格变形技术和动态重叠网格技术处理物体的柔性及刚性运动.首先在生成计算网格时需要围绕每一个物体或者部件生成独立的贴体子网格块, 并采用重叠网格技术将各个子网格块进行组装.子网格块可以采用三棱柱、四面体、金字塔、六边形等多种形式的混合单元(二维情况下为三角形、四边形、多面体等单元); 当物体发生变形和刚性运动之后, 首先每个子网格块根据其所依赖的物面点的运动信息, 在其体轴系内实现内部网格点的变形; 变形之后的子网格块再跟随物体进行刚性运动, 随后采用重叠网格技术将各个子网格块进行重新组装.
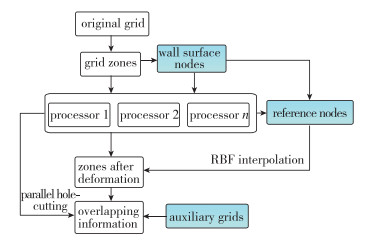
动态混合网格生成流程如图 2所示, 整个过程均在并行环境下进行, 采用了基于网格分区的分布式并行策略.在读入初始计算网格之后, 分别对围绕每个物体的子网格块进行分区并均匀分布至各个进程, 同时提取其中各个物体或部件的物面网格信息并发送至所有进程.该全局的物面网格信息有两个用途: (1)跟随物体进行变形; (2)计算空间网格点或单元的最近壁面距离.动态网格生成过程中, 每个进程仅对其所负责的若干网格分区进行变形和刚性运动的计算, 且采用相同的物面网格以及物面参考点以保证网格分区边界的匹配.隐式重叠网格装配过程中, 需要通过各个进程之间的通讯来确定查询以及逻辑判断结果.
|
| 图 2 动态混合网格生成的整体思路 Fig.2 Sketch map for the dynamic mesh generator |
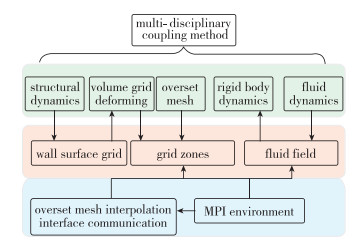
算法的具体实现过程中, 如何建立耦合动态混合网格生成的整体程序框架, 如何保证各个功能模块的封装性、可扩展性是一个非常重要的内容.本文采用了C++面向对象的思想开发计算程序, 网格数据、流场数据是程序的核心, 依据这些数据结构建立MPI底层支撑环境, 并围绕这些数据、底层支撑环境开发具有高度封装性的功能模块, 从而保证各个模块的可扩展、可移植特性, 也提高了代码的容错能力并降低了维护成本. 图 3给出了程序的架构示意图, 各个功能模块之间须根据多学科耦合顶层计算流程的需要建立必要的信息传递接口.
|
| 图 3 程序框架示意图 Fig.3 Framework of the software platform |
重叠网格技术包括挖洞、宿主单元搜索以及流场插值3个方面的内容, 其中挖洞和宿主单元搜索称为重叠网格装配.根据挖洞过程的不同可以分为显式装配[6-9]和隐式装配[10-15]两类.显式装配过程首先要将落在物体内部的点或单元进行标记, 形成初始洞边界(判断点是否在物体内部的方法有矢量判别法[4]、射线求交法[5]、洞映射方法[6]、目标x射线法[7]等.), 然后通过一些优化算法将洞边界进行优化(例如割补法[8-9])并确定出插值单元, 最后查找插值单元的宿主单元.
隐式装配技术须查找所有点或者单元的宿主单元, 通过对比单元的质量确定其属性, 挖洞过程则隐含在查询与判断的过程之中. Lee等[10]在2003提出了隐式装配的概念, 并将单元的尺度作为是否是活跃单元的判则.其实早在1999年Nakahashi等[11]针对非结构重叠网格的方法中就已经采用了隐式装配技术, 其采用节点的最近壁面距离作为活跃点的判则. Togashi等[12]进一步将基于最近壁面距离的该方法推广应用于复杂多体分离问题的数值模拟. Loehner等[13],Luo等[14]采用单元的尺度和壁面距离的组合量作为单元属性的判断标准, 使插值单元和贡献单元的大小匹配, 有助于提高插值稳定性并减少插值误差.非结构重叠网格隐式装配软件PUNDIT[15]亦采用了隐式装配技术.
本文的基于网格分区的并行化装配技术分为两步执行. Step1:通过隐式装配技术划分点的属性; Step2:判断插值单元, 并搜索其宿主单元.
Step1中需要搜索所有网格点的宿主单元, 可以采用两种并行查询策略:
策略1—“整体-局部”查询:搜集所有分区内的网格点, 形成整体的网格点集并发送至所有进程, 然后在每个分区内搜索点集的宿主单元, 并通过MPI规约操作确定最终的查询结果;
策略2—辅助网格查询:围绕各个物体或部件生成稀疏的辅助网格, 分别在各套辅助网格内进行宿主单元搜索, 并通过插值得到网格分区中计算网格点的质量(以最小壁面距离作为质量判则).
在点属性划分过程中, 还采取了一种并行化的阵面推进技术, 能够快速高效地确定出联通的活跃区域.
Step2的搜索过程采用与Step1中策略1类似的方式:首先搜集每个网格分区内的插值单元以形成整体的插值单元集合, 然后在各个网格分区内进行宿主单元查找.
对于多套网格相互嵌套的问题, 可能存在多个宿主单元, 此时需要根据宿主单元的属性以及其最小壁面距离确定唯一的一个.本文将查找的宿主单元分为3个等级:第1等级的为活跃单元, 标记为1;第2等级宿主单元为插值单元, 标记为-1;第3等级的宿主单元为非活跃单元, 标记为-2.优先选择等级较高的宿主单元, 如果存在多个等级相同的, 则进一步比较其最小壁面距离, 选择距离较小的作为最终结果.并行环境下通过如下的MPI通讯流程实现进程之间的逻辑判断:
(1) 通过MPI全局规约命令确定宿主单元的最高等级;
(2) 各个进程内, 如果宿主单元等级小于最高等级, 舍去该宿主单元;
(3) 通过MPI全局规约命令确定宿主单元的最小壁面距离;
(4) 各个进程内, 如果宿主单元的最小壁面距离大于该值, 则舍去该宿主单元;
(5) 将剩下的唯一的宿主单元广播至所有进程.
1.3 并行化网格变形技术常见的网格变形方法有超限插值(transfinite interpolation, TFI)方法[2]、弹簧松弛法[18-19]、Delaunay背景网格映射法[20]、RBF插值法[21-22]等, 这些方法各具特色, 并都已经得到广泛应用.在之前的研究工作中, 作者所在的研究团队发展了弹簧松弛法和Delaunay背景网格映射相结合的网格变形方法[23-25], 并结合了局部网格重构技术, 从而可以模拟大变形、大位移等问题, 在多体相对运动问题中也得到了大量应用.在这些工作的基础上, 本文进一步集成了并行化RBF插值方法.
当物面网格量较大时, RBF方法中的插值矩阵会变得十分庞大, 导致空间网格点的插值计算量急剧增加.为了提高RBF插值效率, 参照文献[22]的做法, 选用有限的物面点作为参考点, 从而可以减少矩阵的规模, 提高空间网格点的插值效率.由于RBF插值过程不需要网格的拓扑关系, 因此其并行计算比较容易实现.其包括两部分的并行: (1)物面点选择过程的并行; (2)插值过程的并行.
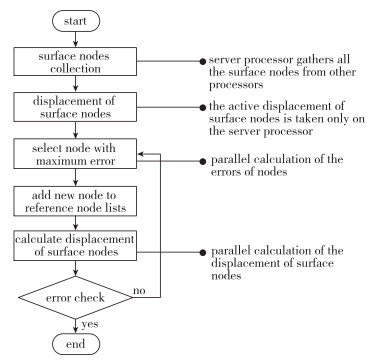
物面参考点的选择采用贪婪算法, 以物面点位移的误差作为准则.首先需要将物面点集平均分配到各个进程.在循环判断的过程中, 每个进程只对其所负责的物面点进行插值运算和比较, 并求出其中的最大误差点, 然后通过MPI通讯确定出所有进程中的误差最大点并加入参考点集, 主进程根据新的参考点集执行插值矩阵的更新以及求逆操作, 并将其广播至其他所有进程, 算法的具体流程如图 4所示.空间点的插值直接基于网格分区进行, 每个进程只针对其所负责的网格分区进行插值运算, 每一个进程中存储相同的插值矩阵, 这样可以保证分区边界上点的匹配.
|
| 图 4 RBF变形网格法中并行化物面参考点选择方法 Fig.4 Reference node selecting method in parallel environment for RBF moving grid generation |
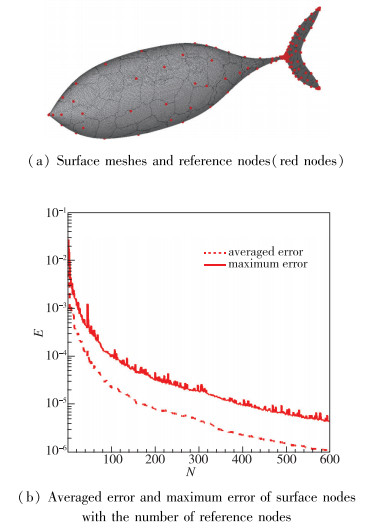
图 5及表 1给出了并行化RBF方法的测试算例.模型为简化的三维金枪鱼外形, 采用了三棱柱、四面体形式的混合网格, 其中物面网格点数9.8×104, 空间网格单元数7.19×106.采用单进程, 选择600个物面参考点耗时约16.2 s, 空间网格变形耗时约30.2 s.采用64进程并行, 物面参考点选择耗时约6.0 s, 空间网格变形耗时约1.5 s.并行效率较低的原因在于:物面参考点选择阶段, 矩阵求逆过程没有并行化; 空间点位移插值阶段, 插值系数的计算过程没有并行化.这两部分计算均由主进程负责, 然后将计算结果发送给其他进程.
|
| 图 5 物面参考点选择测试算例 Fig.5 Test case for reference node selection |
| 下载CSV 表 1 并行RBF插值效率测试 Tab.1 Test for parallel RBF method |
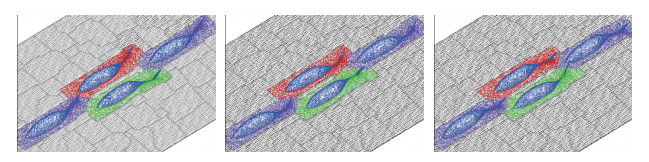
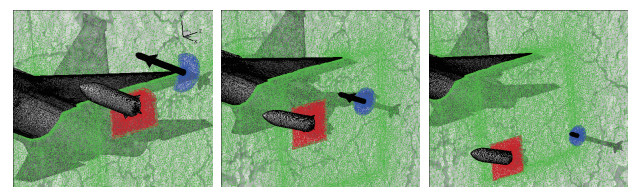
本节展示了采用上述动态混合网格生成技术得到的一些典型应用实例. 图 6所示为三维情况下4条鱼群游过程的动态混合网格, 网格单元由四面体、三棱柱、金字塔等组成, 总数为1.05×107.物面为三角形网格, 网格点数8×104, 选取其中1 200个作为RBF参考点.采用64进程并行, 参考点选择耗时约4.7 s, 执行一次空间网格变形耗时约3.2 s, 重叠网格装配耗时约10 s. 图 7所示为飞机外挂物投放过程的重叠网格, 载机网格单元数2.5×107, 两个外挂物网格单元数约1.2×107.采用256进程并行执行重叠网格装配耗时约7 s.图中给出了分离过程中3个典型时刻的空间网格切面. 图 8给出了机翼外挂物分离的超大规模重叠网格, 网格单元总数为2.88×109, 采用了12 288进程并行计算.此算例采用了并行化的辅助网格查询技术, 结合分布式并行计算, 因此每个进程占用内存较少.
|
| 图 6 三维情况下鱼群游动过程的动态混合网格 Fig.6 Dynamic meshes for the schooling of four fishes in 3D case |
|
| 图 7 战斗机分离投放过程的动态混合网格 Fig.7 Dynamic meshes during the separation process between two missiles and aircraft |

|
| 图 8 超大规模重叠网格装配测试 Fig.8 Hole-cutting for large scale overset mesh |
针对飞行器机动飞行、生物体自主运动等流动、运动和控制等多学科耦合问题, 作者课题组已经发展了流动/运动/控制耦合的一体化数值方法, 并研发了虚拟飞行模拟平台——HyperFLOW[26-28].本文将上述重叠/变形动态混合网格生成技术进一步集成于HyperFLOW平台之中, 使之能够适应于同时存在柔性变形和相对运动的复杂动边界问题.
HyperFLOW平台[26-28]耦合了非定常RANS方程求解、刚体动力学求解和飞行控制律等多学科计算模块, 并有机集成了动态混合网格生成模块, 在统一的理论框架下建立了流动/运动/控制耦合的一体化数值模拟算法.
在运动网格上进行非定常RANS方程计算, 离散后的方程中含有网格几何量对时间的导数项, 为避免由于网格运动引入的额外误差, 几何守恒律(geometric conservation law, GCL)应该和质量守恒、动量守恒、能量守恒一样在“数值”上得到满足.目前满足几何守恒律的算法很多, 作者通过理论分析将其归纳为两类[29]:第1类方法通过在控制方程中引入源项, 从而在整体上消除几何守恒误差.第2类方法通过限制面元的速度、法向、面积等求解方法, 以满足面元扫过体积的守恒.通过截断误差分析以及数值测试, 我们对各种满足几何守恒律的算法进行了分析[29].结果表明:第1类格式在整体上消除了几何守恒律误差, 虽然能够保持均匀流的守恒, 但是在非均匀流情况下添加的源项不能够和几何守恒律误差相互抵消, 会残留一部分误差, 而这部分误差可能会影响数值计算的精度; 第2类格式在理论上更为严格, 能够保证每个面元上体积通量的守恒, 因此对于均匀流或者非均匀流都能够严格满足几何守恒律.详细内容请参见文献[29].
根据耦合计算策略的不同, 耦合计算方法一般可分为全耦合、松耦合和紧耦合3种.全耦合即将各个学科的控制方程视为一个统一、完整的系统进行求解.由于流动控制方程、运动/动力学方程等在性质上存在较大差异, 因此全耦合格式比较难以实现.这里采用解耦方法进行耦合问题的求解, 为了解决不同耦合程度的气动/运动耦合问题, 我们建立了统一的框架, 可通过参数选取实现不同时间精度的松耦合和紧耦合计算[30].我们选用圆柱自激震荡算例对松耦合、紧耦合算法进行了考核, 与文献结果进行了对比, 并对紧耦合、松耦合的适用范围进行了测试.结果表明, 当物体密度远大于周围流体密度时, 采用松耦合或者紧耦合均能够得到较好的计算结果; 但是当物体密度接近或者小于周围流体密度时, 采用松耦合的方式将难以得到收敛的计算结果, 此时采用紧耦合算法是比较合适的选择.最后我们通过一维稳定性分析对该结论进行了验证[30].在此基础上, 进一步耦合了飞行控制律, 实现了“气动/运动/控制”的一体化数值模拟.
在本文中, 我们进一步将基于动态重叠网格的非定常RANS方程求解方法集成于HyperFLOW平台.其中涉及到第1节中介绍的重叠网格并行隐式装配, 以及重叠区的物理量插值.我们将重叠边界视为一种特殊的网格块间交界面信息, 从而很容易在并行分区环境下, 实现重叠区的信息交换.关于重叠插值算法, 我们目前仍采用普遍采用的双线性(2D)或三线性(3D)插值方法.具体的实现过程这里不再详述.
3 一体化算法应用实例本节给出几个一体化算法的应用实例.
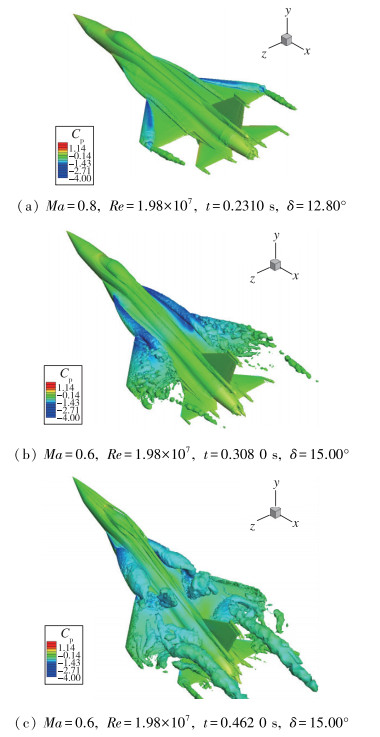
第1个算例为战斗机纵向机动开环控制过程的模拟.通过给定水平尾舵的舵偏规律, 战斗机在气动力作用下其俯仰角逐渐增大并进入俯仰震荡状态.为了模拟该问题, 我们采用非结构重叠网格分别离散机身(含主翼和垂直尾翼)和水平尾舵.物面附近采用各向异性三棱柱网格, 而远场采用各向同性的四面体网格.机身网格随体运动, 水平尾舵根据控制律进行偏转, 通过动态重叠与机身网格进行信息交换. 图 9所示为其纵向机动过程中的典型数值模拟结果(压力云图以及空间的Q等值面).
|
| 图 9 战斗机单自由度纵向机动开环控制过程数值模拟结果(物面压力云图及Q-等值面) Fig.9 Numerical results for the pitching motion of an aircraft with open-loop control(surface pressure contour and Q-isosurface) |
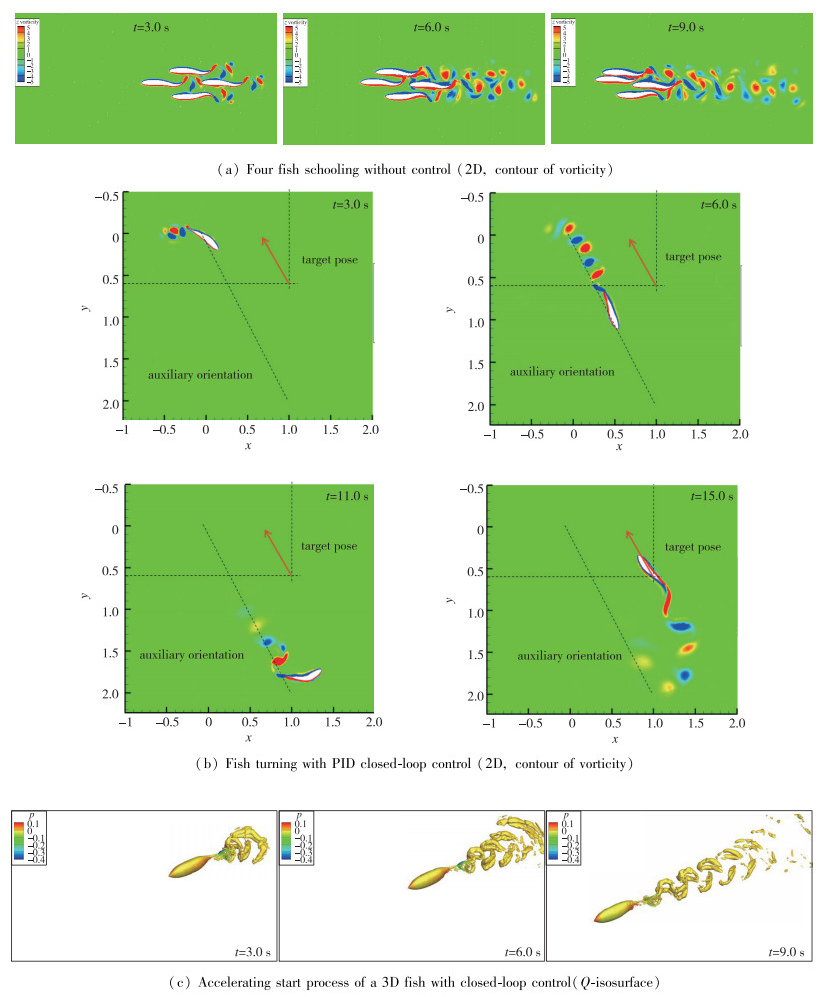
图 10所示为一体化算法在生物外流流体力学方面的典型应用.首先,模拟了二维情况下, 在未考虑控制时4条鱼的自主群游起动过程(见图 10(a)). 4条鱼排成菱形阵形从静止流场中加速游动.鱼体的尾涡之间发生了非常剧烈的相互干扰, 其中后鱼的游速大于前鱼, 说明其受到了有益的流向干扰.
|
| 图 10 一体化算法在生物外流流体力学方面的应用 Fig.10 Applications of HyperFLOW for bio-fluid simulations |
其次, 我们耦合简单的PID控制律, 对二维情况下单个鱼体的转向过程进行了模拟(见图 10(b)).数值模拟结果表明, 建立的控制律能够较好地实现控制目标, 鱼顺利完成了连续转弯及方向控制.
最后, 我们对三维鱼体自主游动的加速过程进行了模拟. 图 10(c)所示为鱼加速起动过程中的流场结构, 起动过程中考虑了尾鳍的闭环控制, 其根据游速适时调节尾鳍的偏转幅度以及摆动频率, 以达到更好的加速效果.
需要指出的是, 以上应用实例仅是初步计算结果, 更为详细的数值模拟及流动结构分析仍在进行之中.因此, 这里我们给出的结果仅为典型时刻的流场, 关于机动过程中气动(水动)力的变化、流场的演化、闭环控制效果的评估等, 我们将在后续的工作中陆续发表.
4 结论本文介绍了作者在重叠/变形耦合动态混合网格生成技术及流动/运动/控制耦合一体化算法方面的研究工作.我们利用面向对象模块化软件设计方法, 初步建立了适用于复杂动边界问题的一体化数值模拟软件平台.典型飞行器俯仰机动过程和鱼体自主游动的数值模拟结果表明, 我们发展的动态混合网格生成技术及一体化数值模拟平台对于复杂动边界问题具有良好的适应性, 展现了广阔的应用前景.
下一步工作中需要在如下几个方面加强研究: (1)自适应网格技术的集成.通过自适应网格和重叠、变形网格技术的结合, 能够进一步提高数值模拟过程的自动化程度和数值模拟效果; (2)DES数值模拟技术的研究与集成, 主要目的是为了提高飞行器在大迎角情况下复杂分离流动的数值模拟精度; (3)多学科耦合模拟软件架构深化研究.我们将采用基于事件驱动的设计思路, 进一步增强软件的模块化、封装性和可扩展性.通过底层网格数据、流场数据的集中管理, 实现各种数值格式在空间上的混合运算, 以进一步提高数值模拟效果; (4)结构动力学模块研制与集成.在飞行器机动飞行过程中, 结构载荷更大, 有可能导致结构的大变形, 进而导致气动力的巨大变化.为了准确模拟机动飞行过程, 必须考虑结构变形带来的影响.
致谢 感谢国家重点研发计划(2016YFB0200701)以及国家自然科学基金(11532016, 11672324)对本文工作的支持.| [1] |
Steger J L, Dougherty F C, Benek J A. A chimera grid scheme[C]. Presented at Applied Mechanics, Bioengineering, and Fluids Engineering Conference, June 20-22, 1983, Houston: American Society of Mechanical Engineers.
|
| [2] |
Nakamichi J. Calculations of unsteady Navier-Stokes equations around an oscillating 3D wing using moving grid system[R]. AIAA 1987-1158, 1987.
|
| [3] |
Kim D, Choi H. Immersed boundary method for flow around an arbitrarily moving body[J]. Journal of Computational Physics, 2006, 212(2): 662-680. DOI:10.1016/j.jcp.2005.07.010 |
| [4] |
Benek J A, Steger J L, Dougherty F A. A flexible grid embedding technique with application to the Euler equa-tions[R]. AIAA 1983-1944, 1983.
|
| [5] |
LaBozzetta W F, Gatzke T D, Ellison S, et al. MACGS-towards the complete grid generation system[R]. AIAA 1994-1923, 1994.
|
| [6] |
Chiu I T, Meakin R. On automating domain connectivity for overset grids[R]. AIAA 1995-0854, 1995.
|
| [7] |
Meakin R L. Object X-rays for cutting holes in composite overset structured grid[R]. AIAA 2001-2537, 2001.
|
| [8] |
Cho K W, Kwon J H, Lee S. Development of a fully systemized chimera methodology for steady/unsteady problems[J]. Journal of Aircraft, 1999, 36(6): 973-980. DOI:10.2514/2.2538 |
| [9] |
李亭鹤, 阎超, 李跃军. 重叠网格技术中割补法的研究与改进[J]. 北京航空航天大学学报, 2005, 31(4): 402-406. Li T H, Yan C, Li Y J. Investigation and enhancement of cut-paste algorithm in overlapping grid[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(4): 402-406. DOI:10.3969/j.issn.1001-5965.2005.04.007 (in Chinese) |
| [10] |
Lee Y L, Baeder J D. Implicit hole cutting-a new approach to overset grid connectivity[R]. AIAA 2003-4128, 2003.
|
| [11] |
Nakahashi K, Togashi F, Sharov D. An intergrid-boundary definition method for overset unstructured grid approach[R]. AIAA 1999-3304, 1999.
|
| [12] |
Togashi F, Ito Y, Nakahashi K, et al. Overset unstructured grids method for viscous flow computations[J]. AIAA Journal, 2006, 44(7): 1617-1623. DOI:10.2514/1.4292 |
| [13] |
Loehner R, Sharov D, Luo H, et al. Overlapping unstructured grids[R]. AIAA 2001-0439, 2001.
|
| [14] |
Luo H, Sharov D, Baum J, et al. An overlapping unstructured grid method for viscous flows[R]. AIAA 2001-2603, 2001.
|
| [15] |
Roget B, Sitaraman J. Robust and efficient overset grid assembly for partitioned unstructured meshes[J]. Journal of Computational Physics, 2014, 260: 1-24. DOI:10.1016/j.jcp.2013.12.021 |
| [16] |
常兴华, 马戎, 张来平. 并行化非结构重叠网格隐式装配技术[J]. 航空学报, 2018, 39(6): 121780. Chang X H, Ma R, Zhang L P. Parallel implicit hole-cutting method for unstructured overset grid[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(6): 121780. (in Chinese) |
| [17] |
Chang X H, Ma R, Wang N H, et al. Parallel implicit hole-cutting method for unstructured Chimera Grid[C]. 10th International Conference on Computational Fluid Dynamics (ICCFD10), 2018, Barcelona, Spain.
|
| [18] |
Blom F J. Considerations on the spring analogy[J]. International Journal of Numerical Methods in Fluids, 2000, 32(6): 647-668. DOI:10.1002/(SICI)1097-0363(20000330)32:6<647::AID-FLD979>3.0.CO;2-K |
| [19] |
Batina J T. Unsteady Euler airfoil solutions using unstructured dynamic meshes[J]. AIAA Journal, 1990, 28(8): 1381-1388. DOI:10.2514/3.25229 |
| [20] |
Liu X Q, Qin N, Hao X. Fast dynamic grid deformation based on Delaunay graph mapping[J]. Journal of Computational Physics, 2006, 211(2): 405-423. |
| [21] |
Rendall T C S, Allen C B. Efficient mesh motion using radial basis functions with data reduction algorithms[J]. Journal of Computational Physics, 2009, 229(17): 6231-6249. |
| [22] |
Rendall T C, Allen C B. Reduced surface point selection options for efficient mesh deformation using radial basis functions[J]. Journal of Computational Physics, 2010, 229(8): 2810-2820. DOI:10.1016/j.jcp.2009.12.006 |
| [23] |
张来平, 段旭鹏, 常兴华, 等. 基于Delaunay背景网格插值和局部网格重构的变形体动态混合网格生成技术[J]. 空气动力学学报, 2009, 27(1): 32-40. Zhang L P, Duan X P, Chang X H, et al. A hybrid dynamic grid generation technique for morphing bodies based on Delaunay graph and local remeshing[J]. Acta Aerodynamica Sinica, 2009, 27(1): 32-40. DOI:10.3969/j.issn.0258-1825.2009.01.006 (in Chinese) |
| [24] |
张来平, 常兴华, 赵钟, 等. 复杂外形静动态混合网格生成技术研究新进展[J]. 气体物理, 2016, 1(1): 42-61. Zhang L P, Chang X H, Zhao Z, et al. Recent progress of static and dynamic hybrid grid generation techniques over complex geometries[J]. Physics of Gases, 2016, 1(1): 42-61. (in Chinese) |
| [25] |
Zhang L P, Chang X H, Duan X P, et al. Applications of dynamic hybrid grid method for three-dimensional moving/deforming boundary problems[J]. Computers & Fluids, 2012, 62: 45-63. |
| [26] |
He X, He X Y, He L, et al. HyperFLOW:A structured/unstructured hybrid integrated computational environment for multi-purpose fluid simulation[J]. Procedia Engineering, 2015, 126: 645-649. DOI:10.1016/j.proeng.2015.11.254 |
| [27] |
常兴华, 马戎, 张来平, 等. 基于计算流体力学的"虚拟飞行"技术及初步应用[J]. 力学学报, 2015, 47(4): 596-604. Chang X H, Ma R, Zhang L P, et al. Study on CFD-based numerical virtual flight technology and preliminary application[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(4): 596-604. (in Chinese) |
| [28] |
Zhang L P, Chang X H, Ma R, et al. A CFD-based numerical virtual flight simulator and its application in control law design of a maneuverable missile model[J]. Chinese Journal of Aeronautics, 2019. |
| [29] |
Chang X H, Ma R, Zhang L P, et al. Further study on the geometric conservation law for finite volume method on dynamic unstructured mesh[J]. Computers & Fluids, 2015, 120: 98-110. |
| [30] |
马戎, 常兴华, 赫新, 等. 流动/运动松耦合与紧耦合计算方法及稳定性分析[J]. 气体物理, 2016, 1(6): 36-49. Ma R, Chang X H, He X, et al. Loose and strong coupling methods for flow/kinematics coupled simulations and stability analysis[J]. Physics of Gases, 2016, 1(6): 36-49. (in Chinese) |




