在工程实际问题中经常涉及边界层、火焰面、多介质界面和激波等流动结构, 具有明显的各向异性特征.为了对这些局部特征进行精确捕捉, 需要在激波、边界层和火焰面等处合理布置网格.
各向异性非结构网格是指网格单元在不同方向上有不同的伸展度, 具有明显的方向性.一方面使得网格密度能随流场特征变化而调整, 大大降低了网格规模; 另一方面网格密度的合理布置, 使得流场结构的计算精度和分辨率大大提高.
流场自适应求解技术则是研究如何自动识别非定常流动的流场特征, 根据识别到的特征和期望的误差控制参数对网格尺寸进行实时控制, 以克服人为定义网格单元尺寸导致的网格规模过大或分布不合理等局限性.
鉴于各向异性非结构网格的前述优点, 国内外许多学者在基于各向异性非结构网格的自适应求解技术方面做了大量研究工作.文献[1~8]等对各向异性网格生成技术以及度量张量的定义方法做了广泛的研究和实践.文献[9~10]则将各向异性网格应用于具有强间断的多介质界面流动问题的自适应求解, 并对计算的可靠性和准确性做了对比研究. Castro-Diaz[11]等应用各向异性网格自适应求解技术对超燃冲压发动机进口段和超声速机翼绕流流场进行了数值模拟, 捕捉到了高分辨率的激波和边界层结构.
可见, 各向异性网格自适应求解技术已经在超声速激波捕捉、界面流等流动问题中得到了很好的实现, 而在湍流燃烧的数值模拟方面, 各向异性网格自适应求解的应用研究还比较缺乏.由于燃烧流场具有明显的各向异性, 如果将这项技术扩展到对火焰面、不同组分交界面和流动涡旋的捕捉上, 对湍流燃烧的大规模数值模拟将起到一定的推动作用.本文基于各向异性非结构网格, 结合大涡模拟技术, 开发了燃烧问题的自适应并行求解程序, 并进行程序代码的验证工作, 最后应用该自适应求解技术对一款富油燃烧-快速淬熄-贫油燃烧(rich-burn, quick-mix, lean-burn, RQL)燃烧室的流场结构进行捕捉和特性分析, 这对低排放燃烧室的设计工作有重要的指导意义.
1 各向异性网格自适应技术各向异性网格自适应求解算法主要包含两个关键性的实现步骤:一是估计流场解插值误差, 构建度量张量; 二是度量空间内的各向异性非结构网格生成.度量张量概念的引入用来刻画流场网格单元的方向性和尺寸信息, 流场中任一点的度量张量均可通过一个对称正定矩阵表示, 这个矩阵中包含了该网格点沿各个方向的尺寸值信息.从本质上说, 自适应技术正是基于流场度量张量提供的网格信息进行各向异性网格的生成.
1.1 流场度量张量构造定义三维R3空间内任意非结构四面体网格单元K=[a, b, c, d], a,b, c, d分别表示4个网格节点. u为R3计算域内的流场精确解, uh代表流场数值解, Πhu为定义在单元K上u的插值函数.
由于缺乏对计算结果的后验性认识, 对精确解和数值解之间的近似误差εh=u-uh往往无法定量描述, 因而采用插值误差ε=u-Πhu来逼近误差的大小.
将网格单元K某一节点(如a)处的插值误差在任意点x附近进行Taylor展开, 如下:
| $\begin{array}{*{35}{l}} \left( u-{{\mathit{\Pi }}_{\rm{h}}}u \right)\left( a \right)=\left( u-{{\mathit{\Pi }}_{\rm{h}}}u \right)\left( x \right)+ \\ \left\langle \mathit{\boldsymbol{ax}},\nabla \left( u-{{\mathit{\Pi }}_{\rm{h}}}u \right)\left( x \right) \right\rangle + \\ \int{_{_{0}}^{^{1}}}\left( 1-t \right)\left\langle \mathit{\boldsymbol{ax}},{{\mathit{\boldsymbol{H}}}_{u}}\left( x+t\ \mathit{\boldsymbol{xa}} \right)\mathit{\boldsymbol{ax}} \right\rangle \rm{d}\mathit{t}. \\ \end{array}$ | (1) |
式(1) 中∇u(x)和Hu(x)分别表示定义在精确解u上的梯度和Hessian矩阵.若插值误差在x处取得最大值时, 有
| $\nabla \left( u-{{\mathit{\Pi }}_{\rm{h}}}u \right)\left( x \right)=0.$ |
则插值误差的范数可以表示为
| $\begin{array}{*{35}{l}} {{\left\| u-{{\mathit{\Pi }}_{\rm{h}}}u \right\|}_{\infty ,K}}= \\ \left| \int \begin{array}{*{35}{l}} ^{1} \\ _{0} \\ \end{array}\left( 1-t \right)\left\langle \mathit{\boldsymbol{ax}},{{\mathit{\boldsymbol{H}}}_{u}}\left( x+t\ \mathit{\boldsymbol{ax}} \right)\mathit{\boldsymbol{ax}} \right\rangle \rm{d}\mathit{t} \right|. \\ \end{array}$ |
网格单元内任意向量ax均可以用单元边e的线性组合表示, 因而可以得出网格单元K的插值误差, 表示如下:
| ${\left\| {u - {\mathit{\Pi }_h}u} \right\|_{\infty ,K}} \le c\left\langle {e,{\mathit{\boldsymbol{H}}_u}\left( x \right)e} \right\rangle ,e\; \in \;{E_K},x\, \in \;K.$ | (2) |
式(2) 表明单元K的插值误差可以用4条单元边的度量长度来衡量, 通过对单元边度量长度的控制, 可以达到控制插值误差的目的.正是基于对插值误差的上述关系式的推导, 给定误差的上限ε, 可以构造一个3×3的度量张量矩阵M,
| $\begin{array}{l} \mathit{\boldsymbol{M = R}}\left( {\begin{array}{*{20}{c}} {{{\tilde \lambda }_1}}&0&0\\ 0&{{{\tilde \lambda }_2}}&0\\ 0&0&{{{\tilde \lambda }_3}} \end{array}} \right){\mathit{\boldsymbol{R}}^{ - 1}},\\ {{\tilde \lambda }_i} = \min \left( {\max \left( {\frac{{c\left| {{\mathit{\lambda }_i}} \right|}}{\varepsilon },\frac{1}{{h_{\max }^2}}} \right),\frac{1}{{h_{\min }^2}}} \right). \end{array}$ |
其中R, λ1, λ2, λ3分别为Hessian矩阵Hu的特征向量和特征值, hmax和hmin分别表示网格单元边长度的限制阈值.这里将最大和最小单元边引入到特征值中, 将保证Hessian矩阵的2阶导数项不出现异常值, 从而使得创建的各向异性网格的单元尺寸和网格规模满足实际流场解析的要求.
1.2 基于燃烧问题多度量张量相交运算对于湍流燃烧问题来说, 由于存在湍流场和温度场的相互耦合作用, 必须要同时考虑多个流场解变量进行度量张量的构造, 这就需要进行多个度量张量的相交运算, 使每个变量的插值误差都在给定的误差极限内.
3阶度量张量可以表示成椭球, 椭球的长轴、中轴和短轴分别对应3个方向的网格尺寸差异, 表示网格的各向异性生长.计算域内任一点存在着对应不同流体变量的多个度量张量, 分别对应着不同尺寸大小的椭球.为了同时满足不同大小椭球尺寸限制, 本文基于体积相交的原则, 选择包含相交体积内的最大椭球作为新的度量张量椭球.具体过程如下(以两个度量张量的相交计算为例, 见图 1):

|
| 图 1 相交椭圆示意图 Fig.1 Schematic of the intersection of two ellipses(2D) |
定义μ1和μ2分别是点P上的两个流场变量解的度量张量, 与之相对应的椭球方程分别为Θμ1和Θμ2, 则椭球方程可以表示为
| ${\mathit{\Theta }_{{\mu _i}}} = \left\{ {M\mathit{\boldsymbol{|}}\sqrt {{{\left( {\mathit{\boldsymbol{PM}}} \right)}^{\rm{T}}}{\mu _i}\mathit{\boldsymbol{PM}}} = 1} \right\}.$ |
用μ1∩2表示新的相交度量张量, 两椭球的相交部分用Θμ1∩Θμ2表示, 则
| ${\mathit{\Theta }_\mu }{\rm{ = max}}\left\{ {M|\sqrt {{{\left( {\mathit{\boldsymbol{PM}}} \right)}^{\rm{T}}}{\mu _i}\mathit{\boldsymbol{PM}}} = 1} \right\} \subset {\mathit{\Theta }_{{\mu _1}}} \cap {\mathit{\Theta }_{{\mu _2}}}.$ |
其中Θμ=max{M}表示相交部分的最大体积椭球.
1.3 基于度量张量的各向异性网格自适应迭代过程非结构网格生成技术早在20世纪90年代初就得到了迅速的发展, 技术相对比较成熟, 目前常用的非结构网格生成方法主要有Delaunay三角化法、阵面推进法(advancing front technique, AFT)及n叉树法.本文采用阵面推进法生成非结构网格, 其在边界的处理方面有很强的适应能力, 对局部网格质量有很好的控制能力.完整的基于度量张量的各向异性网格自适应迭代过程简介如下(以二维情形为例):
(1) 计算域初始网格系统创建
应用基于阵面推进技术的三角形网格生成程序, 对所研究问题的计算域进行三角化网格划分Tk(k=0), 得到计算域的初始网格系统.
(2) 流场解获取
应用CFD求解器, 获得Tk(k≥0) 网格系统上的流场解φk.
(3) 度量张量矩阵计算
基于流场解φk, 计算得到描述流场误差信息的Hessian矩阵Hk及其对应的度量张量矩阵Mk.本章研究的是湍流燃烧问题, 采用了基于Mach数M、温度T、密度ρ这4个物理量场构造的度量张量, 以充分考虑求解动量方程、能量方程和连续性方程对网格解析度的需求.
(4) 网格系统质量判断
如果网格系统质量达到预定值, 则自适应循环结束并退出, 反之则进一步划分.
(5) 基于度量张量矩阵的各向异性网格划分
对计算域执行新的三角划分Tk+1, 以获得在度量张量Mk定义的几何空间内为最优的三角化系统.具体实现过程中, 需要通过增删节点、交换边, 以及移动节点等局部操作以获取最优网格系统.
(6) 返回第(2) 步
利用获得的新网格再次进行流场计算.
2 反应流的大涡模拟技术各向异性自适应求解技术可以直接用于普通意义下的燃烧求解器.由于湍流燃烧过程同时存在着湍流、多相流和化学反应的多尺度耦合, 要想模拟所有尺度的流场结构, 网格要小到能分辨最小尺度的涡和火焰厚度, 但这必然要受到当前计算机发展水平的限制.因此本文采用大涡模拟技术, 通过对流场滤波, 对比网格尺寸大的涡进行直接模拟, 而亚网格尺度涡对湍流流动的影响效应以亚网格尺度模型的形式追加在方程源项中.
在燃烧问题研究中发现, 大多数情况下化学反应区域的厚度在0.1~1mm的量级, 这样的尺度远小于大涡模拟网格尺寸, 导致化学反应区域整体落在了亚网格内, 从而使得大涡模拟技术在模拟燃烧问题时遇到挑战.在本文的燃烧求解器中, 为了对此问题进行解决, 引入了增厚火焰模型.
增厚火焰模型(thickened flame model)由Butler等[12], Colin等[13]提出的原始模型发展而来.该燃烧模型的基本思想是, 通过人为提升组分扩散效应同时降低化学反应速率, 以达到在不改变火焰传播速度的前提下增大火焰面厚度的目的, 从而使在网格分辨率有限的条件下进行火焰面模拟成为可能.
根据燃烧火焰相关理论, 火焰传播速度Uf与
| ${U_{\rm{f}}} \propto \sqrt {D\omega } ,\delta \propto \frac{D}{{{U_{\rm{f}}}}}.$ | (3) |
记增厚因子为F, 从而增厚火焰对应的扩散率为FD, 化学反应源项为ω/F, 火焰面传播速度Uf保持不变, 最终导致火焰面厚度变为Fδ.
如果实际网格尺寸为Δ, N为合理解析火焰结构所需要的网格点数(一般为5~10), 则增厚因子F及增厚火焰厚度δfTF的计算表达式为
| $F = \frac{{N\mathit{\Delta }}}{\delta },\delta _{\rm{f}}^{{\rm{TF}}} = F\delta .$ |
通过调整F到恰当的值, 就能使火焰厚度达到实际求解器和网格系统所能达到的网格尺度.做了增厚处理后燃料组分方程变为
| $\frac{{\partial \rho {Y_k}}}{{\partial t}} + \nabla \cdot \rho u{Y_k} = \nabla \cdot \left( {\rho \left( {DF} \right)\nabla {Y_k}} \right) + \frac{{{\omega _k}}}{F}.$ |
其中, Yk为组分质量分数.
3 典型算例验证本文将各向异性网格生成技术与燃烧大涡模拟技术相结合, 开发了用于湍流燃烧的自适应求解程序.考虑到湍流燃烧流场中经常遇到激波、边界层和火焰面等流动结构, 下面选取了几个典型的有针对性的流动算例进行了详细的对比分析, 以验证程序在激波捕捉和边界层/火焰面解析等方面的准确性和可靠性.
3.1 超声速楔形体绕流美国国家应用软件研究中心CFD研究所(National Project for Application-Oriented Research in CFD, NPARC)的CFD验证与确认网站[14], 提供了高速楔形体绕流问题的Wind软件计算结果.本文首先对该问题进行各向异性网格自适应求解, 以验证该方法对高速流动问题的适应性和优越性.
计算的楔形体与水平方向的夹角为15°, 来流Mach数M为2.5, 波前压力为1atm, 温度T为289K. 图 2展示了自适应求解过程中网格与Mach数分布情况的演变与收敛历程.

|
| 图 2 自适应网格和Mach数演变过程 Fig.2 Evolutions of mesh and Mach number field for anisotropic mesh adaptation process |
从图 2(a)中可以看出, 自适应求解的第1次迭代就产生了显著效果, 网格资源明显向激波附近汇集, 计算得到的激波变得尖锐.经过4次迭代, 自适应求解过程区域收敛, 网格单元被有效分配至激波附近的狭窄区域.
表 1为本文的各向异性网格计算结果与理论分析解及Wind代码模拟结果的定量对比.可以看出, 本文的计算结果不但在定性上能捕捉到相对更加尖锐的激波效应, 与理论分析解的定量对比也吻合得很好, 物理量误差值与Wind代码模拟结果相比有了明显的改善.
| 下载CSV 表 1 激波前后流场数据对比 Tab.1 Comparisons of the present results with theory and Wind code |
选取了几何结构比较简单的一维CH4/air预混层流火焰燃烧算例, CH4和air在化学当量比为1, 压力为1个标准大气压, 绝热条件下自由传播燃烧. 图 3为自适应迭代生成的网格和温度场.

|
| 图 3 自适应网格和温度演变过程 Fig.3 Evolutions of mesh and temperature field for anisotropic mesh adaptation process |
从图 3中可以看出, 初始网格均匀分布, 捕捉到的层流火焰解析度较差.经过4次自适应迭代操作, 网格逐渐向火焰面附近加密, 各向异性特征显著, 而在远离火焰面处, 网格尺度较大, 这样使整个网格规模大大下降.
图 4和图 5分别为火焰面附近温度和组分CO2质量分数的对比验证情况.可以看出, 与均匀网格相比, 各向异性网格的单元数更少, 但其分布更加合理, 对火焰面的解析精度与均匀网格相比更高, 物理量分布与CHEMKIN化学分析软件的计算结果吻合良好.这说明本文自适应求解程序在计算预混燃烧问题上具有很好的精度.

|
| 图 4 火焰面附近温度分布对比 Fig.4 Comparisons of temperature profiles |

|
| 图 5 火焰面附近CO2组分分布对比 Fig.5 Comparisons of CO2 mass fraction profiles |
层流对冲火焰被广泛用于层流非预混燃烧火焰的基础研究.本节以H2/air对冲火焰为例, 分别对基于单变量流场和多变量流场构造的各向异性网格自适应计算进行考察, 其中算例H2喷射速度为2.5m/s, 空气喷射速度为1m/s, 温度为300K.
图 6(a)显示了在各向同性网格下流场温度、速度和OH质量分数等物理量的分布云图, 整体网格节点数为18026, 单元数为35314. 图 6(b)为基于温度度量张量MT进行各向异性网格的创建, 节点数为1500, 单元数为2850, 而图 6(c)则采用了同时考虑温度、密度和速度的多变量度量张量MT∩ρ∩|v|, 网格节点数为8053, 单元数为15553.

|
| 图 6 不同网格系统及对应流场解 Fig.6 Comparisons of the computed solution on different grid systems |
图 6(b)中可以发现, 基于温度度量张量的网格系统仅在温度场变化较剧烈处进行了加密, 与各向同性网格系统相比, 对速度场的捕捉不够精确, 特别是在壁面附近没有对边界层结构进行很好的刻画.而图 6(c)由于构造度量张量时, 同时考虑了温度、密度和速度3个流场变量, 网格在整个对冲区域和壁面附近都有加密, 网格的各向异性特征比较明显.与图 6(b)相比, 图 6(c)对边界层附近的流动有更好的捕捉精度; 与图 6(a)相比, 火焰区附近的虚拟数值振荡得到大幅降低.
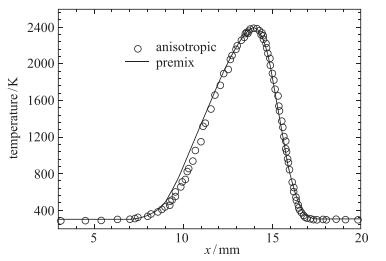
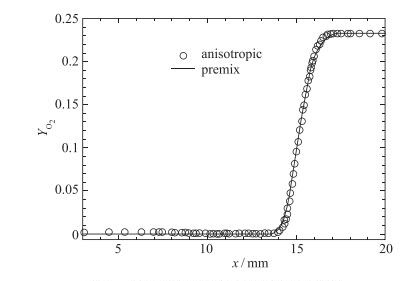
从网格规模和计算结果综合上看, 各向同性网格由于没有采用自适应技术, 虽然对网格局部进行了加密, 但网格数目最多造成计算量过大, 对冲区速度场也出现了数值振荡现象.基于温度度量张量的自适应计算, 网格数目最少且对火焰面结构的计算也较精准, 自适应求解的优势较为突出, 但对速度场的计算结果较差. 图 7~10分别为多变量自适应算例火焰面附近密度、温度和组分质量分数的对比验证, 相关模拟结果与CHEMKIN化学分析软件的计算结果吻合良好.这说明了对于燃烧问题来说, 基于多变量度量张量的自适应计算不但能综合考虑各变量的变化因素, 对整个流场结构的捕捉都比较精确.

|
| 图 7 对冲火焰面附近密度分布 Fig.7 Comparisons of density profiles for a 2D opposed flame |
|
| 图 8 对冲火焰面附近温度分布 Fig.8 Comparisons of temperature profiles for a 2D opposed flame |
|
| 图 9 对冲火焰面附近O2组分质量分布 Fig.9 Comparisons of O2 mass fraction profiles for a 2D opposed flame |

|
| 图 10 对冲火焰面附近OH组分质量分布 Fig.10 Comparisons of OH mass fraction profiles for a 2D opposed flame |
湍流火焰面不像层流火焰那样光滑, 会产生褶皱或分离现象, 多尺度流场涡与火焰面之间的耦合作用, 使得流场呈现非定常性, 对流场结构的捕捉难度增大.本节对三维湍流预混火焰进行算例验证, 选取典型的三维本生灯火焰算例, 混合气体为化学恰当比下的预混CH4/air, 喷孔直径为12mm, 出口速度为30m/s
本节基于多变量流场的自适应求解技术, 同时考虑温度、密度和速度3个物理量的变化. 图 11展现了三维Bunsen火焰的瞬时特征.

|
| 图 11 三维Bunsen火焰瞬时特征(温度场) Fig.11 Instantaneous flame structure for 3D Bunsen flame (temperature field) |
基于多变量度量张量的自适应网格由于同时考虑了速度场和温度场的变化, 因而加密区域沿着中轴线在下游成扩张状, 各向异性的特征较为明显, 特别是在下游火焰面分离区域, 流场还捕捉到了一些精细的小尺度涡结构.
图 12为不同流向位置处计算结果与实验测量的对比.图中显示, 所得的数值预测结果与实验测量吻合良好.由此可以看出, 基于多个流场变量的各向异性网格自适应计算, 对于求解湍流预混燃烧问题是稳定可靠的,并且具有效率.

|
| 图 12 不同轴向位置流场数据的对比验证 Fig.12 Comparisons of radial profiles of velocity and species |
对于航空发动机燃烧室来说, 氮氧化物的排放会导致严重的环境问题.因此, 研究影响NOX生成的关键因素至关重要, 这有利于设计出先进的低污染燃烧室.其中富油-快速混合-贫油燃烧室
就是一种较有前途的低排放燃烧室.如果将基于多变量度量张量的自适应技术应用于实际的燃烧室数值模拟, 这对于工程应用将十分有意义.
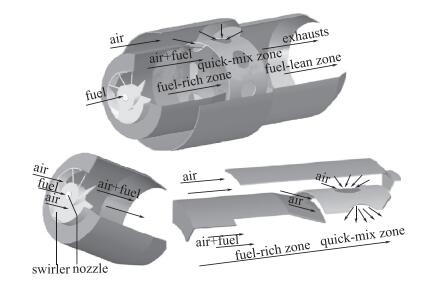
4.1 RQL燃烧室几何结构这里设计的RQL燃烧室主要由5个部分组成:头部、富油区、快速混合区、贫油区和排气段, 其中头部由一级轴向旋流器构成, 用于产生回流区, 起稳定火焰作用.来流空气以两种方式进入燃烧室:头部旋流器和快速混合孔.两种方式的空气质量流量比随着不同的设计工况和燃烧室设计几何而变化.如图 13为RQL燃烧室的三维几何和局部剖析图, 用于描述整个通道空气的流向和化学反应区.
|
| 图 13 RQL燃烧室的三维几何和局部剖析图 Fig.13 Geometry schematic of a RQL combustion chamber |
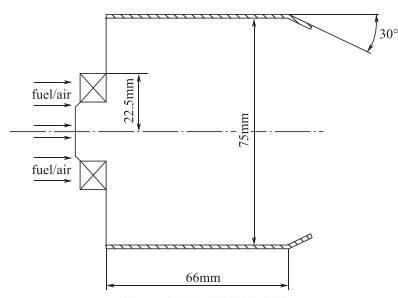
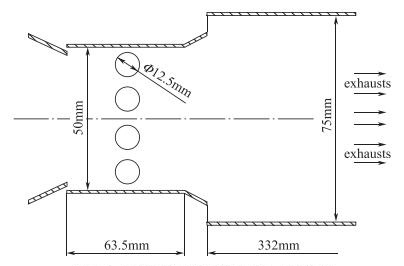
整个燃烧室的设计尺寸以NASA相关报告[15]作为参考依据.头部轴向旋流器出口外径为45mm, 叶片安装角为45°, 叶片数为8, 旋流数SN=0.77.富油区内径为75mm, 长度为66mm, 其后连有一个收缩角为30°的过渡段, 用于连接富油区和快速混合区.快速混合区含有8个直径为12.5mm的稀释圆孔.贫油区长度为332mm, 内径为75mm.具体的尺寸示意如图 14和图 15所示.
|
| 图 14 富油区尺寸示意图 Fig.14 Dimension of the fuel-rich zone |
|
| 图 15 快速混合区和贫油区尺寸示意图 Fig.15 Dimension of the quick-mix zone and the fuel-lean zone |
对于整个RQL燃烧室, 由于头部旋流的作用会在富油区形成回流区, 使来流速度降低, 从而起到稳定火焰的目的. 图 16给出了富油区和贫油区燃烧室内的火焰形状以及轴向速度分布情况.

|
| 图 16 RQL燃烧室内温度场等值面分布(灰度图:轴向速度值) Fig.16 Instantaneous iso-surface of temperature in a RQL combustion chamber (gray level: axial velocity) |
图 17为中心截面速度和反应产物质量分数分布云图, 在富油区流场速度集中在-5~15m/s, 这是由于采用的一级旋流强度较弱, 直接导致下游回流强度的减小, 回流效果不明显.从燃烧产物CO2质量分数分布可以看出, 预混燃气经过富油燃烧后, 由于快速混合空气的稀释作用, 在下游贫油区燃烧反应得到了增强, 从而CO2的生成量较高.

|
| 图 17 中心截面轴向速度和CO2质量分数分布云图 Fig.17 Instantaneous axial velocity and CO2 mass fraction in the central plane |
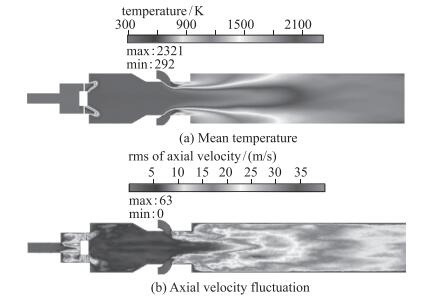
从流场平均温度分布图 18(a)也可以看出, 在快速混合区, 火焰呈扇锥形, 这是由于一方面淬熄射流在快速混合区压缩火焰面, 另一方面火焰在突扩的贫油区域有扩张趋势.淬熄空气一方面对富油区高温燃气起到冷却的作用, 另一方面富油燃料在快速混合区进行了二次点燃, 从而实现了富油向贫油的快速转换.
|
| 图 18 中心截面平均温度场和轴向脉动速度分布 Fig.18 Mean temperature and axial velocity fluctuation in the central plane |
分级燃烧技术虽然有利于减小NOX的生成, 但由于速度场与温度场之间强烈的耦合作用, 也会出现燃烧不稳定现象.从流场轴向脉动速度分布云图 18(b)可以看出, 在快速混合区局部出现了较大的脉动速度(20~40m/s), 并向下游延伸, 进而贫油区脉动速度(20~30m/s)明显大于富油区(2~10m/s).这是由于在快速混合区和贫油区, 流场的各物理参数如压力、密度、成分等均发生了较大变化, 在较大的压力梯度下, 这样直接导致了气流脉动量的增加.
5 结论本文针对燃烧问题的数值模拟, 构造了单变量和多变量的度量张量矩阵, 实现了基于各向异性非结构网格的自适应求解算法.结合大涡模拟技术, 通过对一维层流预混火焰、二维对冲扩散火焰和三维本生灯湍流火焰的自适应计算, 验证了算法的准确性, 展示了各向异性非结构网格技术在准确模拟火焰面流场方面的独特优势, 具体如下:
(1) 自适应技术根据流场解的变化对网格单元资源进行合理的分配和布置, 有效降低了问题的规模.
(2) 具有对层流和湍流火焰面结构进行精确捕捉的能力, 对流场物理量的计算精度较高.
(3) 对于燃烧问题来说, 基于多变量流场的自适应算法比单变量的计算分辨率高.
此外还将自适应技术应用到了实际的富油-快速混合-贫油(RQL)燃烧室的数值模拟工作中, 对流场结构进行了分析, 发现了燃烧室内的热声不稳定问题.
| [1] | Habashi W, Dompierre J, Bourgault Y. Anisotropic mesh adaptation: towards user-independent, mesh-independent and solver-independent CFD. Part Ⅰ: general principles[J]. IInternational Journal for Numerical Methods in Fluids, 2000, 32(6): 725-744. |
| [2] | Dompierre J, Vallet M, Bourgault Y. Anisotropic mesh adaptation: towards user-independent, mesh-independent and solver-independent CFD. Part Ⅲ:unstructured meshes[J]. International Journal for Numerical Methods in Fluids, 2002, 39(8): 675-702.DOI:10.1002/(ISSN)1097-0363 |
| [3] | Tam A, Ait-Ali-Yahia D, Robichaud M. Anisotropic mesh adaptation for 3D flows on structured and unstructured grids[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 189(4): 1205-1230.DOI:10.1016/S0045-7825(99)00374-6 |
| [4] | Dolejsi V. Anisotropic mesh adaption technique for viscour flow simulation[J]. East West Journal of Numerical Mathematics, 2001, 9(1): 1-24.DOI:10.1515/JNMA.2001.1 |
| [5] | Bottasso C. Anisotropic mesh adaption by metric driven optimization[J]. International Journal for Numerical Methods in Engineering, 2004, 60(3): 597-639.DOI:10.1002/(ISSN)1097-0207 |
| [6] | Dolejsi V, Felcman J. Anisotropic mesh adaptation for numerical solution of boundary value problems[J]. Numerical Methods for Partial Differential Equations, 2004, 20(4): 576-608.DOI:10.1002/(ISSN)1098-2426 |
| [7] | Frey P, Alauzet F. Anisotropic mesh adaptation for CFD computation[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(48/49): 5068-5082. |
| [8] | Remacle J, Li X, Shephard M. Anisotropic adaptive simulation of transient flows using discontinuous Galerkin methods[J]. International Journal for Numerical Methods in Engineering, 2005, 62(7): 899-923.DOI:10.1002/(ISSN)1097-0207 |
| [9] | Belhamadia Y, Fortin A, Chamberland E. Anisotropic mesh adaptation for the solution of the Stefan problem[J]. Jounal of Computational Physics, 2004, 194(1): 233-255.DOI:10.1016/j.jcp.2003.09.008 |
| [10] | Belhamadia Y, Fortin A, Chamberland E. Three-dimensional anisotropic mesh adaptation for phase change problems[J]. Jounal of Computational Physics, 2004, 201(2): 753-770.DOI:10.1016/j.jcp.2004.06.022 |
| [11] | Castro-Diaz M, Hecht F, Mohammadi B. Anisotropic unstructured mesh adaption for flow simulations[J]. International Journal for Numerical Methods in Fluids, 1997, 25(4): 475-491.DOI:10.1002/(ISSN)1097-0363 |
| [12] | Butler T D, O Rourke P J. A numerical method for two dimensional unsteady reacting flows[J]. Symposium (International) on Combustion, 1997, 16(1): 1503-1515. |
| [13] | Colin O, Ducros F, Veynante D. A thickened flame model for large eddy simulations of turbulent premixed combustion[J]. Physics of Fluids, 2000, 12(7): 1843-1863.DOI:10.1063/1.870436 |
| [14] | http://www.grc.nasa.gov/WWW/wind/valid/archive.html |
| [15] | Peterson C, Sowa W, Samuelsen G. Performance of a model rich burn-quick mix-lean burn combustor at elevated temperature and pressure[R]. NASA CR-211992, 2002 |



