2. 北京系统工程研究所,北京 100191
2. Beijing Institute of System Engineering, Beijing 100191, China
燃烧室是发动机上重要的热端部件, 燃烧室设计的好坏对发动机的工作性能有直接影响.在航空发动机燃烧室的传统设计中, 主要依靠经验和半经验公式进行初步设计, 然后进行大量的冷态和热态燃烧实验, 对初步设计方案进行选择、校正和优化.这种通过实验的设计方法通常成本高、周期长、难度大, 并且很难模拟发动机真实的工作压力.而且, 对高温高压的燃烧室, 仅能测量其出口参数, 无法测量其内部流场和温度场[1].
随着计算机技术、计算流体力学和计算燃烧学的迅速发展, 航空发动机燃烧室数值仿真设计技术发展速度不断加快.与传统的经验设计方法相比, 这种方法不仅耗费资源少, 还能大大缩短研究周期, 因此利用数值方法辅助燃烧室设计受到越来越多的重视[2].
在实际的燃烧系统中, 旋流火焰以其良好的点火性能和稳定性能得到了广泛的应用, 同时, 旋流火焰还能在非常有限的小体积内进行高效率的能量转化[3-4].目前, 已经有一些学者用数值方法研究了旋流燃烧室的物理现象, 并且找到了计算时间和成本都较为合理, 且不是很复杂的数值方法[5-6].但是由于旋流数的改变会使得流动结构呈现不同的拓扑结构, 为旋流燃烧室的设计和建模增加困难, 而且这些数值仿真结果的验证和优化需要大量实验测量的精确数据[7-8].而真实的燃烧室体积大, 结构复杂, 一方面无法依靠成本昂贵的实验进行详细测量, 另一方面, 数值工具的置信水平也没有达到完全解决这些问题的程度.因此, 研究者们通过建立一个实验室规模的标准燃烧室来代替真实的燃烧室作为研究对象, 为燃烧数值模拟程序的验证和优化, 以及工程上燃烧室的性能模拟提供详细全面的测量值[9].
目前, 使用LES方法和概率密度函数模型相结合的方法来更好地模拟双旋流火焰还没有得到充分的研究, 国内对于这方面的研究更是缺乏.基于此, 本文将用基于LES-PDF方法的AECSC两相程序, 对模型燃烧室(gas turbine model combustor, GTMC)进行数值模拟, 以此验证AECSC程序模拟燃烧室的可行性和可信度, 并对旋流燃烧室的流动和燃烧特性进行分析.
1 计算方法和模型 1.1 AECSC程序本文使用的AECSC程序(aero engine combustor simulation code)是一款基于LES-PDF方法的湍流燃烧仿真软件, 能够对燃烧器中亚声速湍流燃烧过程进行三维仿真模拟.
AECSC程序是基于Fortran 77标准的模块化Fortran程序, 采用gfortan编译器.程序基于有限体积法, 用LES求解连续方程和动量方程, PDF求解能量方程和组分方程. LES的亚格子应力模型选取了动力Smagorinsky-Lilly模型, PDF方程的求解选取了Euler形式的Ito随机场解法, 可自定义随机场的个数.动量和标量输运方程均使用二阶中心差分格式(central difference scheme, CDS)进行空间离散, 除了标量方程中的对流项选用了全变差缩小(total variation diminishing, TVD) 格式离散, 时间的离散均选取了Crack-Nicholson格式.雾化破碎模型为Claudio′s破碎模型, 蒸发模型为Abramzon Sirignano模型, 气液两相耦合过程采用Euler-Lagrange方法,点火模型为能量沉积模型.程序用LES方法对燃料喷雾进行概率模拟, 通过随机模型来表示亚网格速度波动对扩散和蒸发的影响.液相采用Lagrange公式进行跟踪, 而气相采用Euler描述.程序内置了多种两相燃料的化学反应机理, 如煤油、甲烷、甲醇、正庚烷等, 但是这些化学反应机理均为简化后的几步或十几步的化学反应机理, 有文献可以表明其计算精度[10-11].
1.2 湍流燃烧模型AECSC程序用概率密度函数(probability density function, PDF)来求解带反应的湍流流动问题.对于任一标量k, 其单点边缘概率密度函数Pk定义为
| $ P_k = \delta (\psi_k - \phi_k) $ |
其中, ψk表示标量ϕk的样本空间, δ为单步脉冲(Dirac-Delta)函数.对标量ψ=[ψ1, …, ψNS]和ϕ=[ϕ1, …, ϕNS], 离散PDF有如下性质
| $ \begin{array}{l} \int_{ - \infty }^{ + \infty } {\delta (\psi ){\rm{d}}\psi = 1} \\ \int_{{\rm{ - }}\infty }^{{\rm{ + }}\infty } {f\left( \psi \right)\delta \left( {\psi - \phi } \right){\rm{d}}\psi } {\rm{ = }}f\left( \phi \right) \end{array} $ |
其中,
由于湍流反应包含许多标量,所以就有了所有标量的联合概率密度函数F
| $ F\left( {\psi ;\mathit{\boldsymbol{x}}, t} \right){\rm{ = }}\prod\limits_{k = 1}^{{N_S}} {\delta \left( {{\psi _k} - {\phi _k}\left( {x', t} \right)} \right)} $ |
使用Favre滤波法, 对上式进行密度加权, 可以得到NS种标量的联合亚网格PDF
| $ \begin{array}{*{20}{l}} {{{\tilde P}_{{\rm{sgs}}}}\left( {\psi ;x,t} \right) = \frac{1}{{\bar \rho }}\int_V {\rho \prod\limits_{k = 1}^{{N_s}} \delta } \left( {{\psi _k} - {\phi _k}\left( {x',t} \right)} \right) \cdot }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;G\left( {x - x';\Delta } \right){\rm{d}}x'} \end{array} $ |
上式利用了单步脉冲函数的筛选性质, 其中G为滤波函数,
| $ \begin{array}{l} \bar \rho \frac{{\partial {{\tilde P}_{{\rm{sgs}}}}\left( \psi \right)}}{{\partial t}} + \bar \rho {{\tilde u}_i}\frac{{\partial {{\tilde P}_{{\rm{sgs}}}}\left( \psi \right)}}{{\partial {x_i}}} + \sum\limits_{k = 1}^{{N_S}} {\frac{\partial }{{\partial {\psi _k}}}} \left[ {\bar \rho {{\dot \omega }_k}\left( \psi \right){{\tilde P}_{{\rm{sgs}}}}\left( \psi \right)} \right] = \\ - \frac{\partial }{{\partial {x_i}}}\left[ {\overline {\rho \left( \psi \right)F\left( \psi \right){u_i}} - \bar \rho {{\tilde u}_i}{{\tilde P}_{{\rm{sgs}}}}\left( \psi \right)} \right]- \\ \sum\limits_{k = 1}^{{N_S}} {\frac{\partial }{{\partial {\psi _k}}}} \left[ {\frac{\partial }{{\partial {x_i}}}\frac{\mu }{\sigma }\frac{{\partial {\psi _k}}}{{\partial {x_i}}}F\left( \psi \right)} \right] \end{array} $ |
方程等号左侧第3项是封闭的化学反应源项, 可以精确计算, 而无需模拟.等号右侧第1项是亚网格对流项, 引入一个梯度封闭近似, 所得的结果如下
| $ \overline {\rho (\psi )F(\psi ){u_i}} - \bar \rho {\tilde u_i}{\tilde P_{{\rm{sgs}}}}(\psi ) = - \frac{{{\mu _{{\rm{sgs}}}}}}{{{\sigma _{{\rm{sgs}}}}}}\frac{{\partial {{\tilde P}_{{\rm{sgs}}}}}}{{\partial {x_j}}} $ |
等号右侧第2项是分子扩散项, 这一项是离散的, 包含了标量的空间梯度, 因此不能用
| $ \begin{array}{*{20}{l}} -{\sum\limits_{k = 1}^{{N_S}} {\frac{\partial }{{\partial {\psi _k}}}} \left[ {\frac{\partial }{{\partial {x_i}}}\frac{\mu }{\sigma }\frac{{\partial {\psi _k}}}{{\partial {x_i}}}F(\psi )} \right] = \frac{\partial }{{\partial {x_i}}}\left[ {\frac{\mu }{\sigma }\frac{{\partial {{\tilde P}_{\rm sgs }}(\psi )}}{{\partial {x_i}}}} \right]}\\ { - \sum\limits_{k = 1}^{{N_S}} {\sum\limits_{l = 1}^{{N_S}} {\frac{{{\partial ^2}}}{{\partial {\psi _k}{\partial _l}}}} } \left[ {\left( {{{\left. {\frac{\mu }{\sigma }\frac{{\partial {\psi _k}}}{{\partial {x_i}}}\frac{{\partial {\psi _l}}}{{\partial {x_i}}}} \right|}_{\phi = \psi }}} \right){{\tilde P}_{{\rm{sgs}}}}(\psi )} \right]} \end{array} $ |
式中等号右侧第1项是封闭的, 第2项也称为小尺度混合项, 包含了标量耗散率, 表示了亚网格尺度下的混合过程, 并说明了分子扩散对
| $ \begin{array}{*{20}{c}} {\int_{ - \infty }^\infty \psi M(\psi ;x, t){\rm{d}}\psi = 0}\\ {\int_{ - \infty }^{ + \infty } {\left( {{\psi _k} - {{\tilde \phi }_k}} \right)} \left( {{\psi _l} - {{\tilde \phi }_l}} \right)M(\psi ;x, t){\rm{d}}\psi = 2\bar \rho {\chi _{kl}}} \end{array} $ |
式中, χkl是能量耗散率, 表达式如下
| $ {\chi _{kl}} = \frac{\mu }{\sigma }\overline {\frac{{\partial {\psi _k}}}{{\partial {x_i}}}\frac{{\partial {\psi _l}}}{{\partial {x_i}}}} $ |
目前, 对小尺度混合项的模拟主要有两种模型, 分别是IEM确定性模型和Curl颗粒相互作用模型.两者都有一定局限性, 但IEM模型更适合于高Reynolds数下的湍流燃烧问题, 模型方程如下
| $ M(\psi ;x, t) = \frac{{\bar \rho }}{{2{\tau _{ sgs }}}}\sum\limits_{k = 1}^{{N_S}} {\frac{\partial }{{\partial {\psi _k}}}} \left[ {{\psi _k} - {\rm{ }}{\tilde \phi _k}(x, t){{\tilde P}_{{\rm{sgs}}}}(\psi )} \right] $ |
综上所述, 过滤后的亚网格标量输运PDF方程最终可以表示为
| $ \begin{array}{l} \bar \rho \frac{{\partial {{\tilde P}_{{\rm{sgs}}}}(\psi )}}{{\partial t}} + \bar \rho {{\tilde u}_i}\frac{{\partial {{\tilde P}_{{\rm{sgs}}}}(\psi )}}{{\partial {x_i}}} + \sum\limits_{k = 1}^{{N_S}} {\frac{\partial }{{\partial {\psi _k}}}} \left[ {\bar \rho {{\dot \omega }_k}(\psi ){{\tilde P}_{{\rm{sgs}}}}(\psi )} \right] = \\ \;\; - \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\frac{\mu }{\sigma } + \frac{{{\mu _{{\rm{sgs}}}}}}{{{\sigma _{{\rm{sgs}}}}}}} \right)\frac{{\partial {{\tilde P}_{{\rm{sgs}}}}(\psi )}}{{\partial {x_i}}}} \right] - \frac{{\bar \rho }}{{2{\tau _{{\rm{sgs}}}}}}\sum\limits_{k = 1}^{{N_s}} {\frac{\partial }{{\partial {\psi _k}}}} \left[ {{\psi _k} - } \right.\left. {{\phi _k}(x, t){{\tilde P}_{{\rm{sgs}}}}(\psi )} \right] \end{array} $ |
目前PDF方程主要有两种解法, 一种是将输运方程转换为Lagrange方程、利用Monte Carlo法来求解, 另一种是随机Euler场法, 通过推导与联合PDF方程等价的随机偏微分方程, 得到标量的随机Euler场[13].程序采取Euler随机场法求解PDF方程, 这种方法兼顾计算速度, 计算准确性和泛用性, 可以模拟湍流燃烧的燃烧特性、点火性能、燃烧产物生产等.本文工作采用一个随机场进行求解计算.
程序求解Ito形式的随机微分方程
| $ {\rm{d}}{X_m} = {A_m}\left( {{X_m}} \right){\rm{d}}t + {B_m}\left( {{X_m}} \right){\rm{d}}{W^m} $ | (11) |
这是带有Brown运动干扰项的随机微分方程式, Am表示漂移系数, Bm表示第m个随机过程的扩散系数, Xm表示第m个随机样本.通过将Brown运动视为随机干扰并施加于一般运动, 这种随机微分方程能够表示一般化过程, 也被称为Ito过程.其最终推导结果如下[14]
| $ \begin{array}{l} \bar \rho \frac{{{\rm{d}}\xi _k^n}}{{{\rm{d}}t}} + \bar \rho {{\tilde u}_i}\frac{{\partial \xi _k^n}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left( {{\mathit{\Gamma} ^\prime }\frac{{\partial \xi _k^n}}{{\partial {x_i}}}} \right) - \frac{{\bar \rho }}{{{T_{sgs}}}}\left( {\xi _k^n - {{\tilde \phi }_k}} \right) + \\ \bar \rho {{\dot \omega }_k}\left( {\xi _k^n} \right) + \bar \rho \sqrt {\frac{{2{\mathit{\Gamma} ^\prime }}}{{\bar \rho }}} \frac{{\partial \xi _k^n}}{{\partial {x_i}}}\frac{{{\rm{d}}W_i^k}}{{{\rm{d}}t}} \end{array} $ |
式中,
德国航空航天中心的Meier等[15-16]先后于2004年、2006年和2011年设计并给出了3个GTMC的几何结构和详细的实验测量数据, 本文选取2011年的双旋流模型燃烧室GTMC作为模拟对象[15].实验对GTMC的喷雾特性和温度场进行了定量测量, 希望对现有计算方法无法模拟的真实情况下的雾化提供一定的参考, 对数值模拟时旋流燃烧室的进口喷雾边界条件的定义以及喷雾的蒸发和燃烧起到帮助作用.
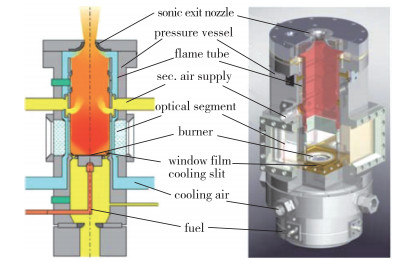
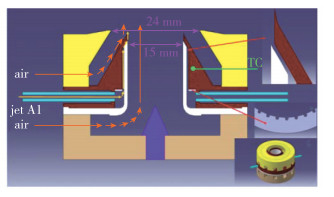
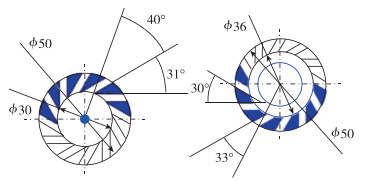
GTMC的几何结构如图 1所示, 燃烧室长264 mm, 截面为102 mm×102 mm的正方形.空气通过中心旋流器和外旋流器进入燃烧室, 两个旋流器均有12个径向通道, 其设计细节如图 2所示. 图 3则展示了空气和航空煤油进口的设计细节.煤油由两个位置相对的燃油管道先进入一个环形的燃油通道, 然后通过圆周均布的36个面积0.2 mm2大小的孔进入垂直槽, 径向通道中的高温空气会在垂直槽中给燃料带来显著的温升和预蒸发, 这样的设计有利于燃烧的稳定.燃料在穿过垂直槽后以31°的倾角进入燃烧室.
|
| 图 2 中心旋流器(左)和外旋流器(右)的轴向截面图[15-16] Fig.2 Axial section of central cyclone and external cyclone [15-16] |
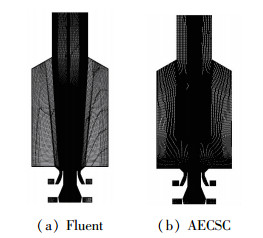
本文使用SolidWorks创建几何模型, 使用ANSYS ICEM软件划分结构化网格.由于AECSC程序只支持1个block在1个CPU上进行计算, 于是划分了用于Fluent计算的网格, 在此基础上重新进行了合并和分割, 将block数从300减小到了144. 图 4分别显示用于Fluent计算和AECSC程序计算的x=0平面的网格.可以看到, 相比于Fluent的网格, 用于AECSC程序的网格在径向的分布稍差一点, 但是在燃烧室轴向的分布更合理一些.旋流器部分的网格如图 5所示, 其中蓝色和绿色的部分为旋流器的空气进口.
|
| 图 4 计算网格示意图 Fig.4 Computational grid |

|
| 图 5 内外旋流器网格 Fig.5 Computational grid of cyclones |
本文分别划分了数量为2.2×106, 2.97×106, 4.4×106的网格, 并使用Fluent对3种网格进行了模型燃烧室冷态流场的计算.计算的结果表明2.2×106网格的表现不是很好, 而2.97×106网格和4.4×106网格的计算结果基本一致.综合考量计算量和精确度, 最终选取2.97×106网格进行后续计算.
2.3 边界条件| 下载CSV 表 1 边界条件测试 Tab.1 Boundary conditions |
其中, 实验文献[15]只给定了总的空气质量流量.前文中使用Fluent软件对4.4×106的网格计算得到的结果表明内外旋流器的流量比约为1:1.65, 按照该流量比分别设置内外旋流器的空气进口边界条件.
3 计算结果与分析 3.1 冷态工况本文使用Fluent软件和AECSC程序分别计算了模型燃烧室的冷态流场.其中, Fluent计算中按照冷态工况设置进口边界条件, 出口采用压力边界条件, 用LES计算冷态流场.速度-压力耦合采用SIMPLE算法, 对于空间离散, 动量方程采用有限中心差分离散, 能量方程采用2阶迎风格式离散, 时间离散采用1阶隐式格式.模拟时, 1个时间步包含20个内迭代循环, 时间步长设置为Δt=5×10-4 s.
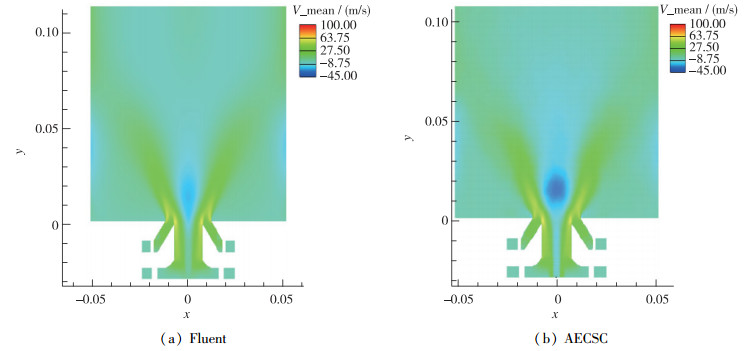
图 6展示了冷态条件下, Fluent和AECSC分别计算得到的x=0平面轴向速度云图.
|
| 图 6 冷态工况下x=0平面平均轴向速度云图 Fig.6 Average axial relocity on x=0 plane under the non-reaction conditions |
可以看到, 两个云图的差异并不大, 最主要的区别在于内回流区的强度和大小.可以明显看到, Fluent结果中的内回流区明显比AECSC的内回流区要窄, 且强度要弱一些.此外还可以观察到轴向速度在h=20 mm以后, 同一高度下AECSC的轴向速度最大值要比Fluent的大一些.
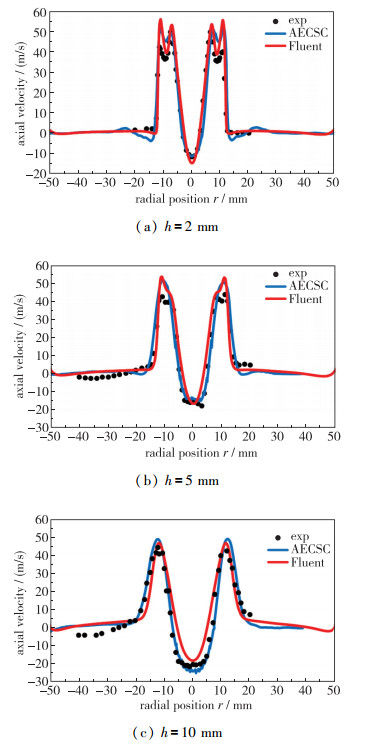
图 7~9分别展示了不同轴向位置处, Fluent和AECSC程序得到的轴向、径向、切向的速度分布和实验结果的比较.其中黑点为实验结果, 红色实线代表Fluent结果, 蓝色实线代表AECSC程序的结果.
|
| 图 7 冷态工况下不同轴向高度上轴向速度比较 Fig.7 Comparisons of axial velocity at different axial heights under the non-reaction conditions |
|
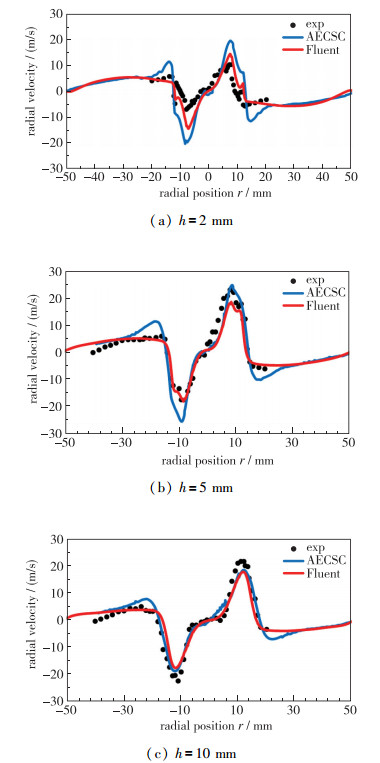
| 图 8 冷态工况下不同轴向高度上径向速度比较 Fig.8 Comparison of radial velocity at different axial heights under the non-reaction conditions |
|
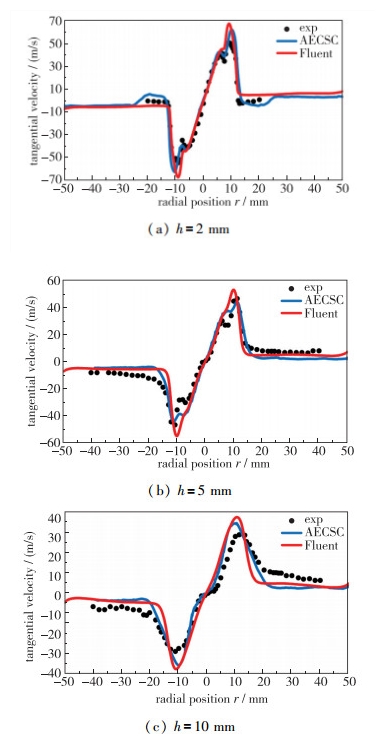
| 图 9 冷态工况下不同轴向高度上切向速度比较 Fig.9 Comparison of tangential velocity at different axial heights under the non-reaction conditions |
可以看到计算得到的3个方向的速度分布和实验的速度分布有相同的趋势. h=2 mm时, 轴向速度有两个正向峰值, 这是因为在h=2 mm的高度处, 两股来自两个旋流器的新鲜空气还没有很好的混合.这两个峰值都在43 m/s附近, 比最大径向速度要大的多.从径向速度曲线图上可以看到在r>10 mm的范围有明显的外回流区, 在此区域内切向速度的变化很小. h=5 mm, h=10 mm的流动特性和h=2 mm的相比变化基本不大, 相比较而言, 速度曲线整体被逐渐拉宽, 轴向速度的两个峰值由于两股气流的渐渐融合, 在h=5 mm时明显变小, 在h=10 mm时已经完全不见.外回流区在变小, 有消失的倾向.
整体来看, Fluent的计算结果和AECSC程序的计算结果都和实验结果比较接近.单就轴向速度分布来看, AECSC程序的计算结果比Fluent的计算结果要好一些. Fluent计算得到的轴向速度分布曲线要略窄一些, 且随着轴向距离的增加, 实验测量的分布逐渐拉宽, 而Fluent的速度曲线拉宽的趋势并不明显, 这使得和实验的误差渐渐加大.相比之下, AECSC程序得到的轴向速度曲线有相同的随着轴向距离增加被拉宽的趋势, 所以轴向距离越大, AECSC的结果和实验值吻合得越好.对于切向速度, Fluent和AECSC的计算结果相差不是很大, AECSC结果的整体平均误差比Fluent计算结果略微低一些.
而在径向速度分布上, 在h=2 mm时, AECSC程序计算得到的最大值大约在20 m/s附近, 而实验测量结果只有10 m/s左右.在其他两个高度处, 两种方法得到的计算结果和实验值都比较吻合.这可能是由AECSC程序的计算网格在由轴向通道进入燃烧室处的径向分布较差, 处理方面有些欠缺, 导致计算时气流刚进入模型燃烧室时的径向速度增长过快.整体看来, 除了在h=5 mm和h=10 mm处的径向速度, AECSC的计算结果比Fluent的结果要更接近实验值.
表 2~4分别给出了程序计算的轴向、径向、切向速度和实验结果的相对误差, 可以看到所有峰值的位置相对误差基本都在10%以内, 而速度峰值的相对误差, 在2 mm处的径向速度误差非常大, 其他地方的误差较小.其中, 表 2中h=2 mm轴向速度的比较位置有两个波峰, 分别指曲线中速度值最大的两处, 即中心旋流器和外旋流器出口气流的最大速度, h=5, 10 mm中波峰指曲线中速度值最大的位置, 波谷均指曲线中速度值最小的地方, 径向速度和切向速度的比较位置也是曲线中速度值最大的地方.选取这些点来比较是因为这些点的位置和速度值能很好地反映出计算值和实验结果之间的偏差.
| 下载CSV 表 2 时间平均轴向速度的相对误差 Tab.2 Relative errors of time-average axial velocity |
| 下载CSV 表 3 时间平均径向速度的相对误差 Tab.3 Relative errors of time-average radial velocity |
| 下载CSV 表 4 时间平均切向速度的相对误差 Tab.4 Relative errors of time-average tangential velocity |
实验中GTMC的燃料为商用航空煤油Jet-A, 本程序使用分子式C12H23代替真实组分, 其化学反应机理用烷烃通用的4步7组分反应机理[17], 步骤如下
| $ {{\rm{C}}_{12}}{{\rm{H}}_{23}} + 6{{\rm{O}}_2} \to 12{\rm{CO}} + 11.5{{\rm{H}}_2} $ | (ⅰ) |
| $ {{\rm{C}}_{12}}{{\rm{H}}_{23}} + 12{{\rm{H}}_2}{\rm{O}} \to 12{\rm{CO}} + 23.5{{\rm{H}}_2} $ | (ⅱ) |
| $ {{\rm{H}}_2} + \frac{1}{2}{{\rm{O}}_2} \to {{\rm{H}}_2}{\rm{O}} $ | (ⅲ) |
| $ {\rm{CO}} + {{\rm{H}}_2}{\rm{O}} \to {\rm{C}}{{\rm{O}}_2} + {{\rm{H}}_2} $ | (ⅳ) |
各步骤的反应速率[18]为
| $ {\dot r_{\rm{i}}} = 4.4 \times {10^{11}}\exp \left( {\frac{{ - 30\;000}}{{RT}}} \right){\rho ^{0.75}}\sqrt {{n_{{{\rm{C}}_{12}}{{\rm{H}}_{23}}}}} n_{{0_2}}^{1.25} $ |
| $ {\dot r_{{\rm{ii}}}} = 3.00 \times {10^8}\exp \left( {\frac{{ - 30\;000}}{{RT}}} \right)\rho {n_{{{\rm{C}}_{12}}{{\rm{H}}_{23}}}}{n_{{{\rm{H}}_2}{\rm{O}}}} $ |
| $ {\dot r_{{\rm{iii }}}} = \frac{{2.5 \times {{10}^{16}}}}{T}\exp \left( {\frac{{ - 40\;000}}{{RT}}} \right){\rho ^{0.75}}\sqrt {{n_{{{\rm{H}}_2}}}} n_{{0_2}}^{2.25}/{n_{{{\rm{H}}_2}0}} $ |
| $ {\dot r_{{\rm{iv}}}} = 2.75 \times {10^9}\exp \left( {\frac{{ - 20\;000}}{{RT}}} \right)\rho {n_{{\rm{CO}}}}{n_{{{\rm{H}}_2}{\rm{O}}}} $ |
热态工况的燃烧模拟是在冷态模拟的基础上进行的.先将边界条件改为热态的边界条件, 在不喷油且不加燃烧的情况下, 用AECSC程序先算出一个冷态的流场, 在此基础上喷油, 然后再利用程序自带的点火模型[19]进行点火、燃烧.实验没有对进口燃油的温度、速度和SMD进行测量, 考虑到燃油在垂直槽中有一个显著的温升和预蒸发, 将初始喷雾边界条件中的SMD设置为15, 温度设置为380 K, 速度设置为50 m/s.使用此进口燃油条件计算, 在燃烧室点火成功, 在流场基本稳定后统计平均了3个周期, 约3×106步.
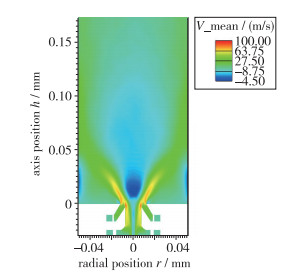
图 10展示了热态工况下的x=0平面平均轴向速度分布.和冷态的流场相比, 热态的进口流量变小了, 温度明显增大, 计算得到的热态下的空气密度变为冷态的将近4倍.所以无法直接比较两种工况下的速度大小.可以发现热态流场内回流区的范围和强度较冷态流场要大得多, 且向燃烧室下游延伸得远, 所以整个回流区非常大.但是流场的总体趋势和形态基本一致, 这说明液体燃料的加入和燃烧的发生对流场形态并没有产生太大的影响.
|
| 图 10 热态工况下x=0平面平均轴向速度云图 Fig.10 Average axial relocity on x=0 plane under the reaction conditions |
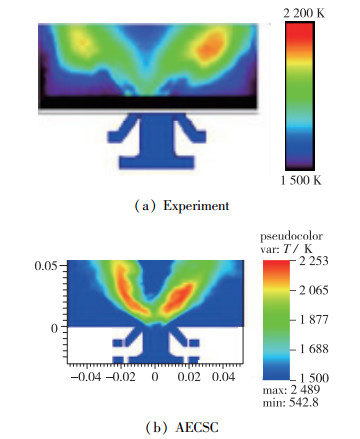
温度场可以直观地表示出燃烧状态. 图 11展示了在x=0平面实验测量的温度云图和AECSC程序计算得到的时间平均温度云图.实验温度是由OH的绝对密度计算出来的, 而OH的绝对密度是由瞬时平面激光诱导荧光技术(plane laser induced florescence, PLIF)测量得到的.可以看到, 程序模拟结果很好地再现了实验的V型火焰和内、外回流区.模拟得到的整体时间平均温度在数值上和实验结果比较接近, 模拟的最高温度为2 253 K, 而实验云图上标注的温度范围为1 500~2 200 K.同时, 模拟结果的内、外回流区的温度均低于1 500 K, 与实验结果吻合, 说明在这两个地方没有发生明显的化学反应.但是, 模拟结果的高温区位置相较实验结果更加靠前, 也很难看到实验中高温区的“耳垂”现象.分析可能是因为初始喷雾边界条件SMD过小或温度过高, 模拟时液体燃料相比实验情况的蒸发更快, 导致高温区提前, 且燃料在h=0.025 mm处就已经基本蒸发完全, 没来得及扩散成“耳垂”的形态.
|
| 图 11 x=0平面时间平均温度云图 Fig.11 Time-average temperatures on x=0 plane |
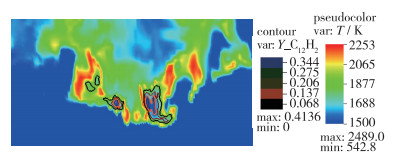
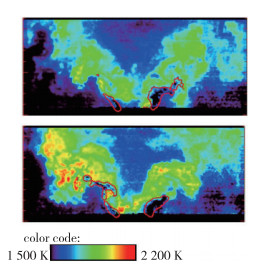
图 12展示了在x=0平面的瞬时温度云图, 图中的轮廓线为燃料蒸气(C12H23)的质量分数等值线. 图 13展示了实验的两个瞬时温度云图, 其中轮廓线代表了煤油在相应云图中下降到其最大值的10%的区域.
|
| 图 12 x=0平面瞬时温度云图和燃料(C12H23)质量分数等值线 Fig.12 Instantaneous temperature and contours of mass fraction of fuel on x=0 plane |
|
| 图 13 实验瞬时温度云图 Fig.13 Instantaneous temperature of experimental result |
可以看到模拟结果的瞬时火焰的分布和形状和实验很接近, 且均能看到明显的回流区.温度最高的区域位于燃料下游, 这是因为燃油初始温度较低, 燃油的蒸发很慢, 所以蒸气浓度过低, 无法快速达到可燃边界, 即使环境温度(大约1 000 K)达到了着火的要求, 在这个地方基本还是没有燃烧发生.反应前沿位于燃料穿透长度上游的区域, 表现出很大的脉冲波动, 所以会导致在时间上平均时, 燃料和平均温度的云图会发生明显重叠.还可以看到, 程序计算结果和实验结果中, 燃油轮廓线内的温度均低于1 500 K, 这是由于其中的当量比太高, 无法达到可燃性条件.
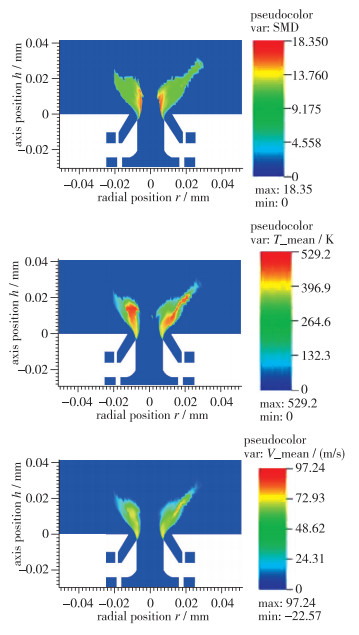
图 14展示的是x=0平面液滴统计情况, 从上到下依次为液滴平均直径、时间平均温度、时间平均轴向速度的云图.可以看到小液滴的扩散速度更快, 因此主要分布在喷雾锥的外部, 而大液滴停留在中心.从物理角度来看, 液滴越大惯性就越大, 而惯性越大就会使液滴通过向前流动平衡其切向速度, 从而使得径向速度就越高.此外, 液滴的温度在较大液滴存在的位置更高, 而且这些液滴的速度也比较大.同时, 液滴平均直径并不是沿锥形喷雾的中心面呈对称分布的, 大液滴要更靠近内回流区一些, 这说明较大的液滴进入了高温区域, 但是需要更长的时间才能完全蒸发.
|
| 图 14 x=0平面液滴平均统计云图 Fig.14 Average statistics of droplets on x=0 plane |
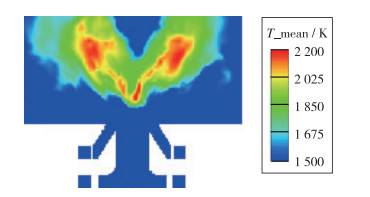
在此基础上, 本文更改了初始喷雾边界条件重新计算, SMD设置为20, 温度设置为340 K, 速度设置为50 m/s.使用此进口燃油条件计算, 在流场基本稳定后统计平均了1.5个周期, 约1.2×105步. 图 15展示了本次计算得到的x=0平面的时间平均温度云图.可以看到在更改了初始喷雾边界条件之后, 计算结果在较好地还原了V型火焰和内、外回流区的同时, 其高温区的位置和大小相较之前, 与实验结果更加接近.由此分析发现, 初始喷雾边界条件对流场以及高温区温度的影响不大, 但是对液滴蒸发速度的影响非常明显, 从而对高温区的位置产生了较大的影响.同时, 本次计算在火焰底部仍和实验结果有一些差异, 实验结果中V型火焰底部的温度较为平均, 约为1 800 K, 而在计算结果中还存在较窄的一部分温度约为2 200 K的高温区, 这可能是计算统计的周期不够, 流场并非完全稳定.
|
| 图 15 x=0平面液滴平均统计云图(修改喷雾边界条件之后) Fig.15 Time-average temperature on x=0 plane (After modifying the boundary conditions of the spray) |
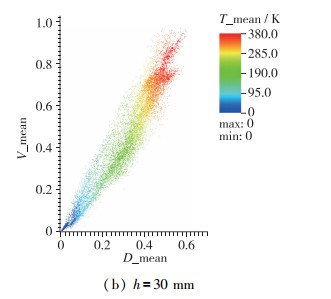
图 16展示了本次计算h=7 mm和h=30 mm的两处轴向位置处液滴平均速度与液滴直径之间的散点图.可以看到, 随着轴向距离的变化, 两者液滴平均速度与液滴直径的关系有所变化, 可以明显看到,图 16(a)中的某些位置上是没有散点的,这表明这些速度范围内的液滴的轴向速度并不是连续的, 在一定的速度区间内发生了断点情况.而随着轴向距离的增加, 可以看到散点图越来越均匀, 但同时范围也缩小了, 轴向速度的范围没有发生太大的变化, 而液滴平均直径的范围明显减小, 从0~0.9变为0~0.6, 说明随着轴向距离的增大, 液滴由于蒸发而慢慢减小, 这与液滴的SMD云图是吻合的.
|
| 图 16 平均液滴速度与直径的散点图 Fig.16 Scatter plot of average droplet velocity and diameter |
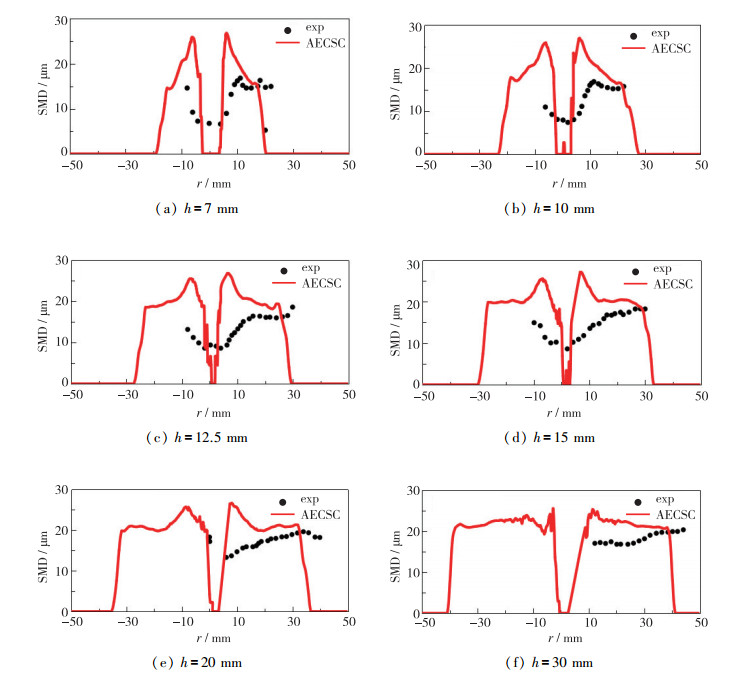
图 17展示了本次计算中6个轴向位置处液滴的Sauter平均直径(Sauter mean diameters, SMD)随径向位置的变化.其中, 黑点为实验结果, 红色实线代表程序模拟的结果.对实验数据进行分析可以得到, 随着轴向距离的增加, SMD的下降幅度很小.在内回流区, 液滴的SMD明显减小, 而在内回流区以外, 液滴的SMD沿径向变化相对较小.这种粒径分布符合典型的空心锥式雾化器的液滴分布, 即粒径较小的液滴出现在靠中心的位置, 而粒径较大的液滴移动到喷雾的边缘.随着液滴被气流带着往下游运动, 它们会慢慢蒸发, 而径向分布趋于更加均匀.
|
| 图 17 不同轴向高度处液滴SMD随径向位置的变化比较 Fig.17 Comparisons of the change of SMD with radial position at different axial height |
程序模拟的结果在上述特征中和实验结果基本符合.但是可以发现, 模拟结果还是存在一定误差.在内回流区处, 模拟结果显示这里的液滴SMD始终为零, 也就是内回流区没有液滴, 但是在实验结果中内回流区是有小液滴存在的.这可能是由于较小的液滴会跟随气体流动, 进入内回流区, 这可以从图 16所示的平均液滴速度与直径的散点图中看出.当这些小液滴获得一个负速度, 并进入温度较高的区域时, 那么它们可能会迅速蒸发, 导致这部分的计算结果上没有液滴.而在定量上的误差可以用图 15的平均温度场来解释.计算和实验的温度场有一定的偏差, 就平均温度场统计而言, 50 K的量级的差异可能是不显著的, 但由于温度对液滴蒸发速率存在很大影响, 液滴温度的等效增加将显著改变液滴尺寸.尤其在流场下游, 流场的预热作用效果逐渐累积, 对液滴的温度影响越来越大, 内回流区内的液滴温度分布和实验结果偏差变得更大, 同时还影响着液滴的速度, 这些都会对液滴的SMD分布产生影响.另外, 未知的初始喷雾条件也对SMD的准确模拟造成了一些困难.
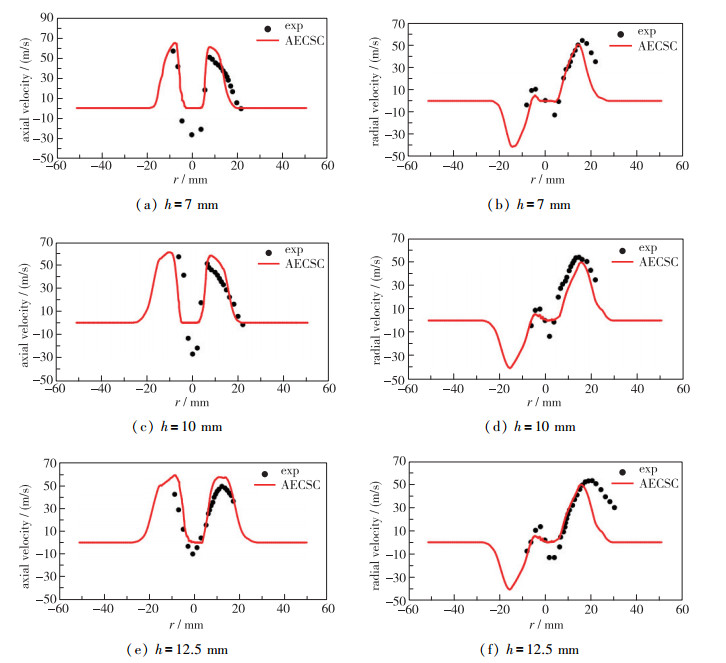
图 18展示了液滴的径向速度和轴向速度沿径向的分布和实验结果的比较, 黑点为实验结果, 红色实线代表程序模拟的结果.可以看到计算得到的液滴沿径向的速度分量和实验结果相比偏差不是很大.尤其在内回流区, 可以看到液滴径向速度和轴向速度和实验结果吻合得都很好.从上面对于液滴SMD分布的分析可以知道, 液滴在内回流区内的尺寸很小, 这些小液滴对于气流的跟随性很好, 所以在速度分布上和实验结果基本没有偏差.但是可以发现, 在3个高度位置, 除了在靠近中心线的位置由于计算结果没有液滴存在, 所以速度自然为零, 这一点和实验的偏差较大之外, 液滴的轴向速度分布和实验结果都吻合较好.而径向速度分布除了10 mm的吻合较好之外, 其他两个位置的外流区都有较大偏差.
|
| 图 18 液滴的速度分量的径向分布比较 Fig.18 Comparisons of the radial distribution of velocity of droplets |
本文用基于LES-PDF的AECSC两相程序对模型燃烧室GTMC分别进行了冷态与燃烧两种条件下的航空煤油燃料湍流燃烧模拟.冷态模拟时, 程序计算的模型燃烧室GTMC的轴向、径向、切向速度与实验结果的位置相对误差基本都在10%以内, 3个速度的峰值相对误差在大多数统计点上在20%以内.且程序计算的结果在一定程度上要比Fluent的LES结果更吻合实验结果, 表明AECSC程序可以用于旋流燃烧室及湍流流动的计算.燃烧模拟时, 程序计算得到的燃烧工况结果很好地再现了V型火焰和内外回流区, 且高温区和内外回流区的温度和实验结果非常接近, 但在高温区位置上存在一定的误差.从定性分析的液滴SMD、温度、速度等方面均符合物理实际和预计假设, 其分布也和实验结果基本吻合.
虽然模拟结果能够比较精确地再现各项实验测量值, 但在热态条件下, 由于喷雾的进口边界条件没有确定的实验数据, 这给模拟结果带来了一定的困难及误差.但是现有的结果还是表明选取了LES-PDF方法的AECSC程序能够比较精确地模拟出湍流燃烧过程, 在模型燃烧室的数值模拟能力和结果准确度方面有一定的优越性, 在航空发动机燃烧室等复杂结构的数值仿真方面有广阔的前景.
| [1] |
曹建国. 航空发动机仿真技术研究现状、挑战和展望[J]. 推进技术, 2018, 39(5): 961-970. Cao J G. Status, challenges and perspectives of aero-engine simulation technology[J]. Journal of Propulsion Technology, 2018, 39(5): 961-970. (in Chinese) |
| [2] |
彭泽琰, 刘刚. 航空燃气轮机原理[M]. 北京: 国防工业出版社, 2000: 274-277. Peng Z Y, Liu G. Principle of aviation gas turbine[M]. Beijing: National Defense Industry Press, 2000: 274-277. (in Chinese) |
| [3] |
Gupta A K, Lilley D G, Syred N. Swirl flows[M]. Tunbridge Wells, Kent England: Abacus Press, 1984.
|
| [4] |
Weber R, Dugué J. Combustion accelerated swirling flows in high confinements[J]. Progress in Energy and Combustion Science, 1992, 18(4): 349-367. DOI:10.1016/0360-1285(92)90005-L |
| [5] |
Syred N, Chigier N A, Beér J M. Flame stabilization in recirculation zones of jets with swirl[J]. Symposium on Combustion, 1971, 13(1): 617-624. |
| [6] |
Syred N, Beér J M. Combustion in swirling flows:A review[J]. Combustion and Flame, 1974, 23(2): 143-201. |
| [7] |
See Y C, Ihme M. LES investigation of flow field sensitivity in a gas turbine model combustor[R]. AIAA 2014-0621, 2014.
|
| [8] |
Wankhede M J, Tap F A, Schapotschnikow P, et al. Numerical study of unsteady flow-field and flame dynamics in a gas turbine model combustor[C]. Proceedings of ASME Turbo Expo 2014: Turbine Technical Conference and Exposition. Düsseldorf, Germany: ASME, 2014.
|
| [9] |
Weigand P, Meier W, Duan X R, et al. Investigations of swirl flames in a gas turbine model combustor:I. Flow field, structures, temperature, and species distributions[J]. Combustion and Flame, 2006, 144(1/2): 205-224. |
| [10] |
Jones W P, Tyliszczak A. Large eddy simulation of spark ignition in a gas turbine combustor[J]. Flow Turbulence and Combust, 2010, 85(3-4): 711-734. DOI:10.1007/s10494-010-9289-9 |
| [11] |
Prasad V N. Large eddy simulation of partially premixed turbulent combustion[D]. Imperial College London, 2011: 167-211.
|
| [12] |
Madnia C K, Jaberi F A, Givi P. Large eddy simulation of heat and mass transport in turbulent flows[M]. John Wiley & Sons, Inc., 2009.
|
| [13] |
Muradoglu M, Pope S B, Caughey D A. The hybrid method for the PDF equations of turbulent reactive flows:consistency conditions and correction algorithms[J]. Jour-nal of Computational Physics, 2001, 172(2): 841-878. DOI:10.1006/jcph.2001.6861 |
| [14] |
Valiño L. A field Monte Carlo formulation for calculating the probability density function of a single scalar in a turbulent flow[J]. Flow, Turbulence and Combustion, 1998, 60(2): 157-172. |
| [15] |
Meier U, Heinze J, Freitag S, et al. Spray and flame structure of a generic injector at aeroengine conditions[C]. Proceedings of ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition. Vancouver, Canada: ASME, 2011.
|
| [16] |
Freitag S, Meier U, Heinze J, et al. Measurement of initial conditions of a kerosene spray from a generic aeroengine injector at elevated pressure[C]. Proceedings of the 23rd Annual Conference on Liquid Atomization and Spray Systems. Brno, Czech Republic: ILASS, 2010.
|
| [17] |
Jones W P, Lindstedt R P. Global reaction schemes for hydrocarbon combustion[J]. Combustion and Flame, 1988, 73(3): 233-249. DOI:10.1016/0010-2180(88)90021-1 |
| [18] |
Jones W P, Marquis A J, Vogiatzaki K. Large-eddy simulation of spray combustion in a gas turbine combustor[J]. Combustion and Flame, 2014, 161(1): 222-239. |
| [19] |
Lacaze G, Richardson E, Poinsot T. Large eddy simula-tion of spark ignition in a turbulent methane jet[J]. Combustion and Flame, 2009, 156(10): 1993-2009. DOI:10.1016/j.combustflame.2009.05.006 |