边界层中层流-湍流的转捩不仅受自由流中扰动的影响,还受壁面粗糙度的影响.对于光滑壁面的情况,自由流扰动主要通过两种途径诱发转捩.若自由流中的湍流度很低,边界层转捩主要通过Tollmien-Schlichting(T-S)波的增长被触发,这一过程通常被称为自然转捩[1].自然转捩一般由感受性(T-S波的产生)线性失稳(T-S波的线性增长)非线性breakdown(扰动的非线性作用)以及湍流4个阶段组成.若自由流中的湍流度较高(一般大于1%的量级),转捩会逾越过T-S波的缓慢增长过程,这一过程被称为旁路转捩[2-4].在这一过程中,边界层内会首先出现流向条带结构[5].该结构可能从前缘产生(由边界区方程描述[6]),也可能在局部产生(由边缘层(edge layer)渐进解描述[7]).这种条带会诱发比T-S波的增长率高一个数量级的二次稳定性扰动,从而快速触发转捩[8-9].
即使壁面存在小粗糙元(一般小于边界层名义厚度的20%), 自然转捩过程也会受到影响.在感受性阶段, 壁面的粗糙元能通过和自由流中的声或涡扰动的相互作用而直接激发T-S波[10-11].这一机制与光滑壁面的前缘感受性机制完全不同, T-S波可以在中性曲线附近被激发, 这导致线性增长阶段的初始幅值增大.在线性稳定性阶段, 粗糙元对上游传播过来的T-S波有散射作用, 表现为幅值的局部突变[12].这两种机制都可以影响转捩的位置.但实验发现, 通过这种机制控制转捩效果有限.
Wheaton等[13]发现, 只有当粗糙元的高度增加到一定值时, 转捩位置才会明显向上游移动, 这一高度被称为临界高度.继续增加粗糙元高度, 当其值达到一定值时, 转捩会提前到紧挨着粗糙元的位置, 此时再增加粗糙元高度不会改变转捩位置, 这一高度被称为有效高度.用大粗糙元触发转捩有重要的工程应用背景, 如用于吸气式发动机的进气道.但是, 目前还缺乏对其转捩机理的理性认识.
工程上, 对粗糙元强制转捩的预测多基于对实验数据的拟合[14-15]. Tani [16]给出了转捩位置与来流Reynolds数和粗糙元高度的关系, 并定义了一个粗糙元Reynolds数Reh, 其长度尺度为粗糙元高度h.对于低速流, 转捩一般发生在Reh=500时.其后, Reshotko等[17]提出了一个改进的方法, 他们认为转捩Reynolds数与粗糙元高度成反比, 即Reθ, tr~(k/θ)-1(Te/Tw)-1/2, 其中Te与Tw分别表示来流与壁面温度, 在这个公式中, 壁面温度的影响也被考虑进来.对于绝热壁, Reshotko [18]进一步给出了公式Reθ, tr~(k/θ)-1Me.但是, 这些公式并没有考虑粗糙元的形状分布形式以及自由流湍流度等诸多因素的影响, 在很多情况预测结果与实际并不相符.
对转捩机理更精细的研究工作要基于稳定性理论. Marxen等[19]针对Mach数为4.8的边界层, 研究了二维大粗糙元(高度为无粗糙元时的当地边界层名义厚度的0.55倍)附近流场的稳定性.他们发现, 在粗糙元附近, T-S波的幅值被突然放大, 但却并不改变下游T-S波的增长率.这与Wu等[12]的结论相同.值得说明的是, 尽管二维粗糙元的高度达到了边界层名义厚度的一半以上, 其对转捩的促进作用仍是有限的, 因为它并没有改变由T-S波诱发自然转捩的机制.而如果粗糙元是三维的, 粗糙元的尾流场会出现流向涡对[20].这些涡对的出现使得基本流沿展向变化剧烈, 从而改变边界层的稳定性特性(表现出二维整体不稳定特性), 进而促进高增长率扰动的演化.这一过程属于旁路转捩范畴, 即T-S波在转捩过程中并不起作用.
对流不稳定性机制是对粗糙元强制转捩机理的一种解释. Chang等[21]计算了Mach数分别为4.1和6.5条件下矩形和圆柱形粗糙元的尾迹流, 并指出该尾迹流中的条带可能会产生对流不稳定性. Choudhari等[22]针对Mach数为3.5的超声速边界层, 分析了钻石型粗糙元尾迹流的二维整体稳定性, 得到了高增长率的余弦(对称)和正弦(反对称)模态的不稳定扰动, 而余弦模态的扰动更不稳定.但是, Choudhari等[23]对Mach数为6条件下粗糙元尾迹流稳定性的分析发现, 正弦模态扰动更不稳定.他们认为, 哪个模态的扰动主导转捩和粗糙元的几何形状参数及流动条件有关. Kegerise等[24]结合实验与数值方法, 究了Mach数3.5工况下粗糙元尾迹流的稳定性特性.他们发现, 当Reh=462时, 余弦模态扰动在转捩过程中起主导作用; 而当Reh=319时, 正弦模态扰动在转捩过程中起主导作用. De Tullio等[25]通过直接数值模拟, 计算了Mach数为2.5条件下大粗糙元诱导的尾迹流场; 并分别采用空间二维整体不稳定性(bi-global)分析与三维抛物化稳定性方程(PSE-3D)对扰动在尾迹流中的演化进行了研究.对于该研究工况, 高增长率的余弦和正弦模态的扰动都被发现, 但余弦模态的增长率更大.在粗糙元下游50倍粗糙元高度的位置处, 扰动增长了e9倍. De Tullio等[26]在对Mach数为6的高速边界层中, 发现粗糙元的尾迹中除了存在传统的余弦和正弦模态以外, 还存在一个额外的余弦模态.这一额外的模态与Blasius边界层中最不稳定的Mack模态有关.
引起粗糙元强制转捩的另一种可能机理是绝对不稳定性[3].这一机制在低速流的实验中被发现. Acarlar等[27]观察到在低速边界层中粗糙元的尾迹中存在发卡涡脱落的现象.但是, 这一现象还没有直接在超声速边界层中发现.另一方面, 一部分基于超声速或高超声速边界层的直接数值模拟研究发现[28-29], 即使不从外界引入任何非定常的扰动, 仍然可以在粗糙元尾迹中得到非定常的涡, 以及下游处的转捩.这说明粗糙元附近的流场可能存在某种绝对不稳定性机制, 它可以把数值误差放大.但是, 由于粗糙元的尾迹中并没有明显的涡脱落现象, 说明其下游流场还是由对流不稳定性主导的.
虽然粗糙元强制转捩的机理还有许多不清楚的地方, 但有一点是明确的, 即粗糙元的尾迹流中的条带结构能支持高增长率的扰动.这些扰动属于对流不稳定机制.这本质上是对旁路转捩理论的扩展. Dong等[3]对旁路转捩的研究发现, 从二次失稳扰动的出现到转捩breakdown的完成并不是一个显然的过程, 在该过程中存在许多复杂的非线性现象. Loiseau等[30]采用直接数值模拟的方法, 研究了不稳定模态在粗糙元尾迹流中的非线性演化.但是, 该研究并未包含转捩的breakdown过程.本文拟以高超声速边界层为研究对象, 研究粗糙元尾迹中从不稳定扰动的产生到触发转捩的全过程, 以探求导致转捩的内在机理.
1 计算条件与数值方法 1.1 物理模型与计算条件本文研究的物理模型是一个带有孤立粗糙元的半无限长平板, 其中粗糙元的高度与边界层厚度量级相当.该模型以小攻角放置在高超声速来流中.
本文的计算参数与Danehy等[31]的实验工况以及Chang等[21]的计算工况相同.来流Mach数为9.65, 来流温度为53.3K, 单元Reynolds数为3.513×106/m.在距离楔形板前缘92.1mm处, 放置一个长1mm, 宽8mm, 高2mm的粗糙元.共计算两个攻角条件, 条件1:攻角为-10°; 条件2:攻角为-20°.楔形板的表面温度为308K.
1.2 无量纲化本文采用无量纲化的N-S方程组进行数值模拟.速度温度密度与黏性系数以来流参数U∞, T∞, ρ∞与μ∞无量纲化, 选取1mm为特征长度L.这样, 定义Reynolds数为
| $Re=\frac{{{ρ}_{\infty }}{{U}_{\infty }}L}{{{\mu }_{_{\infty }}}}.$ |
对于本文的计算工况, Re=3513.
1.3 数值方法对粗糙元强制转捩的数值研究一般有两种方法.一种是用高精度格式直接模拟粗糙元转捩的全过程, 如文献[28-29].研究发现, 即使不引入任何外界非定常扰动, 也可以在粗糙元下游观察到转捩.这一现象可以与静风洞中的实验结果直接比较[32].但是, 由定常的初始流场计算出非定常扰动的原因尚不清楚.一种可能的解释是粗糙元周围存在某些绝对不稳定性机制, 数值扰动在该机制下被放大.但这一绝对不稳定机制并不是导致转捩的直接原因, 否则转捩应该发生在粗糙元附近.只有对流不稳定性机制可能是导致下游转捩的合理解释, 而绝对不稳定机制的作用是给对流不稳定模态提供非定常的初始扰动.这种研究方法的缺点是把所有扰动混在一起计算, 不利于对转捩机理的进一步分析.
另一种研究方法是采用低精度的CFD计算存在粗糙元的边界层的定常基本流动, 如文献[21-23].由于低精度格式耗散较大, 数值扰动不易被放大, 从而可以得到定常的基本流场.该基本流场可作为稳定性分析的基础.
本文采用第2种数值研究方法.首先, 用CFD方法计算存在大粗糙元的边界层流动, 以得到定常的基本流场. CFD代码“openCFD_EC_v0.95”由中国科学院力学研究所李新亮提供.该代码基于有限体积法, 并运用多块结构化网格技术.对流项采用3阶MUSCL格式, 时间上采用1阶显格式.
然后, 选取粗糙元的尾迹流场, 对其网格加密, 并采用高精度格式重新计算, 以得到高精度的基本流.由于此时计算域不包含粗糙元附近的区域, 流场中无绝对不稳定性机制, 所以数值误差不会被放大而激发流场中的非定常扰动.在本文高精度的计算中, 对流项采用5阶迎风格式, 黏性项采用6阶中心型格式, 时间采用2阶Runge-Kutta法.具体数值格式与计算方法详见文献[3]和[33].
基于得到的高精度基本流进一步做稳定性分析.由于粗糙元的尾迹流场中存在定常的流向条带结构, 且其流向尺度远大于法向和展向尺度, 本文引入流向平行流假设, 对尾迹流场进行二维稳定性分析.
最后, 以得到的高增长率的不稳定模态为初始扰动, 用直接数值模拟(DNS)的方法计算扰动的演化直至转捩到湍流.
2 基本流的计算 2.1 CFD的计算域与网格本文的计算采用Descartes坐标, (x, y, z)分别表示流向法向与展向坐标.坐标原点o设置在粗糙元底面的中心处.
计算域和网格如图 1所示.图中给出的是z=0平面内的计算域与网格分布侧视图, 不同灰度表示不同分块.流向计算域为-100≤x≤160, 楔形体的前缘设置在x=-92.1处.粗糙元落在-0.5≤ x ≤0.5, 0≤ y ≤2, -4≤ z ≤4的区域内, 右上角图为局部放大图.网格在粗糙元附近加密.在展向, 由于流场沿着粗糙元中心轴z=0对称, 所以只需计算一半, 而在z=0面上采用对称边界条件.展向计算域为0≤ z ≤10.计算条件中只有计算域的展向宽度与Chang等[21]的不同, 他们选取的是0≤ z ≤20.

|
| 图 1 计算域与网格示意图 Fig.1 Sketch of the computational domain and meshes |
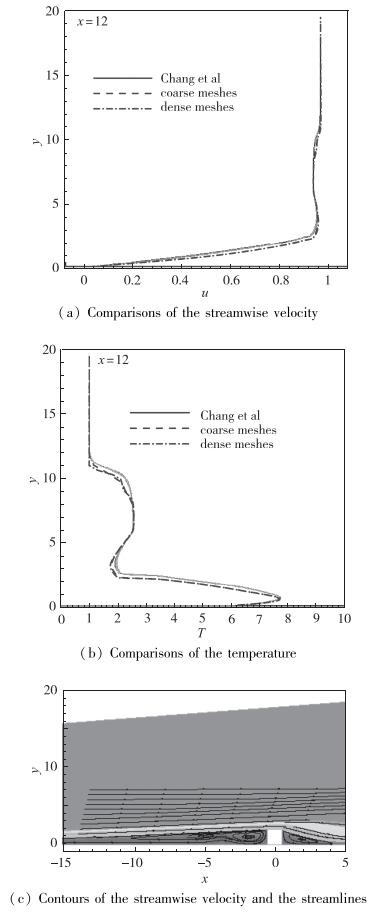
文献[21]同时给出了二维粗糙元情况下的计算结果.首先计算相同的工况以验证CFD计算的可靠性.选取的计算域与图 1相同.本文选择两套不同规模的网格计算:粗网格为35848个网格点, 密网格为111853个网格点. 图 2(a)和(b)分别给出了x=12处速度和温度剖面.两套网格的计算结果完全重合, 这说明本文选取的粗网格已经具有足够的分辨率.同时, 本文的计算结果与文献[21]的结果也吻合得很好. 图 2(c)给出由粗网格计算出的流向速度云图和流线的分布.在粗糙元前后均可观察到明显的分离区, 其规律同样与文献[21]的结果吻合.
|
| 图 2 二维粗糙元的计算结果 Fig.2 Computational results for 2D roughness elements |
首先用CFD方法计算三维粗糙元情况下的基本流场.本文共选取3套规模的网格, 网格数分别为:粗网格4356220, 中网格7292620, 密网格9963620.这3套网格的计算误差趋于收敛, 以下采用密网格的结果做进一步计算.
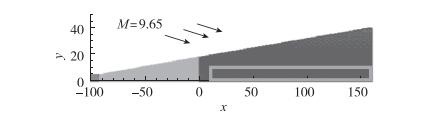
为获得更加精确的粗糙元尾迹流场, 本文在粗网格计算结果的基础上用高精度格式重新计算.此时的计算域不包含粗糙元, 并把展向拓展为-10≤ z ≤10, 以适应后文对扰动演化的模拟.计算域的选取如图 3所示, 即10≤ x ≤150, 0≤ y ≤9.54, -10≤ z ≤10.计算域入口及上边界处的边界条件由之前CFD低精度方法所得的计算结果给定.计算网格为401 × 151 × 128, 并通过网格加密验证了结果的可靠性.
当计算扰动在粗糙元尾迹流中的演化时, 入口取在x=20处, 以舍去入口附近由于格式改变而引起的不光滑流场段.
|
| 图 3 高精度格式的计算域示意图 Fig.3 Sketch of the computational domain for the calculation of the high-order numerical method |
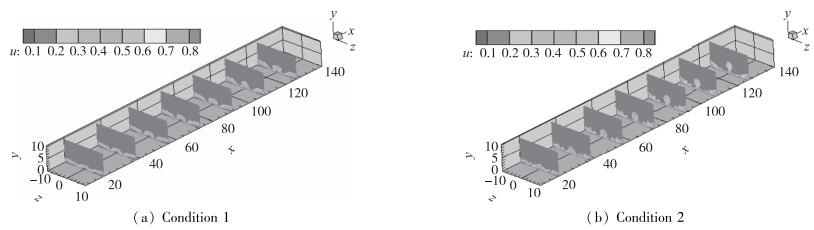
图 4(a)和(b)给出了两种计算条件下不同流向位置的流向速度云图.可以看出在尾流中存在着明显流向涡对, 其分布规律与不可压缩边界层中由自由流涡扰动引起的流向条带结构[4, 8]相似.这很可能导致无黏失稳, 从而产生余弦或正弦模态.
|
| 图 4 粗糙元尾迹流中不同流向位置的流向速度云图 Fig.4 Contours of the streamwise velocity in the wake flow behind the roughness elements at different streamwise locations |
若楔形板表面没有粗糙元, 基本流将满足Blasius相似性解.这一结论也被CFD的计算证实.在背景湍流度很低的条件下, 此时边界层转捩将被T-S波失稳而触发.
对T-S模态的求解来自线性稳定性理论(linear stability theory, LST).由于基本流沿流向变化缓慢, 在平行流假设下流场可被看作是一维的.把扰动写成波动形式并代入线性化的N-S方程组, 可得到Orr-Sommerfeld (O-S)方程.这种分析方法比较基础, 具体介绍可参见文献[34].
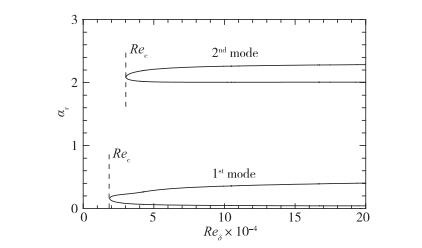
通过CFD计算, 可得到条件1下斜激波后的Mach数约为6.5, 温度约为117.2K.以这一条件下的Blasius解为基本流, 求解O-S方程, 得到了第1和第2模态扰动的中性曲线(展向波数β=0), 如图 5所示, 其中纵轴α表示无量纲的流向波数, 参考长度为边界层的排移厚度δ, 横轴是以排移厚度δ为特征长度的Reynolds数.可以看出, 第1模态和第2模态T-S波失稳的临界Reynolds数Rec分别约为20000与30000.
|
| 图 5 条件1下Blasius边界层的中性曲线 Fig.5 Neutral curves of Blasius boundary layer for Condition 1 |
对于条件1, 通过CFD计算可得到计算域出口(x=150) 附近处边界层的排移厚度为2.62mm, 其对应的以排移厚度为特征长度的Reynolds数是11790.这比临界Reynolds数小很多, 说明在本文条件1下, 没有传统意义的不稳定T-S模态.
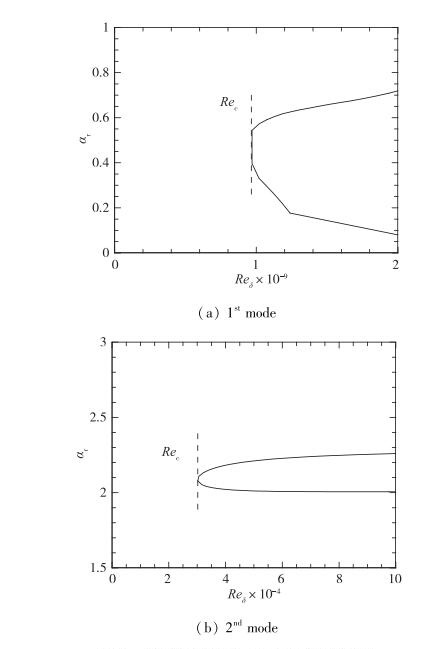
类似地, 对于条件2, 计算得到斜激波后的Mach数约为4.1, 温度约为238K. 图 6给出了该计算条件下第1和第2模态扰动的中性曲线.可以看出, 第2模态的临界Reynolds数Rec大约在30000处, 而第1模态的要大得多.从CFD计算中, 得到计算域出口处的Reynolds数约为9400.这也比临界Reynolds数小很多, 说明在条件2下, 流场中也没有不稳定T-S模态.
|
| 图 6 条件2下Blasius边界层的中性曲线 Fig.6 Neutral curves of Blasius boundary layer for Condition 2 |
因而, 对于本文研究的计算条件而言, 如不对楔形体表面施加人为干扰, 不会发生自然转捩.
3.2 粗糙元尾迹流的二维稳定性分析 3.2.1 二维稳定性分析方法在粗糙元尾迹流中, 流动的流向尺度明显大于法向和展向尺度.因而引入流向平行流假设, 把基本流看作某一给定流向位置x0的二维剖面, 即
| $\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {\mathit{y},\mathit{z};{\mathit{x}_{\rm{0}}}} \right){\rm{ = }}\left[ {\mathit{\boldsymbol{U}},\mathit{\boldsymbol{T}},p} \right]\left( {y,z;{x_{\rm{0}}}} \right),$ | (1) |
其中U =(U, V, W), 分别表示基本流的流向法向和展向速度.扰动也可被写成
| $\mathit{\boldsymbol{\varphi }}\mathit{\boldsymbol{'}}\left( {\mathit{y},\mathit{z},\mathit{t}} \right){\rm{ = }}\left[ {\mathit{\boldsymbol{u'}},\mathit{\boldsymbol{T'}},\mathit{p'}} \right]\left( {\mathit{y},\mathit{z},\mathit{t}} \right),$ | (2) |
其中u′=(u′, v′, w′), 分别表示扰动的流向法向和展向速度, t为时间.
把扰动(2) 代入N-S方程组并对扰动做线性化处理, 可得到扰动随时间的演化方程
| $\frac{{\partial \;\;\mathit{\boldsymbol{\varphi '}}}}{{\partial {\rm{t}}}} = \mathit{\boldsymbol{F}}(\;\mathit{\boldsymbol{\varphi '}}{\mkern 1mu} ;{\mkern 1mu} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}),$ | (3) |
其中, F反映基本流与扰动之间的线性作用.这本质上是一个初值问题, 即
| $\left\{ \begin{array}{l} \frac{{\partial {\mkern 1mu} \mathit{\boldsymbol{\varphi }}\prime }}{{\partial t}} = \mathit{\boldsymbol{A}}({\mkern 1mu} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mkern 1mu} ){\mkern 1mu} \mathit{\boldsymbol{\varphi }}\;\prime \\ \mathit{\boldsymbol{\varphi }}{\mkern 1mu} \prime ({\rm{0}}){\rm{ = }}\mathit{\boldsymbol{\varphi }}{{\mkern 1mu} _{\rm{0}}} \end{array} \right.,$ | (4) |
其中, A=∂F/∂φ′, φ0=(u0, T0, p0), 且u0=(u0, v0, w0).
Bi-global分析是最常用的对二维基本流场做稳定性分析的方法.首先把扰动(2) 写成波动形式, 即
| $\mathit{\boldsymbol{\varphi }}\mathit{'} = \mathit{\boldsymbol{\hat \varphi }}\left( {y,z} \right)\; \cdot {\mkern 1mu} {{\rm{e}}^{{\rm{i}}\left( {\alpha x{\rm{ - }}\omega t} \right)}} + c.c.,$ | (5) |
其中,
采用时间模式进行分析, 即ω包含非0虚部.把式(5) 代入式(4), 可得到一个特征值问题
| $ - {\rm{i}}\omega \mathit{\boldsymbol{\hat \varphi = A}}\left( \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \right)\mathit{\boldsymbol{\hat \varphi }}.$ | (6) |
上式可通过数值方法(如Arnoldi迭代)求解.
研究表明, 若初始条件φ0选择合适, 直接求解初值问题(4) 与bi-global分析(6) 所给出的最不稳定模态完全吻合, 如文献[35].本文采取直接求解初值问题(4) 的方法进行稳定性分析.具体做法是
1) 首先选取一个流向位置x0的基本流剖面(1), 把它平行布置在选定的计算域中作为基本流.流向计算域的长度选取为2π/α, 其中α为流向波数.
(2) 在初始时刻t=0引入任意扰动φ 0.由于要寻找的模态不同, φ 0的选择方法也不同, 如表 1所示.其中a0=10-8, 以保证扰动随线性规律演化;
| 下载CSV 表 1 设置φ0的方法 Tab.1 Methods to choose φ0 |
(3) 再用扰动方程计算扰动随着时间的演化规律.流向的边界条件为周期边界条件.引入的初始扰动并不是特征方程(6) 的解, 但是, 它可以看做是一系列特征模态的线性叠加.这些模态的增长率各不相同.经过一段时间的演化后, 增长率最大的波将成为占压倒优势的波, 因而扰动的幅值A(t)将按eωit的规律增长, 其中ωi对应最不稳定波的时间增长率.于是, 可根据
| ${{\omega }_{\rm{i}}}\to \frac{\rm{ln}\left( \mathit{A}\left( \mathit{t} \right)-\mathit{A}\left( {{\mathit{t}}_{0}} \right) \right)}{\left( t-{{t}_{0}} \right)}\quad \rm{as}\quad \mathit{t}\to \infty, $ |
反求出增长率, 其中t0是一个主导波已经占优的时刻.
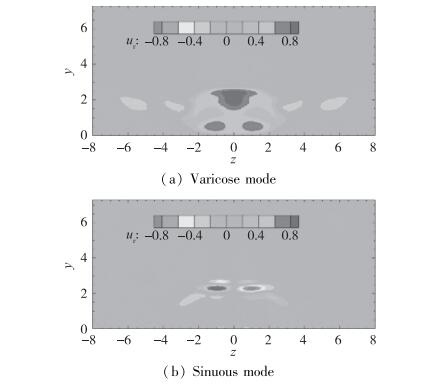
3.2.2 二维稳定性分析结果取条件1下x=37.6处的基本流剖面, 计算了流向波数α=0.6情况下的最不稳定时间模式扰动的特征函数. 图 7分别给出了余弦和正弦模态的流向速度特征分布.对于余弦模态, 流向速度法向速度温度与压力相对于z=0轴对称, 但展向速度则相对于z=0轴反对称.正弦模态的对称性质则正相反.
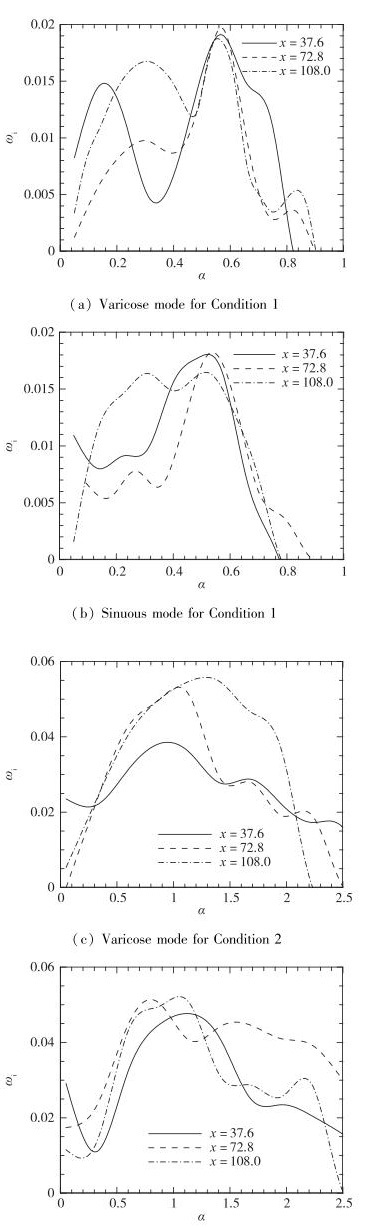
图 8给出了不同流向位置处增长率ωi随流向波数的分布.余弦模态与正弦模态的增长率都在0.01的量级.从数值上来看, 对于同一计算条件, 余弦模态和正弦模态的扰动增长率相近.但是, 条件2下的增长率明显大于条件1.这与实验结果[31]相吻合, 即-20°攻角情况比-10°攻角情况更容易发生转捩.
|
| 图 7 时间模式下流向速度特征函数的实部, 计算条件为条件1, 其中α=0.6 Fig.7 Real parts of the eigen-functions of the streamwise velocities for temporal evolutions under Condition 1, where α=0.6 |
|
| 图 8 时间模式增长率ωi随流向波数α的分布 Fig.8 Temporal mode growth rates vs. streamwise wave numbers |
若扰动沿空间演化, 时间的初值问题(3) 和(4) 要改写成对流向坐标的初值问题.线性化的N-S方程组写成
| $\frac{{\partial \mathit{\boldsymbol{\varphi '}}}}{{\partial x}} = \mathit{\boldsymbol{\bar F}}\left( {\mathit{\boldsymbol{\varphi '}}{\rm{ }};\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right){\rm{ }},$ | (7) |
则对流向坐标的初值问题可写成
| $\left\{ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{\varphi '}}}}{{\partial x}} = \mathit{\boldsymbol{\bar A}}\left( \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \right)\mathit{\boldsymbol{\varphi ',}}\\ \mathit{\boldsymbol{\varphi '}}\left( {{x_0}} \right) = {\mathit{\boldsymbol{\varphi }}_0} \end{array} \right.$ |
其中,
稳定性分析通过直接求解初值问题(7) 来实现:
(1) 首先选取一个流向位置x0的基本流剖面(1), 同样做平行流假设.与时间模式求解方法不同的是, 由于扰动沿流向演化, 流向计算域要足够长.
(2) 然后在入口x=x0处引入任意扰动φ0, 其设置方法见表 1.
(3) 再用扰动方程计算扰动随着空间的演化规律, 流向出口采用嵌边边界条件.在计算域的下游区域, 扰动的幅值A(x)将按e-αix的规律增长, 其中-αi对应最不稳定波的空间增长率.因而可根据
| $ - {\alpha _i} \to \frac{{{\rm{ln}}\left( {A\left( x \right) - A\left( {{x_{\rm{0}}}} \right)} \right)}}{{\left( {x - {x_0}} \right)}}\quad {\rm{as}}\quad x \to \infty ,$ |
反求出增长率, 其中x0是一个主导波已经占优的流向位置.
4.2 空间模式下的二维稳定性分析结果由于条件2下不稳定波的增长率较大, 下面的研究以该计算条件为基础.选取计算域入口为x0=20, 扰动频率为ω=0.8.
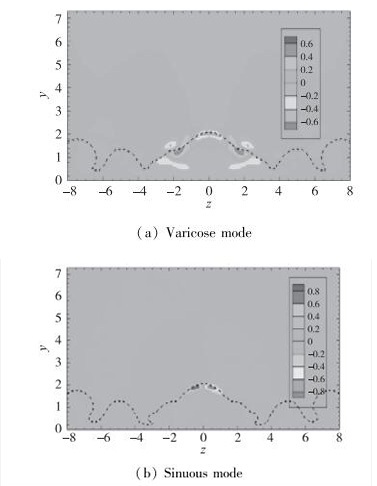
通过计算, 分别得到了余弦和正弦模态的不稳定波, 其特征参数如表 2所示.对于该计算条件, 正弦模态扰动的增长率略大于余弦模态, 且两种模态的相速度接近. 图 9给出两种模态扰动的特征函数分布.图中的虚线表示流向速度与不稳定波相速度相同的位置, 这一层被称为临界层.扰动特征函数的峰值恰好落在临界层上, 这说明该不稳定模态属于无黏模态.
| 下载CSV 表 2 不稳定模态的特征值 Tab.2 Eigen-values of the instability modes |
|
| 图 9 空间模式下流向速度特征函数的实部, 计算参数为条件2, 其中ω=0.8 Fig.9 Real parts of the eigen-function of the streamwise velocity for spatial evolution under Condition 2, where ω=0.8 |
4.2节的稳定性分析都是基于平行流假设得到的, 本节将对扰动在尾迹流中的演化进行直接模拟, 以观察非平行流效应的影响.
选取流向计算域为20≤x≤120, 在入口处分别引入余弦模态扰动(图 9(a))与正弦模态扰动(图 9(b)).为了保证扰动以线性规律演化, 扰动的初始幅值设置为A0=10-8.
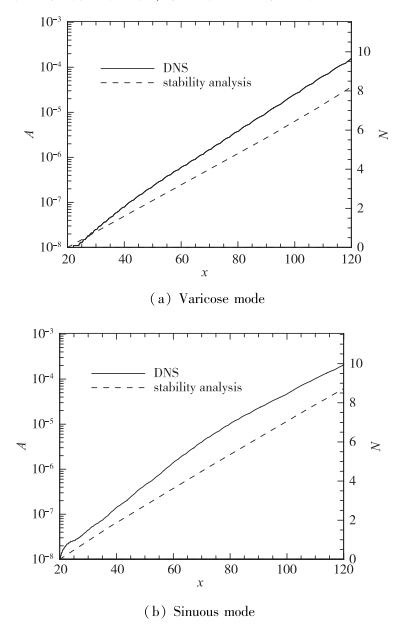
图 10给出了由DNS计算出的不稳定模态的幅值增长曲线, 并与稳定性分析结果进行比较.图中的纵坐标为对数形式, 幅值放大因子N定义为
| $N = {\rm{ln}}\left( {A\left( x \right){\rm{/}}{A_{\rm{0}}}} \right),$ |
其中A(x)是当地幅值.可以看出, 在短短100mm的区域范围内, 两种模态的扰动都几乎放大了10000倍, 放大因子N已接近10.这说明即使初始扰动为10-8, 转捩也可能发生.而对于实际的扰动, 转捩发生位置应远在计算域出口的上游处.另外, 由于非平行流效应的影响, DNS计算出的幅值比稳定性分析的结果大, 但二者的差别只是定量的.
|
| 图 10 不稳定模态在尾迹流中的空间演化过程 Fig.10 Spatial evolutions of the unstable modes in the wake flow |
要想解决转捩问题, 对扰动线性演化的研究是远远不够的, 因而本文对有限幅值扰动的非线性演化进行了模拟, 以观察扰动之间的相互作用以及转捩的过程.另外, 不稳定模态特征函数的峰值只集中在x-o-z平面上的一个小区域, 扰动怎样从局部区域扩散到整个流场, 并导致层流的breakdown, 也是一个值得关注的问题.
选取的计算域仍与图 3相同, 基本流仍选图 4(b)的结果, 计算网格数加密为1151151192.由于在实际情况中, 除了不稳定模态, 流场中还会存在一些其他形式的扰动.因此, 在入口处, 除了引入频率为0.8的余弦模态(扰动Ⅰ, 幅值为AⅠ)和频率为0.6的正弦模态(扰动Ⅱ, 幅值为AⅡ)外, 还引入一系列频率为ωrandom=0.2的随机扰动(扰动III), 随机扰动的分布形式为
| $u{{\mathit{'}}_{\rm{random}}}={{\mathit{A}}_{\rm{Ⅲ}}}\underset{n=1}{\overset{10}{\mathop{\Sigma }}}\, {{\tilde{u}}_{n}}\left( y \right){{\rm{e}}^{\rm{i}\left( n{{\beta }_{0}}z={{\phi }_{n}}-{{\omega }_{random}}\mathit{t} \right)}}, $ |
其中,
本文共计算了3种转捩工况, 各工况下引入扰动的幅值如表 3所示.
| 下载CSV 表 3 各工况下引入扰动的幅值 Tab.3 Amplitudes of the introduced disturbances for different cases study |
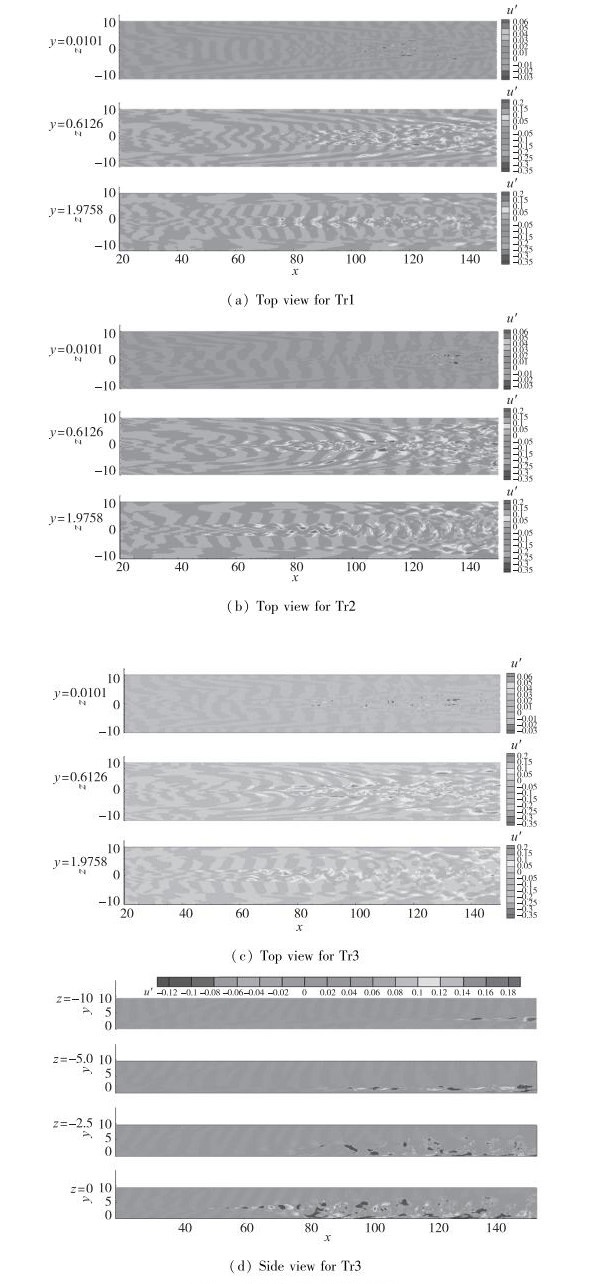
通过计算得到了扰动的非线性演化及转捩的整个过程. 图 11给出了瞬时脉动速度u′的云图, 其中, 图 11(a)~(c)分别为3种工况下不同法向高度处x-o-z平面切片的俯视图.对于Tr1工况, 从y=1.9758切片图可以看出, 在开始阶段, 随机扰动Ⅲ的存在使得流场没有呈现对称规律; 但随着向下游的演化, 扰动Ⅲ的幅值迅速减小.到x=50以后, 扰动沿中心线对称分布的规律非常明显, 表现出余弦模态的特征, 并且其幅值迅速放大.在x=100以后, 扰动的对称性开始被破坏, 这是由于有限幅值的余弦模态扰动与随机扰动的非线性作用所致.余弦模态的峰值分布在y=2左右, 所以在3张切片图中, y=1.9758切片图中的扰动首先达到0.015, 并表现出强非线性作用.随着向下游的演化, 扰动的峰值逐渐向壁面靠近, 最后在近壁区引起较大的脉动.
工况Tr2的非线性演化规律与Tr1相似.只是在不稳定模态的增长阶段, 起主导作用的扰动是反对称的正弦模态.故可以看到扰动的峰值沿中心线交替出现的现象.另外与Tr1相比, Tr2工况更早地进入扰动的非线性作用阶段, 湍斑出现得更早.这是由于引入的扰动Ⅱ的线性增长率大于扰动Ⅰ.
如图 11(c)所示, 工况Tr3同时引入了余弦模态和正弦模态的不稳定波, 故在随机扰动经过一段距离的衰减后, y=1.9758切片图的瞬时扰动既有对称的特征(中心线附近), 又有反对称的特征(z=±1.5附近), 且幅值的峰值分布在z=±1.5附近.与Tr1和Tr2类似, 扰动由在y=2附近的峰值分布向壁面扩散, 并在展向向全流场扩散. 图 11(d)给出了Tr3工况下不同展向位置的侧视图.扰动首先在y=2附近达到有限幅值.随着向下游的演化, 大幅值扰动向着壁面方向扩散, 距离中心线越远的位置湍斑出现得越晚.
|
| 图 11 中文标脉动速度u′的分布云图题 Fig.11 Contours of the fluctuation velocity u′ |
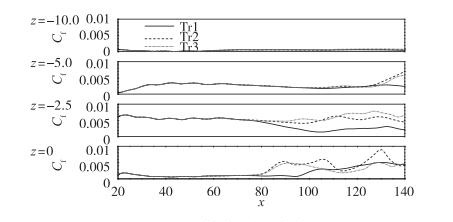
图 12给出了不同展向位置处的壁面摩擦系数曲线(Cf曲线)随流向的分布.Cf曲线的定义为
| ${{C}_{\text{f}}}=\frac{\left( \bar{\mu }\partial \bar{u}/\partial y \right)\text{w}}{{{\rho }_{\infty }}u_{\infty }^{2}/2},$ |
其中
以上说明, 高增长率的不稳定模态的确可以触发转捩, 其过程是在特征函数峰值附近的局部位置首先出现湍斑, 然后随着向下游的演化扰动向全局扩散, 直到进入湍流阶段.
|
| 图 12 Cf曲线的流向分布 Fig.12 Streamwise distributions of Cf curve |
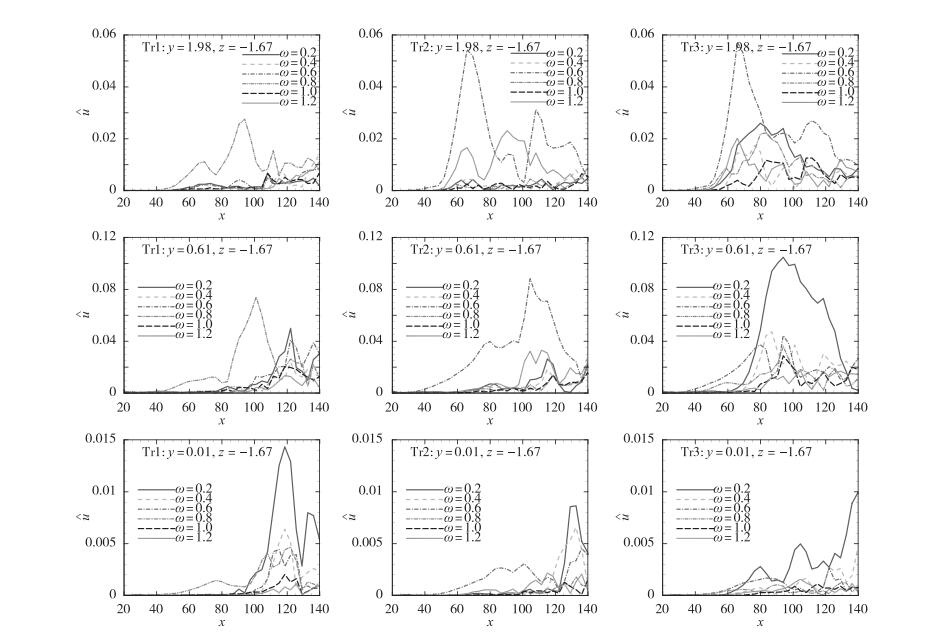
基于这3种工况, 图 13给出了z=-1.67平面3个法向位置处扰动速度Fourier分量û的流向演化.û的定义是
| $\hat u\left( {\mathit{x},y,z,N} \right) = \frac{1}{\mathit{T}}\int \begin{array}{l} T\\ 0 \end{array} u\mathit{'}\left( {x,y,z,t} \right){{\rm{e}}^{{\rm{ - i2 }}{\rm{ \mathsf{ π} }}{\rm{ }}\mathit{Nt}/\mathit{T}}}{\rm{d}}t,$ |
其中, T=31.4.本文也尝试计算T=62.8的情况, 发现结果差别很小.图中6条曲线分别对应N取1到6, 其中N=4(ω=0.8) 对应于引入的余弦模态扰动, N=3(ω=0.6) 对应于引入的正弦模态扰动, N=1(ω=0.2) 对应于随机扰动.第1行选取的法向位置为y=1.98, 对应于不稳定模态的峰值位置.在开始阶段, 工况Tr1与Tr2的主导频率分别为ω=0.8与ω=0.6, 它们分别在x=60与50的位置幅值达到1%.在该位置以后, 非线性效应明显增强, 从而其他频率的扰动被激发并增长, 这导致转捩的发生.由于正弦模态的扰动首先累积到有限幅值, 故工况Tr2和Tr3的转捩位置比工况Tr1发生得早.在工况Tr3的初始阶段, ω=0.8与ω=0.6分量分别与工况Tr1和Tr2的增长规律相似.但是从x=60开始, 由于它们之间的非线性作用, 差频ω=0.2分量的幅值比前两种工况大得多, 其他频率的扰动也由于非线性作用出现比前两种工况大的幅值.
|
| 图 13 3种工况下扰动Fourier分量的流向演化 Fig.13 Streamwise evolutions of the Fourier components of the disturbances for three cases |
在靠近壁面的区域(第2行和第3行图), 扰动迅速增长的起始点晚于y=1.98处, 这与云图的观察结果相同.在工况Tr3中, 各扰动分量迅速增长的位置明显早于工况Tr1和Tr2.值得注意的是, 在第2行最右侧的图中, ω=0.2分量的幅值以及增长率都远远超过了ω=0.6和0.8的分量, 显然这说明ω=0.2分量的快速增长不是由这两个不稳定模态非线性作用引起的. Dong等[3]在对旁路转捩的breakdown过程的研究中发现, 在强非线性作用阶段, 平均流剖面稳定性的迅速变化是转捩过程的关键, 该扰动分量的迅速增长恰是平均流剖面稳定性所决定的.
对于本文研究的工况, Tr2的转捩位置明显早于Tr1.这是由于引入的正弦模态扰动的增长率大于余弦模态.而工况Tr2与Tr3的转捩位置非常接近, 这说明在Tr3中, 虽然存在余弦和正弦模态扰动相互作用的现象, 但它们对转捩的影响并不明显.在整个转捩过程中, 正弦模态仍起主导作用.
Li等[36]在对横流边界层转捩的DNS研究中, 发现了类似的结论, 即余弦和正弦模态扰动的相互作用非常弱.这是由于对于他们的研究工况, 两种模态特征函数的峰值不在同一法向位置, 即相速度不同.而对于本文的工况, 即使两个模态相速度很相近, 它们之间的相互作用仍然非常弱.这是因为余弦和正弦模态扰动特征函数的峰值虽然处于同一法向位置, 但却不在同一展向位置处.从图 9可以看出, 余弦模态特征函数的峰值分布在中心线z=0轴上, 而正弦模态特征函数在z=0轴上的值为0.这说明, 余弦和正弦两种模态的扰动在通常情况下的相互作用是非常弱的.
6 结论由于粗糙元尾迹中存在流向条带结构, 高增长率的余弦和正弦不稳定模态可以在T-S波所对应的临界Reynolds数之前被激发.这表现出旁路转捩的特性.
通过对小幅值不稳定模态在粗糙元尾迹流中演化的模拟, 发现两种不稳定模态都可以在尾迹流中持续地线性增长, 并在短短100 mm距离内, 不稳定波被放大了近10000倍.非平行效应使不稳定模态增长更快.
过对粗糙元尾迹流转捩的模拟, 验证了这些对流不稳定模态是导致转捩的主导因素.转捩过程是首先在余弦或正弦模态的峰值附近出现局部湍斑, 然后逐渐向壁面扩散.在工况Tr3的转捩过程中, 发现低频扰动ω=0.2的增长速度明显高于引入的不稳定模态(ω=0.6和ω=0.8), 这说明扰动的非线性作用在转捩过程中进一步修正了平均流剖面, 使其稳定性发生明显变化.而平均流剖面稳定性的变化是转捩breakdown过程得以快速完成的关键机理.另外, 余弦和正弦模态之间的相互作用很弱, 对于本文的研究工况, 后者在转捩过程中起主导作用.
致谢 感谢中国科学院力学研究所的李新亮研究员为作者提供CFD程序代码, 感谢天津大学力学系的周恒教授张永明博士吴雪松教授和罗纪生教授在本文写作过程中提出的宝贵意见.| [1] |
Kachanov Y S. Physical mechanisms of the laminar-boundary-layer transition[J]. Annual Review of Fluid Mechanics, 1994, 26(1): 411-482. DOI:10.1146/annurev.fl.26.010194.002211 |
| [2] |
Morkovin M V. Bypass transition to turbulence and research desiderata[R]. NASA CP-2386 Transition in Turbines, 1984 : 161-204. http://www.tandfonline.com/doi/ref/10.1080/14685248.2011.573792
|
| [3] |
Dong M, Zhou H. A simulation on bypass transition and its key mechanism[J]. Science China : Physics, Mechanics and Astronomy, 2013, 56(4): 775-784. DOI:10.1007/s11433-013-5036-2 |
| [4] |
Qin H, Dong M. Boundary-layer disturbances subjected to the free-stream turbulence and simulation on bypass transition[J]. Applied Mathematics and Mechanics, 2016, 37(8): 967-986. DOI:10.1007/s10483-016-2111-8 |
| [5] |
Klebanoff P S. Effect of free stream turbulence on a laminar boundary layer[J]. Bulletin of American Physical Society, 1971, 16(11): 1323-1334. |
| [6] |
Lei S J, Wundrow D W, Goldstein M E. Effect of free-stream turbulence and other vortical disturbances on a laminar boundary layer[J]. Journal of Fluid Mechanics, 1999, 380: 169-203. DOI:10.1017/S0022112098003504 |
| [7] |
Dong M, Wu X. On continuous spectra of the Orr-Sommerfeld/Squire equations and entrainment of free-stream vortical disturbances[J]. Journal of Fluid Mechanics, 2013, 732: 616-659. DOI:10.1017/jfm.2013.421 |
| [8] |
Ricco P, Luo J, Wu X. Evolution and instability of unsteady nonlinear streaks generated by free-stream vortical disturbances[J]. Journal of Fluid Mechanics, 2011, 677: 1-38. DOI:10.1017/jfm.2011.41 |
| [9] |
Zhang Y, Zaki T, Sherwin S, et al. Nonlinear response of a laminar boundary layer to isotropic and spanwise localized free-stream turbulence[R]. AIAA 2011-3292, 2011. https://www.researchgate.net/publication/268558548_Nonlinear_Response_of_a_Laminar_Boundary_Layer_to_Isotropic_and_Spanwise_Localized_Free-stream_Turbulence
|
| [10] |
Wu X. Receptivity of boundary layers with distributed roughness to vortical and acoustic disturbances : a second-order asymptotic theory and comparison with experiments[J]. Journal of Fluid Mechanics, 2001, 431: 91-133. DOI:10.1017/S0022112000002962 |
| [11] |
De Tullio N, Ruban A I. A numerical evaluation of the asymptotic theory of receptivity for subsonic compressible boundary layers[J]. Journal of Fluid Mechanics, 2015, 771: 520-546. DOI:10.1017/jfm.2015.196 |
| [12] |
Wu X, Dong M. A local scattering theory for the effects of isolated roughness on boundary-layer instability and transition : transmission coefficient as an eigenvalue[J]. Journal of Fluid Mechanics, 2016, 794: 68-108. DOI:10.1017/jfm.2016.125 |
| [13] |
Wheaton B M, Schneider S P. Roughness-induced instability in a laminar boundary layer at Mach 6[R].AIAA 2010-1574, 2010. https://engineering.purdue.edu/~aae519/BAM6QT-Mach-6-tunnel/tunnelpapers/2010-1574.pdf
|
| [14] |
Reda D C. Review and synthesis of roughness-dominated transition correlations for reentry vehicles[J]. Journal of Spacecraft and Rockets, 2002, 39(2): 161-167. DOI:10.2514/2.3803 |
| [15] |
Schneider S P. Effects of roughness on hypersonic boundary-layer transition[J]. Journal of Spacecraft and Rockets, 2008, 45: 193-209. DOI:10.2514/1.29713 |
| [16] |
Tani I. Boundary layer transition[J]. Annual Review of Fluid Mechanics, 1969, 1: 169-196. DOI:10.1146/annurev.fl.01.010169.001125 |
| [17] |
Reshotko E, Tumin A. Role of transient growth in roughness-induced transition[J]. AIAA Journal, 2004, 42: 766-770. DOI:10.2514/1.9558 |
| [18] |
Reshotko E. Is Reθ/Me a meaningful transition criterion[J]. AIAA Journal, 2007, 44: 1441-1443. |
| [19] |
Marxen O, Iaccarino G, Shaqfeh E S. Disturbance evolution in a Mach 4.8 boundary layer with two-dimensional roughness-induced separation and shock[J]. Journal of Fluid Mechanics, 2010, 648: 435-469. DOI:10.1017/S0022112009992758 |
| [20] |
Asai M, Minagawa M, Nishioka M. The instability and breakdown of a near-wall low-speed streak[J]. Journal of Fluid Mechanics, 2002, 455: 289-314. |
| [21] |
Chang C L, Choudhari M M. Hypersonic viscous flow over large roughness elements[R]. AIAA 2009-0173, 2009.
|
| [22] |
Choudhari M, Li F, Wu M, et al. Laminar-turbulent transition behind discrete roughness elements in a high-speed boundary layer[R]. AIAA 2010-1575, 2010.
|
| [23] |
Choudhari M, Li F, Bynum M, et al. Computations of disturbance amplification behind isolated roughness elements and comparison with measurements[R]. AIAA 2015-2625, 2015. http://www.annualreviews.org/doi/citedby/10.1146/annurev.fl.23.010191.003125
|
| [24] |
Kegerise M, King R, Owens L, et al. An experimental and numerical study of roughness-induced instabilities in a Mach 3.5 boundary layer[R]. RTO-MP-AVT-200. Art. 29, NATO, 2012. https://link.springer.com/article/10.1007/s00193-014-0514-7
|
| [25] |
De Tullio N, Paredes P, Sandham N D, et al. Laminar-turbulent transition induced by a discrete roughness element in a supersonic boundary layer[J]. Journal of Fluid Mechanics, 2013, 735: 613-646. DOI:10.1017/jfm.2013.520 |
| [26] |
De Tullio N, Sandham N D. Influence of boundary-layer disturbances on the instability of a roughness wake in a high-speed boundary layer[J]. Journal of Fluid Mechanics, 2015, 763: 136-165. DOI:10.1017/jfm.2014.663 |
| [27] |
Acarlar M S, Smith C R. A study of hairpin vortices in a laminar boundary layer. Part 1. Hairpin vortices generated by a hemisphere protuberance[J]. Journal of Fluid Mechanics, 1987, 175: 1-41. DOI:10.1017/S0022112087000272 |
| [28] |
Duan Z, Xiao Z. Direct numerical simulation of geometrical parameter effects on the hypersonic ramp-induced transition[R].AIAA 2014-2495, 2014. https://es.scribd.com/document/289311049/Xalatin-Zest
|
| [29] |
Iyer P S, Muppidi S, Mahesh K. Roughness-induced transition in high speed flows[R]. AIAA 2011-566, 2011. https://www.researchgate.net/profile/Prahladh_S_Iyer/publication/268565987_Roughness-Induced_Transition_in_High_Speed_Flows/links/5654fec508ae4988a7b08c50.pdf
|
| [30] |
Loiseau J, Robinet J, Cherubini S, et al. Investigation of the roughness-induced transition : global stability and analyses and direct numerical simulations[J]. Journal of Fluid Mechanics, 2014, 760: 175-211. DOI:10.1017/jfm.2014.589 |
| [31] |
Danehy P M, Garcia A P, Borg S, et al. Fluorescence visualization of hypersonic flow past triangular and rectangular boundary layer trips[R]. AIAA 2007-536, 2007. http://www.academia.edu/15057667/Hypersonic_viscous_flow_over_large_roughness_elements
|
| [32] |
Schneider S P. Developing mechanism-based methods for estimating hypersonic boundary-layer transition in flight : the role of quiet tunnels[J]. Progress in Aerospace Sciences, 2015, 72: 17-29. DOI:10.1016/j.paerosci.2014.09.008 |
| [33] |
Dong M, Zhang Y M, Zhou H. A new method for computing laminar-turbulent transition and turbulence in compressible boundary layers-PSE plus DNS[J]. Applied Mathematics and Mechanics (English Edition), 2008, 29(12): 1527-1534. DOI:10.1007/s10483-008-1201-z |
| [34] |
周恒, 赵耕夫. 流动稳定性[M]. 北京: 国防工业出版社, 2004 : 87-92. Zhou H, Zhao G F. Hydrodynamic stability[M]. Beijing : National Defense Industry Press, 2004 : 87-92(in Chinese). http: //www. oalib. com/paper/4250296 |
| [36] |
Pando M F, Schmid P J, Sipp D. A global analysis of tonal noise in flows around aerofoils[J]. Journal of Fluid Mechanics, 2014, 754: 5-38. DOI:10.1017/jfm.2014.356 |
| [37] |
Li F, Choudhari M M, Duan L. Stationary crossflow breakdown due to mixed mode spectra of secondary instabilities[R].AIAA 2016-3789, 2016. http://scholarsmine.mst.edu/mec_aereng_facwork/3540/
|



