20世纪, 以Prandtl和Von Kármán为代表的德国哥廷根应用力学学派开辟和发展了对应用问题的力学理论分析, 特别是极大地推动了航空工程和航天工程的迅速发展.正如Von Kármán在航空工程开展50年之际写成的《空气动力学的发展》中做出了这样的评价: “空气动力学所经历的路程并不比航空技术的发展有何逊色.我们对于为什么飞行和如何飞行的知识在广度和深度上的增长都是异常惊人的”; “这门科学的发展是数学人和有创造力的工程师通力合作的一个稀有例子.从纯数学家的园地中出来的数学理论居然被发现适宜于用来描写飞行器绕流, 而且异常精确, 可直接应用于飞机设计” [1].
钱学森在加州理工学院期间, 对发展高速空气动力学和火箭技术做出了重大贡献.基于他的前瞻性视野, 他在1948年[2]和1957年[3]提出了“工程科学”的概念, 拓展了应用力学的范畴.他为此开拓了“工程控制论”和“物理力学”.他强调工程科学的目标是要创造工程技术的理论. Von Kármán在其回忆录(1967年)中写道: “钱学森是加州理工学院的火箭小组元老, 第二次世界大战中为美国的火箭研制做出过重大贡献.他36岁时已经是一位公认的天才, 他的研究工作大大地推进了高速空气动力学和喷气推进技术的发展.我有鉴于此, 才举荐他为空军科学顾问团成员. ”钱学森叙述了研究工程科学的思想和方法论, 要求从工程和实践中抽象出科学问题, 基于自然科学理论建立简化力学模型, 通过数学手段求解, 得到理论结果, 再经过实际检验, 从而“创造出工程技术的理论”.这种“从实际中来, 到实际中去”的思想, 在流体力学领域中就体现为应用流体力学.
从上世纪后期到本世纪, 由于工程中的流体力学问题越来越复杂, 随着数值模拟技术迅速发展, 数值计算得到研究人员的广泛使用, 而理论建模的方法成为人们稀缺的手段.这是否意味着应用流体力学的研究手段已经过时了呢?我们有理由为此而担心.
从1999年起, 童秉纲带领博士生和青年教师, 在两个研究方向(生物运动力学和近空间尖头体气动加热预测)尝试采用理论建模方法和流动物理分析的途径, 得到了某些有益的结果.以下两节分别简要介绍我们在这两个研究方向上的具体实践.
1 飞行与游动的生物外部流体力学 1.1 昆虫高频拍翼的理论建模20世纪末期, 人们开始关注飞行器的微型化, 逐渐形成了微型飞行器研制的一股热潮.但是, 空气动力学家们根据相似性原理分析, 发现普通固定翼飞机缩尺后的流动Reynolds数(流体惯性力与黏性力的比值, 缩写为Re)很低, 表面的边界层较厚, 这导致固定翼无法产生足够的气动力来维持飞行.然而, 自然界中飞行昆虫给予了人们更多的灵感, 它们的尺寸大都在cm甚至mm量级, 飞行性能优异, 兼具小巧快速机动和抗干扰等特性.除了蝴蝶采用Weis-Fogh的机制外, 大多飞行昆虫都是依靠高频的拍翼方式来实现了复杂多变的飞行能力, 频率通常在几十至几百Hz, 有的甚至上千.因此, 采用拍翼替换固定翼是微型飞行器的一种选择.
为了揭开昆虫拍翼产生高气动力的机制, 人们通过实验数值计算和理论建模的方法进行了大量的研究. Ellington等[4]通过风洞实验发现, 系留的鹰蛾拍翼飞行时翼前缘存在很强的分离涡, 这引起了高升力; Dickinson等[5]通过模型实验研究了果蝇翼模型拍动, 提出了3个潜在的机制:延迟失速旋转环量和尾迹捕捉; Sun等[6]通过三维数值模拟, 研究了果蝇拍翼, 也提出了高升力的3个作用机制:果蝇翅膀挥拍初期的快加速不失速以及挥拍末期的快速上仰机制; Yu等[7]提出了理论建模的方法, 从理论上把变速运动前缘涡和后缘涡对气动力的贡献分解开来, 提出了高升力的产生和调节主要依靠的流动控制因素:附加惯性效应增强后缘涡抑制前缘涡.
针对昆虫拍翼的强非定常黏性流动, 如何做到理论模化的呢?
第1步, 简化拍翼的物理模型.通常, 昆虫翅膀的展弦比在5.7~11.6之间, 平均值为8.3, 而且翅膀的厚度是翅长度的0.015%~ 0.106%, 平均在0.057%左右[8].所以, 把运动中的昆虫翅膀简化成厚度被忽略的板.进一步地, 作为初次近似, 忽略翅膀的变形, 视其为刚性平板.由于三维拍翼运动产生的升力系数与距翅基回转半径处的昆虫翼剖面的二维拍动所得到的升力系数接近(果蝇的回转半径约为0.6), 故而三维拍翼运动可被简化为距翅基回转半径处的昆虫翼剖面的二维平板做沉浮和俯仰振动的组合.
第2步, 流动特征分析及理论建模.采用拍动翼的弦长为特征长度, 挥拍周期为特征时间, 空气密度为特征密度, 则昆虫拍翼飞行的控制参数有两个:一个是表征非定常性的Strouhal数(流体非定常力与惯性力比值, 缩写为St), 另一个是表征黏性大小的Reynolds数.昆虫的尺度越小, Reynolds数越低.对于尺度为10~1mm的昆虫, Reynolds数为103~101.在航空设计中这意味着空气的黏性足够大, 无法产生足够的飞行升力, 被称作低Reynolds数的气动局限性.另一方面, 昆虫尺度越小, 其拍翼频率越高, 小型昆虫的频率超过100 Hz.对于这类昆虫翅膀高频拍动产生的流动, 其非定常性很强, St数接近于1.对于由昆虫高频拍翼产生的流动而言, 流动的非定常性远大于黏性, 即
| $St \gg 1/{Re}{.}$ |
此不等式成了非定常性抑制黏性效应的判据, 从流动的控制方程(Navier-Stokes方程, 简称N-S方程)来看, 黏性项就显得不是那么重要了.据此, 可对拍翼引起的强非定常低Reynolds数流动进行空气动力学理论建模.
昆虫翼高频拍动的强非定常效应主要表现在以下两个方面:强变速运动引发了流体同步作用——附加惯性效应, 以及因高频拍翼产生的流体迟滞作用——壁面黏性薄层和前后缘脱涡效应.由此, 可以提出这样一个简化气动模型: (1) 由于昆虫振翅的强非定常流动满足$St \gg 1/{Re}{.}$, 可以将流体运动的控制方程做一次近似, 略去黏性项, 把振翅的外部流场看作是无黏势流; (2) 在翅膀表面上附着一层很薄的非定常不可压缩边界层(视为附着涡层), 以及在翅膀的前缘和后缘处自由剪切层形成的前缘涡和后缘涡卷起并脱泻, 这反映了黏性效应的本质, 与流动的物理图像相符.
第3步, 求解及分析.根据以上建模, 采用经典的解析手段求解出速度场, 并由此确定拍翼的非定常气动性能, 结果表明此理论建模方法可以得到定量合理定性正确的分析结果.由此建立了适用于昆虫拍翼飞行的非定常空气动力学分析方法[9].
对昆虫拍翼飞行的空气动力学理论建模的优势在于可以分解出产生非定常高气动力主要因素.通过对昆虫大攻角拍翼的非定常空气动力学的流动物理进行了再探讨, 获得了两点新认识.其一, 理论建模方法的成功应用, 证实了在强非定常黏性流动中, 表征流场非定常运动能够克服由低Reynolds数带来的气动局限性.其二, 昆虫往复拍翼产生和调节高升力的流动控制因素有3个[7, 9] : (1) 拍翼的变速运动带来瞬时的流体动力响应, 这种附加惯性效应可产生瞬时高升力; (2) 增大后缘涡的强度并加速其脱离后缘能够有效地提高升力; (3) 使前缘涡在拍翼行程中不脱离翼面有助于维持高升力.
1.2 鱼类的自主推进建模与流动物理分析对鱼类游动机理的探索始于1936年的Gray佯谬[10]. Gray采用刚性海豚模型估算游动中海豚所受到的阻力, 发现海豚维持游动所需的功率损耗是其肌肉可提供功率的7倍.这引起了人们探究鱼类游动的极大兴趣.随后的几十年中, 关于游动的理论实验和计算工作层出不穷.实验方面包括活体观测和模型实验, 在此不再赘述.而理论和计算方面的工作大致可以分为两个阶段.
第1阶段, 在非自主框架下研究游动机理.这类研究体现在设置来流, 鱼体的运动是指定的.理论工作相继有: Taylor的抗力理论[11], Lighthill的细长体理论[12-13], Wu的二维波动板理论[14-15], Cheng等的三维波动板理论[16].这些理论都是鱼游流体力学领域具有里程碑意义的工作.计算流体力学(CFD)的发展, 使鱼游研究领域多了一个重要的研究手段.比如, Liu等[17-18]对蝌蚪波状摆动数值模拟, Zhu等对金枪鱼的数值研究[19].陆夕云课题组[20-22]从鱼游中抽象出更基础的模型, 数值研究了生物推进的机理.这类研究还扩展到多体相互干扰的复杂问题[23-26].
第2阶段, 自主推进的研究.所谓自主推进, 就是鱼体的运动须通过求解运动控制方程获得, 不是指定的.特别是研究鱼体机动运动时, 如何辨识鱼体的整体运动速度(平动和转动)与变形速度就显得格外重要. Carling等[27]于1998年首次发表了鱼类自主推进的数值模拟工作.随后, 陆续有关于自主推进的国外工作[28-31]以及国内吴锤结课题组[32-34]和童秉纲课题组[35-37]等的工作发表.最初的自主推进模拟方法中都做了一定简化, 与真正的自主游动存在差异, 直到童秉纲课题组明确给出二维变形体动力学控制方程[35-36], 才逐渐认识到自主推进的力学模型必须满足的基本原则.
自主推进的力学模型必须满足这样的流动物理:把生物体与流体介质看作一个系统, 整个系统满足质量守恒动量守恒和动量矩守恒.那么, 鱼体的游动是鱼体与水的相互作用(内力)的结果.在这个问题中, 如何区分变形体的整体运动和变形运动, 如何耦合求解变形体控制方程与流体力学控制方程是实现自主推进的关键.
首先, 把鱼体看作变形体, 鱼体上的任一点的速度可以分解为整体平动速度转动速度和变形速度.其中, 平动速度指质心的速度, 转动速度是该点绕质心的转动速度.把3个速度代入动量和动量矩方程, 化简后得到整体平动和转动的控制方程以及变形速度满足的限制方程, 即变形体动力学控制方程组[35-36], 从而提出了生物体变形速度与整体运动速度的分解准则.
然后, 通过预估-矫正迭代算法来实现变形体动力学方程与流体力学控制方程(N-S方程)的耦合[36].在整个的建模过程中, 提出区分变形体的整体运动速度和变形速度分解准则是关键.
以上的建模使得计算鱼体的自主推进成为可能.对于波状摆动的二维鱼体(鲹科类), 周期性的波动产生了稳定的前游速度, 据此, 鱼体受到的合力为0.那么, 鱼体尾迹中的旋涡该如何排列呢?结果发现, 自主推进的二维鱼体尾迹中正向和反向涡交替排列成一条线, 既不是Karman涡街, 也不是反Karman涡街[35].在对鱼类C型快速起动(鱼体弯曲成C型然后迅速回摆)的研究后发现, 鱼体的转弯角度和转弯末期的游速与实验给出的测量结果相符(在相同的鱼体变形量下).进一步分析表明, 转弯角度和末期游速依赖于C型弯曲程度和弯曲过程中叠加的行波变形, 且对行波的初始相位敏感; C型起动后的尾迹结构清晰干净, 呈三涡结构, 且三涡连线与鱼体垂直, 如图 1所示, 这符合涡量动力学的分析结果[36].

|
| 图 1 仿鱼C型起动的流场结构 Fig.1 Flow structures caused by a fish-like C-start |
无论是昆虫飞行还是鱼类的游动, 都需要从流动问题的主要特征出发, 抓住其中的关键因素, 建立相应的理论模型, 然后通过数学的方法或者计算手段, 获得重要结果, 并与实验数据或者物理图像进行对比, 检验建模的正确性, 从而取得对流动物理的新认识.
2 近空间尖头体气动加热预测 2.1 问题描述最近10多年来, 美国俄罗斯和中国等世界大国都在发展近空间高超声速巡航飞行器[38-40].为了追求较高的升阻比和良好的机动性能, 这类飞行器采用尖头薄翼的外形和低冗余度精细化的热防护系统设计理念, 因而飞行器气动热环境的精确预测成为亟待解决的关键技术之一.
由于近空间空气密度较低, 分子平均自由程较大, 因而以Knudsen数Kn来衡量, 尺寸小至mm量级的前缘局部区域会出现近连续流或稀薄过渡流动, 稀薄气体效应对流动和和传热的影响显著.同时, 由于飞行速度较高, 飞行器头部形成很强的激波, 强激波后高温条件下, 空气中的氧气和氮气分子将发生振动能激发离解-复合等一系列物理化学过程, 称为高温真实气体效应.在低密度条件下, 真实气体效应涉及的过程往往是非平衡的, 即Damköhler数Da为中等大小.我们面对的是高速高温局部稀薄和热-化学非平衡的流动传热问题, 传统的理论方法, 如基于连续介质假设和平衡边界层假设的Fay-Riddell公式[41]已经失效.
稀薄气体效应和非平衡真实气体效应, 成为我们建立新型飞行器气动热预测方法遇到的最主要障碍, 周恒与张涵信称之为当前空气动力学的新问题[42].当两种效应同时起作用时, 传统天地换算相似律也将失效, 我们甚至无法进行地面风洞试验和标模检验.目前, 解决工程实际问题主要依靠数值模拟手段和形成于几十年前的经验公式[43-44], 可靠性和鲁棒性都值得商榷.
为了探讨高超声速稀薄非平衡流动物理, 并为工程标模检验和快速估算提供理论支撑, 我们在前期研究[45-51]中开展了一系列关于尖头体气动加热受稀薄气体效应和非平衡真实气体效应的模型理论分析工作, 得到了一些初步结果, 可视为对“工程科学”思想的一次具体实践.此处省略具体的推导细节, 只对建模过程和主要结果做一简要介绍.
2.2 模型理论分析我们关注的是气动加热最严重的前缘驻点区域, 因而主要的工作是对沿驻点线的准一维流动进行模化分析, 所得部分结果可以向其他区域推广.
真实飞行器的前缘有各种不同的设计, 但在分析基本的流动和传热特征时, 飞行器体前缘或翼前缘模型可近似为一个高超声速来流中前缘曲率半径RN不断缩小的微钝尖锥体或楔体, 如图 2所示, 其中M∞为自由来流Mach数.当RN很大时, 该模型也涵盖了经典的大钝头航天器外形设计.
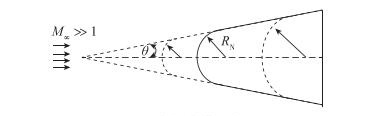
|
| 图 2 尖化前缘示意图 Fig.2 Schematic diagram of a sharp leading edge |
典型的气动加热特征对应着典型的流场结构, 我们首先需要弄清楚当前流动的具体特征.如图 3所示, 前缘驻点附近流动具有典型的3层结构, 其中Δ, δ和d分别表示激波脱体距离驻点边界层厚度和激波本身的厚度.当来流条件和前缘曲率半径变化时, 流动可以从连续极限逐渐过渡到稀薄, 一直到自由分子流极限, 也可以从热-化学平衡极限逐渐过渡到非平衡, 一直到冻结极限.相应地, 流场中激波和边界层的区域也可以不断增长重叠干扰甚至完全混为一体.
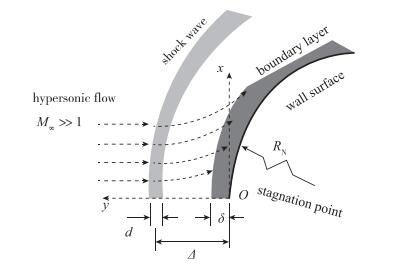
|
| 图 3 高超声速流动前缘驻点流场示意图 Fig.3 Typical hypersonic flow field around a nose |
稀薄气体效应的微观本质是由于分子碰撞率降低导致的碰撞非平衡效应, 我们提出了与之对应的宏观物理模型来描述其对传热的影响, 即non-Fourier传热模型.该模型认为真实热流密度q是两部分之和, 其一是经典的线性Fourier定律预测的ql, 其二是非线性热流密度修正项qnl.基于摄动的思想, 从比Navier-Stokes-Fourier方程更高阶的Burnett方程出发, 在驻点附近区域推导出了qnl的具体表达式, 并进一步把qnl与ql之比值定义为一个流动特征参数, 最终可表示为Wr=2JM∞2ω/Re∞, 其中Re∞=ρ∞V∞RN/μ∞为来流Reynolds数, J=0或1分别对应二维和轴对称外形, ω为气体的黏性-温度幂律的幂指数.
Wr衡量了流动偏离Navier-Stokes-Fourier方程描述的程度, 即流动的稀薄程度, 是一个在当前问题中具体化的Knudsen数, 或称为稀薄流动判据[46, 50].它不但能够归一化预测各种流动稀薄程度下的气动加热特征, 还定量描述了图 3中流场结构随稀薄程度的演化过程.后来, 在研究驻点下游及高超声速平板流动中热流-摩阻广义Reynolds比拟关系时[52-53], 也基于同样思想提出了non-Newton剪切模型, 结果表明Wr是一个在各类高超声速稀薄流动问题中普适的判据, 可以用来构建气动力/热受稀薄气体效应的预测桥函数.这种在近连续领域采用非线性本构关系进行理论分析的思想, 最近也被美国Singh和Schwartzentruber研究组[54-55]所采用, 他们分析了比Burnett方程更高阶的super-Burnett方程, 其所给出的修正参数仍然是Wr, 并证明Wr能够很好地归一化驻点热流及驻点下游热流分布情况.
在当前流动问题中, 高温真实气体效应和稀薄气体效应往往是同时出现且互有关联的.为了研究非平衡真实气体效应对前缘气动加热的影响, 提出了能量沿驻点线传递和转化的广义物理模型, 把流动过程拆解为3个步骤, 分别是强激波后的非平衡流动沿驻点线的等焓滞止流动和驻点边界层流动.
首先, 基于Lighthill和Freemann的理想离解气体模型研究了正激波后化学非平衡流动, 推导得到了气体平衡离解度αe(即原子质量分数)非平衡特征尺度χe(即松弛距离)和非平衡过渡过程α(χ)的近似解析预测算式, 详见文献[48, 50].
其次, 推导出了前缘头激波后驻点线滞止非平衡流动与上述正激波后非平衡流动之间的解析映射关系, 如图 4所示.据此关系, 可以直接预测出驻点线上的非平衡流动状态.特别地, 驻点边界层外缘处的气体离解度相当于正激波后χδ≈Δln (Δ+d/2)/δ处的离解度情况.进一步把χδ和χe之比值定义为前缘驻点线流动的离解非平衡判据Dad, 并基于Dad给出了驻点边界层外缘离解度的归一化预测算式[48, 50].结果发现, 驻点边界层外缘流动并非总是传统气动热预测理论所默认的平衡状态, 在近连续或稀薄条件下, 它往往是离解非平衡的.这正是建立稀薄流动领域气动热预测理论的关键所在, 即不但要讨论边界层内部原子复合反应非平衡程度, 也要讨论边界外的分子离解非平衡流动情况.
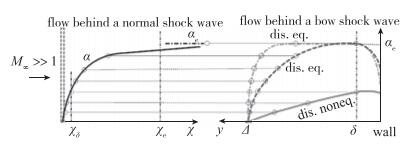
|
| 图 4 正激波和前缘弓形头激波后非平衡流动映射关系示意图 Fig.4 Mapping between flows behind a normal shockwave and a bow shockwave |
最后, 在驻点边界层内部, 流动的主要特征由原子复合反应与扩散控制, 根据二者时间尺度的差异, 定义了一个复合非平衡流动判据Dar, 基于Dar也给出了驻点边界层内部因原子复合反应引起的气体离解度变化.结果表明, 如果把边界层内复合反应的影响等效转化为一个对边界层外缘离解度的削减修正, 那么完全可以把非平衡边界层传热问题当作一个冻结边界层来看待[49-50].
把以上3步组合起来, 就能描述自由来流高速气体经过强激波压缩升温发生非平衡化学反应和传递能量给壁面的整个过程, 从而构建了非平衡真实气体效应下前缘驻点热流的预测桥函数.非平衡流动判据Dad和Dar的具体表达式[49-50]直接显含稀薄流动判据Wr, 表明了流动非平衡程度和稀薄程度的关联.
2.3 主要结果讨论以上先后两阶段研究结果联合起来, 就构成了尖头体气动加热受稀薄气体效应和非平衡真实气体效应的工程理论.除了给出具体的可供工程上使用的气动热快速估算公式, 我们还讨论了两种效应同时存在时的流动相似律.根据相似律要求, 在涉及稀薄非平衡气动加热问题的实验和数值模拟中, 传统的天地换算准则失效, 必须采用全尺寸模型和完全复现真实来流条件, 这就对实验和计算技术提出非常严峻的挑战.当然, 这也说明了模型理论分析途径的重要性和必要性.
在回顾这一研究过程时, 我们还有一些体会, 值得加以强调.
(1) 要解决当前航天工程中跨尺度多物理耦合的流动和加热问题, 须要综合利用实验计算和理论分析手段联合攻关.我们的工作以模型理论分析为主, 同时结合了直接模拟Monte Carlo数值计算和合作单位的风洞实验验证, 在当前该领域研究严重依赖数值计算和经验公式的大背景下, 走出了另一条可行的道路.
(2) 寻找具有真实物理意义的流动判据十分关键.在一个多种复杂因素耦合作用的物理问题中, 如果找到了定量描述主要控制因素对流动和传热影响的无量纲特征参数, 我们就成功了一半.
(3) 对流动宏观的守恒律和相似性的认识非常重要.在研究非平衡流动时, 我们在能量守恒和分子二体碰撞相似律框架下, 可把正激波后扩展到无穷远处的非平衡流动与驻点线上有限范围的非平衡流动进行统一处理, 导出二者之间的映射关系.但是, 同样在驻点线上, 边界层内部的原子复合反应源于三体碰撞, 不满足二体碰撞相似律, 因此, 边界层内外非平衡流动的主控因素不同, 外部是分子离解非平衡, 内部是原子复合非平衡, 二者的判据是不同的.
3 结论人们认识世界靠自然科学, 特别是其中的基础科学(如数理化力天地生等).人们改造世界要靠工程和技术, 工程技术既取决于基础科学的理论指导, 又依赖于经验积累和技术创新.研究基础科学问题称为基础研究, 研究工程技术问题称为应用研究.在社会生产力低下的时代, 与工程相关的科学与技术的研究, 即基础研究与应用研究之间, 极少关联.随着20世纪初期出现的航空工程和其后的航天工程等高新技术发展, 迫切要求科学与技术的结合, 因此在连接基础研究和应用研究的链条之中, 人们添加了应用基础研究这个环节, 造就了一批应用科学的迅猛发展.它们面向工程技术中提炼出的科学问题, 根据基础科学的原理, 构建相应的工程技术理论, 指导工程应用.正是由于应用科学紧密结合工程技术的研究, 使这些高新技术得以前所未有的步伐获得进展[56].
特别须要关注的有以下两点[56] : (1) 要明确工程科学这一研究层次的定位.当前不少人将工程技术的应用研究当做应用基础研究.其实, 工程科学才属于应用基础研究, 要求从工程技术中提炼出兼有学术和应用价值的科学问题, 其研究目标是要“创造出工程技术的理论”. (2) 要使研究结果成为理论, 就须要用数学方法加以表述.
我们的实践证明, 虽然当今遇到的流动问题越来越复杂, 但是理论建模和流动物理分析仍可以发挥重要作用, 仍是应用流体力学的重要研究手段.理论建模也须结合实验观测和数值模拟手段, 彼此相辅相成, 才能得出正确的工程理论.
致谢 感谢《气体物理》编辑部的邀请.感谢国家自然科学基金委的资助(11202224, 11372310).本文的写作目的是为了阐释应用流体力学的理论建模方法在当今的流体力学研究中仍很重要, 不可偏废.| [1] |
Von Kármán. 空气动力学的发展[M]. 姜可宗, 译. 上海: 上海科学技术出版社, 1954 : 1-2. Von Kármán. Aerodynamics[M]. Jiang K Z, translated. Shanghai : Shanghai Scientific & Technical Publishers, 1954 : 1-2(in Chinese). http: //www. doc88. com/p-7592063371186. html |
| [2] |
Tsien H S. Engineering and engineering sciences[J]. CIE Journal, 1948(6): 550-563. |
| [3] |
钱学森. 论技术科学[J]. 科学通报, 1957(2): 97-104. Tsien H S. On engineering sciences[J]. Chinese Science Bulletin, 1957(2): 97-104. (in Chinese) |
| [4] |
Ellington C P, van den Berg C, Willmott A P, et al. Leading-edge vortices in insect flight[J]. Nature, 1996, 384: 626-630. DOI:10.1038/384626a0 |
| [5] |
Dickinson M H, Lehmann F O, Sane S P. Wing rotation and the aerodynamic basis of insect flight[J]. Science, 1999, 284: 1954-1960. DOI:10.1126/science.284.5422.1954 |
| [6] |
Sun M, Tang J. Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion[J]. Journal of Experimental Biology, 2002, 205: 55-70. |
| [7] |
Yu Y, Tong B, Ma H. An analytic approach to theoretical modeling of highly unsteady viscous flow excited by wing flapping in small insects[J]. Acta Mechanica Sinica, 2003, 19(6): 508-516. DOI:10.1007/BF02484543 |
| [8] |
Ellington C P. The aerodynamics of hovering insect flight. II. Morphological parameters[J]. Philosophical Transactions of the Royal Society B, 1984, 305(1122): 17-40. DOI:10.1098/rstb.1984.0050 |
| [9] |
余永亮, 童秉纲, 马晖扬. 昆虫拍翼方式的非定常流动物理再探讨[J]. 力学学报, 2005, 37(3): 257-265. Yu Y L, Tong B G, Ma H Y. Unsteady flow mechanisms revisited in insect flapping flight[J]. Acta Mechanica Sinica, 2005, 37(3): 257-265. (in Chinese) |
| [10] |
Gray J. Studies in animal locomotion VI. The propulsive powers of the dolphin[J]. Journal of Experimental Biology, 1936, 13: 192-199. |
| [11] |
Taylor G I. Analysis of the swimming of long narrow animals[J]. Proceedings of the Royal Society(A), 1952, 214: 158-183. DOI:10.1098/rspa.1952.0159 |
| [12] |
Lighthill M J. Note on the swimming of slender fish[J]. Journal of Fluid Mechanics, 1960, 9(2): 305-317. DOI:10.1017/S0022112060001110 |
| [13] |
Lighthill M J. Large-amplitude elongated-body theory of fish locomotion[J]. Proceedings of the Royal Series B : Biological Sciences, 1971, 179(1055): 125-138. DOI:10.1098/rspb.1971.0085 |
| [14] |
Wu T Y. Swimming of a waving plate[J]. Journal of Fluid Mechanics, 1961, 10(3): 321-344. DOI:10.1017/S0022112061000949 |
| [15] |
Wu T Y. Hydromechanics of swimming propulsion. Part 1. Swimming of a two-dimensional flexible plate at variable forward speeds in an inviscid fluid[J]. Journal of Fluid Mechanics, 1971, 46(2): 337-355. DOI:10.1017/S0022112071000570 |
| [16] |
Cheng J Y, Zhuang L X, Tong B G. Analysis of swimming three-dimensional waving plates[J]. Journal of Fluid Mechanics, 1991, 232: 341-355. DOI:10.1017/S0022112091003713 |
| [17] |
Liu H, Wassersug R, Kawachi K. A computational fluid dynamics study of tadpole swimming[J]. Journal of Experimental Biology, 1996, 199: 1245-1260. |
| [18] |
Liu H, Wassersug R, Kawachi K. The three-dimensional hydrodynamics of tadpole locomotion[J]. Journal of Experimental Biology, 1997, 200: 2807-2819. |
| [19] |
Zhu Q, Wolfgang M J, Yue D K, et al. Three-dimensional flow structures and vorticity control in fish-like swimming[J]. Journal of Fluid Mechanics, 2002, 468: 1-28. |
| [20] |
Zhang J, Liu N S, Lu X Y. Route to chaotic state in flow past an inclined flat plate[J]. Physical Review E, 2009, 79: 045306. |
| [21] |
Zhang J, Liu N S, Lu X Y. Locomotion of a passively flapping flat plate[J]. Journal of Fluid Mechanics, 2010, 659: 43-68. DOI:10.1017/S0022112010002387 |
| [22] |
Tian F B, Luo H, Zhu L, et al. Interaction between a flexible filament and a downstream rigid body[J]. Physical Review E, 2010, 82(2): 26301. DOI:10.1103/PhysRevE.82.026301 |
| [23] |
Dong G J, Lu X Y. Characteristics of flow over traveling wavy foils in a side-by-side arrangement[J]. Physics of Fluids, 2007, 19: 057107. DOI:10.1063/1.2736083 |
| [24] |
Deng J, Shao X M, Yu Z S. Hydrodynamic studies on two traveling wavy foils in tandem arrangement[J]. Physics of Fluids, 2007, 19(11): 113104. DOI:10.1063/1.2814259 |
| [25] |
Shao X, Pan D, Deng J, et al. Hydrodynamic performance of a fishlike undulating foil in the wake of a cylinder[J]. Physics of Fluids, 2010, 22: 111903. DOI:10.1063/1.3504651 |
| [26] |
Tian F B, Luo H, Zhu L, et al. Coupling modes of three filaments in side-by-side arrangement[J]. Physics of Fluids, 2011, 23: 111903. DOI:10.1063/1.3659892 |
| [27] |
Carling J, Williams T L, Bowtell G. Self-propelled anguilliform swimming : simultaneous solution of the two-dimensional Navier-Stokes equations and Newton′s laws of motion[J]. Journal of Experimental Biology, 1998, 201(23): 3143-2819. |
| [28] |
Leroyer A, Visonneau M. Numerical methods for RANSE simulations of a self-propelled fish-like body[J]. Journal of Fluids and Structures, 2005, 20(7): 975-991. DOI:10.1016/j.jfluidstructs.2005.05.007 |
| [29] |
Kern S, Koumoutsakos P. Simulations of optimized anguilliform swimming[J]. Journal of Experimental Biology, 2006, 209(24): 4841-4857. DOI:10.1242/jeb.02526 |
| [30] |
Gazzola M, van Reesa W M, Koumoutsakos P. C-start : optimal start of larval fish[J]. Journal of Fluid Mechanics, 2012, 698: 5-18. DOI:10.1017/jfm.2011.558 |
| [31] |
van Rees W M, Gazzola M, Koumoutsakos P. Optimal shapes for anguilliform swimmers at intermediate Reynolds numbers[J]. Journal of Fluid Mechanics, 2013, 722. |
| [32] |
Wu C J, Wang L. Numerical simulations of self-propelled swimming of 3D bionic fish school[J]. Science in China Series E : Technological Sciences, 2009, 52(3): 658-669. DOI:10.1007/s11431-009-0064-x |
| [33] |
Wu C J, Wang L. Where is the rudder of a fish? : the mechanism of swimming and control of self-propelled fish school[J]. Acta Mechanica Sinica, 2010, 26(1): 45-65. DOI:10.1007/s10409-009-0305-z |
| [34] |
Xin Z Q, Wu C J. Numerical simulations and vorticity dynamics of self-propelled swimming of 3D bionic fish[J]. Science China : Physics, Mechanics & Astronomy, 2012, 55(2): 272-283. |
| [35] |
Yang Y, Wu G H, Yu Y L, et al. Two-dimensional self-propelled fish motion in medium : an integrated method for deforming body dynamics and unsteady fluid dynamics[J]. Chinese Physics Letters, 2008, 25(2): 597-600. DOI:10.1088/0256-307X/25/2/066 |
| [36] |
Liu G, Yu Y L, Tong B G. Flow control by means of a traveling curvature wave in fishlike escape responses[J]. Physical Review E, 2011, 84(5): 056312. DOI:10.1103/PhysRevE.84.056312 |
| [37] |
Liu G, Yu Y L, Tong B G. Optimal energy-utilization ratio for long-distance cruising of a model fish[J]. Physical Review E, 2012, 86(1): 016308. DOI:10.1103/PhysRevE.86.016308 |
| [38] |
Kontinos P. Aerothermal performance constraints for hypervelocity small radius unswept leading edges and nosetips[R]. NASA Technical Memorandum 112204, 1997.
|
| [39] |
Reuther J, Kinney D, Smith S, et al. A reusable space vehicle design study exploring sharp leading edges[R].AIAA 2001-2884, 2001.
|
| [40] |
McClinton C R. High speed/hypersonic aircraft pro-pulsion technology development[R]. Advances on Propulsion Technology for High-Speed Aircraft, RTO-EN-AVT-150, 2007 : 12-15.
|
| [41] |
Fay J A, Riddell F R. Theory of stagnation point heat transfer in dissociated air[J]. Journal of the Aeronautical Sciences, 1958, 25(2): 73-85. |
| [42] |
周恒, 张涵信. 空气动力学的新问题[J]. 中国科学:物理学力学天文学, 2015, 45(10): 104709. Zhou H, Zhang H X. New problems of aerodynamics[J]. Scientia Sinica : Physica, Mechanica & Astronomica, 2015, 45(10): 104709. (in Chinese) |
| [43] |
Lutz S A. Heating correlations for bluff cylinder hypersonic rarefied flows[R]. AIAA 2003-4060, 2003. https://www.researchgate.net/publication/268558611_Heating_Correlations_for_Bluff_Cylinder_Hypersonic_Rarefied_Flows
|
| [44] |
Lips T, Fritsche B. A comparison of commonly used re-entry analysis tools[J]. Acta Astronaut, 2005, 57: 312-323. DOI:10.1016/j.actaastro.2005.03.010 |
| [45] |
Wang Z H, Bao L, Tong B G. Variation character of stagnation point heat flux for hypersonic pointed bodies from continuum to rarefied flow states and its bridge function study[J]. Science in China Series G : Physics, Mechanics & Astronomy, 2009, 52(12): 2007-2015. |
| [46] |
Wang Z H, Bao L, Tong B G. Rarefaction criterion and non-Fourier heat transfer in hypersonic rarefied flows[J]. Physics of Fluids, 2010, 22: 126103. DOI:10.1063/1.3525289 |
| [47] |
Wang Z H, Bao L, Tong B G. Theoretical modeling of the chemical non-equilibrium flow behind a normal shock wave[J]. AIAA Journal, 2012, 50(2): 494-499. DOI:10.2514/1.J051044 |
| [48] |
Wang Z H, Bao L, Tong B G. An analytical study on nonequilibrium dissociating gas flow behind a strong bow shockwave under rarefied conditions[J]. Science China : Physics, Mechanics & Astronomy, 2013, 56(4): 671-679. |
| [49] |
Wang Z H, Bao L, Tong B G. Theoretical modeling of chemical nonequilibrium stagnation point boundary layer heat transfer under rarefied conditions[J]. Science China : Physics, Mechanics & Astronomy, 2013, 56(5): 866-874. |
| [50] |
Wang Z H. Theoretical modelling of aeroheating on sharpened noses under rarefied gas effects and nonequilibrium real gas effects[M]. Berlin : Springer-Verlag, 2015. http://www.doc88.com/p-9943452592389.html
|
| [51] |
王智慧, 鲍麟, 童秉纲. 尖化前缘的稀薄气体化学非平衡流动和气动加热相似律研究[J]. 气体物理, 2016, 1(1): 5-12. Wang Z H, Bao L, Tong B G. Similarity law of aero-heating to sharpened noses in rarefied chemical nonequilibrium flows[J]. Physics of Gases, 2016, 1(1): 5-12. (in Chinese) |
| [52] |
Chen X X, Wang Z H, Yu Y L. Nonlinear shear and heat transfer in hypersonic rarefied flows past flat plates[J]. AIAA Journal, 2015, 53(2): 413-419. DOI:10.2514/1.J053168 |
| [53] |
Chen X X, Wang Z H, Yu Y L. General Reynolds analogy for blunt-nosed bodies in hypersonic flows[J]. AIAA Journal, 2015, 53(8): 2410-2416. DOI:10.2514/1.J053962 |
| [54] |
Singh N, Schwartzentruber T E. Heat flux correlation for high-speed flow in the transitional regime[J]. Journal of Fluid Mechanics, 2016, 792: 981-996. DOI:10.1017/jfm.2016.118 |
| [55] |
Singh N, Schwartzentruber T E. Heat flux and drag correlations for high speed flight at any Knudsen number[R]. AIAA 2016-3841, 2016.
|
| [56] |
童秉纲, 余永亮, 鲍麟. 技术科学要求创造工程技术的理论——纪念钱学森先生百年诞辰[J]. 工程研究, 2011, 3(1): 1-7. Tong B G, Yu Y L, Bao L. Engineering science research requires foundings of new theories for specific problems in engineering and technology : in honor of 100th birthday of Qian Xuesen[J]. Journal of Engineering Studies, 2011, 3(1): 1-7. (in Chinese) |



