经过亿万年自然选择, 鱼类进化出非凡高效的游动能力.例如处于海洋生物链顶端的海洋水生动物巡游时流体的推进效率高达80%[1], 白斑狗鱼的加速度可以达到20倍重力加速度[2], 天使鱼的转弯半径只有身体体长的6%左右[3].它们的运动能力远远超过现有水下航行器的性能.因此研究鱼类游动推进机理, 可为人类设计更高效水中载运工具提供参考[4].研究生物游动的理论分析往往只能通过一些近似与假设来分析运动方式比较简单的模化运动.对于复杂流体中的非定常运动, 理论分析很难精确给出复杂涡系结构.活体实验则存在难以对生物运动进行控制重复性差测力困难等缺点[5].随着并行计算技术飞速发展, 使用数值模拟手段研究仿生非定常运动问题, 弥补了理论分析与实验测量的不足, 逐渐成为当前CFD研究领域的热点.鱼类仿生游动非定常流场的求解是一种典型的具有运动边界流场求解问题[6].采用基于贴体网格的有限体积或有限差分N-S方程求解器求解此类动边界问题, 需要在每一个时间步重新生成网格, 对于复杂固体边界运动计算效率低且对于大幅度运动边界容易发散.
浸入边界法(immersed boundary method, IBM)处理动边界问题时, 无需在每一个时间步重新生成网格[7], 因此在生物游动生物戈行生物瓣膜运动流体颗粒输运和纤丝摆动等非定常流体机理研究中获得了广泛的应用, 成为目前计算流体力学领域的新手段[8].不同于贴体网格流场求解器, 格子Boltzmann方法(lattice Boltzmann method, LBM)以Boltzmann输运方程为控制方程, 采用固定Descartes网格从介观尺度模拟宏观复杂流动, 无需处理从物理平面到计算平面的坐标和网格转化问题.同时LBM方法容易实施及天然并行, 在大规模并行流动模拟中受到广泛关注[9], 在许多领域取得精确的结果[10-15].由于IBM与LBM都采用Descartes网格, 因此将两种方法结合起来模拟复杂动边界非定常流动问题成为备受关注的方向.
Feng等首先提出了IB-LBM方法[16-17].在其研究中, 形变产生的回复力由惩罚力方法计算得到.惩罚力法中引入了一个自定义弹簧参数, 针对不同问题恰当选取该参数可以获得良好模拟效果.直接力法从N-S方程求出壁面受力,尽管比较准确但却损失了IBM方法的简单性. Niu等[19]在2006年根据动量交换的思想提出了一种新的IB-LBM方法, 其力项通过对格子点分布函数的动量交换进行Lagrange插值得到, 从而使得边界上力项计算更简单.但在该方法中速度校正固定不变, 因此边界上通过插值获得的速度不等于壁面速度, 从而导致无滑移边界条件不能精确满足.针对这种情况, Wu等[20]在2009年提出了基于速度隐式迭代的IB-LBM方法, 提高了边界上无滑移条件的满足度.该方法既保持了传统IB-LBM方法的简易与光滑性, 同时力项计算更加方便准确. Tian等[21]在2011年针对二维弹性纤丝提出了一种鲁棒性较高的IB-LBM计算框架. Suzuki等[22]对比了无内部质量效应刚体近似和Lagrange点近似3种方法, 讨论了IBM方法内部质量效应对流场模拟结果的影响. IB-LBM特别适合求解固体边界变形较大与固体边界几何形状复杂的问题,广泛应用于仿生运动数值模拟[24-25].
总之, IB-LBM具有算法简单并行性高无需每步更新网格算法鲁棒性高等优点, 因此特别适合复杂仿生运动模拟.由于LBM对高Reynolds数流动问题需要在足够细密网格下可以获得较高模拟精度, 因此本文基于Wu提出的IB-LBM方法开发了面向天河-2超级计算机的三维仿生运动并行求解器, 该求解器适合动边界及大网格情况下的数值模拟.同时以鳗鱼等鱼类游动过程抽象出的一种仿生波动翼为研究对象, 通过分析波动翼在不同相角和不同波动幅值下的涡量图和Q变量图, 清晰展示了波动翼非定常涡系结构的产生与演化过程, 给出了升阻力系数与波动幅值的关系.
1 数值模拟方法 1.1 IBM方法IBM首先由Peskin提出[26], 其基本思想是将浸入边界模化为流场中的力而不再处理为边界条件.浸入边界施加给流场的力被离散为施加在浸入边界周围网格上的体力, 然后体力被添加到N-S方程中来模拟边界.
为了方便叙述IB-LBM,考虑边界为Γ的柔性细丝沉浸在二维不可压缩黏性流体中(流体区域用Ω表示).柔性细丝的边界Γ用Lagrange坐标s表示,流体区域Ω由Euler坐标x表示,柔性细丝上的坐标可以表示为x=X(s, t).下面引入不可压N-S方程结合IBM的整个系统,详细方法可参考文献[27].
| $ \rho \left[{\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + \left( {\mathit{\boldsymbol{u}} \cdot \nabla \mathit{\boldsymbol{u}}} \right)} \right] = - \nabla p + \mu {\nabla ^2}\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{f}} $ | (1) |
| $ \nabla \cdot \mathit{\boldsymbol{u}} = 0 $ | (2) |
| $ \mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{x}}, t} \right) = \int {_\varGamma } \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{s}}, t} \right)\delta \left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{X}}\left( {\mathit{\boldsymbol{s}}, t} \right)} \right){\rm{d}}\mathit{\boldsymbol{s}} $ | (3) |
| $ \frac{{\partial \mathit{\boldsymbol{X}}}}{{\partial t}} = \mathit{\Omega } \mathit{\boldsymbol{u}}\left( {\mathit{\boldsymbol{x}}, t} \right)\delta \left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{X}}\left( {\mathit{\boldsymbol{s}}, t} \right)} \right){\rm{d}}\mathit{\boldsymbol{x}} $ | (4) |
| $ \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{s}}, t} \right) = S\left( {\mathit{\boldsymbol{X}}\left( {\mathit{\boldsymbol{s}}, t} \right), t} \right) $ | (5) |
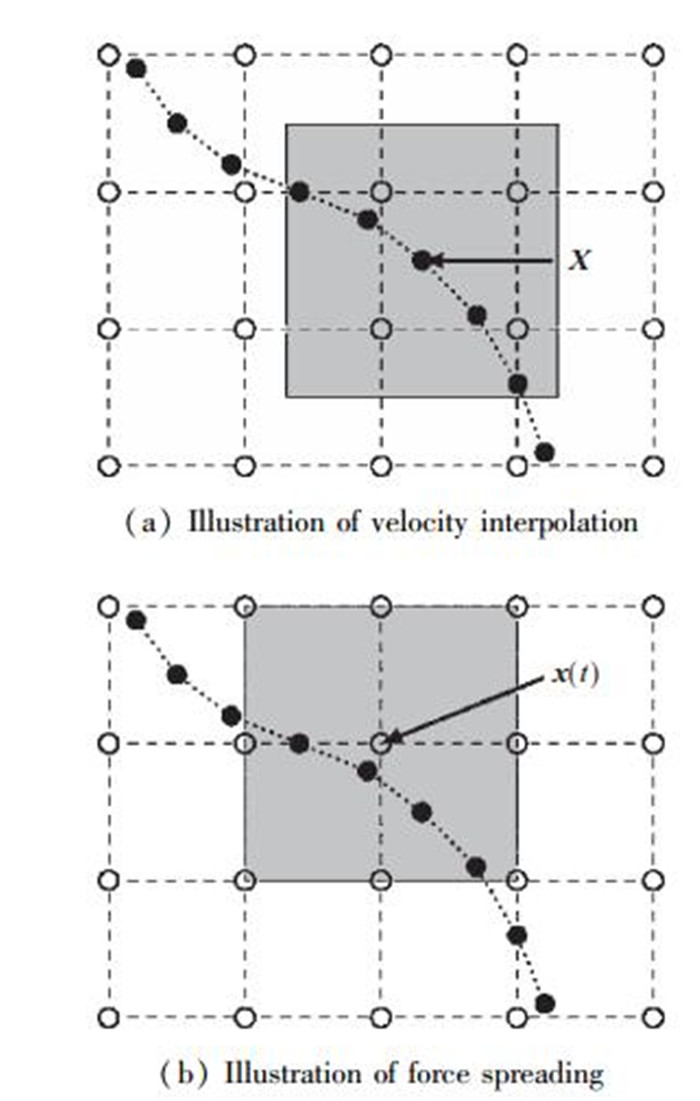
上述公式中p(x, t)为流体压力,ρ为流体密度,μ为流体黏度系数,F(s, t)为浸入边界上的集中力密度,f(x, t)为流体体力密度.式(1) 和(2) 为不可压黏性N-S方程.式(3) 表示浸入边界上的集中作用力F(s, t)分散到周围流体力密度f(x, t)的过程,δ(x-X(s, t))为Dirac delta函数.式(4) 则表示流体网格点上的速度通过加权关系集中到浸入边界上速度的过程,本质上为无滑移边界条件.式(5) 表示浸入边界上某点集中力是由外形决定的,S(X(s, t), t)为与形变相关的函数,在惩罚力法中,近似于弹簧的变形特性.边界节点X的速度值由阴影中包含的流场格点速度差值得到(对应于式(4)), 如图 1(a)所示[28].作用在流场格点x上的力可以通过阴影部分包含的边界格点组合得到(对应于式(3)), 如图 1(b)所示.图中空心点代表Euler坐标表示的流场格点, 实心点代表用Lagrange描述的运动边界点.
|
| 图 1 IBM数值方法示意图 Fig.1 Numerical method of IBM |
LBM由格子气自动机发展而来[29]. LBM将流体域划分为一系列规则的静止的网格.流体被模拟成只能在节点间运动或者保持静止的“质点”.本文采用Boltzmann-BGK模型, 表述为[30]
| $ \frac{{\partial {f_i}}}{{\partial t}} + {\mathit{\boldsymbol{e}}_i} \cdot \nabla {f_i} = - \frac{{\left( {{f_i} - f_i^{{\rm{eq}}}} \right)}}{\lambda } $ | (6) |
fi为粒子密度分布函数, ei为i方向的粒子速度, λ为松弛时间, fieq为当地平衡态分布函数.
| $ f_i^{{\rm{eq}}} = \rho {w_i}\left[{1 + 3{\mathit{\boldsymbol{e}}_i} \cdot \mathit{\boldsymbol{u}} + \frac{9}{2}{{\left( {{\mathit{\boldsymbol{e}}_i} \cdot \mathit{\boldsymbol{u}}} \right)}^2}-\frac{3}{2}\mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{u}}} \right] $ | (7) |
ωi为权系数, 具体取值与计算模型有关.
将式(6) 在空间x和时间t离散后得到:
| $ {f_i}\left( {\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{e}}_i}\delta t, t + \delta t} \right) - {f_i}\left( {\mathit{\boldsymbol{x}}, t} \right) = \frac{{{f_i}\left( {\mathit{\boldsymbol{x}}, t} \right) - f_i^{{\rm{eq}}}\left( {\mathit{\boldsymbol{x}}, t} \right)}}{\tau } $ | (8) |
式(8) 中τ=λ/(δt)为无量纲松弛参数, δt为时间步长.
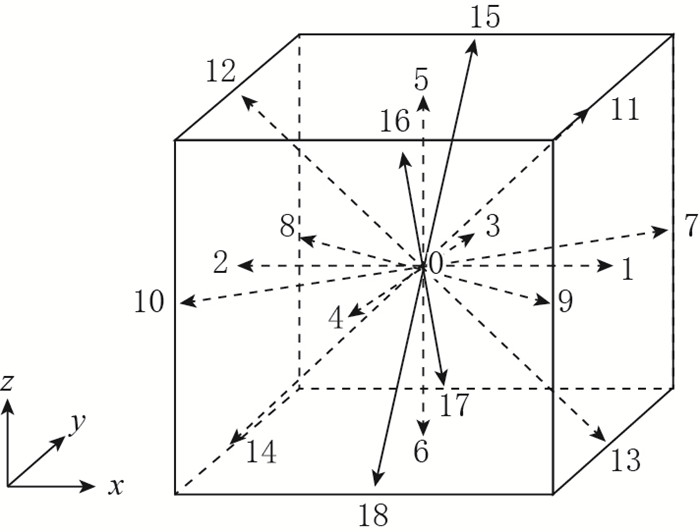
本文中, LBM模型选用D3Q19模型, 离散模型如图 2所示. D3Q19模型中对应的权系数为ω0=1/3, ω1-ω6=1/18, ω7-ω18=1/36.
|
| 图 2 D3Q19离散模型 Fig.2 Discretization model of D3Q19 |
公式(8) 通常被分为两步求解:
碰撞步:
| $ {{\tilde{f}}_{i}}\left( \mathit{\boldsymbol{x}},t+\delta t \right)={{f}_{i}}\left( \mathit{\boldsymbol{x}},t \right)=-\frac{{{f}_{i}}\left( \mathit{\boldsymbol{x}},t \right)-f_{i}^{\rm{eq}}\left( \mathit{\boldsymbol{x}},t \right)}{\tau } $ | (9) |
迁移步:
| $ {f_i}\left( {\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{e}}_i}\delta t, t + \delta t} \right) = {{\tilde f}_i}\left( {\mathit{\boldsymbol{x}}, t + \delta t} \right) $ | (10) |
将IBM和LBM耦合起来的关键是将体力项添加到BGK模型中.本文中IB-LBM算法采用Wu提出的隐身速度修正, 其中LBM采用D3Q19模型求解.
IB-LBM的控制方程为[20]
| $ {f_i}\left( {\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{e}}_i}\delta t, t + \delta t} \right) - {f_i}\left( {\mathit{\boldsymbol{x}}, t} \right) = - \frac{{{f_i}\left( {\mathit{\boldsymbol{x}}, t} \right) - f_i^{{\rm{eq}}}\left( {\mathit{\boldsymbol{x}}, t} \right)}}{\tau } + {F_i}\delta t $ | (11) |
| $ \rho \mathit{\boldsymbol{u}} = \sum\limits_i {{\mathit{\boldsymbol{e}}_i}} {f_i} + \frac{1}{2}\mathit{\boldsymbol{f}}\delta t $ | (12) |
| $ {F_i} = \left( {1 - \frac{1}{{2\tau }}} \right){w_i}\left( {\frac{{{\mathit{\boldsymbol{e}}_i} - \mathit{\boldsymbol{u}}}}{{c_s^2}} + \frac{{{\mathit{\boldsymbol{e}}_i} \cdot \mathit{\boldsymbol{u}}}}{{c_s^4}} \cdot {\mathit{\boldsymbol{e}}_i}} \right)\mathit{\boldsymbol{f}} $ | (13) |
f为Euler点上体力密度,ωi为平衡态分布函数的权系数,cs为格子声速, 其值为1/3.
如果定义中间速度u*为:
| $ \rho {\mathit{\boldsymbol{u}}^*} = \sum\limits_i {{\mathit{\boldsymbol{e}}_i}} f $ | (14) |
定义校正速度δu为:
| $ \rho \delta \mathit{\boldsymbol{u}} = \frac{1}{2}\mathit{\boldsymbol{f}}\delta t $ | (15) |
传统IB-LBM方法中,中间速度u*与δu分别通过显示计算得到,当通过u插值计算边界上的速度时,并不能严格保证无滑移条件,为此Wu提出隐式算法计算u与δu,有兴趣的读者可以参考文献[19],本文不再赘述.
对于基于速度的隐式算法,体力密度通过式(16) 得到:
| $ \mathit{\boldsymbol{f}} = 2\rho \frac{{\delta \mathit{\boldsymbol{u}}}}{{\Delta t}} $ | (16) |
对流流体宏观量密度与压力按式(17) 计算.
| $ \rho = \sum\limits_i {{f_i}, p = c_s^2} \rho $ | (17) |
该算法可以归纳为[19]:
(1) 设定初值,计算隐式速度法中速度修正项的相关变量.
(2) 通过式(11) 计算t=tn时刻的密度分布函数(最初时刻设定Fi=0), 然后式(14) 与(17) 计算宏观变量.
(3) 通过隐身算法计算浸入边界点上的校正速度项,然后计算Euler点上的速度校正项.
(4) 计算Euler点上的速度项,用式(16) 获得体力密度.
(5) 通过式(7) 计算平衡态分布函数.
(6) 重复步骤(2)~(5),直到结果收敛.
基于上述Wu提出的隐式算法, 编写了可适用于天河-2的求解器, 该求解器保证了浸入固体边界上的速度无滑移条件.
2 正弦波动翼参数研究鱼类游动现象对开发高性能低噪音仿生水中航行器具有重要指导作用.考虑到复杂边界运动连续性函数均可通过三角级数展开逼近, 因此本文从鳗鱼等鱼类游动过程抽象出一种正弦仿生波动翼, 从而可以近似简化模拟此类鱼类典型运动模式又不失一般性.
2.1 波动翼运动形式的数学描述一个起始位置位于x-y平面的无厚度平板翼, 设沿着x方向为长度方向, y方向为宽度方向, 并且长宽比为2:1.模拟开始后, 平板上的节点沿平行z轴的方向进行变形, 平板在t时刻的位移沿x轴呈现为一个周期的正弦曲线, 其数学形式为
| $ Z = A\left( L \right)\sin \left( {\pi \frac{x}{L}} \right)\sin \left( {\varPhi \left( t \right)} \right) $ |
其中, L为翼型的宽度, x为几何节点的x坐标, 在变形中保持不变, Z为几何节点的z坐标, A为正弦波的最大振幅, 与翼型宽度L为线性关系即A(L)=KL. Φ(t)为随时间变化的相角:
| $ \varPhi \left( t \right) = 2\pi wt $ |
式中ω为波动频率, 取值为0.1.
Z向的速度为
| $ \dot Z = 2\pi wA\left( L \right)\sin \left( {\pi \frac{x}{L}} \right)\cos \left( {\mathit{\Phi} \left( t \right)} \right) $ |
其中在上下扑动的极限位置自动满足速度为0的条件, 符合物理的真实情况.再次强调的是, 波动平板上节点的X, Y坐标在变形中均保持不变.正弦波动翼型运动的Reynolds数定义为
| $ Re = \frac{{{U_\infty }L}}{v} $ |
其中, U∞为来流速度, L为平板宽度, υ为运动黏度.
升阻力系数设定为
| $ {C_x} = \frac{{ - \int {_\Omega {f_x}{\rm{d}}x} }}{{\frac{1}{2}\rho U_\infty ^2L}}, {C_z} = \frac{{ - \int {_\varOmega {f_z}{\rm{d}}z} }}{{\frac{1}{2}\rho U_\infty ^2L}} $ |
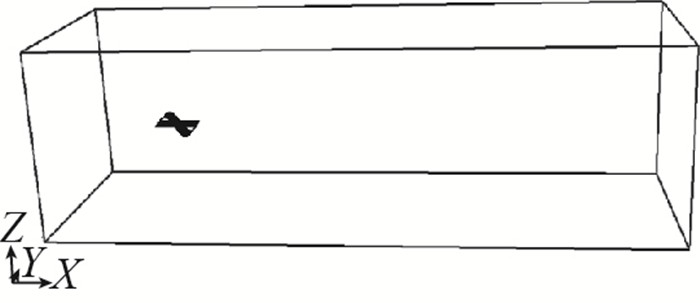
波动翼计算模型中, 波动翼采用隐式浸入边界条件, 4个侧面采用周期性边界条件, 最左侧采用速度入口边界条件, 最右侧为速度出口边界条件.波动翼相关参数为无量纲参数. Reynolds数为450, 流体来流速度为1, 波动翼的宽度为1, 长度为2, 远场尺寸为29.5×9.5×9.5, 平板左侧中心位点(4.5, 4.5, 4.5).取宽度1中有34个网格长度, 即空间步长dx=1/34=0.0294, 时间步长dt=0.001, 模拟步数100000步.整个流场被离散为1004×323×323的长方体网格区域, 如图 3所示.其中, 黑色水平放置的平板为初始时刻平板位置.呈正弦形状的翼型对应的相角为π/2.取最大振幅A为变量, 通过计算3个不同幅值下的工况, 分析幅值对非定常流场涡系结构及升力和阻力的影响.本文算例网格量约为1×108, 在广州超算中心天河-2超级计算上采用8个节点共192个计算核, 单个工况计算时间约为9 h.
|
| 图 3 波动翼模拟区域 Fig.3 Simulation domain of waving airfoil |
为了研究正弦波动翼运动时的非定常流动, 本小节列出当最大幅值为0.5时, 不同时刻即不同相角下的涡量图, 如图 4所示.涡量图为y=4.5时, xz平面内的二维涡量分布.

|
| 图 4 各相角下的涡量图 Fig.4 Vorticity at different phase angles |
从涡量图可得到:
(1) 相角从π到1.5π的变化过程中, 翼型(x=2L)处尾涡逐渐增强, 当相角从1.5π变化到2π的过程中, 尾涡在压强梯度的作用下继续增强;当相角为2π时, 尾涡脱离翼型, 并且向下游扩散.
(2) 相角为π到1.5π的过程中, 前段翼型凹陷处(x=0.5L)的流体受到压强驱动而产生涡, 该涡逐渐增强, 在相角为1.5π时强度达到最大.当相角从1.5π变化到2π时, 该涡逐渐脱离翼型, 向后扩散.
(3) 相角为π时, 翼型处于xy平面.当相角逐渐增加时, 前段翼型(0~0.5L)下侧与后段翼型(1L~1.5L)上侧, 由于翼型对流体的摩擦作用, 有涡产生.相角为1.5π时, 平板处于极限位置, 涡继续产生同时向下游扩散.当相角变化为2π时, 翼型处于水平位置, 涡将会在翼型另一侧面产生并向下游扩散.
(4) 翼型波动关于xy平面对称, 会产生关于xy平面对称的涡系.翼型运动在下一个周期相同相角时, 具有同样的涡系结构.正是柔性翼型波动产生的反涡系结构, 使翼型下游产生“喷流”, 提供鱼类前进的动力.
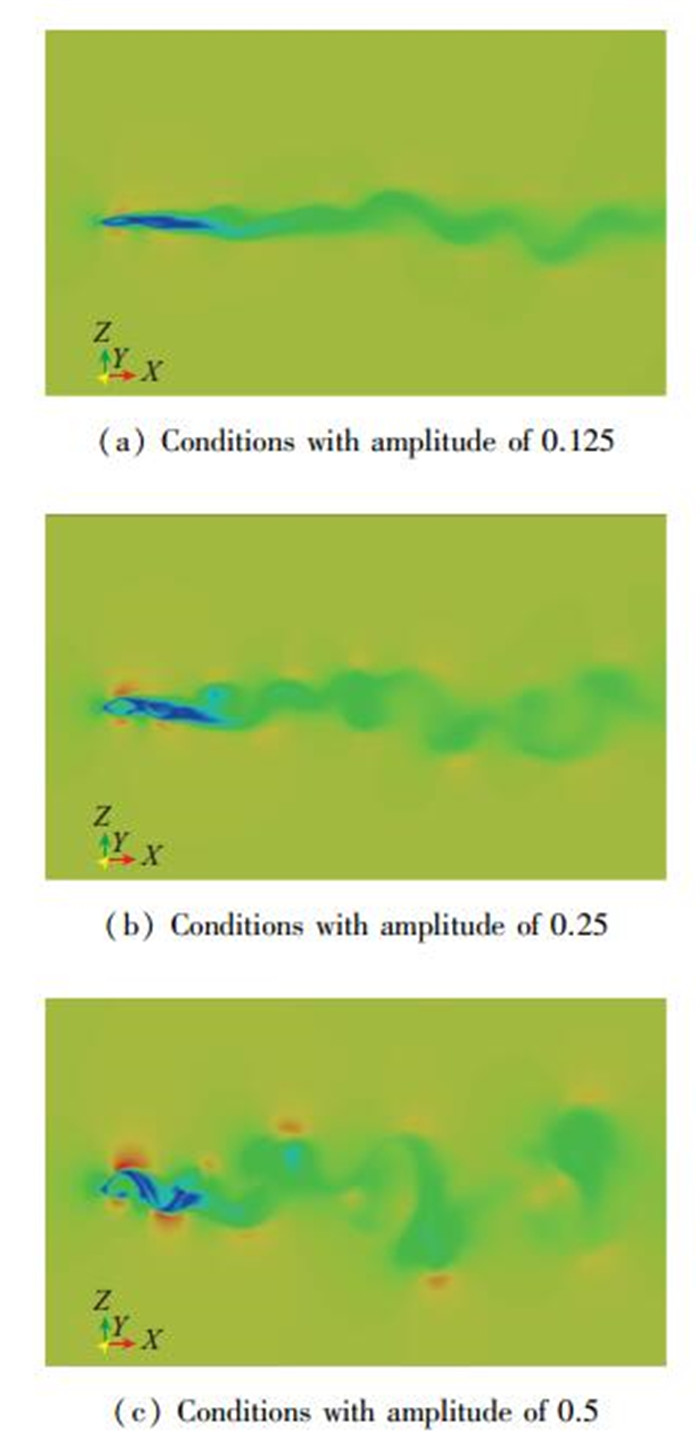
3.2 不同幅值的速度云图为了研究波动幅值对流场的影响, 图 5给出了A=0.125, 0.25, 0.5这3种工况下, 相角为π/2时, 翼型中间切面(y=4.5时, xz平面)的速度云图.
|
| 图 5 不同波动幅值下, 翼型附近的速度云图 Fig.5 Velocity coutours around the wing in different amplitudes |
翼型附近处速度为0, 符合无滑移边界条件. 3幅速度云图的速度最大位置发生在波峰波谷处.流体在翼型起始点处, 速度为0, 压强最大, 流体沿着翼型在压强梯度作用下, 速度逐渐增加, 到波峰处速度达到最大.流体经过翼型的扰动后, 流体速度发生变化.当幅值为0.125时, 翼型对流场的扰动较小, 速度变化的区域集中在中线附近, 如图 5(a)所示.随着幅值增加, 当幅值为0.5时, 翼型对流场扰动增大, 速度变化的区域明显增大, 如图 5(c)所示.
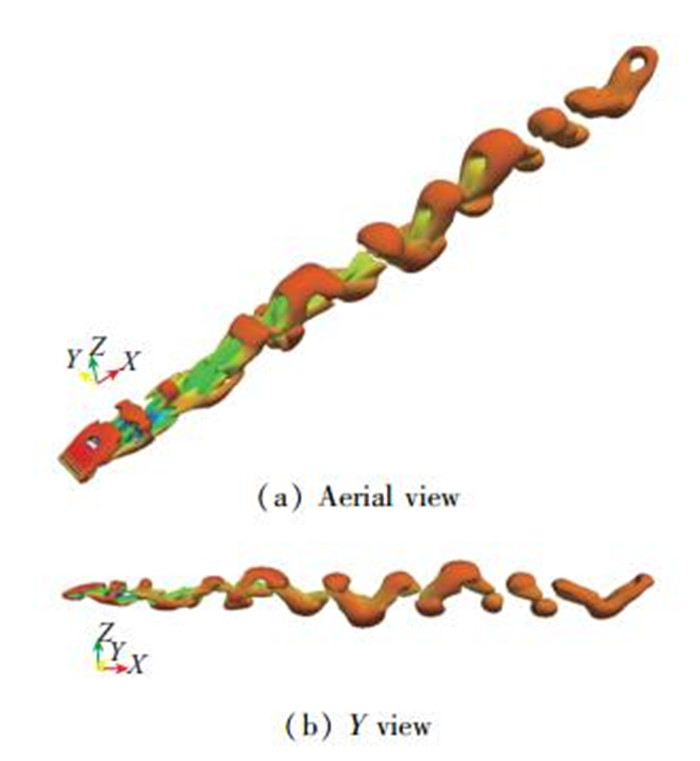
3.3 波动翼涡结构的演化图 6~8列出了A=0.125, 0.25, 0.5这3种工况下, t=3.25T(T为波动周期)时翼型流场瞬时涡系结构.本文中涡结构的识别采用Q准则, Q准则的定义为Q=1/2(ΩijΩij-SijSij) 图 6(a)为鸟瞰图, 图 6(b)为Y向视图.波动翼型的相角从0~π/2的过程中, 波动翼表面的涡脱离翼型, 在向后扩散的过程中和翼稍涡相连, 在尾流场中形成涡环结构.由于翼型中心对称, 因此尾流中的涡环呈现出相连的双涡环结构.双涡环结构见图 6(a), 7(a), 8(a).涡系结构选取于第4周期开始时刻, 因此在图 6(b), 7(b), 8(b)中均呈现6个相连的双涡环结构.
|
| 图 6 幅值为0.125, t=3.25T, Q(Q=0.0001) 准则定义的瞬时涡系结构 Fig.6 Vortical structure visualized by Q-criterion at 3.25T, with amplitude of 0.125 |
|
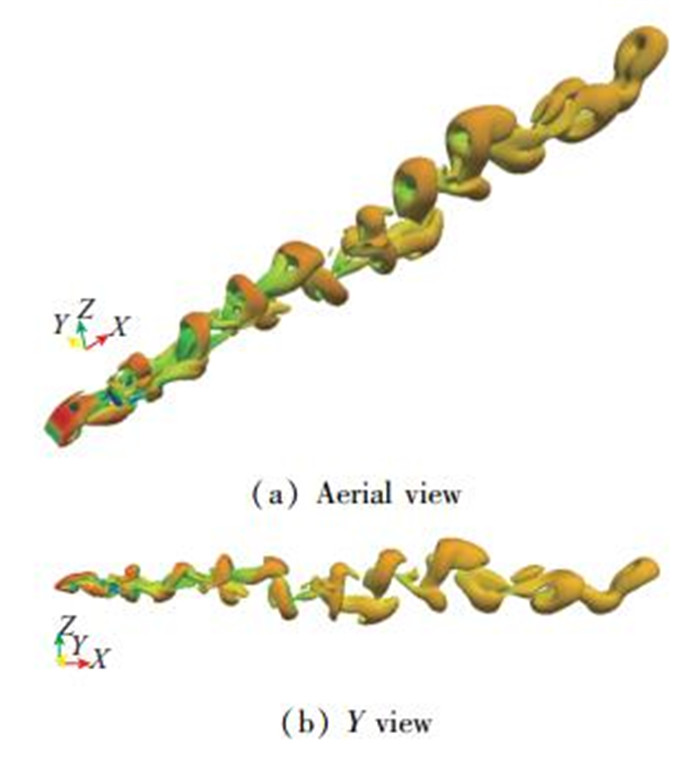
| 图 7 幅值为0.25, t=3.25T, Q(Q=0.0001) 准则定义的瞬时涡系结构 Fig.7 Vortical structure visualized by Q-criterion at 3.25T, with amplitude of 0.25 |
|
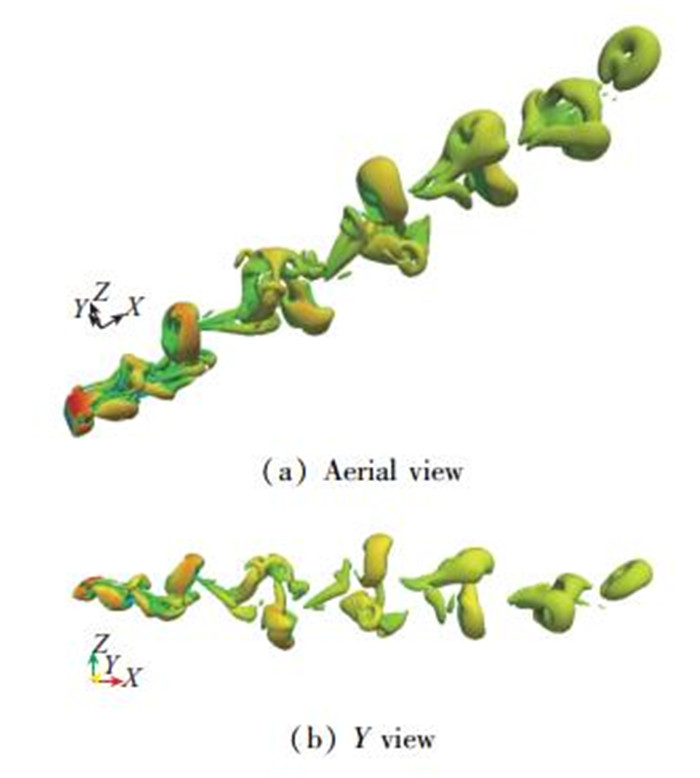
| 图 8 幅值为0.5, t=3.25T, Q(Q=0.0001) 准则定义的瞬时涡系结构 Fig.8 Vortical structure visualized by Q-criterion at 3.25T, with amplitude of 0.5 |
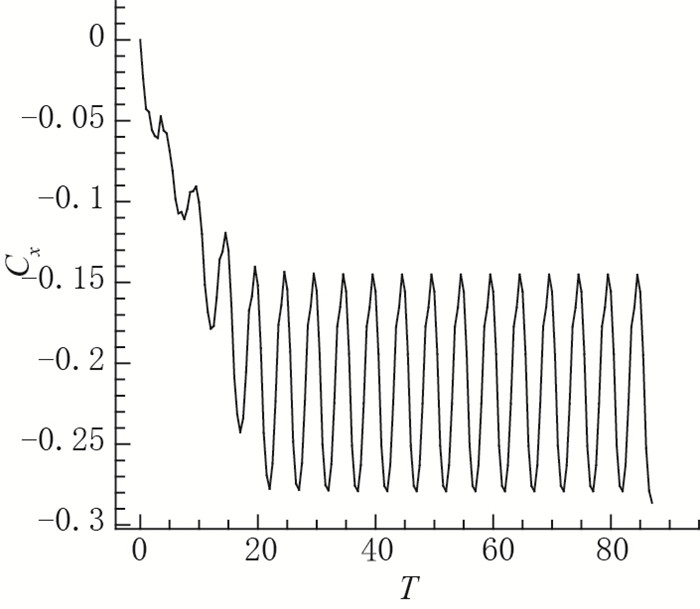
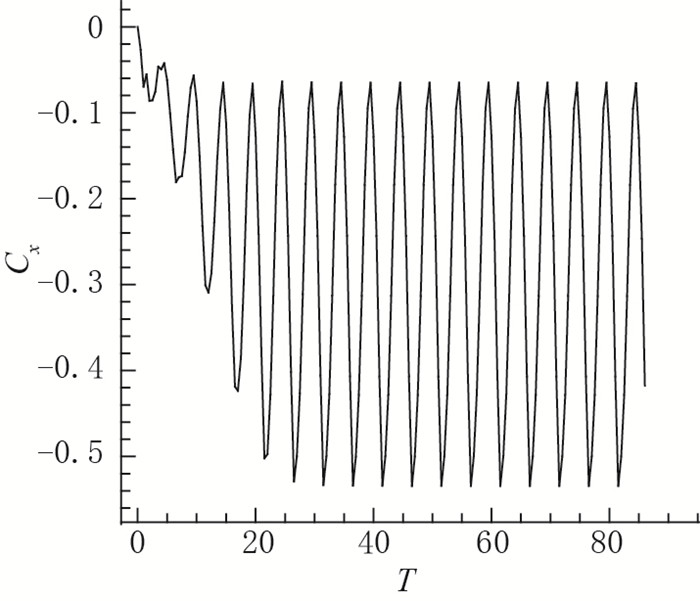
当幅值为0.125时, 推力系数平均值为-0.22;当幅值为0.25时, 推力系数平均值为-0.3;当幅值为0.5时, 推力系数的平均值为-0.5.本文中流体流动方向为正x方向, 负的推力系数与波动翼运动方向一致.随着翼型波动幅值增加, 涡的强度增加, 诱导出流体的速度也越大, 上述速度云图同样说明幅值增加流体的扰动区域增加.根据动量定理, 翼型受到的冲量增加, 因此推力系数也增加, 如图 9~11所示.
|
| 图 9 幅值为0.125时, X方向推力系数随时间变化 Fig.9 Coefficient in x-direction with an amplitude of 0.125 |
|
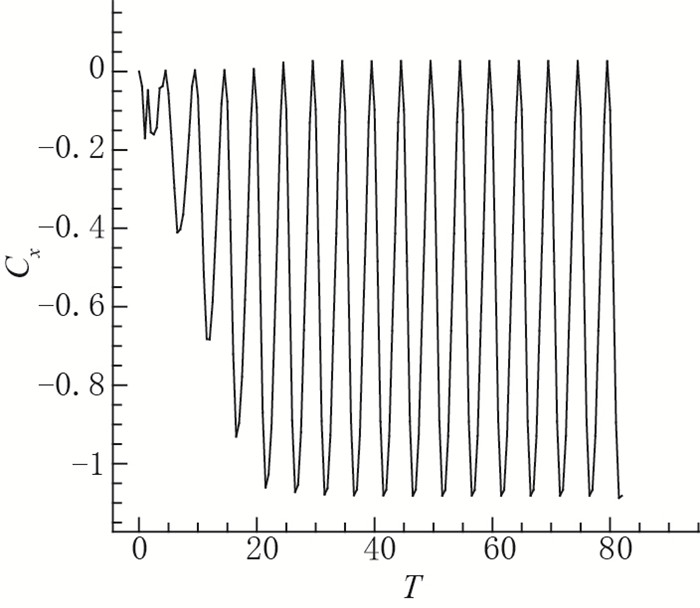
| 图 10 幅值为0.25时, X方向推力系数随时间变化 Fig.10 Coefficient in x-direction with an amplitude of 0.25 |
|
| 图 11 幅值为0.5时, X方向推力系数随时间变化 Fig.11 Coefficient in x-direction with an amplitude of 0.5 |
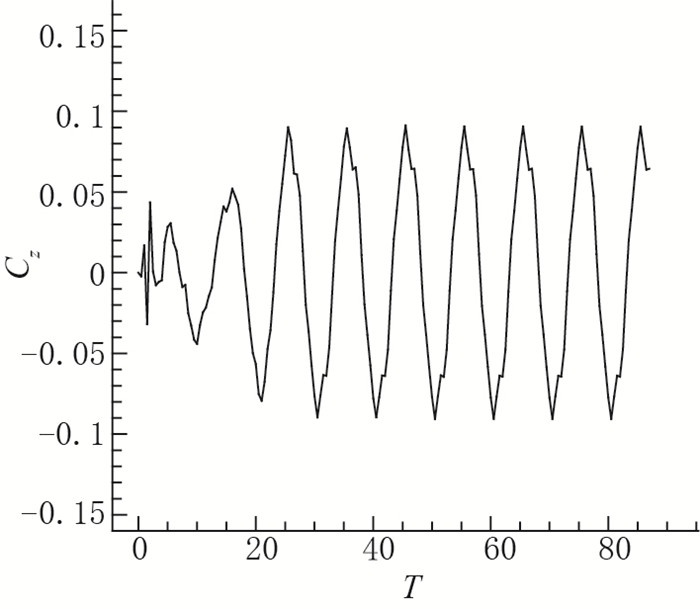
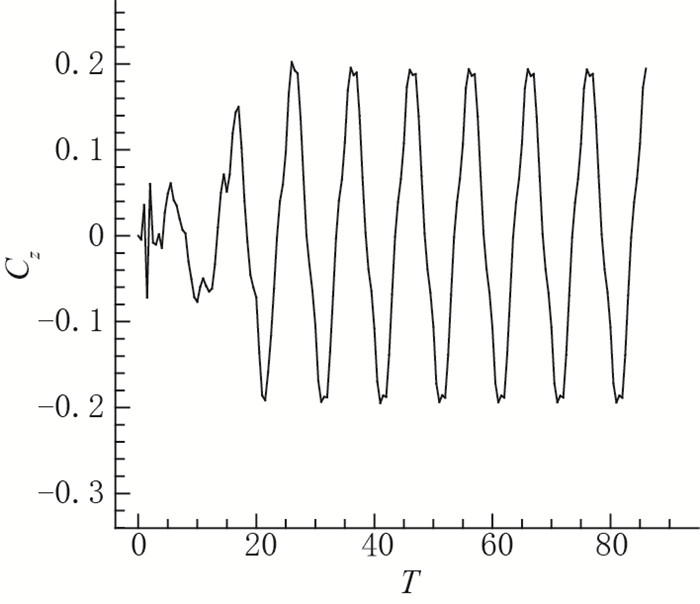
Z向力系数平均值为0.当翼型的波动幅值为0.125时, 最大力系数为0.09;当波动幅值为0.25时, 最大力系数为0.2;当幅值为0.5时, 最大力系数为0.44.翼型的最大力系数随着波动幅值的增大而增加, 如图 12~14所示.由于翼型的反对称运动, 升力的变化周期是阻力变化周期的两倍.对于类鳗鱼正弦运动游动, 其摆动幅值越大, 获得的推力越大, 但是同时类鳗鱼受到周期性的侧向力也越大, 这对于鱼类游动稳定极为不利.单从升阻力系数来看, 现实世界中鳗鱼的游动, 身体摆动的幅值保持在一个合理的范围内.
|
| 图 12 幅值为0.125时, Z方向力系数随时间的变化曲线 Fig.12 Coefficient in z-direction with an amplitude of 0.125 |
|
| 图 13 幅值为0.25时, Z方向力系数随时间的变化曲线 Fig.13 Coefficient in z-direction with an amplitude of 0.25 |

|
| 图 14 幅值为0.5时, Z方向力系数随时间的变化曲线 Fig.14 Coefficient in z-direction with an amplitude of 0.5 |
本文以水下航行器仿生推进为背景, 采用基于IB-LBM的面向天河-2超级计算机求解器, 选取了模拟结果更精确的三维平板波动翼模型, 采用1×108计算网格开展了非定常流场并行模拟.给出了不同幅值下涡系结构演化过程, 发现翼型往复波动时将边界层中的涡泄出, 泄出的涡相互作用, 形成个数固定成周期性的涡向后脱落, 涡的诱导作用使翼型后边的流体速度加快, 翼型从而获得推力.仿生波动翼波动幅值越大, 翼型的两个凹陷处的反对称涡系越明显.翼型平均阻力系数随着幅值增加而增加, 平均升力系数始终为0, 最大升力系数随着幅值的增加而增加.在仿生潜水器的设计中, 波动幅值越大, 获得的推力越大, 但是侧向稳定性会被破坏, 因此波动幅值应该选择一个合理范围.
| [1] |
董根金. 波状摆动变形体非定常粘性绕流的数值研究[D]. 合肥: 中国科学技术大学, 2006.
Dong G J. Study of unsteady viscid flow past body undulation[D]. Hefei: University of Science and Technology of China, 2006(in Chinese). |
| [2] | Frith H, Blake R. The mechanical power output and hydromechanical efficiency of northern pike (Esox lucius) fast-starts[J]. Journal of Experimental Biology, 1995, 198(9): 1863-1873. |
| [3] | Domenici P, Blake R W. The kinematics and performance of the escape response in the angelfish (Pterophyllum eimekei)[J]. Canadian Journal of Zoology, 2011, 71(11): 2319-2326. |
| [4] |
潘定一. 基于沉浸边界法的鱼游运动水动力学机理研究[D]. 杭州: 浙江大学, 2011.
Pan D Y. Studies on the hydrodynamics mechanism of fish-like swimming with immersed boundary method[D]. Hangzhou: Zhejiang University, 2011(in Chinese). |
| [5] |
李高进. 三维拍动板推进特性的数值研究及理论分析[D]. 合肥: 中国科学技术大学, 2012.
Li G J. Numerical and theoretical study on the three-dimension flapping locomotion[D]. Hefei: University of Science and Technology of China, 2012(in Chinese). |
| [6] | Wu J, Shu C. A coupled immersed boundary-lattice Boltzmann method and its simulation for biomimetic problems[J]. Theoretical & Applied Mechanics Letters, 2015, 5(1): 16-19. |
| [7] |
丁一宸. 蝌蚪游动的IB-LBM数值模拟[D]. 北京: 北京理工大学, 2015.
Ding Y C. IB-LBM numerical modeling of a tadpole swimming[D]. Beijing: Beijing Institute of Technology, 2015(in Chinese). |
| [8] | Tian F B, Luo H, Zhu L, et al. Interaction between a flexible filament and a downstream rigid body[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2010, 82(2): 530-539. |
| [9] | Aidun C K, Clausen J R. Lattice-Boltzmann method for complex flows[J]. Annual Review of Fluid Mechanics, 2009, 42(1): 439-472. |
| [10] | Jourabian M, Farhadi M, Rabienataj D A, et al. Lattice Boltzmann simulation of melting phenomenon with natural convection from an eccentric annulus[J]. Thermal Science, 2013, 17(3): 877-890.DOI:10.2298/TSCI110510012J |
| [11] | Miguel A F. Non-Darcy porous media flow in no-slip and slip regimes[J]. Thermal Science, 2012, 16(1): 167-176.DOI:10.2298/TSCI100929001M |
| [12] | Sajjadi H, Gorji M, Kefayati G H, et al. Lattice Boltzmann simulation of turbulent natural convection in tall enclosures using Cu/water nanofluid[J]. Numerical Heat Transfer, Part A: Applications, 2012, 62(6): 512-530.DOI:10.1080/10407782.2012.703054 |
| [13] | Shangguan Y, Wang X, Li Y. Large-scaled simulation on the coherent vortex evolution of a jet in a cross-flow based on lattice Boltzmann method[J]. Thermal Science, 2015, 19(3): 977-988.DOI:10.2298/TSCI150606101S |
| [14] | Tian Z, Xing H, Tan Y, et al. Reactive transport LBM model for CO2 injection in fractured reservoirs[J]. Computers & Geosciences, 2016, 86: 15-22. |
| [15] | Ammer R, Rüde U, Markl M, et al. Validation experiments for LBM simulations of electron beam melting[J]. International Journal of Modern Physics C, 2015, 25(12): 1441009 |
| [16] | Feng Z G, Michaelides E E. The immersed boundary-lattice Boltzmann method for solving fluid-particles interaction problems[J]. Journal of Computational Physics, 2004, 195(2): 602-628.DOI:10.1016/j.jcp.2003.10.013 |
| [17] | Feng Z G, Michaelides E E. Proteus—a direct forcing method in the simulation of particulate flows[J]. Journal of Computational Physics, 2005, 202(1): 20-51.DOI:10.1016/j.jcp.2004.06.020 |
| [18] | Niu X D, Shu C, Chew X T, et al. A momentum exchange-based immersed boundary-lattice Boltzmann method for simulating incompressible viscous flows[J]. Physics Letters A, 2006, 354(3): 173-182.DOI:10.1016/j.physleta.2006.01.060 |
| [19] | Wu J, Shu C. Implicit velocity correction-based immersed boundary-lattice Boltzmann method and its applications[J]. Journal of Computational Physics, 2009, 228(6): 1963-1979.DOI:10.1016/j.jcp.2008.11.019 |
| [20] | Tian F B, Luo H, Zhu L, et al. An efficient immersed boundary-lattice Boltzmann method for the hydrodynamic interaction of elastic filaments[J]. Journal of Computational Physics, 2011, 230(19): 7266-7283.DOI:10.1016/j.jcp.2011.05.028 |
| [21] | Suzuki K, Inamuro T. Effect of internal mass in the simulation of a moving body by the immersed boundary method[J]. Computers & Fluids, 2011, 49(1): 173-187. |
| [22] | Kimura Y, Suzuki K, Inamuro T. Flight simulations of a two-dimensional flapping wing by the IB-LBM[J]. International Journal of Modern Physics C, 2013, 25(1): 265-284. |
| [23] | Wu J, Qiu Y L, Shu C, et al. Pitching-motion-activated flapping foil near solid walls for power extraction: A numerical investigation[J]. Physics of Fluids, 2014, 26(8): 083601DOI:10.1063/1.4892006 |
| [24] | Zhang J. Locomotion of a passively flapping flat plate[J]. Journal of Fluid Mechanics, 2010, 659(659): 43-68. |
| [25] | Rosis A D. On the dynamics of a tandem of asynchronous flapping wings: lattice Boltzmann-immersed boundary simulations[J]. Physica A: Statistical Mechanics & Its Applications, 2014, 410(12): 276-286. |
| [26] | Peskin C S. The immersed boundary method[J]. Acta Numerica, 2002, 11: 479-517. |
| [27] | Feng Z G, Michaelides E E. The immersed boundary-lattice Boltzmann method for solving fluid-particles interaction problems[J]. Journal of Computational Physics, 2004, 195(2): 602-628.DOI:10.1016/j.jcp.2003.10.013 |
| [28] | Krüger T. Introduction to the immersed boundary method[C]. LBM Workshop, Edmonton, Canada, 2011 |
| [29] | Frisch U, Hasslacher B, Pomeau Y. Lattice-gas automata for the Navier-Stokes equation[J]. Physical Review Letters, 1986, 56(14): 1505-1508.DOI:10.1103/PhysRevLett.56.1505 |
| [30] | Bhatnagar P L, Gross E P, Krook M. A model for collision processes in gases[J]. Physical Review, 1954, 94(3): 511-525.DOI:10.1103/PhysRev.94.511 |



