20世纪涡轮机研制过程中发现:叶片尖端速度不能超过305~450m/s[1].否则效率迅速降低、结构应力将过高.究其原因, 叶片尖端速度超过声速, 流场中出现了激波.控制激波成为涡轮机设计的一项重要内容.由此联想起:高速火车通过隧道时如果产生激波, 也会使列车周围气流压力升高, 导致车辆结构应力过高、运行能耗上升以及隧道出口噪声剧增等严重问题.
我和几位长期从事飞行器气动研究的老朋友交流这个想法时, 他们对我说:你的思想是不是解放过头了?飞行器速度超过声速才会形成激波.高速火车最高运行速度还不到0.5M, 担心车前形成激波, 岂非杞人忧天!
然而飞行器是在无边界限制的空中飞行, 火车通过隧道时, 受隧道壁面的约束, 两者环境是截然不同的.激波相对于波前气体的传播速度必须高于气体的声速.由于飞行器的头激波为驻定激波, 其速度与飞行器相同, 因而亚声速飞行器不可能出现头激波.活塞在管道中运动, 受管壁约束, 活塞前方激波为运动激波, 其速度大于活塞.即便活塞速度很低, 前驱激波速度也大于声速, 满足激波存在条件, 因而低速活塞前能够形成激波.
火车通过隧道受壁面约束,类似活塞在管道中运动受到管壁的约束.活塞在管中运动, 无论活塞速度高低都会产生激波.虽然火车开行已相当久远, 高铁运行也已半个多世纪, 仍未听说列车通过隧道时会出现激波!火车通过隧道时究竟会不会产生激波?在什么条件下会产生激波?这就是本文探究的中心问题.
1 活塞在管中运动激波管流动是典型的一元不定常流动.激波管结构及流动波图示于图 1.

|
| 图 1 激波管结构及流动波图 Fig.1 Schematic diagrams of shock tube and wave diagram |
激波管流动从破膜开始, 破膜后高压段中的气体膨胀加速流向低压段, 驱动低压气体向前流动, 受扰动的低压气体前沿会形成一个强间断——运动激波.假定气体为完全气体、无黏以及忽略热交换, 激波Mach数与气体分界面(分隔原先在高、低压段的气体)速度的关系式如下:
| $\frac{{{U_G}}}{{{a_1}}} = \frac{2}{{{\gamma _1} + 1}}\left( {{M_{\rm{s}}} - \frac{1}{{{M_{\rm{s}}}}}} \right).$ | (1) |
式(1) 中MS为激波Mach数, UG为气体分界面速度, a1和γ1分别为未受扰动气体的声速和比热比, 数值结果见表 1.
| 下载CSV 表 1 数值结果 Tab.1 Numerical results |
从表 1中数据可以看出:激波速度或Mach数始终大于气体分界面速度或Mach数; 即便气体分界面速度很低, 激波Mach数也大于1.
激波管实验结果表明:高、低压气体压力比很小, 破膜后形成的分界面速度很低时, 也能产生入射激波.在管中运动的活塞就像激波管流动中气体分界面.据此可以得到:活塞运动速度即便很低, 其前方也会产生一个运动激波.
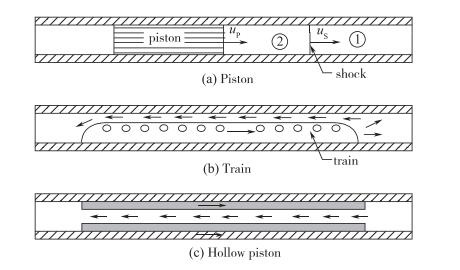
2 空心活塞在管中运动火车通过隧道与活塞在管道中运动, 两者存在本质差别:活塞与管壁紧密接触, 不会漏气, 被活塞推动的气体只能向前流动; 而火车与隧道壁面之间空隙相当大, 受火车推动的气体既可向前流动, 也可通过火车与隧道壁面之间的空隙返流回火车后方.因而空心活塞才能真实模拟火车通过隧道(见图 2).
|
| 图 2 活塞、空心活塞在管中运动和火车通过隧道示意图 Fig.2 Schematic diagrams of piston and hollow piston travelingthrough tube, and train through tunnel |
空心活塞与普通活塞在管道中运动产生的气体流动究竟存在什么本质差别?将坐标系固定在活塞上就会看得比较清晰.
坐标变换后, 活塞静止不动, 管道入口处的气体则以活塞速度流入(见图 3).
|
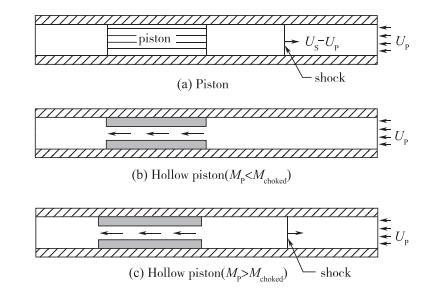
| 图 3 活塞静止流动示意图 Fig.3 Schematic diagrams of flow in tube with a stationary piston |
图 3(a)为变换坐标后普通活塞在管中运动的示意图.流入管中的气体碰撞活塞就像激波管中的② 区气流碰撞管尾壁面一样, 气流速度被滞止并立即反射回一个激波.
图 3(b)为变换坐标后空心活塞在管中低速运动的示意图.由于入口处气流Mach数较低, 气流可通过空心活塞中心孔顺利流出, 管中不会出现激波.
在管道流动中, 管道横截面积变化, 壁面摩擦和热交换均可使流动参数随之改变.假定流动过程绝热且忽略黏性效应, 则流动参数仅随横截面积的改变而变化.若入口处为亚声速流, 横截面缩小, 则当地气流Mach数升高.当最小横截面处气流Mach数上升至1时, 流量达极大值, 出现壅塞现象.此时入口处气流Mach数定名为壅塞Mach数.
如果管入口处气流Mach数大于壅塞Mach数, 管中就会像普通活塞在管中运动一样, 在活塞前方出现一个运动激波, 见图 3(c).
为何入口气流Mach数大于壅塞Mach数, 管中会出现运动激波呢?当气体流入量超过活塞中心孔最大流量, 超过最大流量的多余气体必须有出路.新增一个激波, 使进入管中的气流通过该激波后气流Mach数降低到壅塞Mach数, 气流才能顺利通过活塞中心孔.前面已经提到,激波相对于波前气体的传播速度必须高于气体的声速.亚声速气流中不可能存在驻定激波, 对于运动激波, 其上游气流可以是超声速流, 也可以是亚声速流, 甚至是静止的或同方向运动的气流.因而可出现运动激波.
为何新出现的运动激波刚好能将上游超过壅塞Mach数的气流降到壅塞Mach数?原因是产生运动激波的根源为超过最大流量的多余流量.如果上游气流通过运动激波后, 气流Mach数降低但仍高于壅塞Mach数, 则还是有多余流量通不过最小截面, 这些多余气流将增强反向激波强度, 使穿过激波的气流Mach数刚好降低到壅塞Mach数.这种状态下, 气流可顺利通过最小截面.由于不再有多余气体使运动激波的强度进一步加强, 运动激波后的气流Mach数不会降得更低.
活塞运动Mach数是否超过壅塞Mach数是空心活塞在管中运动时能否产生激波的判定基准.普通活塞堵塞气流通道, 始终处于壅塞状态.空心活塞运动Mach数超过壅塞Mach数, 出现壅塞状态后, 才像普通活塞一样, 在管中运动时驱动产生运动激波.流动中气流壅塞是出现激波的基础条件.
3 空心活塞壅塞Mach数假定流动过程绝热, 除活塞中心孔内流动考虑黏性外, 其他流动均忽略气体黏性.活塞中心孔为等截面管.若入口处气流为亚声速流, 摩擦作用使气流速度或Mach数随管长延伸逐渐增大, 中心孔出口端气流Mach数最高.当出口端气流Mach数达到1, 流量达最大值, 即出现壅塞现象.此时空心活塞中心孔入口处Mach数Min可按式(2)[1]求出
| $\frac{{4\bar fL}}{D} = \frac{{1 - M_{{\rm{in}}}^2}}{{{\mathit{\gamma }_1}M_{{\rm{in}}}^2}} + \frac{{{\mathit{\gamma }_1} + 1}}{{2{\mathit{\gamma }_1}}}\ln \frac{{\left( {{\mathit{\gamma }_1} + 1} \right)M_{{\rm{in}}}^2}}{{2\left( {1 + \frac{{{\mathit{\gamma }_1} - 1}}{2}M_{{\rm{in}}}^2} \right)}}.$ | (2) |
因为流动介质为空气, γ1=1.4, 式(2) 可改写为
| $\frac{{4\bar fL}}{D} = \frac{{1 - M_{{\rm{in}}}^2}}{{1.4M_{{\rm{in}}}^2}} + \frac{6}{7}\ln \frac{{1.2M_{{\rm{in}}}^2}}{{1 - 0.2M_{{\rm{in}}}^2}}.$ | (3) |
式(2) 和式(3) 中, L、D和
求出空心活塞中心孔出口端气流Mach数为1时入口处的气流Mach数Min后, 再根据中心孔和管道横截面积按式(4)[1]可求出壅塞Mach数(Mchoked):
| $\frac{{{A_{{\rm{tube}}}}}}{{{A_{{\rm{hole}}}}}} = \frac{{{M_{{\rm{in}}}}}}{{{M_{{\rm{choked}}}}}}{\left( {\frac{{1 + 0.2M_{{\rm{choked}}}^2}}{{1 + 0.2M_{{\rm{in}}}^2}}} \right)^3}.$ | (4) |
火车车箱与隧道壁面之间的空隙断面为不规则的非圆截面.为了计算火车通过隧道不出现激波的最大Mach数, 先要求出等效水力直径D(4倍车箱与隧道壁面之间空隙横截面积除以火车车箱断面外周长), 将圆截面转化为等效圆.再按计算空心活塞壅塞Mach数的方法, 求出火车通过隧道不出现激波的火车最大Mach数.这是气动效应限制的最高车速.
如果火车速度、长度、车箱横断面积以及列车平均摩阻系数已定, 则可求出隧道最小横截面面积.这就是气动效应限制的隧道最小横截面.
隧道最小截面还有其他各种限制因素, 如车辆气密性、车辆抗震性等[2].当前这些技术水平限制的隧道最小截面比气动效应限制的隧道最小横截面大得多, 还不到考虑气动效应限制的时候.但各种技术因素与气动效应限制的隧道最小横截面积差距, 可以作为评估这些技术发展水平的参考.
5 测量列车摩阻的新方法用于克服火车气动阻力的动力消耗随车速的3次方急剧增大, 气动阻力的动力消耗已经成为高铁列车能耗的重要部分.
运动物体的气动阻力分为压差阻力和摩擦阻力两部分.由于列车是特别细长的物体, 摩擦阻力成为气动阻力的主要组成部分.降低列车摩擦阻力的重要性不言而喻.
要有效降低列车的摩擦阻力, 测准摩擦系数极其关键.然而算准或测准摩擦系数, 长期以来一直是难以解决的问题.摩擦系数难以测准的原因是布置在物面附近或物体表面上的传感器会严重破坏当地流场特性, 从而大大降低了测量结果的可靠性.
依据本论文的成果, 提出一种间接测量列车全长平均摩擦系数的设想.新方法的基本构思如下:火车通过隧道时, 检测列车前是否出现了激波, 即是否出现了壅塞现象.如果出现了激波, 则列车全长平均摩擦系数可由列车速度、列车长度、车厢横截面周长以及隧道和列车横截面积求出.新方法只需判定列车前出现了激波, 就可获得列车平均摩擦系数.由于不需要使用摩擦传感器, 从而提高了数据的可靠性.
提出的间接测量列车全长平均摩擦系数的新方法, 既适用于缩尺模型试验, 也可用于实车试验.两者所需设备及测量仪器都相当简单.
6 结束语《气体物理》杂志批准正式出版后, 编辑部邀我向首期投送一篇论文.
在我着手选择论文内容时, 着重思考了两个问题.一是庄逢甘先生在《气体物理》发刊词中提出的希望.他认为《气体物理》的英文译名与美国著名刊物《Physics of Fluids》类似, 希望《气体物理》办成与《Physics of Fluids》性质相同的杂志.二是论文应该有点创新性.
当前国内大家十分喜欢使用“创新”一词, 含意十分广泛.我追求的“创新”是什么含意呢?庄逢甘先生在《气体物理》发刊词中引用了《Science》关于创新的观点:“创新不是对已有结论进行简单的重复论证, 而是对自然或理论提出新的见解, 它应具有冲击性和启发性, 并包含广泛的科学意义.如沉寂领域的先锋思想, 活跃领域的重大进展, 分散领域的有机融合. ”这与我遵照的钱学森的“创新”含义是一致的.
思考后我将论文针对的问题定为“高速火车穿越隧道时会不会驱动产生激波?产生激波的条件是什么?”.前些时候, 我向几位资深专家通报有关想法时, 他们听后面露惊异的表情.回忆当时的情景,我猜想这些内容可能具有冲击性.这是我选定论文题目的一个重要原因.
气动力学在高铁技术发展进程中的作用随着车速的提高而急剧增加, 相关研究工作日益受到人们重视.但是当前开展的研究工作大多是与飞行器研究工作类似的内容, 采用的方法也是从那里扩展过来的.这些工作当然很有实用价值, 将有力促进高铁技术的发展.
但是像高速火车穿越隧道、桥梁、车站及靠近其它物体通过有关的流动问题, 不论国内或国外都很少有人问津.当前我国高铁技术已处于国际先进水平, 不应该回避这些难题.然而这些流动问题, 具有很强的非定常性, 相关研究先例很少, 开展工作难度很大.
作者决定试探一下这类流动问题, 先从最简单的开始, 着重认识流动现象和特性, 同时探求各种可能的实际应用.论文获得的结果并不深入, 错误也难免.投送并发表本论文, 目的为抛砖引玉, 提醒青年同志关注这类重要但十分困难的工作, 希望有人选做这类工作, 收获优异成果.
致谢: 本文写作过程中, 曾和李进平副研究员多次讨论.他还为本文制图和公式, 在此一并致谢!| [1] |
Shapiro A H. 可压缩流的动力学与热力学(上册)[M]. 陈立子, 译. 北京: 科学出版社, 1966: 164~173
Shapiro A H. The dynamics and thermodynamics of compressible flow(volume Ⅰ)[M]. Chen L Z, translated. Beijing:Science Press, 1966: 164~173(in Chinese) |
| [2] |
赵有明, 马伟斌, 程爱君, 等.高速铁路隧道气动效应[M].北京:中国铁道出版社, 2012: 5~11
Zhao Y M, Ma W B, Cheng A J, et al. High-speed railway tunnel aerodynamic effect[M]. Beijing: China Railway Publishing House, 2012: 5~11(in Chinese) |



