2. 航天神舟飞行器有限公司,天津 300000
2. Aerospace Shenzhou Aerial Vehicle Co., Ltd, Tianjin 300000, China
飞行器大攻角飞行时, 三维非定常流动特征明显, 存在复杂的流动分离、涡破碎等现象.准确预测气动特性, 对气动力进行有效建模是飞行仿真和性能评估的基础.在大攻角状态下, 气动力不仅和当前的状态相关, 也和飞行历史状态相关.传统由静态气动力和动导数构成的气动模型, 已经不能满足大攻角状态下飞行稳定性分析、飞行仿真和控制的需要[1], 必须建立一套能够包含充分非定常非线性特性的气动模型.
目前, 飞行器大迎角范围内的气动力建模, 需要在高精度计算流体力学方法的预测结果和必要的动态风洞试验验证的基础上建立空气动力模型, 从而提供大攻角飞行过程中任意时刻的非定常气动力.随着计算机和数值方法的发展[2], 采用强迫振荡运动的CFD预测方法, 在飞行器动态稳定性参数预测中已经有了较为广泛的应用[3], 在大攻角动态气动力的性能预测上也得到了推广[4].
一套成熟的气动预测和建模方法可以有效地评估飞行器的设计方案[5], 降低飞行器设计风险, 节约研发成本[6].
不少研究人员针对大攻角气动建模问题, 采用了两类研究方法[7], 一类是建立气动力和飞行物理量相关的数学类的气动模型, 如代数模型[8-9]、阶跃响应模型[10]、微分方程模型、状态空间模型[11-12]; 另一类是智能学习类的气动模型, 如模糊逻辑法[13]、支持向量机[14]、神经网络法[15-17]等.传统分析方法是进行大量的气动数值计算和风洞试验来进行分段线性气动建模, 在一定程度上解决了工程问题, 随着人工智能技术的发展, 神经网络技术在气动建模中得到了一定的应用[18-20].神经网络方法可以建立多输入多输出的任意非线性模型, 非常适合大攻角非线性、非定常气动力特性建模[21-22].
本文利用CFD方法, 对某典型轴对称导弹外形飞行器大攻角气动力进行了数值预测, 通过复杂飞机标模动态气动力的数值算例验证, 证明了该数值方法的有效性.针对不同运动频率的数值气动力数据, 进行了线性动导数模型、多项式模型和神经网络模型的气动建模.通过对比分析, 确定了神经网络模型是适合于描述大攻角非线性非定常特性的气动模型.探索了基于人工智能的神经网络模型在飞行器大机动条件下气动力建模中的应用, 表征飞行器的气动力/力矩与飞行状态和控制输入之间的函数关系.结果表明, 神经网络方法对于高度非线性的大攻角非定常气动力模型具有较高的拟合精度.
1 研究方法为了建立飞行器大攻角气动特性的模型, 需要获得大量的非定常样本数据, 本文采用CFD方法获得气动建模的气动数据, 探索传统数学类模型和基于人工智能思想的神经网络方法进行气动建模.
1.1 数值计算控制方程数值计算采用基于RANS的N-S方程[23], 运动计算采用建立在机体轴系的强迫运动方程[24], 流体运动控制方程如下
| $ \frac{{\partial \hat U}}{{\partial t}} + \frac{{\partial \hat F}}{{\partial \xi }} + \frac{{\partial \hat G}}{{\partial \eta }} + \frac{{\partial \hat H}}{{\partial \zeta }} = \frac{1}{{R{e^*}}}\left( {\frac{{\partial {{\hat F}_{\rm{v}}}}}{{\partial \xi }} + \frac{{\partial {{\hat G}_{\rm{v}}}}}{{\partial \eta }} + \frac{{\partial {{\hat H}_{\rm{v}}}}}{{\partial \zeta }}} \right) $ |
其中,
补充理想气体方程和网格运动方程
| $ \begin{array}{*{20}{c}} {P = \rho RT}\\ {{\mathit{\boldsymbol{V}}_{\rm{i}}} = {\mathit{\boldsymbol{V}}_{\rm{c}}} + \mathit{\boldsymbol{\omega }} \times {\mathit{\boldsymbol{r}}_{{\rm{i - c}}}}} \end{array} $ |
式中,P为压强, ρ为大气密度, R为气体常数, T为来流温度, Vi为气流总速度, Vc为来流速度, ω为飞行器运动角速度, r为气体到飞行器质心的距离.
1.2 数值计算方法非定常气动特性计算采用经典的Roe格式进行空间离散, 具体见文献[25].时间推进采用隐式LU-SGS格式的双时间步方法.由于采用刚性动网格, 网格的体积保持不变, 自动满足了几何守恒律.边界条件采用恒温壁无滑移物面边界, 远场采用基于Riemann不变量的无反射远场边界[26].大规模的气动计算在中国航天空气动力技术研究院高性能计算中心进行.
1.3 气动建模方法飞行器大攻角机动过程中主导飞行运动的呈现高度非线性特性, 其中非定常非线性气动力是非线性特性的主要来源.为了描述飞行器运动, 需要建立六自由度运动方程, 从而建立气动力和运动状态及其导数的形式[27].常用的气动建模方法有线性动导数模型、多项式模型和神经网络模型等[28].
线性气动模型, 也就是工程上常用的气动导数模型, 目前国内外飞行动力学分析与控制设计最常用的也都是这种线性气动模型.动导数模型早在1911年, Bryan[29]分析飞机飞行稳定性时就提出了, 该模型基于准定常假设, 气动力和力矩仅仅依赖于飞行器的速度和角速度的瞬时值, 气动建模的标准函数为
| $ f = {f_0} + {f^\alpha }\alpha + {f^\omega }\omega $ | (1) |
式中, f0为常数项, fα为静导数项, fω为动导数项.
多项式气动模型, 考虑影响气动特性的高阶项、耦合项的拟合建模[30].多项式形式的气动建模物理是处理非线性气动力建模的快速计算方法, 物理意义较为明确[31].针对纵向情况, 考虑纵向攻角和俯仰角速度两个影响因子, 考虑2阶和3阶两种形式, 拟合函数分别为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f = {f_0} + m_1^\alpha \alpha + m_1^\omega \omega + m_2^{\alpha \omega }\alpha \omega + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} m_2^{{\alpha ^2}}{\alpha ^2} + m_2^{{\omega ^2}}{\omega ^2}\\ f = {f_0} + m_1^\alpha \alpha + m_1^\omega \omega + m_2^{\alpha \omega }\alpha \omega + m_2^{{\alpha ^2}}{\alpha ^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} m_2^{{\omega ^2}}{\omega ^2} + m_3^{\alpha {\omega ^2}}\alpha {\omega ^2} + m_3^{{\alpha ^2}\omega }{\alpha ^2}\omega + m_3^{{\omega ^3}}{\omega ^3} \end{array} $ | (2) |
动导数气动模型和多项式气动模型内部系数的计算采用最小二乘法, 计算公式为
| $ \mathit{\boldsymbol{A}} = {({\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}})^{ - 1}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{Y}} $ |
式中,A为拟合系数矩阵, T表示矩阵转置, X,Y分别为敏感因变量矩阵和样本矩阵.
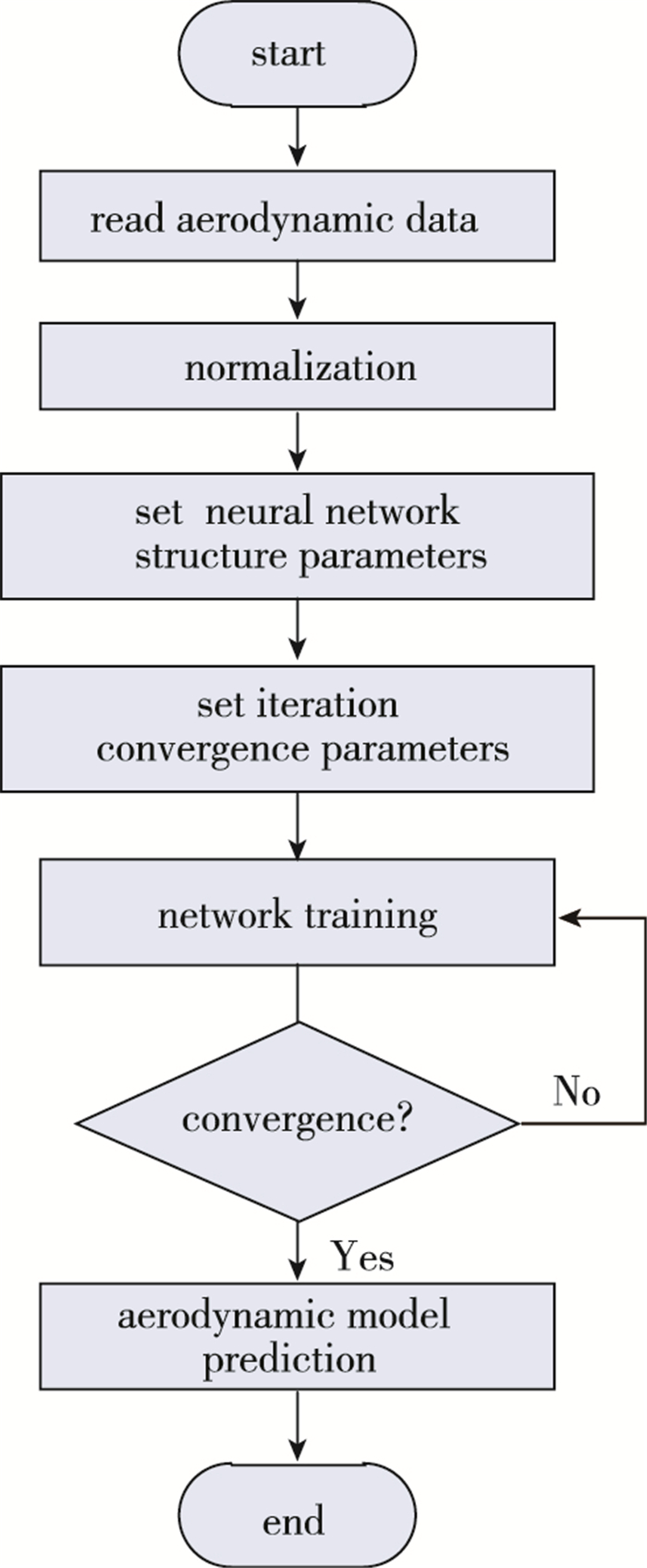
神经网络的气动模型, 具有良好的学习能力、较强的非线性拟合和预测能力, 因而适用于进行强非线性非定常气动特性建模[32].反向传播(back propagation,BP)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念, 是一种按照误差逆向传播算法训练的多层前馈神经网络, 是目前应用最广泛的神经网络. BP神经网络的训练算法称为误差反向传播的BP算法, 简称BP算法. BP神经网络的训练过程采用文献[32]的方法, 具体见图 1.首先读入气动力和气动样本, 进行归一化处理; 其次设置BP神经网络的结构参数和训练指标参数; 然后进行神经网络训练, 训练满足要求后即可以进行气动预测.
|
| 图 1 神经网络气动建模算法流程 Fig.1 Flowchart of the neural network aerodynamic modeling algorithm |
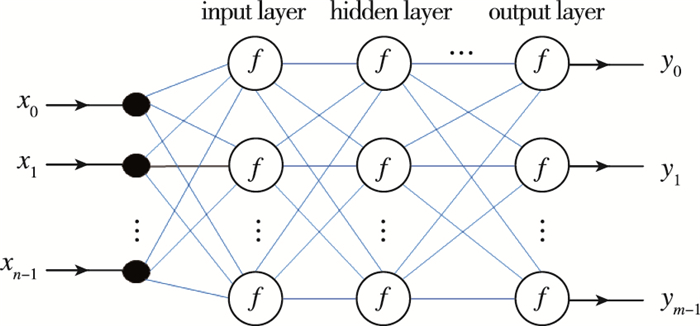
BP网络算法的基本思想是最小二乘法, 采用梯度搜索技术, 通过前向反馈误差来改变权值和阈值, 当使网络的实际输出值与期望输出值的误差均方误差低于某个阈值或学习达到一定的次数时, 训练结束.采用Levenberg-Marquardt(LM)方法作为神经网络的训练方法, 它是梯度下降法里最优的二阶训练方法. BP神经网络结构分3层, 输入层、隐含层和输出层, 如图 2所示.
|
| 图 2 BP神经网络的结构 Fig.2 Structure of BP neural networks |
训练输出的均方差误差为
| $ {E_{\rm{A}}} = \frac{1}{2}\sum\limits_{p = 1}^p {\sum\limits_{i = 0}^{m - 1} {{{(d_i^{(p)} - y_i^{(p)})}^2}} } $ |
式中,EA为目标网络参数, m为输出节点个数, p为训练样本个数, d为样本值, y为训练输出值.
设一个多输入多输出的BP神经网络有m个输入节点,n个隐层系数,p个输出节点.则BP网络的输出为
| $ {\hat y_p} = \sum\limits_{j = 1}^n {(\sum\limits_{i = 1}^m {{\omega _{ij}}} {x_{ij}} + {b_{ij}})} $ |
式中,j为输出节点, i为输入节点, 每个节点输入值xi, wij为权值公式, bij为节点的阈值.
权值更新公式
| $ {w_{ki}} = w_{ki}^\prime - \eta \nabla E({w_{ki}}) $ |
式中,k为隐含层节点数, i为输出节点个数, wki为第k个隐含节点到第i个输出节点之间的权重, η为学习率, ΔE(wki)是EA关于权值wki的梯度.即
| $ \nabla E({w_{ki}}) = \frac{{\partial {E_{\rm{A}}}}}{{\partial {w_{ki}}}} = \sum\limits_{p = 1}^p {\frac{{\partial {E_{\rm{A}}}}}{{\partial y_i^{(p)}}}} \frac{{\partial y_i^{(p)}}}{{\partial u_i^{(p)}}}\frac{{\partial u_i^{(p)}}}{{\partial {w_{ki}}}} $ |
其中
| $ \begin{array}{*{20}{l}} {u_i^{(p)} = \sum\limits_{k = 1}^k {{w_{ki}}} \cdot x_k^{(p)}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y_i^{(p)} = \frac{1}{{1 + {{\rm{e}}^{ - u_i^{(p)}}}}}} \end{array} $ |
因此
| $ \nabla E({w_{ki}}) = \sum\limits_{p = 1}^p {(d_i^{(p)} - y_i^{(p)})} \cdot y_i^{(p)} \cdot (1 - y_i^{(p)}) \cdot x_k^{(p)} $ |
为了验证CFD计算方法的有效性, 进行了标模的气动计算.校核计算选择的SDM标模是AEDC基于F-16简化外形提出的一个标准动态模型[33], 如图 3所示, 由机身、机翼、前缘边条、平尾、垂尾、腹鳍、座舱以及进气道组成.计算网格总数为5×105, 图 4展示了表面网格分布.计算参数为: Ma=0.6, 纵向质心位置Xcg=0.584, 减缩频率kr=0.034.为了节省计算量, 俯仰方向采用了半模计算.
|
| 图 3 SDM几何外形 Fig.3 SDM geometry |

|
| 图 4 SDM表面网格分布 Fig.4 SDM surface grids |
在定常计算基础上, 分别数值模拟了SDM绕体轴的俯仰和滚转强迫振荡运动的流场, 通过对非定常气动系数的辨识, 给出了各直接阻尼导数随攻角变化情况.
图 5给出的是俯仰阻尼导数Cmq+

|
| 图 5 俯仰阻尼随攻角变化曲线 Fig.5 Pitch damping curve with angle of attack |

|
| 图 6 滚转阻尼随攻角变化曲线 Fig.6 Roll damping curve with angle of attack |
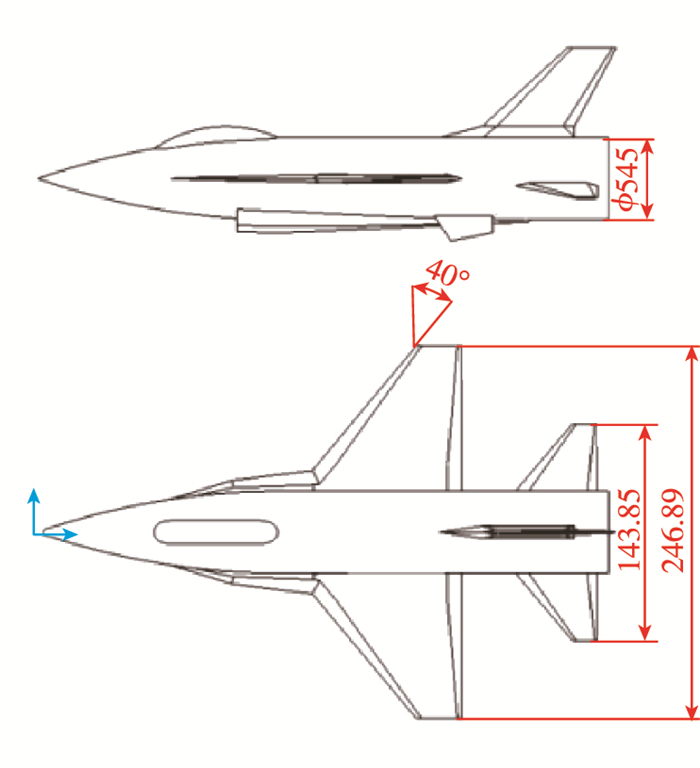
采用轴对称导弹简化模型作为研究对象, 外形尺寸和计算坐标如图 7所示:前面为锥形, 后面为光弹身, 无尾翼, 采用国内航天系, 机体坐标表示为: x轴为轴向,y轴为法向, z轴为侧向.模型全长1 000 mm, 底部直径100 mm, 参考长度为底部直径, 参考面积为底部面积.质心为距头部顶点500 mm处.

|
| 图 7 飞行器外形及坐标 Fig.7 Aircraft configuration and coordinate |
计算网格采用结构网格, 拓扑结构为O型, 网格量为3.2×105, 网格拓扑及对称面示意图见图 8.

|
| 图 8 导弹算例网格 Fig.8 Mesh generation for a missile |
计算状态为: Ma=0.4, 振荡运动的平衡攻角为70°, 振幅10°, 频率分别为1,2,3,5,10 Hz.气动力模型的一般函数形式为
| $ F = f(Ma,\alpha ,{\omega _z}) $ |
俯仰角的计算公式
| $ \theta = 70 + 10{\rm{sin}}(2\pi t + {\alpha _0}) $ |
角速度模型为
| $ {\omega _z} = 20\pi {\rm{cos}}(2\pi t) $ |
由于飞行器非定常气动影响因素多, 包含攻角、侧滑角、高度、速度、俯仰角速度、偏航角速度、滚转角速度、升降舵、偏航舵和滚转舵等信息, 且信息的非线性强.传统动导数模型和多项式模型很难对该种状态进行全面而准确的建模.根据2.3节所述状态, 俯仰力矩气动计算结果见图 9.

|
| 图 9 俯仰力矩系数计算结果 Fig.9 Pitch moment coefficient results |
飞行器空间流场如图 10所示, 在大攻角飞行时, 背风区出现了较大的涡流动, 气动非线性、非定常特性明显.

|
| 图 10 飞行器空间流场 Fig.10 Flow field of aircraft |
(1) 建模精度评价方法
为了避免局部除零, 出现异常值, 通过采用平均误差的形式综合评价建模误差, 平均误差是一个统计的概念即采用样本预测值和标准值偏差的平方和与样本平方和之比, 再开根号[32], 计算公式为
| $ E = \sqrt {\frac{{\sum\limits_{i = 1}^{i = n} {{{({C_{\rm{f}}} - {C_i})}^2}} }}{{\sum\limits_{i = 1}^{i = n} {C_i^2} }}} $ | (3) |
式中, Cf为模型预测值, Ci为样本值.
(2) 动导数模型建模结果
基于式(1), 俯仰力矩系数Cmz的气动模型为
| $ {C_{{\rm{m}}z}} = {C_{{\rm{m}}z0}} + C_{{\rm{m}}z}^\alpha \alpha + C_{{\rm{m}}z}^{{\omega _z}}{\omega _z} $ |
式中, Cmz0为常数项, Cmzα为静导数项, Cmzωz为俯仰阻尼动导数项, 该模型在飞行力学特性分析中最为广泛使用.为了研究方便, ωz常常进行无量纲化处理[34], 即
| 下载CSV 表 1 动导数建模结果 Tab.1 Aerodynamic derivative modeling results |
(3) 多项式建模结果
基于式(2), 俯仰力矩系数表达式为
| $ \begin{array}{*{20}{l}} {{C_{{\rm{m}}z}} = {C_{{\rm{m}}z0}} + C_{{\rm{m}}z}^\alpha \alpha + C_{{\rm{m}}z}^{{\omega _z}}{\omega _z} + C_{{\rm{m}}z}^{\alpha {\omega _z}}\alpha {\omega _z} + C_{{\rm{m}}z}^{{\alpha ^2}}{\alpha ^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} C_{{\rm{m}}z}^{\omega _z^2}\omega _z^2 + C_{{\rm{m}}z}^{\alpha \omega _z^2}\alpha \omega _z^2 + C_{{\rm{m}}z}^{{\alpha ^2}{\omega _z}}{\alpha ^2}{\omega _z} + C_{{\rm{m}}z}^{\omega _z^3}\omega _z^3} \end{array} $ |
计算得到的气动模型的系数如表 2所示.动导数模型和多项式模型和原始数据的对比见图 11, 可见频率越高, 动导数模型误差相对越明显.
| 下载CSV 表 2 3阶多项式建模结果 Tab.2 3rd order polynomial modeling results |

|
| 图 11 动导数和多项式建模结果 Fig.11 Dynamic derivatives and polynomial modeling results |
(4) 神经网络模型建模结果
考虑1,2,3,5,10 Hz全部样本频率数据的气动建模, 采用神经网络模型进行建模, 得到了所有频率下的统一模型.为了对比分析, 也采用1阶线性动导数模型、3阶多项式模型进行了建模, 图 12给出了针对俯仰力矩系数的3种气动建模结果对比.从图中可以看出, 神经网络气动模型对大攻角非定常气动特性的描述最为精确, 多项式模型次之, 动导数模型偏差最大.
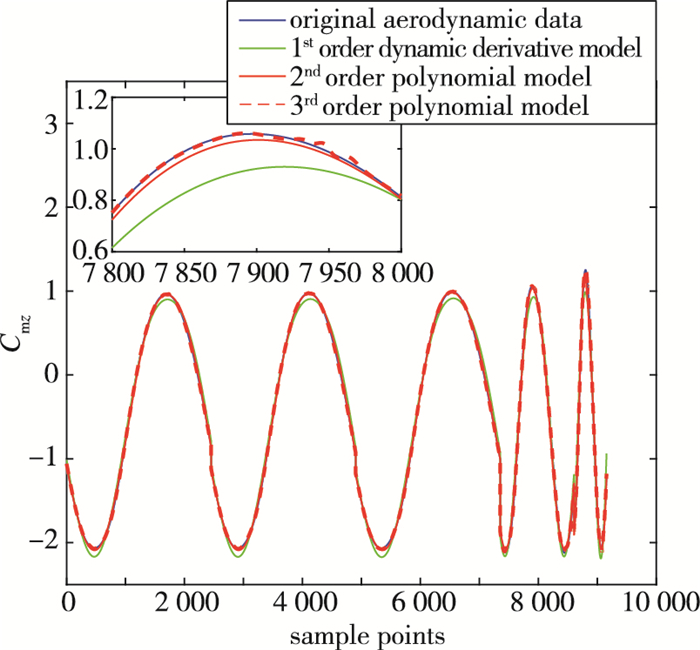
|
| 图 12 俯仰力矩建模结果对比图 Fig.12 Comparison of pitch moment modeling results |
为了对比分析3种建模方法的有效性, 分别进行了建模精度分析, 误差计算方式采用式(3).
表 3给出3种建模方法对于大攻角气动特性的建模误差统计结果, 线性动导数模型误差高达10%, 多项式气动模型建模误差约1%, 而人工神经网络气动模型误差为0.5%.
| 下载CSV 表 3 非定常气动建模精度对比 Tab.3 Comparison of unsteady aerodynamic modeling accuracy |
基于RANS的飞行器大攻角非线性/非定常气动数值计算和基于线性动导数、多项式和神经网络的气动建模方法进行了论述, 并基于轴对称简化导弹模型进行了非定常气动力特性数值计算, 分别采用上述3种方法进行了气动建模分析.结论如下:
(1) 采用基于RANS的数值模拟方法, 针对SDM标模的数值预测结果和风洞实验值一致性较好, 表明该方法可以作为飞行器大攻角非定常气动力特性进行模拟的研究有效方法之一;
(2) 大攻角下的非定常气动力具有较强的非线性特性, 1阶动导数模型具有较大的误差, 须考虑更高精度的建模方式;
(3) 基于神经网络气动建模方法, 气动模型能够模拟大攻角下强非线性非定常的气动特性, 建模精度较高, 可以作为非定常非线性气动建模的有效方法之一.
| [1] |
汪清, 钱炜祺, 丁娣. 飞机大迎角非定常气动力建模研究进展[J]. 航空学报, 2016, 37(8): 2331-2347. Wang Q, Qian W Q, Ding D. A review of unsteady aerodynamic modeling of aircrafts at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2331-2347. (in Chinese) |
| [2] |
袁先旭, 张涵信, 谢昱飞. 基于CFD方法的俯仰静、动导数数值计算[J]. 空气动力学学报, 2005, 23(4): 458-463. Yuan X X, Zhang H X, Xie Y F. The pitching static/dynamic derivatives computation based on CFD methods[J]. Acta Aerodynamica Sinica, 2005, 23(4): 458-463. DOI:10.3969/j.issn.0258-1825.2005.04.012 (in Chinese) |
| [3] |
刘绪, 刘伟, 柴振霞, 等. 飞行器动态稳定性参数计算方法研究进展[J]. 航空学报, 2016, 37(8): 2348-2369. Liu X, Liu W, Chai Z X, et al. Research progress of numerical method of dynamic stability derivatives of aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2348-2369. (in Chinese) |
| [4] |
Wang F J. Numerical prediction of stability derivatives for complex configurations[R]. APISAT2014, 2014.
|
| [5] |
陈农.大攻角非定常气动力建模研究[D].北京: 中国航天空气动力技术研究院, 2007. Chen N. High angles of attack unsteady aerodynamic modeling[D]. Beijing: China Academy of Aerospace Aerodynamics, 2007(in Chinese). |
| [6] |
黄达.飞行器大振幅运动非定常空气动力特性研究[D].南京: 南京航空航天大学, 2007. Huang D. Unsteady aerodynamic characteristics for the aircraft oscilation in large amplitude[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10287-2007193997.htm |
| [7] |
蔡金狮. 飞行器系统辨识[M]. 宇航出版社, 1995. Cai J S. System identification for flight vehicles[M]. China Astronautic Publishing House, 1995. (in Chinese) |
| [8] |
王贵东.航天飞行器气动参数辨识研究[D].中国航天空气动力技术研究院, 2010. Wang G D. Study on aerodynamic parameter identification for aerospace vehicle[D]. China Academy of Aerospace Aerodynamics, 2010(in Chinese). |
| [9] |
Lin G F, Lan C E. A Generalized dynamic aerodynamic coefficient model for flight dynamics application[R]. AIAA-97-3643, 1997.
|
| [10] |
Allwine D A, Strhaler J A, Lawernee D A, et al. Nonlinear modeling of unsteady aerodynamics at high angle of attack[R]. AIAA 2004-5275, 2004.
|
| [11] |
Goman M, Khrabrov A. State-space representation of aerodynamic characteristics of an aircraft at high angles of attack[R]. AIAA 1992-4651, 1992.
|
| [12] |
陈海萍, 高正红. 大迎角非定常气动力数学模型研究[J]. 飞行力学, 2008, 26(5): 10-12, 16. Chen H P, Gao Z H. Large angle of attack unsteady aerodynamic modeling study[J]. Flight Dynamics, 2008, 26(5): 10-12, 16. (in Chinese) |
| [13] |
刘志涛, 孙海生, 姜裕标, 等. 非线性非定常气动力的模糊逻辑建模方法[J]. 实验流体力学, 2005, 19(1): 99-103. Liu Z T, Sun H S, Jiang Y B, et al. Fuzzy logic modeling of nonlinear unsteady aerodynamics[J]. Journal of Experiments in Fluid Mechanics, 2005, 19(1): 99-103. DOI:10.3969/j.issn.1672-9897.2005.01.020 (in Chinese) |
| [14] |
吴辰, 姚宏, 彭兴钊, 等. 支持向量回归机在飞机气动力建模中的应用[J]. 计算机仿真, 2013, 30(10): 128-132. Wu C, Yao H, Peng X Z, et al. Application of support vector regression for aerodynamic modeling[J]. Computer Simulation, 2013, 30(10): 128-132. DOI:10.3969/j.issn.1006-9348.2013.10.030 (in Chinese) |
| [15] |
Chan Y Y, Zhu Z W. Neural network modeling of aerodynamic[R]. AIAA 99-0685, 1999.
|
| [16] |
Steck J, Rokhsaz K. Some applications of artificial neural networks in modeling of nonlinear aerodynamics and flight dynamics[R]. AIAA 1997-0338, 1997.
|
| [17] |
陈海, 钱炜祺, 何磊. 基于深度学习的翼型气动系数预测[J]. 空气动力学学报, 2018, 36(2): 294-299. Chen H, Qian W Q, He L. Aerodynamic coeffient prediction of airfoils based on deep learning[J]. Acta Aerodynamica Sinica, 2018, 36(2): 294-299. DOI:10.7638/kqdlxxb-2017.0098 (in Chinese) |
| [18] |
张瑞民, 张石玉, 赵俊波. 基于神经网络的非定常气动力建模研究[J]. 计算机仿真, 2017, 34(2): 106-110. Zhang R M, Zhang S Y, Zhao J B. The research of neural network in modeling of unsteady aerodynamics[J]. Computer Simulation, 2017, 34(2): 106-110. DOI:10.3969/j.issn.1006-9348.2017.02.024 (in Chinese) |
| [19] |
龚正, 沈宏良. 非定常气动力的结构自适应神经网络建模方法[J]. 飞行力学, 2007, 25(4): 13-16. Gong Z, Shen H L. Structure self-adapting ANN method in modeling of unsteady aerodynamic[J]. Flight Dyna-mics, 2007, 25(4): 13-16. DOI:10.3969/j.issn.1002-0853.2007.04.004 (in Chinese) |
| [20] |
王博斌, 张伟伟, 叶正寅. 基于神经网络模型的动态非线性气动力辨识方法[J]. 航空学报, 2010, 31(7): 1379-1388. Wang B B, Zhang W W, Ye Z Y. Unsteady nonlinear aerodynamics identification based on neural network model[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(7): 1379-1388. (in Chinese) |
| [21] |
史志伟, 王峥华, 李俊成. 径向基神经网络在非线性非定常气动力建模中的应用研究[J]. 空气动力学学报, 2012, 30(1): 108-119. Shi Z W, Wang Z H, Li J C. Numerical study of flow characteristics of a plunging rigid airfoil with elastic trailing-edge plate[J]. Acta Aerodynamic Sinica, 2012, 30(1): 108-119. DOI:10.3969/j.issn.0258-1825.2012.01.019 (in Chinese) |
| [22] |
付军泉, 史志伟, 陈坤, 等. 基于EKF的实时循环神经网络在非定常气动力建模中的应用[J]. 空气动力学学报, 2018, 36(4): 658-663. Fu J Q, Shi Z W, Chen K, et al. Applications of real-time recurrent neuralnetwork based on extended Kalman filter in unsteady aerodynamics modeling[J]. Acta Aero-dynamic Sinica, 2018, 36(4): 658-663. DOI:10.7638/kqdlxxb-2016.0131 (in Chinese) |
| [23] |
王刚, 刘钧圣, 王琨, 等. 一种亚声速导弹气动力计算方法[J]. 弹箭与制导学报, 2018, 38(2): 65-68. Wang G, Liu J S, Wang K, et al. A method to predict aerodynamic characteristics for subsonic missile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2018, 38(2): 65-68. (in Chinese) |
| [24] |
吴子牛. 计算流体力学基本原理[M]. 北京: 科学出版社, 2001. Wu Z N. The basic principles of computational fluid mechanics[M]. Beijing: Science Press, 2001. (in Chinese) |
| [25] |
杨云军.飞行器非稳定运动的流动物理及动力学机理[D].北京: 中国航天空气动力技术研究院, 2008. Yang Y J. Flow physics and dynamic mechanism of non-stable motion of aircraft[D]. Beijing: China Academic of Aerospace Aerodynamics, 2008(in Chinese). |
| [26] |
张瑞民, 时晓天. 有翼导弹动态气动特性数值研究[J]. 弹箭与制导学报, 2017, 37(1): 117-120, 128. Zhang R M, Shi X T. Research on numerical virtual flight of spinning projectile[J]. Journal of Projectiles, Roc-kets, Missiles and Guidance, 2017, 37(1): 117-120, 128. (in Chinese) |
| [27] |
孙海生, 张海酉, 刘志涛. 大迎角非定常气动力建模方法研究[J]. 空气动力学报, 2011, 29(6): 733-737. Sun H S, Zhang H Y, Liu Z T. Comparative evaluation of unsteady aerodynamics modeling approaches at high angle of attack[J]. Acta Aerodynamica Sinica, 2011, 29(6): 733-737. (in Chinese) |
| [28] |
史志伟, 吴根兴. 大攻角非定常气动力建模与模型比较[J]. 空气动力学学报, 1999, 17(4): 454-461. Shi Z W, Wu G X. Comparison between the modeling and model of the non-fixed normal gas power of the large attack angle[J]. Acta Aerodynamica Sinica, 1999, 17(4): 454-461. (in Chinese) |
| [29] |
Bryan G H. Stability in aviation[M]. Lonton: Macmil-lan and Co., 1911: 20-105.
|
| [30] |
沈霖.大攻角非定常气动力建模及尾旋仿真研究[D].南京: 南京航空航天大学, 2013. Shen L. Research on unsteady aerodynamic models at high angle of attack and spin simulation of aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013(in Chinese). |
| [31] |
白斌, 徐敏, 祝小平, 等. 正交多项式在非定常气动建模上的运用[J]. 飞行力学, 2013, 31(5): 398-401. Bai B, Xu M, Zhu X P, et al. Nonlinear aerodynamic modeling using on orthogonal polynomials[J]. Flight Dynamics, 2013, 31(5): 398-401. DOI:10.3969/j.issn.1002-0853.2013.05.004 (in Chinese) |
| [32] |
王超, 王贵东, 白鹏. 飞行仿真气动力数据机器学习建模方法[J]. 空气动力学学报, 2019, 37(3): 488-497. Wang C, Wang G D, Bai P. Method of flight test aerodynamic modeling based on machine learning[J]. Acta Aerodynamic Sinica, 2019, 37(3): 488-497. DOI:10.7638/kqdlxxb-2019.0024 (in Chinese) |
| [33] |
赵忠良, 任斌, 黄叙辉. SDM标模大攻角动导数试验[J]. 航空学报, 1998, 19(2): 137-141. Zhao Z L, Ren B, Huang X H. High angle of attack dynamic derivative experiment of standard dynamic model[J]. Acta Aerodynamica Sinica, 1998, 19(2): 137-141. (in Chinese) |
| [34] |
钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 北京: 北京理工大学出版社, 2000. Qian X F, Lin R X, Zhao Y N. Missile flight dyna-mics[M]. Beijing: Beijing Institute of technology, 2000. (in Chinese) |



