高超声速飞行器的快速发展对地面试验模拟提出了新的要求, 但是, 现有设备的模拟能力达不到这些要求, 由于“高超声速发展的未来直接取决于试验设施的可用性和试验能力[1]”, 因此, 分析高超声速气动试验模拟的现状及其面临的挑战, 是一件非常有意义的事情.
高超声速设备建设可简单分为3个阶段.第1个阶段是20世纪五六十年代, 人们建设了小尺寸的高超声速力热设备, 解决了再入弹头的防热问题以及烧蚀外形对气动力的影响问题.第2个阶段是20世纪80年代初期开始, 建设了大尺寸的高超声速力热设备, 解决了航天飞机中的高Mach数高Reynolds数真实气体效应等问题.第3个阶段从20世纪90年代开始, 人们建设了多学科综合性高超声速设备, 例如高超声速推进试验设备热结构试验设备, 以满足吸气式发动机全尺寸部件地面模拟的需要.
目前, 以空天飞机高超滑翔高超吸气式巡航飞行器为代表的临近空间飞行器对高超声速设备的模拟能力提出了新的挑战[2, 3].首先, 这些飞行器要求地面设备能够模拟宽速域(M=5~25) 和大空域(20~100km)范围的飞行环境, 但是, 地面模拟设备尚未能覆盖这些条件, 存在气体物理性质不相似的问题, 显著影响了稀薄流真实气体高温气体等热力学和化学非平衡流动的模拟结果.其次, 在烧蚀热结构等地面试验中因受巨大模拟能量需求的限制而无法做到力与热同时模拟.同样由于能量限制, 在全尺寸推进试验中只能采用燃气加热方式, 产生了燃气污染问题.最后, 复杂气动现象如边界层转捩-湍流[4]激波-边界层干扰[5]边界层分离与再附[6]旋涡流化学反应流/壁面催化化学反应流壁面烧蚀[7]混合流[8]多相流[9]燃烧流[10]等通常具有非线性多尺度特征, 对环境变量十分敏感, 地面设备难以复现这些现象对气动力热的影响.这些问题导致地面试验模拟获得的气动力热数据与实际飞行数据存在天地差异.
那么, 能否在现有条件下有效地开展地面试验研究, 获取设计所需的数据是现阶段一个亟需回答的问题.为此, 本文从相似理论出发, 对该问题进行了论述, 提出了一些建议.
1 缩比模型气动试验模拟理论简述地面气动试验的理论基础是相似准则.对于两个同类的物理现象, 如果在相应的时刻与相应的空间点上与物理现象有关的物理量一一对应成比例, 则称此两现象彼此相似.气动相似[11, 12]的含义包括:
(1) 几何相似:缩比模型相似于它的原型, 缩比模型上任意两点的距离与原型上相应两点的距离比值为常数, 即几何缩比因子.
(2) 运动学相似:如果一个流动系统的任意点的速度与另一流动系统相应点的速度比值为常数, 即等于速度缩比因子, 且方向相同, 那么这2个流动系统运动学相似.
(3) 动力学相似:除几何相似和运动学相似外, 如果作用力也存在类似关系, 那么这2个系统满足动力学相似.
(4) 边界条件相似:即无量纲后的边界条件一致.
(5) 物理条件相似:即介质组分的种类及其浓度构成, 以及输运性质和热物性一致;也包括模型的导热传热刚度系数等热力学特性一致.
凡是相似的物理现象, 其物理场一定可以用一个统一的无量纲场来表示, 即所有同名特征数(无量纲参数)对应相等, 表 1给出了一组常见的参数.相似准则决定了地面试验设施理论上应当具有的能力.
| 下载CSV 表 1 气动热试验相似参数 Tab.1 Similarity parameters in aerothermodynamic tests |
从空气动力学微分方程系统出发可以获得高超声速气动试验所需的相似参数.以一维多组分量热完全气体有化学反应流动的控制方程为例:
| $ \left\{ \begin{align} & \frac{\partial \rho }{\partial t}+\frac{\partial \rho u}{\partial x}=0 \\ & \frac{\partial \rho u}{\partial t}+\frac{\partial (\rho uu+p)}{\partial x}=\frac{\partial }{\partial x}\left( \begin{matrix} \mu & \frac{\partial u}{\partial x} \\ \end{matrix} \right) \\ & \frac{\partial \rho E}{\partial \rm{t}}+\frac{\partial (\rho E+p)u}{\partial x}=\frac{\partial }{\partial x}\left( \begin{matrix} \mu u & \frac{\partial u}{\partial x} \\ \end{matrix} \right)+\frac{\partial }{\partial x}\left( \begin{matrix} \lambda & \frac{\partial T}{\partial x} \\ \end{matrix} \right)+{{\sum\limits_{i}^{I}{Qi}}^{\centerdot }} \\ & \frac{\partial \rho {{y}_{s}}}{\partial t}+\frac{\partial \rho u{{y}_{s}}}{\partial x}=\frac{\partial }{\partial x}\left( \begin{matrix} D & \frac{\partial {{y}_{s}}}{\partial x} \\ \end{matrix} \right)+\overset{\centerdot }{\mathop {{\omega }_{s}}}\, \\ \end{align} \right. $ | (1) |
其中, 下标s代表第s种组分,且
| $ p=\sum\limits_{s}{\rho {{y}_{s}}}{{R}_{\text{g}s}}T, $ |
Rg表示气体常数,E为总能密度,定义为
| $ \begin{matrix} E=e+\frac{\left( {{u}^{2}}+{{v}^{2}}+{{w}^{2}} \right)}{2}, \\ e=\sum\limits_{s}{{{y}_{s}}}\int{{{c}_{\text{p}s}}}dT-\sum\limits_{s}{{{y}_{s}}}{{R}_{\text{g}s}}T, \\ \overset{\centerdot }{\mathop{{{\omega }_{s}}}}\,=\sum\limits_{i=1}^{I}{{{k}_{\text{f}}}_{i}}{{p}^{2}}{{y}_{s}}{{y}_{j\centerdot }} \\ \end{matrix}$ |
kfi为第i个化学反应的反应速率常数,一般采用如下形式
| $ {{k}_{\text{f}}}_{i}={{A}_{i}}{{T}^{\beta i}}\exp \left( \frac{-{{E}_{i}}}{RT} \right). $ |
选取无量纲系统(u∞, L, T∞, ρ∞, μ∞)对式(1) 进行无量纲化, 为简便书写, 略去无量纲记号, 得
| $ \left\{ \begin{align} & \frac{\partial \rho }{\partial t}+\frac{\partial \rho u}{\partial x}=0 \\ & \frac{\partial \rho u}{\partial t}+\frac{\partial \left( \rho uu+p \right)}{\partial x}=\frac{1}{\operatorname{Re}}\frac{\partial }{\partial x}\left( \mu \frac{\partial u}{\partial x} \right) \\ & \frac{\partial \rho E}{\partial t}+\frac{\partial \left( \rho E+p \right)u}{\partial x}=\frac{1}{\operatorname{Re}}\frac{\partial }{\partial x}\left( \mu u\frac{\partial u}{\partial x} \right)+ \\ & \frac{1}{\left( \gamma -1 \right)\Pr \operatorname{Re}{{M}^{2}}_{\infty }}\frac{\partial }{\partial x}\left( \begin{matrix} \lambda & \frac{\partial T}{\partial x} \\ \end{matrix} \right)+{{D}_{I}}{{\sum\limits_{i=1}^{I}{{{Q}_{i}}}}^{\centerdot }} \\ & \frac{\partial \rho {{y}_{s}}}{\partial t}+\frac{\partial \rho u{{y}_{s}}}{\partial x}=\frac{1}{\operatorname{Re}Sc}\frac{\partial }{\partial x}\left( \begin{matrix} \mu & \frac{\partial {{y}_{s}}}{\partial x} \\ \end{matrix} \right)+ \\ & \frac{{{\rho }_{\infty }}L}{{{u}_{\infty }}}\sum\limits_{i=1}^{I}{{{A}_{i}}}T_{\infty }^{\beta i}{{T}^{\beta i}}\exp \left( \frac{-{{E}_{i}}}{RT} \right){{y}_{s}}{{y}_{j}} \\ \end{align} \right. $ | (2) |
其中,
| $ \begin{matrix} \gamma ={{c}_{\text{p}}}/{{c}_{\text{v}}}, \\ {{c}_{\text{p}}}=\frac{1}{T}\sum\limits_{s}{{{y}_{s}}}\int{{{c}_{\text{p}s}}}dT, \\ {{c}_{\text{v}}}={{c}_{\text{p}}}-{{R}_{\text{g}}}, \\ {{R}_{\text{g}}}=\sum\limits_{s}{{{y}_{s}}}{{R}_{\text{g}s}}. \\ \end{matrix} $ |
采用这些关系, 状态方程仍满足
| $ p=\rho {{R}_{\text{g}}}T. $ |
内能形式上可以写为
| $ e=\frac{p}{\left( \gamma -1 \right){{\rho }^{\centerdot }}} $ |
声速仍可表述为
| $ a=\sqrt{\gamma {{R}_{\text{g}}}T}\cdot $ |
控制方程形式上与单一理想气体(或量热完全气体)的流动控制方程一样.但是, 由于
从无量纲方程组(2) 可以看到, 高超声速气动试验如做到完全模拟, 在几何相似边界相似和物理相似的前提下, 需模拟的相似参数除表 1所列的Re, Pr, M∞, γ, DI, Sc外, 对于化学反应源项, 还需
上述仅仅是流动问题的相似准则, 对于多场耦合问题, 除此之外, 还需满足其他物理场的相似准则.例如, 对于风洞自由飞试验, 还需满足刚体运动的相似准则, 质量质心及转动惯量等物理量构成的相似参数必须一致;对于气动力/热耦合试验, 还需满足材料结构的热学和力学性能相似[15].
2 关于气动试验模拟难题的思考地面试验的理想情形是实现完全相似模拟, 但是现实中几乎不可能做到, 因此, 不得不在众多相似律中做出取舍, 对关心的物理量进行模拟, 采取的方式通常有主要参数模拟部件模拟局部模拟和燃气加热模拟等方法.
2.1 主要参数模拟方法主要参数模拟的思想在很多模拟方法中得到应用, 例如在气流速度较高时不考虑气体重力.该方法通过对主要参数的模拟抓住问题的主要矛盾, 实现大部分动量和能量交换过程的模拟, 达到对真实结果的良好近似, 但是, 参数的重要性与问题有关, 在某些时候通常认为的次要参数也可以转变为主要参数.例如, 对常规静态测力试验, 通常认为主要的相似参数为Mach数和Reynolds数, 但是, 航天飞机飞行试验中遇到了机身襟翼偏角在实际飞行中比预测值大1倍的高超声速异常问题[16], 分析认为主要原因是地面模拟设备未能正确模拟Mach数效应和真实气体效应, 这表明此时真实气体效应已经成为一个主要因素.
当这些重要因素的地面模拟能力不足时, 应通过设备建设条件改造等提升能力, 尽量模拟.例如, 动态试验中由于涉及流动与刚体运动, 在系统中会引入减缩频率ωL/u∞(Strouhal数)这样一个重要参数, 它表征模型刚体运动与扰流运动在时域上的同时性.由于高超声速飞行器重点关注20km高度以上空间的动稳定特性, 此时动压较低, 飞行器短周期模态频率较低空大幅降低, 同时, 高超声速飞行器静稳定裕度也较低, 通过减缩频率参数转化到风洞中需要模拟的机构振动频率一般集中在10Hz左右甚至更低, 这意味着模拟一个完整运动周期需风洞的有效运行时间达到100ms.以前, 中国航天空气动力技术研究院脉冲式高超声速风洞有效工作时间约为30ms, 自由振动试验和自由飞试验只能模拟0.3个周期的非定常运动, 不能获得有效动导数, 通过新建FD-16高超声速风洞, 有效工作时间接近20s, 从而具备这一参数的模拟能力.
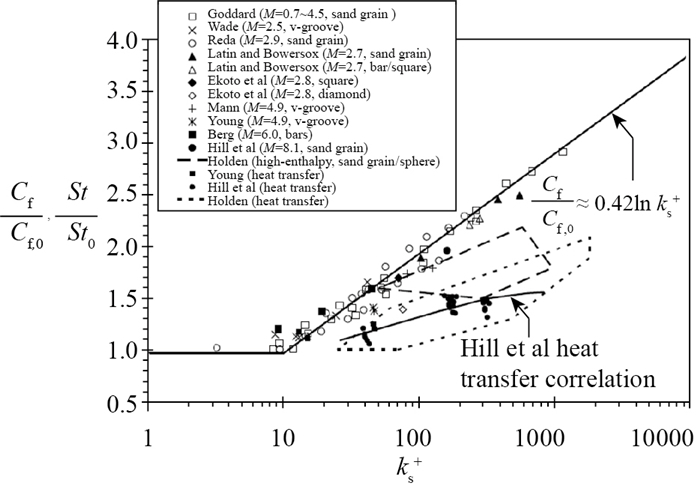
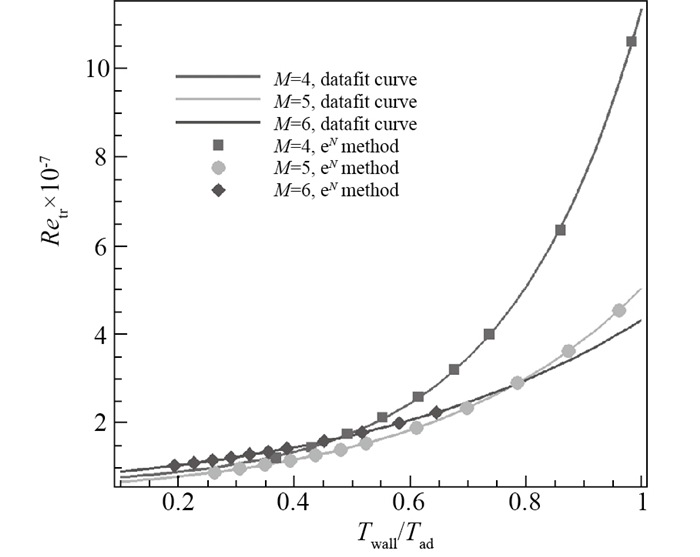
然而, 不管如何努力, 在实际中有一些参数都不可能被完全模拟, 例如壁面粗糙度壁温比噪声度等.当这些参数的影响变得重要时, 一条思路是通过规律性研究来开展天地相关性, 对数据进行修正或外推.例如, 在摩阻和热流测量中, 粗糙度的影响会变得重要, 图 1示意了国外关于摩阻系数和Stanton数与粗糙度的相关性研究结果[17, 18].又如, 壁温比对静态测力试验的影响很小, 但是, 它对转捩试验具有显著影响.最近, 我们采用eN方法研究了壁温比这一单一因素对转捩的影响, 发现壁温比对转捩Reynolds数有显著影响, 在高超声速条件下, 壁温升高, 转捩Reynolds数增加, 转捩位置后移, 且在一定范围以内, 转捩Reynolds数与壁温比之间存在很好的规律性, 结果如图 2所示.
|
| 图 1 摩阻系数和Stanton数与粗糙度的相关性[18] (平板边界层结果) Fig.1 Relations of friction factor and Stanton number against roughness[18](planar boundary layer) |
|
| 图 2 转捩Reynolds数随恢复温度系数的变化规律(平板边界层结果) Fig.2 Variations of transitional Reynolds number with temperature ratio (planar boundary layer) |
另一条思路是适当放宽某个方向的自由度, 降低模拟参数的硬性约束.例如, 对于高速投放模型试验(如图 3所示), 除模型几何相似外, 还需满足刚体动力学相似.刚体动力学相似要求模型质量与模型缩比的平方成正比, 而体积是模型缩比的3次方, 因此, 实际上要求模型的比重很大.当风洞尺寸较小, 模型缩比很大, 现实中不存在比重如此之大的材质, 因此, 一种有效模拟方法是采用轻模型法代替重模型法.在轻模型法中, 保证Mach数模拟, 模型惯性力与气动力之比和实际情形相同, 仅垂直运动因重力与气动力之比与实际情形不符而存在差别, 其余方向运动严格相似, 模型有正确的弹射运动和俯仰振动[19].
2.2 部件相似与局部相似模拟方法从气动试验模拟理论可知, 对于含化学反应的流动, 完全模拟是在物理相似的前提下, 保证T∞, u∞与ρ∞L参数一致.双尺度参数ρ∞L表明, 对于含化学反应的流动, 缩比试验实际不可能做到完全相似模拟, 换言之, 此类流动的模拟必须采用全尺寸模型.这类流动包括热非平衡[20]和化学非平衡流动[21].一般而言, 受能量限制, 全模的全尺寸试验很难实现, 因此, 只能开展部件的全尺寸试验.
部件相似模拟是一种常见的试验模拟方法, 例如翼型起落架等试验.它要求部件流动与全模中的部件流动相似, 实际上要求部件的边际效应对气动力热数据的影响可以忽略.
全尺寸模拟的优势是保证几何完全相似.例如, 2010年, Wadhams等[22]在CUBRC(Calspan University at Buffalo Research Center)的LENS Ⅱ风洞中开展了X-51A前体的全尺寸试验(如图 4所示), 研究人工转捩技术与进气道起动性能.相比于飞行器特征尺度, X-51A前缘钝度和人工转捩装置的尺度是个小量, 在模型缩比严重时它们的加工精度无法保证几何相似, 但是, 这些尺度却能对边界层转捩产生显著影响, 全尺寸模拟的优势是能够保证这些小尺度结构的几何外形与实物完全一致.

|
| 图 4 X-51A进气道转捩与起动性能全尺寸部件试验[22] Fig.4 Tests of boundary layer transition and starting performance of X-51A full scale model[22] |
又如Clemente等[23]在CIRA PWT风洞中开展了高超声速机翼热结构试验(如图 5所示), 机翼全尺寸模拟, 实现了力热耦合模拟.

|
| 图 5 高超声速机翼热结构试验[23](CIRA PWT风洞试验结果) Fig.5 Thermal structural tests of hypersonic wing[23] (wind-tunnel results in CIRA PWT) |
由于气流的动能密度与速度的3次方成正比, 获取大流量高焓气流需要非常巨大的能量, 一些材料性能和热结构考核试验往往还需要模拟成百甚至上千秒的时间, 导致对总能量的需求更加巨大, 此时, 人们不得不采取局部相似模拟方法.球头驻点热流试验是局部相似模拟的典型案例, 该试验中模拟参数为驻点总焓和驻点压力, 根据试验总结出的Lees公式Fay-Riddell公式和Goulard修正公式使用至今.
包罩试验可以看成是局部相似模拟的进一步简化.该试验方法集中热气流对局部流动进行模拟, 以亚声速代替超/高超声速气流, 减小了能量需求, 避免了超声速气流中激波引起的非均匀性, 模拟准则为表面加热率冲刷力和压力载荷相同.但是, 实际过程中由于未能模拟流动, 放宽了对压力载荷的模拟要求.
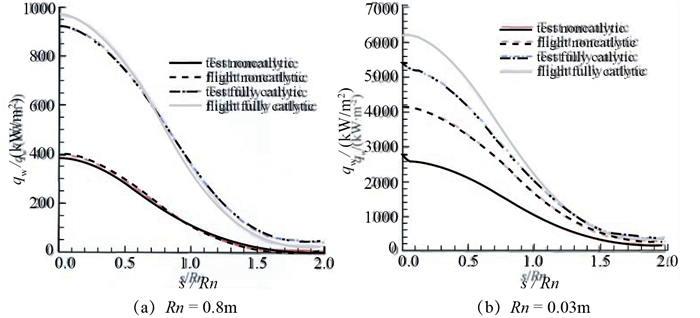
部件相似与局部相似模拟为高超声速气动热试验提供了可行的技术途径, 但是, 一个很重要的问题是需要评估热化学非平衡对局部相似模拟结果的影响[24].袁军娅等[25]研究了高焓非平衡气动热环境对试验结果的影响(如图 6所示),结果表明, 对于球头模型, 当模型尺度较大时, 试验条件和飞行条件下的边界层外缘均达到平衡状态, 局部相似模拟理论是适用的, 试验条件可以模拟飞行环境, 对材料性能的评价是可靠的;当模型尺度较小时, 试验条件与飞行条件均存在非平衡现象, 局部相似模拟理论不再适用, 表面热流模拟程度偏低, 非催化壁热流降低更明显, 而目前正在研究的高超声速飞行器多具有面对称外形, 以及尖化前缘特征, 恰好属于这种情形.
|
| 图 6 不同尺度下非平衡热环境对壁面热流的影响[25] Fig.6 Variations of surface heat flux with non-equilibrium thermal environment at different scales[25] |
同样, 由于未完全模拟, 局部相似模拟所获结果也需要开展天地相关性来外推实际飞行结果.董维中等[26]分析了高焓风洞试验和飞行试验相关性问题, 指出在高焓风洞试验中, 由于来流存在组分和振动能量的非平衡冻结效应, 试验条件的激波脱体距离比飞行条件的大, 激波层中NO质量分数比飞行条件的高, 对于钝锥体模型, 在头部区域, 保证总焓和双尺度参数ρ∞L一致, 热流数据可以从试验条件外推到飞行条件, 但在尾部区域, 当把热流数据从试验条件外推到飞行条件时存在较大误差.可见, 气动热数据的天地相关性尚存在很多难题.
2.3 燃气加热模拟方法虽然, 人们试图实现高超声速飞行器全尺寸模拟, 但是, 大流量高焓气流的获取需要超大功率的加热器, 目前并不具备这一条件, 不得已采用燃烧加热方式, 也因此带来燃气污染问题.
Auslender等[29]在NASA Langley中心8ft高温风洞中进行X-51A发动机全尺寸试验(如图 7所示).该风洞采用燃气加热, 气体热物性偏离真实空气, 引起进气道性能燃料的混合/点火/燃烧性能等均偏离实际飞行状态. X-51A第4次飞行试验获得成功, 但它实际上是在飞行Mach数5.1时实现推阻平衡, 与此前地面研究预测的Mach数6相去甚远, 暴露出地面模拟存在问题.
常用的燃气加热燃料有氢气甲烷酒精和煤油.以文献[30]的一组数据为例, 重新分析可以发现存在3方面的燃气污染问题.不同于文献[30]中把水视为气态, 此处把来流中的水看成液态(因为静温为221.66K), 模拟状态见表 2.
| 下载CSV 表 2 不同加热方式下推进风洞的模拟参数 Tab.2 Simulation parameters in wind tunnels with different heating methods |
(1) 比热比不相似.燃气比热比低于实际飞行时的纯净空气.比热比能够对推阻性能评估产生重要影响.考虑总压与静压关系
| $ \frac{{{p}^{*}}}{p}={{\left( 1+\frac{\gamma -1}{2}{{M}^{2}} \right)}^{\frac{\gamma }{\gamma -1}}}\centerdot $ |
可以看到, Mach数为6, 匹配静压时, 比热比为1.27时所需的总压是比热比为1.4时的2.6倍, 即地面风洞运行总压远高于实际飞行条件, 很容易影响推力性能评估.试验中也发现比热比不同能够对高Mach数气动力模拟产生显著影响[27].
(2) 发动机燃料为碳氢燃料, 燃气的组分构成也是碳氢燃料燃烧产物, 根据化学反应的质量作用定律, 产物浓度增加, 相关的化学反应会受到抑制, 即污染气体对化学反应动力学过程存在影响[28].
(3) 水在激波前后发生相变, 由液态水变为气态水, 引起混合气体比热比的改变, 从1.27变为1.37, 做简单估算, 会额外带来3%左右的压力增益.而实际飞行时不存在这种物理过程.
从上述分析还可以看到, 试验条件的匹配不能再用常值比热比下的激波关系式, 而是通过计算的手段根据间断关系迭代给出.
对于推进试验, 欲消除燃气污染问题, 理想的方式是设法获取纯净无污染的高焓空气.例如美国CUBRC的LENS Ⅱ激波风洞, 运行介质可以是氮气或空气, 总温最高可达到2500K, Mach数为5~8时喷管直径为1.524m, 具有很强的复制飞行条件的模拟能力.
3 结束语高超声速气动试验的理论基础是相似准则, 通过对气动力气动热和推进试验的现状分析可知, 现行主要参数相似部件相似局部相似和燃烧相似模拟方法仍然有效, 但是, 这些模拟与理论准则间存在差距, 带来了结果的天地差异, 而这正是高超声速气动试验所面临的主要问题和挑战.为应对这些问题和挑战, 建议:
(1) 开展必要的尽可能完全模拟的条件建设, 提高对物理环境的高保真模拟能力.例如, 发展清洁空气加热器技术或大功率电弧加热器设备, 支持大尺寸纯净空气介质高焓风洞的建设.
(2) 加强理论计算与试验的结合, 扩展地面模拟能力.通过理论和计算来分析不完全相似引起的问题, 实现对试验方案设计的指导, 科学取舍地面模拟参数, 获取实用的地面模拟准则.
(3) 加强对气体材料/结构等物理化学特性, 以及转捩/湍流真实气体燃烧等流动机理的理论研究, 科学构建数理模型和CFD手段, 以支撑天地相关性研究, 从而能够在不完全相似模拟时对试验结果进行外推, 给出飞行条件下的结果.
(4) 设立专门项目, 开展面向科学认知探索和技术创新发展的飞行试验, 为地面模拟(主要参数模拟部件相似模拟局部相似模拟燃气加热模拟等)提供科学实践和认知确认的手段.
| [1] |
Leslie J D, Marren D E. Hypersonic test capabilities overview[R]. AIAA 2009-1702, 2009.
|
| [2] |
李建林. 临近空间高超声速飞行器发展研究[M]. 北京: 中国宇航出版社, 2012: 264-269. Li J L. Development of near space hypersonic flight vehicles[M]. Beijing: China Aerospace Press, 2012: 264-269. (in Chinese) |
| [3] |
于登云. 新型航天器发展对力学学科的挑战[J]. 科学通报, 2015, 60(12): 1085-1094. Yu D Y. Mechanical challenges in advanced spacecraft development[J]. Chinese Science Bulletin, 2015, 60(12): 1085-1094. (in Chinese) |
| [4] |
Berry S, Daryabeigi K, Wurster K, et al. Boundary-layer transition on X-43A[J]. Journal of Spacecraft and Rockets, 2010, 47(6): 922-934. DOI:10.2514/1.45889 |
| [5] |
Holden M S, Wadhams T P. A review of experimental studies for DSMC and Navier-Stokes code validation in laminar regions of shock/shock and shock/boundary layer interaction including real gas effects in hypervelocity flows[R]. AIAA 2003-3641, 2003.
|
| [6] |
Frost M A, Gangurde D Y, Paull A, et al. Boundary-layer separation due to combustion-induced pressure rise in a supersonic flow[J]. AIAA Journal, 2009, 47(4): 1050-1053. DOI:10.2514/1.40868 |
| [7] |
Ewing M E, Laker T S, Walker D T. Numerical modeling of ablation heat transfer[J]. Journal of Thermophysics and Heat Transfer, 2013, 27(4): 615-632. DOI:10.2514/1.T4164 |
| [8] |
Agarwal K K, Krishna S, Ravikrishna R V. Mixing enhancement in a compact trapped vortex combustor[J]. Combustion Science and Technology, 2013, 185(3): 363-378. DOI:10.1080/00102202.2012.721034 |
| [9] |
Gross M L, Beckstead M W, Puduppakkam K V, et al. Multi-phase combustion modeling of ammonium dinitramide using detailed chemical kinetics[R]. AIAA 2006-4747, 2006.
|
| [10] |
Motoe M, Shimada T. Large eddy simulation of swirling combustion flow in a modeled hybrid rocket with wall fuel blowing[R]. AIAA 2013-3644, 2013.
|
| [11] |
吴建民. 高等空气动力学[M]. 北京: 北京航空航天大学出版社, 1992: 91-102. Wu J M. Advanced Aerodynamics[M]. Translated by Chen Z L, Wu W Z. Beijing: Beihang University Press, 1992: 91-102. (in Chinese) |
| [12] |
杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 1998: 150-161. Yang S M, Tao W Q. Heat Transfer[M]. Beijing: Higher Education Press, 1998: 150-161. (in Chinese) |
| [13] |
张涵信. 真实气体流动的相似规律[J]. 空气动力学学报, 1990, 8(1): 1-8. Zhang H X. The similarity law for real gas flow[J]. Acta Aerodynamica Sinica, 1990, 8(1): 1-8. (in Chinese) |
| [14] |
陈伟芳, 石于中, 曹登泰, 等. 流动相似律研究[J]. 国防科技大学学报, 1999, 21(4): 5-8. Chen W F, Shi Y Z, Cao D T, et al. Study of flow's similitude law[J]. Journal of National University of Defense Technology, 1999, 21(4): 5-8. (in Chinese) |
| [15] |
刘磊. 高超声速飞行器热气动弹性特性及相似准则研究[D]. 北京: 中国空气动力研究与发展中心, 2014. Liu L. Study on the characteristics and similarity criteria of aerothermoelasticity for hypersonic vehicles[D]. Beijing: China Aerodynamics Research and Development Center Graduate School, 2014 (in Chinese). |
| [16] |
Romere P O, Kanipe D B, Young J C. Space shuttle entry aerodynamic comparisons of flight 1 with preflight predictions[J]. Journal of Spacecraft and Rockets, 1983, 20(1): 15-21. DOI:10.2514/3.28351 |
| [17] |
Holden M S, Mundy E P, Wadhams T P. A review of experimental studies of surface roughness and blowing on the heat transfer and skin friction to nosetips and slender cones in high Mach numbers flows[R]. AIAA 2008-3907, 2008.
|
| [18] |
Bowersox R. Survey of high-speed rough wall boundary layers: invited presentation[R]. AIAA 2007-3998, 2007.
|
| [19] |
Johnson R A, Stanek M J, Grove J E. Store separation trajectory deviations due to unsteady weapons bay aerodynamics[R]. AIAA 2008-188, 2008.
|
| [20] |
Neville A G, Nompelis I, Subbareddy P K, et al. Effect of thermal non-equilibrium on decaying isotropic turbulence[R]. AIAA 2014-3204, 2014.
|
| [21] |
Rini P, Thmel J, Chazot O, et al. Analysis of chemical nonequilibrium and elemental demixing within carbon dioxide plasma flows for Mars entry application[R]. AIAA 2007-1356, 2007.
|
| [22] |
Wadhams T P, MacLean M G, Holden M S, et al. A review of transition studies on full-scale flight vehicles at duplicated flight conditions in the LENS tunnels and comparisons with prediction methods and flight measurement[R]. AIAA 2010-1246, 2010.
|
| [23] |
Clemente M D, Rufolo G C, Ianiro A, et al. Aerothermal coupling methodology for the rebuilding of a plasma wind tunnel test and comparison with an advanced infrared measurement technique[R]. AIAA 2009-7236, 2009.
|
| [24] |
Gkcen T. Effects of flowfield nonequilibrium on convective heat transfer to a blunt body[J]. Jounal of Thermophysics and Heat Transfer, 1997, 11(2): 289-295. DOI:10.2514/2.6236 |
| [25] |
袁军娅, 蔡国飙, 杨红亮, 等. 高焓非平衡气动热环境的试验模拟及影响[J]. 实验流体力学, 2012, 26(6): 35-39. Yuan J Y, Cai G B, Yang H L, et al. Test simulation of heat environment in high enthalpy nonequilibrium flow and effects[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(6): 35-39. (in Chinese) |
| [26] |
董维中, 乐嘉陵, 高铁锁. 钝体标模高焓风洞试验和飞行试验相关性的数值分析[J]. 流体力学实验与测量, 2002, 16(2): 1-8. Dong W Z, Le J L, Gao T S. Numerical analysis for correlation of standard model testing in high enthalpy facility and flight test[J]. Experiments and Mearsurements in Fluid Mechanics, 2002, 16(2): 1-8. (in Chinese) |
| [27] |
Erickson W D. Real-gas correction factors for hypersonic flow parameters in Helium[R]. NASA TN D-462, 1960.
|
| [28] |
郭帅帆, 宋文艳, 李建平, 等. 燃烧加热污染空气对超燃冲压发动机性能影响研究[J]. 推进技术, 2013, 34(4): 493-498. Guo S F, Song W Y, Li J P, et al. Numerical investigation of effects of vitiated air on scramjet performance[J]. Journal of Propulsion Technology, 2013, 34(4): 493-498. (in Chinese) |
| [29] |
Auslender A H, Suder K L, Thomas S R. An overview of the NASA FAP hypersonics project airbreathing propulsion research[R]. AIAA 2009-7277, 2009.
|
| [30] |
邢建文, 李卫强, 肖保国. 不同燃料燃烧加热对超燃冲压发动机性能影响的分析与评估[J]. 推进技术, 2013, 34(12): 1636-1642. Xing J W, Li W Q, Xiao B G. Effects of different fueled combustion heater on scramjet performance[J]. Journal of Propulsion Technology, 2013, 34(12): 1636-1642. (in Chinese) |





