矢量气动声学的理论研究进展及应用
西安交通大学能源与动力工程学院，陕西西安 710049
摘要：气动声学的声比拟理论以密度、声压等标量为波动算子变量，建立非齐次波动方程，描述流体运动及与边界作用诱发声音的辐射，但标量无法直接描述声能量的传播过程和途径.在流体力学研究中，标量用于描述当前当地的物质状态，而矢量用于描述质量和能量的传输.借鉴上述思想，开展了矢量气动声学的研究，概述矢量气动声学的理论研究进展及应用，主要包括：（1）以声粒子速度为变量，采用声比拟理论的思想直接从Navier-Stokes方程出发推导建立了气动声学的矢量波动方程及两种频域解；（2）综合利用声压和声粒子速度的积分解，直接求解声源周围的瞬时和有功声强矢量场，直观显示声能量的传播途径，应用于旋转声源辐射声能量的传播分析，揭示了亚音速旋转声源辐射声能量的3种传播模式：螺旋模式、声学黑洞模式和R-A模式；（3）采用球谐级数展开方法建立旋转点/紧凑声源辐射噪声的声压和声粒子速度的频域解析解，在此基础上推导了声功率谱的频域解析解，建立了识别旋转叶片声源在空间域和频域分布特征的方法；（4）综合利用矢量气动声学方法和等效源方法，显示声源和散射边界周围声强矢量场的分布特征和能量传播途径，直接揭示了阻抗边界主要的吸声位置以及直接计算得到阻抗边界的吸收声功率.
关键词：声比拟理论 矢量气动声学 声强 辐射模式 声源识别
Research Advancement and Application on Vector Aeroacoustics
School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
Abstract: In acoustic analogy theory, the perturbation of density or acoustic pressure is used as variable of the wave operator to describe the noise generated from fluid and its interaction with solid surfaces, but it is unable to directly describe the acoustic energy propagation with the acoustic scalars. In fluid mechanics, scalars are used to characterize the instantaneous and local states of fluid, while vectors are used to describe the transfers of mass and energy. Inspired by this idea, the vector aeroacoustics was developed and this paper presented the overview of recent advancement on this research. Some advancements were as summarized as follows. (1) The vector wave equation of aeroacoustics and the corresponding solutions have been proposed, in which the acoustic velocity was regarded as the variable of the wave operator. (2) The acoustic intensity vector field around rotating sources was visualized, revealing the following three radiation modes of acoustic energy:spiral mode, R-A mode and acoustically black-hole mode. (3) Analytical acoustic power spectrum formulations for the rotating point sources have been developed to identify the spatial and frequency features of the source on rotating blades. (4) Vector aeroacoustics method and the equivalent source method were combined to show the acoustic intensity vectors around the sources and scattering surfaces, visualizing the primary absorption position as well as calculating the acoustic power absorbed by impedance surfaces.
Key words:
acoustic analogy theory vector aeroacoustics acoustic intensity radiation mode source identification
引言
2 应用示例
2.1 旋转声源辐射能量模式
2.3 边界散射噪声分析
3 总结与展望
声比拟理论是现代气动声学的建立标志, 它首先由Lighthill提出, 然后经过Curle和FfowcsWilliams等学者的发展, 目前已成为工程领域中预测和分析气动噪声的最广泛应用方法.声比拟理论建立了声压等标量与不同类型声源之间的响应关系, 能够直接预测出声源周围的声压场分布.但是, 声压等标量不能够直接描述声能量在场中的传播途径和机理.近年来, 我们借鉴流体力学中用标量(如压力)描述流体的当前当地状态, 用矢量(如速度)描述流动的运动方向和能量输运特征的思路, 开展了矢量气动声学的理论及应用研究.本文对主要的研究进展进行了综述.
1 气动声学矢量波动方程及其解 1.1 气动声学矢量波动方程Ffowcs Williams等[1]引入广义函数建立了同时适用于整个可压缩流体和刚性固体区域的广义Navier-Stokes方程:
| $ \frac{{\partial \left[{H\left( f \right)\rho } \right]}}{{\partial t}} + \frac{{\partial [H\left( f \right)\rho {u_j}]}}{{\partial {x_j}}} = Q\delta \left( f \right) $ | (1) |
| $ \frac{{\partial \left[{H\left( f \right)\rho {u_i}} \right]}}{{\partial t}} + \frac{{\partial [H\left( f \right)(\rho {u_i}{u_j} + p{\delta _{ij}}-{\sigma _{ij}})]}}{{\partial {x_j}}} = {L_i}\delta \left( f \right) $ | (2) |
其中,
| $ \begin{array}{l} Q = {\rho _0}{v_n} + \rho ({u_n} - {\rm{ }}{v_n})\\ {L_i} = [(p-{p_0}){\delta _{ij}}-{\sigma _{ij}}]{n_j} + \rho {u_i}({u_n} - {v_n}) \end{array} $ |
在上述方程基础上, 推导了流体与固体作用诱发噪声的非齐次波动方程, 其中波动算子中的变量为密度或声压扰动.采用声比拟理论的思路, 期望建立以速度矢量为变量的波动方程.需要强调, 上述方程中矢量u描述的是当地流体的运动速度, 在非线性声源区域外即为描述声波运动的声粒子速度或声振速.对方程(1) 求空间偏导, 对方程(2) 求时间偏导, 并经过恒等变形后可以得到如下矢量波动方程, 具体推导步骤和分析参见文献[2].
| $ \begin{array}{*{20}{l}} {\frac{1}{{c_0^2}} \cdot \frac{{\partial \left[ {H\left( f \right)\rho {\bf{u}}} \right]}}{{\partial {t^2}}} - {\nabla ^2}\left[ {H\left( f \right)\rho {\bf{u}}} \right] = - \nabla \left[ {\delta \left( f \right)Q} \right] + }\\ {\frac{1}{{c_0^2}} \cdot \frac{{\partial \left[ {\delta \left( f \right){\bf{L}}} \right]}}{{\partial t}} + \int_0^t {\left\{ {\nabla \times \left[ {\nabla \times \left( {\delta \left( f \right){\bf{L}}} \right)} \right]} \right\}y{\rm{d}}{t^{\rm{*}}} - } }\\ {\frac{1}{{c_0^2}} \cdot \frac{{\partial \left[ {\nabla \cdot H\left( f \right){\bf{T}}} \right]}}{{\partial t}} - \int_0^t {\left\{ {\nabla \times \left( {\nabla \times \left( {\nabla \cdot \left( {H\left( f \right){\bf{T}}} \right)} \right)} \right)} \right\}} {\rm{d}}{t^{\rm{*}}}} \end{array} $ | (3) |
方程(3) 右端为源项, 第1, 2和3行分别表示单、偶和四极子源.
1.2 波动方程的解沿用Farassat求解FW-H方程的思路, 可以建立上述矢量波动方程的时域积分解, 其中单极子和偶极子源时域积分解可以见Ghorbaniasl等[3]的工作.针对旋转声源的情形, 可以分别沿用Tang等[4]和Mao等[5-6]的思路建立频域积分解以及适用于紧凑/点声源的球谐级数展开解, 具体求解过程参见文献[7].本文仅给出频域积分解的表达形式:
| $ \begin{array}{l} 4\pi {p_0}{{\tilde u}_{{\rm{T}}i}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\omega }}) = \int_{ - \infty }^\infty {\int_{f = 0} {\frac{{Q{{\hat r}_i}(1 - ikr)}}{{{r^2}}}} } {{\rm{e}}^{{\rm{i}}kr}}{{\rm{e}}^{{\rm{i}}\omega \tau }}{\rm{d}}S{\rm{d}}\tau \\ 4\pi {p_0}{c_0}{{\tilde u}_{{\rm{T}}i}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\omega }}) = - \int_{ - \infty }^\infty {\int_{f = 0} {\left( {\frac{{ik{L_r}{{\hat r}_i}}}{r} + \frac{{{L_i} - 3{L_r}{{\hat r}_i}}}{{{r^2}}} + \frac{{{\rm{i}}\left( {{L_i} - 3{L_r}{{\hat r}_i}} \right)}}{{k{r^3}}}} \right)} } \\ {{\rm{e}}^{{\rm{i}}kr}}{{\rm{e}}^{{\rm{i}}\omega \tau }}{\rm{d}}S{\rm{d}}\tau \\ 4\pi {p_0}{c_0}{{\tilde u}_{{\rm{Q}}i}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\omega }}) = - {k^2}\int_{ - \infty }^\infty {\int_{f > 0} {\frac{{{T_{rr}}{{\hat r}_i}{{\rm{e}}^{{\rm{i}}kr}}{{\rm{e}}^{{\rm{i}}\omega \tau }}}}{r}{\rm{d}}y{\rm{d}}\tau + } } \\ {\rm{i}}k\int_{ - \infty }^\infty {\int_{f > 0} {\frac{{\left[{\left( {{T_{jj}}-6{T_{rr}}} \right){{\hat r}_i} + 2{T_{ri}}} \right]{{\rm{e}}^{{\rm{i}}kr}}{{\rm{e}}^{{\rm{i}}\omega \tau }}}}{{{r^2}}}} } {\rm{d}}y{\rm{d}}\tau - \\ \int_{ - \infty }^\infty {\int_{f > 0} {\frac{{\left[{\left( {3{T_{jj}}-15{T_{rr}}} \right){{\hat r}_i} + 6{T_{ri}}} \right]{{\rm{e}}^{{\rm{i}}kr}}{{\rm{e}}^{{\rm{i}}\omega \tau }}}}{{{r^3}}}} } {\rm{d}}y{\rm{d}}\tau \\ - \frac{{\rm{i}}}{k}\int_{ - \infty }^\infty {\int_{f > 0} {\frac{{\left[{\left( {3{T_{jj}}-15{T_{rr}}} \right){{\hat r}_i} + 6{T_{ri}}} \right]{{\rm{e}}^{{\rm{i}}kr}}{{\rm{e}}^{{\rm{i}}\omega \tau }}}}{{{r^4}}}} } {\rm{d}}y{\rm{d}}\tau \end{array} $ |
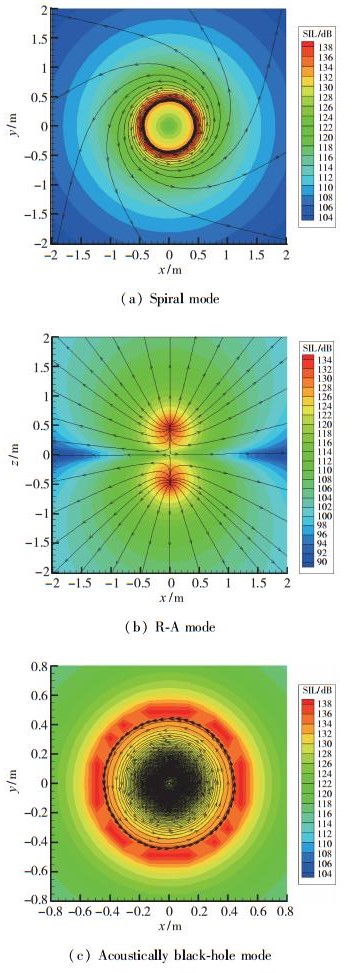
采用Tang等建立的频域声压积分公式和上节给出的频域声粒子速度积分公式, 直接计算出旋转声源周围的声强矢量场分布, 在此基础上, 类似于流体力学中通过速度矢量绘制流线, 可以绘制出声源向空间辐射声能量的声能流线.以亚音速声源为例, 得到如图 1所示的声能流线[8], 它揭示了辐射噪声的3种模式:螺旋模式、R-A模式以及声学黑洞模式.上述声能量的辐射模式有利于分析旋转叶片声能量传播模式, 优化布置吸声材料.具体分析参见文献[8].
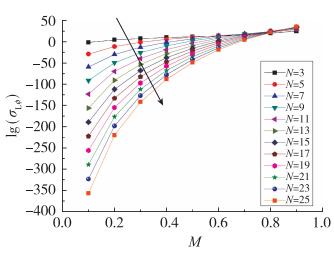
2.2 旋转声源辐射声功率频谱
另一方面, 应用球谐级数展开方法推导旋转点源辐射声压和声粒子速度的级数展开解, 在此基础上进一步推导得到声功率谱的解析公式[9].解析公式可以应用于旋转叶片气动噪声的分析: (1) 基于该公式可以快速直观分析叶片转速、动静叶片数、叶片安装角、直径等参数对输出声功率的影响, 因此可以在叶片式流体机械的初步方案设计阶段开展相关参数的匹配优化设计, 如图 2所示; (2) 在叶片详细设计完成后获取叶片壁面的压力脉动分布特征, 基于该声功率频谱的解析解能够从能量输出的角度快速识别出旋转叶片的主要声源位置以及声能量的分布频率.
|
| 图 2 叶片数和旋转Mach数对周向偶极子源辐射声能量的影响[9] Fig.2 Effects of blades number and rotating Mach number on the acoustic energy output of circumferential dipole source[9] |
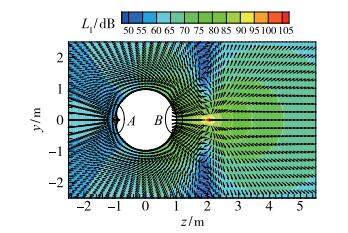
基于上述矢量声学方法并结合等效源法可以计算散射边界周围的声强矢量场分布, 其中声粒子速度可以直接作为边界条件用于求解等效源的源强, 具体步骤参见文献[10].由于在噪声预测过程中, 同时计算出声压标量和声粒子速度、声强矢量场的分布, 因此不仅能计算噪声的量级, 而且能显示声能量的传播途径.当散射边界为阻抗边界时, 可以直观观察出主要的吸声部位, 如图 3所示, 图中箭头指向散射边界内即表示部分声能量在此区域被吸收.通过对散射表面法向声强(声压和法向声粒子速度共轭值组合)的数值积分可以直接计算吸收声功率.以吸收声功率最大为目标函数, 优化散射表面吸声材料的位置和声阻抗参数, 即可以进一步开展噪声控制方法的优化设计.应用上述方法可以分析旋转叶片噪声受到边界散射的影响[11].
|
| 图 3 单极子源和阻抗散射边界周围的声强矢量场[10] Fig.3 Acoustic intensity vector field around monopole source and impedance scattering surface[10] |
本文主要介绍了矢量气动声学及研究进展.开展矢量气动声学研究的主要目的是直观展示声强矢量场, 从而深入理解声能量的传播机理.以旋转叶片噪声为研究背景, 分析了旋转声源辐射及边界散射噪声的能量传输特征.计划继续进一步深入开展矢量气动声学的理论研究, 如考虑运动介质效应等, 同时将其应用于指导叶片的气动声学设计和吸声材料的优化设计.
参考文献
| [1] | Ffowcs Williams J E, Hawkings D. Sound generation by turbulence and surfaces in arbitrary motion[J]. Philosophical Transactions of the Royal Society of London A:Mathematical, Physical and Engineering Sciences, 1969, 264(1151): 321-342. DOI:10.1098/rsta.1969.0031 |
| [2] | Mao Y J, Tang H T, Xu C. Vector wave equation of aeroacoustics and acoustic velocity formulations for quadrupole source[J]. AIAA Journal, 2016, 54(6): 1922-1931. DOI:10.2514/1.J054687 |
| [3] | Ghorbaniasl G, Carley M, Lacor C. Acoustic velocity formulation for sources in arbitrary motion[J]. AIAA Journal, 2013, 51(3): 632-642. DOI:10.2514/1.J051958 |
| [4] | Tang H T, Qi D T, Mao Y J. Analysis on the frequency-domain numerical method to compute the noise radiated from rotating sources[J]. Journal of Sound and Vibration, 2013, 332(23): 6093-6103. DOI:10.1016/j.jsv.2013.06.020 |
| [5] | Mao Y J, Gu Y Y, Qi D T, et al. An exact frequency-domain solution of the sound radiated from the rotating dipole point source[J]. Journal of the Acoustical Society of America, 2012, 132(3): 1294-1302. DOI:10.1121/1.4742972 |
| [6] | Mao Y J, Xu C, Qi D T, et al. Series expansion solution for sound radiation from rotating quadrupole point source[J]. AIAA Journal, 2014, 52(5): 1086-1095. DOI:10.2514/1.J052706 |
| [7] | Mao Y J, Zhang Q L, Xu C, et al. Two types of frequency-domain acoustic-velocity formulations for rotating thickness and loading sources[J]. AIAA Journal, 2015, 53(3): 713-722. DOI:10.2514/1.J053230 |
| [8] | Mao Y J, Xu C, Qi D T. Computation of instantaneous and time-averaged active acoustic intensity field around rotating source[J]. Journal of Sound and Vibration, 2015, 337: 95-115. DOI:10.1016/j.jsv.2014.10.023 |
| [9] | Mao Y J, Xu C. Analytical acoustic power spectrum formulations for rotating monopole and dipole point sources[J]. Journal of Vibration and Acoustics, 2016, 138(2): 021009 DOI:10.1115/1.4032139 |
| [10] | Mao Y J, Cai J C, Gu Y Y, et al. Direct evaluation of acoustic intensity vector field around impedance scattering body[J]. AIAA Journal, 2015, 53(5): 1362-1371. DOI:10.2514/1.J053431 |
| [11] | Mao Y J, Gu Y Y, Xu C. Validation of frequency-domain method to compute noise radiated from rotating source and scattered by surface[J]. AIAA Journal, 2016, 54(4): 1188-1197. DOI:10.2514/1.J053674 |