高超声速飞行器是航空航天技术的重要发展方向.随着新材料、轻质结构在高超声速飞行器中的广泛应用以及设计中对结构质量的要求越来越严苛, 新一代高超声速飞行器设计中遇到的气动弹性问题将越来越严峻.
20世纪五六十年代, Lighthill[1], Ashley等[2], Van Dyke[3], Garrick[4]采用各种版本的活塞理论和其他气动力模型研究高超声速气动弹性.同一时期, Gibson[5], Doggett[6-7], Goetz等[8-9], Morgan等[10], Hanson[11], Rainey[12]通过大量的高超声速风洞颤振试验研究了不同舵翼面模型的颤振特性, 从翼型形状、翼面厚度、攻角、前缘钝度、翼体干扰效应等方面探索了高超声速颤振的规律.这些工作对认识高超声速颤振特性和机理有重要作用, 并且为航天飞机的研发提供了重要的支撑.
但之后的高超声速气动弹性研究主要侧重于理论和数值计算方面, 很少有试验方面的研究报道.如Liu等[13]提出了结合活塞理论和面元法优点的统一升力面理论用于高超声速非定常气动力计算; 陈劲松等[14]、Zhang等[15]、杨炳渊等[16-18]、史晓鸣等[19]发展和完善了当地活塞流理论, 进一步提高了该方法的适用性; Löehner等[20], Nydick等[21], Friedmann等[22], McNamara[23], Gupta等[24], 徐敏等[25], 窦怡彬等[26]通过基于CFD计算的颤振分析方法研究了高超声速气动弹性和热气动弹性问题.
为满足高超声速飞行器研发需求和CFD非定常计算技术发展的需要, 中国航天空气动力技术研究院在国内首先研发了高超声速风洞颤振试验技术[27-31].笔者为研究钝前缘翼面高超声速颤振特性和校验高超声速非定常CFD计算方法及程序, 采用一组具有相同结构动力学特性和气动外形的钝前缘梯形翼模型, 在FD-07高超声速风洞中开展了颤振试验研究, 试验Mach数为4.95和5.95.本文将在试验的基础上结合统一升力面理论计算讨论该模型的高超声速颤振特性, 并提供相关模型参数和试验数据.
1 试验设备 1.1 风洞中国航天空气动力技术研究院FD-07风洞是一种暂冲式高超声速风洞(见图 1), 具备固定Mach数连续变动压的试验能力, 常用风洞试验Mach数为4.5, 5.0, 6.0, 7.0和8.0, 试验段喷口直径为500 mm.

|
| 图 1 FD-07高超声速风洞 Fig.1 FD-07 hypersonic wind tunnel |
采用Coinv INV 3060A数据采集系统, 该系统具有16个数据采集通道, 24位采样精度, 最大采样频率51.2 kHz.试验采用应变电桥测量模型振动响应.试验中结构响应和风洞流场参数同步测量.
1.3 试验装置风洞试验装置如图 2所示, 主要由模型支撑系统、模型保护系统组成[29-30].模型支撑系统用于支撑弹性模型并使其免受风洞本体振动等影响; 模型保护系统用于保护模型以避免其受到风洞启动和停止的流场冲击影响, 同时可以用于在临近颤振发生时保护模型.

|
| 图 2 高超声速风洞颤振试验装置 Fig.2 Rig for hypersonic wind tunnel flutter test |
模型外形为等厚钝前缘直角梯形翼, 其中翼面部分裸露在流场中(见图 2, 图 3), 根部由板梁悬臂支撑.

|
| 图 3 翼面模型 Fig.3 Wing model |
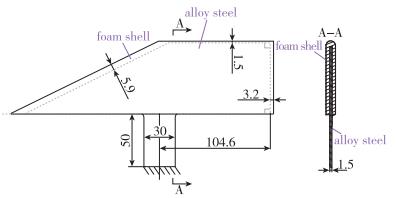
模型结构为合金钢芯板和泡沫组成的夹层结构(见图 3, 图 4); 合金钢芯板和支撑板梁等厚且一体切割成型, 并提供模型的主要刚度和质量特性; 合金芯板翼面部分外部由泡沫包裹以维持翼面气动外形.
|
| 图 4 模型结构示意图 Fig.4 Model structure construction |
该合金钢芯板的材料属性通常为:弹性模量2.06×1011 Pa, Poisson比0.3, 密度7 850 kg/m3; 该泡沫材料的材料属性通常为:弹性模量5.5×107 Pa, 剪切模量2.5×107 Pa, 密度80 kg/m3.
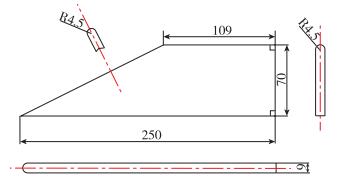
2.2 几何参数翼面模型气动外形参数如图 5所示, 为直角梯形翼, 翼尖弦长109 mm, 翼根理论弦长250 mm(实际弦长247 mm), 展长70 mm, 前缘和翼尖倒角半径4.5 mm.
|
| 图 5 翼面模型气动外形 Fig.5 Wing model configuration |
如图 4所示, 支撑板梁长50 mm, 宽30 mm, 其中心距离合金芯板后缘104.6 mm.合金芯板外形用虚线表示, 为直角梯形外形, 其边缘与泡沫外形边缘的距离如图 4所示.
合金钢芯板和支撑板梁由钢板整体切割而成, 厚度为1.5 mm, 模型翼面部分总厚度9 mm.
2.3 结构动力学参数研究中采用两个具有相同气动外形和结构动力学特性的模型进行试验, 模型编号为H-151和H-152, 对应的试验Mach数分别为4.95和5.95.
采用锤击法测量模型模态参数.
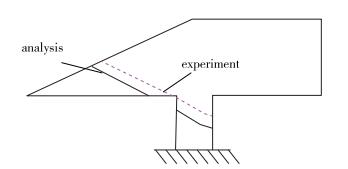
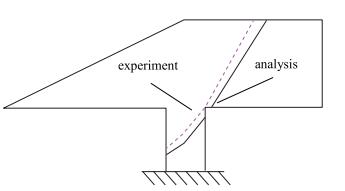
H-151和H-152试验模型的前2阶模态频率(fm)和阻尼比(g)的试验值见表 1; 试验模态振型节线位置如图 6, 图 7所示.
| 下载CSV 表 1 模型结构动力学参数(计算和试验) Tab.1 Calculated and measured structural dynamic properties |
|
| 图 6 1阶模态振型节线 Fig.6 Node line of the first mode |
|
| 图 7 2阶模态振型节线 Fig.7 Node line of the second mode |
风洞颤振试验采用固定Mach数连续变动压的风洞开车方式, 即试验中保持Mach数不变, 通过持续增加总压实现动压的增加, 直到模型发生颤振.试验采用粘贴于模型根部的应变片测量模型振动, 纹影仪观测模型附近流场.
试验过程由如下步骤组成:
(1) 选用对应Mach数的喷管, 并安装模型;
(2) 锁止模型, 弹出模型保护罩, 以低动压启动风洞并开始数据采集;
(3) 流场稳定后撤出保护罩并解锁模型;
(4) 缓慢增加动压直至模型发生颤振;
(5) 颤振发生时锁止模型并弹出保护罩;
(6) 风洞关车, 停止试验.
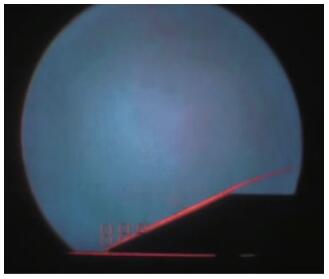
4 分析与讨论 4.1 试验结果和分析纹影仪流场观测显示(见图 8), 翼面前缘产生一道斜激波, 反射板附近流场未受到其他部件激波干扰且反射板附面层未影响翼面流场.
|
| 图 8 试验纹影图 Fig.8 Schlieren photograph of model |
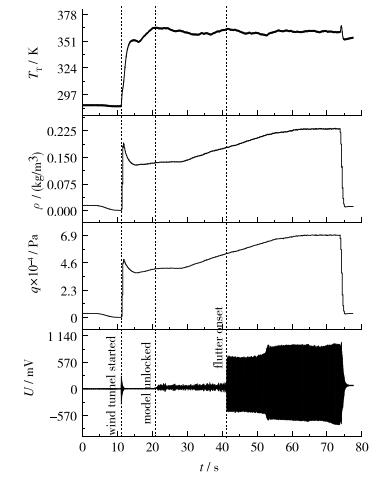
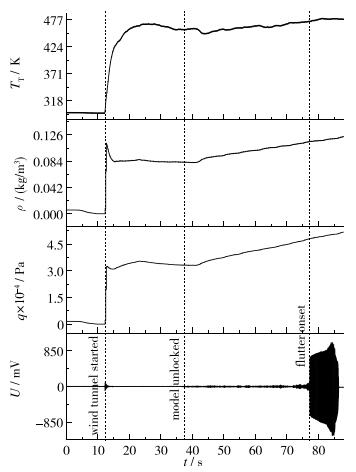
试验中的流场总温、密度、动压和模型应变响应如图 9, 图 10所示.试验过程中, 总温基本保持恒定, 通过增加总压提高试验段动压.试验通过增加动压直接观测到模型振动发散并破坏.
|
| 图 9 H-151模型高超声速颤振试验(Ma=4.95) Fig.9 H-151 hypersonic flutter test (Ma=4.95) |
|
| 图 10 H-152模型高超声速颤振试验(Ma=5.95) Fig.10 H-152 hypersonic flutter test (Ma=5.95) |
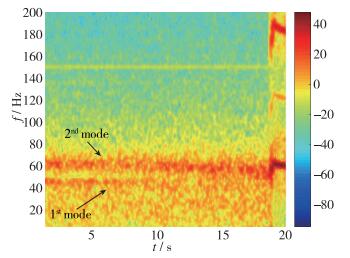
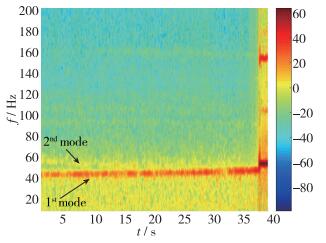
截取如图 9, 图 10所示解锁后的振动响应试验数据进行分析, 采用小波时频域分析方法[32], 选用Morlet小波作为小波基函数.两个模型振动响应时频谱如图 11和图 12所示, 由时频域分析可得:模型1阶模态和2阶模态随着试验动压的增加发生频率聚合, 因此试验中模型发生了1阶、2阶模态的耦合颤振.
|
| 图 11 时频谱图(Ma=4.95) Fig.11 Time-frequency spectrum (Ma=4.95) |
|
| 图 12 时频谱图(Ma=5.95) Fig.12 Time-frequency spectrum (Ma=5.95) |
通过直接观测法获得的模型试验颤振参数如表 2所示.
| 下载CSV 表 2 试验颤振临界参数 Tab.2 Measured flutter onset parameters |
H-151模型在Ma=4.95的试验颤振动压(qfm)为54 142 Pa, 试验颤振频率(ffm)为50.3 Hz, 对应的气流密度(ρ)为0.178 8 kg/m3, 气流总温(TT)为363.87 K.
H-152模型在Ma=5.95的试验颤振动压(qfm)为48 077 Pa, 试验颤振频率(ffm)为44.5Hz, 对应的气流密度(ρ)为0.115 2 kg/m3, 气流总温(TT)为474.24 K.
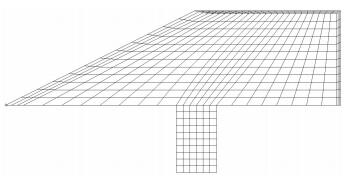
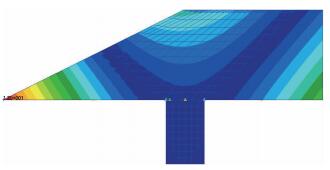
4.2 结构动力学建模和分析采用板壳单元(见图 13)建立结构有限元模型, 并进行结构动力学分析.计算得到的前4阶模态频率和振型如图 14~图 17所示, 其中1阶模态主要为翼面弯曲模态, 2阶模态为翼面扭转模态.
|
| 图 13 结构有限元模型 Fig.13 Structural finite element model |

|
| 图 14 1阶振型, fa=36.0 Hz Fig.14 1st mode, fa=36.0 Hz |

|
| 图 15 2阶振型, fa=56.6 Hz Fig.15 2nd mode, fa=56.6 Hz |
|
| 图 16 3阶振型, fa=136.3 Hz Fig.16 3rd mode, fa=136.3 Hz |

|
| 图 17 4阶振型, fa=261.1 Hz Fig.17 4th mode, fa=261.1 Hz |
与加工模型的地面振动试验(ground vibration test, GVT)结果相比(如表 1和图 7), 计算模型的频率略高、节线位置更靠近翼面根部.
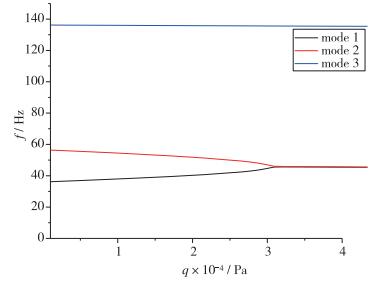
4.3 颤振计算分析采用统一升力面理论计算高超声速非定常气动力, K方法计算颤振临界参数, 结构模型为4.2节有限元模型. Ma=4.95工况下颤振计算动压-频率(q-f)曲线如图 18所示, 表明该模型的颤振是由1阶模态和2阶模态的耦合产生, 与试验响应的时频域分析一致.
|
| 图 18 颤振计算q-f曲线 Fig.18 Calculated flutter q-f plot |
试验中动压随试验总压的变化而变化(见图 9, 图 10), 相应的气流密度也随之变化; 而计算中为密度不变, 速度增加.为了评估计算密度对计算颤振动压的影响, 计算涵盖了试验范围内的密度区间.
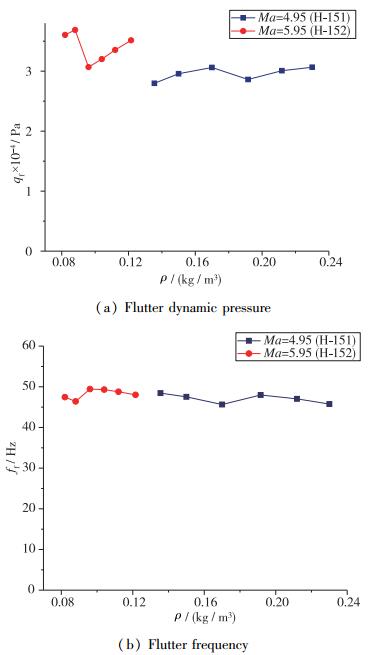
计算结果(结构阻尼比为0时)如图 19所示, 不同的计算密度对颤振动压(qf)和颤振频率(ff)的计算结果有一定影响:
|
| 图 19 不同气流密度颤振计算结果 Fig.19 Calculated flutter results at different fluid densities |
(1) 不同计算密度下的颤振动压并不完全一致, Mach数4.95和5.95时不同密度下的计算颤振动压相对于平均值分别有±2.9%和±5.8%的平均变化量, 并且最大偏差量分别达5.4%和9.9%;
(2) 颤振频率随计算密度的变化较小, Mach数4.95和5.95时相对于计算颤振频率平均值的平均变化都为±1.9%, 最大偏差量分别为3.0%和3.8%.
4.3.2 结构阻尼影响实际模型的结构阻尼不为零, 本试验模型的结构阻尼由GVT实验测得, 如表 1所示.
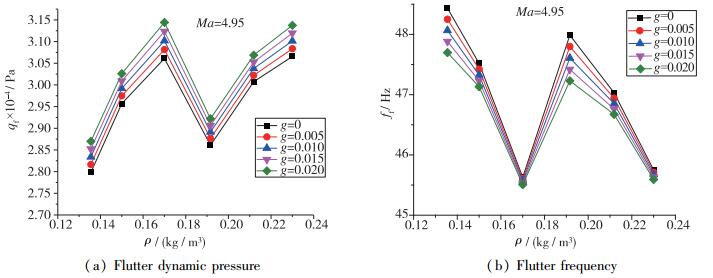
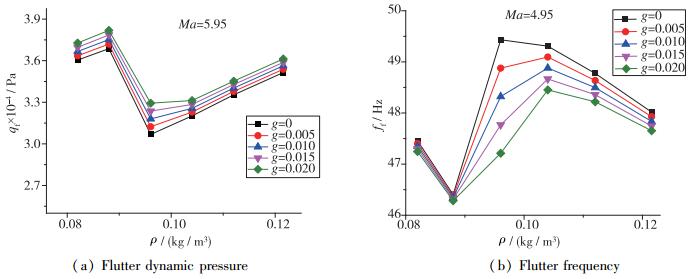
研究中计算了不同气流密度下结构阻尼比为0, 0.005, 0.01, 0.015和0.02时的颤振动压(qf)和颤振频率(ff), 计算结果如图 20, 图 21所示, 结果表明:
|
| 图 20 不同气流密度和结构阻尼颤振计算结果(Ma=4.95) Fig.20 Calculated flutter results at different fluid densities and structural dampings (Ma=4.95) |
|
| 图 21 不同气流密度和结构阻尼颤振计算结果(Ma=5.95) Fig.21 Calculated flutter results at different fluid densities and structural dampings (Ma=5.95) |
(1) 计算颤振动压随结构阻尼的增加而增加, Mach数4.95和5.95条件下计算颤振动压分别平均增加了2.3%和3.8%;
(2) 计算颤振频率随结构阻尼的增加而减小, Mach数4.95和5.95条件下颤振频率分别平均降低了0.9%和1.5%.
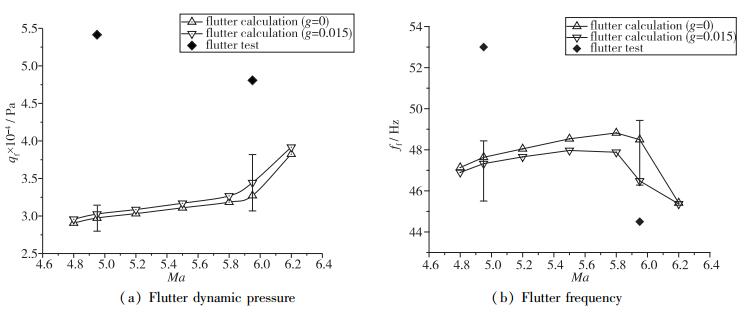
4.3.3 Mach数影响按照气流密度0.15 kg/m3, 计算结构阻尼为0和0.015时Ma=4.8~6.2的颤振动压(qf)和颤振频率(ff).计算结果如图 22所示, 理论计算认为:在分析Mach数范围内, 不同结构阻尼下颤振动压和颤振频率变化趋势一致, 颤振动压基本随Mach数增加而增加, 而颤振频率随着Mach数的增加先增后降.
|
| 图 22 试验和计算颤振动压 Fig.22 Experimental and calculated flutter results |
综合4.3节的分析, 考虑实际模型结构阻尼范围和风洞试验流场密度范围的因素, 在Mach数4.95和5.95下得到的计算颤振动压分别在27 980~31 442 Pa和30 682~38 183 Pa范围内(如图 22(a)中所示Mach数4.95和5.95下的颤振动压计算偏差带); Mach数4.95和5.95下得到的计算颤振频率分别在45.5~48.4 Hz和46.3~49.4 Hz范围内(如图 22(b)中所示Mach数4.95和5.95下的颤振频率计算偏差带).
对比风洞颤振试验结果和统一升力面理论的计算结果可以得出如下结论:
(1) 对于该模型, 计算Mach数范围内颤振动压要低于试验颤振动压. Mach数4.95和5.95下的平均计算颤振动压分别比试验值低45.1%和28.4%, 最大计算颤振动压分别比试验值低41.9%和20.6%(如表 3所示).
| 下载CSV 表 3 计算和试验颤振动压 Tab.3 Calculated and tested flutter dynamic pressures |
(2) 该模型在Mach数4.95时的计算颤振频率低于试验值, 而Mach数5.95时的计算颤振频率高于试验值(如表 4所示).
| 下载CSV 表 4 计算和试验颤振频率 Tab.4 Calculated and tested flutter frequencies |
可见, 在将气流密度、结构阻尼因素考虑在内之后得到的理论计算颤振动压范围与试验值之间仍存在较大的偏差, 这种偏差的主要来源可能有如下几个方面:
(1) 结构有限元模型与实物模型之间的结构动力学特性偏差, 即结构有限元建模带来的偏差;
(2) 试验结果散布, 即本身试验值也存在一定的散布区间;
(3) 气动力建模的局限性, 即理论计算模型无法考虑模型前缘钝度因素, 而模型的前缘特性对翼面的高超声速流场有重要影响.
文献[31]采用试验的方法研究了一组结构动力学特性类似的舵面模型的颤振特性, 试验Mach数为4.95.试验发现, 尽管模型与模型之间的结构动力学特性由于加工等因素存在一定范围的偏差, 但是试验得到的颤振动压偏差较小, 涵盖结构动力学特性偏差和试验结果散布因素在内的颤振动压最大相对偏差为3.8%.
因此, 有理由相信, 对于本文的研究模型, 结构动力学特性的偏差和试验结果的散布特性还不至于使得理论计算与试验颤振动压之间存在如此大的偏差.而对于前缘钝度的影响, 目前的高超声速非定常理论计算模型无法评估, 因此有必要对此进行进一步的研究, 探寻前缘钝度对高超声速非定常气动力的影响特性和规律.
5 结论本文设计了一组具有简单结构动力学特性的钝前缘翼面模型, 并给出了结构材料、尺寸、气动外形和结构动力学参数.在高超声速风洞中采用直接观测法获得了模型在Mach数4.95和5.95下的颤振动压、颤振频率、气流密度、总温等颤振临界参数.
对于该试验模型和试验Mach数, 统一升力面理论计算得到的颤振动压低于试验值.分析认为, 计算气流密度、计算结构阻尼、结构建模偏差、试验结果散布特性等因素均会构成计算值和试验值之间的偏差, 但即便在计算中考虑上述因素, 计算结果与试验值仍存在较大偏差.因此, 高超声速非定常气动力计算理论中对前缘钝度的忽略值得进一步研究.
致谢: 感谢国家自然科学基金(项目: 11702285)对本研究的支持.| [1] |
Lighthill M J. Oscillating airfoils at high Mach number[J]. Journal of the Aeronautical Sciences, 1953, 20(6): 402-406. DOI:10.2514/8.2657 |
| [2] |
Ashley H, Zartarian G. Piston theory-a new aerody-namic tool for the aeroelastician[J]. Journal of the Aeronautical Sciences, 1956, 23(12): 1109-1118. DOI:10.2514/8.3740 |
| [3] |
Van Dyke M D. A study of second-order supersonic flow theory[R]. Technical Reports 1081, 1951. https://authors.library.caltech.edu/82829/
|
| [4] |
Garrick I E. A survey of aerothermoelasticity[J]. Aerospace Engineering, 1963, 22(1): 140-147. |
| [5] |
Gibson F W. Flutter investigation of models having the planform of the North American X-15 airplane wing over a range of Mach numbers from 0. 56 to 7. 3[R]. NASA-TM-X-460, 1961.
|
| [6] |
Doggett R V Jr. An observation on the pictorial representation of aeroservothermoelasticity[R]. NASA TM 104058, 1991.
|
| [7] |
Doggett R V Jr. Experimental flutter investigation of some simple models of a boost-glide-vehicle wing at Mach numbers of 3. 0 and 7. 3[R]. NASA TM X-37, 1959.
|
| [8] |
Goetz R C, Sewall J L. Experimental flutter study of a wing-fuselage configuration at a Mach number of 15. 4 and comparison with theory[R]. NASA-TN-D-3046, 1965.
|
| [9] |
Goetz R C. Hypersonic flutter analysis using measured static aerodynamic derivatives, and comparison with ex-periment[R]. NASA-TN-D-5233, 1969.
|
| [10] |
Morgan H G, Miller R W. Flutter tests of some simple models at a Mach number of 7. 2 in helium flow[R]. NASA-MEMO 4-8-59L, 1959.
|
| [11] |
Hanson P W. Aerodynamic effects of some configuration variables on the aeroelastic characteristics of lifting sur-faces at Mach numbers from 0. 7 to 6. 86[R]. NASA-TN-D-984, 1961.
|
| [12] |
Rainey A G. Aeroelastic research at high speeds[R]. NASA-TM-X-326, 1960.
|
| [13] |
Liu D D, Yao Z X, Sarhaddi D, et al. From piston theory to a unified hypersonic-supersonic lifting surface me-thod[J]. Journal of Aircraft, 1997, 34(3): 304-312. DOI:10.2514/2.2199 |
| [14] |
陈劲松, 曹军. 超声速和高超声速翼型非定常气动力的一种近似计算方法[J]. 空气动力学学报, 1990, 8(3): 339-344. Chen J S, Cao J. An approximate calculating method of supersonic/hypersonic unsteady aerodynamic[J]. Acta Aerodynamica Sinica, 1990, 8(3): 339-344. (in Chinese) |
| [15] |
Zhang W W, Ye Z Y, Zhang C A, et al. Supersonic flu-tter analysis based on a local piston theory[J]. AIAA Journal, 2009, 47(10): 2321-2328. DOI:10.2514/1.37750 |
| [16] |
杨炳渊. 颤振的工程计算方法, 防空导弹结构与强度[M]. 北京: 中国宇航出版社, 1993. Yang B Y. The engineering approximate method for flutter calculation, structure and strength of anti-aircraft mi-ssile[M]. Beijing: China Aerospace Publishing House, 1993. (in Chinese) |
| [17] |
杨炳渊, 史晓鸣, 梁强. 高超声速有翼导弹多场耦合动力学的研究和进展(上)[J]. 强度与环境, 2008, 35(5): 55-63. Yang B Y, Shi X M, Liang Q. Investigation and development of the multi-physics coupling dynamics on the hypersonic winged missiles(I)[J]. Structure & Environ-ment Engineering, 2008, 35(5): 55-63. (in Chinese) |
| [18] |
杨炳渊, 史晓鸣, 梁强. 高超声速有翼导弹多场耦合动力学的研究和进展(下)[J]. 强度与环境, 2008, 35(6): 55-62. Yang B Y, Shi X M, Liang Q. Investigation and development of the multi-physics coupling dynamics on the hypersonic winged missiles(Ⅱ)[J]. Structure & Environ-ment Engineering, 2008, 35(6): 55-62. (in Chinese) |
| [19] |
史晓鸣, 杨炳渊, 李海东, 等. 基于当地流活塞理论的翼-身组合体飞行器大攻角超声速颤振分析[J]. 空气动力学学报, 2012, 30(5): 664-667. Shi X M, Yang B Y, Li H D, et al. Supersonic flutter analysis of wing-fuselage complete vehicle of high attack angle with local piston theory based on CFD techno-logy[J]. Acta Aerodynamica Sinica, 2012, 30(5): 664-667. (in Chinese) |
| [20] |
Löehner R, Yang C, Cerbal J, et al. Fluid-structure-thermal interaction using a loose coupling algorithm and adaptive unstructured grids[R]. AIAA 1998-2419, 1998.
|
| [21] |
Nydick I, Friedmann P P. Aeroelastic analysis of a trim-med generic hypersonic vehicle[C]. Proceedings of the 39th AIAA/ASME/ASCE/AHS/ASC Structures, Struc-tural Dynamics, and Materials Conference and Exhibit, Long Beach, CA, USA: AIAA, 1999: 777-810. http://arc.aiaa.org/doi/abs/10.2514/6.1998-1807
|
| [22] |
Friedmann P P, McNamara J J, Thuruthimattam B J, et al. Aeroelastic analysis of hypersonic vehicles[J]. Jour-nal of Fluids and Structures, 2004, 19(5): 681-712. DOI:10.1016/j.jfluidstructs.2004.04.003 |
| [23] |
McNamara J J. Aeroelastic and aerothermoelastic behavior of two and three dimensional lifting surfaces in hypersonic flow[D]. Ann Arbor, MI, USA: University of Michi-gan, 2005. http://adsabs.harvard.edu/abs/2005PhDT.......163M
|
| [24] |
Gupta K K, Voelker L S. Aeroelastic simulation of hypersonic flight vehicles[J]. AIAA Journal, 2012, 50(3): 717-723. DOI:10.2514/1.J051386 |
| [25] |
徐敏, 安效民, 陈士橹. 一种CFD/CSD耦合计算方法[J]. 航空学报, 2006, 27(1): 33-37. Xu M, An X M, Chen S L. CFD/CSD coupling numerical computational methodology[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(1): 33-37. (in Chinese) |
| [26] |
窦怡彬, 徐敏, 安效民, 等. 高超声速舵面颤振分析[J]. 工程力学, 2009, 26(11): 232-237. Dou Y B, Xu M, An X M, et al. Flutter analysis for a fin in hypersonic flow[J]. Engineering Mechanics, 2009, 26(11): 232-237. (in Chinese) |
| [27] |
Ji C, Zhu J, Chen N, et al. Development of a hypersonic flutter test capability[R]. AIAA 2016-3820, 2016.
|
| [28] |
Ji C, Cheung C, Liu Z Q, et al. Design, build and test of a wind tunnel rig for hypersonic flutter research[C]. Proceedings of the 5th Aircraft Structural Design Conference, Manchester, UK: Royal Aeronautical Society, 2016.
|
| [29] |
季辰, 李锋, 刘子强. 高超声速风洞颤振试验技术研究[J]. 实验流体力学, 2015, 29(4): 75-80. Ji C, Li F, Liu Z Q. Research on flutter test technique in hypersonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(4): 75-80. (in Chinese) |
| [30] |
季辰, 赵玲, 朱剑, 等. 高超声速风洞连续变动压舵面颤振试验[J]. 实验流体力学, 2017, 31(6): 37-44. Ji C, Zhao L, Zhu J, et al. Hypersonic wind tunnel flutter test research on rudder models by continuously varying dynamic pressure[J]. Journal of Experiments in Fluid Mechanics, 2017, 31(6): 37-44. (in Chinese) |
| [31] |
季辰. 舵翼面高超声速气动弹性特性试验研究[D]. 北京: 中国航天空气动力技术研究院, 2015. Ji C. Experimental research on aeroelastic characteri-stics of rudder and wing models in hypersonic flow[D]. Beijing: China Academy of Aerospace Aerodynamics, 2015(in Chinese). |
| [32] |
Marty B, Eric F, Marty B, et al. Wavelet analysis of F/A-18 aeroelastic and aeroservoelastic flight test data[R]. AIAA 1997-1216, 1997.
|



