超燃冲压发动机燃烧室内Mach数可达2以上, 气流在燃烧室的驻留时间只有ms量级, 而且气流的压力和温度均比较低, 在这样的条件下要组织稳定高效的燃烧相当困难.为促进超声速燃烧时燃料与氧化剂的掺混与火焰稳定, 先后采用的方案有壁面燃料垂直喷射斜坡支板后向台阶和凹腔.与其他方案相比, 凹腔结构简单, 且在点火燃烧效率阻力总压损失热防护实现等方面更具优势[1-3].因此, 近年来, 凹腔作为超声速燃烧室中增强混合与稳定火焰的装置得到非常广泛的研究和应用. Stalling等[4]将凹腔按照剪切层发展分为开式闭式过渡3类, 闭式凹腔最大的特点是凹腔自由剪切层可以撞击在凹腔底壁, 凹腔内部形成两个驻定的回流区; 开式凹腔的自由剪切层无法撞击在凹腔底壁, 凹腔内存在一个大的回流区, 阻力较小, 流动存在自激振荡现象.目前, 超燃冲压发动机中主要采用开式凹腔作为火焰稳定器.开式方腔流动会产生强烈的振荡, 振荡的诱因幅值抑制方法等都很值得研究, 涉及流动失稳波涡非线性作用自持振荡等许多理论问题, 20世纪50年代以来, 许多研究者对此进行了研究[5]. Krishnamutry [6]最早从实验得到方腔声场结构. Rossiter [7]总结了预测振荡频率的半经验公式. Rowley等[5, 8-9]对方腔的空间稳定性降维模型理论模型控制等问题进行了一系列研究. Shieh [10]对高Reynolds数下不同构型方腔进行了湍流数值模拟研究.
但这些研究主要针对外流低Reynolds数亚声速或跨声速条件下凹腔流动.与常规外流凹腔不同, 超燃冲压发动机凹腔流动属于内流问题, 并且来自于隔离段的气流处于高速和高温状态. Hassan等[11]采用动态网格RANS/LES混合方法对三维超声速进行了数值模拟, 并与IDDES的结果进行了对比. Li等[12]采用LES方法对超声速开式凹腔进行数值模拟, 并采用POD对结果进行分析. Gruber等[13]和Settles等[14]在超声速条件下对不同长深比和后缘角的凹腔进行风洞实验.王振国等[15]从理论分析的角度对超声速气流中稳焰凹腔吹熄极限进行了分析和建模. Sun等[16]基于Menter的k-ω SST湍流模型构建了一种混合RANS/LES模拟方法, 并对超燃冲压发动机凹腔二维超声速流动进行数值模拟.
在获得流动结构的众多方法中, 本征正交分解方法(proper orthogonal decomposition, POD)被广泛使用[17]. POD方法是一种高效的降阶方法, 其核心思想是寻找一组最佳的标准正交基, 使得样本数据在该标准正交基上的投影依次迅速递减, 截取投影较大(包含能量较高)的前几阶模态, 从而可以用较少的基展开获得较高阶数据的近似描述. Lumley [17]首先将POD方法引入湍流研究, 接着Sirovich [18]引入了快照方法来研究波动流的动力学问题.很多学者应用POD进行流动分析开展了大量的工作, 如圆柱尾迹流[19]平板边界层[20]自然对流[21]等.
动力学模态分解(dynamic mode decomposition, DMD)是近年来从整体稳定性Koopman分析的基础上发展起来的一种低维系统分解技术[22]. DMD方法基于流动快照而不受流动类型的限制, 可以得到流动在时间和空间上的主要特征, 且可通过特征值得到流动频率并判断其稳定性. DMD方法由Schmid [22]提出, 并将其分别对在数值方法和实验得到流场数据进行分析. Rowley等[23]采用DMD方法对横向射流中的非线性流动进行分析, 结果表明, 该方法可以提取主要的流动结构以及频率, 通过与DNS线化N-S方程以及POD方法得到的频率进行对比, 发现DMD得到频率与DNS的结果相同, 而其他方法的结果均与DNS结果相差较大. Roy等[24]将DMD方法和POD方法应用于反应流的稳定性分析中, 并对比了两种方法的结果.潘翀等[25]将DMD应用在TR-PIV测量得到的NACA0015翼型加装Gurney襟翼后的尾流速度场.在凹腔流动方面, Seena等[26]采用DMD方法对低Reynolds数不可压缩条件下的开式凹腔流动进行分析. Sun等[27]对亚声速和跨声速下的开式凹腔流动进行了DMD分析.
上述研究工作主要关于开式凹腔在外流低Reynolds数亚声速或跨声速条件下的流动.然而, 超燃冲压发动机凹腔流动与此均有明显的区别:(1) 属于内流问题;(2) 来流Mach数较高, 通常在2左右, 同时Reynolds数较高.根据笔者查阅的文献, 现在还没有以超燃冲压发动机凹腔流动为研究背景并采用DMD方法对其进行稳定性分析的文献.超声速凹腔流动稳定性的研究对深入理解凹腔增强混合和稳焰机理以及凹腔的设计有着重要的学术意义和工程应用价值.
本文首先基于LES方法对超燃冲压发动机凹腔流动进行数值模拟, 进而分别采用DMD和POD方法对自激振荡流动进行稳定性分析, 并将其提取的频率与压力脉动FFT分析结果以及Rossiter模型预测结果进行对比.
1 计算方法及验证算例 1.1 流场计算方法LES方法的本质是用非定常的Navier-Stokes方程来直接模拟大尺度的涡运动, 而通过亚格子模型来模拟小尺度涡的运动, 即大涡直接求解, 小涡使用模型.
应用滤波函数可将一个瞬态流动变量分为两个部分, 瞬态变量有如下公式:
| $\mathit{\Phi }\,\mathit{=}\,{{\mathit{\Phi }}_{\mathit{0}}}\mathit{+}\,\mathit{\Phi '}\mathit{.}$ |
其中, Φ0为大尺度涡的平均分量, 是LES方法中直接计算的部分; Φ′为小尺度涡的分离, 该部分是通过亚格子模型表示的.滤波后的变量Φ可以通过下式得到
| $\mathit{\Phi =}\int{\begin{matrix} {} \\ _{\mathit{D}} \\ \end{matrix}}G\left( x,x\mathit{'} \right)\rm{d}\mathit{x'}\mathit{.}$ | (1) |
其中, D为流动区域, x′为实际流动区域中的空间坐标, x为滤波后大尺度涡的空间坐标.
用式(1) 表示的滤波函数处理瞬态下的连续方程和Navier-Stokes方程, 可以得到
| $\begin{align} & \frac{\partial \rho }{\partial t}=\frac{\partial }{\partial {{x}_{i}}}\left( \rho {{u}_{i}} \right)=0, \\& \frac{\partial }{\partial t}\left( \rho {{u}_{i}} \right)+\frac{\partial }{\partial {{x}_{i}}}\left( \rho {{u}_{j}}{{u}_{i}} \right)=-\frac{\partial \rho }{\partial {{x}_{i}}}+\frac{\partial }{\partial {{x}_{j}}}\left( \mu \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}} \right)-\frac{\partial {{\tau }_{ij}}}{\partial {{x}_{j}}}. \\ \end{align}$ | (2) |
其中, ρ为流体密度, ui为流体平均速度, p为平均压力, μ为流体分子黏性系数, τij为亚格子尺度剪应力张量.
方程(2) 还不能直接求解, 为使其能够求解, 须构造亚格子尺度应力的数学表达式.最早的亚格子尺度模型由Smagorinsky提出, 基本亚格子尺度应力模型的形式为
| $\tau {_{ij}} - \frac{1}{3}{\tau _{kk}}{\delta _{ij}} = - 2{\mu _t}{\mathit{\boldsymbol{S}}_{ij}}.$ | (3) |
其中, μt为亚格子尺度的湍动黏度, δij为亚格子尺度应力, τkk为亚格子尺度各向同性的一部分, Sij为亚格子尺度的应变率张量. μt用式(4) 进行计算:
| ${\mu _{\rm{t}}} = {\left( {{C_{\rm{s}}}\Delta } \right)^2}\left| \mathit{\boldsymbol{S}} \right|.$ | (4) |
其中, S为拉伸率张量,
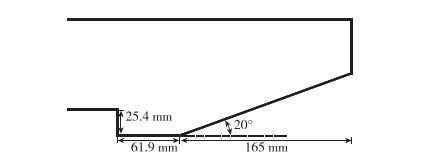
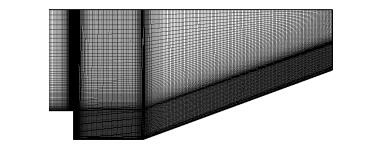
Settles等[14]关于凹腔可压缩湍流自由剪切层的实验作为凹腔流动数值模拟的验证算例被广泛采用.实验来流条件为:M=2.92, ReL=6.7×107/m, T0=258K, P0=0.69MPa, 图 1为凹腔模型尺寸, 凹腔深度D为25.4mm, 底壁长度L为61.9mm, 入口处的湍流边界层厚度为2.9mm, 流动中凹腔前缘产生自由剪切层, 剪切层向下游发展并再附着于凹腔后壁, 形成撞击激波, 实验结果表明该流场具有很好的二维特性.各壁面采用无滑移绝热边界条件. 图 2为计算网格, 采用O-H结构网格, 网格单元总数为45242, 第1层网格高度为1.4×10-4mm, 壁面y+小于1.本文计算中凹腔入口处的湍流边界层由225mm长度的平板湍流边界层得到.
|
| 图 1 凹腔实验模型 Fig.1 >Experiment cavity model |
|
| 图 2 计算网格 Fig.2 Computation grids |
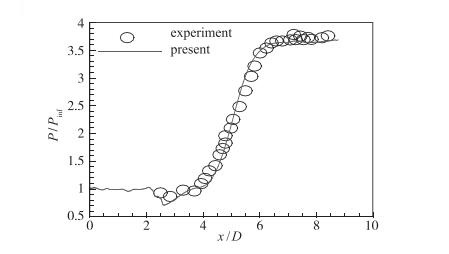
图 3为凹腔壁面上时均压力分布与实验数据的对比.可以看出, 计算结果与实验结果吻合较好.这说明本文计算方法可以较好地模拟凹腔流动, 并说明超声速凹腔流动具有很好的二维特性.
|
| 图 3 计算压力分布与实验结果的对比 Fig.3 Comparisons of pressure distributions between numerical calculation and experiment |
DMD方法只基于流动快照而不受模型限制, 通过提取流动中的模态, 从而准确地描述流动结构.对于线化流动而言, 被提取的模态可以用来表征全局稳定模态; 对于非线性流动而言, DMD的模态描述了在数据序列中起支配作用的流动结构, 以下为数学推导过程.
动态模态分解的数据来源于数值仿真或者物理实验, 可以快照序列的形式呈现, 序列由矩阵V1N表示.
| $\mathit{\boldsymbol{V}}_1^N = \left\{ {{\mathit{\boldsymbol{v}}_1},{\mathit{\boldsymbol{v}}_2},{\mathit{\boldsymbol{v}}_3}, \cdots ,{\mathit{\boldsymbol{v}}_N}} \right\}.$ |
其中,vi代表第i个流场,vi∈CM,CM为M维复向量空间.在上述定义中,下标1表示序列中的第1个元素,下标N表示进入序列中的最后1个元素,即矩阵V1N的第1列和最后1列.假设这个序列的时间间隔为常量Δt.
第1步, 假设线性映射A是快照v i到v i+1的映射, 即
| ${\mathit{\boldsymbol{v}}_{i = 1}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_i}.$ |
且在全部区域和整个时间段内的采样都满足上述映射关系.对于缓慢变化的系统, 乘法准则是上述假设的基础.
| $\begin{array}{l} \mathit{\boldsymbol{V}}_2^N = \left\{ {{\mathit{\boldsymbol{v}}_2},{\mathit{\boldsymbol{v}}_3},{\mathit{\boldsymbol{v}}_4}, \cdots ,{\mathit{\boldsymbol{v}}_N}} \right\}\\ = \left\{ {\mathit{A}{\mathit{\boldsymbol{v}}_1},\mathit{A}{\mathit{\boldsymbol{v}}_2},\mathit{A}{\mathit{\boldsymbol{v}}_3}, \cdots \mathit{A}{\mathit{\boldsymbol{v}}_{N - 1}}} \right\}\\ = A\mathit{\boldsymbol{V}}_1^{N - 1}. \end{array}$ |
系统矩阵A能够将时-空物理场沿时间维度平移Δt, 因此, A的特征值刻画了V1N的时间演化特性.然而, 实际应用中A是一个含有数据量极大的矩阵, 因此, 希望将A转化为一个小型矩阵, 用小型矩阵的特征值来估算A的特征值, 这样DMD方法才能应用于实际动力学问题.
对于秩为r的数据列V1N-1, A与其简化后的矩阵可以通过V 1N-1的POD模态联系起来,
| $\mathit{\boldsymbol{A}} \approx \mathit{\boldsymbol{UF}}{\mathit{\boldsymbol{U}}^*}.$ | (5) |
其中, F∈C r×r, U*为POD模态U的复共轭转置矩阵, U可以由V1N-1的奇异值分解得到, 即
| $\mathit{\boldsymbol{V}}_1^{N - 1} = \mathit{\boldsymbol{U \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{V}}^*}.$ | (6) |
其中, Σ为一个r×r的对角矩阵, 有非0的对角元素{σ1, …, σr}, 并且, U和V为酉矩阵.
| $\begin{array}{l} \mathit{\boldsymbol{U}} \in {\mathit{\boldsymbol{C}}^{M{\rm{xr}}}},{\rm{ 且}}{\mathit{\boldsymbol{U}}^*}\mathit{\boldsymbol{U}} = I.\\ \mathit{\boldsymbol{V}} \in {\mathit{\boldsymbol{C}}^{{\rm{rxN}}}},{\rm{ 且}}{\mathit{\boldsymbol{V}}^*}\mathit{\boldsymbol{V}} = I. \end{array}$ |
将式(5) 和式(6) 代入式(3) 中, 可得:
| $\mathit{\boldsymbol{F}}{\rm{ = }}{\mathit{\boldsymbol{U}}^{\rm{*}}}\mathit{\boldsymbol{V}}_{\rm{2}}^N\mathit{\boldsymbol{V}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{{\rm{ - 1}}}}.$ |
F即为A的最优低维估计矩阵, 由此, 通过求解F的特征值和特征向量即可得到DMD分析结果.
假设F是一个r维子空间内的精确映射矩阵, 而不是对A的估计, 那么,
| ${\mathit{\boldsymbol{x}}_{k + 1}}{\rm{ = }}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{x}}_k}.$ |
则A的POD模态U可以看作从x k到v k的近似映射, 则
| ${\mathit{\boldsymbol{v}}_k} \approx \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{x}}_k}.$ |
如果F的特征向量个数与秩相等且都线性独立, 那么F可以写做如下形式
| $\mathit{\boldsymbol{F}} = \left[ {{\mathit{\boldsymbol{y}}_1} \cdots {\mathit{\boldsymbol{y}}_r}} \right]\left[\begin{matrix} {{\mu }_{1}} & {} & {} \\ {} & \ddots & {} \\ {} & {} & {{\mu }_{r}} \\ \end{matrix} \right]\left[\begin{align} & \mathit{z}_{1}^{*} \\ & \vdots \\ & z_{r}^{*} \\ \end{align} \right].$ |
其中, yi为其特征向量, μi为其特征值, 每一个yi的模为一个单位长度, yi* yi=1, zi*是F*的特征向量, F*相应的特征值为μi, zi*和yi满足如下的条件:
| $\mathit{\boldsymbol{z}}_i^*{\mathit{\boldsymbol{y}}_j} = \left\{ \begin{array}{l} 1,i = j\\ 0,i \ne j \end{array} \right.$ |
则
| ${\mathit{\boldsymbol{x}}_k} = \mathit{\boldsymbol{YD}}_\mu ^K{\mathit{\boldsymbol{Z}}^*} = \sum\limits_{i = 1}^r {{\mathit{\boldsymbol{y}}_i}\mu _i^k\mathit{\boldsymbol{z}}_i^*{\mathit{\boldsymbol{x}}_0} = \sum\limits_{i = 1}^r {{\mathit{\boldsymbol{y}}_i}\mu _i^k{\alpha _i}} .} $ |
其中, αi= zi* x 0表示初始条件对第i个模态的影响程度, 所以, 可以利用DMD模态的线性组合来估计数据快照, 模态为Φi=Uyi, 则:
| ${\mathit{\boldsymbol{v}}_k} \approx \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{x}}_k} = \sum\limits_{i = 1}^r {{\mathit{\boldsymbol{\phi}} _i}\mu _i^k{\alpha _i}} .$ |
由此可得
| $\left[ {{\mathit{\boldsymbol{v}}_1},{\mathit{\boldsymbol{v}}_2}, \cdots ,{\mathit{\boldsymbol{v}}_{N - 1}}} \right] \approx \left[ {{\mathit{\boldsymbol{\phi}} _1},{\mathit{\boldsymbol{\phi}} _2}, \cdots {\mathit{\boldsymbol{\phi}} _r}} \right]\left[ {\begin{array}{*{20}{c}} {{\alpha _1}}&{}&{}&{}\\ {}&{{\alpha _2}}&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{{\alpha _r}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&{{\mu _1}}& \cdots &{\mu _1^{N - 1}}\\ 1&{{\mu _2}}& \cdots &{\mu _2^{N - 1}}\\ \vdots & \vdots & \ddots & \vdots \\ 1&{{\mu _r}}& \cdots &{\mu _r^{N - 1}} \end{array}} \right].$ |
动态模态分解获得的最重要的结果是模态φi和模态对应的特征值μi, log μi/Δt的实部为对应模态的放大率, 其虚部表示对应模态的频率.在进行稳定性判断时, 放大率为正, 则对应的模态发散; 放大率为负, 则对应的模态收敛; 若放大率为0, 则对应的模态为稳定极限环模态.同样也可以将μi置于复平面的单位圆上进行判断, 若在单位圆内, 则收敛; 单位圆外, 则发散; 单位圆上, 则为稳定周期性模态.
3 POD方法POD方法的核心思想是从一组时间序列的空间数据中寻找在均方意义上的最优正交基函数空间, 用较少正交基展开获得较高阶数据的近似描述, 具体推导过程如下.
选取N个瞬态速度场, 定义vi代表第i个速度场, 选取数据库中N个的时刻瞬态速度场V1N构成快照集合, 将快照写成平均值与脉动量的和.
| ${{\mathit{\boldsymbol{u}}}_{i}}={{\mathit{\boldsymbol{v}}}_{i}}-\frac{1}{N}\sum\limits_{i=1}^{N}{{{\mathit{\boldsymbol{v}}}_{i}}}.$ |
利用V1N构成一组时间序列的空间数据集合, 寻找一组最优正交基
| $F = \frac{1}{N}\sum\limits_{i = 1}^N {\left( {\left\| {{\mathit{\boldsymbol{u}}_i} - \mathit{\Phi }{\mathit{\boldsymbol{u}}_i}} \right\|} \right)} .$ |
这一问题等价于使得正交基函数满足最大值问题:
| $\mathop {\max }\limits_{\mathit{\boldsymbol{\varphi }} \in {L^2}\left( \mathit{\Omega } \right)} \left( {\left\langle {{{\left| {\left( {\mathit{\boldsymbol{u}},\mathit{\boldsymbol{\varphi }}} \right)} \right|}^2} > {{\left\| \mathit{\boldsymbol{\varphi }} \right\|}^2}} \right\rangle } \right).$ |
其中:L2(Ω)为定义在空间区域Ω上的L2函数空间; (·, ·)表示该函数空间上的内积; ‖φ‖2=(φ, φ)1/2; 〈·〉表示算术平均运算.
利用变分法, 该最大值问题可转化为特征值问题:
| $\int {_\mathit{\Omega }} C\left( {x,y} \right)\mathit{\boldsymbol{\varphi }}\left( \mathit{y} \right){\rm{d}}\mathit{\Omega } = \lambda \mathit{\boldsymbol{\varphi }}\left( x \right).$ | (7) |
其中, C(x, y)=〈 u (x, t)⊗u(y, t)〉为u的自相关函数, 也称为POD的核; (φ i, φ j)=δij, 求解此特征值问题可以得到相应的特征向量, 即为POD模态.
由于实际应用中快照都是在离散空间点上的实验数据或数值模拟结果, 这时的自相关函数可以表示为
| $C\left( x, y \right)=\frac{1}{N}\sum\limits_{i=1}^{N}{\mathit{\boldsymbol{u}}}\left( x, {{t}_{i}} \right){{\mathit{\boldsymbol{u}}}^{\rm{T}}}\left( y, {{t}_{i}} \right).$ |
对于计算流体力学问题, 快照包含的空间点数M远大于所选取的快照数N.如果直接求解特征值问题, 则待求解的矩阵阶数为M×M, 将使求解过程变得困难, 且造成较大的误差.为了解决这一问题, Sirovich [18]提出了快照技术, 该技术使得在流体动力系统中更高效快捷地提取POD模态成为可能.该方法的主要思想是利用原函数空间元素与特征值问题中的特征模态处在同一线性空间中, 从而可以利用原有函数空间快照的线性组合来表示特征模态, 即
| $\mathit{\boldsymbol{\varphi }}{_i} = \sum\limits_{k = 1}^N {A_i^k} {\mathit{\boldsymbol{u}}_k}.$ | (8) |
将式(8) 代入式(7) 中, 得到RA =λA.其中, Ai为对应特征值λi的特征函数.
| ${{R}_{ij}}=\frac{1}{N}\left( {{\mathit{\boldsymbol{u}}}_{i}}, {{\mathit{\boldsymbol{u}}}_{j}} \right)\left( i, j=1, 2, 3, \cdots, \mathit{N} \right).$ |
这样, 所需求解的特征值问题只有N阶, 远小于空间点, M的量级, 即可通过求解相关矩阵, R的特征值和特征向量得到POD模态.
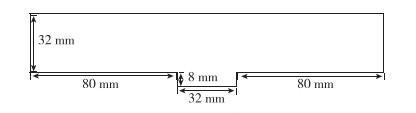
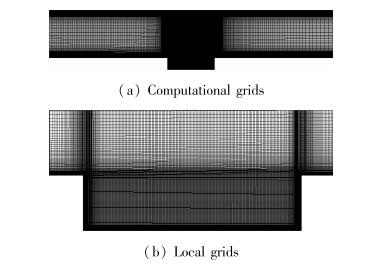
4 计算结果及分析 4.1 计算模型本文设计的超燃冲压发动机凹腔模型如图 4所示, 长深比L/D=4, 后缘角为90°, 该模型尺寸参考了文献[16].计算网格如图 5所示, 对凹腔区域的网格进行加密, 网格单元总数为101502, 物面第1层网格的高度为1×10-6m, 壁面y+小于1.采用LES方法进行数值模拟时, 为了降低计算量, 仅将二维网格沿展向拉伸1层.进口来流条件为:M=2.0, T0=1476K, P0=7.928MPa.非定常计算中的时间步长为Δt=1×10-6s.所有壁面均采用无滑移绝热边界条件.
|
| 图 4 凹腔模型 Fig.4 Cavity model |
|
| 图 5 计算网格 Fig.5 Computational grids |
目前, 对凹腔流场振荡机制的认识存在两种观点.一种观点认为, 振荡是自持的.腔体内外流体的剪切诱导Kelvin-Helmholtz不稳定性, 产生涡卷起; 涡卷起后向下游运动, 进而与后拐角撞击压缩产生往前传的声波; 声波到达方腔前端会再次激发剪切层失稳, 使新涡卷起, 完成自持振荡过程.所以, 在无任何外部持续激励时, 方腔流动仍会持续地振荡.此时方腔流动的动力学系统可认为是一个关于不稳定平衡点(Navier-Stokes方程定常解)的稳定的极限环, 振荡的幅值取决于非线性效应, 如剪切层失稳中扰动增长达到饱和.还有一种观点认为, 方腔流动是稳定的轻微衰减的系统, 只有在外界持续激励下(如边界层内湍流脉动, 壁面粗糙引起扰动等)才能维持振荡[5, 9], 撤除激励, 振荡现象也将消失.本文支持第1种观点.
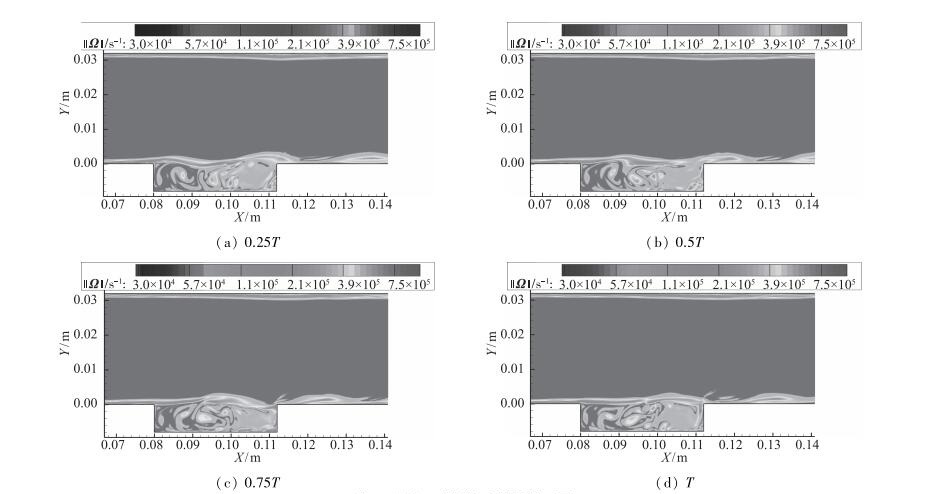
图 6和图 7分别为凹腔一个周期内的涡量云图和密度梯度云图, 由图可以看出剪切层失稳的发展过程.由图可见, 凹腔剪切层的发展大致可以分为3个阶段:第1个阶段表现为Kelvin-Helmholtz不稳定波发展, 对应图中的0.25T时刻, 主要集中在凹腔的前半段, 高速主流与低速回流形成的剪切层中只有涡量而没有形成漩涡, 上游来流及凹腔内前传压缩波在前缘形成的扰动进入凹腔剪切层后, 以不稳定波的形式发展, 不稳定波的作用使扰动在剪切层中得到选择性放大, 最大模态成为优势模态, 同时使原来相对均匀的涡量分布变得相对集中.
|
| 图 6 凹腔一个周期内的涡量云图 Fig.6 Vorticity contours of cavity in one period |

|
| 图 7 凹腔一个周期内的密度梯度云图 Fig.7 Density gradient contours of cavity in one period |
第2个阶段为非线性失稳区, 主要集中在凹腔的后半段, 对应图中的0.5T时刻, 由于剪切层增厚, 相应Reynolds数增加, 第1阶段形成的展向涡结构的周期性流动又处于不稳定条件, 并再次失稳而发生涡的配对与合并; 在这个阶段, 涡尺度和波长均成倍增加, 剪切层厚度增加非常快.
第3个阶段对应图中0.75T和1T时刻, 发展到后壁附近的剪切层下潜并撞击凹腔后壁, 大尺度拟序结构破碎, 涡量重新分布, 一部分流向下游, 一部分进入凹腔, 同时向凹腔内注入质量并产生撞击激波和前传压缩波.
4.3 压力脉动的FFT分析很多学者已对凹腔的自激振荡做了大量的研究工作, 并提出了一些解释其振荡机理的物理模型. Rossiter [7]提出的涡运流声反馈模型是比较成功且应用较广的一种, 该模型认为凹腔剪切层由凹腔前缘脱落的一系列涡组成并以一定的速度向下游运动, 涡与腔后壁碰撞, 产生压缩波并以声速向上游传播, 当这一压缩波运动到前壁面时, 在前缘处会诱导出新的涡脱落, 特别是当流场涡与反馈声波组成的反馈回路满足一定的相位关系时, 流动将出现自激振荡.由此, Rossiter提出的凹腔流动振荡频率方程为
| $S{{t}_{n}}=\frac{{{f}_{n}}L}{{{U}_{\infty }}}=\frac{n-\alpha }{{{M}_{\infty }}+1/{{\mathit{K}}_{\upsilon }}}, n=1, 2, 3\cdots .$ |
其中, Stn和, fn分别为振荡的第n阶Strouhal数和频率, L为凹腔长度, U∞和, M∞分别为来流速度和Mach数, n为模态阶数, α和, Kv是由实验确定的常数, 一般对浅凹腔(L/D≥2), α=0.25, Kv=0.57. Heller等[28]基于Rossiter的涡运动流声反馈模型, 提出向上游的扰动声波传播速度应当是凹腔内的当地声速, 并由此得到修正的Rossiter公式:
| $S{{t}_{n}}=\frac{{{f}_{n}}L}{{{U}_{\infty }}}=\frac{n-\alpha }{{{M}_{\infty }}/\sqrt{1=\left[\left( {{\rm{ }\!\!\gamma\!\!\rm{ }}_{\infty }}-1 \right)/2 \right]M_{\infty }^{2}}=1/{{K}_{\upsilon }}}.$ |
其中, n=1, 2, …, γ∞为气体的比热比.
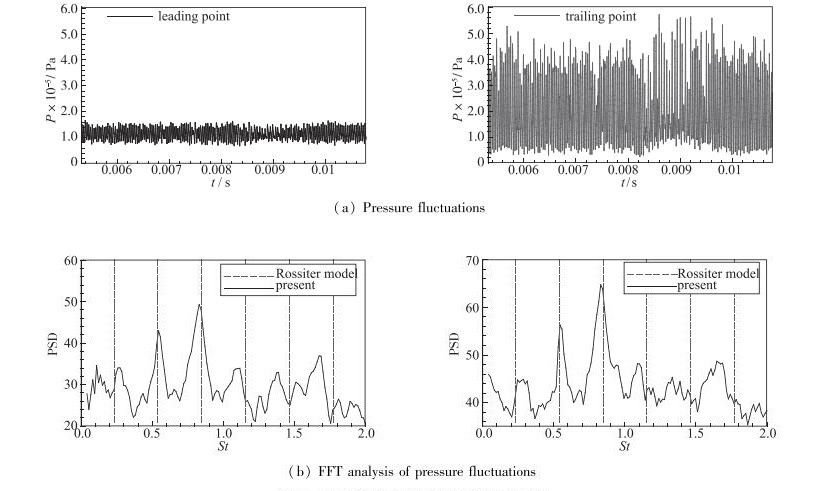
采用LES方法对凹腔进行数值模拟时, 对凹腔前缘点和后缘点处的压力进行监测, 图 8为压力脉动随时间的变化曲线及FFT分析结果.可以看出, 后缘点处的压力脉动的幅值较大, 两处的FFT分析的频率比较一致, 相同主频率下, 后缘点处功率谱密度较高, 其前3阶主频与Rossiter模型预测的前3阶频率非常接近, 按功率谱密度幅值对前3阶主频进行排序, 由大到小的顺序为模态3, 模态2, 模态1.因此, 在本文流动条件下, 流动中RossiterⅢ模态占据主导地位.这与文献[29]中, 0.3 < M < 0.6, 流动中RossiterⅠ模态占据主导作用, 以及文献[27]中, 当M进一步增加到0.8时, 流动中RossiterⅡ模态占据主导作用的结果有所不同.
|
| 图 8 压力脉动随时间变化及其FFT分析 Fig.8 >Comparisons of FFT results of pressure and Rossiter model |
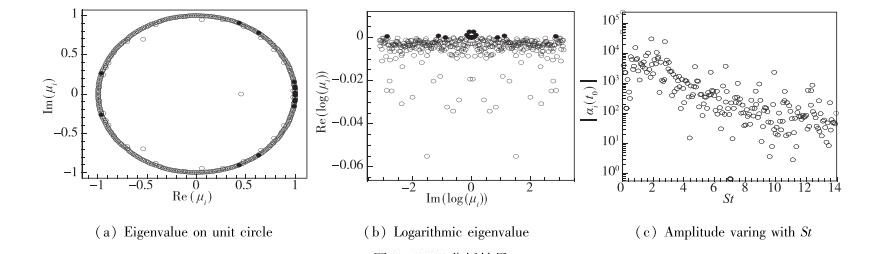
提取非定常计算中400个连续的瞬态流场, 并采用DMD方法对速度场进行分析. 图 9为DMD方法得到的特征值和特征值取对数后的分布以及系数幅值随St数的变化.其中实心点对应的模态为不稳定模态, 可以看出, 绝大部分的模态为稳定模态, 且其对应的特征值比较靠近单位圆, 因此, 大部分模态基本表现为稳定极限环模态.不稳定模态和收敛模态都较少.其中DMD方法提取得到的St数的范围为0~14, 为Rossiter Ⅰ模态对应St数的0~60倍.且其中最小非0的St数为6.7935×10-2, 为Rossiter Ⅰ模态对应频率的29.4%, 这说明在对自激振荡的低频提取上, DMD方法比Rossiter模型更具有优势.
|
| 图 9 DMD分析结果 Fig.9 Analysis results of DMD |
表 1为Rossiter模型压力脉动FFT分析以及DMD方法得到的St对比.对于前3阶模态的St数而言, 3种方法的结果均较接近, 对于后3阶模态而言, 压力脉动FFT分析结果与另外两种方法的结果均相差很大, Rossiter模型与DMD方法的结果依然比较接近, 这说明, 相比于压力脉动的FFT分析, DMD方法在对凹腔自激振荡中的流动结构高阶频率的提取上具有优势, 同时也说明, Rossiter提出的涡运流声反馈模型的合理性.
| 下载CSV 表 1 Rossiter模型, 压力脉动FFT分析以及DMD方法得到的St对比 Tab.1 Comparisons of St among Rossiter model, pressure FFT analysis and DMD method |
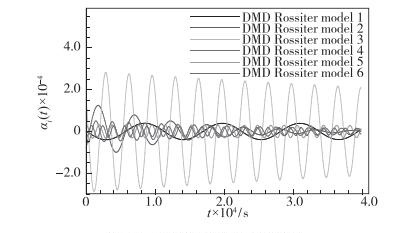
图 10为前6阶模态系数随时间的变化, 可以看出, 所有模态系数均表现为缓慢地趋于收敛, 这与表 1中模态放大率为负相对应.系数幅值的大小反应了该模态对流动贡献的大小, 即该模态在流动中的重要程度, 按系数的最大幅值对模态进行排序, 由大到小的顺序为模态3, 模态2, 模态1, 模态4, 模态5, 模态6, 其中前3阶的顺序与压力脉动FFT分析的按功率谱密度排序的结果一致.
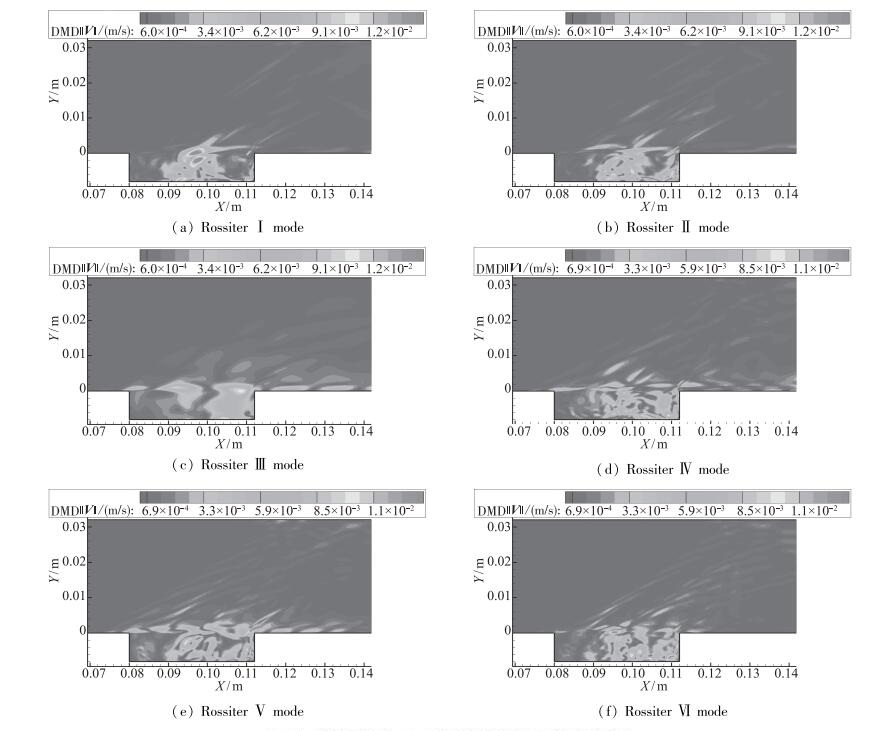
DMD方法不仅可以提取与Rossiter模型对应的频率, 且可提取到该频率对应的流动结构.图 11为与Rossiter前6阶频率对应的DMD模态速度云图.可以看出, 其中1阶2阶4阶6阶模态主要表现为模态的凹腔中部剪切层与分离涡之间相互作用, 3阶和5阶模态主要表现为剪切层中的分离涡结构和后缘下游区域的涡结构, 以及剪切层与凹腔后缘的撞击.
|
| 图 10 模态系数随时间的变化 Fig.10 DMD mode amplitudes varying with times |
|
| 图 11 与前6阶Rossiter模态对应的DMD模态速度云图 Fig.11 Velocity contours of the DMD modes corresponding to the first six Rossiter modes |
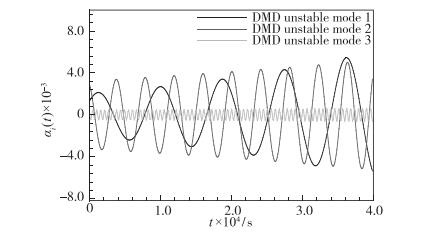
基于放大率对DMD模态进行排序, 提取前3阶不稳定模态, 表 2为此3阶模态对应的St数和放大率.其中1阶不稳定模态的St数处于RossiterⅠ与RossiterⅡ之间, 2阶不稳定模态的St数处于RossiterⅡ与RossiterⅢ之间, 3阶不稳定模态的St数比较大, 所有模态的放大率均较小. 图 12和图 13为此3阶模态对应的模态系数随时间的变化以及速度云图.可以看出, 所有模态系数均缓慢地趋于发散. 1阶不稳定模态中的涡结构主要集中在中部剪切层和凹腔中, 2阶不稳定模态中的涡结构主要集中在中部剪切层以及凹腔后壁面附近的区域, 且涡尺度变小. 3阶不稳定模态中的涡结构主要集中在凹腔后缘, 以及底部下游区域, 涡尺度进一步变小.
| 下载CSV 表 2 DMD不稳定模态对应的St及放大率 Tab.2 Unstable modes correspond St and growth rates |
|
| 图 12 模态幅值随时间的变化 Fig.12 DMD mode amplitude varying with time |

|
| 图 13 DMD中前3阶不稳定模态 Fig.13 First three order unstable DMD modes |
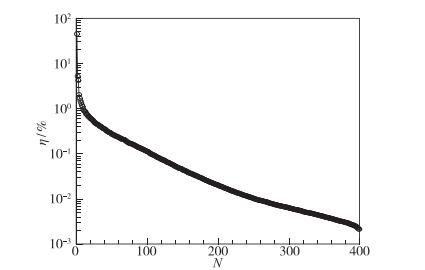
进一步采用POD方法对以上400个连续的瞬态流场进行分析, 图 14为POD模态能量比的分布, 模态能量比按下式计算:
| $\eta = \mathit{\lambda }{_i}/\sum\limits_{k = {\rm{1}}}^N {\mathit{\lambda }{_k}} .$ |
其中λi为第i阶模态对应的特征值.可以看出能量比衰减得较快, 按能量比的大小对模态进行排序, 提取前6阶模态进行分析.
|
| 图 14 POD模态能量比的分布 Fig.14 Distributions of POD mode energy rates |
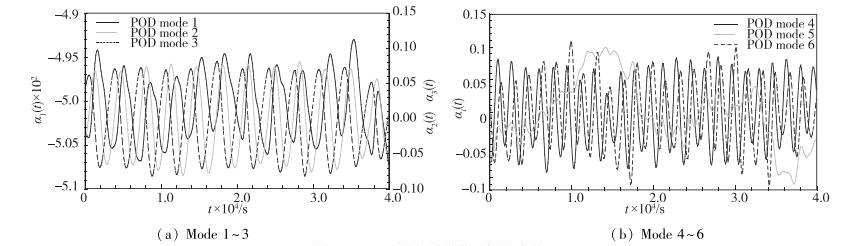
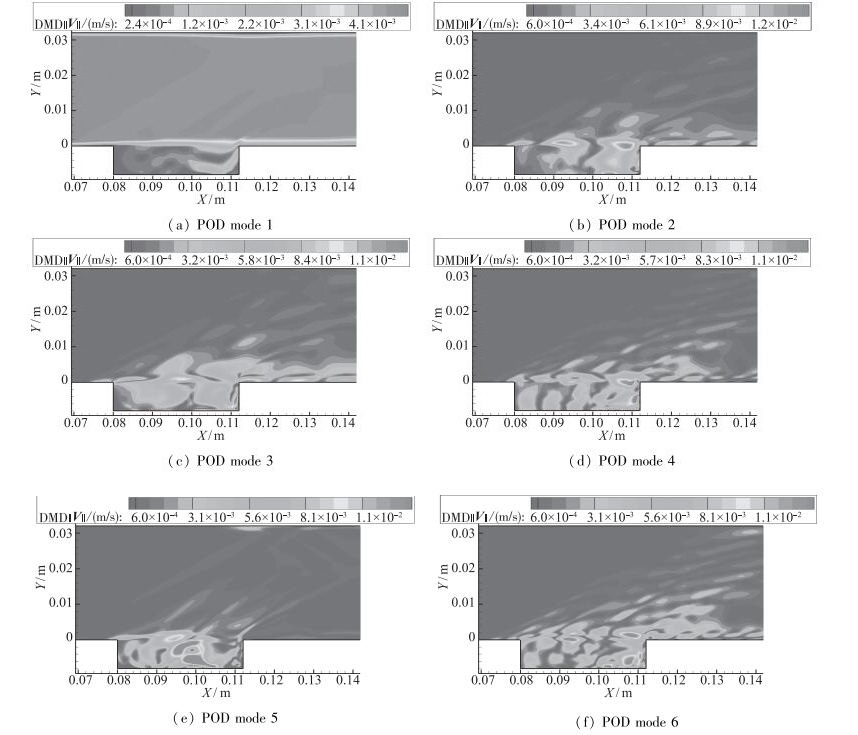
图 15为前6阶POD模态系数随时间的变化.表 3为模态系数进行FFT分析的结果.表中2阶模态至6阶模态中存在两个频率, 其中main表示主频, second表示次频. 图 16为前6阶POD模态对应的速度云图.可以看出, 相比于其他模态系数, 1阶模态系数较小, 且变化范围也较小, 其频率与Rossiter Ⅲ模态的频率较为接近, 该模态对应为瞬态流动中的时均流场. 2阶模态和3阶模态系数的主频也与Rossiter Ⅲ模态的频率较为接近, 但同时包含一个频率为其2倍的次频.其对应的速度云图与DMD提取的Rossiter Ⅲ模态较为类似, 但又有所不同, 说明POD 2阶模态和3阶模态中存在高频和低频耦合的现象.4阶5阶和6阶模态的系数的主频与Rossiter Ⅵ模态的频率较为接近, 但包含的次频不一样, 其中4阶模态对应的次频为3.2835, 5阶和6阶模态对应的次频为2.515.三者对应的速度云图也差别较大, 其中4阶和6阶模态主要反映的是剪切层和凹腔后缘处的涡结构, 5阶模态主要反映的是凹腔中部区域处的涡结构.这说明对于这3阶模态, 次频对模态的影响较大.
对于本文的凹腔流动, POD方法可以高效地提取流场的主要结构, 较少的POD模态占据了流场的主要能量.但是, 与Rossiter模型预测的频率相比, 通过POD方法提取的模态频率在分辨率上效果不佳, 提取到最低频率为Rossiter 3阶模态对应的频率, 而DMD方法提取的最低模态频率为RossiterⅠ模态对应频率的29.4%, 分辨率约为POD方法的10倍.同时, 除1阶模态以外, 其余5阶模态中均存在次频, 次频与主频之间的耦合导致模态的形态相差较大.且与DMD方法相比, POD方法无法判断所提取模态的稳定性.
|
| 图 15 POD模态系数随时间的变化 Fig.15 mode amplitudes varying with times |
|
| 图 16 POD中前6阶模态 Fig.16 First six order POD modes |
| 下载CSV 表 3 POD模态系数FFT分析的St Tab.3 FFT of the selected POD modes amplitude |
基于大涡模拟方法对超燃冲压发动机开式凹腔超声速内流进行数值模拟, 并采用DMD和POD方法对凹腔自激振荡流动进行稳定性分析.对于本文计算模型及状态, 得到以下结论:
(1) DMD方法可准确提取凹腔的振荡频率, 与Rossiter模型以及压力脉动FFT分析得到的频率吻合较好, 且DMD中对应Rossiter前3阶频率的模态在流动中的主导作用顺序也与FFT分析结果一致, 其中RossiterⅢ模态占据主导作用.同时DMD方法对Rossiter 3阶以上模态频率的预测能力明显强于FFT分析方法.在对低频的提取上, DMD方法比Rossiter模型更具有优势.
(2) 与前6阶Rossiter模态频率对应DMD模态的稳定性均表现为弱收敛, 其中1阶2阶4阶6阶模态主要表现为凹腔中部剪切层与分离涡之间相互作用, 3阶和5阶模态主要表现为剪切层中的分离涡结构和后缘下游区域的涡结构, 以及剪切层与凹腔后缘的撞击.
(3) 凹腔中不稳定的DMD模态均表现为弱发散趋势, 按放大率对模态进行排序, 前3阶模态中的流动结构主要集中在中部剪切层以及凹腔后壁面附近的区域.
(4) POD方法可以高效地提取流场的主要结构, 较少的POD模态就占据了流场的主要能量.但是, 通过POD方法提取的模态频率在分辨率上效果不佳, 提取到最低频率为Rossiter 3阶模态对应的频率, 且模态中均存在次频, 次频与主频之间的耦合导致模态的形态相差较大.另外, 与DMD方法相比POD方法无法判断所提取的模态的稳定性.
通过DMD和POD方法对凹腔流动稳定性的分析, 有利于进一步理解凹腔自激振荡的机理, 对凹腔中的流动控制也具有一定的参考价值.进一步的工作中将采用LES方法对三维凹腔流动进行模拟, 得到更加细致流动细节, 并进行稳定性分析.
| [1] |
Roudakov A S, Schikhmann Y, Semenov V, et al. Flight testing of an axisymmetric scramjet—Russian recent advances[A]. //44th Congress of the International Astronautical Federation[C]. Graz, 1993. https://ar.scribd.com/document/212770403/NASA-SCRAMJET-DEVLPMNT-pdf
|
| [2] |
Rodriguez C G. CFD analysis of the CIAM/NASA scramjet[R]. AIAA 2002-4128, 2002. https://hapb-www.larc.nasa.gov/Public/Engines/Ciam/Ciam.html
|
| [3] |
贾真. 超声速燃烧室中壁面凹腔结构的稳焰机理[J]. 航空动力学报, 2013, 28(6): 1392-1401. Jia Z. Flame-holding mechanism of cavity structure in supersonic combustor[J]. Journal of Aerospace Power, 2013, 28(6): 1392-1401. (in Chinese) |
| [4] |
Stalling R L, Wilcox F J. Experimental cavity pressure distributions at supersonic speeds[R]. NASA TP-2683, 1987. http://journals.sagepub.com/doi/abs/10.1243/09544100JAERO445
|
| [5] |
Rowley C W, Williams D R. Dynamics and control of high Reynolds number flow over open cavities[J]. Annual Review Fluid Mechanics, 2006, 38: 251-276. DOI:10.1146/annurev.fluid.38.050304.092057 |
| [6] |
Krishnamutry K. Sound radiation from surface cutouts in high speed flow[D]. Pasadena : California Institute of Technology, 1956. https://ar.scribd.com/doc/54302427/02-05-Architectural-Record
|
| [7] |
Rossiter J E. Wind-tunnel expriments on the flow over rectangular cavities at subsonic and transonic speed[R]. Aeronautical Research Council Reports and Memoranda, Technical Reports 3438, 1964.
|
| [8] |
Rowley C W, Colonlus T, Basu A J. On self-sustained oscillations in two-dimensional compressible flow over rectangular cavities[J]. Journal of Fluid Mechanics, 2002, 445: 315-346. |
| [9] |
Rowley C W, Williams D R, Colonius T, et al. Linear model for control of cavity flow oscillation[J]. Journal of Fluid Mechanics, 2006, 547: 317-330. DOI:10.1017/S0022112005007299 |
| [10] |
Shieh C M. Parallel numerical simulations of subsonic, turbulent, flow-induced noise from two and three dimensional cavities[D]. Pennsylvania : Pennsylvania State University, 2000. https://www.researchgate.net/profile/Chingwei_Shieh/publications
|
| [11] |
Hassan E, Peterson D M, Walters K, et al. Dynamic hybrid RANS/LES computations of a supersonic cavity[R]. AIAA 2016-1118, 2016. http://www.sciencedirect.com/science/article/pii/S0142727X17301583
|
| [12] |
Li W P, Nonomura T, Oyama A, at al. LES study of feedback-loop mechanism of supersonic open cavity flows[R]. AIAA 2010-5112, 2010. https://www.researchgate.net/publication/276854195_RIT_by_Cavity
|
| [13] |
Gruber M R, Baurle R A. Fundamental studies of cavity based name holder concepts for supersonic combustors[J]. Journal of Propulsion Power, 2001, 17(1): 146-153. DOI:10.2514/2.5720 |
| [14] |
Settles G S, Williams D R. Reattachment of a compressible turbulent free shear layer[J]. AIAA Journal, 1982, 20(1): 60-67. DOI:10.2514/3.51047 |
| [15] |
王振国, 杨揖心, 梁剑寒, 等. 超声速气流中稳焰凹腔吹熄极限分析与建模[J]. 中国科学:技术科学, 2014, 44: 961-972. Wang Z G, Yang Y X, Liang J H, et al. Analysis and modeling of blowout limits of cavity flame in supersonic flows[J]. Scientia Sinica : Technologica, 2014, 44(9): 961-972. (in Chinese) |
| [16] |
Sun M B, Liang J H, Wang Z G. Study on self-sustained oscillation characteristics of cavity flameholders for scramjet application[R]. AIAA 2007-3401, 2007. http://www.sciencedirect.com/science/article/pii/S0360319917300058
|
| [17] |
Lumley J L. The structure of inhomogeneous turbulence flows[J]. Atmospheric Turbulence and Radio Wave Propagation, 1967, 166-176. |
| [18] |
Sirovich L. Turbulent and the dynamics of coherent structures. Parts I :coherent structures[J]. Quarterly of Applied Mathematics, 1987, 45(3): 561-571. DOI:10.1090/qam/1987-45-03 |
| [19] |
Ma X, Karniadakis G. A low-dimensional model for simulating three-dimensional cylinder flow[J]. Journal of Fluid Mechanics, 2002, 458: 181-190. |
| [20] |
Aubry N, Holmes P, Lumley J L, et al. The dynamics of coherent structures in the wall region of a turbulent boundary layer[J]. Journal of Fluid Mechanics, 1988, 192: 115-173. DOI:10.1017/S0022112088001818 |
| [21] |
何江, 符松. 竖直平板间自然对流大尺度相干结构的POD分析[J]. 力学学报, 2003, 35(4): 385-392. He J, Fu S. POD analysis of large-scale coherent structures in natural convection between two vertical plates[J]. Acta Mechanica Sinica, 2003, 35(4): 385-392. (in Chinese) |
| [22] |
Schmid P J. Dynamic mode decomposition of numerical and experimental data[J]. Journal of Fluid Mechanical, 2010, 656: 5-28. DOI:10.1017/S0022112010001217 |
| [23] |
Rowley C W, Mezic I, Bagheri S, et al. Spectral analysis of nonlinear flows[J]. Journal of Fluid Mechanical, 2009, 641(12): 115-127. |
| [24] |
Roy S, Hua J C, Barnhill W, et al. Deconvolution of reacting-flow dynamics using proper orthogonal and dynamic mode decompositions[J]. Physical Review E, 2015, 91. |
| [25] |
潘翀, 陈皇, 王晋军. 复杂流场的动力学模态分解[A]. //第八届全国实验流体力学会议[C]. 广州, 2010, 77-82. Pan C, Chen H, Wang J J. Dynamic mode decomposition of complex flow field[A]. //Eighth Annual Meeting of Experiment Fluid Dynamics[C]. Gaung Zhou, 2010 : 77-82(in Chinese). |
| [26] |
Seena A, Sung H J. Dynamic mode decomposition of turbulent cavity flows for self-sustained oscillations[J]. International Journal of Heat and Fluid Flow, 2011, 32: 1098-1110. DOI:10.1016/j.ijheatfluidflow.2011.09.008 |
| [27] |
Sun Y Y, Nair A G, Taira K, et al. Numerical simulations of subsonic and transonic open cavity flows[R]. AIAA 2014-3092, 2014. https://link.springer.com/article/10.1007/s00162-016-0412-y
|
| [28] |
Heller H H, Bliss D B. The physical mechanism of now induced pressure fluctuations in cavities and concepts for their suppression[R]. AIAA 1975-0491, 1975. http://www.academia.edu/13969921/Large-eddy_simulation_of_a_compressible_flow_in_a_three-dimensional_open_cavity_at_high_Reynolds_number
|
| [29] |
Brès G A. Numerical simulations of three-dimensional instabilities in cavity flows[D]. Pasadena : California Institute of Technology, 2007.
|



