在传统武器上配备有大杀伤半径和纵深比打击能力的战斗部是今后武器的发展方向之一, 而子母弹对不同的运载器具有高度的适配能力, 能够同时打击地面多个目标.同时无控子母弹分离后无需制导使其制造成本较低, 具有极低的费效比, 在现代战略武器的应用日益广泛.对于超声速飞行的子母弹, 子弹在抛撒时历经二次发射, 需要穿过母弹附近的剪切层和激波后, 才能进入均匀的流场.由于在这一区域内存在强烈的涡流和弹体间复杂的气动力干扰, 因而子弹在分离初期飞行极不稳定, 极有可能发生弹体间碰撞或分离偏离设计轨道的问题, 因此准确预测子母弹的分离轨迹是仿真工作的关键所在.
国外对于多体分离的研究工作起步较早, 并进行了一系列的风洞实验. Panneerselvam等[1]和Holden等[2]对子母弹分离时的气动干扰现象开展了研究, 并进行了风洞实验; Cavallo等[3]基于有限体积法, 使用自适应动网格方法, 对多体分离过程进行了数值模拟; Rizk等[4]编写了嵌套网格程序, 对多体分离过程进行数值模拟, 取得了较好的计算结果; Bhange等[5]耦合了六自由度刚体运动学方程对穿甲弹的脱壳过程进行了数值模拟, 精确地捕捉了流场细节, 此外又提出了优化设计等相关准则; Harris等[6]使用OVERFLOW-2程序在耦合了CFD与六自由度刚体运动学方程的基础上加入了碰撞预测模型, 能够对大批量子弹分离过程进行仿真.
在国内三维非定常N-S方程和刚体运动方程耦合计算已经广泛地应用于工程实践[7-9]; 曾铮等[10]以径向基函数(radical basis function, RBF)网格变形技术为基础, 通过引入一种改进的Laplace光顺算法, 对多体分离轨迹进行了数值模拟.雷娟棉等[11]对俄9M55K型火箭弹子母战斗部的第一次抛撒进行了数值模拟, 并指出母弹头部产生的激波反射是对子弹产生气动干扰的主要原因; 张玉东等[12]采用网格变形的结构动网格技术, 数值模拟子弹穿越母弹激波的过程; 陶如意等[13]采用了风洞试验与数值模拟相结合的方法对子母弹分离进行研究.
综合国内外的研究来看, 大多数研究者对于子母弹分离进行数值模拟时都将母弹设置为静止固壁边界条件, 锁定母弹的自由度, 忽略了母弹运动时激波位置变化对子弹气动力的干扰.本文选取多舱段子母弹为计算模型, 子弹采取横向抛撒方式, 数值模拟了锁定母弹自由度和同时释放母弹自由度两种计算状态.
1 数值方法 1.1 非定常N-S方程求解为了考虑固壁边界的六自由度运动, 流动控制方程采用任意Lagrange-Euler方法(arbitrary Lagrangian Eulerian,ALE)方法描述的N-S方程. ALE方法允许计算网格的刚体运动和任意变形, 通过在流动方程中加入网格运动速度, 将流体力学中的Lagrange方法和Euler方法进行统一描述.采用ALE方法描述的三维非定常Reynolds平均Navier-Stokes方程的积分形式为:
| $ \frac{\partial }{\partial t}\iiint_{\mathit{\boldsymbol{ }}{\mathit{\Omega}}\text{ }}{{{{\mathit{\boldsymbol{Q}}}}_{\text{d}}}V}+\iint_{\partial {\mathit{\Omega}} }{F({\mathit{\boldsymbol{Q}}})}\cdot {\mathit{\boldsymbol{n}}}\text{d}S=\iint_{\partial {\mathit{\Omega}} }{G({\mathit{\boldsymbol{Q}}})}\cdot {\mathit{\boldsymbol{n}}}\text{d}S $ | (1) |
在式(1)中,Ω为控制体, ∂Ω表示控制体单元边界, Q为守恒变量, Q=[ρ ρu ρv ρω ρE]T, ρ为流体密度, u, v, w分别为旋转弹在体轴系下3个轴向的运动速度, E为总内能; vgrid为网格运动速度, n为控制体单元边界外法线方向分量, F(Q)和G(Q)分别表示N-S方程的无黏通量项和有黏通量项.方程(1)经过格心有限体积法空间离散后, 可以得到在网格单元i上的半离散形式:
| $ \frac{\text{d}{{{\mathit{\boldsymbol{Q}}}}_{i}}}{\text{d}t}+{{R}_{i}}({\mathit{\boldsymbol{Q}}}_{i}^{n+1})=0 $ | (2) |
| $ {{R}_{i}}({\mathit{\boldsymbol{Q}}}_{i}^{n+1})=\frac{1}{{\mathit{\Omega}} }[F({\mathit{\boldsymbol{Q}}}_{i}^{n+1}, {{v}_{grid}})-G({\mathit{\boldsymbol{Q}}}_{i}^{n+1})]\cdot {{n}_{i}}{{S}_{i}} $ | (3) |
其中, R为残差, S为网格单元面积, n为时间步.为了获得高阶时间精度, 使用2阶隐式双时间方法求解方程(2)[14]
| $ \frac{3{\mathit{\boldsymbol{Q}}}_{i}^{n+1}-4{\mathit{\boldsymbol{Q}}}_{i}^{n}+{\mathit{\boldsymbol{Q}}}_{i}^{n-1}}{2\Delta t}+{{R}_{i}}({\mathit{\boldsymbol{Q}}}_{i}^{n+1})=0 $ | (4) |
在式(4)中Δt代表时间步长, 上标n代表真实时间迭代的步数.方程(4)为隐式表达式, 直接求解较为复杂, 一般采用伪时间迭代的方法对方程进行求解, 为此我们在方程左端加入一个守恒变量对虚拟时间τ的导数, 方程的解可以等价为一个关于τ的1阶常微分方程组在τ趋近无穷时的渐进解:
| $ \frac{\text{d}{\mathit{\boldsymbol{Q}}}_{i}^{n+1}}{\text{d}\tau }+R_{i}^{*}({\mathit{\boldsymbol{Q}}}_{i}^{n+1})=0 $ | (5) |
| $ R_{i}^{*}({\mathit{\boldsymbol{Q}}}_{i}^{n+1})=\frac{3{\mathit{\boldsymbol{Q}}}_{i}^{n+1}-4{\mathit{\boldsymbol{Q}}}_{i}^{n}+{\mathit{\boldsymbol{Q}}}_{i}^{n-1}}{2\Delta t}+{{R}_{i}}({\mathit{\boldsymbol{Q}}}_{i}^{n+1}) $ | (6) |
式中
在多体分离问题中, 子母弹作为刚体在空中运动一般有6个自由度, 对应6个动力学方程, 其中3个描述平动, 3个描述转动.此外还有6个动力学方程对应物体的空间位置和姿态[18-19]. Euler角示意图见图 1, 图中x指向地平面某任意选定的方向, z轴铅垂向下, y轴垂直于zx平面(按右手定则确定方向), 其中φ为滚转角, θ为俯仰角, ψ为偏航角.
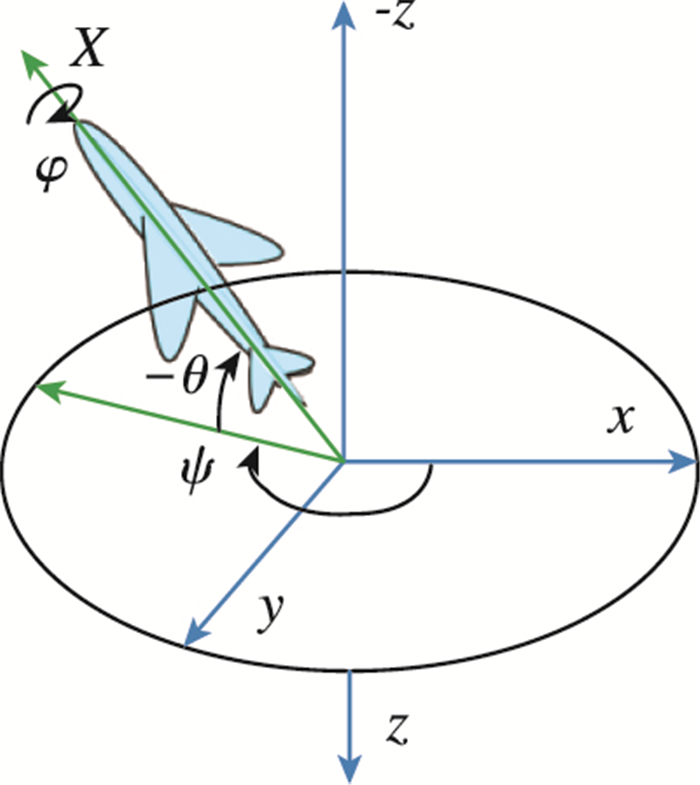
|
| 图 1 Euler角示意图 Fig.1 Schematic diagram of the Euler angle |
惯性系下质心的平动方程:
| $ \begin{align} &m{{{\dot{V}}}_{x}}=F_{x\text{a}}^{\text{i}}+F_{x\text{e}}^{\text{i}}+F_{x\text{g}}^{\text{i}} \\ &m{{{\dot{V}}}_{y}}=F_{\text{ya}}^{\text{i}}+F_{\text{ye}}^{\text{i}}+F_{\text{yg}}^{\text{i}} \\ &m{{{\dot{V}}}_{z}}=F_{z\text{a}}^{\text{i}}+F_{z\text{e}}^{\text{i}}+F_{z\text{g}}^{\text{i}} \\ \end{align} $ | (7) |
体轴系下绕质心的转动方程:
| $ \begin{align} &\dot{\omega }_{x}^{\text{b}}=[M_{x}^{\text{b}}+(I_{yy}^{\text{b}}-I_{zz}^{\text{b}})\omega _{y}^{\text{b}}\omega _{z}^{\text{b}}]/I_{xx}^{\text{b}} \\ &\dot{\omega }_{y}^{\text{b}}=[M_{y}^{\text{b}}+(I_{zz}^{\text{b}}-I_{xx}^{\text{b}})\omega _{z}^{\text{b}}\omega _{x}^{\text{b}}]/I_{yy}^{\text{b}} \\ &\dot{\omega }_{z}^{\text{b}}=[M_{z}^{\text{b}}+(I_{xx}^{\text{b}}-I_{yy}^{\text{b}})\omega _{x}^{\text{b}}\omega _{y}^{\text{b}}]/I_{zz}^{\text{b}} \\ \end{align} $ | (8) |
刚体质心的运动学方程:
| $ {{[{{{\dot{x}}}^{\text{i}}}\ \ {{{\dot{y}}}^{\text{i}}}\ \ {{{\dot{z}}}^{\text{i}}}]}^{\text{T}}}={{{\mathit{\boldsymbol{R}}}}_{\text{B}-\text{I}}}{{[V_{x}^{\text{b}}\ \ V_{y}^{\text{b}}\ \ V_{z}^{\text{b}}]}^{\text{T}}} $ | (9) |
刚体姿态角的运动学方程:
| $ \left[ \begin{array}{l} {\dot \varphi }\\ {\dot \theta }\\ {\dot \psi } \end{array} \right] = \left[ {\begin{array}{*{20}{c}} 1&{\sin \varphi \tan \theta }&{\cos \varphi \tan \theta }\\ 0&{\cos \varphi }&{ - \sin \varphi }\\ 0&{\sin \varphi /\cos \theta }&{\cos \varphi /\cos \theta } \end{array}} \right]\left[ \begin{array}{l} \omega _x^{\rm{b}}\\ \omega _y^{\rm{b}}\\ \omega _z^{\rm{b}} \end{array} \right] $ | (10) |
以上各式中, m表示物体的质量, V表示物体的运动速度, F表示物体受到的力, M表示物体所受力矩, I表示物体的惯性矩, ω表示物体的角速度.上标i和b分别表示惯性系和体轴系, 而下标a, e, g分别表示物体受到的气动力, 发动机推力和体积力. RB-I表示体轴系到惯性系的过渡矩阵.
方程组(7)和(8)为刚体动力学方程组, 方程组(9)和(10)为刚体运动学方程组, 在进行六自由度轨迹仿真时, 方程组的右端项全部已知, 因此对方程(7)到(10)求解属于常微分方程的初值问题, 一般采用Adams预估-校正法求解.
如图 2所示, 利用CFD方法获取某一时刻的气动力和气动力矩, 并将其传递至刚体六自由度中的动力学方程以获得飞行器对气动力的响应, 再通过刚体运动学方程计算出下一时刻的运动姿态.根据这些信息调整计算网格, 进行下一时刻的CFD计算以获取新的气动力, 重复以上耦合过程, 至此, CFD/RBD耦合计算平台基本搭建完成.
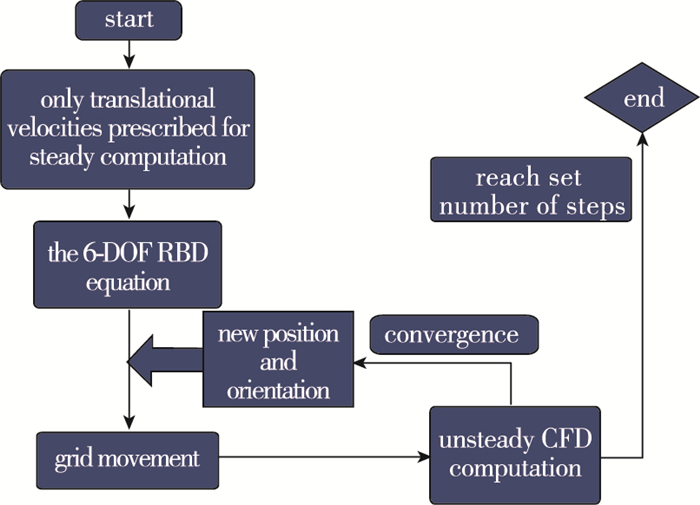
|
| 图 2 数值模拟过程的流程图 Fig.2 Flow chart of the numerical simulation process |
在嵌套网格实现过程中, 本文采取的策略是根据壁面距离判定的方法进行嵌套边界的确定[20-25].
如图 3所示, 虚线所对应的网格是包含物面A的网格, 实线是包含物面B的网格.对于虚线中的i点, 分别计算i点到物面A的距离d1, 到物面B的距离d2, 若d1<d2, 则i点属于激活单元; j点到物面A的距离d1, 到物面B的距离d2, 若d1>d2, 则j点属于非激活单元.如果一个单元上的节点全部是激活状态则标记该网格单元为激活状态, 若一个网格的所有网格节点全部是激活状态, 则该网格为激活的网格单元; 若全为非激活状态, 则该网格为非激活单元; 若既有激活又有非激活状态的节点, 则该网格单元为需要进行数值传递的网格.
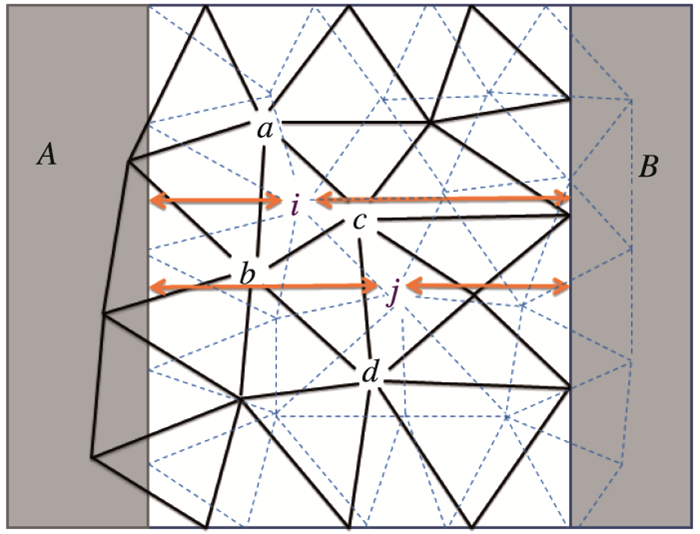
|
| 图 3 节点距离判定示意图 Fig.3 Schematic diagram of node distance determination |
由于HUNS3D求解器在构造网格交界面上的值时采用的策略是在计算中先将格点的值重构到格点上, 而后用格心和格点的值通过线性组合构造交界面的值.因此, 在嵌套网格组装完成后, 需要对其进行扩宽操作, 即在重叠边界上, 将与边界单元相连且处于关闭区域的单元选中也放入重叠区域.
如图 4所示, 在贡献单元搜索上, 采用蛇形查找的策略.即连接起始出发单元和要查找的点, 判断该线穿过该单元哪个边, 之后把相邻的单元作为下一个出发单元, 如果这条线和所有的边都不相交, 则判定当前的单元就是包含这个点的贡献单元.

|
| 图 4 蛇形查找示意图 Fig.4 Schematic representation of a serpentine look |
在流场信息传递的部分, 采用径向基函数插值的策略, 径向基函数的基本形式是:
| $ {\mathit{\boldsymbol{F}}}({\mathit{\boldsymbol{r}}})=\sum\limits_{i=1}^{N}{{{\omega }_{i}}\phi (\parallel {\mathit{\boldsymbol{r}}}-{{{\mathit{\boldsymbol{r}}}}_{i}}\parallel )} $ |
其中,下标i代表支撑点,r代表该点的位置矢量,N代表网格节点的总数,ϕ(‖r-ri‖代表所采用的基函数的形式,代表与第i个支撑点相关的权重系数.径向基函数的类型有很多, 这里简单介绍本文使用的一种逆二次径向基函数.
| $ \varphi (\eta )=1/({{\eta }^{2}}+d), \eta =\parallel {{{\mathit{\boldsymbol{r}}}}_{i}}-{\mathit{\boldsymbol{r}}}\parallel $ |
在对重叠区域的P点进行传递时进行流场信息传递时, 根据之前查找得到的贡献单元, 将贡献单元以及它的相邻单元一起作为径向基函数的插值模版构建径向基函数的系数矩阵.如图 5所示, i网格是P的贡献单元, 则使用i, j, k, l这4个网格用于构建径向基函数系数矩阵.

|
| 图 5 插值模版示意图 Fig.5 Schematic diagram of the interpolation template |
如图 5所示, 为了选取比较光滑的模版值, 因此在选取模版时, 每个物理量减去它们的平均值, 最后再加上被减去的值.将各个点的流场信息做差后ΔZ带入到RBF插值函数之中, 得到的线性方程组如下:
| $ {\mathit{\pmb{\Phi}}} {\mathit{\boldsymbol{W}}}=\Delta {\mathit{\boldsymbol{Z}}} $ |
| $ {\mathit{\pmb{\Phi}}} =\left| \begin{matrix} \varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{i}}-{{{\mathit{\boldsymbol{r}}}}_{i}}\parallel )&\varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{i}}-{{{\mathit{\boldsymbol{r}}}}_{j}}\parallel )&\varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{i}}-{{{\mathit{\boldsymbol{r}}}}_{k}}\parallel )&\varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{i}}-{{{\mathit{\boldsymbol{r}}}}_{l}}\parallel ) \\ \varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{j}}-{{{\mathit{\boldsymbol{r}}}}_{i}}\parallel )&\varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{j}}-{{{\mathit{\boldsymbol{r}}}}_{j}}\parallel )&\varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{j}}-{{{\mathit{\boldsymbol{r}}}}_{k}}\parallel )&\varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{j}}-{{{\mathit{\boldsymbol{r}}}}_{l}}\parallel ) \\ \varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{k}}-{{{\mathit{\boldsymbol{r}}}}_{i}}\parallel )&\varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{k}}-{{{\mathit{\boldsymbol{r}}}}_{j}}\parallel )&\varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{k}}-{{{\mathit{\boldsymbol{r}}}}_{k}}\parallel )&\varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{k}}-{{{\mathit{\boldsymbol{r}}}}_{l}}\parallel ) \\ \varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{l}}-{{{\mathit{\boldsymbol{r}}}}_{i}}\parallel )&\varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{l}}-{{{\mathit{\boldsymbol{r}}}}_{j}}\parallel )&\varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{l}}-{{{\mathit{\boldsymbol{r}}}}_{k}}\parallel )&\varphi (\parallel {{{\mathit{\boldsymbol{r}}}}_{l}}-{{{\mathit{\boldsymbol{r}}}}_{l}}\parallel ) \\ \end{matrix} \right| $ |
| $ {\mathit{\boldsymbol{W}}}=[{{\omega }_{i}}, {{\omega }_{j}}, {{\omega }_{k}}, {{\omega }_{l}}] $ |
其中, ‖ri-rj‖为欧式距离, 即各个基网格格心之间的距离.求解方程后得到每个基网格的权重.
1.4 求解器精度验证选择AEDC外挂物投放标模作为算例来考察本文所使用的求解器在多体分离问题中的可靠性[26-30].计算模型尺寸与嵌套区域划分如图 6和图 7所示.

|
| 图 6 外挂物投放标模几何外形 Fig.6 Geometric shape of the external model |

|
| 图 7 嵌套区域划分示意图 Fig.7 Schematic diagram of nested area division |
分离外挂物的主要数据如表 1所示. AEDC外挂物的模型尺寸如下表所示,机翼为一个具有45°倾斜角的三角翼,根弦长为7.62 m,半展长6.6 m,机翼展向截面为NASA-64A010翼型.挂架的构造为一个对称的弧面-平面-弧面组合体,对称线沿展向距翼根弦线的距离为3.3 m,挂架顶点距机翼前缘的距离为0.61 m.外挂物带有4个对称尾翼,其中心圆柱体直径为0.5 m,实际长度为3.017 5 m,质量约为907 kg.每个尾翼都带有45°的倾斜角,展向翼型为NACA008.外挂物和挂架之间的距离只有3.66 cm.外挂物质心前后作用2个弹射力分别为10.7 kN和42.7 kN,作用时间0.054 s,作用距离约为0.1 m.
| 下载CSV 表 1 分离外挂物的主要数据 Tab.1 Main data of the separated external objects |
由图 8所示, 由于弹射力矩的作用, 外挂物一开始会有一个抬头的效应, 0.054 s之后弹射力消失, 气动俯仰力矩会逐渐使外挂物低头.外挂物在前0.05 s先向右偏航, 而后会逐渐左偏, 本文CFD/RBD仿真结果真实地反映了这些现象.

|
| 图 8 外挂物分离过程压力云图 Fig.8 Pressure cloud diagram of the separation process of the hanging object |
图 9为弹体物面压力系数站位图, 图 10和图 11分别为质心速度和质心位移随时间变化的曲线, 图 12和图 13分别为姿态角和气动力矩随时间变化的曲线, 计算结果与实验结果吻合良好, 验证了本文所使用求解器的可靠性.

|
| 图 9 弹体截面压力系数分布 Fig.9 Distributions of pressure coefficient of the section of the projectile |

|
| 图 10 质心速度与实验对比图 Fig.10 Comparison of centroid velocity and experiment |

|
| 图 11 质心位移与实验的对比图 Fig.11 Comparison of centroid displacement and experiment |
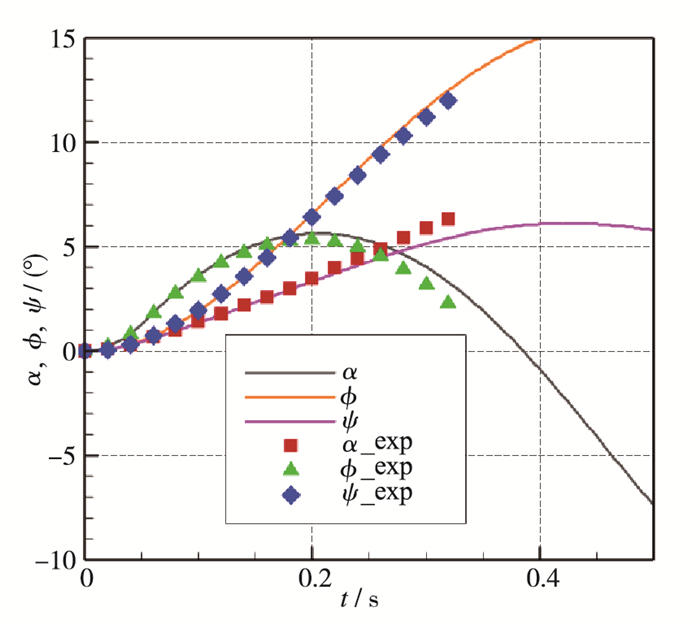
|
| 图 12 姿态角与实验值的对比图 Fig.12 Comparison of attitude angle and experimental value |

|
| 图 13 气动力矩与实验值的对比图 Fig.13 Comparison of aerodynamic torque and experimental values |
本文选取多舱段的子母弹为计算模型, 如图 14所示, 其中子弹质量M1=28 kg, 直径D1=170 mm, 长度L1=595 mm, 母弹直径D2=440 mm, 母弹质量M2=525 kg, 母弹弹舱长度L2=1 200 mm, 中间隔板厚度δ=10 mm, 弹体质心位置距离子弹尾部246.8 mm, 子弹距离母弹弹舱d=110 mm.子弹初始位置距离母弹弹舱有一个弹射气囊膨胀后的间隔高度.

|
| 图 14 子母弹计算模型 Fig.14 Submunition calculation model |
计算网格采用非结构嵌套网格, 围绕母弹和子弹分别生成其计算网格.如图 15所示, 红色区域是激活的区域, 彩色部分则是嵌套区域的网格, 其中母弹网格数量约为420万, 子弹网格数量约为80万, 为保证子弹运动区域中的网格质量, 对网格进行局部加密.

|
| 图 15 子母弹计算网格 Fig.15 Submunition calculation grid |
边界条件包括物面边界条件和远场边界条件, 本文设计了两种计算状态, 第1种只释放子弹的自由度, 将母弹设置为静止固壁边界条件; 第2种计算状态同时释放子弹与母弹的自由度, 将子弹和母弹都设置为移动固壁边界条件.物面边界条件同时还应该满足无滑移条件, 即u=v=w=0.由于能量方程的引入, 计算中需要补充边界上的传热条件为绝热壁条件.对于远场边界条件, 在实际数值计算中, 计算区域的大小是有限的, 因而在计算区域的远场边界处需要引入无反射边界条件, 以保证物体所产生的扰动波不被反射回内场这一流动的物理特征, 本文采用被广泛运用的Riemann不变量关系来处理远场无反射边界条件.流场初始参数为:来流Mach数Ma=3, 压力P=101 325 Pa, 子弹初始速度v=20 m/s, 方向竖直向上, 俯仰角速度大小为ω=200(°)/s, 方向使得子弹具有抬头的趋势, 转动惯量Ixx=0.39 kg·m2, Iyy=Izz=3.435 kg·m2.
2.3 算例结果对比子母弹非定常流场计算结果如图 16和图 17, 对于前舱子弹, 分离初期, 母弹激波作用于子弹上表面, 在子弹下表面形成低压区; 当t=5 ms时, 子弹头部开始穿越母弹激波, 随后母弹激波逐渐扫过子弹的下表面, 并向弹尾运动, 同时与子弹激波产生相交波系, 反射激波作用于母弹弹舱后再次形成反射波系作用于子弹弹身; 当t=25 ms时, 子弹完全穿越母弹激波.对于后舱子弹, 由于轴向距离靠后, 分离时受到母弹的干扰作用相对于前舱子弹较弱, 当t=20 ms时, 后舱子弹弹头开始穿越母弹激波.

|
| 图 16 前舱子弹分离过程压力云图 Fig.16 Pressure cloud diagram of the separation process of the front cabinsubmunition |

|
| 图 17 后舱子弹分离过程压力云图 Fig.17 Pressure cloud diagram of the separation process of the rear cabinsubmunition |
图 18为锁定母弹自由度时前舱与后舱子弹运动轨迹对比曲线, 由图 18(a)图可知, 由于空气阻力和初始弹射力的作用, 子弹沿x方向上的位移呈现不断增加的趋势. 图 18(b)为子弹分离过程中俯仰角速度变化曲线, 对于前舱子弹, 分离初期, 在初始角速度的作用下, 子弹的俯仰角逐渐增加.此时母弹激波作用于子弹上表面, 在子弹下表面形成低压区, 导致上表面压强高于下表面, 使子弹角速度增加的速率变缓, 与空气阻力共同作用, 致使角速度增加缓慢.当t=5 ms时, 子弹头部开始穿越母弹激波, 母弹激波作用于子弹下表面, 并逐渐向弹尾移动, 前舱子弹的角速度值再次增加.当t=25 ms时, 子弹脱离母弹激波, 在空气阻力的作用下, 子弹的角速度继续增加; 后舱子弹由于轴向位置靠后, 分离前期在自身角速度和气动干扰的共同作用下, 使得角速度减小, 随后子弹逐渐穿越母弹激波, 其角速度总体上呈现先减小后增加的趋势.

|
| 图 18 锁定母弹自由度前舱与后舱子弹运动轨迹对比 Fig.18 Comparison of the movement trajectories of the front and rear cabin submunition after locking the freedom of the projectile |
图 18(c)描述了锁定母弹自由度后子弹沿z方向相对速度变化曲线, 对于前舱子弹, 分离初期(前5 ms内), 母弹激波作用于子弹上表面, 导致弹身上表面压力高于下表面, 沿z方向相对速度呈现减小的趋势.当t=5 ms时, 母弹激波开始作用于子弹下表面, 沿z方向速度达到最小值. 5 ms后, 子弹沿z方向速度呈现增大的趋势.由于后舱子弹的轴向位置相对靠后, 导致后舱子弹穿越母弹激波的时间较长, 沿z轴方向速度整体上小于前舱子弹. 图 18(d)描述了锁定母弹自由度后子弹沿z方向气动力变化曲线, 从图中可以看出, 分离初始阶段, 由于母弹激波作用于子弹上表面, 在下表面形成低压区域, 加上重力的作用, 子弹沿z方向的气动力呈现减小的趋势, 当t=5 ms时, 前舱子弹弹头穿越母弹激波, 母弹激波作用于子弹下表面并逐渐向弹身中部移动, 子弹沿z方向所受气动力的方向发生改变; 当t=15 ms时, 母弹激波扫过子弹弹身中部区域, 并逐渐向弹尾移动, 此时沿z方向的气动力增加较为缓慢; 当t=25 ms时, 前舱子弹穿越母弹激波, 在自身角速度作用下, 迎角增加, 使得沿z方向的气动力继续增加.与前舱子弹相比, 后舱子弹长期处于母弹干扰流场作用下, 沿z方向气动力较前舱相比变化较为缓慢.
图 19和图 20为锁定母弹自由度与释放母弹自由度后子弹运动轨迹对比, 由图(a)、(b)可知, 释放母弹自由度后, 子弹沿x方向位移在分离前期变化不明显, 在分离中后期子弹头部已经穿越母弹激波后相比于锁定母弹自由度时有所减小; 释放母弹自由度后子弹的俯仰角速度在分离前期无明显变化, 分离中后期整体高于锁定母弹自由度后子弹的俯仰角速度.由图(c)、(d)可知, 释放母弹自由度后, 沿z轴方向的速度和气动力在分离中后期整体高于锁定母弹自由度时子弹沿z轴方向的速度和气动力.造成这一现象的原因是, 释放母弹自由度后母弹的空间位置发生变化, 使得激波干扰区域发生变化, 当子弹进入母弹激波干扰区域后, 所受气动力干扰发生改变.

|
| 图 19 锁定母弹自由度与释放母弹自由度前舱子弹运动轨迹对比 Fig.19 Comparison of the trajectory of the front cabin sub- munition after locking and releasing the freedom of the projectile |

|
| 图 20 锁定母弹自由度与释放母弹自由度后舱子弹运动轨迹对比 Fig.20 Comparison of the trajectory of the rear submunition after locking and releasing the freedom of the projectile |
图 21与图 22为释放母弹自由度后母弹沿x方向和z方向相对位移的变化曲线, 由图 22可知, 由于前舱子弹分离时与母弹的相互激波干涉作用要强于后舱子弹, 所以释放前舱子弹时母弹沿z方向上的相对位移要整体高于释放后舱子弹时母弹沿z方向上的相对位移. 图 23和图 24描述的是释放母弹自由度与锁定母弹自由度前后舱子弹与母弹的分离轨迹对比.由图可知, 在空气阻力作用下, 母弹沿x方向相对位移不断增加; 在自身重力和子弹激波干涉的共同作用下, 母弹沿z方向上的位移不断增加, 且释放前舱子弹时要整体高于释放后舱子弹时母弹沿z方向上的相对位移.

|
| 图 21 母弹沿x方向相对位移变化曲线 Fig.21 Relative displacement curves of the projectile in the x direction |

|
| 图 22 母弹沿z方向位移变化曲线 Fig.22 Relative displacement curves of the projectile in the z direction |
|
| 图 23 释放与锁定母弹自由度时前舱子弹分离轨迹对比 Fig.23 Comparison of the separation trajectory of the front cabin submunition when releasing and locking projectile freedom |

|
| 图 24 释放与锁定母弹自由度时后舱子弹分离轨迹对比 Fig.24 Comparison of the separation trajectory of the rear cabin submunition when releasing and locking projectile freedom |
为研究分离时前舱子弹对后舱子弹气动干扰特性的影响, 对前后舱子弹同时抛撒和对后舱子弹单独抛撒状态进行了数值模拟.计算条件为:来流Mach数Ma=1.5, 压力P=101 325 Pa, 子弹初始速度v=20 m/s, 角速度ω=200(°)/s.同时释放前后舱子弹及母弹的自由度.前后舱子弹分离轨迹如图 25所示.

|
| 图 25 前后舱子弹分离轨迹示意图 Fig.25 Schematic diagram of the separation of the front and rear cabin submunition |
计算结果如图 26、27所示, 由于初始阶段后舱子弹受前舱子弹的干扰, 导致同时释放子弹时后舱子弹要小于单独释放后舱子弹沿x方向上的相对位移; 由于前舱子弹的持续干扰作用, 母弹激波前期未能作用于子弹上表面并提供一个反向的俯仰力矩, 使得同时释放时后舱子弹的角速度整体上大于单独释放后舱子弹时的角速度.

|
| 图 26 后舱子弹沿x方向上的相对位移变化 Fig.26 Relative displacement of the rear cabin submunition in the x direction |

|
| 图 27 后舱子弹的俯仰角速度变化 Fig.27 Pitch angular velocity change of the rear cabin submunition |
本文以双层轴向排布子母弹为计算模型, 采用课题组开发的非结构混合网格Reynolds平均Navier-Stokes方程求解程序HUNS3D, 结合非结构嵌套网格技术, 耦合六自由度刚体运动方程, 对锁定与放开母弹自由度及同时释放前后舱子弹的分离过程进行了数值模拟, 得到了不同情况下子弹分离的干扰流场特性, 分析了释放母弹自由度后对子弹分离的影响.
仿真结果说明, 在分离前期, 由于激波之间的多次反射, 导致前舱子弹与母弹之间有较强的耦合作用, 在子弹与弹舱之间形成壅塞区域.随着时间的推进, 子弹逐渐穿越母弹激波, 母弹激波逐渐扫过子弹弹身下表面, 改变了子弹的俯仰力矩, 子弹在分离中期气动力发生较大变化.而后舱子弹由于轴向位置靠后, 母弹激波的干扰作用相对较弱, 整体气动力参数相对于前舱子弹变化较为缓慢.
当释放母弹自由度时, 子弹的气动力参数发生较大的变化, 主要体现在在释放母弹自由度后, 子弹沿x方向位移相比于锁定母弹自由度时有所减小, 子弹的俯仰角速度整体高于锁定母弹自由度后子弹的俯仰角速度; 释放母弹自由度后, 沿z轴方向的速度和气动力高于锁定母弹自由度时子弹沿z轴方向的速度和气动力.造成这一现象的原因是, 放开母弹自由度后母弹的空间位置发生变化, 使得激波干扰区域发生变化, 当子弹进入母弹激波干扰区域后, 所受气动力干扰发生改变.
同时释放前后舱子弹时, 由于前舱子弹的尾激波及干扰作用, 导致同时释放子弹时后舱子弹要小于单独释放后舱子弹沿x方向上的相对位移; 同时释放时后舱子弹的角速度整体上大于单独释放后舱子弹时的角速度.
本文通过对不同舱段的子弹在锁定母弹自由度和释放母弹自由度分离时的三维非定常流场进行数值模拟, 得到了子弹在不同流场下的分离干扰特性.但在研究过程中忽略了侧向子弹在分离前期对纵向子弹的干扰作用.在下一步工作中, 将对周向的4枚子弹同时分离进行仿真, 研究侧向子弹在分离前期对纵向子弹的干扰作用.
| [1] |
Panneerselvam S, Nagarajan V, Soundararajan P. Dispenser induced aerodynamic interference loads on submunition during dispense[C]. Proceedings of the 15th Applied Aerodynamics Conference. Atlanta, GA, USA: AIAA, 1997.
|
| [2] |
Holden M S, Harvey J, MacLean M, et al. Development and application of a new ground test capability to conduct full-scale shroud and stage separation studies at dupli-cated flight conditions[C]. Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada: AIAA, 2005.
|
| [3] |
Cavallo P A, Dash S M. Aerodynamics of multi-body separation using adaptive unstructured grids[C]. Procee-dings of the 18th Applied Aerodynamics Conferenc. Denver, CO, USA: AIAA, 2000.
|
| [4] |
Rizk M, Jolly B. Aerodynamic simulation of bodies with moving components using CFD overset grid methods[C]. Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada: AIAA, 2006.
|
| [5] |
Bhange N P, Sen A, Ghosh A K. Technique to improve precision of kinetic energy projectiles through motion study[C]. Proceedings of the AIAA Atmospheric Flight Mechanics Conference. Chicago, Illinois: AIAA, 2009.
|
| [6] |
Harris R E, Liever P A, Luke E A, et al. Towards a predictive capability for multiple-body proximate-flight in high-speed air-delivered systems[C]. Proceedings of the 42nd AIAA Fluid Dynamics Conference and Exhibit. New Orleans, Louisiana: AIAA, 2012.
|
| [7] |
蒋跃文.基于广义网格的CFD方法及其应用[D].西安: 西北工业大学, 2013. Jiang Y W. Numerical solution of Navier-Stokes equations on generalized mesh and its application[D]. Xi'an: Northwestern Polytechnical University, 2013(in Chinese). |
| [8] |
段旭鹏, 常兴华, 张来平. 基于动态混合网格的多体分离数值模拟方法[J]. 空气动力学学报, 2011, 29(4): 447-452. Duan X P, Chang X H, Zhang L P. A CFD-and-6DOF-coupled solver for multiple moving object problems based on dynamic hybrid grids[J]. Acta Aerodynamica Sinica, 2011, 29(4): 447-452. DOI:10.3969/j.issn.0258-1825.2011.04.008 (in Chinese) |
| [9] |
张来平, 邓小刚, 张涵信. 动网格生成技术及非定常计算方法进展综述[J]. 力学进展, 2010, 40(4): 424-447. Zhang L P, Deng X G, Zhang H X. Reviews of moving grid generation techniques and numerical methods for unsteady flow[J]. Advances in Mechanics, 2010, 40(4): 424-447. (in Chinese) |
| [10] |
曾铮, 王刚, 叶正寅. RBF整体网格变形技术与多体轨迹仿真[J]. 空气动力学学报, 2015, 33(2): 170-177. Zeng Z, Wang G, Ye Z Y. Enhanced RBF mesh deformation method and multi-body trajectory simulation[J]. Acta Aerodynamica Sinica, 2015, 33(2): 170-177. DOI:10.7638/kqdlxxb-2014.0143 (in Chinese) |
| [11] |
雷娟棉, 苗瑞生, 居贤铭. 战术火箭子母战斗部第一次抛撒分离多体干扰流场数值模拟[J]. 北京理工大学学报, 2004, 24(9): 766-769, 785. Lei J M, Miao R S, Ju X M. Numerical investigation of multi-body flow fields in the first separation of tactical rocket's submunitions[J]. Transactions of Beijing Insti-tute of Technology, 2004, 24(9): 766-769, 785. DOI:10.3969/j.issn.1001-0645.2004.09.004 (in Chinese) |
| [12] |
张玉东, 纪楚群. 多体分离非定常气动特性数值模拟[J]. 空气动力学学报, 2006, 24(1): 1-4. Zhang Y D, Ji C Q. The numerical simulation of unsteady multi-body separating flows[J]. Acta Aerodynamica Sinica, 2006, 24(1): 1-4. DOI:10.3969/j.issn.0258-1825.2006.01.001 (in Chinese) |
| [13] |
陶如意, 张丁山, 赵润祥, 等. 超音速子母弹分离干扰流场数值模拟与试验研究[J]. 空气动力学学报, 2010, 28(3): 310-315. Tao R Y, Zhang D S, Zhao R X, et al. Numerical and experimental study of interference flow field on separation of supersonic cluster munition[J]. Acta Aerodynamica Sinica, 2010, 28(3): 310-315. DOI:10.3969/j.issn.0258-1825.2010.03.013 (in Chinese) |
| [14] |
王刚, 叶正寅. 三维非结构混合网格生成与N-S方程求解[J]. 航空学报, 2003, 24(5): 385-390. Wang G, Ye Z Y. Generation of Three dimensional mixed and unstructured grids and its application in solving Navier-Stokes equations[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(5): 385-390. DOI:10.3321/j.issn:1000-6893.2003.05.001 (in Chinese) |
| [15] |
Jameson A. Time dependent calculations using multigrid, with applications to unsteady flows past airfoils and wings[C]. Proceedings of the 10th Computational Fluid Dynamics Conference. Honolulu, HI, USA: AIAA, 1991.
|
| [16] |
Gaitonde A L. A dual-time method for the solution of the unsteady Euler equations[J]. The Aeronautical Journal, 1994, 98(978): 283-291. DOI:10.1017/S0001924000026786 |
| [17] |
Wang G, Jiang Y W, Ye Z Y. An improved LU-SGS implicit scheme for high Reynolds number flow computations on hybrid unstructured mesh[J]. Chinese Journal of Aeronautics, 2012, 25(1): 33-41. DOI:10.1016/S1000-9361(11)60359-2 |
| [18] |
高浩, 朱培申, 高正红. 高等飞行动力学[M]. 北京: 国防工业出版社, 2004. Gao H, Zhu P S, Gao Z H. The advanced flight dyna-mics[M]. Beijing: National Defense Industry Press, 2004. (in Chinese) |
| [19] |
韩子鹏. 弹箭外弹道学[M]. 北京: 北京理工大学出版社, 2008. Han Z P. Exterior ballistics of projectiles and rockets[M]. Beijing: Beijing Institute of Technology Press, 2008. (in Chinese) |
| [20] |
杜超, 李孝伟. 基于动态嵌套网格方法的摆动翼型粘性绕流数值模拟[J]. 上海大学学报(自然科学版), 2007, 13(3): 304-307. Du C, Li X W. Numerical analysis of viscous flow around oscillatoring wing using dynamic chimra grid method[J]. Journal of Shanghai University (Natural Science), 2007, 13(3): 304-307. DOI:10.3969/j.issn.1007-2861.2007.03.017 (in Chinese) |
| [21] |
李立, 麻蓉, 郝海兵, 等. 嵌套网格计算的一种实用初始洞面构造方法及应用[J]. 应用力学学报, 2016, 33(2): 262-267. Li L, Ma R, Hao H B, et al. A practical method for efficient creation of initial hole boundary in chimera grid computation[J]. Chinese Journal of Applied Mechanics, 2016, 33(2): 262-267. (in Chinese) |
| [22] |
徐春光, 董海波, 刘君. 基于单元相交的混合网格精确守恒插值方法[J]. 爆炸与冲击, 2016, 36(3): 305-312. Xu C G, Dong H B, Liu J. An accurate conservative interpolation method for the mixed grid based on the intersection of grid cells[J]. Explosion and Shock Waves, 2016, 36(3): 305-312. (in Chinese) |
| [23] |
Meakin R L. On the spatial and temporal accuracy of overset grid methods for moving body problems[C]. Proceedings of the 12th Applied Aerodynamics Conference. Colorado Springs, CO, USA: AIAA, 1994.
|
| [24] |
Suhs N E, Rogers S E. PEGASUS 5: an automated pre-processor for overset-grid CFD[C]. Proceedings of the 32nd AIAA Fluid Dynamics Conference and Exhibit. St. Louis, Missouri: AIAA, 2002.
|
| [25] |
Nakahashi K, Togashi F, Sharov D. An intergrid-boundary definition method for overset unstructured grid approa-ch[C]. Proceedings of the 14th Computational Fluid Dynamics Conference. Norfolk, VA, USA: AIAA, 1999.
|
| [26] |
李孝伟, 范绪箕. 基于动态嵌套网格的飞行器外挂物投放的数值模拟[J]. 空气动力学学报, 2004, 22(1): 114-117. Li X W, Fan X J. Simulation of the release of store based on the moving chimera grid technique[J]. Acta Aerodynamica Sinica, 2004, 22(1): 114-117. DOI:10.3969/j.issn.0258-1825.2004.01.022 (in Chinese) |
| [27] |
肖中云, 江雄, 牟斌, 等. 并行环境下外挂物动态分离过程的数值模拟[J]. 航空学报, 2010, 31(8): 1509-1516. Xiao Z Y, Jiang X, Mou B, et al. Numerical simulation of dynamic process of store separation in parallel environ-ment[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(8): 1509-1516. (in Chinese) |
| [28] |
Wang Z J, Parthasarathy V, Hariharan N. A fully automated Chimera methodology for multiple moving body prob-lems[C]. Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit. Reno, NV, USA: AIAA, 1998.
|
| [29] |
Newman Ⅲ J C, Baysal O. Transonic solutions of a wing/pylon/finned store using hybrid domain decomposi-tion[C]. Proceedings of the Astrodynamics Conference. Hilton Head Island, SC, USA: AIAA, 1992.
|
| [30] |
Newman Ⅲ J C, Baysal O. Transonic solutions of a wing/pylon/finned store using hybrid domain decomposition[C]. Proceedings of the Astrodynamics Conference. Hilton Head Island, SC, USA: AIAA, 1992.
|




