两相流动问题指流动区域内同时存在两种不同组分或同组分不同相的流体, 它们彼此相互作用, 共同发展.与单相流动相比, 两相流现象的表现形式更加复杂, 包括自由界面变化和相变两种, 前者如液滴破裂, 后者如空化和液化.对于很多问题, 两种流体的压力条件速度条件和物质属性迥异, 给两相流问题的求解带来巨大挑战[1-3].
计算机技术的发展和数值模拟方法的改进使两相流问题的解决方法取得了长足进步.在众多两相流模拟方法中, 借助体积分数变量进行两相流模拟的方法是一种通用的做法.体积分数表示某种流体所占控制单元的体积百分比, 当控制单元体积无限小时, 体积分数在全场变为一个非0即1的台阶状分布函数:颜色函数(colour function)[4].依此理论建立的模型称为EFM(effective field modeling)模型[5-6], 具体形式见公式(1). EFM模型虽然较好地描述了两相流体的流动规律, 但其应用仍存在如下两个问题:
(1) 在EFM模型中, 补充了相应的状态方程后, 方程数目和未知量数目相等, 但是两种流体的空间分布是未知的, 因而方程仍不能求解.
(2) 在EFM控制方程中, 包含体积分数(颜色函数)的微分项, 由于其空间的不连续性而不可进行空间求导, 因此特征分析方法在两相流领域的推广遇到困难.
在借助体积分数进行两相流模拟的方法中, 有一种气液两相流全流速数值模拟方法由Liou等[7]Chang等[8-9]研究者提出, 它通过分层流(stratified flow)模型得到控制单元内不同流体的空间分布, 并利用AUSM系列格式[10-12], 将通量分解为对流通量和压力通量, 从而不必如Godunov格式那样显式求解特征值和特征向量.不过, 该方法所能表示的体积分数为(0, 1) 开区间, 对于纯水或纯气需加入微量的另一组分流体来近似.此外, 对于EFM模型存在的非守恒项和非双曲项, 数值模拟中也需要特别的处理[7].
本文在借鉴现有基于EFM模型的两相流模拟方法的基础上, 吸收并融合界面重构思想和AUSM通量分裂的思想, 发展了一种基于密度的气液两相流模拟方法.该方法采用体积分数变量区分流体组分, 并通过自由界面重构技术得到流体空间分布, 一方面,这些做法具有VOF(volume of fluid)方法的特点; 另一方面, 它利用AUSM+-up格式进行通量计算, 通过基于密度的方法进行流场求解, 因此本文将新方法称为ρ-VOF方法.该方法可同时模拟气液流场中的激波现象与自由界面现象, 并能有效抑制自由界面的非物理耗散.
1 数值方法 1.1 控制方程本文采用的方法是在Liou等提出的全流速模拟方法[7]的基础上发展得来的, 其中全流速数值模拟方法的控制方程如下所示:
| $\frac{{\partial {\mathit{\boldsymbol{U}}_k}}}{{\partial t}} + \frac{{\partial {\mathit{\boldsymbol{F}}_k}}}{{\partial x}} = \mathit{\boldsymbol{P}}_k^{{\rm{int}}} + {\mathit{\boldsymbol{S}}_k},k \in \{ 1,2\} .$ | (1) |
其中,
| $\begin{array}{l} {\mathit{\boldsymbol{U}}_k} = \left( {\begin{array}{*{20}{c}} {{\alpha _k}{\rho _k}}\\ {{\alpha _k}{\rho _k}{u_k}}\\ {{\alpha _k}{\rho _k}{E_k}} \end{array}} \right),{\mathit{\boldsymbol{F}}_k} = \left( {\begin{array}{*{20}{c}} {{\alpha _k}{\rho _k}{u_k}}\\ {{\alpha _k}{\rho _k}u_k^2}\\ {{\alpha _k}{\rho _k}{u_k}{H_k}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0\\ {{\alpha _k}{p_k}}\\ 0 \end{array}} \right),\\ \quad \quad \quad \mathit{\boldsymbol{P}}_k^{{\rm{int}}} = {\left( {0,p_k^{{\rm{int}}}\frac{{\partial {\alpha _k}}}{{\partial x}}, - p_k^{{\rm{int}}}\frac{{\partial {\alpha _k}}}{{\partial t}}} \right)^{\rm{T}}}. \end{array}$ |
下标k为参与计算的流体的标识, αk为流体k的体积分数, Pkint向量为与自由界面压强有关的量, Sk为源项.
假设用于数值计算的控制单元尺度(网格尺度)远小于流场发生显著变化的特征尺度, 则认为控制单元内流场变量近似为均一值, 即控制单元内的所有流体在同一瞬时共用相同的速度温度和压强.如此, 将方程(1) 中的不同流体的同类型方程相加, 便可消除自由界面的压力项Pkint, 得到一个简化的EFM模型, 其一维形式如下:
| $\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}}{\rm{ = }}\mathit{\boldsymbol{S}}.$ | (2) |
其中,
| $\begin{array}{l} \quad \quad \quad \mathit{\boldsymbol{U}} = {(\bar \rho ,\bar \rho u,\bar \rho \bar E,{\alpha _1}{\rho _1})^{\rm{T}}},\\ \mathit{\boldsymbol{F}} = {(\bar \rho u,\bar \rho {u^2},\bar \rho \bar Eu,{\alpha _1}{\rho _1}u)^{\rm{T}}} + {(0,p,0,0)^{\rm{T}}}. \end{array}$ |
ρ, E分别为控制单元内两种流体的平均密度和平均总能;u, p分别为控制单元内的速度和压强;α1, ρ1分别为流体1(以下称为参考流体)在控制单元内所占的体积百分比和密度;S为源项, 可包括重力相变和热传导等项.
方程(2) 由4个标量方程组成, 每一个方程均具有明确的物理意义, 其中前3个方程分别表示控制单元内的流体整体上遵守质量守恒动量守恒和能量守恒定律, 第4个方程表示参考流体在传输过程中遵守质量守恒定律.最后1个标量方程间接控制着自由界面的运动, 与VOF方法中的相位场方程类似.
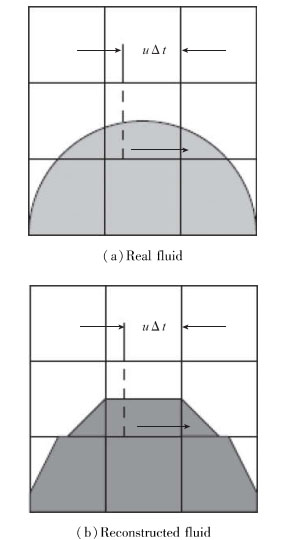
1.2 通量计算通过重构技术得到控制单元内不同流体的空间分布以后, 可采用AUSM+-up格式[7]计算控制单元边界处的通量, 该通量分为对流通量和压力通量两部分.本文采用VOF方法中“贡献单元-接收单元”的思想进行对流通量的计算[13], 如图 1所示.
|
| 图 1 通量计算示意图 Fig.1 Sketch map of flux calculation |
在图 1中, (a)为真实流体分布, (b)为重构后的流体分布. Δt时间内中间单元向右传输的物质为该控制单元内虚线右侧的部分, 质量动量和能量的对流通量根据传输的气体和液体的量分别计算得到, 而压力通量则根据AUSM+-up格式推荐的方法计算得到[7], 具体操作如下:
(1) 对流通量
记对流通量为F1/2(c), 满足
| $\begin{array}{l} \quad \quad \quad {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{{\rm{L}}/{\rm{R}}}}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\rm{R}}},} & {{{\dot m}_{1/2}} > 0}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\rm{L}}},} & {{{\dot m}_{1/2}} \le 0} \end{array}} \right..\\ {{\dot m}_{1/2}}{\rm{ = }}{u_{1/2}}{\rho _{1/2,{\rm{L}}/{\rm{R}}}} = {u_{1/2}}\left\{ {\begin{array}{*{20}{l}} {{\rho _{\rm{L}}},} & {{u_{1/2}} > 0}\\ {{\rho _{\rm{R}}},} & {{u_{1/2}} \le 0} \end{array}} \right.. \end{array}$ |
下标1/2表示控制体边界处的变量, 如u1/2为控制体边界处的速度, 以下类同.由相邻控制体的Mach数决定, 再加上两控制体的压力差量的函数作为修正项, 则其表达式为
| ${u_{1/2}} = {a_{1/2}}\left[ {M_{(4)}^ + ({M_{\rm{L}}}) + M_{(4)}^ - ({M_{\rm{R}}}) + {M_{\rm{p}}}} \right].$ |
其中, ML/R为左/右Mach数, Mp为速度计算中的压力项, 定义如下:
| $\begin{array}{l} \quad \quad \quad \quad \quad \quad \quad {M_{{\rm{L}}/{\rm{R}}}} = \frac{{{u_{{\rm{L}}/{\rm{R}}}}}}{{{a_{1/2}}}},\\ {M_{\rm{p}}} = - {K_{\rm{p}}}{\rm{max}}\left( {1 - {{\bar M}^2},{\rm{ }}0} \right)\frac{{{p_{\rm{R}}} - {p_{\rm{L}}}}}{{{\rho _{1/2}}a_{1/2}^2}},{\rm{ }}0 \le {K_{\rm{p}}} \le 1. \end{array}$ |
本文取Kp = 0.25.
其中,
| $\begin{array}{l} {\rho _{1/2}} = ({\rho _{\rm{L}}} + {\rho _{\rm{R}}})/2,{{\bar M}^2} = (M_{\rm{L}}^2 + M_{{\rm{LR}}}^2)/2,\\ \quad \quad \quad {a_{1/2}} = \frac{1}{2}({a_{{\rm{g,}}1/2}} + {a_{{\rm{l}},1/2}})/2. \end{array}$ |
Mach数分裂函数如下:
| $M_{(4)}^ \pm \left( M \right) = \left\{ {\begin{array}{*{20}{l}} {M_{(1)}^ \pm ,} & {\left| M \right| \ge 1}\\ {M_{(2)}^ \pm \left( {1 \mp 2M_{(2)}^ \pm } \right),} & {\left| M \right| < 1} \end{array}} \right..$ |
其中,
| $\begin{array}{l} M_{(1)}^ \pm \left( M \right) = \frac{1}{2}\left( {M \pm \left| M \right|} \right),\\ M_{(2)}^ \pm \left( M \right) = \pm \frac{1}{4}{\left( {M \pm 1} \right)^2}. \end{array}$ |
(2) 压力通量计算
压力通量由边界相邻控制体的加权压力决定, 再附加速度差量的函数作为修正, 其定义如下:
| ${p_{1/2}} = P_{(5)}^ \pm ({M_{\rm{L}}}){p_{\rm{L}}} + P_{(5)}^ - ({M_{\rm{R}}}){p_{\rm{R}}} + {P_u}.$ |
其中,
Pu=-KuP(5)+(ML)P(5)-(MR)ρ1/2a1/2(uR-uL), 0≤Ku≤1, 取Ku = 0.75.
压力分裂函数为
| $P_{(5)}^ \pm (M) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{M}M_{(1)}^ \pm ,} & {\left| M \right| \ge 1}\\ {M_{(2)}^ \pm \left[ {\left( { \pm 2 - M} \right) \mp 3MM_{(2)}^ \pm } \right],} & {\left| M \right| < 1} \end{array}} \right..$ |
控制方程需补充适当的状态方程才能封闭, 本文采用的stiffened状态方程是一种应用广泛的气液通用状态方程, 具有形式简单的特点[7, 8], 其压强和比内能的计算公式见式(3).
| $\left\{ {\begin{array}{*{20}{l}} {p = \left( {\gamma - 1} \right)\rho e - \gamma {p_\infty }}\\ {e = \frac{{{C_{\rm{p}}}}}{\gamma }T + \frac{{{p_\infty }}}{\rho }} \end{array}} \right..$ | (3) |
其中, p为压强, e为流体的比内能, γ为比热比, p∞为stiffened状态方程中流体所具有的一个固有属性参量, Cp为定压比热.对于水和空气, 相关参数见表 1.
| 下载CSV 表 1 水气状态参数表 Tab.1 Parameters for water and air |
数值计算中需要用到流体的声速公式, 本文从流体声速的原始概念出发, 通过一种不同于文献[14]中声速求解方法的途径, 利用流体等熵关系求得.
流体等熵变化时流体对外做功则内能减少, 满足微分方程(4), 其中V为流体的比容, e为流体的比内能.
| $p{\rm{d}}V = - {\rm{d}}e.$ | (4) |
结合状态方程(3) 进行整理, 得到压强与密度的等熵关系:
| $p = \frac{{\gamma - 1}}{\gamma }{C_{\rm{p}}}\left( {C{\rho ^\gamma }} \right) - {p_\infty }.$ |
根据定义, 则声速表达式为:
| $a = {\left. {\sqrt {\frac{{\partial p}}{{\partial \rho }}} } \right|_{\rm{s}}} = \sqrt {\frac{{\gamma \left( {p + {p_\infty }} \right)}}{\rho }} .$ |
特别的, 对于理想气体而言, 将p∞= 0代入上式, 则得到声速表达式
在N-S方程的求解过程中, 需要根据新时刻的守恒变量反求压强和温度等原始变量, 以便进行下一时刻的计算.对于单相理想气体而言, 通过守恒变量可以很容易求得压强和温度等变量, 公式如下所示, 其中E为单位质量的总能.
| $\begin{array}{l} p = \left( {\gamma - 1} \right)\rho \left[ {E - \frac{1}{2}(\mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{u}})} \right],\\ T = \frac{p}{{\left( {\gamma - 1} \right)\rho }} = E - \frac{1}{2}\left( {\mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{u}}} \right). \end{array}$ |
而在本文的气液两相流计算中, 流场随时间更新后, 仅得到控制单元内两种流体整体的守恒变量, 因此不能简单照搬单相流的公式, 而需要通过重新推导得到.
已知控制单元内守恒变量(ρ, ρu, ρv, ρw, ρE, ρ1α1)T, 由于控制单元内的两种流体共用一个速度, 因此容易得到控制单元内的平均密度, 平均内能和参考流体的表观密度:
| $\left\{ {\begin{array}{*{20}{l}} {{\alpha _1}{\rho _1}\left( {p,T} \right) = A\quad ①}\\ {{\alpha _2}{\rho _2}\left( {p,T} \right) = C\quad ②}\\ {{\alpha _1}{\rho _1}{e_1} + {\alpha _2}{\rho _2}{e_2} = B\quad ③}\\ {{\alpha _1} + {\alpha _2} = 1\quad ④}\\ {{\rho _i}\left( {p,{\rm{ }}T} \right) = \frac{{p + {p_{\infty i}}}}{{T{C_{{\rm{pi}}}}}} \cdot \frac{{{\gamma _i}}}{{{\gamma _i} - 1}},i \in \left\{ {1,{\rm{ }}2} \right\}{\rm{ }}\quad ⑤}\\ {{e_i}\left( {p,{\rm{ }}T} \right) = \frac{{T{C_{{\rm{pi}}}}}}{{{\gamma _i}}} \cdot \frac{{p + {\gamma _i}{p_{\infty i}}}}{{p + {p_{\infty i}}}},i \in \left\{ {1,{\rm{ }}2} \right\}\quad ⑥} \end{array}} \right..$ | (5) |
式(5) 共有8个标量方程, 含有8个标量未知量αi, ei, ρi, p, T,其中i∈{1, 2}, 方程数和未知量数相等, 方程可解.
式(5) 中的①, ② 式联立消除T, 得:
| $\begin{array}{l} {\left( {\frac{{{\alpha _1}}}{{{\alpha _2}}}} \right)^2} = \frac{A}{C} \cdot \frac{{\frac{{{\gamma _2}}}{{{\gamma _2} - 1}} \cdot \frac{1}{{{C_{{\rm{p}}2}}}}\left( {p + {p_{\infty 2}}} \right)}}{{\frac{{{\gamma _1}}}{{{\gamma _1} - 1}} \cdot \frac{1}{{{C_{{\rm{p1}}}}}}(p + {p_{\infty 1}})}}\\ \quad \quad \quad \quad = \frac{{{n_2}\left( {p + {p_{\infty 2}}} \right)}}{{{n_1}\left( {p + {p_{\infty 1}}} \right)}}. \end{array}$ | (6) |
其中,
代入式(5) 中第③ 式, 并结合式④~⑥, 整理得到:
| $\begin{array}{l} \left( {\frac{{{n_2}}}{{{\gamma _1} - 1}} + \frac{{{n_1}}}{{{\gamma _2} - 1}}} \right){p^2} + \left[ {\frac{{{n_2}}}{{{\gamma _1} - 1}}\left( {{p_{\infty 2}} + {\gamma _1}{p_{\infty 1}}} \right) + } \right.\\ \left. {\frac{{{n_1}}}{{{\gamma _2} - 1}}\left( {{p_{\infty 1}} + {\gamma _2}{p_{\infty 2}}} \right) - B\left( {{n_1} + {n_2}} \right)} \right]p + \\ {p_{\infty 1}}{p_{\infty 2}}\left( {\frac{{{n_2}{\gamma _1}}}{{{\gamma _1} - 1}} + \frac{{{n_1}{\gamma _2}}}{{{\gamma _2} - 1}}} \right) - B\left( {{n_1}{p_{\infty 1}} + {n_2}{p_{\infty 2}}} \right) = 0. \end{array}$ | (7) |
由于式(7) 为关于压强p的一元二次方程, 共含有两个根, 但仅有1个是合理的.本文所研究的对象为气液两相流问题, 其中含有一相气相, 具有一般性, 假设第1组分为气相, 则该组分的状态方程中的压强参量p∞1=0.
对于一般的一元二次方程可写成如下形式:
| $a{p^2} + bp + c = 0.$ |
对于式(7), 有:
| $\begin{array}{l} \quad \quad \quad a = \frac{{{n_2}}}{{{\gamma _1} - 1}} + \frac{{{n_1}}}{{{\gamma _2} - 1}} > 0,\\ c = {p_{\infty 1}}{p_{\infty 2}}\left( {\frac{{{n_2}{\gamma _1}}}{{{\gamma _1} - 1}} + \frac{{{n_1}{\gamma _2}}}{{{\gamma _2} - 1}}} \right) - B({n_1}{p_{\infty 1}} + {n_2}{p_{\infty 2}})\\ = - B{n_2}{p_{\infty 2}} < 0. \end{array}$ |
则
| $4ac < 0 \Rightarrow {b^2} - 4ac > {b^2} \Rightarrow \sqrt {{b^2} - 4ac} > \left| b \right|.$ |
一元二次方程的两个根为
| $p = \frac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}.$ |
一个为正根, 一个为负根.由于压强只能为正, 因此p只有1个有效解, 即
| $p = \frac{{ - b + \sqrt {{b^2} - 4ac} }}{{2a}}.$ |
得到压强p后, 再通过式(5) 和(6) 可得到体积分数和温度的表达式:
| $\begin{array}{l} {\alpha _1} = \frac{{{n_2}\left( {p + {p_{\infty 2}}} \right)}}{{{n_1}\left( {p + {p_{\infty 1}}} \right) + {n_2}\left( {p + {p_{\infty 2}}} \right)}},\\ T = \frac{{\sum\limits_{i = 1}^2 {\frac{{{\alpha _i}\left( {p + {p_{\infty i}}} \right)}}{{{C_{{\rm{pi}}}}}}\frac{{{\gamma _i}}}{{{\gamma _i} - 1}}} }}{{A + C}}. \end{array}$ |
则控制单元内两种流体的参数均可求得.
2 计算结果与分析 2.1 一维液体激波管问题本节模拟了文献[7]的一维水下激波管问题, 计算区域为[0, 1], 其初始状态如下:
| $\begin{array}{l} {({\alpha _{\rm{g}}},p)_{\rm{L}}} = (0,10\;{\rm{bar}}),\\ {({\alpha _{\rm{g}}},p)_{\rm{R}}} = (0,1\;{\rm{bar}}). \end{array}$ |
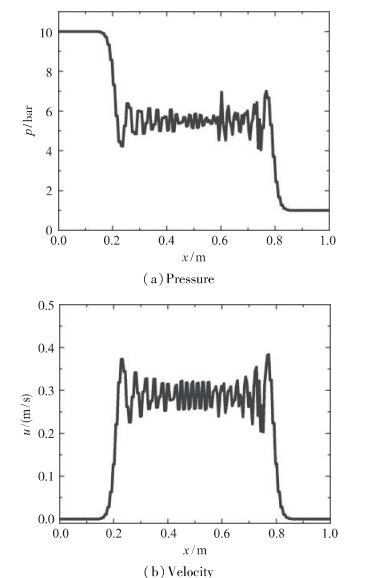
计算开始后, 激波管内不同区域的流体在原始压强梯度的驱动下开始运动. 图 2为文献[7]在未考虑低Mach数修正时得到的结果, 出现非物理震荡现象.
|
| 图 2 文献[7]液体激波管压强和速度曲线(未考虑低Mach数修正) Fig.2 Distributions of pressure and velocity in liquid shock tube problem (without low Mach modification) in reference[7] |
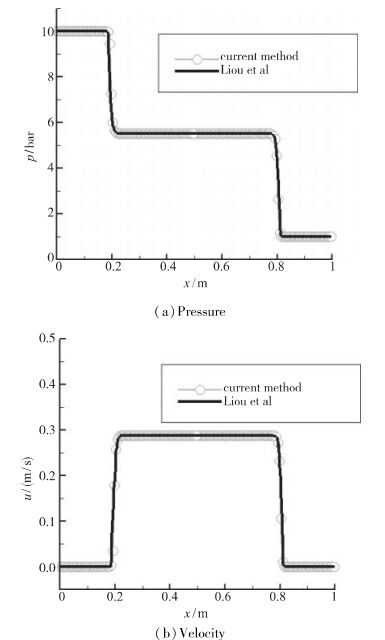
ρ-VOF方法不存在上述现象, 其计算结果见图 3.图中实线为文献[7]经过修正后的计算值, 虚线带圈为本文计算值, 本文计算结果与文献结果完全吻合, 从而验证了ρ-VOF方法对水下激波现象的模拟能力.
|
| 图 3 液体激波管压强和速度曲线 Fig.3 Distributions of pressure and velocity for water in shock tube problem |
为考察ρ-VOF方法对存在气液自由界面时的高速流动问题的模拟能力, 本节考核了气体和液体的激波传播的问题.考虑一维激波管, 长度为10 m, 以中间刻度5 m为分界面, 左右两侧变量如下所示[7]:
| $\begin{array}{l} {(p,{\alpha _{\rm{g}}},u,T)_{\rm{L}}} = ({10^9}\;{\rm{Pa}},{\rm{ }}1,{\rm{ }}0\;{\rm{m/s}},{\rm{ }}308.15\;{\rm{K}}),\\ {(p,{\alpha _{\rm{g}}},u,T)_{\rm{R}}} = ({10^5}\;{\rm{Pa}},{\rm{ }}0,{\rm{ }}0\;{\rm{m/s}},{\rm{ }}308.15\;{\rm{K}}). \end{array}$ |
其中,αg为气相的体积百分比.注意到文献[7]在本算例初始气体的体积分数设置为1-ε, 液体为ε, 其中ε=10-7, 这是由于文献采用的方法不允许体积分数为0或1, 而本文的方法无此限制, 因此本文取ε= 0.在本算例中, 由于气液存在压差, 随着时间的推进, 气体能量通过自由界面进入液体并形成激波, 同时, 在气体侧形成膨胀波.
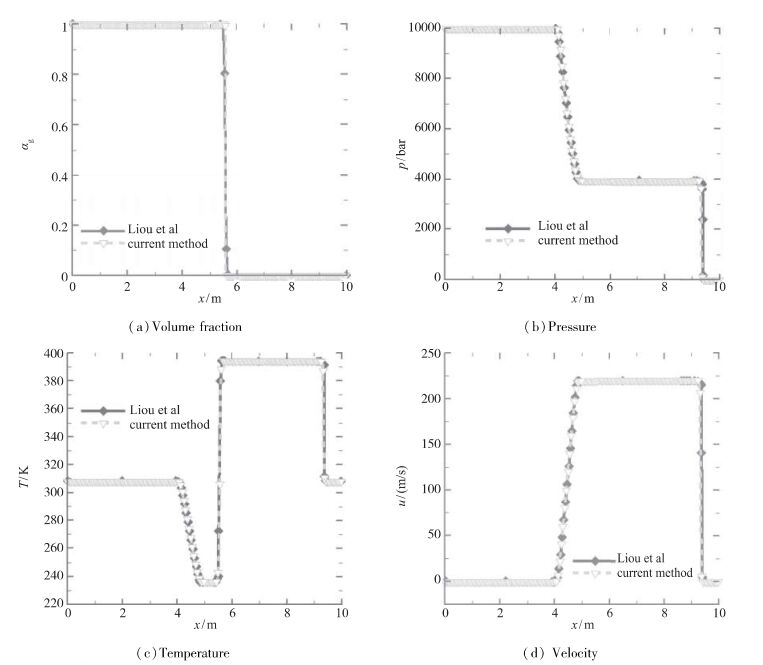
图 4为气体体积分数压强温度和速度随空间的变化曲线, 菱形标记的曲线为文献计算值, 三角标记的曲线为本文计算值.对比发现, 本文计算值与文献计算值完全吻合, 从而验证了新方法对激波跨自由界面传播问题的模拟能力.
|
| 图 4 气体激波向水中传播的流场参数变化曲线 Fig.4 Flowfield variables distributions in shock transition from air to water |
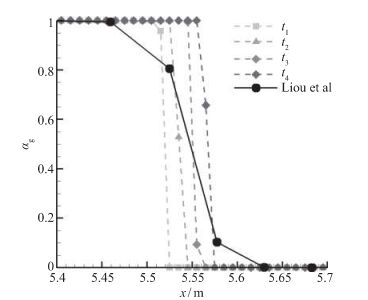
为展示ρ-VOF方法对气液自由界面的高分辨率特性, 将图 4(a)在自由界面附近放大, 如图 5所示.图中实线为文献[7]计算值, 4条虚线为本文计算值, 分别对应计算过程中的4个不同时刻.注意到文献给出的标记点是经过采样后的结果, 采样频率为6, 因此图中文献计算值有两个点位于0和1之间, 意味着自由界面至少被模糊到了7个点的宽度.而对于本文的方法, 从t1时刻到t4时刻, 体积分数介于0和1的单元在每一时刻均只有1个, 表示自由界面始终被约束在一个网格的尺度内, 这说明本文所发展的计算方法对气液自由界面拥有很高的分辨率, 明显优于文献的计算方法.文献[15]指出Liou等的全流速模拟方法不能清晰模拟自由界面, 而本文ρ-VOF方法可以做到.
|
| 图 5 气液激波问题中自由界面位置的变化 Fig.5 Free interface distributions in gas-liquid shock tube problem |
本节考核ρ-VOF方法对二维激波和气液自由界面的相互作用的模拟能力, 所选取的算例为文献[7]算例D激波跨二维液滴传播问题, 其中液体为水, 气体为空气, 激波移动的Mach数为1.47, 波前为1个大气压, 流场静止, 温度为293.15 K.根据驻波条件, 波后的压强为2.3548倍大气压, 流场流向速度为225.86 m/s, 法向速度为0, 温度均为381.85 K, 液滴直径为6.4 mm, 单位直径的网格点数为160.
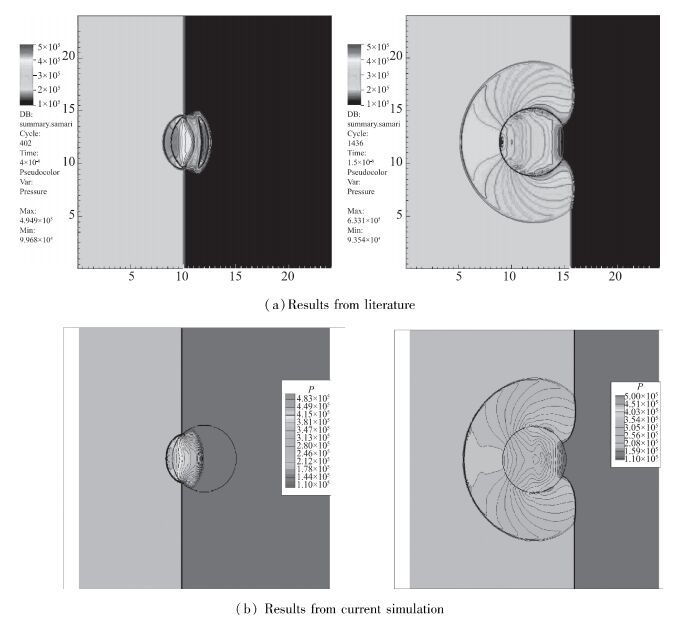
图 6为文献计算结果和本文计算得到的不同时刻的压强云图对比, 其中图 6(a)为文献计算结果, 图 6(b)为本文计算结果.计算发现, 由于激波在液体中的传播速度快于在气体中的传播速度, 液体内的激波先于外部气体激波到达液滴后缘, 并在到达自由界面后反射, 在液滴后侧出现低压区.随后, 液体内压力波在液滴内不断反射, 几乎不对外部气体流场产生作用, 本文模拟结果与文献计算结果一致, 验证了ρ-VOF方法对气液两相流问题中的激波间断与接触间断相互作用的模拟能力.
|
| 图 6 激波跨二维液滴传播模拟图 Fig.6 Simulation of shockwave passing by droplet |
本文在Liou等提出的全流速气液两相流模拟方法的基础上进行改进, 得到了一种新的气液两相流方法: ρ-VOF方法.它对控制单元内的流体进行空间重构, 获得自由界面位置和不同组分流体的空间分布, 并采用AUSM+-up格式得到包含气液自由界面接触间断信息的数值通量.该方法可实现气液两相流问题中不同组分区域的统一求解, 有效模拟气液接触间断和气液流场中的激波间断.此外, 与原方法相比, 它还具有如下优点:
(1) 提高了鲁棒性, 减少了计算量
采用简化的EFM模型, 减少了待求解方程的数目, 从而减少了计算量; 简化形式的方程还消除了原模型中的非守恒项和非双曲特性项, 提高了鲁棒性, 降低程序实现过程中的复杂度.
(2) 拓展体积分数的取值空间, 更清晰地模拟自由界面
新方法拓展了流场中体积分数的取值空间, 使原方法的取值范围从(0, 1) 的开区间拓展到[0, 1]的闭区间. ρ-VOF方法采用了重构技术, 使气液自由界面在计算中始终保持无厚度的形态, 模拟得到的自由界面可被定位在一个网格的尺度内, 比原方法更好地保持了气液自由界面的尖锐性, 具有更高的分辨率.
通过对气液两相流典型算例的考核, 验证了ρ-VOF方法对两相流问题的模拟能力, 为气液两相流问题的研究提供一个新的选择.
| [1] |
Scardovelli R, Zaleski S. Direct numerical simulation of free-surface and interfacial flow[J]. Annual Reviews Fluid Mechanics, 1999, 31(1): 567-603. DOI:10.1146/annurev.fluid.31.1.567 |
| [2] |
Saurel R, Abgrall R. A multiphase Godunov method for compressible multifluid and multiphase flows[J]. Journal of Computational Physics, 1999, 150(2): 425-467. DOI:10.1006/jcph.1999.6187 |
| [3] |
曾卓雄, 亢力强, 姜培正, 等. 用双流体模型模拟湍流两相流场[J]. 空气动力学学报, 2003, 21(1): 98-103. Zeng Z X, Kang L Q, Jiang P Z, et al. Simulation of two-phase turbulent flow using a two-fluid model[J]. Acta Aerodynamica Sinica, 2003, 21(1): 98-103. (in Chinese) |
| [4] |
Pilliot J E, Puckett E G. Second order accurate volume-of-fluid algorithms for tracking material interfaces[J]. Journal of Computational Physics, 2004, 199: 465-502. DOI:10.1016/j.jcp.2003.12.023 |
| [5] |
Drew D A, Passman S L. Theory of multicomponent fluids[M]. New York: Springer-Verlag, 1998.
|
| [6] |
Ishii M, Hibiki T. Thermo-fluid dynamic theory of two-phase flow[M]. New York: Springer Science & Business Media, 2010.
|
| [7] |
Liou M S, Chang C H, Nguyen L, et al. How to solve compressible multifluid equations: a simple, robust, and accurate method[J]. AIAA Journal, 2008, 46(9): 2345-2356. DOI:10.2514/1.34793 |
| [8] |
Chang C H, Liou M S. A new approach to the simulation of compressible multifluid flows with AUSM+ scheme[R]. AIAA 2003-4107, 2003.
|
| [9] |
Chang C H, Liou M S. A robust and accurate approach to computing compressible multiphase flow: stratified flow model and AUSM+-up scheme[J]. Journal of Computational Physics, 2007, 225: 840-873. DOI:10.1016/j.jcp.2007.01.007 |
| [10] |
Liou M S, Charistopher J S. A new flux splitting scheme[J]. Journal of Computational Physics, 1991, 107: 23-39. |
| [11] |
Liou M S. A sequel to AUSM: AUSM+[J]. Journal of Computational Physics, 1996, 129: 364-382. DOI:10.1006/jcph.1996.0256 |
| [12] |
Liou M S. A sequel to AUSM, Part Ⅱ: AUSM+-up for all speeds[J]. Journal of Computational Physics, 2006, 214: 137-170. DOI:10.1016/j.jcp.2005.09.020 |
| [13] |
Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39: 201-225. DOI:10.1016/0021-9991(81)90145-5 |
| [14] |
Ding L, Sankaran V, Lindau J W, et al. A unified computational formulation for multi-component and multi-phase flows[R]. AIAA 2005-1391, 2005.
|
| [15] |
Edwards J R. A comparison of interface sharpening scheme for multiphase mixture flows[R]. AIAA 2008-1236, 2008.
|



