在计算气动声学(computational aeroacoustics, CAA)问题和湍流的直接数值模拟(direct numerical simulation, DNS)中, 有许多波数比较高而波幅较小的波需要准确模拟, 这要求数值格式有好的短波分辨率[1].谱方法的短波分辨率非常好, 但是该方法对问题的几何外形以及边界条件有很高的要求.紧致差分格式通常用来处理该类问题, 相比普通差分格式, 具有相同阶收敛精度的紧致格式有着更小的模板以及更好的谱分辨率[2].但是紧致格式在使用时一般需求解方程组, 这会导致计算效率的降低和并行处理上的困难.
优化格式是为处理该类问题而构造的一类数值格式.这种格式通过牺牲一部分收敛精度来对某一特定范围波数的波形(比如短波)分辨率进行优化[3].对于长波, 即使是低阶格式也能很精确地模拟, 因此此类格式可能有着更好的整体分辨率.但是, 优化格式除了精度略低之外还有其他不足之处.该类格式不适宜于长距离的波形传播模拟, 并且, 如果波形中含有大量长波成分, 优化格式也通常没有较好的表现, 甚至不及相同模板上的最高阶格式[4].
本文尝试结合模板上最高阶精度格式与优化格式的特点, 构造一种混合优化格式.格式由最高阶精度格式与优化格式加权组合得到.下文首先介绍差分格式的收敛精度与波数误差的关系, 然后设计合适的权系数, 构造相应的混合优化格式, 最后是数值算例测试.
1 差分格式的收敛精度与波数误差Fourier方法对分析差分格式性质非常有用.通过该方法可以得到差分格式的线性稳定性以及谱分辨率性质[5].下面通过该方法给出差分格式的波数误差.以线性对流方程为例, 对于初值问题
| $ \left\{\begin{array}{l}{\frac{\partial u}{\partial t}+c \frac{\partial u}{\partial x}=0} \\ {u(x, 0)=f(x)=\mathrm{e}^{\mathrm{i} k x}}\end{array}\right. $ | (1) |
其解析解为
| $ u(x, t)=f(x-c t)=\mathrm{e}^{\mathrm{i} k(x-c t)} $ | (2) |
数值模拟中采用等距网格xj=jh, 这里h为网格间距.对于半离散差分格式
| $ \frac{\partial u_{j}}{\partial t}=-c \tilde{u}_{j}^{\prime} $ | (3) |
其中,
若空间离散格式对于问题(1)可写为
| $ \widetilde{u}_{j}^{\prime}=\mathrm{i} \tilde{k} u_{j} $ | (4) |
其中,i为虚数单位,
| $ \widetilde{u}(x, t)=\mathrm{e}^{\mathrm{i}(\kappa x-c \tilde{\kappa} t) / h} $ | (5) |
比较该式与原方程的解析解式(2)可知,
考虑光滑函数f(x), 其Fourier变换为
| $ \mathscr{F}(f(x))=F(k) $ |
则
| $ \mathscr{F}\left(f^{\prime}(x)\right)=\operatorname{i}k F(k) $ | (6) |
若逼近f′(x)的某差分格式为q阶精度, 且有效波数为
| $ \mathscr{F}\left(\tilde{f}^{\prime}(x)\right)=\text {i} \tilde{k} F(k) $ | (7) |
根据Taylor展开, 差分格式的截断误差为
| $ \begin{aligned} T_{h}=& \tilde{f}^{\prime}(x)-f^{\prime}(x)=M f^{(q+1)}(x) h^{q}+\\ & O\left(f^{(q+2)}(x) h^{q+1}\right) \end{aligned} $ |
其中, h为空间步长, M是由差分格式决定的常数.对上式做Fourier变换得
| $ \mathscr{F}\left(\tilde{f}^{\prime}(x)-f^{\prime}(x)\right)=M(\mathrm{i} k)^{q+1} F(k) h^{q}+O\left(k^{q+2} h^{q+1}\right) $ | (8) |
结合前面两个Fourier变换等式以及κ=kh,
| $ \tilde{\kappa}-\kappa=M \mathrm{i}^{q} \kappa^{q+1}+O\left(\kappa^{q+2}\right) $ | (9) |
由该式可知, 高阶精度的格式在波数0附近的波数误差更小.优化格式由于精度相对较低, 以至于对含有大量长波成分波形的远距传播可能没有好的表现.
2 混合优化格式 2.1 两个子格式本节将通过加权混合最高阶格式和一个优化格式来融合两者的优点.权系数由局部波数指示子[6]确定.本节格式采用的模板为7点对称模板, 所用差分格式的形式为
| $ \tilde{f}_{j}^{\prime}=\frac{1}{h} \sum\limits_{l=-3}^{3} a_{l} f_{j+l} $ | (10) |
在7点对称模板上的最高阶格式为6阶格式, 其表达式记为
| $ \begin{array}{c}{a_{0}^{\mathrm{S}}=0} \\ {a_{1}^{\mathrm{S}}=-a_{-1}^{\mathrm{S}}=\frac{3}{4}} \\ {a_{2}^{\mathrm{S}}=-a_{-2}^{\mathrm{S}}=-\frac{3}{20}} \\ {a_{3}^{\mathrm{S}}=-a_{-3}^{\mathrm{S}}=\frac{1}{60}}\end{array} $ | (11) |
对于优化格式, 这里采用单位波长所含网格点数[7]PPW=6(对应无量纲波数κ=π/3)时波数误差为0的4阶格式, 其表达式记为
| $ \begin{array}{c} a_{0}^{{\rm O}} =0\\a_{1}^{{\rm O}} =-a_{-1}^{{\rm O}}=0.772998940 \\ a_{2}^{{\rm O}} =-a_{-2}^{{\rm O}}=-0.168399152 \\ a_{3}^{{\rm O}} =-a_{-3}^{{\rm O}}=0.021266455 \end{array} $ | (12) |
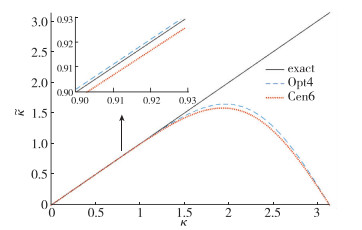
图 1为两个子格式的有效波数图.从图中可以看出, 在无量纲波数为0.91附近时, 6阶格式Cen6的有效波数偏小, 而优化格式Opt4则偏大.通过在不同区域进行局部放大, 可知在0 < κ < π/3间均有上述结果.因而可以通过加权平均两种格式来降低波数误差.由于相速度为
|
| 图 1 两个子格式的修正波数图 Fig.1 Modified wavenumbers of two schemes |
仿照文献[6]给出一种局部波数指示子
| $ \begin{array}{l}{I W_{j}=} \\ {\frac{\left(f_{j-2}-4 f_{j-1}+6 f_{j}-4 f_{j+1}+f_{j+2}\right)^{2}+\left(-f_{j-2}+2 f_{j-1}-2 f_{j+1}+f_{j+2}\right)^{2}}{\left(f_{j-1}-2 f_{j}+f_{j+1}\right)^{2}+\left(-f_{j-1}+f_{j+1}\right)^{2}+\varepsilon}}\end{array} $ | (13) |
ε是一个小的正数, 用来防止分母为0, 这里取10-40.那么对于单色波f(x)=asin(kx+φ)+C(C为常数项)
| $ I W_{j}=16 \sin ^{4}\left(\frac{\kappa}{2}\right) $ |
其中,κ=kh为无量纲波数.
下面考虑由IWj构造对单色波相位误差较小的混合格式.最直接的方法是先求解无量纲波数κ, 再构造权系数.
7点对称差分格式的有效波数为
| $ \tilde{\kappa}=-\mathrm{i} \sum\limits_{l=-3}^{3} a_{l} \mathrm{e}^{\mathrm{i} l \kappa} $ | (14) |
则
| $ \tilde{\kappa}^{\mathrm{S}}=2 \sum\limits_{l=1}^{3} a_{l}^{\mathrm{S}} \sin (l \kappa), \tilde{\kappa}^{{\rm O}}=2 \sum\limits_{l=1}^{3} a_{l}^{{\rm O}} \sin (l \kappa) $ | (15) |
若令
| $ \lambda_{j}^{\mathrm{E}}=\frac{\kappa-\tilde{\kappa}^{\mathrm{S}}}{\widetilde{\kappa}^{{\rm O}}-\tilde{\kappa}^{\mathrm{S}}} $ | (16) |
则加权优化格式
λjE的求解过程需要计算反三角函数和几个三角函数, 计算量相对较大.因此,可以采用一个简单的公式来逼近
| $ \lambda_{j}=\min \left(1, \gamma_{j}\right) $ | (17) |
| $ \begin{array}{c} \lambda_{j}=\min \left(1, \gamma_{j}\right) \gamma_{j}=0.7764332858 \sqrt{I W_{j}}+0.2235667142 I W_{j} \end{array} $ |
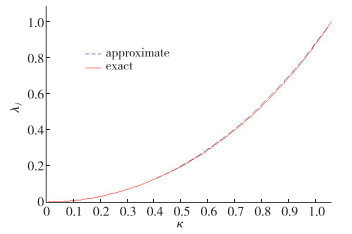
这使得混合格式为两个子格式的凸组合. 图 2给出了精确权系数与逼近权系数的比较, 横坐标为无量纲波数, 取值范围为[0, π/3], 对应于0≤IW≤1.从图中可见看出逼近权系数与精确值之间的误差很小.
|
| 图 2 加权系数的比较 Fig.2 Comparison of the weighted coefficients |
本文构造的混合优化格式为
| $ \tilde{f}_{j}^{\prime}=\left(1-\lambda_{j}\right) \tilde{f}_{j}^{\prime \mathrm{S}}+\lambda_{j} \tilde{f}_{j}^{\prime {\rm O}} $ | (18) |
其中,λj由式(17)给出, 显然该格式为非线性格式.下文中以HybOpt表示该格式.
记
|
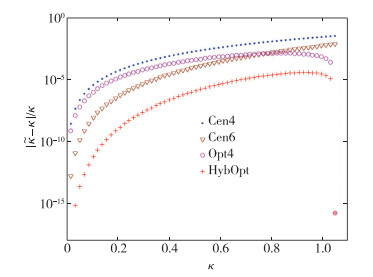
| 图 3 相对波数误差的比较 Fig.3 Comparison of relative wave number errors of four schemes |
本节分析该格式的收敛精度.由于该格式为非线性格式, 而非线性格式可能在极值点附近降阶, 如WENO格式[8-10], 因此下面对该混合格式在极值点附近的精度进行讨论.
两个子格式的收敛精度分别为
| $ \tilde{f}_{j}^{\prime \mathrm{S}}=f_{j}^{\prime}+O\left(h^{6}\right), \tilde{f}_{j}^{\prime {\rm O}}=f_{j}^{\prime}+O\left(h^{4}\right) $ | (19) |
当h→0时
| $ I W_{j}=\frac{\left(f_{j}^{(4)} h^{4}\right)^{2}+4\left(f_{j}^{(3)} h^{3}\right)^{2}+O\left(h^{8}\right)}{\left(f_{j}^{(2)} h^{2}\right)^{2}+4\left(f_{j}^{\prime} h\right)^{2}+O\left(h^{4}\right)} $ |
下面分3种情况讨论:
(1) 当xj附近没有极值点时
| $ f_{j}^{\prime}=O(1), I W_{j}=\frac{\left(f_{j}^{(3)}\right)^{2}}{\left(f_{j}^{\prime}\right)^{2}} h^{4}+O\left(h^{5}\right) $ |
则λj=O(h2), 根据式(18),(19)易知, 混合格式精度为6阶;
(2) 当xj附近有极值点时, 记xj到极值点的距离为ch, 若该极值点处2阶导数不为0, 则
| $ \begin{array}{c}{f_{j}^{\prime}=c f_{j}^{(2)} h+O\left(h^{2}\right), I W_{j}=\frac{\left(f_{j}^{(3)}\right)^{2}}{\left(1+c^{2} / 4\right)\left(f_{j}^{(2)}\right)^{2}} h^{2}+} \\ {O\left(h^{3}\right), \lambda_{j}=O(h)}\end{array} $ |
混合格式精度为5阶;
(3) 当xj附近有极值点且该极值点处2阶导数为0时, 则IWj=O(1), λj=O(1), 混合格式精度为4阶.
综上, 若求解问题是光滑的, 且极值点处2阶导数不为0, 则混合格式除极值点附近为5阶外均为6阶, 则L1收敛精度为了6阶, L∞收敛精度为5阶.若极值点处2阶导数为0, 则混合格式L1收敛精度为5阶, L∞收敛精度为4阶.
显然, 混合格式的收敛精度比原优化格式高.下面通过数值计算验证收敛精度, 考虑如下线性对流方程的初值问题
| $ \left\{\begin{array}{ll}{u_{t}+u_{x}=0} & {-1 \leqslant x \leqslant 1} \\ {u(x, 0)=u_{0}(x)} & {\text { periodic }}\end{array}\right. $ | (20) |
其中,下标t和x分别表示对相应变量求偏导数.计算终止时间为T=1.采用的初值条件为
| $ u_{0}(x)=\sin \left({\rm \mathsf{ π}} x-\frac{\sin ({\rm \mathsf{ π}} x)}{{\rm \mathsf{ π}}}\right) $ |
边界条件为周期边界.时间格式采用3阶TVD Runge-Kutta方法[11], 时间步长设为Δt~h2以使得时间格式的精度实际为6阶, 这里h为空间步长.计算结果的L1误差, L∞误差以及相应收敛精度列在表 1中.从表中可以看到, 混合格式的L∞收敛精度为5阶, L1收敛精度达到了6阶.易知该函数在极值点处2阶导数不为0, 则数值结果与前面的分析一致.
|
下载CSV
表 1 混合格式精度测试, |
本节通过数值算例来测试混合格式.作为比较, 同时测试的有2个子格式以及5阶迎风格式.这里的5阶迎风格式为6点迎风模板上的最高阶线性格式, 其模板为Cen6所用模板去掉顺风向最远端的点得到, 记该格式为Up5.测试问题为一维对流问题和球面波的传播问题.时间格式采用了3阶TVD Runge-Kutta方法[11], 在实际计算中也可采用低耗散低色散Runge-Kutta方法[12-13].
4.1 一维线性对流方程本小节采用对流方程进行测试, 对流速度设为1, 其方程为
| $ u_{t}+u_{x}=0 $ | (21) |
初值包括正弦波、Gauss波、调制正弦波.
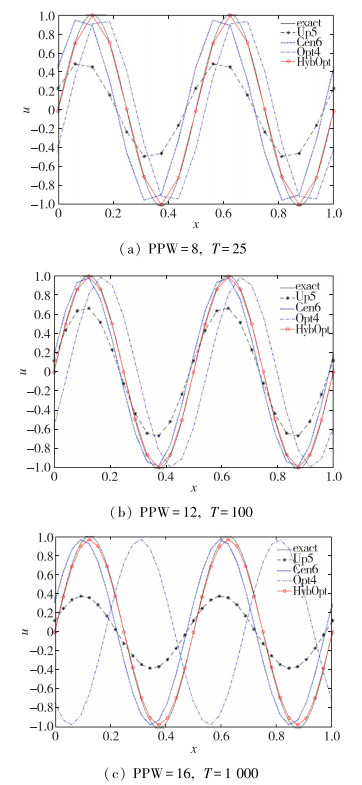
(1) 首先测试的是正弦波的传播问题, 初值为u0(x)=sin(4πx), 求解区域为[0, 1], 计算的CFL数均取0.1. PPW分别取8, 12和16, 推进时间分别为T=25, 100, 1 000. 图 4中给出了计算的结果.显然混合格式HybOpt在3种情况下的相位误差均几乎为0, 表现最佳.迎风格式Up5由于耗散项的存在, 导致波幅有明显减小.相对于精确解, Cen6的相位落后, 而Opt4的相位领先.而当PPW增加且推进时间大幅延长时, Opt4的相位误差也相对较大, 这与前面的结论一致.
|
| 图 4 正弦波的传播问题 Fig.4 Advection of sine waves |
(2) 计算一个Gauss波的传播问题, 初始波形为[14]
| $ u_{0}(x)=0.5 \exp \left(-\ln (2)\left(\frac{x}{3 h}\right)^{2}\right) $ | (22) |
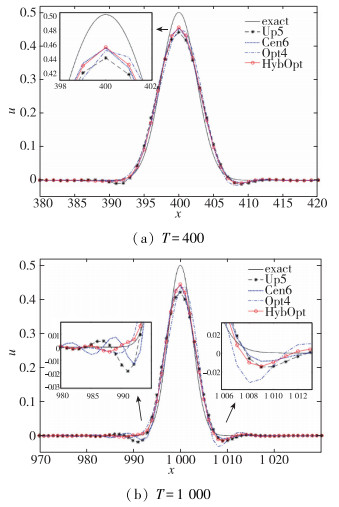
其中, h=1为空间步长, 取时间步长dt=0.5.计算终止时间为T=400, 1 000, 计算结果见图 5. 图 5(a)中, 在波峰处混合格式HybOpt与6阶格式Cen6表现最优. 图 5(b)中, Gauss波左侧下方优化格式Opt4和混合格式HybOpt表现较好, 而在右侧下方, 优化格式Opt4存在较大的波动, 其他格式表现较好.这是由于该Gauss波主要由长波(波数较小)构成, 优化格式Opt4的相速度偏大, 导致Gauss波前方有波动, 而6阶格式Cen6刚好相反.综上, 混合格式HybOpt能在传播中更好地保持波形.
|
| 图 5 Gauss波的传播问题 Fig.5 Advection of Gaussian wave |
下面考虑计算效率, 将终止时间设为T=10 000, 以同一计算条件进行计算, 计算时间见表 2.该混合格式的计算时间约为其他格式的2.5倍, 这是需要计算两种子格式的权系数并加权所致.
| 下载CSV 表 2 Gauss波传播计算时间测试 Tab.2 Computational time of the advection of Gaussian wave |
(3) 计算一个调制正弦波的传播问题, 初始波形为[15]
| $ u_{0}(x)=\exp \left(-16(x-0.5)^{2}\right) \sin (40 {\rm \mathsf{ π}} x) $ | (23) |
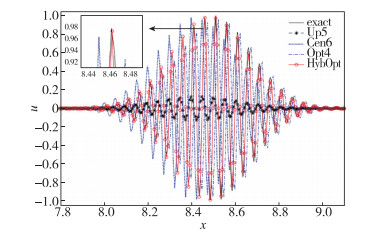
令h=1/160为空间步长, CFL数取0.1, 计算终止时间为T=8, 计算结果显示在图 6中.与正弦波的结果相似, 混合格式HybOpt由于其最小的相位误差表现最佳.
|
| 图 6 调制正弦波的传播问题 Fig.6 Advection of modulated sine wave |
球面波传播问题是一个计算气动声学的标准测试算例[14], 其控制方程为
| $ \frac{\partial u}{\partial t}+\frac{u}{r}+\frac{\partial u}{\partial r}=0 $ | (24) |
计算区域为[5,450], 初始条件为u=0, 在r=5处的边界条件为u=sin(ωt).
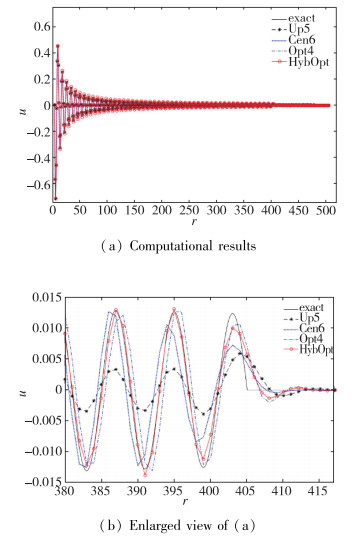
取ω=π/4, 计算终止时间为T=400, 空间步长为dr=1.为减小时间推进误差的影响, 时间步长取dt=0.1.计算结果如图 7所示, 实线为精确解.从图中可以看到, 混合格式HybOpt得到了与精确解几乎一致的相位.
|
| 图 7 球面波传播问题 Fig.7 Advection of spherical wave |
本文构造了一种混合优化格式.通过对优化格式和最高阶格式谱误差的比较与分析, 构造两种格式的加权平均来融合它们各自的优点.加权系数由局部的离散函数值分布得到.该格式比原优化格式精度高, 并且对于单色波问题相位误差很小, 其波数误差明显低于最高阶格式和线性优化格式.该格式对Gauss波的波形保持能力也较好, 对于近似单色波问题也有很好的表现.但是由于需要额外计算权系数, 计算时间约为相应线性格式的2.5倍.
本文所构造格式为中心格式, 对于一般的传输问题, 通常需要增加滤波过程[2, 16]; 而对于包含间断的问题, 还须加入特别的处理, 如限制器或者引入WENO处理[17].
| [1] |
Tam C K. Recent advances in computational aeroa-coustics[J]. Fluid Dynamics Research, 2006, 38(9): 591-615. DOI:10.1016/j.fluiddyn.2006.03.006 |
| [2] |
Lele S K. Compact finite difference schemes with spectral-like resolution[J]. Journal of Computational Physics, 1992, 103(1): 16-42. |
| [3] |
Tam C K, Webb J C. Dispersion-relation-preserving finite difference schemes for computational acoustics[J]. Journal of Computational Physics, 1993, 107(2): 262-281. DOI:10.1006/jcph.1993.1142 |
| [4] |
Zingg D W. Comparison of high-accuracy finite-difference methods for linear wave propagation[J]. SIAM Journal on Scientific Computing, 2000, 22(2): 476-502. DOI:10.1137/S1064827599350320 |
| [5] |
Vichnevetsky R, Bowles J B. Fourier analysis of numeri-cal approximations of hyperbolic equations[M]. Philadelphia: SIAM, 1982.
|
| [6] |
武从海.流体力学高精度高分辨率差分格式的研究[D].南京: 南京航空航天大学, 2012. Wu C H. Research on high order accurate and high resolution difference methods of fluid dynamics[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1014005377.htm |
| [7] |
Lockard D P, Brentner K S, Atkins H L. High-accuracy algorithms for computational aeroacoustics[J]. AIAA Journal, 1995, 33(2): 246-251. DOI:10.2514/3.12436 |
| [8] |
Jiang G S, Shu C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. |
| [9] |
Henrick A K, Aslam T D, Powers J M. Mapped weighted essentially non-oscillatory schemes:achieving optimal order near critical points[J]. Journal of Computational Physics, 2005, 207(2): 542-567. DOI:10.1016/j.jcp.2005.01.023 |
| [10] |
Borges R, Carmona M, Costa B, et al. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J]. Journal of Computational Physics, 2008, 227(6): 3191-3211. DOI:10.1016/j.jcp.2007.11.038 |
| [11] |
Shu C W. Total-variation-diminishing time discretiza-tions[J]. SIAM Journal on Scientific and Statistical Computing, 1988, 9(6): 1073-1084. DOI:10.1137/0909073 |
| [12] |
Hu F Q, Hussaini M Y, Manthey J L. Low-dissipation and low-dispersion Runge-Kutta schemes for computa-tional acoustics[J]. Journal of Computational Physics, 1996, 124(1): 177-191. |
| [13] |
Berland J, Bogey C, Bailly C. Low-dissipation and low-dispersion fourth-order Runge-Kutta algorithm[J]. Computers & Fluids, 2006, 35(10): 1459-1463. |
| [14] |
Hardin J C, Ristorcelli J R, Tam C K. Benchmark problems and solutions, ICASE/LaRC workshop on benchmark problems in computational aeroacoustics[R]. NASA CP-3300, 1995: 1-14.
|
| [15] |
Trefethen L N. Group velocity in finite difference sch-emes[J]. SIAM Review, 1982, 24(2): 113-136. DOI:10.1137/1024038 |
| [16] |
Koutsavdis E K, Blaisdell G A, Lyrintzis A S. Compact schemes with spatial filtering in computational aeroacou-stics[J]. AIAA Journal, 2000, 38(4): 713-715. DOI:10.2514/2.1016 |
| [17] |
Wang Z J, Chen R F. Optimized weighted essentially nonoscillatory schemes for linear waves with discontinui-ty[J]. Journal of Computational Physics, 2001, 174(1): 381-404. |



