2. 中国航天空气动力技术研究院,北京 100074
2. China Academy of Aerospace Aerodynamics, Beijing 100074, China
液滴的气动破碎是指液滴在突然遇到均匀高速气流时出现的变形和溃裂现象, 通常发生在激波后.它的实际应用十分广泛, 例如内燃发动机、核裂变装置、农业和环境喷雾等[1-2].
气动破碎是多物理过程不稳定性的结果, 对于高Weber数和高Reynolds数等高参数情形下的Newton液滴气动破碎, 弱黏性耗散和表面张力可导致高波数扰动快速增长.由于界面处极高的声阻抗失谐, Richtmeyer-Meshkov(R-M)不稳定性可忽略, 所以Rayleigh-Taylor(R-T)不稳定性和Kelvin-Helmholtz(K-H)不稳定性被看作是主要机制. Harper等[3]和Joseph等[4]最初认为液滴迎风界面指数增长的R-T不稳定性引起液滴剧烈的溃裂, 然而Theofanous等[5-7]根据实验观测和简单估计, 指出其主导机制是具有明显径向分量的剪切诱导运动, 以及由此产生并拉伸的液片上的不稳定性, 这更类似于K-H不稳定性.不管怎样, 目前实验常用的摄像机的空间分辨率约200 pixel/mm, 时间分辨率为50 kHz[5], 尚无法分辨高参数情形下的气动破碎, 只用实验方法难以验证其机制.
本文采用数值模拟方法研究超声速情形下液滴气动破碎初期的R-T不稳定性和K-H不稳定性两种机制, 给出激波与液滴相互作用演化过程.
1 数值方法数学上, 将问题理想化为二维可压缩Newton流动, 黏性耗散和表面张力趋于0.流动控制方程可写作守恒形式
| $ \frac{{\partial \, {\mathit{\boldsymbol{U}}}}}{{\partial \, t}} + \nabla \cdot {\mathit{\boldsymbol{F}}} = 0 $ | (1) |
其中, 守恒变量向量 U=(ρ, ρv, E)T依次由密度、动量向量、单位体积总能量组成, 向量F为相应的通量函数.流动区域Ω被相界面分成气相“g”和液相“l”两个子区域, 状态方程分别取完全气体方程和Tait方程.方程(1)采用低耗散守恒锐界面方法数值求解[8-9], 该方法是对一种基于5阶低耗散迎风WENO(weighted essentially non-oscillatory)格式的标准有限体积方法的改进, 考虑了与气液界面相切的计算单元.
将气液界面、气相子区域、液相子区域分别记作Γ(t), Ωg(t), Ωl(t), 气液界面的演化由气液Riemann问题的界面条件确定
| $ R({{\mathit{\boldsymbol{U}}}_{\rm{g}}}, {{\mathit{\boldsymbol{U}}}_{\rm l} }) = 0 $ | (2) |
现以气相子区域Ωg(t)为例, 对网格间距为Δx和Δy的二维Descartes网格的Ωg(t)中的气体应用方程(1).在被气体占据的网格单元(i, j)的时空体积Δij ∩ Ωg(t)上, 通过积分方程(1)可获得有限体积离散形式
| $ \int_{{\kern 1pt} {\kern 1pt} n}^{{\kern 1pt} n + 1} {[\int_{{\Delta _{ij}} \cap {{\mathit{\Omega}} _{\rm g}}(t)}^{} {(\frac{{\partial {\mathit{\boldsymbol{U}}}}}{{\partial t}} + \nabla \cdot {\mathit{\boldsymbol{F}}}){\kern 1pt} {\kern 1pt} {\rm{d}}x{\rm{d}}y]} } \, {\rm{d}}t = 0 $ |
其中, Δij=ΔxΔy为网格单元体积. Δij ∩Ωg(t)可用αij(t)ΔxΔy代替, 且αij(t)为依赖于时间的所求气体体积分数系数, 满足0≤αij(t)≤1.应用Gauss定理, 可得
| $ \int_{{\kern 1pt} {\kern 1pt} n}^{{\kern 1pt} n + 1} {[\int_{{\Delta _{ij}} \cap {{\mathit{\Omega}} _{\rm g}}(t)}^{} {\frac{{\partial {\mathit{\boldsymbol{U}}}}}{{\partial t}}{\kern 1pt} {\kern 1pt} {\rm{d}}x{\rm{d}}y]} } \, {\rm{d}}t + \int_{{\kern 1pt} {\kern 1pt} n}^{{\kern 1pt} n + 1} {[\int_{\partial {\Delta _{ij}} \cap {\mathit \Gamma} (t)}^{} {{\mathit{\boldsymbol{F}}} \cdot {\mathit{\boldsymbol{n}}}{\kern 1pt} {\kern 1pt} {\rm{d}}x{\rm{d}}y]} } \, {\rm{d}}t = 0 $ | (3) |
其中, ∂Δij为网格在特定4个点下的4个单元面的直角截边, 即
| $ \begin{align} &({{x}_{i}}+\Delta x/2, {{y}_{j}}), \ \ \ \ \ \ ({{x}_{i}}, {{y}_{j}}+\Delta y/2), \\ &({{x}_{i}}-\Delta x/2, {{y}_{j}}), \ \ \ \ \ ({{x}_{i}}, {{y}_{j}}-\Delta y/2). \\ \end{align} $ |
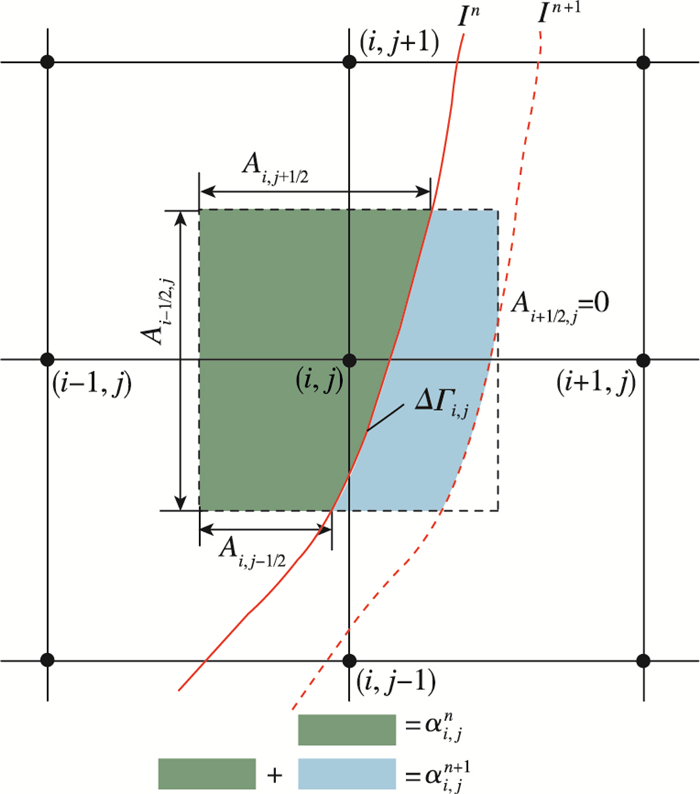
如图 1所示, Γ(t)和∂Δij ∩ Ωg(t)可由两部分表示:一部分是气液界面切割单元面的4段直角截边的集合, 可写作
|
| 图 1 切割单元的守恒离散示意图 Fig.1 Schematic of conservative discretization for a cut cell |
| $ \begin{align} &{{A}_{i+1/2, j}}(t)\Delta y, \ \ \ \ \ \ {{A}_{i, j+1/2}}(t)\Delta x, \\ &{{A}_{i-1/2, j}}(t)\Delta y, \ \ \ \ \ \ {{A}_{i, j-1/2}}(t)\Delta x. \\ \end{align} $ |
其中, 孔隙A满足0≤A≤1;另一部分是Γ(t)在网格单元(i, j)内的部分, 记作ΔΓi, j(t).因此, 式(3)可写作
| $ \begin{align} &\alpha _{ij}^{n+1}{\mathit{\boldsymbol{U}}}_{ij}^{n+1}-\alpha _{ij}^{n}{\mathit{\boldsymbol{U}}}_{ij}^{n}= \\ &\ \ \ \ \ \int_{n}^{n+1}{{\rm{d}}t}\frac{1}{\Delta x}[{{A}_{i+1/2, j}}(t){{{\mathit{\boldsymbol{\hat{F}}}}}_{i+1/2, j}}-{{A}_{i-1/2, j}}(t){{{\mathit{\boldsymbol{\hat{F}}}}}_{i-1/2, j}}]+ \\ &\ \ \ \ \ \int_{n}^{n+1}{{\rm{d}}t}\frac{1}{\Delta y}[{{A}_{i, j+1/2}}(t){{{\mathit{\boldsymbol{\hat{F}}}}}_{i, j+1/2}}-{{A}_{i, j-1/2}}(t){{{\mathit{\boldsymbol{\hat{F}}}}}_{i, j-1/2}}]+ \\ &\ \ \ \ \ \int_{n}^{n+1}{{\rm{d}}t}\frac{1}{\Delta x\Delta y}\mathit{\boldsymbol{\hat{X}}}[{{{\mathit{\Gamma}} }_{ij}}(t)] \\ \end{align} $ | (4) |
其中, αijUij和Uij分别为切割单元内的守恒变量和平均守恒变量,
| $ \begin{align} &\alpha _{ij}^{n+1}\mathit{\boldsymbol{U}}_{ij}^{n+1}= \\ &\ \ \ \ \ \ \alpha _{ij}^{n}\mathit{\boldsymbol{U}}_{ij}^{n}+\frac{\Delta t}{\Delta x}[{{A}_{i+1/2, j}}(t){{{\mathit{\boldsymbol{\hat{F}}}}}_{i+1/2, j}}-{{A}_{i-1/2, j}}(t){{{\mathit{\boldsymbol{\hat{F}}}}}_{i-1/2, j}}]+ \\ &\ \ \ \ \ \ \frac{\Delta t}{\Delta y}[{{A}_{i, j+1/2}}(t){{{\mathit{\boldsymbol{\hat{F}}}}}_{i, j+1/2}}-{{A}_{i, j-1/2}}(t){{{\mathit{\boldsymbol{\hat{F}}}}}_{i, j-1/2}}]+ \\ &\ \ \ \ \ \ \frac{\Delta t}{\Delta x\Delta y}\mathit{\boldsymbol{\hat{X}}}[{{{\mathit{\Gamma}} }_{ij}}(t)] \\ \end{align} $ | (5) |
其中, Δt为时间步长, 等号右边的所有项均赋予第n层时间的值.具体计算中, 根据式(5)采用3步3阶TVD型Runge-Kutta方法进行高阶时间推进, 同时保证离散的守恒性.同理, 液相子区域Ωl(t)中的数值离散与之类似.
气液界面条件由符号距离函数ϕ重构, 即水平集函数, 在界面处赋0水平集[10].气液界面的对流运动方程为
| $ \frac{\partial \, \phi }{\partial \, t}+\mathit{\boldsymbol{v}}\cdot \nabla \phi =0 $ |
它与式(5)中的通量函数均由一种5阶低耗散迎风WENO格式数值求解[11].同时, 设置阶跃条件得到通过界面的通量, 在通过界面的宽度为2b的窄段内求解Riemann问题, 以此确定沿法向n的界面速度和压强. Riemann问题的一侧状态由实际流体状态获得, 另一侧状态通过求解扩展方程由相应的流体插值获得[11].值得一提的是, 当求解Riemann问题得到沿法向的共同界面速度时, 保持了沿切向τ的速度阶跃.
2 结果与分析考虑Chang等[12]最先建议的一个典型问题, 空气中的一个二维水滴被Mach数为3的运动平面激波驱动.取定无量纲化参考值, 压强为1.013 25×105 Pa, 密度为1 kg/m3, 长度为1 cm, 则水滴的密度为1 000, 直径为0.35;激波前空气的密度为1.2, 未扰动压强为1.计算网格等距分布, 网格间距Δ=2.5×10-3.初始界面未显式施加扰动, 以数值误差替代.
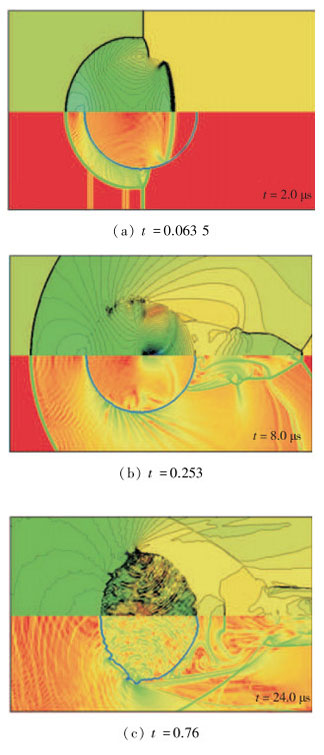
2.1 界面演化特性图 2是激波冲击液滴后t=0.063 5, 0.253, 0.76时刻的等值线, 反映了初期界面不稳定性发展的3个阶段, 相应的有量纲时刻依次为2.0, 8.0, 24.0 μs. 图 2中, 蓝色粗实线表示空气-水界面, 上半部分为压强, 取值范围-20~70, 等分为55条等值线; 下半部分为流动速度, 取值范围0.1~4, 等分为20条等值线.
|
| 图 2 不同时刻压强和流动速度 Fig.2 Pressures and flow velocities at different times |
开始阶段(见图 2(a)), 激波像环绕固体圆柱一样环绕液滴衍射, 在液滴内部传播的激波运动得快于空气中.随着压强等值线光滑地穿过气液界面, 驻点和外环之间中段附近迎风界面处形成了压强梯度阶跃, 数值逐渐增大.从气相一侧到液相一侧的压强梯度数值也呈现类似的变化.同时, 较靠近驻点的迎风界面处出现切向速度阶跃, 并在外环达到最大值.
第2阶段(见图 2(b)), 在迎风界面附近, 随着压强等值线光滑地穿过气液界面, 可清晰地看到扰动向外环逐渐增长.还可观察到, 主导扰动始于驻点和外环之间中段附近处, 对应于图 2(a)所示的压强梯度阶跃出现的相同位置.远离外环的压强等值线重新变得光滑, 但气相中依然存在压强梯度阶跃, 远远弱于迎风界面处和液滴内部的压强梯度阶跃.不管怎样, 切向速度阶跃的数值是一直增大的, 直到流动分离区域.
第3阶段(见图 2(c)), 液滴显著变形, 流动分离区域延伸至外环.在压强扰动形成处, 产生了波皱和一些离散的小液滴.迎风界面相对较光滑, 只有很小程度的波皱.波皱上端的切向速度阶跃被抹平, 形成一个有限厚度的剪切层, 随后导致一些微小的流动分离区域.此外, 还可对比发现, 在主弓形激波和液滴之间存在小的波状声波往复反射, 液滴内部的声波形态十分复杂.
需要特别指出的是, 一些文献中分辨率远远高于本研究的数值模拟表明, 上述3个阶段的压强和流动速度特征不依赖于网格尺度[13-14].这些液滴气动破碎初期界面变形及波动的数值预测结果同Theofanous等[5-6]的实验观测结果十分吻合, 迎风界面也是相对较光滑的, 且主导扰动始于从迎风界面到外环之间中段附近处.
2.2 线性稳定性分析R-T不稳定性和K-H不稳定性在气动破碎过程中的作用可由线性稳定性理论预测分析.当气相和液相的密度比ρg/ρl << 1时, 扰动增长率为
| $ s={{\left[ k\frac{{{(\rho a)}_{\rm gl }}}{{{\rho }_{\rm g}}+{{\rho }_{\rm l}}}+{{k}^{2}}\frac{{{\rho }_{\rm g}}{{U}_{\rm gl }}}{{{\rho }_{\rm g}}+{{\rho }_{\rm l}}} \right]}^{1/2}} $ | (6) |
其中, 假设初始扰动特征波数k的量阶是O(Δ-1); (ρa)gl为压强梯度诱导的沿界面法向的加速度阶跃, Ugl=Ug-Ul为沿界面切向的流动速度阶跃.式(6)中括号里的第1项和第2项分别由R-T不稳定性和K-H不稳定性引起. R-T不稳定性依赖于(ρa)g和(ρa)l的结构, 它仅当(ρa)gl >0时才导致不稳定, 否则界面是稳定的.特别地, 本文的R-T不稳定性分析与以往Harper等[3]和Joseph等[4]的研究不同, 他们假设了一个从气相到液相的总体加速度.
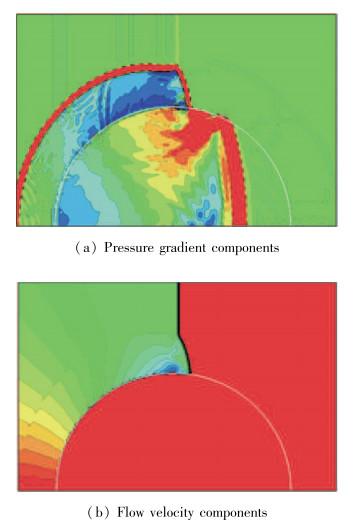
为了厘清气动破碎初期阶段中两种不稳定性机制的贡献, 图 3取t =0.063 5时刻, 给出了压强梯度和流动速度分别沿界面法向和切向分量的等值线.压强梯度沿界面法向的分量即为沿界面法向的加速度, ρa= Δp·N,N的指向从气相到液相.图中, 白色粗实线表示空气-水界面, 压强梯度分量Δp·N取值范围-200~200, 等分为11条等值线; 流动速度分量v·τ取值范围0.2~4, 等分为20条等值线.由图可知, 在驻点区域附近, (ρa)g < 0, 压强从激波阵面到驻点逐渐增大, 并且(ρa)l >0, 因而界面被加速度的这种结构稳定化.注意到驻点区域附近的流动速度的切向分量是连续的, K-H不稳定性的影响较小, 于是基于R-T不稳定性的界面稳定化清晰地解释了实验观测到的迎风界面光滑的现象.还可观察得到, 从驻点到外环, (ρa)g和(ρa)l都改变了符号.在迎风界面上, 过(ρa)l=0等值线后, 呈现出(ρa)g >0和(ρa)l < 0的结构, 这意味着气相和液相中的加速度使界面失稳引起了R-T不稳定性的增长率大幅度地增大.另外, 切向速度阶跃从驻点到外环逐渐增大, 导致K-H不稳定性的增长率增大.第2阶段的界面演化很好地支持了这些预测与分析, 如图 2(b)所示, 在(ρa)l改变符号的位置出现明显的扰动.该改变符号的位置处于从驻点到外环之间中段附近, 同时也是压强梯度阶跃的开始位置.这些观察结果清楚地显示了R-T不稳定性的本质贡献.然而, K-H不稳定性的增长率也沿着迎风界面增大, 它的贡献不可去除.就本文的数值模拟而言, 式(6)可由k=O(10-2)替代, Ugl的典型值为3, (ρa)gl沿外环附近的迎风界面的值为200~300, 可见K-H不稳定性对于高波数扰动的贡献大于R-T不稳定性.当然, 对于低波数和中间波数的扰动, R-T不稳定性也可具有相当或更高的增长率.
|
| 图 3 压强梯度和流动速度沿界面法向和切向的分量(t =0.063 5) Fig.3 Pressure gradient components normal to the interface and flow velocity components parallel to the interface at t = 0.063 5 |
为了进一步验证R-T不稳定性和K-H不稳定性的作用, 特别进行了一项改进的数值模拟.在该数值模拟中, 界面附近气相流动速度vg的切向分量修改为
| $ {{\mathit{\boldsymbol{v}}}_{\rm{g}}}\leftarrow (1-\alpha ){{\mathit{\boldsymbol{v}}}_{\rm{g}}}+\alpha \, {{\mathit{\boldsymbol{v}}}_{\rm l}}+\alpha ({{\mathit{\boldsymbol{v}}}_{\rm{g}}}-{{\mathit{\boldsymbol{v}}}_{\rm l}})\cdot \mathit{\boldsymbol{N}} $ |
这里, 若|ϕ| < b则α=(b-|ϕ|)2/b2, 否则α=0.这种改进通过消除穿过界面的切向速度阶跃和在界面上端引入一个厚度约为b的剪切层, 显著降低K-H不稳定性的影响, 与此同时保持了其他流动特性不变.
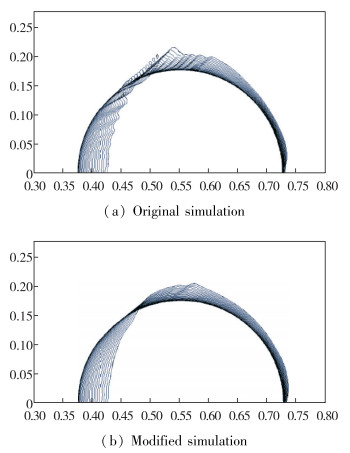
图 4对比了原始模拟和改进模拟获得的气动破碎初期界面的时间演化过程, 即t =0~0.76.同原始模拟相比, 改进模拟的界面演化由大尺度变形主导, 高波数扰动基本未增长.除了外环附近区域, 如图 3(a)所示, (ρa)gl在那里达到最大值.该结果明确地揭示, 若仅靠R-T不稳定性, 则高波数扰动难以充分发展, K-H不稳定性也在本质上起到重要的作用.值得注意的是, 原始模拟和改进模拟都预测到了迎风界面比下游界面有更显著的径向运动.这种现象与Theofanous[5]的实验发现一致, 意味着该径向运动主要由R-T不稳定性引起.
|
| 图 4 液滴气动破碎初期界面演化(t =0~0.76) Fig.4 Early-time interface evolution during aero- breakup of a liquid drop from t =0 to 0.76 |
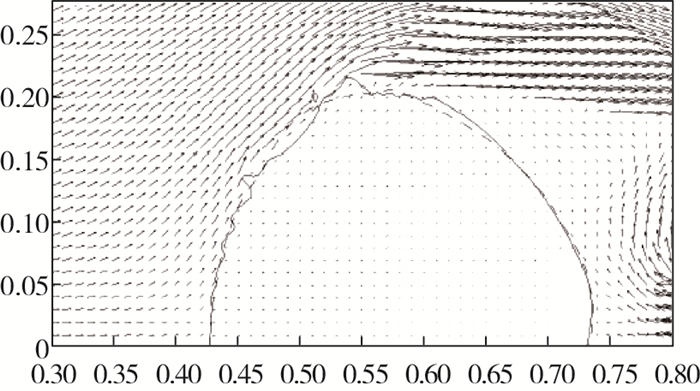
现进一步进行界面对比, 取定t =0.76时刻. 图 5是叠加了原始模拟流动速度向量场的原始模拟和改进模拟的界面, 两者的迎风界面和下游界面几乎吻合, 表明在驻点区域和流动分离区域, K-H不稳定性的增长率较小, 改进模拟保持了R-T不稳定性的发展.此外, 类似于固体圆柱绕流, 流动速度向量显示了气流自驻点开始, 从迎风界面到下游界面的压缩、膨胀、再压缩的过程, 在液滴下游尾流区域发展出旋涡结构.
|
| 图 5 原始模拟流动速度向量场及原始模拟和改进模拟的界面(t =0.76) Fig.5 Flow velocity field of the original simulation and the interface of the original (solid line) and modified (dash line) simulations at t = 0.76 |
尽管前述分析证明R-T不稳定性和K-H不稳定性都在液滴气动破碎初期起到重要的作用, 但是定量估计两者在整个气动破碎过程中的贡献及其相互作用仍很困难.线性稳定性理论已在初期中预测得知, 高波数扰动具有较大的增长率, 而在中期和后期中则须考虑非线性效应.如图 2(c)和图 5所示, 在初期不稳定性之后, 切向速度阶跃被抹平, 形成一个剪切层.该剪切层的厚度与界面波动的大小有关, 后者可导致扰动增长率急剧下降.不管怎样, 对于非线性R-T不稳定性, 多模态增长率甚至可能比线性阶段的增长率更大[15-17].另外, 非线性R-T不稳定性还可导致二次K-H不稳定性, 进一步极大地促使界面失稳.
界面不稳定性的另一个问题是可压缩性效应.以往的研究表明, 流体的可压缩性既可使界面稳定也可使之失稳.对于R-T不稳定性, 可压缩性改变了密度比而影响扰动增长率[18-19].由于密度比已经很高, 所以液滴气动破碎问题中的这种改变相对很小, 可压缩性效应对R-T不稳定性的影响很可能并不明显.对于K-H不稳定性, 即便可压缩性通常会使界面稳定[20], 受限区域里的声波共振效应也可引起高波数扰动增长率的增大[21].声波共振效应可用以解释在主弓形激波和液滴迎风界面之间的波状声波, 以及液滴内部的高波数声波形态.这些声波与K-H不稳定性相关的证据是, 它们在改进模拟的结果中几乎都消失了.基于线性理论的简单预测显示, 这些声波因其增长率相对较小而不起太大的作用[21].不管怎样, 为了详细研究这些效应, 针对液滴气动破碎中期和后期的高分辨率数值模拟将是必要的[22].
4 结论本文采用守恒锐界面方法, 对空气中的一个二维水滴被Mach数为3的运动平面激波驱动问题进行了数值分析, 给出了气动破碎初期界面演化特性.引入线性稳定性分析理论, 并构造了一项改进的数值模拟, 详细对比探讨了R-T不稳定性和K-H不稳定性在液滴超声速气动破碎初期过程中的作用.研究表明:
(1) 初期界面不稳定性发展可分成3个阶段, 主导扰动源于驻点和外环之间中段附近处, 并受到R-T不稳定性和K-H不稳定性的共同作用;
(2) R-T不稳定性主导引起了界面的径向运动, 迎风界面的径向运动比下游界面更显著, 而K-H不稳定性对于高波数扰动的贡献大于R-T不稳定性;
(3) 在初期界面不稳定性发展的末段, 在主弓形激波和液滴迎风界面之间构成了受限区域, 声波共振效应是该区波状声波以及液滴内部高波数声波形态的形成机制.
| [1] |
刘金元, 祝成民. 脉冲爆震发动机流动形态与推力相关性研究[J]. 兵器装备工程学报, 2018, 39(3): 51-56. Liu J Y, Zhu C M. Investigation of correlation between flow structure and thrust of pulse detonation engine[J]. Journal of Ordnance Equipment Engineering, 2018, 39(3): 51-56. DOI:10.11809/bqzbgcxb2018.03.011 (in Chinese) |
| [2] |
张永亮, 范文欣, 田野. 气液压弹射动力学影响参数分析[J]. 四川兵工学报, 2015, 36(1): 56-59. Zhang Y L, Fan W X, Tian Y. Study on dynamic ejection force of numerical parameters of pneumatic and hydraulic launching[J]. Journal of Sichuan Ordnance, 2015, 36(1): 56-59. DOI:10.11809/scbgxb2015.01.016 (in Chinese) |
| [3] |
Harper E Y, Grube G W, Chang I D. On the breakup of accelerating liquid drops[J]. Journal of Fluid Mechanics, 1972, 52(3): 565-591. |
| [4] |
Joseph D D, Belanger J, Beavers G S. Breakup of a liquid drop suddenly exposed to a high-speed airstream[J]. International Journal of Multiphase Flow, 1999, 25(6/7): 1263-1303. |
| [5] |
Theofanous T G. Aerobreakup of Newtonian and viscoelastic liquids[J]. Annual Review of Fluid Mechanics, 2011, 43(1): 661-690. |
| [6] |
Theofanous T G, Li G J. On the physics of aerobreakup[J]. Physics of Fluids, 2008, 20(5): 052103. DOI:10.1063/1.2907989 |
| [7] |
Theofanous T G, Li G J, Dinh T N. Aerobreakup in rarefied supersonic gas flows[J]. Journal of Fluids Engineering, 2004, 126(4): 516-527. DOI:10.1115/1.1777234 |
| [8] |
Hu X Y, Adams N A, Iaccarino G. On the HLLC Rie-mann solver for interface interaction in compressible multi-fluid flow[J]. Journal of Computational Physics, 2009, 228(17): 6572-6589. DOI:10.1016/j.jcp.2009.06.002 |
| [9] |
Hu X Y, Khoo B C, Adams N A, et al. A conservative interface method for compressible flows[J]. Journal of Computational Physics, 2006, 219(2): 553-578. |
| [10] |
Osher S, Sethian J A. Fronts propagating with curvature-dependent speed:algorithms based on Hamilton-Jacobi formulations[J]. Journal of Computational Physics, 1988, 79(1): 12-49. |
| [11] |
Fedkiw R P, Aslam T, Merriman B, et al. A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method)[J]. Journal of Computational Physics, 1999, 152(2): 457-492. |
| [12] |
Chang C H, Liou M S. A robust and accurate approach to computing compressible multiphase flow:stratified flow model and AUSM+-up scheme[J]. Journal of Computational Physics, 2007, 225(1): 840-873. |
| [13] |
Chang C H, Deng X L, Theofanous T G. Direct numerical simulation of interfacial instabilities:a consistent, conservative, all-speed, sharp-interface method[J]. Journal of Computational Physics, 2013, 242: 946-990. DOI:10.1016/j.jcp.2013.01.014 |
| [14] |
Han L H, Hu X Y, Adams N A. Adaptive multi-resolu-tion method for compressible multi-phase flows with sharp interface model and pyramid data structure[J]. Journal of Computational Physics, 2014, 262: 131-152. DOI:10.1016/j.jcp.2013.12.061 |
| [15] |
Kull H J. Theory of the Rayleigh-Taylor instability[J]. Physics Reports, 1991, 206(5): 197-325. DOI:10.1016/0370-1573(91)90153-D |
| [16] |
Sharp D H. An overview of Rayleigh-Taylor instability[J]. Physica D:Nonlinear Phenomena, 1984, 12(1/3): 3-10, IN1-IN10, 11-18. |
| [17] |
Sohn S I. Vortex model and simulations for Rayleigh-Taylor and Richtmyer-Meshkov instabilities[J]. Physical Review E, 2004, 69(3): 036703. DOI:10.1103/PhysRevE.69.036703 |
| [18] |
Bernstein I B, Book D L. Effect of compressibility on the Rayleigh-Taylor instability[J]. Physics of Fluids, 1983, 26(2): 453-458. DOI:10.1063/1.864158 |
| [19] |
Livescu D. Compressibility effects on the Rayleigh-Taylor instability growth between immiscible fluids[J]. Physics of Fluids, 2004, 16(1): 118-127. |
| [20] |
Gerwin R A. Stability of the interface between two fluids in relative motion[J]. Reviews of Modern Physics, 1968, 40(3): 652-658. DOI:10.1103/RevModPhys.40.652 |
| [21] |
Rajaee L, Shokri B. Resonant instability of tangential discontinuity in a compressible fluid[J]. Journal of Physics D:Applied Physics, 2007, 40(11): 3512-3517. DOI:10.1088/0022-3727/40/11/038 |
| [22] |
马英杰, 郝继光. 水液滴撞击导流面成膜过程数值模拟[J]. 兵器装备工程学报, 2017, 38(3): 175-179. Ma Y J, Hao J G. Numerical simulation of liquid film formed by a water droplet impinging onto a diversion surface[J]. Journal of Ordnance Equipment Engineering, 2017, 38(3): 175-179. DOI:10.11809/scbgxb2017.03.039 (in Chinese) |



