| 基于自适应模糊滑模观测器的永磁同步电机无位置传感器运行 |
2. 江苏科技大学 电子信息学院,镇江 212003
2. School of Electrical and Information, Jiangsu University of Science and Technology, Zhenjiang 212003, China
当下永磁同步电机多采用PID或其改进的算法控制。文献[1]提供了电梯用永磁同步电机BP神经网络PID调速控制方法的研究,利用BP神经网络改进PID,其控制效果相对于传统PID来说精度有所提高。文献[2]介绍了永磁同步电机的模型预测电流控制器研究,提出了表贴式永磁同步电机的模型预测电流控制法,实现了对电流的前馈和反馈控制,本质上也是一种改进的PID控制器。文献[3]提出了一种永磁同步电机变论域自适应模糊PID控制,通过变论域模糊控制来实现控制参数自整定和控制规则的自调整。该算法较为复杂,虽控制性能良好,但不易于实现。文献[4]介绍了永磁同步电机单神经元自适应PID控制,利用神经元自适应来改进PID,其鲁棒性有所提高,但是相对于传统PID动态响应速度有所下降。文献[5]提出基于模糊PID控制的永磁同步电机控制器研究。模糊PID相对于其他的智能改进型的PID来说是目前比较成熟的一种算法,但其模糊规则相对比较复杂。文献[6]提出一种永磁同步电机伺服控制系统的灰色PID控制,设计出一种结合传统PID控制与灰色预测补偿的灰色PID控制器,由于灰色预测对未知量的处理能力较强,所以其抗干扰能力比较出色,但与此同时,它的响应速度却有所下降。以上六种方案都是在传统PID的基础上利用各种先进的算法进行改进,其性能都只是略微提高,并且这些方案由于算法的复杂性,其鲁棒性并不是很强。
针对以上问题,提出了基于自适应模糊滑模观测器的永磁同步电机无位置传感器运行。利用模糊控制对滑模增益设计了模糊控制规则,根据滑模变结构选取了滑膜面,并搭建自适应模糊滑模观测器的永磁同步电机无位置传感器运行实验平台。实验结果表明,提出的自适应模糊滑模观测器的永磁同步电机无位置传感器运行精度高、性能稳定。
1 永磁同步电机控制系统根据永磁同步电机工作原理,可以得到永磁同步电机分析模型,如图 1所示。其中d-q轴为实际转子位置,θ为实际转子位置角。
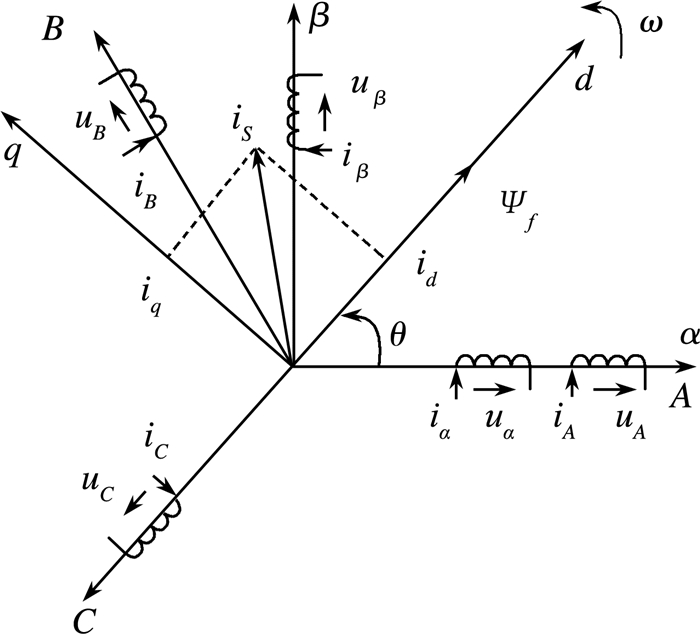 |
| 图 1 永磁同步电机分析模型 |
在α-β参考轴坐标系下的永磁同步电机动态模型可以表示如下:
| $ {{\dot i}_\alpha } = - \frac{R}{L}{i_\alpha } + \frac{{{\psi _f}}}{L}\omega \sin \theta + \frac{{{u_\alpha }}}{L} $ | (1) |
| $ {{\dot i}_\beta } = - \frac{R}{L}{i_\beta } + \frac{{{\psi _f}}}{L}\omega \sin \theta + \frac{{{u_\beta }}}{L} $ | (2) |
| $ \dot \theta = \omega $ | (3) |
| $ \dot \omega = - \frac{B}{J}\omega + \frac{{P_n^2{\psi _f}}}{L}{i_\beta }\cos \theta - \frac{{P_n^2{\psi _f}}}{L}{i_\alpha }\sin \theta - \frac{{{P_n}}}{J}{T_L}. $ | (4) |
式中:uα和uβ分别为α和β轴定子电压;iα和iβ分别为α和β轴定子电流;L为定子绕组电感;R为定子电阻;ψf为永磁体的磁通;Pn为极对数;TL为负载转矩;J为转动惯量;B为阻尼系数;ω为转子速度。
在d-q参考轴坐标系下的永磁同步电机数学模型可以表示如下:
| $ \frac{{di}}{{dt}} = Ai + Bu + D $ | (5) |
式中:
永磁同步电机的电流闭环系统如图 1所示。iq的值由
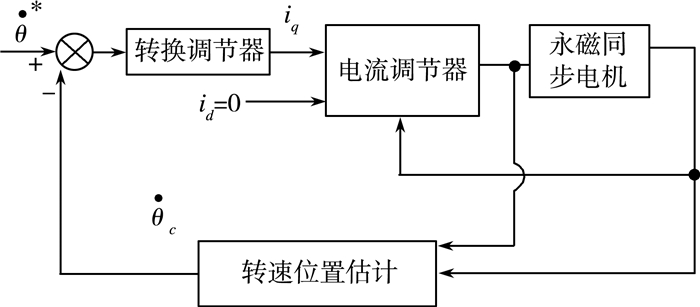 |
| 图 2 永磁同步电机电流闭环系统 |
2 自适应滑模观测器 2.1 自适应模糊滑模观测器的设计
永磁同步电机在α-β坐标系下的状态方程:
| $ \left\{ \begin{array}{l} \frac{{d{i_\alpha }}}{{dt}} = - \frac{{{R_s}}}{{{L_s}}}{i_\alpha } + \frac{1}{{{L_s}}}{u_\alpha } - \frac{1}{{{L_s}}}{e_\alpha }\\ \frac{{d{i_\beta }}}{{dt}} = - \frac{{{R_s}}}{{{L_s}}}{i_\beta } + \frac{1}{{{L_s}}}{u_\beta } - \frac{1}{{{L_s}}}{e_\beta } \end{array} \right. $ | (6) |
反电势方程:
| $ \left\{ \begin{array}{l} {e_\alpha } = - {\psi _f}\omega \sin \theta \\ {e_\beta } = {\psi _f}\omega \cos \theta \end{array} \right. $ | (7) |
定义滑模切换函数:
| $ s\left( x \right) = \begin{array}{*{20}{c}} {\left\lceil {{{\hat i}_\alpha } - {i_\alpha }} \right\rceil }\\ {\left\lfloor {{{\hat i}_\beta } - {i_\beta }} \right\rfloor } \end{array} $ | (8) |
式中:
| $ \left\{ \begin{array}{l} \frac{{d{{\hat i}_\alpha }}}{{dt}} = - \frac{{{R_s}}}{{{L_s}}}{{\hat i}_\alpha } + \frac{1}{{{L_s}}}{u_\alpha } - \frac{{{k_s}}}{{{L_s}}}sign\left( {{{\hat i}_\alpha } - {i_\alpha }} \right)\\ \frac{{d{{\hat i}_\beta }}}{{dt}} = - \frac{{{R_s}}}{{{L_s}}}{{\hat i}_\beta } + \frac{1}{{{L_s}}}{u_\beta } - \frac{{{k_s}}}{{{L_s}}}sign\left( {{{\hat i}_\beta } - {i_\beta }} \right) \end{array} \right. $ | (9) |
构造李雅普诺夫函数为:
| $ V = {s^T}s/2 $ | (10) |
则自适应模糊滑模观测器的稳定条件为:
| $ \dot V = {s^T}\dot s \le 0 $ | (11) |
则自适应模糊滑模观测器的稳定条件可以表示为:
| $ \begin{array}{l} \dot V = {s^T}\dot s = {s_\alpha }{{\dot s}_\alpha } + {s_\beta }{{\dot s}_\beta }\\ = \frac{1}{{{L_s}}}\left( {{{\hat i}_\alpha } - {i_\alpha }} \right)\left[ {{e_\alpha } - {k_s}sign\left( {{{\hat i}_\alpha } - {i_\alpha }} \right)} \right]\\ + \frac{1}{{{L_s}}}\left( {{{\hat i}_\beta } - {i_\beta }} \right)\left[ {{e_\beta } - {k_s}sign\left( {{{\hat i}_\beta } - {i_\beta }} \right)} \right]\\ - \frac{{{R_s}}}{{{L_s}}}\left[ {{{\left( {_\alpha ^{\hat i} - {i_\alpha }} \right)}^2} + {{\left( {_\alpha ^{\hat i} - {i_\alpha }} \right)}^2}} \right] \end{array} $ | (12) |
式(12)中,
| $ {k_s} > \max \left( {\left| {{e_\alpha }} \right|,\left| {{e_\beta }} \right|} \right) $ | (13) |
自适应模糊滑模观测器原理图如图 3所示。
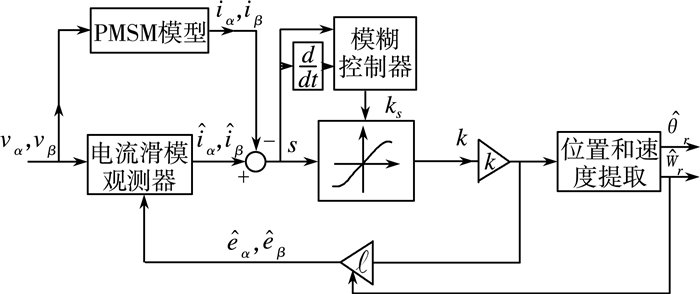 |
| 图 3 自适应模糊滑模观测器原理图 |
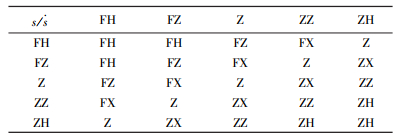
模糊控制系统的输入变量是s和
| 表 1 模糊控制规则 |
 |
3 实验结果
实验平台中所使用的永磁同步电机参数如表 2所示。
| 表 2 实验电机参数 |
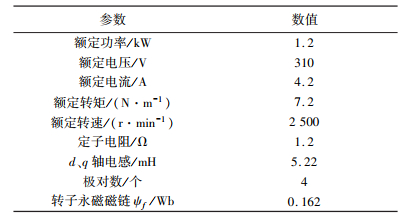 |
图 4是基于自适应模糊滑模观测器的永磁同步电机转子位置估算。
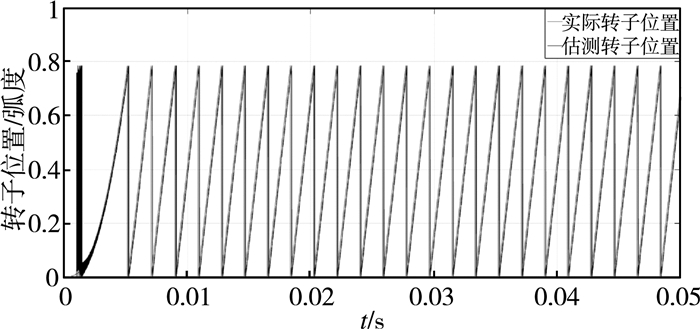 |
| 图 4 估算转子位置 |
图 5是基于自适应模糊滑模观测器的永磁同步电机转子位置估算误差。从图中可以看出误差稳定在一个范围值内,且误差较小、精度较高。
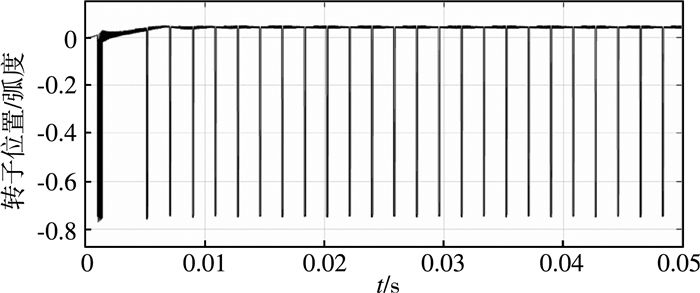 |
| 图 5 估算转子位置误差 |
4 结论
针对传统滑模观测器存在的抖振问题,提出了基于自适应模糊滑模观测器的永磁同步电机无位置传感器运行。
1) 为滑模增益制定了模糊控制规则。设计了自适应模糊滑模观测器,并利用李雅普诺夫定理给出了稳定条件。
2) 搭建实验平台,实验中发现转子位置估算精确度高。从而验证了所提出的基于自适应模糊滑模观测器的永磁同步电机无位置传感器运行的有效性。
| [1] |
王同旭, 马鸿雁, 聂沐晗. 电梯用永磁同步电机BP神经网络PID调速控制方法的研究[J]. 电工技术学报, 2015, 30(1): 43-47. |
| [2] |
王东文, 李崇坚, 吴尧, 等. 永磁同步电机的模型预测电流控制器研究[J]. 电工技术学报, 2014, 29(1): 73-79. |
| [3] |
崔家瑞, 李擎, 张波, 等. 永磁同步电机变论域自适应模糊PID控制[J]. 中国电机工程学报, 2013, 33(1): 190-194. |
| [4] |
西佳军, 孙斌, 赵化启. 永磁同步电机单神经元自适应PID控制[J]. 电力自动化设备, 2003, 24(10): 59-61. DOI:10.3969/j.issn.1006-6047.2003.10.017 |
| [5] |
欧峰, 陈洪, 陈胜来. 基于模糊PID控制的永磁同步电机控制器研究[J]. 计算机测量与控制, 2017, 25(4): 40-43. |
| [6] |
梁中华, 韩殷, 法乃光. 永磁同步电机伺服控制系统的灰色PID控制[J]. 沈阳工业大学学报, 2008, 30(6): 619-622;638. |
 2018, Vol. 32
2018, Vol. 32


