| 基于深度学习的信号调制自动识别 |
在通信技术日益进步的今天, 信号的调制方式也变得多种多样。无线信号传输过程中频率已定, 带宽已定, 只有得知信号的调制类型才能方可实现信号的解调或其他操作, 获得信号调制类型的这一技术被称为调制方式自动识别(Automatic Modulation Classification, 即AMC)[1]。
通常情况下, 调制方式识别技术分为两大类。基于假设检验的最大似然信号识别方法[1]和基于特征提取的统计模式信号识别方法[2]。最大似然算法理论上通过最小化误报概率来实现最佳识别性能, 识别率高表现性能好。但这类方法有以下缺点:
1) 最大似然算法需要事先了解信号的符号率、载波速率、信号功率、噪声功率、脉冲整形函数、信道响应信息等。
2) 计算量大。算法本身的计算量已经很大, 为能减小计算量导致算法中未知参数增多, 系统及时性不能保障。
3) 无法做到盲识别, 稳健性不够好。
统计模式信号识别的计算过程简单、实用。它主要分为三步。首先是分析预处理模块, 获取输入信号的特征, 然后对上一步中的参数训练恰当的分类器, 最后一步训练得到的分类器进行操作, 最终得到结果。现阶段这种方法应用范围比较广。该方法的缺点为:
1) 需要信号的长度足够长以保证信号携带调制信息。
2) 很难确定适应噪声影响的共同阈值。
3) 常因参数不足导致识别率过低。
星座图也是判定通信信号调制号类别的重要方法[3-4], 本文摒弃传统的AMC方法, 利用深度卷积神经网络优异的分类性能提出一种基于深度学习的多种信号调制自动识别方法。
1 系统模型系统提出的基于卷积神经网络的自动调制识别系统模型如图 1所示。
 |
| 图 1 帽形试样尺寸 |
输入信号经过系统的发送端, 经过解调器得到调制信号, 经过加性高斯白噪声信道传送到系统的接受端。信号经过系统的接受端的预处理器、星座图转换(Constellation Drawing Transform, 即CDT)模块, 以及VGGNet(Visual Geometry Group Network)识别模块, 识别出信号的调制方式, 解调器接收到调制信号以及信号的调制信息完成对信号的解调, 恢复原始信号。下文将对信号的信号模型、预处理模块、星座转算法模块、以及VGGNet模块做出说明。
1.1 信号模型幅度以及相位是信号的重要参数, CDT模块以及VGGNet通过幅相结合构成重要参数, 在时间Ts内, 接收端受到的信号的表达式为:
| $ \begin{array}{l} r(t) = \mathit{Re}\left[ {{s_l}(t)ej\left( {{w_c}t + {\varphi _c}} \right) + n(t)} \right]\\ = \mathit{Re}\left[ {\sum\limits_{k = 1}^N s (k)g\left( {t - (k - 1){T_s}} \right)ej\left( {{w_c}t + {\varphi _c}} \right) + n(t)} \right] \end{array} $ | (1) |
其中:
| $ {\theta _k} \in \left\{ {\frac{{2\pi }}{M}i, i = 0, \cdots , M - 1} \right\} $ |
公式1中表示的数字通信信号对应的复包络信号r(t)为:
| $ \begin{array}{l} \begin{array}{*{20}{c}} {r(t) = {s_l}(t)ej\left( {{w_c}t + {\varphi _c}} \right) + n(t)}\\ { = \sum\limits_{k = 1}^N s (k)g\left( {t - (k - 1){T_s}} \right)ej\left( {{w_c}t + {\varphi _c}} \right)} \end{array}\\ + n\left( t \right) \end{array} $ | (2) |
其中:
| $ {\theta _k} \in \left\{ {\frac{{2\pi }}{M}i, i = 0, \cdots , M - 1} \right\} $ |
式中g(t)为脉冲信号, s(k)表示恢复出的码元, sl(t)为复基带信号, Ts为码元时间间隔, N是码元数目。
公式1中r(t)采样可得到r(n), r(n)又是下一模块的输入。由此可以得到我们下一模块-预处理模块的流程如下。
1.2 预处理模块图 2为信号预处理流程图。
 |
| 图 2 预处理模块 |
预处理模块首先对信号序列r(n)进行离散傅里叶变换。
| $ \hat f = \frac{{{f_s}\sum\limits_{i = 0}^{\frac{N}{2} - 1} i |X(i)|2}}{{N\sum\limits_{i = 0}^{\frac{N}{2} - 1} {|X(i)|2} }} $ | (3) |
公式(3)对信号式中fs是中频信号采样频率, N是截断信号中包含的采样点数, 最重得到信号的频谱。
带宽估计用于信号进行低通滤波, 带宽精度不高, 可以在FFT变换中的粗略估计中获得。之后信号经下变频和低通滤波去除载波影响;然后进行符号率估计, 根据信号的带宽Bw设置符号率谱线的搜索范围为Bw/2范围内对符号率进行估计, 然后确定最优的时间点对r(n)采样, 最后可得到原始的r(n)[5]。
预处理模块在完成上述操作后可恢复出码元数据矩阵R=[r[1]r[2]…, r[N]]T, 其中r[k]=[r[k]ir[k]q], k=1, 2…, N是一个二维向量, r[k]i
表示数量为k个的码元信号的正分量, N为码元数目。预处理模块对输入信号进行分析处理并得到矩阵R, 此模块可以r[k]i为横坐标, 以r[k]q为纵坐标恢复出的码元矩阵R即得到接收端信号的星座图。
1.3 CDT模块从数字图像处理的概念来看, 图像识别的大小在深度学习中受到限制, CDT模块可以将恢复的符号序列投影到长度为L的人造图像的大小。CDT模块有两步, 首先将图片按照固定宽度进行分解, 宽度由码元序列样点值确定;第二步将码元进行分配, 以正交分量和同向分量为依据配置到合适的区域[6]。
单位小网格的宽度取决于L的大小和恢复的符号序列的样本值。基于同相和正交分量将每个符号划分为特定区域。星座图投影算法中L的值表示将图片划分为L*L个区域, 具体步骤如下:
1) 预处理后的复信号码元表示为r(k), k=1, 2, …, N, 这些复信号组成输入矩阵R=[r[1]r[2]…, r[N]]T, 其中N为码元数。
2) 对输入矩阵进行分析计算:
| $ \begin{array}{l} Q = {\mathop{\rm real}\nolimits} [R]I = {\mathop{\rm imag}\nolimits} [R]\\ {Q_d} = \frac{{{Q_{\max }} - {Q_{\min }}}}{L}\\ {I_d} = \frac{{{I_{\max }} - {I_{\min }}}}{L}\\ {Q_b} = {Q_{\min }} - {Q_d}\\ {I_b} = {I_{\max }} - {I_d} \end{array} $ | (4) |
Qmax是信号中正交分量的最大值, 同理Qmin为最小值, 而I则表示的是通向分量。Qb以及Ib则是最大值与最小值之间的长度。
3) 对于每一个r(k), 计算:
| $ \begin{array}{l} {Q_n}(k) = \left[ {\left( {{\mathop{\rm real}\nolimits} (r(k)) - {Q_b}} \right)/{Q_d}} \right]\\ {I_n}(k) = \left[ {\frac{{{\mathop{\rm imag}\nolimits} (r(k)) - {I_b}}}{{{I_d}}}} \right] \end{array} $ | (5) |
如果Qn(k)=L+1则In(k)=L。
4) 形成图片化星座图, 对于每一个数据
| $ \begin{array}{*{20}{l}} {\left[ {{Q_n}(k), {I_n}(k)} \right]:}\\ {\quad \mathit{mapdata}\left( {{Q_n}(k), {I_n}(k)} \right)}\\ {\quad = \mathit{mapdata}\left( {{Q_n}(k), {I_n}(k)} \right) + 1} \end{array} $ | (6) |
得到输出L×L的输出矩阵。
在CDT模块中, 将码元投影到图片上的方法简单方便。利用此方法得到的图片输入到VGGNet分类器完成分类工作, 得到信号的调制方式。当经过CDT模块后, 信号的特征就转化为图片的特征, 算法复杂度低。
1.4 VGG网络模型卷积神经网络(Convolution Neural Network, CNN)是一种前向反馈的多层神经网络。一般网络结构的深度与提取特征的能力成正比, 若复杂度与时间成正比, 卷积核的大小与网络的深度相比, 网络深度更加重要。VGG通过小卷积核串联卷积层进而深度网络结构, 并通过这种方式提升网络性能。
VGG网络的模型图如图 3所示:
 |
| 图 3 VGG神经网络参数表 |
本文选取VGG-19网络进行训练, 正如上图所示, 包含16个卷积层, 5个下采样层和3个全连接层。卷积层均采用3*3的卷积核。采样层通过最大值进行采样, filter大设置为3*3, 固定步长为3, 激活函数采用ReLU函数。
2 仿真结果分析 2.1 数据集预备为了获得针对通信信号调制方式分类的神经网络模型, 需要获取大量的星座图作为监督训练的样本数据。在神经网络模型中, 测试样本以及训练样本为在不同信噪比环境下不同调制方式的经过标注的星座图。本文所使用的数据集采用Matlab仿真平台, 对通信系统中常见的MPSK和MQAM信号进行仿真, 其中包括4PSK、8PSK、16PSK、4QAM、8QAM、16QAM、32QAM、64QAM、128QAM、64QAM这10种信号进行仿真。
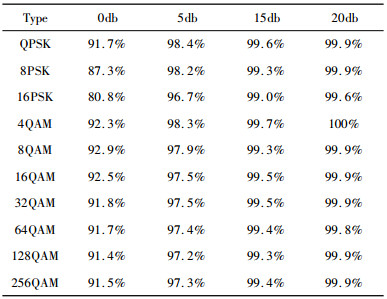
2.2 模型训练与测试在本文中, VGG-16网络应该通过最广泛使用的Tensorflow框架构建。我们略微改变了VGG-16网络的三层, 将网络的输出层1 000改为与信号调制类型一致的数字10, 并将整个连接层的第17层和第8层的神经元数量减少到512, 因为原来4 096个神经元在实际训练中总是导致收敛的困难。除了改变基本结构外, 还针对信号调制优化了一些网络参数。训练集样本数为2 500, 测试集样本数为500, SNR范围为0-20 db。在该模拟中, 采用高斯白噪声信道。VGG-16神经网络采用准备好的数据集进行训练, 学习率α=0.01, 优化算法采用动量优化算法[7], 训练结果显示在表 1中。可以看出, 当SNR超过5 db时, MPSK类的调制信号可以达到96%的精度, 而当SNR为0 db时, MQAM类的调制信号可以达到91%的准确度, 97%的识别精度。当SNR为20 db时, SNR为5 db, 精度为99%。通过分析tabel1的识别结果, 可以发现, 在相同的SNR条件下, 识别精度随着调整顺序的增加而略有下降。随着SNR的增加, 六种调制方法的准确性得到显着提高。当SNR大于5时, 这些调制方法的识别精度高于96%。
| 表 1 识别准确率 |
 |
为了证明该算法在识别精度方面的优越性, 该方法与基于SVD和AF主脊(SVD-AF)方法的雷达发射信号识别一起使用[8], 基于模糊函数的雷达信号识别特征和云模型相似性(AF_CMS)[9], 以及基于模糊函数特征和云模型相似性(MWC_STFT)[10-11]和AlexNet模型的雷达信号Echo用于比较。我们通过上述方法选择16PSK和16QAM信号进行调制识别。图 4为用于测试的不同信噪比下的16QAM信号的星座图, 图 5为用于测试的不同信噪比下的16PSK信号的星座图。
 |
| 图 4 用于测试的不同信噪比下的16QAM信号的星座图 |
 |
| 图 5 用于测试的不同信噪比下的16PSK信号的星座图 |
如图 6和图 7所示, 本文使用的VGG-16网络模型在0 db时的16PSK信号的总识别率分别为80.8%和92.5%, 20 db的识别准确率分别为99.6%和99.9%。
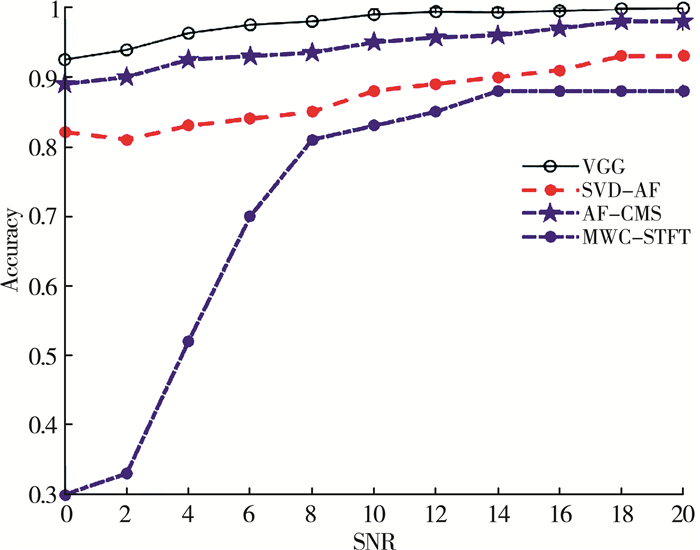 |
| 图 6 16QAM信号在不同方法下的识别准确率 |
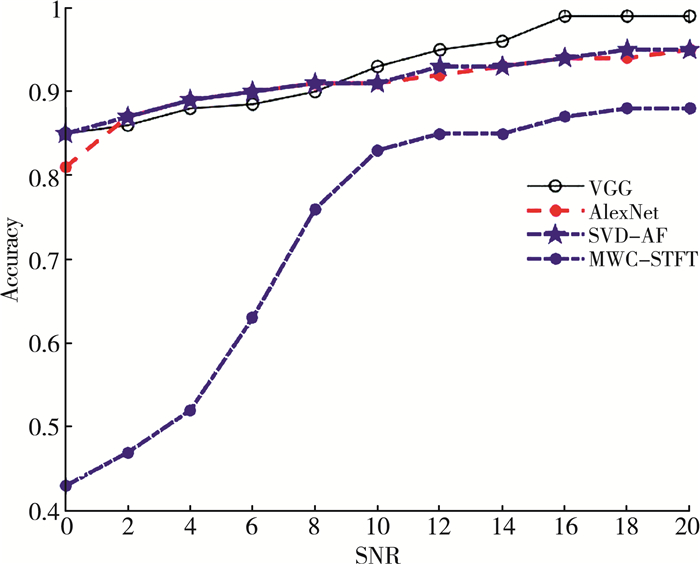 |
| 图 7 16PSK信号在不同方法下的识别准确率 |
SVD-AF, AF-CMS和MWC-STFT中16PSK信号的识别率分别为82.3%, 88.7%和30%。当SNR为20 dB时, SVD-AF, AlexNet和MMWC-STFT的识别率分别为91.3%, 98.4%和83.3%。SVD-AF, AlexNet和MMWC-STFT的信噪比下16QAM信号识别率分别为81.9%, 85.4%和42.3%, 识别准确率分别为95.1%, 95.1%和88%。信噪比为20 db。
通过比较, 可以看出上述方法对信号特征的提取有限且对噪声敏感, 不如VGGNet方法的信号特征的完全提取和良好的抗噪性能。
3 结束语调制方式作为区分不同系统通信信号的重要特征, 是通信信号调制识别的基本任务, 具有重要的研究意义。基于深度卷积神经网络的信号调制自动识别技术避免了传统算法中特征提取和选择的问题, 实现了分类特征的自学习和调制方式识别。仿真结果表明算法有效可行。研究结果发现:在低信噪比的情况下, 算法的性能稳定性存在一些问题, 并且不同调制的识别能力存在差异, 这是下一步的研究重点。
| [1] |
LIU A, ZHU Q.. Automatic modulation classification based on the combination of clustering and neural network[J]. The Journal of China Universities of Posts and Telecommunications, 2011, 18(04): 251-27. |
| [2] |
POLYDOROS A, KIM K. On the detection and classification of quadrature digital modulations in broad-band noise[J]. IEEE Transactions on Communications, 1990, 38(8): 1199-1211. DOI:10.1109/26.58753 |
| [3] |
LIEDTKE F F. Computer simulation of an automatic classification procedure for digitally modulated communication signals with unknown parameters[J]. Signal Processing, 1984, 6(4): 311-323. DOI:10.1016/0165-1684(84)90063-X |
| [4] |
BIJAN G.MOBASSERI. Digital modulation classification using constellation shape[J]. Signal Processing, 2000, 80(2): 251-227. DOI:10.1016/S0165-1684(99)00127-9 |
| [5] |
SCHREYOGG, C., REICHERT, J.Modulation classification of QAM schemes using the DFT of phase histogram combined with modulus information[P].MILCOM 97 Proceedings, 1997: 1372-1376.
|
| [6] |
BOITEAU, D., Le Martret, C.A general maximum likelihood framework for modulation classification[P].Acoustics, Speech and Signal Processing, 1998.Proceedings of the 1998 IEEE International Conference on, 1998: 2165-2168.
|
| [7] |
HINTON G E. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-7. DOI:10.1126/science.1127647 |
| [8] |
GUO QIANG, NAN PU-LONG, et al. Recognition of radar emitter signals based on SVD and A F main ridge[J]. Journal of Communications and Networks, 2015, 17(5): 491-498. DOI:10.1109/JCN.2015.000087 |
| [9] |
GUO QIANG, NAN PU-LONG, WAN JIAN.Radar signal recognition based on ambiguity function features and c loud model similarity[C]IEEE International Conference on Ultrawideb and & Ultrashort Impulse Signals, O dessa, Ukraine, 2016: 128-134.
|
| [10] |
CHEN TAO, LIU LI-ZHI, GUO LI-MIN. Intra-pulse modulation recognition of radar signals based on MWC compressed sampling wideband receiver[J]. Journal of Electonic & Informatin Technology, 2018, 40(4): 867-874. |
| [11] |
ZHANG MING, LIU LU-TAO, DIAO MING. LPI radar waveform recognition based on time-frequency distributin[J]. Sensor, 2016, 16(10): 1682-1688. DOI:10.3390/s16101682 |
 2020, Vol. 34
2020, Vol. 34


