| 基于多属性决策的电力通信网可靠性评估方法 |
2. 漳州供电公司,漳州 363000
2. Zhangzhou Provincial Electric Power Company, Zhangzhou 363000, China
电力通信网是电网安全稳定可靠运行的三大支柱之一[1], 在电网大规模互联的趋势下, 电网的规模越来越大, 电力通信网规模也日益庞大, 结构愈加复杂, 电力通信网面临的风险也越来越多。因此, 如何采用合理的方法评估电力通信网的可靠性, 具有越来越重要的研究意义[2]。现阶段对于电力通信网的可靠性研究也取得了一定的成果:文献[3]从非冗余系统、完全冗余系统、部分冗余系统以及备用系统的可靠性模型出发, 分析建立了典型电力通信系统的可靠性模型;文献[4]通过研究层次的划分, 提出了以网络拓扑层、网络设备层、网络路由层、网络运行层作为测度指标, 分析电力通信网的可靠性;文献[5]基于复杂网络理论, 对电力通信网进行建模, 拓扑统计特性分析, 评估电力通信网的可靠性;文献[6]构建效能模型, 依据网络效能变化, 间接反映电力通信网可靠性变化;这些研究从各个方面研究了电力通信网的可靠性, 在通信网的规划维护方面也起了较大的作用, 但是由于考虑因素比较单一, 因此不能全面评价电力通信网可靠性。
构建电力通信网可靠性指标评价体系, 从网络拓扑, 通信设备, 运行环境, 运维管理等指标评估电力通信网的可靠性, 在每个指标下又细分了多个小的指标, 分层次进行分析。较为全面的考虑电力通信网可靠性影响因素。采用主观和客观相结合的方法计算各个指标的权重, 最后采用多属性决策的方法, 评价出通信网可靠性。
1 电力通信网可靠性评估体系的构建电力通信网可靠性评估体系的构建需要遵循一定的原则。既要保证实用性, 又要保证其完整性和必要性。这就要求指标体系含义明确, 评价全面, 指标不能出现冗余[7]。依据这一原则, 针对电力通信网的特点, 从网络拓扑, 通信设备, 运行环境, 运维管理四个方面, 构建电力通信网可靠性评估指标体系。如图 1所示。
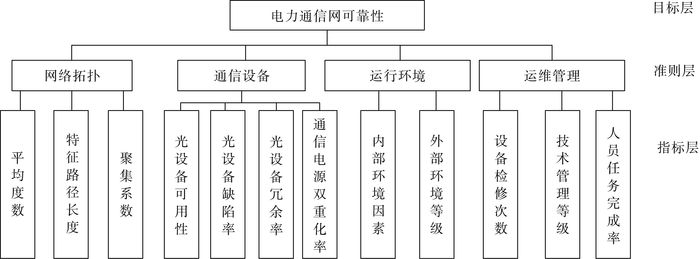 |
| 图 1 电力通信网可靠性评估指标 |
1.1 网络拓扑
基于图论的方法, 构建电力通信网网络拓扑图, 设G=(V, E)为网络的拓扑结构, 其中, V={v1, v2, …, vN}是网络节点集, |V|=N。E={e1, e2, …, eM}是网络无向链路集[8], |E|=M。使用平均度数, 特征路径长度, 聚集系数几个指标评判电力通信网网络拓扑可靠性, 其概念如下:
1) 平均度数
平均每个节点连接的通信线路数, 反映了网架的强度。计算公式为:
| $ K = 2M/N $ |
其中, K为平均度数, M为通信网中边数, 即通信线路数目, N为通信网中节点数, 即通信站点数目。
2) 特征路径长度
最短路径算法下, 通信网中任意2个站点间进行通信所需的平均跳数[9]。计算公式为:
| $ L = \frac{1}{{N\left( {N - 1} \right)}}\sum\limits_{i \ne j} {{d_{ij}}} $ | (1) |
其中, L为特征路径长度, N表示通信站点数目;dij表示在最短路径算法下节点i到节点j所经过的节点数目。
3) 聚集系数
描述节点与其邻接节点之间相互连接的程度。节点i的局部聚集系数表示为:
| $ C\left( i \right) = \frac{{\lambda \left( i \right)}}{{\lambda \left( i \right) + \tau \left( i \right)}} $ | (2) |
其中, λ(i)与τ(i)分别表示与节点i相连的闭三角数与开三角函数[10]。
网络的全局聚集系数C等于所有节点局部聚集系数的平均值:
| $ C = \left[ {\sum\limits_{i = 1}^N {C\left( i \right)} } \right]/N $ | (3) |
| $ {U_1} = \frac{{{T_f}}}{{{T_r}}} $ |
通信设备细分为光设备可用性、光设备缺陷率、光设备冗余率、通信电源双重化率四个指标。
1) 光设备可用性
定义为设备在任意随机时刻处于可执行状态的能力[11]。可用下式计算:
| $ {U_1} = \frac{{{T_f}}}{{{T_r}}} $ | (4) |
其中, U1为光设备可用性, Tf为平均无故障工作时间, Tr为平均故障修复时间[11]。
2) 光设备缺陷率
| $ {U_2} = \frac{{光传输设备缺陷总次数}}{{所维护光传输设备总数}} \times 100\% $ | (5) |
3) 光设备冗余率
| $ {U_3} = \frac{{光设备中实现冗余的设备数}}{{光设备总数}} \times 100\% $ | (6) |
4) 通信电源双重化率
| $ {U_4} = \frac{{通信电源实现双重化站点数}}{{所辖通信站总数}} \times 100\% $ | (7) |
运行环境分为内部环境因素和外部环境等级两个细化指标。
1) 内部环境因素
| $ {V_1} = \frac{{环境合格机房数}}{{机房总数}} \times 100\% $ | (8) |
2) 外部环境等级
包括气象因素和地质因素[12]。综合主要气象灾害及地质灾害发生频率以及专家经验, 将外部环境等级分为三级, 分别对应0.8、0.9、0.95的打分。
1.4 运维管理运维管理因素包括设备检修次数, 技术管理等级, 人员任务完成率三个细化指标。
其中设备检修次数, 人员任务完成率均按照一年内统计数据计算, 技术管理等级按照专家打分的方法计算[13]。
2 电力通信网可靠性评价方法TOPSIS算法是一种多属性决策方法, 根据有限个评价对象与理想化目标的接近程度进行排序, 从而比较评价对象的优劣程度。将电力通信网不同的规划方案纳入该体系中进行比较, 可以评价出不同方案下电力通信网的可靠性。
基于多属性决策方法的电力通信网可靠性评价流程如图 2所示。
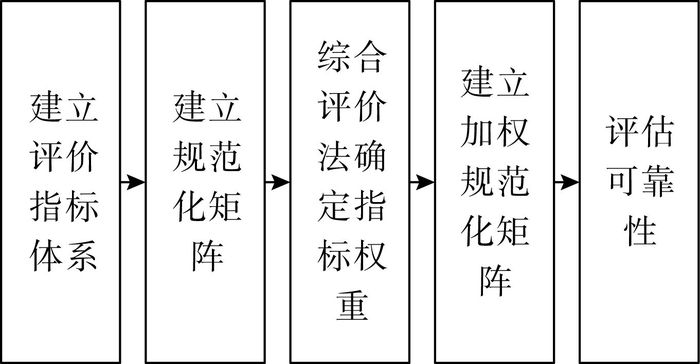 |
| 图 2 电力通信网可靠性评价流程 |
设依据电力通信网可靠性评价体系, 总共有P种方案, a表示准则层的第a项指标(例如:网络拓扑, 通信设备), 准则层每项指标下有m个分类细化指标(例如:平均度数, 特征路径长度, 聚集系数), i、j分别表示第i种方案, 第j个分类细化指标。
1) 构造规范化矩阵
构造第a项指标的决策矩阵Xa = (xij)P×m。
| $ {X_a} = \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1m}}}\\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2m}}}\\ \vdots&\vdots&\cdots&\vdots \\ {{x_{P1}}}&{{x_{P2}}}& \cdots &{{x_{Pm}}} \end{array}} \right] $ |
其中, xij为第i种方案的第j个分类细化指标的值, 为了消除量纲影响, 需要对决策矩阵Xa进行标准化处理, 构成规范决策矩阵Ra = (rij)P×m。
| $ {r_{ij}} = \frac{{{x_{ij}} - x_j^{\min }}}{{x_j^{\max } - x_j^{\min }}} $ | (9) |
| $ {r_{ij}} = \frac{{x_j^{\max } - {x_{ij}}}}{{x_j^{\max } - x_j^{\min }}}。$ | (10) |
对于效益型指标和成本型指标分别使用(9)(10)式进行计算, 其中, xjmax=max{xij|1≤i≤P}, xjmin=min{xij|1≤i≤P}。
2) 计算权重Wa向量
采用综合权重, 即将熵权法和层次分析法结合起来, 确定综合权重。
层次分析法将相同层的各个指标进行两两比较, 用专家打分的方式, 根据其重要性不同得到不同的分数。将准则层第a项指标下的各个分类细化指标两两比较, 构造出比较判断矩阵A。
根据各元素相对重要性的不同, 赋予其不同的值, 采用1~9及其倒数的标度方法, 如表 1所示。
| 表 1 判断矩阵标度表 |
 |
判断矩阵A的最大特征根λmax对应的特征向量w1, w1即是单排序权值[14]。
为了确保评价的合理性, 需要进行一致性检验, 计算一致性指标
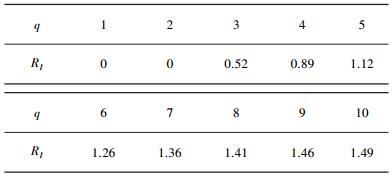
| 表 2 平均随机一致性指标 |
 |
通常认为CR<0.1时, 判断矩阵具有满意的一致性。将w1归一化, 得到每项分类细化指标的主观权重waj′。
熵权法是一种客观赋权法, 各个指标的权重是根据其所包含的信息量的大小来确定[15]。
计算第a项分类指标下的第j个分类细化指标的熵值eaj:
| $ {P_{ij}} = {r_{ij}}/\sum\limits_{i = 1}^P {{r_{ij}}} , $ | (11) |
| $ {e_{aj}} = - k\sum\limits_{i = 1}^P {{P_{ij}}\ln {P_{ij}}} , $ | (12) |
其中,
| $ {w_{aj''}} = \frac{{1 - {e_{aj}}}}{{\sum\limits_{j = 1}^m {\left( {1 - {e_{aj}}} \right)} }}。$ | (13) |
因此, 第j项分类细化指标的综合权重:
| $ {w_{aj}} = \frac{{{w_{aj'}}{w_{aj''}}}}{{\sum\limits_{j = 1}^m {{w_{aj'}}{w_{aj''}}} }}, $ | (14) |
其中, waj满足0≤waj≤1,
1) 构造加权规范化矩阵Ya
将权重向量乘入规范化矩阵, 构造加权规范化矩阵Ya。
| $ \begin{array}{l} \mathit{\boldsymbol{Y}}a = \left( {{y_{ij}}} \right) = \\ \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1m}}}\\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2m}}}\\ \cdots&\cdots&\cdots&\cdots \\ {{r_{i1}}}& \cdots &{{r_{ij}}}& \cdots \\ \cdots&\cdots&\cdots&\cdots \\ {{r_{P1}}}&{{r_{P2}}}& \cdots &{{r_{Pm}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{w_{a1}}}&0& \cdots &0\\ 0&{{w_{a2}}}& \cdots &0\\ \cdots&\cdots&\cdots&\cdots \\ 0& \cdots &{{w_{aj}}}& \cdots \\ \cdots&\cdots&\cdots&\cdots \\ 0&0& \cdots &{{w_{am}}} \end{array}} \right] \end{array} $ |
| $ \mathit{\boldsymbol{Y}}a = \left[ {\begin{array}{*{20}{c}} {{y_{11}}}&{{y_{12}}}& \cdots &{{y_{1m}}}\\ {{y_{21}}}&{{y_{22}}}& \cdots &{{y_{2m}}}\\ \cdots&\cdots&\cdots&\cdots \\ {{y_{i1}}}& \cdots &{{y_{ij}}}& \cdots \\ \cdots&\cdots&\cdots&\cdots \\ {{y_{P1}}}&{{y_{P2}}}& \cdots &{{y_{Pm}}} \end{array}} \right]。$ |
2) 计算相对贴近度
确定第j项分类细化指标的正负理想解。正理想解和负理想解分别用式(15)、(16)计算:
| $ {F_{a{j^ + }}} = \left\{ {\mathop {\max }\limits_{i \in L} \left( {{y_{i1}}, \cdots ,{y_{im}}} \right)} \right\} = \left\{ {y_1^{\max }, \cdots ,y_m^{\max }} \right\} $ | (15) |
| $ {F_{a{j^ - }}} = \left\{ {\mathop {\min }\limits_{i \in L} \left( {{y_{i1}}, \cdots ,{y_{im}}} \right)} \right\} = \left\{ {y_1^{\min }, \cdots ,y_m^{\min }} \right\} $ | (16) |
其中, L={1, …, P}。
然后, 计算每种方案到正负理想解的距离:
到正理想解和到负理想解的距离分别用公式(17)、(18)计算:
| $ D_{ai}^ + = \sqrt {\sum\limits_{j = 1}^m {{{\left( {{y_{ij}} - y_j^{\max }} \right)}^2}} } ,i = 1,2, \cdots P, $ | (17) |
| $ D_{ai}^ - = \sqrt {\sum\limits_{j = 1}^m {{{\left( {{y_{ij}} - y_j^{\min }} \right)}^2}} } ,i = 1,2, \cdots P $ | (18) |
最后计算第i种方案第a项指标的相对贴近度:
| ${Z_{ai}} = D_{ai}^ - /\left( {D_{ai}^ + + D_{ai}^ - } \right),i = 1,2, \cdots P$ | (19) |
根据式(19)可得到每种方案准则层各指标的相对贴近度, 分别计算出每种方案准则层网络拓扑相对贴近度Z1=[Z11, …, Z1i, …, Z1P]T, 通信设备相对贴近度Z2=[Z21, …, Z2i, …, Z2P]T, 运行环境相对贴近度Z3=[Z31, …, Z3i, …, Z3P]T, 运维管理相对贴近度Z4=[Z41, …, Z4i, …, Z4P]T,并以此作为电力通信网可靠性的指标值, 组成新的决策矩阵X。
| $ \mathit{\boldsymbol{X}} = \left[ {{\mathit{\boldsymbol{Z}}_1},{\mathit{\boldsymbol{Z}}_2},{\mathit{\boldsymbol{Z}}_3},{\mathit{\boldsymbol{Z}}_4}} \right] $ |
根据公式(9)、(10)进行规范化处理, 得到规范化决策矩阵R, 根据公式(11)至(14)计算权重向量W, 得到加权规范化矩阵Y, 最后根据公式(15)至(19)计算出每种方案相对贴近度Zi, 从而可以得出每种方案的可靠性。
3 算例分析选取某区域局部电力通信网作为评价对象。以2014年为例, 2015年为规划年。该区域有500 kV变电站5座, 220 kV变电站6座, 110 kV变电站2座。规划后, 新投入运营110 kV变电站1座。更换了使用年限长的设备, 增加了备用设备。对人员进行培训, 提高维护管理水平。
依据评价指标体系, 对规划前和规划后的指标进行计算。由于篇幅有限, 只列出了部分指标计算值, 结果如表 3所示。
| 表 3 评价指标数据(部分) |
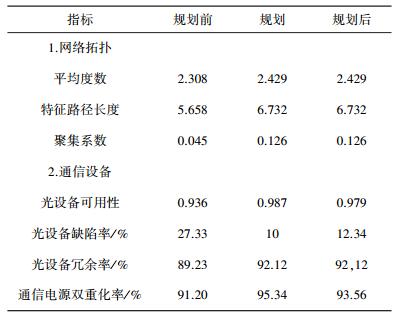 |
由规划前、规划和规划后的平均度数, 特征路径长度, 聚集系数的值, 可以构建网络拓扑指标的决策矩阵X1。
| $ {X_1} = \left[ {\begin{array}{*{20}{c}} {2.308}&{5.658}&{0.045}\\ {2.429}&{6.732}&{0.126}\\ {2.429}&{6.732}&{0.126} \end{array}} \right] $ |
对数据进行标准化处理, 得到规范化决策矩阵R1。
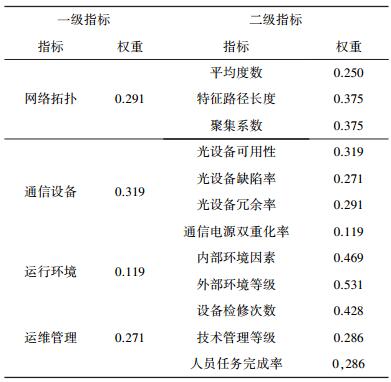
采用层次分析法和熵权法结合的方法, 求得各个指标的权重[16]。结果如表 4所示。
| 表 4 指标权重设置 |
 |
结合权重, 可求得加权规范化矩阵Y1。最后求得规划前、规划和规划后网络拓扑指标的相对贴近度Z1。
同样可以求得通信设备指标的相对贴近度Z2, 运行环境的相对贴近度Z3, 运维管理的相对帖进度Z4。构造可靠性的决策矩阵X=[Z1, Z2, Z3, Z4], 用同样的方法, 最后求得规划前、规划、规划后电力通信网可靠性评分。结果如表 5所示。
| 表 5 综合评分 |
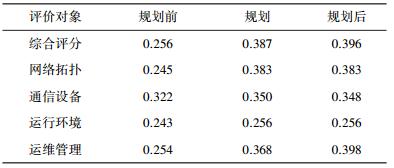 |
由仿真结果可以看出, 规划后电力通信网的可靠性得到了较大的提高。其中, 运维管理在规划后提高幅度较大, 这说明加强人员培训可以在短期内提高人员任务完成率, 是一种快速提高电力通信网可靠性的方法。网络拓扑也在一定程度上得到了提高, 因为增加投入运营的变电站, 使得通信网拓扑结构发生变化, 提高了其稳定性。通信设备也在规划后得到了较大幅度的提高, 因为光设备的更新替换以及增加冗余设备, 使得光设备缺陷率降低、可用性提高, 这也是提高电力通信网可靠性的较为简便可行的方法。
4 结语构建了电力通信网可靠性评估体系, 采用多属性决策算法, 将电力通信网的网络拓扑、通信设备、运行环境、运维管理情况结合起来, 最后评价出电力通信网的可靠性。
相对于以往的评价方法, 该方法既考虑了复杂网络的拓扑结构, 又考虑了设备、环境以及管理情况,评价更为全面。同时, 该方法具有很好的扩展性, 后续可以增加指标, 完善评价体系, 具有较大的应用价值, 为电力通信网的规划提供了重要依据。
| [1] |
姚致清. 通信规约实现与系统可靠性、安全性[J]. 电力系统保护与控制, 2008, 36(6): 68-70. DOI:10.7667/j.issn.1674-3415.2008.06.016 |
| [2] |
姚致清, 于飞, 赵倩, 等. 基于模块化多电平换流器的大型光伏并网系统仿真研究[J]. 中国电机工程学报, 2013, 33(36): 27-33. |
| [3] |
熊小伏, 田娟娟, 周家启, 等. 电力通信系统可靠性模型研究[J]. 电力系统保护与控制, 2007, 35(14): 28-32. |
| [4] |
黄邵远, 王斌, 田森平. 电力通信网可靠性工程的测度指标研究[J]. 电力系统通信, 2008, 29(10): 61-64. DOI:10.3969/j.issn.1005-7641.2008.10.016 |
| [5] |
刘涤尘, 冀星沛, 王波, 等. 基于复杂网络理论的电力通信网拓扑脆弱性分析及对策[J]. 电网技术, 2015, 39(12): 3615-3621. |
| [6] |
邓雪波, 王小强, 陈曦, 等. 基于效能模型的电力通信网可靠性研究[J]. 重庆邮电大学学报(自然科学版), 2012, 24(3): 378-382. DOI:10.3979/j.issn.1673-825X.2012.03.022 |
| [7] |
黄邵远, 王斌, 田森平. 电力通信网可靠性工程的测度指标研究[J]. 电力系统通信, 2008, 29(10): 61-64. DOI:10.3969/j.issn.1005-7641.2008.10.016 |
| [8] |
王江. 复杂网络的可靠性[J]. 电子技术与软件工程, 2017(3): 17. |
| [9] |
周仁, 任海鹏. 复杂网络系统的拓扑结构辨识方法[J]. 西安理工大学学报, 2017, 33(1): 80-85. |
| [10] |
周漩, 张凤鸣, 李克武, 等. 利用重要度评价矩阵确定复杂网络关键节点[J]. 物理学报, 2012, 61(5): 1-6. |
| [11] |
汤奕, 李峰, 王琦, 等. 通信系统故障对电力系统实时负荷控制影响的量化评价方法[J]. 电力自动化设备, 2017, 37(2): 90-96. |
| [12] |
樊冰, 唐良瑞. 电力通信网脆弱性分析[J]. 中国电机工程学报, 2014, 34(7): 1191-1197. |
| [13] |
赵子岩, 张书林, 李扬, 等. 电力通信运维体系建设的思考[J]. 电力信息与通信技术, 2013, 11(12): 58-61. DOI:10.3969/j.issn.1672-4844.2013.12.012 |
| [14] |
PATIL S K, KANT R. A fuzzy AHP-TOPSIS framework for ranking the solutions of knowledge management adoption in supply chain to overcome its barriers[J]. Expert Systems with Applications, 2014, 41(2): 679-693. DOI:10.1016/j.eswa.2013.07.093 |
| [15] |
聂宏展, 吕盼, 乔怡, 等. 基于熵权法的输电网规划方案模糊综合评价[J]. 电网技术, 2009(11): 60-64. |
| [16] |
娄云永. 电力通信网可靠性评价指标体系的研究[D]. 保定: 华北电力大学(保定), 2010.
|
 2017, Vol. 31
2017, Vol. 31

