| 一种基于偏置随机游走的属性网络嵌入方法 |
网络嵌入, 又叫做网络表示学习, 研究对象是现实世界中结构化的网络, 例如QQ等社交软件用户之间的构成的社交网络、蛋白质分子结构之间构成的生物网络、文献数据库中论文之间构成的引文网络等。机器学习能够有效的处理大量的矢量数据, 而网络数据作为生活中最普适、广泛的数据形式之一, 对其进行有效表示并且运用成熟的机器学习算法来分析网络数据也成为近几年数据挖掘和机器学习的研究热点[1]。本文将偏置随机游走策略结合属性网络的嵌入, 开展相关研究工作。
1 相关工作现实生活中很多数据可以用网络来建模, 对网络数据进行低维嵌入的研究也越来越受到重视。网络嵌入旨在将网络中每一个节点映射到一个低维、稠密、实值的向量空间中, 使在网络中相似的节点在新的向量空间中同样有相似的表示[2]。网络嵌入算法学习到的表示向量保留了网络的拓扑结构信息和节点的特征信息, 不仅可以克服网络数据的高维性、稀疏性, 更重要的是这些表示向量可以当做特征向量作为机器学习算法的输入进行网络分析任务来更深入的挖掘网络数据背后的信息, 从而有利于节点分类[3-4], 信息推荐[5], 链路预测[6]等各种应用任务。
较早的网络嵌入方法主要基于计算关系矩阵的特征向量和特征分解[7-8]。谱聚类算法通过对网络的邻接矩阵或者拉普拉斯矩阵进行特征分解得到节点的低维向量表示。这种基于谱聚类的方法时间复杂度比较高, 并且这种方法将关系矩阵整体存入内存中, 空间复杂度也比较高, 所以不能胜任大规模复杂网络的分析任务, 同时这类方法不能融合节点的属性信息。
最近基于随机游走与深度学习的网络嵌入方法被提了出来。DeepWalk[9]受语言模型Word2vec的启发, 中心词汇可以由上下文词汇来表示。DeepWalk采用截断随机游走的方式, 从网络中每个节点出发, 游走遍历网络中的其他节点得到若干节点序列, 根据窗口获取采样节点的上下文节点, 然后使用skip-gram模型最大化随机游走序列的似然概率。LINE[10]算法在图上定义了一阶相似度和二阶相似度, 最小化表示相似度与实际相似度的KL散度得到节点的表示。Node2vec[11]为了挖掘网络结构的局部特性和全局特性, 引入两个超参数p和q控制随机游走的策略, 得到特定的节点序列后也运用skip-gram模型学习节点表示。上述方法只考虑了网络的拓扑结构信息, 没有将节点的属性信息考虑进去。
现实世界中的网络通常包含节点的属性信息, 例如社交网络中用户的个人信息;论文引用网络中论文的关键词等。这些属性信息可以为网络嵌入提供很好的信息来源。TirDNR[12]、TADW[13]、GAT2VEC[14]综合运用了网络的结构信息和属性信息, 进一步提升了网络嵌入的效果。
Node2vec进行偏置随机游走得到特定的节点序列, 使表示向量更能反映网络的拓扑结构信息, 但是它没有考虑节点的属性信息。GAT2VEC在原网络生成的反映拓扑结构的结构图和结合属性信息的二部图上进行随机游走得到融合属性信息的节点序列, 运用skip-gram模型学习表示向量。但是GAT2VEC在结构图上随机游走时没有充分的考虑网络的局部信息和全局信息从而使表示学习结果不能准确表达网络的真实结构。
为了充分利用节点的属性信息, 并更好地捕捉网络的拓扑结构, 借鉴Node2vec和GAT2VEC模型, 提出一种基于偏置随机游走的属性网络嵌入方法ANEBRW。ANEBRW在结构图上进行偏置随机游走兼顾节点的局部特性和全局特性;在属性二部图上随机游走补充节点属性信息, 运用skip-gram模型学习到更高质量的节点表示, 并在节点分类实验中获得了较好的效果。
2 问题定义为了更好阐述所提出的算法, 首先给出相关定义:
定义1属性网络。给定属性网络G=(V, E, A), 其中V是网络节点的集合, E是网络的边的集合, A是属性集合。
定义2属性网络嵌入。在给定属性网络G的情况下, 网络嵌入的目标是学习一个映射函数Φ:V→Rd, 将G中每个节点vi(vi∈V)映射到一个低维、稠密实值的向量空间中, 其中d≪|V|, |V|是网络中节点的个数, Φ要保持网络的结构相似性和属性相似性。
3 基于偏置随机游走的网络嵌入ANEBRWANEBRW模型通过引入偏置游走参数来更好的捕捉网络的拓扑结构信息, 并且结合节点的属性信息共同学习网络的低维向量表示。本章按照图生成、随机游走和表示学习对ANEBRW模型进行详细介绍。
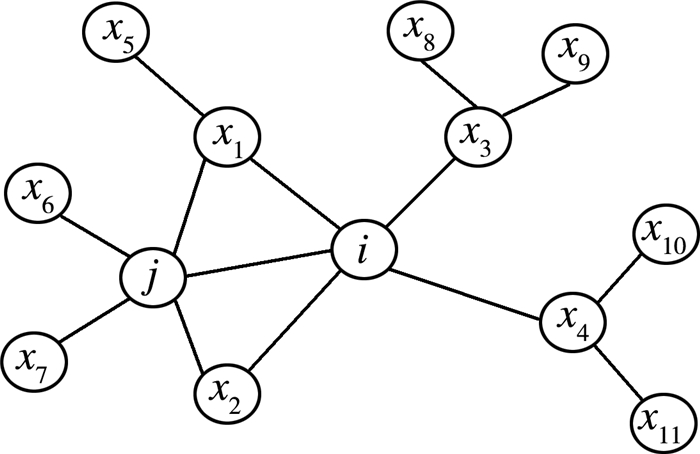
3.1 图生成根据原(图)网络, 如图 1所示, 生成一个结构图Gs和一个二部图Ga, 其中Gs=(Vs, Es)是由原网络中相连的节点构成的网络, 如图 2所示;Ga=(Va, A, Ea)是一个二部图, 其中Va∈V是原网络中带有属性的节点, A是属性节点, 最后Ea是连接Va和A的边集, 在Ga中有共同属性的节点会有边相连, 如图 3所示。
 |
| 图 1 属性网络G |
 |
| 图 2 结构图GS |
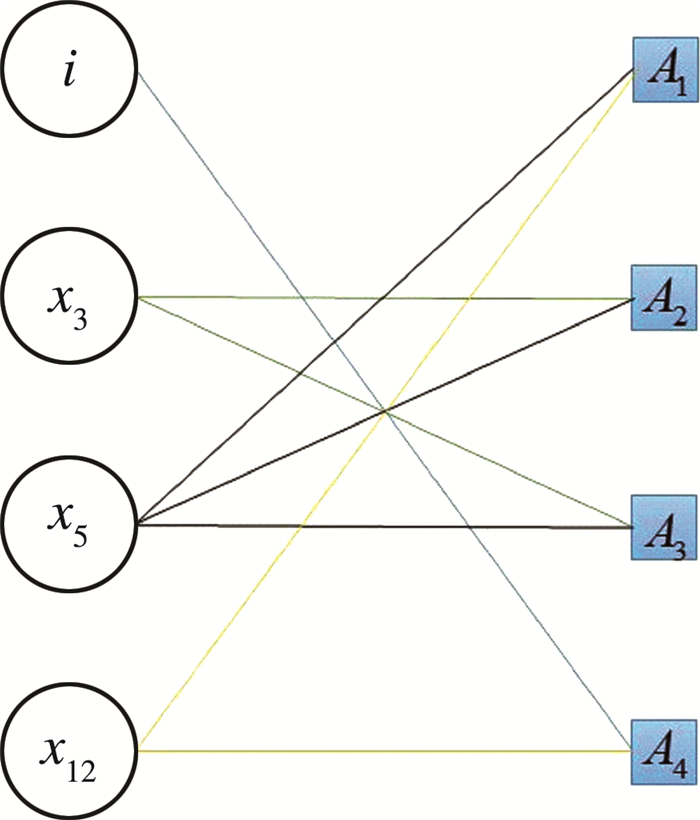 |
| 图 3 二部图Ga |
3.2 随机游走
ANEBRW要在Gs和Ga上进行随机游走采样得到节点的若干近邻序列, 类比文档中的句子输入到skip-gram模型中。
3.2.1 偏置随机游走为了使表示结果能兼顾网络中节点的局部性和更高阶节点的全局性, 在图GS上进行偏置随机游走, 引入参数p和参数q, 使随机游走过程中兼顾宽度优先搜索和广度深度优先搜索进行采样。
在给定当前节点i, 访问下一个节点x的概率如式(1)所示:
| $ P(x|i) = \left\{ {\begin{array}{*{20}{l}} {\frac{{{\pi _{ix}}}}{Z}} \ \ \ \ {如果(i, x) \in E}\\ 0\ \ \ \ \ \ \ \ \ \ \ \ {否则} \end{array}} \right., $ | (1) |
其中πix是节点i和节点x未归一化的转移概率, Z是归一化常数。
引入两个超参数p和q控制随机游走方式。假定当前随机游走经过边(j, i)到达节点i, 设式(1)中πix=α(j, x)·wix, 其中wix是节点i和节点x之间边的权重, α(j, x)定义如式(2)所示, 其中djx是节点j和节点x之间的最短距离。
| $ {\alpha _{pq}}(j, x) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{p}}&{if{d_{jx}} = 0}\\ 1&{{d_{jx}} = 1}\\ {\frac{1}{q}}&{if{d_{jx}} = 2} \end{array}} \right. $ | (2) |
参数p和参数q的作用方式如图 4所示:参数p控制跳向上一个节点概率, 仅作用于djx=0的情况。若p较小, 则下一跳访问节点i之前访问过的节点的概率大, 反之概率小。参数q控制跳向上一个节点非邻居的概率, 如果q>1, 随机游走倾向于访问和j接近的节点, 偏向BFS;如果q < 1, 则下一跳访问距离j较远的节点, 偏向DFS。
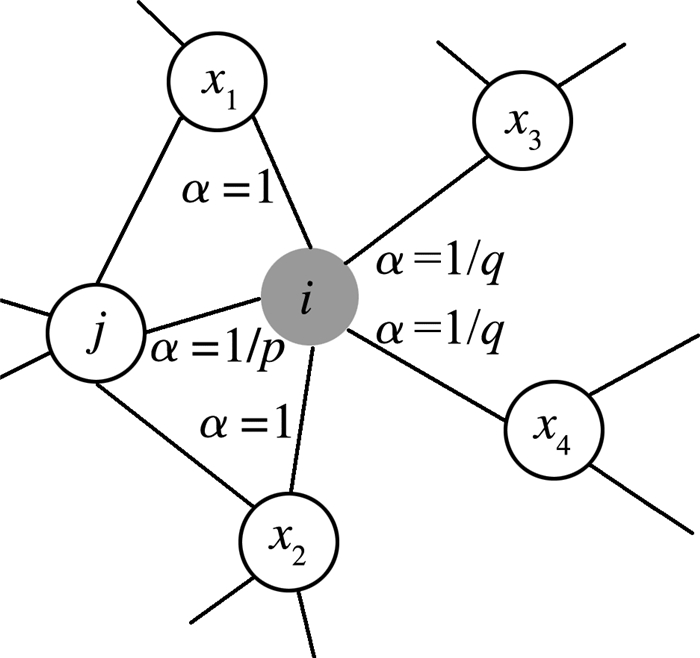 |
| 图 4 偏置随机游走示意图 |
3.2.2 二部图随机游走
在二部图Ga上, 有属性的节点通过属性建立关系, 随机游走在两类节点之间来回游走, 直到节点数量达到固定长度停止游走。这样有共同属性的节点在采样的序列中距离更近, 即使在网络中距离较远或者没有边连接的节点, 属性相同或者相近节点的表示向量会更相似。例如在G中, 节点x12与节点i、节点x5并没有边直接相连, 但是它们有共同的属性A1或A4, 在二部图中, 如图 3所示, 节点x12就会与节点i通过属性节点A4有边连接, 通过属性节点A1与x5有边相连, 则在随机游走过程中, 节点x12, i和x5就可能出现在同一条随机游走序列中, 则即使x12、i和x5没有边连接, 它们的向量表示也是相近的, 能够更好的还原网络的特性。
3.3 表示学习通过在Gs和Ga上的随机游走获得了大量的节点序列, 这里沿用DeepWalk算法的思想, 将随机游走采样得到的节点序列类比文档中的句子输入到skip-gram模型对随机游走序列中每个局部窗口内的节点对进行概率建模, 最大化随机游走序列的似然概率, 并最终使用随机梯度下降学习得到模型参数, 也就是节点的嵌入向量[4]。算法的目标函数如式(3)所示:
| $ \mathop {{\rm{min}}}\limits_\Phi \sum\limits_{u \in V} - {\rm{logPr}} (N(u)|\Phi (u)), $ | (3) |
其中Φ(u)是当前节点的嵌入向量, N(u)是u的邻居节点, 这里的邻居节点是从Gs和Ga中随机游走采样得到。假设采样得到的每个邻居节点相互独立, 上式(3)可简化为:
| $ \Pr (N(u)|\Phi (u)) = \prod\limits_{{c_i} \in N(u)} { \Pr } ({c_i}|\Phi (u)), $ | (4) |
其中Pr(ci|Φ(u))由式(5)定义的softmax函数得到:
| $ \Pr ({c_i}|\Phi (u)) = \frac{{ \exp (\varphi ({c_i}) \cdot \Phi (u))}}{{\sum\limits_{v \in V} { \exp } (\varphi (v) \cdot \Phi (u))}}, $ | (5) |
其中Φ(·)是中心节点的嵌入向量, φ(·)是中心节点的上下文节点的嵌入向量。
3.4 ANEBRW算法描述综合上述3个过程, 下面给出ANEBRW算法的整体描述:
Input:属性网络G=(V, E, A);嵌入维度d;每个节点作为初始节点生成的随机游走序列个数r;随机游走长度l;上下文窗口宽度k;偏置参数p、q
Output:节点的嵌入向量Φ:V→Rd
Step1:由原网络G生成结构图Gs和二部图Ga
Step2:根据p、q计算转移概率π
Step3:在Gs上进行偏置随机游走R1=BiasedRandomWalk(Gs, π, r, l);在Ga上进行随机游走R2=RandomWalk(Ga, r, l)
Step4:将R1、R2作为skip-gram模型的输入的得到网络嵌入Φ=skip-gram(d, k, R1, R2)
4 实验与分析我们在3个广泛使用的数据集上通过节点分类任务来评估所提方法的有效性。
4.1 数据集介绍本文使用了3个真实的广泛使用的数据集, 社交网络数据集BlogCatalog, 还有两个引文网络数据集DBLP和CiteSeer。表 1总结了这三个数据集的节点和连边情况。
| 表 1 数据集概况 |
 |
在使用DBLP和CiteSeer数据集时, 论文的标题作为节点属性, 本文对这些标题进行了预处理删除了停用词。BlogCatalog是博客用户构成的社交网络, 属性是用户的博客提取出来的关键字。在每个数据集中选择至少出现3次以上的单词作为节点的属性。预处理后, DBLP、CiteSeer、BlogCatalog分别有8 168、3 986、5 413个属性。
4.2 对比算法DeepWalk:在网络中采用截断随机游走获取固定长度的节点序列, 用skip-gram模型学习节点的向量表示。
Node2vec:使用有偏随机游走捕获网络的局部结构和全局结构。
GAT2VEC:将随机游走策略应用到属性网络, 结合网络的拓扑结构和属性信息进行网络嵌入。
4.3 评价指标首先使用上述对比算法和ANEBRW进行网络嵌入, 然后在节点分类任务中评价不同算法的性能。基本思想是通过网络嵌入算法学习得到的表示向量在节点分类任务中能够较准确的对未标注的节点进行预测, 则可以更加有效地提取原网络中节点的信息。对于多分类问题一般采用Macro-F1和Micro-F1得分作为评价结果。Macro-F1是将n分类的评价转换成n个二分类的评价, 计算每个二分类的F1得分, 然后计算n个F1得分的算术平均值;Micro-F1则是n个不同类别标签上的F1得分的加权平均值。Macro-F1、Micro-F1得分越高, 分类效果越好。
4.4 参数设定为了保证各对比算法的公平性, 节点表示向量的维度均设置为d=128。ANEBRW算法的参数设置为r=10, l=80, k=5。在Node2vec中, 作者通过实验得出p、q的最佳取值在{0.25, 0.50, 1, 2, 4}中取得, 在本文中, 通过在上述集合中进行超参搜索, 在DBLP数据集上取p=4, q=0.25;CiteSeer数据集上取p=1, q=0.5;BlogCatalog数据集上取p=0.25, q=0.25。
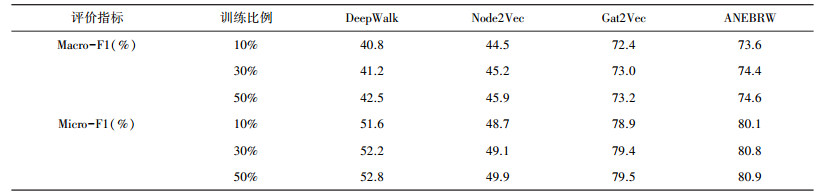
4.5 实验结果分析本文在DBLP和CiteSeer数据集上执行多分类任务, 在BlogCatalog数据集上执行多标签分类任务, 随机选取10%、30%、50%的节点嵌入表示作为训练集, 剩下的作为测试集, 本文以Macro-F1和Micro-F1得分作为与其他基线方法的比较评价指标。训练以及验证过程重复10次取平均值作为最终结果。表 2、表 3、表 4分别展示了DBLP、CiteSeer和BlogCatalog在对比算法和本文所提ANEBRW算法进行网络嵌入后节点分类任务的Macro-F1和Micro-F1值。从表中可以观察出:
| 表 2 DBLP数据集上的分类结果 |
 |
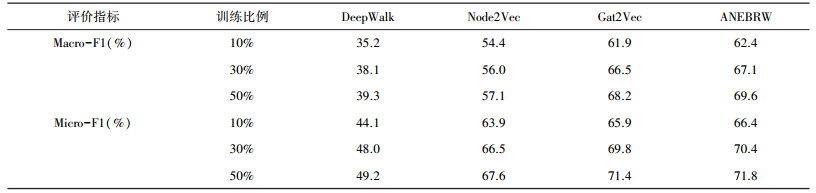
| 表 3 CiteSeer数据集上的分类结果 |
 |
| 表 4 BlogCatalog数据集上的分类结果 |
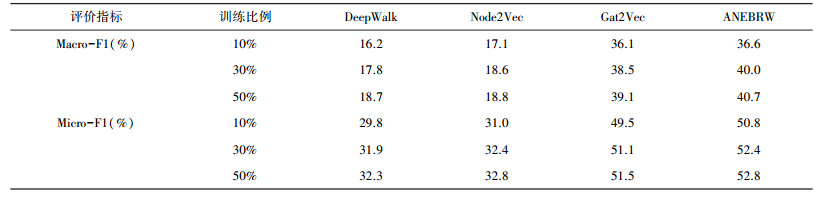 |
1) 在三个数据集上, ANEBRW算法优于所有的对比算法, 即使在只有10%训练样本的情况下, ANEBRW取得的效果也优于其他算法。这表明ANEBRW可以利用节点间的连接关系以及少量的标签对大量没有标签的节点进行分类, 适合真实的标签稀疏的网络数据。
2) ANEBRW在三个数据集上的分类效果均优于DeepWalk和Node2Vec, 这在一定程度上表明, 网络中节点的属性可以为网络嵌入提供很好的信息来源, 将网络的拓扑信息结合节点的属性信息之后, 网络嵌入效果有很大的提升。
3) ANEBRW在三个数据集上的分类效果也均优于GAT2VEC模型, ANEBRW在计算复杂度上相比于GAT2VEC只是提前计算了游走的转移概率, 是与节点数量呈线性关系的, 因此可以应用于大规模网络数据, 这表明在融合节点属性信息基础之上, 随机游走过程中根据不同的网络结构, 采用不同的游走策略, 综合考虑网络表示的局部性和全局性, 可以得到比GAT2VEC更优质的网络表示。
因此, ANEBRW网络嵌入算法有效结合了网络的拓扑信息和节点的属性信息, 兼顾网络嵌入的局部性和全局性, 学习到的嵌入向量能更好的表达网络中的结构信息。
5 结论本文提出了一种基于偏置随机游走的网络嵌入方法ANEBRW, 在融合节点属性信息的基础之上, ANEBRW引入偏置随机游走策略更好的捕捉网络的拓扑信息, 使最终学习到的表示向量兼顾节点的局部特征和全局特征。在三个真实的网络数据上进行节点分类的实验结果表明, ANEBRW算法可以学习到更高质量的网络嵌入, 更好的保留了网络中的结构信息, 因此本文所提出的ANEBRW方法是有效的、可行的。
| [1] |
涂存超, 杨成, 刘知远, 等. 网络嵌入综述[J]. 中国科学:信息科学, 2017(8): 32-48. |
| [2] |
齐金山, 梁循, 李志宇, 等. 大规模复杂信息网络嵌入:概念、方法与挑战[J]. 计算机学报, 2018, 41(10): 222-248. |
| [3] |
BHAGAT S, CORMODE G, MUTHUKRISHNAN S. Node classification in social networks[J]. Computer Science, 2011, 16(3): 115-148. |
| [4] |
LI J, ZHU J, ZHANG B.Discriminative deep random walk for network classification[C]//Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics(Volume 1: Long Papers).2016: 1004-1013.
|
| [5] |
MALLIAROS F D, VAZIRGIANNIS M. Clustering and community detection in directed networks:A Survey[J]. Physics Reports, 2013, 533(4): 95-142. DOI:10.1016/j.physrep.2013.08.002 |
| [6] |
LINYUAN LU, ZHOU T. Link prediction in complex networks:A survey[J]. Physica A Statistical Mechanics & Its Applications, 2011, 390(6): 1150-1170. |
| [7] |
ROWEIS S.T. Nonlinear Dimensionality Reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323-2326. DOI:10.1126/science.290.5500.2323 |
| [8] |
BELKIN M, NIYOGI P.Laplacian eigenmaps and spectral techniques for embedding and clustering[C]//Advances in neural information processing systems.2002: 585-591.
|
| [9] |
PEROZZI B, AL-RFOU R, SKIENA S.Deepwalk: Online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD international conference on knowledge discovery and data mining.ACM, 2014: 701-710.
|
| [10] |
TANG J, QU M, WANG M, et al.Line: Large-scale information network embedding[C]//Proceedings of the 24th international conference on world wide web.International World Wide Web Conferences Steering Committee, 2015: 1067-1077.
|
| [11] |
GROVER A, LESKOVEC J.node2vec: Scalable feature learning for networks[C]//Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining.ACM, 2016: 855-864.
|
| [12] |
PAN S, WU J, ZHU X, et al. Tri-party deep network representation[J]. Network, 2016, 11(9): 12. |
| [13] |
YANG C, LIU Z, ZHAO D, et al.Network representation learning with rich text information[C]//Twenty-Fourth International Joint Conference on Artificial Intelligence, 2015.
|
| [14] |
SHEIKH N, KEFATO Z, MONTRESOR A. gat2vec:representation learning for attributed graphs[J]. Computing, 2019, 101(3): 187-209. |
 2019, Vol. 33
2019, Vol. 33


