| 输电线路上行波故障信号的去噪及仿真 |
2. 山东工业技师学院, 潍坊 256410
2. Shandong Institute of Technology, Weifang 256410, China
电能是当今社会最常用的能源之一, 是一种绿色清洁无污染的能源。并且由于社会发展的日新月异以及科技的不断进步, 电力系统深入触及到社会的各个角落, 这也导致了电力系统的结构日益庞大, 设施日益复杂, 所以用来传输电力的高压输电线也变得尤为重要。但是在现实中, 担负传输电力重任的高压输电线极易受到周围环境的干扰, 一旦发生故障干扰, 城市居民用电以及工业用电就会受到重大影响, 造成人力物力财力上的损失[1]。
在实际生活中, 测得的信号都会由于各种原因使得原始信号中含有大量的噪声, 导致在分析信号时产生不必要的干扰。因此, 在分析原始故障信号时尽可能的消除或者降低噪声进而为下一步分析故障原因及检测打下基础。并且通过对采集到的行波信号进行分析, 发现其噪声成份, 主要是所谓的白噪声或加性噪声为主。
目前常用的信号去噪方式为傅里叶变换去噪和小波去噪两种去噪方式, 其中小波阈值去噪最为常见。
傅里叶变换进行信号去噪的核心就是将信号进行傅里叶变换在利用低通或者带通的滤波器进行信号去噪, 之后再将去噪后的信号进行傅里叶的逆变换。傅里叶变换暴露出的缺点就是很难将噪声中的高频部分和有用信号高频部分区分开来, 以至于高频部分可能还存在噪声[2]。
小波去噪法是一种当前最火热的去噪方式, 是去噪能力强, 适应范围大的一种基于离散小波变换基础的信号处理方法。小波去噪法的核心就是根据信号与噪声不同的性质, 也就是说需要的信号部分和噪声分布在不同频率范围具有不同性质的特点, 将对应频域上和噪声有关的相关系数置0, 并且把需要的有用信号部分保持不变, 完整的保留下来。最后用小波重构的方式重新构建原信号[3]。
但是使用小波阈值去噪时常常使用无偏似然估计阈值的阈值规则而忽略其他几种阈值规则, 造成去噪效果不一定是最理想。本论文主要利用MATLAB软件, 将实际测得的输电线路上的行波故障信号导入到MATLAB中, 通过MATLAB的仿真, 对比分析了几种不同阈值选取方法的去噪效果, 得出获取最纯净的输电线路上行波故障信号的去噪方法。
1 小波变换的基本理论 1.1 傅里叶变换的基本概念傅里叶变换(Fourier Transformation)涉及到众多自然科学领域, 特别是在信号处理、图像处理、量子物理等学科中的一个非常重要的应用工具。通常, 傅里叶变换分析指的是傅里叶变换和傅里叶级数这两种概念。同时, 傅里叶变换也可以认为是信号进行了相干累计从而得出正弦波信号的频率、振幅和相位。经典的傅里叶变换(FT)定义为:
| $ F\left( \omega \right) = \int\limits_{ - \infty }^{ + \infty } {f\left( t \right)} e - j\omega tdt $ | (1) |
傅里叶逆变换为:
| $ f\left( t \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int\limits_{ - \infty }^{ + \infty } {F\left( \omega \right)} ej\omega td\omega $ | (2) |
其中, F(ω)是函数f(t)的频谱密度函数或频谱函数, f(t)是F(jω)的原函数。
一般来说, 人们所说的傅里叶变换包含两部分, 其中一个是连续傅里叶变换, 另一个指的是离散傅里叶变换。
从现代数学分析的方式和角度去观察, 可以看出傅里叶变换是一种特殊的积分变换。它可以把某个特定函数在符合特定条件时表示成正弦基函数的积分形式。连续傅里叶变换和离散傅里叶变换则是在不同研究范围内的变体[4]。
在计算傅里叶变换时, 需要在选取的定义域R上的离散点进行计算。但实际应用时人们希望很直接的来分析出信号的变化以及特性, 那样必须要求信号是有限的, 在一定频域和时域上, 信号也是离散的, 所以人们把它定义为离散傅里叶变换。另外, 傅里叶变换也具有如下的特性:线性性质、位移性质、频移性质、卷积定理、对称性质、能量积分性质。
1.2 小波变换的基本概念小波变换(Wavelet Transform, WT)的概念是由法国科学家Jean Morlet和A.Grossman在1984年提出的, 当时因为种种原因没有受到大家的重视。但是最近, 小波分析已经发展成非常火热的一种数学方法。它主要应用在应用数学及工程科学领域。小波分析是基于傅里叶变换而延展不断深化的学科, 并且它为许多领域提供了新的思路、新的解决方法, 在科研界极为受欢迎。小波分析既是一种理论十分丰富和合理的数学方法, 也是在工程实践中起到关键作用的一种特殊工具[5]。
从数学角度来说, 可以将小波定义为对给定函数局部化的新领域。人们通常用有限区域的函数ψ(x)来定义小波, ψ(x)可以叫做母小波或者基本小波, 一组小波基函数是通过平移或者缩放来实现的, 具体的公式如下:
| $ {\varphi _{a, b}}\left( x \right) = \frac{1}{{\sqrt a }}\varphi \left( {\frac{{x - b}}{a}} \right) $ | (3) |
a为缩放参数, b为平移参数。
其中, 还存在一个特殊情况, 当a=2j和b=ia的情况下也可以将小波基函数序列定义为:
| $ {\varphi _{i, j}}\left( x \right) = 2 - j/2\varphi \left( {2 - j/2x - 1} \right) $ | (4) |
i为平移参数, j为缩放因子。
函数f(x)以小波ψ(x)为基的连续小波变换定义为函数f(x)和ψa, b(x)的内积:
| $ {w_{a, b}}\left( x \right) = < f, {\varphi _{a, b}} \ge \int\limits_{ - \infty }^{ + \infty } {f\left( x \right)\frac{1}{{\sqrt a }}} \varphi \left( {\frac{{x - b}}{a}} \right)dx $ | (5) |
与时域函数对应, 在频域上则有:
| $ {\varphi _{ab}}\left( x \right) = \sqrt a e - j\omega \varphi $ | (6) |
通过小波的定义和公式可以看出, 当|a|减小时, 对应的时域宽度同样减小, 但是它的频域宽度要增大, ψa, b(x)的朝着|ω|增大方向移动。相反当|a|增大时, 对应的时域宽度增大, 但是它的频域宽度却减小, ψa, b(x)的朝着|ω|减小方向移动。这可以清楚地体现连续小波的变化是局部的, 高频和低频分别对应着高分辨和低分辨。总体说来, 小波变换拥有更好的窗口特性[6]。
2 小波去噪 2.1 小波阈值法去噪在实际生活中, 人们把任何能够影响信号中有用信息的一切声音信号都称为噪声。在本论文中, 输电线路上的行波信号经过检测发现都为加性白噪声, 所以本论文以加性白噪声为主。通常人们把实际信号定义为f(t)=s(t)+ε(t), 其中f(t)为含噪实际信号, s(t)为含有有用信息的信号, ε(t)为含有噪声的信号。因为有用信号和噪声信号的不同特性, 在进行小波变换后, 他们得到的小波系数会有所不同, 噪声信号变换得到的小波系数是低于有用信号的小波系数的。所以, 小波阈值法去噪的关键就是因为噪声的小波系数远远小于所选取信号的小波系数。
简单来说, 阈值去噪法就是先对含有噪声的信号进行小波分解, 再对其中的小波系数进行阈值化也就是阈值处理。对处理完的小波系数进行判断, 看它是否大于或者小于某个阈值, 最后再利用之前处理过的结果进行信号重构, 重构出原信号。其中最重要的两个环节分别是选取合适的阈值以及选择哪一种阈值函数。其中, 本文采用的就是小波阈值法对输电线路中行波故障信号进行分析[7-9]。
下图 2为4层小波分解的示意图, 其中S为原始信号;A1、A2、A3、A4为分解后所得到的低频系数, D1、D2、D3、D4则为高频系数[10]。
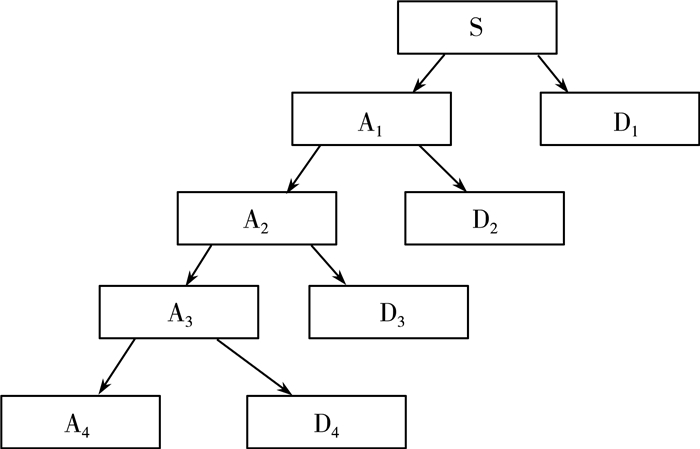 |
| 图 1 4层小波分解示意图 |
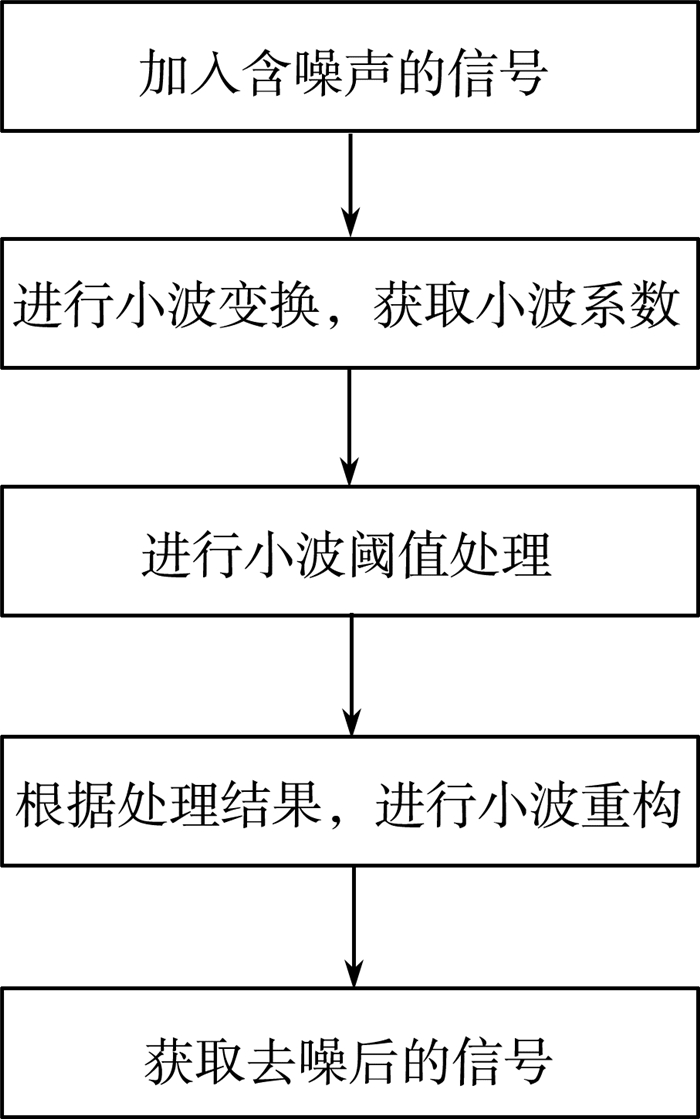 |
| 图 2 小波阈值去噪步骤 |
2.2 小波阈值变换的步骤
小波阈值去噪的步骤有以下三个步骤, 如图 2所示, 其中, 最重要的是如何选择合适的阈值以及进行阈值量化。而对于小波基函数的选择, 常使用Daubechies(Db)小波系和Symlets(Sym)小波系。信号最终的去噪效果, 由于小波基函数选择的差异而有所不同。通常选择小波系中对称性和正则性比较好的小波基函数对信号进行处理, 从而能够获得相对较好的去噪信号[11]。
2.3 软、硬阈值在进行小波变换时, 通常会定义一个变量阈值λ, 当信号的小波变量系数高于阈值λ时, 此时的信号为有用信号, 低于这个阈值λ时, 就把它定义为实际信号中的噪声信号, 将它进行消除。所以阈值的选择很重要。现如今, 有两种常用的阈值函数, 分别是软阈值和硬阈值这两种函数。
1) 硬阈值函数
| $ \eta \left( \omega \right) = \left\{ {\begin{array}{*{20}{c}} {\omega , \left| \omega \right| \ge T}\\ {0, \left| \omega \right| < T} \end{array}} \right. $ | (7) |
2) 软阈值函数
| $ \eta \left( \omega \right) = \left\{ {\begin{array}{*{20}{c}} {\left( {\left| \omega \right| - T} \right)sign\left( \omega \right), \left| \omega \right| \ge T}\\ {0, \left| \omega \right| < T} \end{array}} \right. $ | (8) |
上述所说的硬阈值与软阈值选取的不同体现了两种不同的信号去噪思路, 硬阈值法是将信号的绝对值与阈值λ进行比较, 小于阈值的点置为零, 其他保持不变。软阈值法是将信号的绝对值和阈值λ进行比较, 小于阈值λ的点置为零, 大于或等于阈值λ的点则向零收缩, 变为该点值与阈值λ之差。
本论文采用的是软阈值函数去噪。因为软阈值去噪信号更平滑, 而硬阈值去噪后的结果波形更尖锐, 去噪效果不稳定。
2.4 几种阈值规则除了上述所说的软硬阈值的选取, 阈值规则的选取同样至关重要, 不同阈值规则下, 选取的阈值标准不一样, 同样会影响最终的去噪效果[12-15]。
其中, 小波阈值去噪的阈值选择方法有:固定阈值估计法、极值阈值估计法、无偏似然估计法以及启发式估计法这4种阈值选取规则[16-17]。
1) 固定阈值估计法sqtolog
固定阈值估计法是指采用固定的阈值进行小波阈值去噪。产生的阈值是:
| $ sqrt\left( {2 * \mathit{log}\left( {length\left( X \right)} \right)} \right) $ | (9) |
2) 启发式阈值法heursure
启发式估计法是指将无偏似然估计和固定阈值估计法结合的方法。一般在信号含有很大噪声时采用这种阈值方法。
3) 无偏似然估计rigrsure
无偏似然估计是将给定阈值t使用无偏似然估计的理论将阈值t最小化, 从而得到我们所需要的阈值。
4) 极值阈值估计法minimaxi
极值阈值估计法是指将应用极大极小值的原理进行阈值选取, 产生一个最小均方误差的机制。
3 MATLAB仿真实验与结果本论文采用的是上述论文提到的Sym8小波系, 分解层数为5层, 利用MATLAB软件的wden小波自动去噪的小波去噪函数对输电线路上的行波故障信号进行小波阈值去噪处理。
其中, matlab仿真程序设计参数为利用5层分解的sym8小波系, 选择采用wden函数作为小波阈值去噪的函数, 利用matlab程序仿真, 分别使用rigrsure、sqtwolog、heursure、minimaxi的阈值选取规则, 获得最终的去噪效果, 如下图 3、图 4、图 5、图 6、图 7所示。
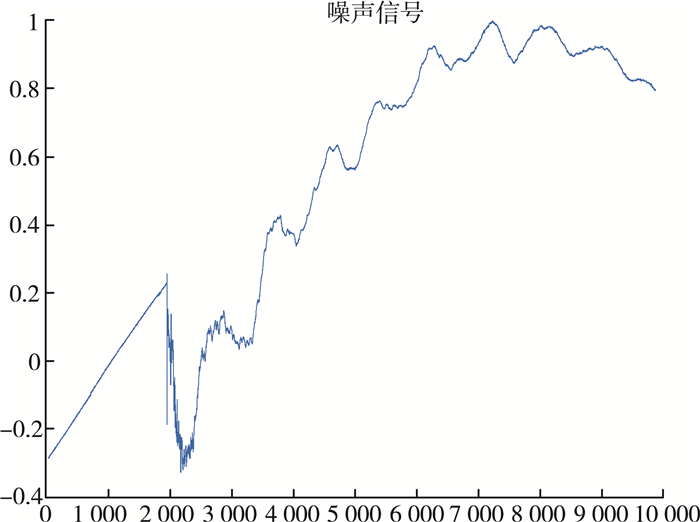 |
| 图 3 输电线路上的行波故障原始信号 |
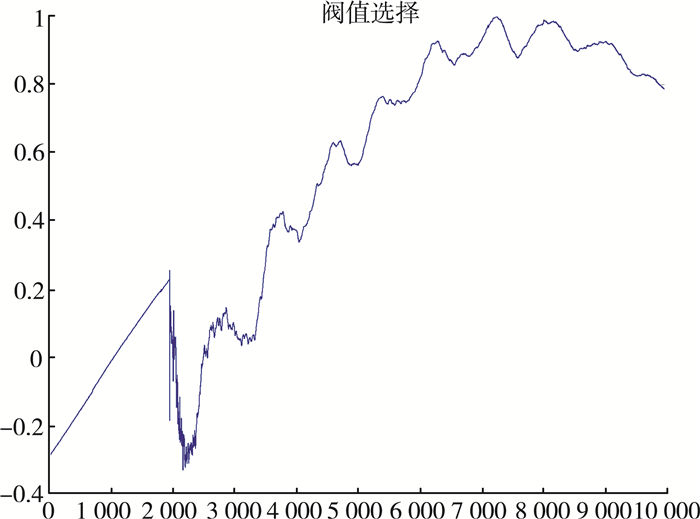 |
| 图 4 无偏似然估计法的去噪 |
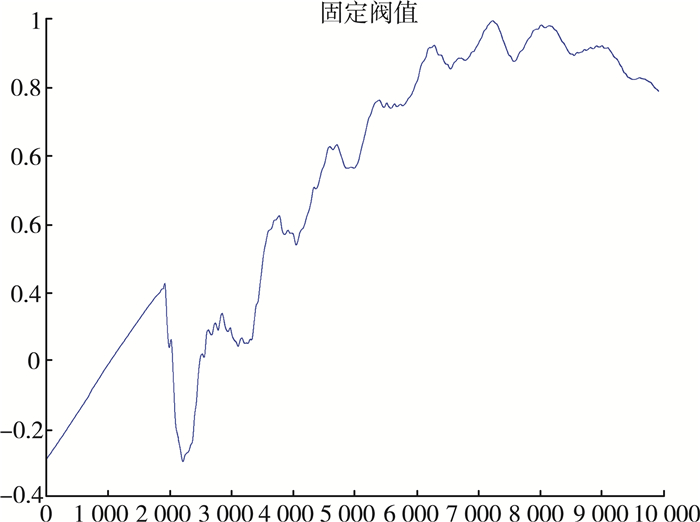 |
| 图 5 固定阈值估计法的去噪 |
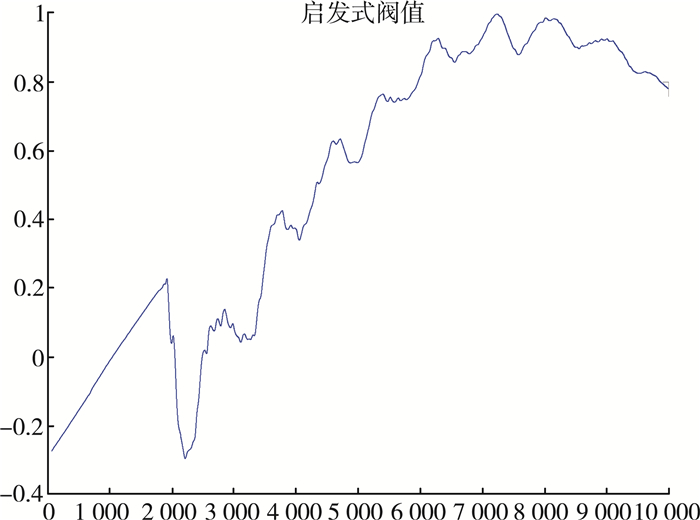 |
| 图 6 启发式估计法的去噪 |
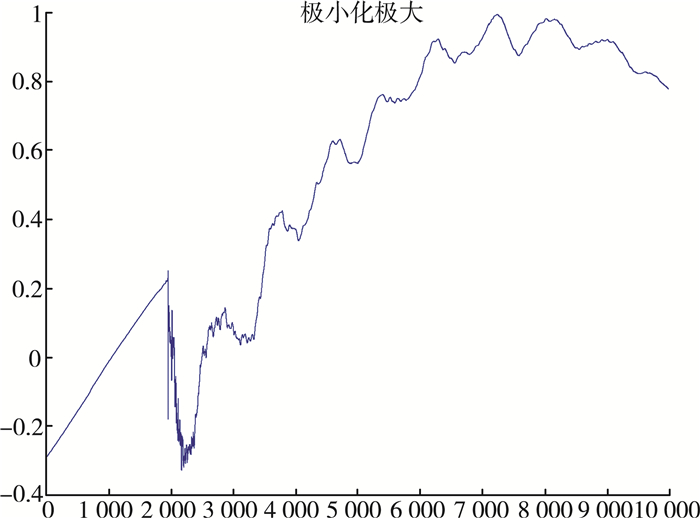 |
| 图 7 极值阈值估计法的去噪 |
其中图 3为输电线路上的行波故障原始信号, 图 4为无偏似然估计法的去噪, 图 5为固定阈值估计法的去噪, 图 6启发式估计法的去噪, 图 7极值阈值估计法的去噪。
通过matlab仿真程序获取了不同阈值选取规则下的阈值分别如下表 1所示:
| 表 1 不同阈值规则仿真得到的阈值大小 |
 |
通过在MATLAB仿真实验环境下的4种不同小波阈值规则下对输电线路上的行波故障信号去噪效果与原始输电线路上含噪故障信号的对比试验, 可以看出4种不同阈值选取规则的去噪图像的颜色都比原始含噪故障信号图像的颜色要浅, 这说明4种不同阈值规则的小波阈值去噪都有效果。但是无偏似然估计法和极值阈值估计法在2 000~3 000在这一段有较大尖峰和突变的噪声范围内去噪效果很不理想, 这是因为无偏似然估计法和极值阈值估计法阈值选择规则很保守, 仅仅将一部分的小波系数置零, 所以在信号的高频信息只有很少一部分的噪声范围内, 效果不理想。同时由表 1的对比可以看出阈值选取较小, 也会导致一些噪声被忽略。而对比另外两种去噪效果, 这两种方法在有较大尖峰和突变的噪声区间去噪效果依然十分明显。综上所述, 本论文采用小波固定形式阈值sqtwolog以及启发式阈值heursure形式来对输电线路上的行波故障信号进行去噪。
4 总结针对输电线路上由于各种原因导致输电线路发生故障, 在分析处理输电线路上的行波故障信号时,无法最准确最简单的获取纯净的行波故障信号导致输电线路发生故障,影响人们的日常生活。本文通过分析傅里叶去噪法和小波阈值去噪法的优劣性, 选择使用小波阈值去噪法对故障信号进行处理, 创新性的提出通过在MATLAB环境下通过对比分析不同阈值规则下的小波阈值去噪的阈值大小以及对比图像, 发现4种不同阈值规则下的去噪都对信号有一定的去噪效果, 但是无偏似然估计法和极值阈值估计法在有较大尖峰和突变的噪声范围去噪效果很不理想, 这是由于这两种阈值规则选取比较保守, 仅仅一部分小波系数置零, 造成噪声信息有所保留。而另外两种阈值选取规则下, 去噪效果十分理想并且在有较大尖峰和突变的噪声范围内去噪效果依然十分清晰, 得到了我们想要的去噪效果和清晰纯净的故障信号, 这也为进一步通过故障信号来进行分析故障原因的分析方法打下基础。
| [1] |
曹银萍, 郭璐. 基于MATLAB的小波分析在信号去噪中的应用[J]. 信息记录材料, 2018, 19(07): 85-87. |
| [2] |
陈文会, 刘芹, 刘小民, 等. 小波阈值去噪在FMCW雷达信号处理中的应用[J]. 计算机工程与应用, 2015, 51(08): 195-199. DOI:10.3778/j.issn.1002-8331.1307-0083 |
| [3] |
李杨.小波分析在输电线路故障诊断定位中的研究[D].淮南: 安徽理工大学, 2018.
|
| [4] |
姜波. 基于MATLAB的小波降噪研究[J]. 电子制作, 2019(13): 87-88, 99. DOI:10.3969/j.issn.1006-5059.2019.13.034 |
| [5] |
司祯祯. 傅里叶变换与小波变换在信号去噪中的应用[J]. 电子设计工程, 2011, 19(04): 155-157. DOI:10.3969/j.issn.1674-6236.2011.04.045 |
| [6] |
高清维, 李海鹰, 庄镇泉, 等. 基于平稳小波变换的心电信号噪声消除方法[J]. 电子学报, 2003(02): 238-240. DOI:10.3321/j.issn:0372-2112.2003.02.022 |
| [7] |
林东升. 小波阈值图像去噪中小波基选择[J]. 电脑知识与技术, 2018, 14(30): 245-246. |
| [8] |
殷青松, 戴曙光. 基于改进的小波阈值图像去噪算法研究[J]. 软件导刊, 2018, 17(01): 89-91. |
| [9] |
张金玲, 郑鑫. 平稳小波变换和新阈值函数用于心电信号去噪[J]. 北京邮电大学学报, 2017, 40(01): 28-31. |
| [10] |
方海荣. 基于小波变换的光电传感器信号去噪技术[J]. 电子设计工程, 2019, 27(19): 145-149. DOI:10.3969/j.issn.1674-6236.2019.19.032 |
| [11] |
申莎莎. 基于小波变换与傅里叶变换对比分析及其在信号去噪中的应用[J]. 山西师范大学学报(自然科学版), 2018, 32(03): 27-32. |
| [12] |
李传文, 魏圆圆, 张俊卿, 等. 基于小波变换的非接触式电导信号去噪研究[J]. 仪表技术, 2019(11): 1-6. DOI:10.3969/j.issn.1002-1841.2019.11.001 |
| [13] |
许子非, 李春, 杨阳, 等. 基于改进小波阈值及多重分形的风力机轴承振动信号分析[J]. 热能动力工程, 2019, 34(09): 191-198. |
| [14] |
韩先平. 基于M估计的外弹道数据小波阈值去噪方法[J]. 电子测量技术, 2019, 42(15): 18-23. |
| [15] |
曲天书, 戴逸松, 王树勋. 基于SURE无偏估计的自适应小波阈值去噪[J]. 电子学报, 2002(02): 266-268. DOI:10.3321/j.issn:0372-2112.2002.02.030 |
| [16] |
董文永, 丁红, 董学士, 等. 一种小波自适应阈值全频降噪方法[J]. 电子学报, 2015, 43(12): 2374-2380. DOI:10.3969/j.issn.0372-2112.2015.12.005 |
| [17] |
蔡静. MATLAB R2015a小波分析[M]. 北京: 清华大学出版社, 2016: 42-357.
|
 2020, Vol. 34
2020, Vol. 34


