| 基于目标导向的双向RRT路径规划算法 |
2. 齐鲁工业大学(山东省科学院)电子信息工程学院(大学物理教学部), 济南 250353;
3. 济南市人机智能协同工程实验室, 济南 250353
2. School of Electronic and Information Engineering(Department of Physics), Qilu University of Technology(Shandong Academy of Sciences), Jinan 250353, China;
3. Jinan Engineering Laboratory of Human-machine Intelligence Cooperation, Jinan 250353, China
随着工业生产对圆盘移动机器人要求的不断提高, 路径规划已经成为圆盘移动机器人在工业生产上的一个重要研究领域, 传统路径规划算法主要有A*算法[1]、蚁群算法[2]、人工势场算法[3]、遗传算法[4]等。尽管这些路径规划问题在处理低维空间路径规划问题方面具有一定的优越性, 但是当机器人路径规划的构型空间维度较高时, 算法在精确表达构型空间上需要占用大量的计算资源。基于采样思想的路径规划算法, 如PRM算法[5-7]、RRT算法[8-14], 不需要精确表达构型空间, 而是通过在构型空间内获取自由构型形成构型图, 以构型图描述构型空间的连通性, 这类算法在机械臂、人型机器人等高维构型空间上的所体现出的优势更为明显。
Lavalle等[9]首次提出了快速扩展随机树(rapidly exploring random trees, RRT)算法, 基于随机采样的思想获取自由构型qfree, 用以构建一个树形网络表达自由构型空间。该算法避免了对整个环境空间建模, 在高维构型空间的路径规划问题中优势更为明显, 得到了广泛的关注。但是RRT算法采用的随机采样思想, 也导致了节点的扩展无目标导向性, 容易出现大量冗余节点, 算法的收敛速度过慢。针对RRT算法生成构型无目标导向性、收敛速度慢等缺点, Urmson等[11]提出了路径代价函数的概念以表征路径的优化程度, 面向目标路径越优则路径代价越小。该算法在扩展中, 不再选择距离随机构型qfree距离最近的节点, 而是选择k个较近的节点进行扩展, 提升了已扩展RRT树内距离随机构型较近节点的搜索性能。代价函数的引入使得RRT树的扩展算法具有较好的目标导向性, 可有效提升算法的收敛速度。但是该算法在狭窄空间或障碍物密集等复杂环境下, 算法收敛性能会有明显下降。
在RRT算法研究初期, RRT及相应变种均采用单一随机树生成的思想, 由初始构型作为随机扩展树的初始节点, 在环境空间内进行扩展。单随机扩展算法构造简单, 但是无论是基础RRT算法还是其改进算法, 均存在收敛速度过慢的缺点。
基于双向搜索的思想, Pohi等[12]提出了双向随机扩展算法(bidirectional RRT, BI-RRT), 构造两棵分别以起始构型和目标构型为初始点的随机扩展树, 递归进行节点扩展以构建可表达构型空间的树形网络。相较于RRT算法, BI-RRT算法的收敛速度更快。但是该算法采用RRT算法的随机节点扩展思想, 这导致BI-RRT算法也存在构型无目标导向性的缺点。为提升BI-RRT算法的收敛速度, 结合贪心思想, Kuffner等[10]提出了RRT-connect算法。在BI-RRT算法扩展过程中, 从qnear到qrand仅步进一个固定步长, 即使在无障碍物空间内也需多次扩展过程才可到达qrand。在RRT-connect算法的扩展过程中, 从qnear到qrand会持续步进, 直至遇到障碍物或到达qrand。贪心思想的应用使得RRT-connect算法具有更高的扩展效率, 在自由构型空间内这一提升更为明显。但该算法扩展过程是以自由采样构型qrand为目标点进行扩展, 没有改变其导向性差的缺点。Akgun等[13]基于目标导向采样策略, 提出了概率优化的RRT*算法, 提升了RRT*算法的收敛速度及路径质量, 但是该算法采样过程中使用的局部偏置思想在复杂环境中的适应性较差, 存在导致算法收敛速度变缓慢的可能。李晓伟等[14]将一种目标偏向的思想加入到BI-RRT, 避免了随机树搜索全局空间, 很大程度降低了算法的复杂度, 但是该算法采样过程中选取的目标点是另一棵树的上一个节点, 目标导向性不明确, 存在导致算法收敛速度缓慢的可能。上述所提的RRT算法均存在收敛速度缓慢的缺点, 没有考虑到圆盘移动机器人的碰撞检测问题。
针对BI-RRT算法研究中存在目标导向性差、收敛速度慢的问题, 提出了一种目标导向的BI-RRT算法(goal-oriented BI-RRT, GOBI-RRT)。该算法是在BI-RRT算法的基础上引入了目标导向的思想。通过搜索两棵树的最近节点, 利用目标导向思想产生随机点, 新增节点具有良好的目标导向性, 加快了路径收敛速度。本文在机器人模型选择中, 以圆盘移动机器人为模型, 替代质点模型, 可更好的匹配真实机器人构型。为适应这一改进, 还提出了适用于圆盘机器人的k点碰撞检测算法, 该碰撞算法可有效检测新增节点是否为自由构型。本文算法不同于文献[14]中的算法, 该算法新增节点是通过搜索一棵树的最近节点和另一棵树的上一节点来生成, 而本文中的GOBI-RRT算法新增节点是通过搜索两棵树的最近节点来生成。最后, 将本文方法与文献[12]基本BI-RRT算法和文献[14]中的算法作仿真实验对比, 验证所提出GOBI-RRT算法在路径规划中的优势。通过实验可知, 所提出的方法可以更加快速地寻得路径。本文算法的这一优势, 可促进圆盘底座移动机器人能够在较短时间内获取可行路径, 节约能源消耗。
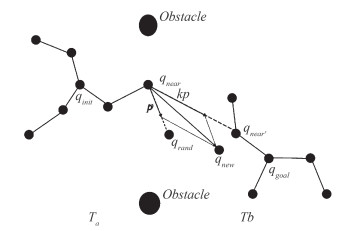
1 目标导向的双向快速搜索随机树算法 1.1 BI-RRT算法在BI-RRT中, 定义了两棵随机树Ta和Tb, 树Ta以qinit为树的根节点(起始点)开始扩展, 树Tb以qgoal为目标点开始扩展, qrand为任意扩展的随机节点, 为每次扩展时任选两棵树中距离qnear最近的节点, 以qnew为新节点。首先在整个搜索空间中采取随机的方式生成随机树的随即扩展节点qrand, 然后遍历当前已有的随机树, 从树中的节点寻找距离qrand最近的节点qnear, 在qnear向qrand延伸一定步长p之后可以得到新节点qnew, 之后需要对新节点qnew进行碰撞检测, 若qnew碰到障碍物便将这个节点舍去;反之, 即将qnew添加到树中, 可知此时qnew的父节点是qnear, 按照上述方式继续扩展, 直到两棵树的qnew小于一定的步长阈值时, 则可确定Ta和Tb连通, 即路径规划成功。图 1表示BI-RRT算法随机树的生长过程。
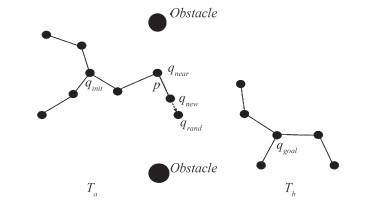 |
| 图 1 BI-RRT算法随机树生长图 |
1.2 GOBI-RRT算法 1.2.1 改进节点生成方式
基本思想:原方案仅采用随机生成采样点, 以树中最近点沿当前方向扩展得到新的节点, 该过程主要的计算任务在碰撞检测阶段。所提出的基于目标导向的方案, 尽管在目标导向阶段增加了计算量, 但节点的选择更具有导向性, 使树的生成更偏向目标点。图 2表示基于目标导向思想生成新节点的过程。
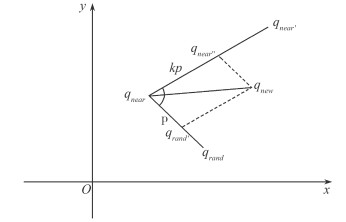 |
| 图 2 GOBI-RRT算法生成qnew |
改进了BI-RRT算法只生成一个qrand确定qnew, 增加目标导向思想是以随机点qrand和树Ta的最近节点qnear生成扩展方向, 树的最近节点qnear和树Tb的最近节点qnear'生成扩展方向, 再分别以步长p和kp(k为导向系数)生成qrand'和qnear'', 最后通过平行四边形法则求新的节点qnew。
假设基于目标导向思想下,
| $ y=\left(y_{ {rand }}-y_{ {near }}\right) /\left(x_{ {rand }}-x_{ {near }}\right) * x+b \text { , } $ | (1) |
其中,b是
假设qrand'的坐标为(xrand', yrand'), 步长p表示为:
| $ p = \sqrt {{{\left( {{x_{rand'{\rm{ }}}} - {x_{near{\rm{ }}}}} \right)}^2} + {{\left( {{y_{rand'{\rm{ }}}} - {y_{near{\rm{ }}}}} \right)}^2}} , $ | (2) |
依据
| $ \begin{array}{*{20}{l}} {\left( {{y_{rand{\rm{ }}}} - {y_{near{\rm{ }}}}} \right)/\left( {{x_{rand{\rm{ }}}} - {x_{near{\rm{ }}}}} \right) = }\\ {\left( {{y_{rand{\rm{ }}}} - {y_{near{\rm{ }}}}} \right)/\left( {{x_{rand{\rm{ }}}} - {x_{near{\rm{ }}}}} \right), } \end{array} $ | (3) |
由(2)和(3)得到qrand'的坐标。
假设qnear''的坐标为(xnear'', ynear''), 步长kp表示为:
| $ kp = \sqrt {{{\left( {{x_{near{{\rm{ }}^{\prime \prime }}}} - {x_{near{\rm{ }}}}} \right)}^2} + {{\left( {{y_{near{{\rm{ }}^{\prime \prime }}}} - {y_{near{\rm{ }}}}} \right)}^2}} , $ | (4) |
依据
| $ \begin{array}{*{20}{l}} {\left( {{y_{near'}} - {y_{near{\rm{ }}}}} \right)/\left( {{x_{near'}} - {x_{near{\rm{ }}}}} \right) = }\\ {\left( {{y_{near^{\prime \prime }}} - {y_{near{\rm{ }}}}} \right)/\left( {{x_{near{{\rm{ }}^{\prime \prime }}}} - {x_{near{\rm{ }}}}} \right), } \end{array} $ | (5) |
由(4)和(5)得到qnear''的坐标。
依据qrand'和qnear''的坐标, qnear的坐标, 假设qnew的坐标为(xnew, ynew), 依据平行四边形法则可得:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{new{\rm{ }}}} = {x_{near{{\rm{ }}^{\prime \prime }}}} + {x_{rand{\rm{ }}^\prime }} - {x_{near{\rm{ }}}}}\\ {{y_{new{\rm{ }}}} = {y_{near{{\rm{ }}^{\prime \prime }}}} + {y_{rand{{\rm{ }}^\prime }}} - {y_{near{\rm{ }}}}} \end{array}, } \right. $ | (6) |
针对一次节点扩展, 利用目标导向得到新节点qnew的计算过程如下:
Step1:给定树Ta的最近点qnear和随机点qrand的坐标, 给定树Tb的最近点qnear'的坐标。
Step2:根据给定的步长p和kp求解式(2)、(3)、(4)和(5)得到qrand'、qnear''的坐标。
Step3:对
假设圆盘的圆心坐标为(x0, y0), 半径为r。将圆盘以圆心将周长k等分, 设圆上任意一点坐标为(xi, yi), i=1, 2, 3……k, 设该点与圆心的连线和平行于x轴的直线y=y0的夹角为α。图 3表示圆盘k点碰撞检测算法。
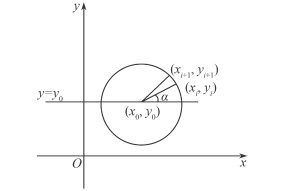 |
| 图 3 圆盘k点碰撞检测算法 |
坐标(xi, yi)表示为:
| $ \left\{\begin{array}{l} x_{i}=x_{0}+r cos \alpha \\ y_{i}=y_{0}+r sin \alpha \end{array}\right.。$ | (7) |
单节点扩展总的计算复杂度由两部分组成:
第一部分:目标导向的复杂度
由式(3)可以得到
| $ \begin{array}{*{20}{l}} {{y_{rand'}} = \left( {{y_{rand{\rm{ }}}} - {y_{near{\rm{ }}}}} \right)\left( {{x_{rand{\rm{ }}}} - {x_{near{\rm{ }}}}} \right) \cdot }\\ {\left( {{x_{rand'}} - {x_{near{\rm{ }}}}} \right), } \end{array} $ | (8) |
再将yrand'带入到式(2)中得到
| $ \begin{array}{*{20}{l}} {p = {{\left( {{x_{rand'{\rm{ }}}} - {x_{near{\rm{ }}}}} \right)}^2} + \left[ {\left( {{x_{rand'{\rm{ }}}} - {x_{near{\rm{ }}}}} \right)} \right. \cdot }\\ {{{\left. {\left( {{y_{rand{\rm{ }}}} - {y_{near{\rm{ }}}}} \right)\left( {{x_{rand{\rm{ }}}} - {x_{near{\rm{ }}}}} \right) - {y_{near{\rm{ }}}}} \right]}^2}}。\end{array} $ |
xrand、xnear、yrand、ynear都是已知的。而复杂度最高的是求开方部分, 依据1997年RICHARD P的论文[15], 假设地图表示为n×n矩阵, 该复杂度包括乘法运算和加法运算, 乘法运算复杂度表示为: O(μ(n))≈O(n2), 而加法运算复杂度可以忽略, 目标导向的复杂度为O(n2)。如图 4所示, 蓝色线为重合
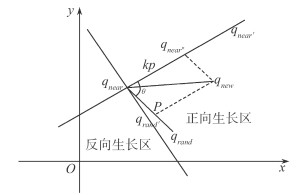 |
| 图 4 正、反向生长区 |
第二部分:圆盘k点碰撞检测复杂度
由式(7), 可见求解(xi, yi)包含二次乘法和二次加法, 圆盘多点碰撞检测算法的复杂度为2k次乘法和2k次加法。圆盘多点碰撞检测的复杂度为O(n2log2k)。
图 5为BI-RRT和GOBI-RRT复杂度对比图, 蓝色线为BI-RRT计算复杂度, 红色线为GOBI-RRT计算复杂度, 与随机采样比较, 目标导向可以减少无效随机采样点生成, 随着扩展节点数量的增长, 通过目标导向思想的算法改进的更明显。
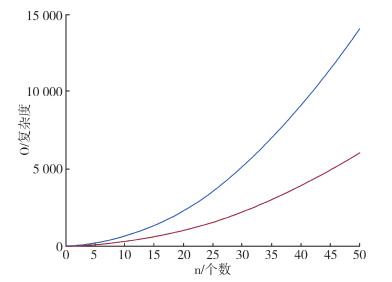 |
| 图 5 BI-RRT和GOBI-RRT复杂度对比图 |
2 伪代码实现 2.1 BI-RRT算法
算法1给出了BI-RRT算法的轮廓, 首先初始状态被添加到搜索树, 主循环是line3-24, 在n次迭代后终止。显然, BI-RRT算法通过采样随机点, 扩展完树Ta的新节点qnew后, 以qnew作为Tb的扩展方向。同时树Tb首先会扩展第一步得到qnew', 如果没有碰撞, 继续向着相同的方向扩展第二步, 直到扩展失败或者qnew=qnew'表示与树Ta相连了, 即整个算法结束。每次迭代中必须考虑两棵树的平衡性, 即两棵树的节点数的多少(也可以考虑两棵树总共花费的路径长度), 交换次序选择“小”的那棵树进行扩展, BI-RRT的构造方法如表 1所示。
| 表 1 BI-RRT算法 |
 |
2.2 GOBI-RRT算法 2.2.1 改进节点生成方式
在节点生成子程序中, 改进了BI-RRT算法通过树上最近点和产生的随机点来确定的新节点, 并提出目标导向的思想生成新节点。首先随机生成qrand, 通过qrand与树Ta上的最近点qnear产生一个新节点qrand', 再通过qnear与树Tb的最近节点qnear'来生成另一个新节点qnear'', 基于目标导向的思想, 对
 |
| 图 6 目标导向生成qnew |
| 表 2 节点生成 |
 |
2.2.2 圆盘k点碰撞检测算法
Checkpath:改进了单点碰撞检测函数, 提出了一种圆盘多点碰撞检测算法, 具体操作:假设圆盘机器人的圆心为xd, 首先将圆盘机器人分割成k等份, 本文中取k=50, 再对分割出来点的坐标合成一个集合{qi}, i=1, 2, 3…50, 对{qi}碰撞检测, 来检测圆盘上的点是否在障碍物上, 当这50个点都不在障碍物里和地图外时, 将qnew加入到路径中。Checkpath构造方法如表 3所示。
| 表 3 k点碰撞检测 |
 |
3 实验与分析
仿真实验是在Windows10, 内存为16GB的电脑安装有Mtalab R2019a仿真平台。仿真实验环境设定在不同的环境(宽阔环境、通道环境、栅格环境、迷宫环境)中的路径规划, 设置实验空间尺寸为500 m×500 m, 起始点坐标设置成(10, 10), 终点坐标设置成(490, 490)。考虑到是现实生活, 本文取圆盘移动机器人直径为1 m。分别对文献[12]BI-RRT算法、文献[14]目标偏向BI-RRT算法和本文GOBI-RRT算法在四种不同地图上进行仿真对比, 每种对比实验进行50次仿真, 取均值进行比较。图 7至图 10, 分别表示宽阔环境、通道环境、栅格环境、迷宫环境下的路径规划图, 图a)表示文献[11], 图b)表示文献[14], 图c)表示本文算法, 蓝色线为树Ta的路径规划, 红色线为树Tb的路径规划, 绿色线为树Ta和树Tb节点的相连。
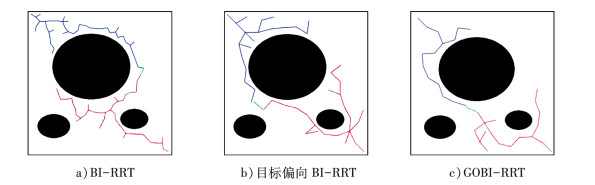 |
| 图 7 宽阔环境下的路径规划 |
 |
| 图 8 通道环境下的路径规划 |
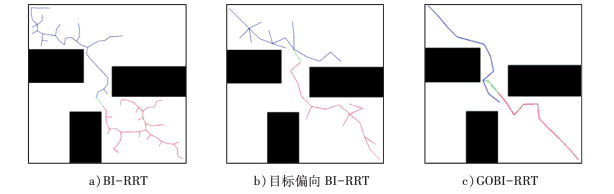 |
| 图 9 栅格环境下的路径规划 |
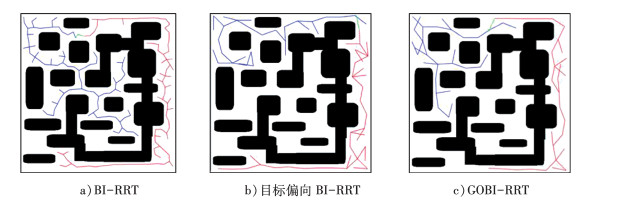 |
| 图 10 迷宫环境下的路径规划 |
通过在四种不同的环境下的仿真实验, 可以明显看出, 相比BI-RRT算法和目标偏向BI-RRT算法, GOBI-RRT算法使随机树向着目标点生长, 提高了收敛速度并减少了大量的节点。
表 4至表 7表示分别在宽阔地图、通道地图、栅格地图、迷宫地图四种环境下, 选取路径长度、航迹点数、规划时间三方面进行对比并得到的仿真实验数据。上述实验数据, 均通过Matlab内运行仿真算法提取。
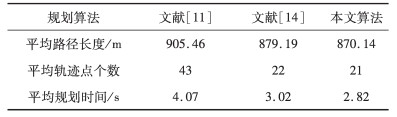
| 表 4 宽阔地图下的仿真数据比较 |
 |
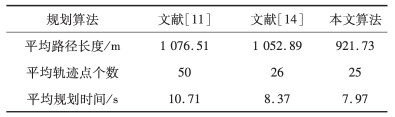
| 表 5 通道地图下的仿真数据比较 |
 |
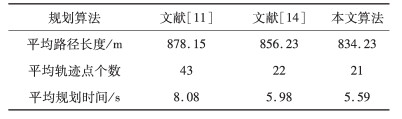
| 表 6 栅格地图下的仿真数据比较 |
 |
| 表 7 迷宫地图下的仿真数据比较 |
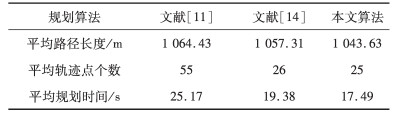 |
在宽阔地图上, GOBI-RRT算法相比BI-RRT算法平均轨迹点减少了53.49%、平均规划时间减少了14.2%, 相比目标偏向BI-RRT算法平均轨迹点减少了5%、平均规划时间减少了6.5%。
在通道环境上, GOBI-RRT算法相比BI-RRT算法平均轨迹点减少了50%、平均规划时间减少了25.58%, 相比目标偏向BI-RRT算法平均轨迹点减少了3.8%、平均规划时间减少了4.78%。
在栅格环境上, GOBI-RRT算法相比BI-RRT算法平均轨迹点减少了51.16%、平均规划时间减少了30.71%, 相比目标偏向BI-RRT算法平均轨迹点减少了4.5%、平均规划时间减少了6.6%。
在迷宫环境上, GOBI-RRT算法相比BI-RRT算法平均轨迹点减少了54.54%、平均规划时间减少了30.5%, 相比目标偏向BI-RRT算法平均轨迹点减少了3.8%、平均规划时间减少了10.78%。
由表 4至表 7可知, GOBI-RRT算法能够在很短的时间里寻得路径。在同样的环境和参数下, 本文算法的平均轨迹点的个数约为BI-RRT算法的一半, 相比目标偏向BI-RRT算法平均减少了4.28%;在平均规划时间上, 本文算法相比BI-RRT算法平均减少了25.25%, 相比目标偏向BI-RRT算法平均减少了6.64%。GOBI-RRT算法相比目标偏向BI-RRT算法更具有目标导向性, 随着节点数量的增加, GOBI-RRT算法相比BI-RRT算法复杂度得到了优化。因此本文提出的GOBI-RRT算法适用于多种不同环境, 能够以更少的搜索节点、更快的收敛速度得到路径, 有较大的实用价值。
4 结论针对BI-RRT算法路径规划中存在目标导向性差、收敛速度缓慢的问题提出了GOBI-RRT算法。该算法通过目标导向思想对随机树中随机点的产生进行改进, 同时和圆盘k点碰撞算法相结合, 通过数学模型分析, 相比于BI-RRT算法, 降低了算法复杂度。在4种不同地图环境的仿真实验中, 验证了GOBI-RRT算法在圆盘移动机器人上的优势。通过与BI-RRT算法和目标偏向BI-RRT算法相比, 该算法大幅减少了平均航迹点的个数和平均规划时间, 在路径规划中, 有较大的实用价值。在后续的研究中, 将考虑在平均路径长度与路径平滑上进行持续优化。
| [1] |
HART P E, NILSSON N J, RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2): 100-107. DOI:10.1109/TSSC.1968.300136 |
| [2] |
朱颢东, 孙振, 吴迪, 等. 基于改进蚁群算法的移动机器人路径规划[J]. 重庆邮电大学学报(自然科学版), 2016, 28(6): 849-855. |
| [3] |
唐志荣, 冀杰, 吴明阳, 等. 基于改进人工势场法的车辆路径规划与跟踪[J]. 西南大学学报(自然科学版), 2018, 40(6): 174-182. |
| [4] |
王勇臻, 陈燕, 于莹莹. 求解多旅行商问题的改进分组遗传算法[J]. 电子与信息学报, 2017, 39(1): 198-205. |
| [5] |
陈艳, 禹继国. 基于概率路线图的动态环境下移动机器人路径规划的神经网络方法[J]. 曲阜师范大学学报(自然科学版), 2019, 45(4): 38-42. |
| [6] |
谭建豪, 肖友伦, 刘力铭, 等. 改进PRM算法的无人机航迹规划[J]. 传感器与微系统, 2020, 39(1): 38-41. |
| [7] |
KAVRAKI L E, P SVESTKA J, et al. Probabilistic roadmaps for path planning in high-dimensional configuration spaces[J]. IEEE Transaction Robotics and Automation, 1996, 12(4): 566-580. DOI:10.1109/70.508439 |
| [8] |
HUADONG, GRANICHIN, OLEG N, et al. 3D motion planning for flexible needle insertion based on rapidly-exploring random trees with environment-adaptive sampling and central angle control[J]. Journal of Medical Imaging and Health Informatics, 2019, 9(7): 1524-1533. |
| [9] |
LAVALLE S M, KUFFNER J. Randomized kinodynamic planning[J]. The International Journal of Robotics and Research, 1999, 15(5): 378-400. |
| [10] |
KUFFNER J J, LAVALLE S M.RRT-connect: an efficient approach to single-query path planning[C]//International Conference on Robotics and Automation. San Franciso: USA IEEE.2002: 995-1001.
|
| [11] |
URMSONC, SIMMONS R.Approaches for heuristically biasing RRT growth[C]//International Conference on Intelligence Robots & System.San Franciso: USA IEEE.2003: 1178-1183.
|
| [12] |
POHⅡ.Bi-directional and heuristic search in path problems[C]//Stanford Linear Accelerator Center.Calif: Technical report, 1969.
|
| [13] |
AKGUN B.Sampling heuristics for optimal motion planning in high dimensions[C]//International Conference on Intelligence on Intelligence Robots and System.San Franciso: USA IEEE.2011: 2640-2645.
|
| [14] |
李晓伟, 于会山. 基于双向生长改进的RRT机器人路径规划算法[J]. 现代计算机, 2019, 21(4): 28-31. |
| [15] |
BRENT, RICHARD P. Fast multiple-precision evaluation of elementary functions[J]. Journal of the Acm, 1997, 23(2): 242-251. |
 2021, Vol. 35
2021, Vol. 35


