| 基于Canny算法的图像边缘提取研究 |
在图像中的一个区域中如果出现了突变或者不连续的微小区域(一组相连的像素集合), 那么就会出现两个具有相对不同灰度值特性的区域的边界线, 那么我们把这个边界线就可以视为图像的边缘。图像边缘的提取算法优劣, 对于后续进一步的图像处理至关重要[1]。边缘提取是提取图像特征的重要一步, 其中关键是要保证能够充分的抑制噪声和保证得到图片的完整。如今存在的边缘监测算法通常包括:Roberts算子、Sobel算子和Prewitt[2]。上述的这些算子推导过程相对简单, 对于计算机来说也较容易实现, 但是带来的缺点是边缘检测的准确度不高、噪声影响较大, 极大的增加了图像边缘提取的难度。
为了解决上述算法存在的问题, 改进算法中存在对噪声敏感等问题, 基于小波变换结合数学形态学处理的思想改进candy算子, 具备提升图像信噪比和改善图像边缘的连续性的优点, 对于后续图像进一步处理起到了非常关键的作用。
1 图像边缘预处理中的灰度化问题红绿蓝RGB(Red, Green, Blue)三通道的亮度值构成了彩色图像, 我们在对彩色图像进行处理的时候, 我们要分别对红绿蓝三个通道进行逐个通道进行处理, 对于彩色图像来说, 它不仅占用非常大的空间, 信息数量多对计算机带来严重的计算负担, 最为重要的是红绿蓝不能反映图片的特征、纹理, 只是灰度图像进行修饰。图像灰度化常用以下几种方法[3]:
1.1 分量法图像的灰度值就是将彩色红绿蓝三个分量的亮度值作为依据, 根据需要采用的公式选择一种灰度图像。公式如下:
| $ \mathit{Gra}{\mathit{y}_1}(i,j) = R(i,j) $ | (1) |
| $ \mathit{Gra}{\mathit{y}_2}(i,j) = G(i,j) $ | (2) |
| $ \mathit{Gra}{\mathit{y}_3}(i,j) = B(i,j) $ | (3) |
分量法应根据实际情况进行选择, 如果选择的亮度不合适对后面的进一步处理, 否则会产生较大的干扰[4]。
1.2 最大值法| $ \mathit{Gray}(i,j) = \mathit{max}\{ R(i,j),G(i,j),B(i,j)\} $ | (4) |
该方法同样会有较大的主观性, 如果选择的RGB三通道的最大亮度值, 就会忽略其他两个通道的亮度值, 图像的一些关键信息可能存在丢失问题[5]。
1.3 平均值法将彩色图像的三个分量亮度求平均得到一个灰度值
| $ \mathit{Gray}(i,j) = (R(i,j),G(i,j),B(i,j))/3 $ | (5) |
由上述公式的表达式我们可以知道, 该图像灰度化方法用数学的平均法将三个亮度的总和进行平均, 该处理方法简单高效, 但是仍需加以改进[6]。
1.4 加权平均法依据三个通道不同的重要性和一些其他依据, 将三个亮度值用不同的系数进行加权之后再平均。对于人类来说, 人眼对于绿色的敏感程度最高, 对于蓝色的敏感程度最低, 因此, 按照以下公式对RGB三个分量进行加权平均得到比较合理的灰度图像[7]。
| $ \begin{array}{*{20}{c}} {\mathit{Ggray}{\rm{ }}(i,j) = 0.299{\rm{*}}R(i,j) + 0.578*}\\ {G(i,j) + 0.114*B(i,j)} \end{array} $ | (6) |
本文将采用加权平均法, 根据多次实验结果表明, 按照上述公式对RGB三个分量进行加权平均得到的是较为合理的灰度图像。
2 边缘检测算子分析与研究 2.1 传统边缘检测算法分析1) Roberts算子
Roberts算子, 它在图像处理中是基本也是较为重要的一种算子, 它的原理是利用局部差分寻找边缘的算子。根据对角线方向上的两个最靠近的两像素之间的梯度近似值来对图像的边缘信息进行检测。检测垂直边缘的效果远远好于斜向边缘, 定位精度高, 对噪声敏感, 无法抑制噪声的影响[8]。
2) Prewitt算子
Prewitt算子是一种一阶微分算子的边缘检测, 它利用像素点的四个相邻方向的像素的灰度值的差, 判断像素的机制来检测是否是图像的边缘, 去除虚假的边缘信息, 对噪声具有平滑作用[9]。它的原理是选择不同的方向然后与图像进行最相近邻域进行卷积操作, 其中一个方向用来可以检测到垂直方向的边缘信息, 而对于另一个方向来说可以检测到水平方向的卷积信息。
定义f(x, y)为图像的二阶灰度值, Prewitt算子有一下的定义:
| $ \begin{array}{*{20}{c}} {G(i) = \{ [f(i - 1,j - 1) + f(i - 1,j) + f(i - }\\ {1,j + 1)]\} - [f(i + 1,j - 1) + f(i + 1,j) + f(i + }\\ {1,j + 1)]} \end{array} $ | (7) |
| $ \begin{array}{*{20}{c}} {G(j) = \{ [f(i - 1,j + 1) + f(i,j + 1) + f(i + }\\ {1,j + 1)] - [f(i - 1,j - 1) + f(i,j - 1) + f(i + }\\ {1,j - 1)]\} } \end{array} $ | (8) |
| $ \begin{array}{l} {\rm{则 }}P(i,j) = \max [G(i),G(j)]\\ {\rm{或}}P(i,j) = G(i) + G(j) \end{array} $ | (9) |
3) Sobel算子
Sobel算法是像素图像边缘检测中最重要的算子之一, 在机器学习、数字媒体、计算机视觉等信息科技领域起着举足轻重的作用。在技术上, 它的一阶差分算子是离散的, 它的主要用途是用来计算图像一阶梯度的最逼近值, 同时它也是计算亮度函数之一。用这个算子计算图像上大其他点, 就会出现这个点所映射出的法矢量或者是梯度矢量[10]。
4) 高斯-拉普拉斯算子
该算法就是直接对我们的高斯模型求二阶导数
高斯卷积函数定义为:
| $ {G_\sigma }(x,y) = \frac{1}{{\sqrt {2\pi {\sigma ^2}} }}\exp \left( { - \frac{{x2 + y2}}{{2{\sigma ^2}}}} \right) $ | (10) |
而原始图像f(x, y)与高斯卷积定义为:
| $ \begin{array}{*{20}{c}} {\left[ {{G_\sigma }(x,y)*f(x,y)} \right] = \left[ {{G_\sigma }(x,y)} \right]*}\\ {f(x,y) = {\mathop{\rm LoG}\nolimits} *f(x,y)} \end{array} $ | (11) |
因为:
| $ \begin{array}{*{20}{c}} {\frac{d}{{dt}}[h(t)*f(t)] = \frac{d}{{dt}}\int f (\tau )h(t - \tau )d\tau = }\\ {\int f (\tau )\frac{d}{{dt}}h(t - \tau )d\tau = f(t)*\frac{d}{{dt}}h(t)} \end{array} $ | (12) |
在上述模板形式容易看出, 如果在图像中一个较暗的区域出现亮点, 那么用拉普拉斯-高斯算子会使得这个亮点变的更亮[11]。这是因为在图像中的边缘就是那些灰度发生跳变的区域, 拉普拉斯高斯算子在边缘检测中很有用, 一般增强技术对于陡峭的边缘和缓慢变化的边缘是不好确定边缘的位置, 但是这个算子却可以用二次微分正峰和负峰之间的过零点来确定, 对孤立点和端点更为敏感, 因此特别适合于以突出图像中的孤立点、孤立线或者线端点为目的的场合。
对于噪声干扰信息来说canny方法不够敏感, 对于一些不够明显的不易检测的边缘信息它也能很好的检测出来。它的最明显的好处是, 它使用了不一样的阈值用来识别易被检测的边缘和不易被检测的边缘, 当容易检测的边缘信息和不易检测的边缘信息相连的时候, 它也会把不易检测到的边缘信息输出到处理的图像中[12]。
结合gasussian滤波的优势采用canny方法能够极大的弱化噪声, 减少不良信息对图像的危害, 增加图像的信噪比, 同时该方法在降噪的同时能够保留图像的奇异点的信息, 克服奇异点“有毛刺和轻微的振荡”的现象。
为了从整体上计算图像的噪声以及更可靠的求出图像的边缘幅值和图像的梯度, 我们在Canny算子中加入了高斯滤波, 计算公式如下:
第一步:求图像与高斯滤波器的卷积:
| $ S[i,j] = G[i,j:\sigma ]*I[i,j] $ | (13) |
第二步:使用一阶有限差分计算偏导数的两个列阵P与Q:
| $ \begin{array}{*{20}{c}} {P[i,j] \approx (S[i,j + 1] - S[i,j] + S[i + }\\ {1,j + 1] - S[i + 1,j])/2} \end{array} $ | (14) |
| $ \begin{array}{l} Q[i,j] \approx (S[i,j] - S[i + 1,j] + S\\ [i,j + 1] - S[i + 1,j + 1])/2 \end{array} $ | (15) |
第三步:计算赋值和方位角:
| $ M[i,j] = \sqrt {P[i,j]2 + Q[i,j]2} $ | (16) |
| $ \theta [i,j] = \arctan (Q[i,j]/P[i,j]) $ | (17) |
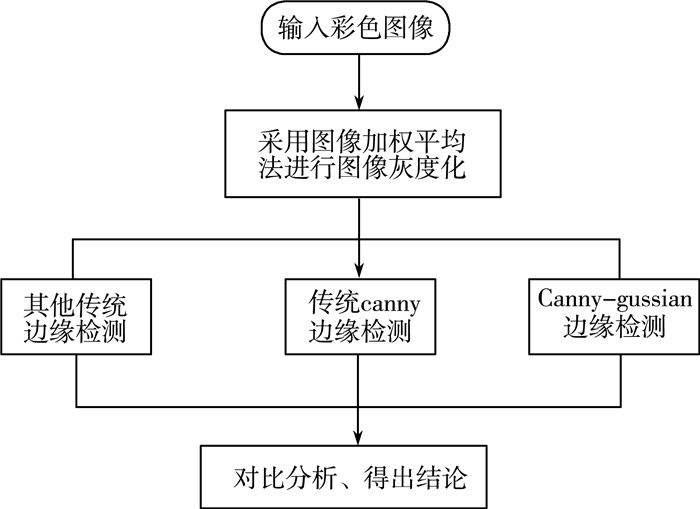 |
| 图 1 图像边缘提取仿真流程 |
在仿真及验证分析中, 本文通过与多个传统边缘检测算子以及Canny算子进行比较, 通过对比仿真得出结论[13]。
首先对测试样图(图 2)进行灰度化处理, 让图像的关键信息得以保存, 取出不重要的大量信息[14]。图像灰度化后如下图所示(图 3):
 |
| 图 2 测试样图 |
 |
| 图 3 加权平均值法灰度化 |
通过与原图对比得知采取加权平均值法进行灰度化不仅保留了原图像的纹理等关键特征, 同时使得文件的空间大大减小, 减少了后续的处理工作。
传统边缘提取算法与Gussian-Canny算法的对比结果如下:
 |
| 图 4 Sobel算子测试图 |
 |
| 图 5 Robert算子测试图 |
 |
| 图 6 Canny算子测试图 |
 |
| 图 7 Gussian-Canny算子测试图 |
4 结论
通过上述仿真结果分析, Sobel与Robert算子对噪声较为敏感, 不能有效的提取图像的边缘信息, 很难用于边缘提取, 传统的Canny算子虽然能够准确的提取到图像的边缘信息, 但是图像的连续性较差, 本文基于Canny算法的图像边缘算子, 加入高斯滤波联合处理可以有效的得到图像的边缘信息, 同时图像的噪声干扰得到了有效的抑制, 得到了较好的效果, 达到了预想的边缘提取成果。
| [1] |
王玉凡. 基于Canny边缘检测和Harris角点检测的图像拼接方法[J]. 内蒙古科技与经济, 2019(17): 90-91. |
| [2] |
王正存, 肖中俊, 严志国.逻辑回归分类识别优化研究[J/OL].齐鲁工业大学学报, 2019, 33(5): 47-51. http://sqgx.cbpt.cnki.net/WKD/WebPublication/paperDigest.aspx?paperID=22ac3202-9b57-4dcc-8313-a0ab89374159
|
| [3] |
巨志勇, 王超男. 基于二次曲面拟合的子像素边缘检测算法[J]. 电子科技, 2016, 29(6): 8-10. |
| [4] |
杨少令, 刁燕, 罗华, 等. 一种改进的Canny图像分割算法[J]. 计算机与现代化, 2018(8): 57-60. DOI:10.3969/j.issn.1006-2475.2018.08.011 |
| [5] |
李强.基于多层次融合与卷积神经网络的道路交通标线检测与识别[D].西安: 长安大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10710-1018790503.htm
|
| [6] |
罗文婷, 李中轶, 李林, 等. 基于改进CANNY边缘检测算法的道路标线自动识别及定位[J]. 西南交通大学学报, 2018, 53(6): 1253-1260. DOI:10.3969/j.issn.0258-2724.2018.06.022 |
| [7] |
刘森斌, 汪国有. 基于改进Fast-MBD显著性检测和多特征融合匹配的靶纸区域快速检测算法[J]. 计算机测量与控制, 2018, 26(9): 23-28, 33. |
| [8] |
WAMG Y G, LIN C J, CHEN S M. Applying fuzzy methodto vision-based lane detection and departure warning system[J]. Expert Systems With Applications, 2010, 37(1): 113-126. |
| [9] |
姜炳旭, 刘杰, 孙可. Sobel边缘检测的细化[J]. 沈阳师范大学学报(自然科学版), 2010, 28(4): 503-506. DOI:10.3969/j.issn.1673-5862.2010.04.014 |
| [10] |
孙根云, 柳钦火, 刘强, 等. 图像的模糊边缘检测算法[J]. 光电工程, 2007, 34(7): 141-144. DOI:10.3969/j.issn.1003-501X.2007.07.031 |
| [11] |
谭艳, 王宇俊, 李飞龙, 等. 几种典型的图像边缘检测算法的分析比较[J]. 电脑知识与技术, 2012, 8(7): 1604-1608. DOI:10.3969/j.issn.1009-3044.2012.07.046 |
| [12] |
张瑞华, 吴谨. 基于曲波变换和Susan种子点生长的边缘检测算法[J]. 华中师范大学学报(自然科学版), 2011, 45(3): 386-390, 411. |
| [13] |
欧温暖. 几种常见边缘检测算子的分析比较[J]. 现代计算机(专业版), 2010, 27(5): 75-77. |
| [14] |
贺智龙, 肖中俊, 严志国. 基于HSV与边缘信息的车牌定位与字符分割方法[J]. 齐鲁工业大学学报, 2019, 33(3): 44-48. |
 2020, Vol. 34
2020, Vol. 34


