| 采用卷积神经网络的数字手写体识别的研究 |
数字作为日常生活中随处可见的符号, 其重要性不言而喻。随着信息化社会的发展, 人们需要处理大量的数字信息。为节省人力、物力、财力、提高数字信息处理效率, 应用计算机进行自动数字识别成为了一个热门研究话题。
目前手写体数字识别的方法主要有模板匹配法、统计决策法、句法结构法、模糊判别法、逻辑推理法和神经网络法等[1-5], 但是以上方法都有提取特征困难的缺陷, 因此识别效果不佳。而深度学习的提出, 使得这一问题有了新的解决渠道。
深度学习[6-9]的概念由Hinton等人于2006年提出, 是机器学习研究中一个新的领域, 目的在于建立模拟人脑进行分析学习的神经网络。而LeCun等人提出的卷积神经网络(Convolutional Neural Networks, CNN)是第一个真正意义上的多层结构学习算法, 它以减少参数数目来提高网络的训练性能。
卷积神经网络通过一系列方法, 将数据量庞大的图像识别问题不断降维, 最终使其能够被训练[10-12]。卷积神经网络最早由Yann LeCun提出并应用在手写字体识别上, 而之后几年中, 由于该模型在反向传播算法中梯度弥散以及收敛速度慢等问题, 对于该神经网络模型的研究被支持向量机(Support Vector Machine, SVM)和贝叶斯网络等方法所取代。而深度学习被提出后, 卷积神经网络渐渐得到改良, 被重新提出并应用。
神经网络具有强大的学习能力以及自适应能力, 并拥有并行处理能力、容错能力、特征自动提取能力。因此, 本文基于LeCun等人提出的卷积神经网络模型, 针对其梯度弥散和收敛速度慢等问题, 对传统的几种激活函数进行结合和改良, 得到一种新的CNN模型, 并将其应用于数字手写体的识别。
1 卷积神经网络模型 1.1 卷积神经网络的基本原理简单来说, 卷积神经网络是一个多层的神经网络, 其每一层由多个二维平面组成, 每个平面又由多个独立神经元组成。卷积神经网络的概念示范图如图 1所示。
 |
| 图 1 卷积神经网络结构示意图 |
一般地, CNN的基本结构包括两层:其一为卷积层(特征提取层), 每个神经元的输入都与前一层的局部感受野相连, 并提取该局部的特征, 一旦该局部特征被提取后, 它与其他特征间的位置关系也随之确定下来; 其二是池化层(特征映射层), 每个计算层由多个特征映射组成, 每个特征映射即为一个平面, 平面上所有神经元的权值相等。特征映射结构采用对函数核影响小的Sigmoid函数作为卷积网络的激活函数, 使得特征映射具有位移不变性。
总的来说, 卷积网络的核心思想是:将局部感受野、权值共享以及时间或空间亚采样这三种结构思想结合起来获得某种程度的位移、尺度、形变不变性。
1.2 卷积经过经验得知, 传统神经网络的每个层次通常采用全连接, 这造成很多不必要的浪费。实验证明, 只需要提取输入图像的一些特征, 将参数数目降低, 如图 2所示。卷积过程包括:用一个可训练的滤波器(卷积核)fx去卷积一个输入的图像, 然后加一个偏置bx, 得到卷积层Cx。卷积的过程可以理解为使用一个卷积核来过滤图像的各个区域, 从而得到这些区域的特征值。而在实际训练过程中, 卷积核的值是在学习过程中学到的。
 |
| 图 2 卷积和下采样过程 |
1.3 池化
池化其实简单地说就是下采样, 是模拟大脑的视觉皮层抑制效应的操作, 可以在减少参数的同时保留特征信息。如图 2所示, 下采样过程包括:每个邻域四个像素求和变为一个像素; 然后通过标量Wx+1加权, 再增加偏置bx+1; 最后通过一个Sigmoid激活函数, 产生一个大概缩小四倍的特征映射图Sx+1。池化的作用是即使减少了许多数据, 特征的统计属性仍能够描述图像, 而且由于降低了数据维度, 有效地避免了过拟合。在实际应用中, 下采样的方法有:最大值下采样、高斯下采样、平均值下采样、权值可训练下采样。根据下采样的方法, 池化分为最大值下采样与平均值下采样, 这两种方法均能得到较好的结果。
1.4 全连接层全连接层是在输出层前的最后一个层, 它的作用是连接所有的特征, 将输出值送给分类器, 得出最终结果。卷积层、池化层等操作是将原始数据映射到隐层特征空间, 全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。在实际使用中, 全连接层可由卷积操作实现。
2 卷积神经网络算法卷积神经网络在本质上是一种输入到输出的映射, 它能够学习大量的输入与输出之间的映射关系, 而不需要任何输入和输出之间的精确的数学表达式, 只要用已知的模式对卷积网络加以训练, 网络就具有输入输出对之间的映射能力。它的训练算法与传统的BP算法差不多, 主要包括4步, 这4步被分为两个阶段, 即前向传播阶段和反向传播阶段。通过卷积神经网络不断将两个阶段进行迭代、参数不断进行更新, 网络对于训练集的学习越来越深, 误差逐渐降低。
2.1 前向传播阶段前向传播阶段的过程为:1)首先从训练集中取一个样本命为(X, Yp), 将X输入网络; 2)计算相应的实际输出Op。即:
| $ \begin{array}{l} {O_p} = {F_n}\left( { \cdots \left( {{F_2}\left( {{F_1}\left( {X * {W_1} + {b_1}} \right) * {W_2} + {b_2}} \right) \cdots } \right) * } \right.\\ \left. {{W_n} + {b_n}} \right) \end{array} $ | (1) |
式中:Wi和bi分别为各卷积层的权值和偏置矩阵; Fi代表各卷积层的激活函数和池化层的下采样函数。在此阶段, 信息从输入层经过逐级变换, 传送到输出层。
下面对网络前向传过程中涉及到的激活函数进行介绍。
激活函数是卷积神经网络中的一个重要组成部分, 它的目的是为了解决训练集中的数据可能存在的非线性问题。实验证明, 单纯地只用一个激活函数对数据进行处理时, 其准确率差强人意。因此, 结合传统的激活函数选择方案并进行改进, 选择出合适的激活函数十分必要。
卷积神经网络中激活函数分为饱和的非线性激活函数和不饱和的非线性激活函数。其中, 饱和非线性激活函数包括Sigmoid函数和Tanh双曲正切函数; 不饱和的非线性激活函数包括ReLUs函数和Softplus函数。
Sigmoid函数的表达式为:
| $ f\left( x \right) = \frac{1}{{1 + {e^{ - x}}}} $ | (2) |
双曲正切函数Tanh的表达式为:
| $ f\left( x \right) = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^x}}} $ | (3) |
ReLUs函数的表达式为:
| $ f\left( x \right) = \max \left( {0,x} \right) $ | (4) |
Softplus函数的表达式为:
| $ f\left( x \right) = \lg \left( {{e^x} + 1} \right) $ | (5) |
以上四种激活函数图像如图 3所示。
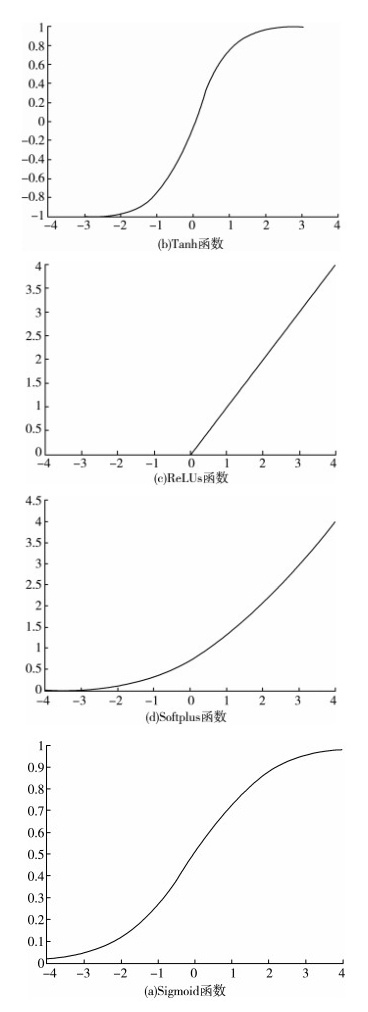 |
| 图 3 激活函数图像 |
传统的卷积神经网络中通常采用饱和非线性激活函数Sigmoid以及双曲正切函数Tanh作为激活函数, 然而这两种函数在使用时存在收敛速度慢以及梯度弥散造成的网络不收敛等问题。如今越来越多的人选择使用更符合生物学的不饱和非线性激活函数ReLUs和Softplus, 它们相对于饱和的非线性激活函数更具有稀疏性。
对比以上几种激活函数的特点和优势发现:在输入特征相差比较复杂或是相差不是特别大, 需要进行更细微的分类判断时, Sigmoid函数的效果比较好; 然而, 若采用Sigmoid作为激活函数, 则需对输入特征数据进行归一化, 否则激活后的值会进入平坦区, 使隐层的输出全部趋同。ReLUs激活函数具有稀疏性, 而Softplus激活函数作为比ReLUs函数更光滑的表示方式, 使激活函数在x≥0处更具优势。
基于Sigmoid和Softplus函数的特征, 本文对激活函数进行改进, 在图 1所示的卷积神经网络的结构中, 全连接层采用的改进后的激活函数如下:
| $ f\left( x \right) = \left\{ \begin{array}{l} \ln \left( {{e^x} + 1} \right)\left( {x \ge 0} \right)\\ \frac{1}{{1 + {e^{ - x}}}}\left( {x < 0} \right) \end{array} \right. $ | (6) |
对于激活函数Sigmoid和Softplus相结合进行的相关测试, 在下文中会进行描述。
2.2 后向传播阶段向后传播阶段的过程为:1)计算实际输出Op与相应的理想输出Yp的差; 2)然后按极小化误差的方法反向传播调整权矩阵。
首先将整个神经网络加上函数的结构视为一串函数(其中每层对应一个函数)级联成的一个新函数, 每个函数的导数都可通过数学表达式解析求得:
| $ h\theta \left( x \right) = \left( {f\left( {L + 1} \right) * \cdots * f\left( 1 \right)\theta 1 * \cdots * f\left( 2 \right)\theta 2f\left( 1 \right)} \right)\left( x \right) $ | (7) |
其中, θ是该神经网络的参数。f(1)=x, f(L+1)=hθ(x), 通过数值计算将误差信号后向传递到第1层:
| $ \begin{array}{l} \delta 1 = \partial \partial f\left( 1 \right)J\left( {\theta ,x,y} \right) = \partial J\partial f\left( {1 + 1} \right)\partial f\left( {1 + 1} \right)\partial f\left( 1 \right)\\ = \delta \left( {1 + 1} \right)\partial f\left( {1 + 1} \right)\partial f\left( 1 \right) \end{array} $ | (8) |
在第1层求J关于该层参数θ(l)的梯度:
| $ \begin{array}{l} \nabla \theta \left( l \right)J\left( {\theta ,x,y} \right) = \partial \partial \theta \left( l \right)J = \partial J\partial f\left( 1 \right)\partial f\left( 1 \right)/\partial \theta \left( l \right) = \\ \delta 1\partial f\left( 1 \right)\partial \theta \left( l \right) \end{array} $ | (9) |
将所有样本的梯度相加得到总梯度:
| $ \nabla \theta \left( l \right)J\left( \theta \right) = \sum {{m_i}} = \nabla \theta \left( l \right)J\left( {\theta ,x\left( i \right),y\left( i \right)} \right) $ | (10) |
对于不同的网络结构, 公式(2-4)和公式(2-5)中根据具体的∂f(l+1)∂f(l)和∂f(l)∂(l)θ就可以求得所有参数的梯度。
3 应用CNN进行数字手写体识别流程利用CNN对数字手写体进行识别流程如图 4所示。首先对网络中的参数进行初始化, 然后输入训练集数据, 网络经过多次前向传播与反向传播的迭代, 最终达到最大迭代次数或训练集实际输出与理论输出值误差在允许范围内。在此过程中, 每一步迭代所生成的权重、偏置等特征参数不断地进行更新、保存, 最后得到数字手写体的CNN识别网络。然后将测试集数据输入到训练好的CNN识别网络, 即可得到相应的识别结果。
 |
| 图 4 CNN数字手写体识别结构框图 |
4 实验设置与实验结果
使用的训练集数据是LeCun所构建的MNIST手写体数据训练库。训练集数据1是根据MNIST数据库的格式从该数据库中分离出的部分数据, 与测试集没有重叠部分。测试集数据2是自己收集的1000个数字手写体的图像。训练过程中, CNN迭代一次所需要的时间约为200 s。
下面首先进行测试集数据库1对于改进算法前后数字手写体识别率的测试。
为了对比不同迭代次数下的网络识别正确率, 设置了七种不同的迭代次数, 将测试集数据1分别输入到改进前后的CNN网络中, 进行数字手写体识别测试。识别结果如图 5所示。
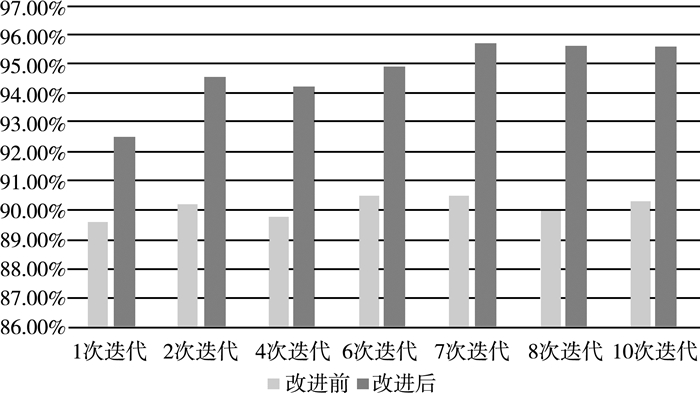 |
| 图 5 数据集1在改进前和改进后在不同迭代次数下的准确率 |
由图 5可以看出, 改进后的CNN网络识别结果要优于改进前的网络识别结果。
为了验证本文提出的CNN识别网络具有更好的实际应用价值, 将自行收集的测试集2分别输入到改进后的CNN网络模型中。识别结果如图 6所示。
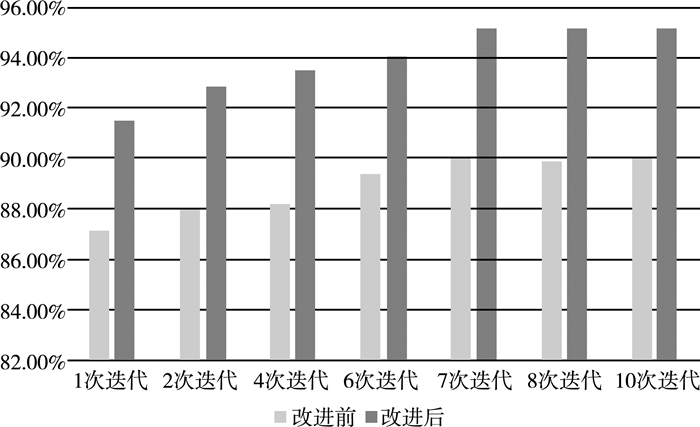 |
| 图 6 数据集2在改进前和改进后在不同迭代次数下的准确率 |
实验结果表明, 官方测试集与实际中应用的测试集识别率误差在可接受范围内, 改进算法后的识别率较之前有了很大提高, 具有实际应用意义。
5 结论所描述的卷积神经网络是在深度学习的环境下, 模仿人脑的神经网络完成数据的处理、分类功能。实验过程中, 首先将较为官方的训练集作为输入, 使卷积神经网络自动学习提取训练集中数字手写体的特征并与其标签一一对应。训练成熟后, 将测试集作为输入, 使计算机根据学习结果自动识别分类图像特征, 并以标签分类, 从而得到最终结果。仿真实验中所使用的训练集MNIST及测试集数据1都具有一定的权威性, 得到的结果客观真实; 又通过测试集数据2中比较实际的数据进行测试, 使得实验结果具有参考性和实际应用意义。采用基于LeCun提出的模型进行改进, 并对卷积神经网络中涉及的激活函数进行改良对比, 使得卷积神经网络对于数字手写体的识别的准确率有所提高; 同时, 改进后减少了网络的训练参数, 使神经网络结构变得更简单, 适应性更强。
总之, 所改进的识别模型使卷积神经网络在数字手写体识别方面达到较好效果, 是一种较为简单、容易实现且具有实际意义的提高数字手写体识别准确率的方法。
| [1] |
马媛媛, 史加荣. 卷积神经网络及其在手写体数字识别中的应用[J]. 湖北工程学院学报, 2017, 37(06): 66-72. DOI:10.3969/j.issn.2095-4824.2017.06.014 |
| [2] |
张翼成, 陈欣, 杨红军, 等. 基于组合特征的BP神经网络数字识别方法[J]. 计算机系统应用, 2013, 22(3): 113-116, 54. DOI:10.3969/j.issn.1003-3254.2013.03.026 |
| [3] |
刘高平, 赵杜娟, 黄华. 基于自编码神经网络重构的车牌数字识别[J]. 光电子·激光, 2011, 22(1): 144-148. |
| [4] |
刘洋洋, 嵇启春. 一种改进的模板匹配的数字识别算法[J]. 工业控制计算机, 2010, 23(5): 76-77. DOI:10.3969/j.issn.1001-182X.2010.05.035 |
| [5] |
杜选, 高明峰. 人工神经网络在数字识别中的应用[J]. 计算机系统应用, 2007(2): 21-22, 27. DOI:10.3969/j.issn.1003-3254.2007.02.006 |
| [6] |
胡侯立, 魏维, 胡蒙娜. 深度学习算法的原理及应用[J]. 信息技术, 2015(2): 175-177. |
| [7] |
余涛. 基于稀疏自编码器的手写体数字识别[J]. 数字技术与应用, 2017(1): 66. |
| [8] |
陈浩翔, 蔡建明, 刘铿然, 等. 手写数字深度特征学习与识别[J]. 计算机技术与发展, 2016, 26(7): 19-23, 29. |
| [9] |
宋志坚, 余锐. 基于深度学习的手写数字分类问题研究[J]. 重庆工商大学学报(自然科学版), 2015, 32(8): 49-53. |
| [10] |
代贺, 陈洪密, 李志申. 基于卷积神经网络的数字识别[J]. 贵州师范大学学报(自然科学版), 2017, 35(5): 96-101. DOI:10.3969/j.issn.1004-5570.2017.05.016 |
| [11] |
徐姗姗.卷积神经网络的研究与应用[D].南京: 南京林业大学, 2013.
|
| [12] |
李飞腾.卷积神经网络及其应用[D].大连: 大连理工大学, 2014.
|
 2018, Vol. 32
2018, Vol. 32

