| 基于云模型的永磁同步电机直接转矩控制仿真研究 |
传统永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)直接转矩控制技术,存在定子电阻参数变化以及转速环PI参数变化问题,影响电机运行效率。针对以上问题,国内外学者提出许多针对永磁同步电机直接转矩控制技术的改进方法。
文献[1]在研究电机转速误差对于PI参数影响的基础上,提出一种模糊增益自整定PI控制策略,解决了电机在连续加减速工况下的控制问题。文献[2]、[3]采用预测控制器代替传统的PID控制器检测定子电流,利用滑模模型自适应系统方法,检测电机转子位置和速度,实现永磁同步电机无传感器控制。文献[4]提出两种定子电阻的在线识别方法:第一种采用谐波信号注入法,另一种采用基于Hammerstein模型的牛顿-高斯法,将电机分为动态线性和静态非线性两种状态,并在实际电机中进行测试,实验证明了这两种方法的有效性。文献[5]在传统滑模观测器的基础上采用可变边界层厚度的Sigmoid函数取代Sign函数,并结合转速大小动态调整观测器增益,同时运用李雅普诺夫函数设计电阻参数在线识别算法,实时修正滑模观测器参数。文献[6]、[7]采用基于神经网络的定子电阻估计器,对定子电阻实现在线估计。文献[8]分析了定子电阻对永磁同步电机直接转矩控制系统性能的影响。文献[9]提出一种二维云模型的永磁同步电机电压模型控制方法,对电机内部参数摄动及外部负载扰动具有较强的鲁棒性。
永磁同步电机的传统直接转矩控制技术,忽略了定子电阻变化及PI参数对电机运行性能的影响,现有的改进方法通常只对某一方面进行改进,虽然提高了电机运行性能,但仍有不足。我们在传统直接转矩控制技术的基础上,加入基于电流误差控制的定子电阻估计器,采用云模型理论构建智能PID控制器,实现对转速环PI参数的自整定。仿真表明,提出的改进方法有效改善了电机运行时的动态性能。
1 永磁同步电机直接转矩控制PMSM转子磁场在αβ两相静止坐标系下的数学模型:
定子电压方程:
| $ \left\{ \begin{array}{l} {u_\alpha } = {R_s}{i_\alpha } + {L_\alpha }p{i_\alpha } + {L_{\alpha \beta }}p{i_\beta } - \omega {\psi _f}{\rm{sin}}\theta \\ {u_\beta } = {R_s}{i_\beta } + {L_\beta }p{i_\beta } + {L_{\alpha \beta }}p{i_\alpha } + \omega {\psi _f}{\rm{sin}}\theta \end{array} \right.。$ | (1) |
定子磁链方程:
| $ \left\{ \begin{array}{l} {\psi _\alpha } = \int {\left( {{u_\alpha } - {R_s}{i_\alpha }} \right)dt} \\ {\psi _\beta } = \int {\left( {{u_\beta } - {R_s}{i_\beta }} \right)dt} \end{array} \right.。$ | (2) |
电磁转矩方程:
| $ {T_e} = 1.5{n_p}\left( {{\psi _\alpha }{i_\beta } - {\psi _\beta }{i_\alpha }} \right),$ | (3) |
uα、uβ为定子电压矢量的αβ轴分量;Rs为定子电枢相电阻;θ为转子轴线与a轴夹角的电气角度;iα、iβ为定子电流矢量的αβ轴分量;p为微分算子;ψf为转子磁链;Te表示永磁同步电动机电磁转矩;np为极对数;ψα、ψβ为定子磁链的αβ轴。
永磁同步电机直接转矩控制原理如图 1所示。首先测量电机的端电压和端电流;然后进行坐标变换;计算定子磁链ψs、转矩Te,并判断出磁链所在的扇区, 将给定的磁链ψs*和转矩Te*分别与计算得到的磁链|ψs|和转矩Te相比较;误差进入滞环比较器进行控制,通过误差值与扇区值选择相应的电压空间矢量,从而实现对电机磁链和转矩的直接控制。
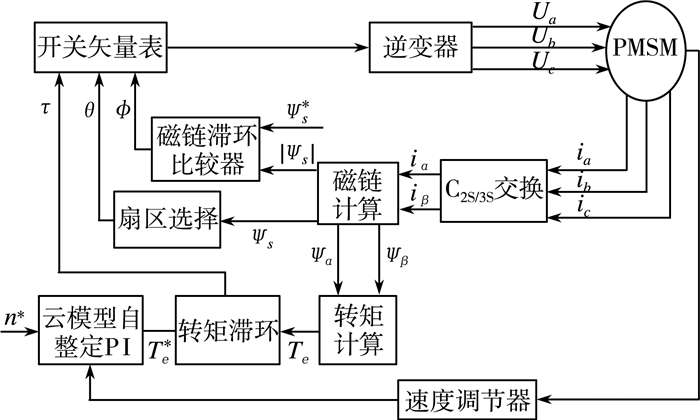 |
| 图 1 PMSM直接转矩控制系统原理图 |
2 云模型 2.1 模型的定义
设U是一个用数值表示的定量论域, C是U上的定性概念。若定量数值x∈U是定性概念C的一次随机实现,x对C的确定度μ(x)∈[0, 1]是具有稳定倾向的随机数,即:
| $ \mu :U \to [0, 1],$ | (4) |
| $ \forall x \in U, x \to u(x), $ | (5) |
则x在论域U上的分布称为云,记为C(x),每一个x称为一个云滴。
2.2 云模型的数学特征云模型用期望Ex、熵En和超熵He三个数字特征来整体表征一个定性概念。
期望Ex:是云滴在论域空间中分布的期望,是论域中最能代表定性概念的点,也是这个概念量化的最典型样本。
熵En:是定性概念不确定性的度量,同时受到定性概念的模糊性和随机性的制约。
超熵He:反映了熵的不确定性,是熵的熵,同时受到熵的模糊性与随机性的制约。
设U是一个用数值表示的定量论域, C是U上的定性概念。若定量数值x∈U是定性概念C的一次随机实现,若x满足:
x~N(Ex, En′2)[其中,En′~N(En, He2)],且x对C的确定度满足:
| $ \mu = {e^{\frac{{{{\left( {x - Ex} \right)}^2}}}{{2{{\left( {En\prime } \right)}^2}}}}}, $ | (6) |
则x在论域U上的分布称为正态云。
3 云模型自整定PI控制器 3.1 基于云模型的自整定PI控制器原理基于云模型的自整定PI控制器的原理为:通过对电机运行时刻转速偏差值e,求微分得到偏差变化值eci, 将e和eci作为输入构建双条件云规则推理器,利用云模型推理规则进行PI参数自整定。如图 2所示。
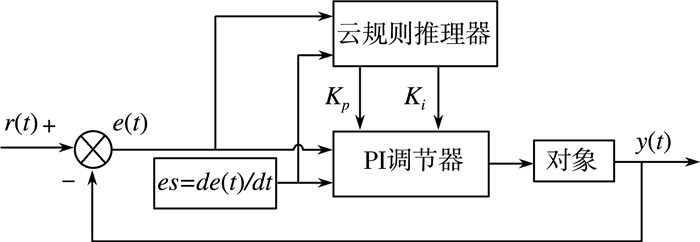 |
| 图 2 自整定PI控制器原理图 |
3.2 云模型自整定PI推理规则设计 3.2.1 PI参数原理
根据PID控制基本原理,Kp和Ki在系统校正环节中分别具有以下作用:
Kp:调节系统对于误差信号的响应速度。Kp越大,响应速度越快;但Kp值过大会产生超调,影响系统稳定性。
Ki:消除系统稳态误差,提高系统无差度。
根据参数Kp和Ki在系统校正环节中的作用,制定以下调节规则:
1) 当误差较大时,增大Kp, 提高系统响应速度;当误差较小时,减小Kp, 控制系统的超调量。
2) 在响应初期,减小Ki, 防止积分饱和;随着误差和误差变化率的减小,适当增大Ki。
3.2.2 云模型推理规则根据Kp、Ki与误差e、误差变化率eci之间的关联,设e、eci、ΔKp、ΔKi的变化范围为四个独立的定量论域,NB、NM、NS、Z、PS、PM、PB为该定量论域上的定性概念,分别代表负大、负中、负小、零、正小、正中、正大。误差e和误差变化率eci构成一个二维论域,分别和ΔKp、ΔKi构成两个条件云发生器,其中e、eci为条件云发生器输入,ΔKp、ΔKi为条件云发生器输出,数字特征见表 1。
| 表 1 自整定PI控制器ΔKp、ΔKi云模型数学特征 |
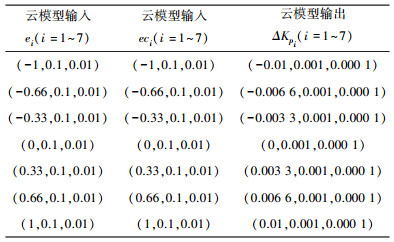 |
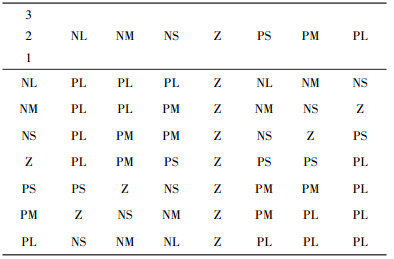
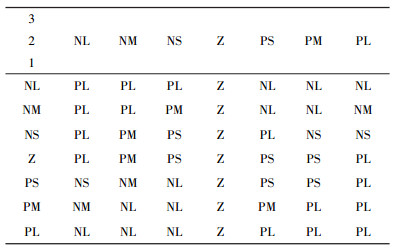
云模型自整定PI控制器以误差e及其误差变化率eci作为输入,对应表中区域1、2,通过规则推理得到输出ΔKp、ΔKi为表中区域3。推理规则表符合表 2、表 3,根据表 2、表 3可知,设计的云模型推理规则共49条。
| 表 2 ΔKp云规则推理表 |
 |
| 表 3 ΔKi云规则推理表 |
 |
设Kp0、Ki0为常规整定方法得到的PI参数,则上述利用云模型推理规则,实际PI参数的整定式为:
| $ {K_p} = {K_{p0}} + \Delta {K_p},$ | (7) |
| $ {K_i} = {K_{i0}} + \Delta {K_i}。$ | (8) |
PI参数整定流程如图 3所示。
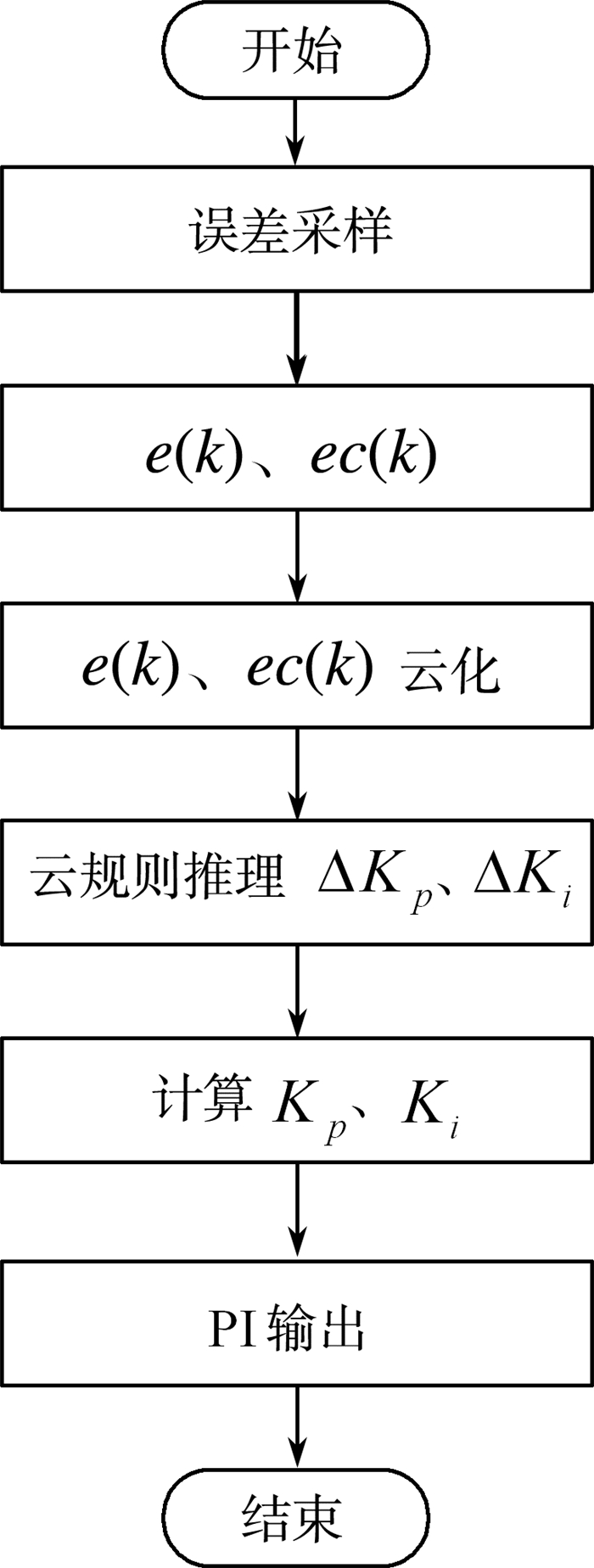 |
| 图 3 PI参数整定流程图 |
4 定子电阻估计器 4.1 定子电阻对电机控制影响
由式(2)定子磁链方程可知,定子磁链的计算通过输入电压及定子电阻压降的差值进行积分得到,因此,定子电阻阻值对于磁链计算的准确度有很大影响,在电机低速运行时,这种影响更为明显。在传统直接转矩控制系统中,通常忽略定子电阻阻值变化,这会影响电机的控制性能。
假设电机实际运行过程中定子电阻阻值变化为ΔR,引起电流变化为Δi,则实际磁链和转矩值为:
| $ \left\{ \begin{array}{l} \psi _\alpha ^ * = \int {\left[{{u_\alpha }-\left( {{R_s} + \Delta R} \right)\left( {{i_\alpha } + \Delta {i_\alpha }} \right)} \right]dt} \\ \psi _\beta ^ * = \int {\left[{{u_\beta }-\left( {{R_s} + \Delta R} \right)\left( {{i_\beta } + \Delta {i_\beta }} \right)} \right]dt} \end{array} \right., $ | (9) |
| $ T_e^ * = \frac{3}{2}{n_p}[\psi _\alpha ^ * \left( {{i_\beta } + \Delta {i_\beta }} \right)-\psi _\beta ^ * ({i_\alpha } + \Delta {i_\alpha })]。$ | (10) |
采用传统直接转矩控制的磁链和转矩估计值为:
| $ \left\{ \begin{array}{l} {\psi _\alpha } = \int {\left[{{u_\alpha }-{R_s}\left( {{i_\alpha } + \Delta {i_\alpha }} \right)} \right]dt} \\ {\psi _\beta } = \int {\left[{{u_\beta }-{R_s}\left( {{i_\beta } + \Delta {i_\beta }} \right)} \right]dt} \end{array} \right., $ | (11) |
| $ {T_e} = \frac{3}{2}{n_p}[{\psi _\alpha }\left( {{i_\beta } + \Delta {i_\beta }} \right)-{\psi _\beta }({i_\alpha } + \Delta {i_\alpha })], $ | (12) |
则实际值与估计值间的差值为:
| $ \left\{ \begin{array}{l} \mathit{\Delta }{\psi _\alpha } = \int {\left[{\Delta {R_s}\left( {{i_\alpha } + \Delta {i_\alpha }} \right)} \right]dt} \\ \mathit{\Delta }{\psi _\beta } = \int {\left[{\Delta {R_s}\left( {{i_\beta } + \Delta {i_\beta }} \right)} \right]dt} \end{array} \right., $ | (13) |
| $ \mathit{\Delta }{T_e} = \frac{3}{2}{\rm{ }}{n_p}[\Delta {\psi _\alpha }\left( {{i_\beta } + \Delta {i_\beta }} \right)-\Delta {\psi _\beta }({i_\alpha } + \Delta {i_\alpha })]。$ | (14) |
由式(9)~式(14)可知,定子电阻阻值变化对于点及控制性能有很大影响。
4.2 定子电阻估计器设计在传统直接转矩控制基础上,采用定子磁链观测器,通过在线观测定子电阻误差,对定子电阻进行补偿,提高系统控制性能。
定子电阻估计器利用定子电流矢量变化和定子电阻变化之间的关系,采用PI控制原理,通过定子电流变化来跟踪定子电阻变化。
定子电阻估计器原理图如图 4所示:
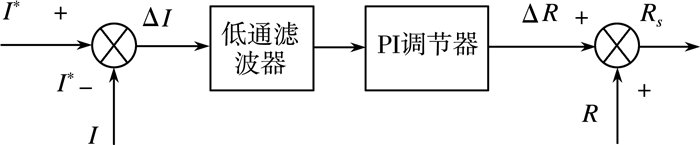 |
| 图 4 定子电阻估计器 |
5 仿真结果分析
设计的基于云模型的永磁同步电机自整定PI控制系统原理图如图 5所示。
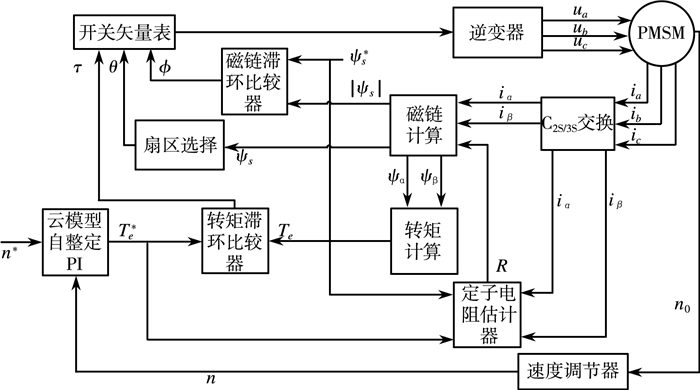 |
| 图 5 PMSM自整定PI控制系统原理图 |
在仿真实验中,将永磁同步电机的参数设置如下:给定电机转速为1 000 r·min-1, 采样周期TS=1e-005 s,仿真时间0.2 s, 直流母线电压为Udc=300 V, 极对数p=2, 定子电阻RS=2.873 Ω,定子磁链Ψref=0.507 2 wb,交轴电感Ld=0.008 5 H,直轴电感Lq=0.008 5 H,转矩惯量J=0.000 8 kg·m2,,负载转矩Te=3 N·m。
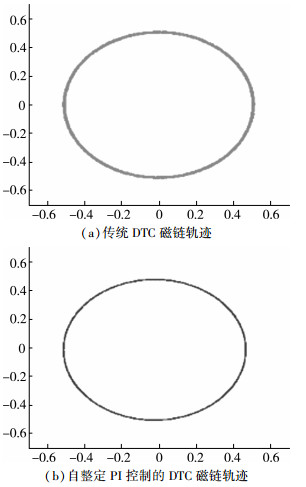 |
| 图 6 DTC磁链轨迹对比 |
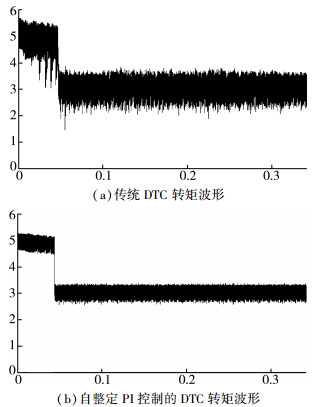 |
| 图 7 DTC转矩波形对比 |
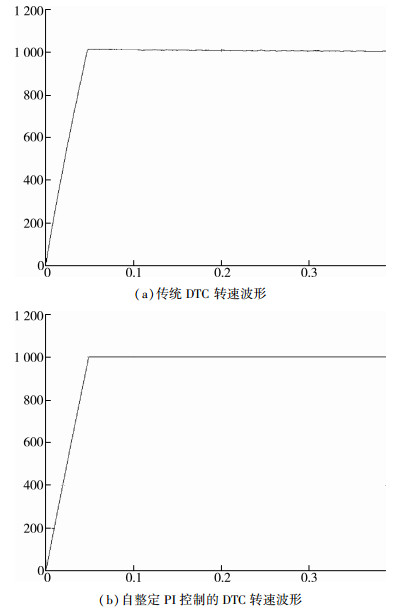 |
| 图 8 DTC转速波形对比 |
对比图 6(a)和图 6(b)可知, 传统直接转矩控制技术磁链脉动较大,采用定子电阻估计器的改进型直接转矩控制在电机运行过程中磁链轨迹平滑,磁链脉动减小。
对比图 7(a)和图 7(b)可知, 传统直接转矩技术转矩脉动过大,过大的转矩脉动会引起系统震荡,采用自整定PI控制的永磁同步电机在运行过程中转矩波形脉动明显减小。
对比图 8(a)和图 8(b)可知, 采用自整定PI控制的永磁同步电机在运行过程中转速脉动小,转速无超调。
6 结论1) 提出以云模型理论改进的自整定PI控制器和基于PI控制器的定子电阻估计器,改进了传统永磁同步电机直接转矩控制技术中忽略定子电阻变化影响电机运行性能的缺点。
2) 搭建基于云模型自整定PI控制器的改进型直接转矩控制仿真模型,仿真结果表明,所提出控制策略有效减小了永磁同步电机运行过程中的磁链和转矩脉动,转速无超调,提高了电机运行性能。
| [1] |
胡勤丰, 陈威振, 邱攀峰, 等. 适用于连续加减速的永磁同步电机模糊增益自调整PI控制研究[J]. 中国电机工程学报, 2017, 37(3): 907-915. |
| [2] |
张勇军, 汪伟, 张小庆, 等. 带电阻在线辨识的改进型永磁同步电机滑模观测方法[J]. 电机与控制学报, 2017, 21(6): 10-17; 2. |
| [3] |
刘计龙, 肖飞, 沈洋, 等. 永磁同步电机无位置传感器控制技术研究综述[J]. 电工技术学报, 2017, 32(16): 76-88. |
| [4] |
VESELY I, POHL L. Stator resistance identification of PMSM[J]. IFAC Papers on Line, 2016, 49(25): 223-228. DOI:10.1016/j.ifacol.2016.12.038 |
| [5] |
林茂, 李颖晖, 吴辰, 等. 基于滑模模型参考自适应系统观测器的永磁同步电机预测控制[J]. 电工技术学报, 2017, 32(6): 156-163. |
| [6] |
胡雪峰. 基于定子电阻观测器的永磁同步电动机滑模变结构直接转矩控制研究[J]. 河南科技大学学报(自然科学版), 2008, 29(2): 42-46; 110. |
| [7] |
徐艳平, 钟彦儒, 于宏全. 永磁同步电机的直接转矩控制的定子电阻的在线估计[J]. 电气传动, 2006(4): 24-26. |
| [8] |
梅柏杉, 陈晖. 直接转矩控制系统中定子电阻的影响分析[J]. 微特电机, 2009, 37(4): 13-15. |
| [9] |
魏海峰, 韦汉培, 张懿. 二维云模型在线优化永磁同步电机无传感器电压模型控制[J]. 电工技术学报, 2017, 32(23): 51-60. |
 2018, Vol. 32
2018, Vol. 32


