| 基于对比度受限自适应直方图多种路面裂缝检测与识别 |
2. 齐鲁工业大学(山东省科学院) 机械与汽车工程学院,济南 250353
2. School of Mechanical and Automotive Engineering, Qilu University of Technology(Shangdong Academy of Sciences), Jinan 250353, China
目前, 我国的道路交通发展十分快速, 对于路面造成的压力逐渐加剧。而路面的保养以及修复也成为了一个热门的研究问题[1-3]。路面的检测、维修、养护, 如果仅靠人工处理不仅会造成人力资源的浪费, 检测时检测人员的安全问题也将是一项隐患。因此, 道路检测应该从人工检测转变为智能化检测。
人工智能的发展使得智能化路面裂缝检测装置得以实现, 其中利用车载检测系统、攀爬机器人[4]等均可对路面进行检测。文献[5]提出了一种基于BP神经网络的沥青路面裂缝识别方法, 文献[6]提出了一种基于形状分析的沥青路面检测算法, 文献[7]提出了一种基于深度学习的裂缝检测算法。这些算法虽然能对特定的裂缝进行识别, 但是并不通用, 而且算法本身的鲁棒性和准确率也有待提高。
1 系统结构组成 1.1 算法流程图本系统借助人工驾驶的车辆, 利用CCD相机完成对行驶路面图像的采集。该系统对相机采集到的图像作如图 1所示处理。
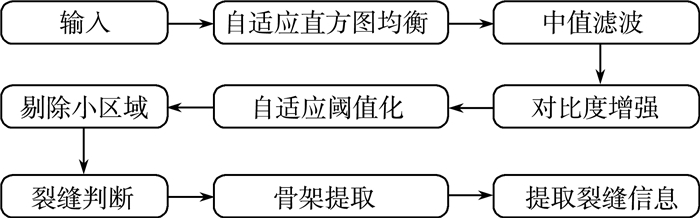 |
| 图 1 算法流程 |
1.2 图像直方图处理 1.2.1 对比度受限自适应直方图均衡法
直方图均衡化(histogram equalization, HE)是一种很常用的图像增强方法[7]。然而HE是对图像整体增强, 对于局部的信息不能有效地提高, 图像中有明暗区域, 此时信息会丢失。而自适应直方图均衡化(adaptive histogram equalization, AHE)[8]能对局部细节进行强化, 但是图像中噪声也会增强。而有限制的自适应直方图均衡化(contrast-limited adaptive histogram equalization, CLAHE)[9]则通过设定AHE中的高度来限制局部对比度的强度[10]。
CLAHE算法流程如下:
1) 将图像分为M*N个连续不重叠的子区域, M*N的大小取决于局部细节的增强强度。
2) 计算每个子区域的灰度直方图H(i)。
3) 如图 2所示:设定一个限制值T, 当H(i)≥T, H(i)=Hmax; 当H(i) < T, H(i)=Hmax。
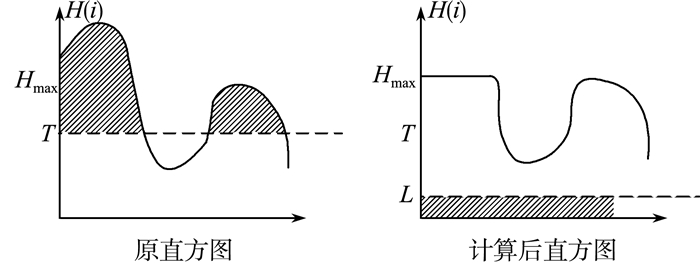 |
| 图 2 算法直方图对比 |
| $ H\left( i \right) = \left\{ \begin{array}{l} H\left( i \right) + L\;\;\;\;H\left( i \right) < T\\ {H_{\max }}\;\;\;\;H \ge T \end{array} \right. $ | (1) |
其中:H(i)、L、Hmax三者关系应为:
| $ {H_{\max }} = L + T $ | (2) |
L的取值为:
| $ L = \frac{{{N_{\sum {阴影} }}}}{{{N_{\rm{g}}}}} $ | (3) |
其中:Ng为子区域灰度级数量, NΣ阴影为阴影部分总像素数目。
a) 对受限制每一个子区域进行直方图均衡化。
b) 选取每个子区域的中心为参考点, 如图 3所示。
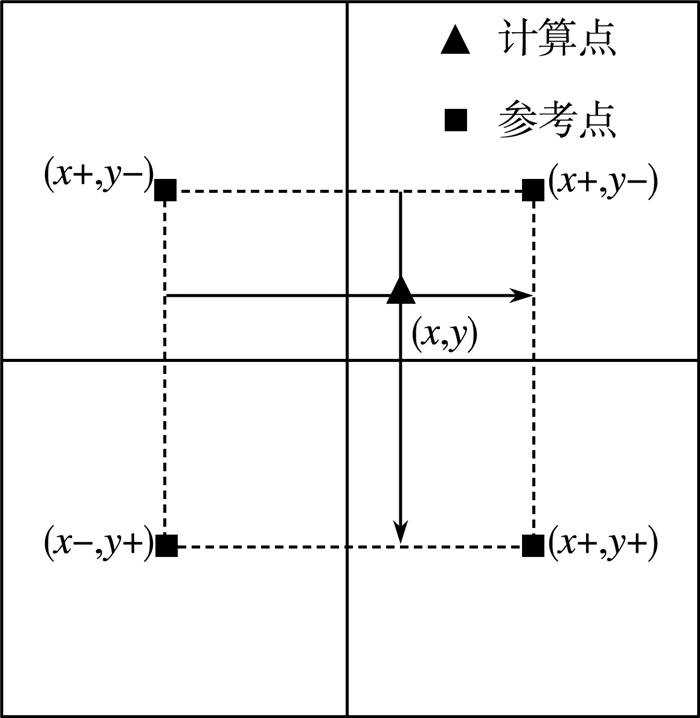 |
| 图 3 双线性插值运算 |
其中:三角形标志为计算点, 正方形标志为参考点。
计算点的插值公式如下:
| $ \begin{array}{l} P\left( i \right) = a\left[ {b{P_{ - - }} - \left( i \right) + \left( {1 - b} \right){P_{ + - }}\left( i \right)} \right] + \pm \left( {1 - a} \right)\\ \left[ {b{P_{ - + }}\left( i \right) + \left( {1 - b} \right){P_{ + + }}\left( i \right)} \right] \end{array} $ | (4) |
其中:
| $ a = \frac{{y - {y_ - }}}{{{y_ + } - {y_ - }}} $ | (5) |
| $ b = \frac{{x - {x_ - }}}{{{x_ + } - {x_ - }}} $ | (6) |
上式中:P(i)代表点(x, y)处的灰度值[7]。利用MATLAB进行仿真。在图 4中:(a)为表示原始图像, (b)为被噪声干扰后的图像, (c)为直方图均衡化后的灰度图像, (d)为经过有限制的直方图均衡化后的灰度图像。由这些图像可以看出:普通的直方图均衡化, 图像中的噪声干扰较大; 而经过CLAHE后的噪声干扰较小, 比较清晰。
 |
| 图 4 直方图均衡化 |
图 5中:(a)为被噪声污染后的灰度直方图; (b)为直方图均衡化后的灰度图像, 可以看出噪声污染较大; (c)为经过2×2模板CLAHE后的直方图, 无大范围的噪声影响; (d)为经过8×8模板后的直方图, 相较于图b、c, 噪声干扰更小。
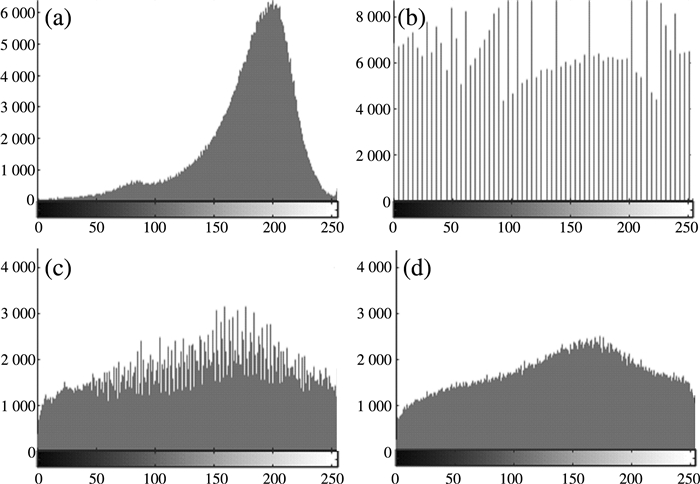 |
| 图 5 直方图前后对比 |
图 6沥青路面在不同模板下CLAHE后的效果。
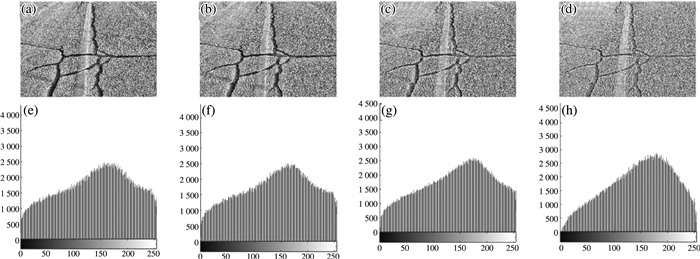 |
| 注:a)12×12模板CLAHE后; b)16×16模板CLAHE后; c)32×32模板CLAHE后; d)64×64模板CLAHE后; e)12×12模板CLAHE后灰度直方图; f)16×16模板CLAHE后灰度直方图; g)32×32模板CLAHE后灰度直方图; h)64×64模板CLAHE后灰度直方图 图 6 沥青路面不同模板下的CLAHE图 |
图 7水泥路面在不同种直方图算法下的效果。
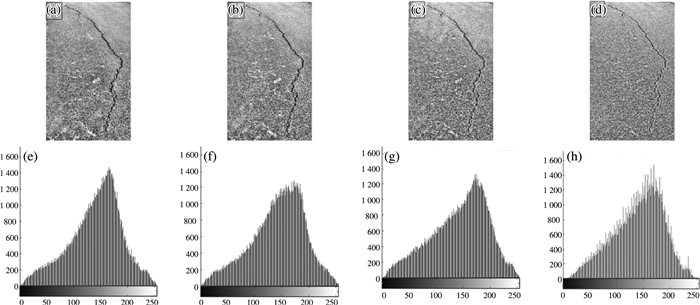 |
| 注:a)12×12模板CLAHE后; b)16×16模板CLAHE后; c)32×32模板CLAHE后; d)64×64模板CLAHE后; e)12×12模板CLAHE后水泥路面灰度直方图; f)16×16模板CLAHE后灰度直方图; g)32×32模板CLAHE后灰度直方图; h)64×64模板CLAHE后灰度直方图 图 7 水泥路面不同算法的结果对比 |
1.2.2 算法质量测评
1) 峰值信噪比
峰值信噪比(peak signal to noise ratio, PSNR)是一种基于对应像素间误差的全参考图像质量评价指标[11-14]。对于一幅大小为M*N的数字图像f0(x, y)和对比图像f(x, y), 均方差(MES)为:
| $ {\rm{MES}} = \frac{{\sum\limits_{x = 0}^{M - 1} {\sum\limits_{y = 0}^{N - 1} {{{\left[ {f\left( {x,y} \right) - {f_0}\left( {x,y} \right)} \right]}^2}} } }}{{MV}} $ | (7) |
峰值信噪比(PSNR)则为:
| $ {\rm{PSNR}} = 10\lg \frac{{{{\left( {{2^{{\rm{bits}}}} - 1} \right)}^2}}}{{{\rm{MES}}}} $ | (8) |
其中:M、N分别为数字图像的高度与宽度, bits为每像素的比特数。PSNR数值越小失真越严重。
2) 结构相似性
结构相似性(structural similarity index, SSIM)也是一种图像评估的方法, 它主要是从亮度、对比度、结构三个方面度量图像的相似性[12-14]。
评价模型:
| $ {\rm{SSIM}}\left( {{f_0},f} \right) = l{\left( {{f_0},f} \right)^\alpha } \cdot c{\left( {{f_0},f} \right)^\beta } \cdot s{\left( {{f_0},f} \right)^y} $ | (9) |
式中:
| $ l\left( {{f_0},f} \right) = \frac{{2{\mu _{{f_0}}}{\mu _f} + C1}}{{\mu _{{f_0}}^2 + \mu _\alpha ^2 + C1}} $ | (10) |
| $ c\left( {{f_0},f} \right) = \frac{{2{\sigma _{{f_0}}}{\sigma _f} + C2}}{{\sigma _{{f_0}}^2 + \sigma _f^2 + C2}} $ | (11) |
| $ s\left( {{f_0},f} \right) = \frac{{{\sigma _{{f_0}f}} + C3}}{{{\sigma _{{f_0}f}} + C3}} $ | (12) |
上式中:μf0、μf分别表示图像f0(x, y)、f(x, y)的均值, σf0、σf分别表示图像f0(x, y)、f(x, y)的方差, σf0f表示协方差。即:
| $ {\mu _{{f_0}}} = \frac{{\sum\limits_{x = 1}^M {\sum\limits_{y = 1}^V {{f_0}\left( {x,y} \right)} } }}{{MN}} $ | (13) |
| $ {\sigma _{{f_0}}} = \frac{{\sum\limits_{x = 1}^{M - 1} {\sum\limits_{y = 1}^{N - 1} {{{\left( {{f_0}\left( {x,y} \right) - {\mu _{{f_0}}}} \right)}^2}} } }}{{MN - 1}} $ | (14) |
| $ {\sigma _{{f_0}f}} = \frac{{\sum\limits_{x = 1}^{M - 1} {\sum\limits_{y = 1}^{N - 1} {\left( {\left( {{f_0}\left( {x,y} \right) - {\mu _{{f_0}}}} \right)\left( {f\left( {x,y} \right) - {\mu _f}} \right)} \right)} } }}{{MN - 1}} $ | (15) |
其中:C1、C2、C3是为了防止分母为零而设置的常数。
SSIM取值范围[0, 1], SSIM值越小, 则图像失真越严重。故平均结构相似性MSSIM为:
| $ {\rm{MSSIM}}\left( {{f_0},f} \right) = \frac{{\sum\limits_{k = 1}^N {{\rm{SSIM}}\left( {{x_k},{y_k}} \right)} }}{N} $ | (16) |
上式中:N为原始数字图像与对比图像的分块数量。
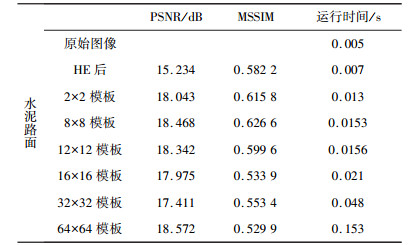
表 1、表 2为对不同路面进行识别检测的对比结果。其中通过对沥青、水泥路面识别可以发现:本文算法的峰值信噪比、平均结构相似性都比HE处理的效果好, 但是在运行时间上CLAHE算法的时间要比HE时间长, 但是时间差较短, 可以忽略不计。
| 表 1 水泥路面算法评估 |
 |
| 表 2 沥青路面算法评估 |
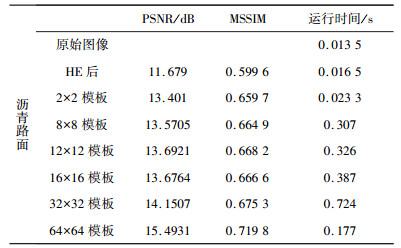 |
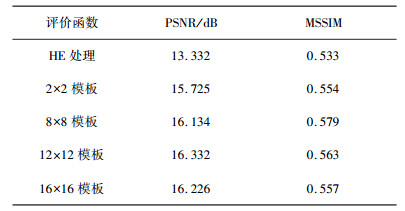
表 3为对100幅沥青水泥路面裂缝图像进行直方图处理的评价结果。由此可知, 对图像进行8*8模板CLAHE时效果最佳。
| 表 3 评价函数 |
 |
2 裂缝识别结果分析
裂缝识别系统主要识别裂缝的形状信息, 比如长、宽、面积等, 以及裂缝的骨架和裂缝形状走势。本文算法运用MATLAB R2018a进行系统仿真, 将识别的信息以Excel表格的形式存储。
图 8截取了识别反馈结果Excel信息表的一部分, 由表格中的信息可以清晰地观察到算法的识别信息。
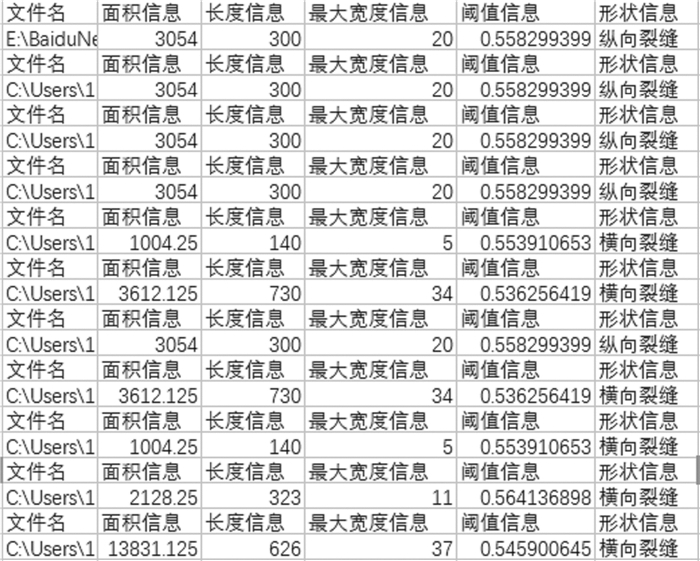 |
| 图 8 识别结果Excel表(部分) |
图 9为裂缝识别系统模块处理的效果图。其中:(a)为输入图像的原始灰度图像, 图片中含有噪声, 对后续的识别造成干扰; (b)为本文算法的对比度受限的自适应直方图均衡化后的灰度图; (c)为经过中值滤波区噪声后的效果展示图; (d)为运用迭代法对图像进行二值化处理的效果图; (e)为去除二值化图像中的小区域, 通过连通区域的选择, 去除非裂缝区域; (f)为裂缝区域判断; (g)为对识别的裂缝进行骨架提取; (h)为对识别的裂缝进行标定。裂缝识别中裂缝的参数通过Excel表格的形式进行存储, 如图 8所示。
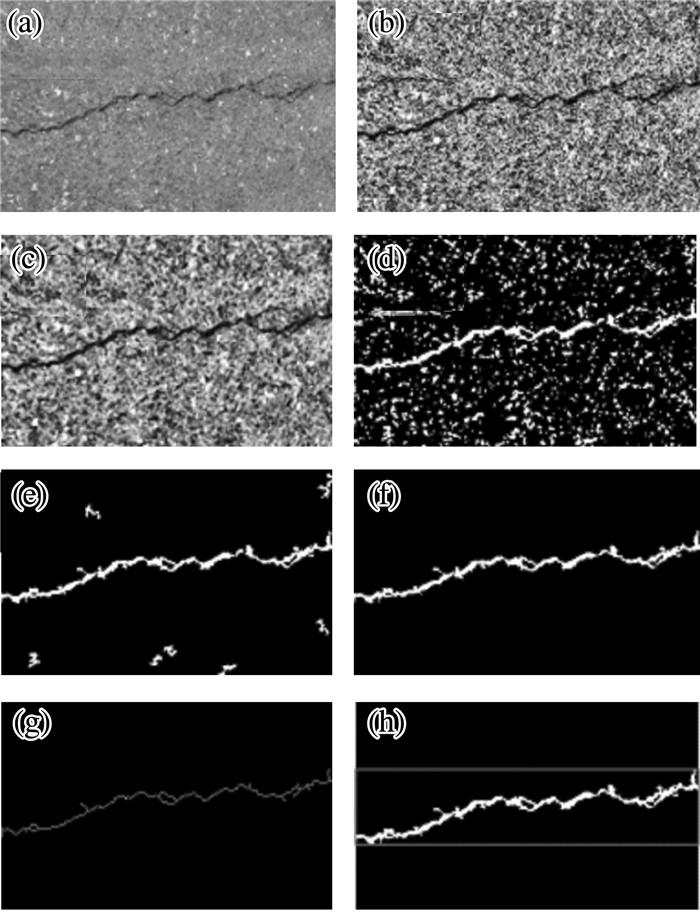 |
| 注:a为原始灰度图; b为对比度受限自适应直方图; c为中值滤波去噪; d为迭代处理; e为删除小区域; f为裂缝识别; g为骨骼提取; h为裂缝标定 图 9 识别效果图 |
本算法对水泥、沥青路面各100幅图像进行裂缝识别检测, 其中水泥路面裂缝检测正确率达93%, 沥青裂缝路面识别正确率达91%。在识别失败的裂缝图像中, 因路面网状裂缝部分的裂缝黏连而导致的识别失败有10个, 占62.5%, 噪声因素导致识别失败的有三个, 占18.75%, 网状裂缝、线性裂缝误诊的有三个, 占18.75%。
3 结论研究了沥青路面与水泥路面的裂缝识别, 对有噪声干扰的图像进行处理, 主要通过有限制对比度的自适应直方图均衡化、中值滤波、自适应二值化、连通区域标定、信息提取等, 最终实现裂缝识别、裂缝信息提取, 平均识别准确率达92%, 可适用于现今大多数路面监测系统中。本算法虽然可用于多种裂缝的检测与识别, 但是对于网状裂缝密集区域的细化与识别仍然存在缺陷。
| [1] |
马荣贵, 徐琨, 刘飞飞. 高速公路路面裂缝识别算法研究[J]. 交通信息与安全, 2014, 32(02): 90-94. DOI:10.3963/j.issn.1674-4861.2014.02.018 |
| [2] |
孙朝云. 基于双相扫描监测的路面三维裂缝识别方法[J]. 中国公路学报, 2015, 2(28): 26-32. |
| [3] |
彭博. 路面裂缝图像自动识别算法综述[J]. 中国交通科技, 2014, 31(7): 19-25. |
| [4] |
戴启凡.桥梁检测攀比机器人及其自适应控制技术研究[D].南京: 南京理工大学, 2013.
|
| [5] |
英红, 丁海明, 侯新月, 等. 基于BP神经网络的沥青路面裂缝识别方法研究[J]. 河南理工大学学(自然科学版), 2018, 37(4): 105-111. |
| [6] |
XU Z G. Asphalt pavement crack recognition algorithm using shape analysis[J]. ICIC Express Letters, Part B:Applications, 2011, 2(3): 671-678. |
| [7] |
PETROU M, PETROU C. Image Processing:The Fundamentals[M]. 2nd edition. New York: Thomson Engineering, 2013.
|
| [8] |
LI Q T.Image recognition of shield tunnel cracks by deep learning[C].In: Proceedings of the Structural Health Monitoring of Intelligent Infrastructure Conference, 2017: 676-685.
|
| [9] |
ZUIDERVELD K.Contrast limited adaptive histogram equalization[A]//HECKBERT P.Graphics Gems IV, Academic Press Professional Inc., 1994: 474-485.
|
| [10] |
张丽. 对比度受限自适应直方图均衡方法[J]. 电脑知识与技术, 2010, 9(6): 2238-2241. |
| [11] |
杨嘉琛. 基于PSNR立体图像质量客观评价方法[J]. 天津大学学报(自然科学与工程技术版), 2008, 12(41): 1448-1452. |
| [12] |
靳鑫. 基于结构相似度的自适应图像质量评价[J]. 光电子·激光, 2014, 2(25): 378-385. |
| [13] |
褚江. 全参考图像质量评价综述[J]. 计算机应用研究, 2013, 1(31): 13-22. |
| [14] |
WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment from error visibility to structural similarity[J]. IEEE Transaction on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
 2018, Vol. 32
2018, Vol. 32


