| 基于电磁寻迹的智能车仿真 |
2. 日照市技术监督信息研究所,日照 276825;
3. 齐鲁理工学院 机电学院,济南 250200
2. Rizhao technical supervision institute of information, Rizhao 276825, China;
3. School of Mechanical and Electrical Engineering, Qilu Institute of Technology, Jinan 250200, China
智能车辆作为智能交通系统的关键技术之一,体现了车辆工程、人工智能、自动控制及计算机技术于一体的综合技术,是未来汽车的发展趋势[1]。
本文研究的智能车是通过电磁传感进行路径识别、通过霍尔传感测速、通过姿态检测系统实时采集车体姿态信息,再由控制算法控制车轮的速度和转向,即整个控制过程中控制车轮是关键环节。本研究重点是对整个过程中车轮速度进行控制,即通过电磁传感器和霍尔传感器采集的信号,经转换成数字量发送给控制器,控制器根据集成的模糊算法调节车轮速度。方向控制主要由陀螺仪和加速度计组成的姿态检测系统对车体实时采集姿态信息,再经滤波处理,输出理想值。
由于直流电机伺服系统存在非线性、强耦合及结构参数变化范围大等特点,本文首先对其建模,再用PID控制算法对其模型进行仿真,根据仿真分析控制性能。其次,针对PID控制性能存在缺陷,又设计了一个以模糊理论为基础的二维模糊控制器,由编码器实时采集速度信号y(t),再与理想控制设定值r(t)比较。本文选取小车速度误差e(t)=y(t)-r(t)和误差变化率ec=e(t2)-e(t1)作为模糊控制器的输入量,设计模糊规则,并用Matlab/Simulink对已建模型进行仿真,根据仿真分析对比模糊算法和PID算法控制性能的优劣。
1 智能车系统设计 1.1 智能车系统框图智能车系统框图如图 1所示。控制器选用低功耗、处理速度快的STM32系列;姿态检测模块由陀螺仪和加速度计构成,实时检测车身姿态信息;电磁传感是通过前瞻电感检测铺设的导线实现寻迹功能。本文主要研究对象是直流电机,对其建模并搭建Matlab/Simulink仿真平台。
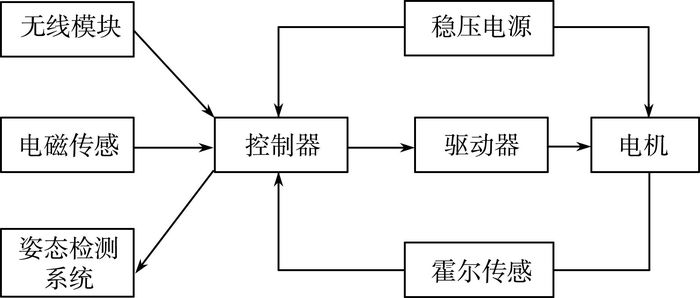 |
| 图 1 智能车系统框图 |
1.2 电磁寻迹原理
智能车寻迹目前主要有激光传感、红外传感、CCD传感和电磁传感,目前较流行的是电磁传感和CCD传感。电磁寻迹主要利用前瞻电感检测与赛道中心线的偏差距离,再根据相应算法实现寻迹要求。
飞思卡尔电磁组的寻迹方案存在一个共性问题:小车偏离中心线一定距离后,随着偏离距离的增加,左右电感检测到的电压经过一系列计算后得到偏差反而会逐渐减小,高速情况下容易引起循迹误判。
本文采用比值法寻迹方案:分别将左右两电感的感应电动势开根号后作差,再比上两电感的和值,将所得值Bias作为最后的偏差值,即:[2]
| $Bias = \frac{{\sqrt {{E_1}} - \sqrt {{E_2}} }}{{{E_1} + {E_2}}}$ | (1) |
本文研究的是两轮智能车,所以平衡控制是关键问题。针对平衡控制问题,采用陀螺仪和加速度计组成的姿态检测系统实时采集姿态信息,但由于惯性传感器固有特性导致累积偏差,造成检测精度不高,便采用滤波算法对多传感器的数据进行融合。由于上述两种传感器之间的互补性,选用如图 2所示的互补滤波算法,这里不再赘述。
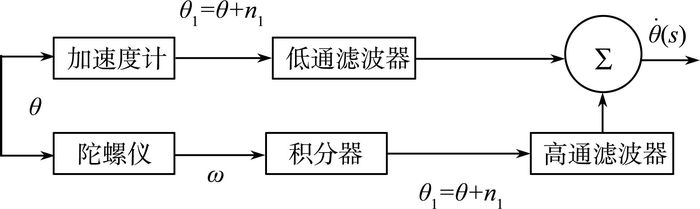 |
| 图 2 滤波算法原理图 |
为了弥补加速度计和陀螺仪各自的缺点,采用图 2所示的互补滤波算法融合加速度计的角度值和陀螺仪的角速度值,补偿加速度计的动态误差和陀螺仪的累积误差,得到更优的平衡车姿态估计值[3]。
1.4 电机转速测量根据霍尔效应原理,首先将一块永久磁钢固定在车轮侧方,磁钢跟着车轮同步旋转,在车轮侧方安装一个霍尔器件。车轮旋转时,霍尔器件输出脉冲信号,其频率和转速成正比。脉冲信号周期与电机转速之间存在以下关系:
| $n = \frac{{60}}{{PT}}$ | (2) |
式中:P为电机转一圈的脉冲数;T为输出方波信号周期。
1.5 直流电机数学模型建模假设励磁电流不变,以电压为输入量、转速为控制量,根据KVL定律得直流电机电枢回路电压平衡方程:
| ${U_d} = {L_d}\frac{{d{I_d}}}{{dt}} + {I_d}{R_d} + {C_e}n$ | (3) |
式中:Ud、Rd、Id、Ld分别为电枢回路的电压、电阻、电流和电感;Ce为反电动势常数;n为电动机角速度。[4]
根据刚性转体定律,若不计摩擦,得电机轴上的转矩平衡方程:
| $M - {M_f} = J\frac{{dn}}{{dt}}$ | (4) |
式中:M、Mf分别为电动机轴上的电磁力矩和负载力矩;J为电动机轴上的(包括负载折算过来的)转动惯量。[4]
当磁通不变时有:M=CmId,Mf=CmIf。Cm为电机的转矩常数。整理得电机微分方程:
| ${T_d}{T_m}\frac{{dn}}{{dt}} + {T_m}\frac{{dn}}{{dt}} + n = \frac{1}{{{C_e}}}{U_d}$ | (5) |
式中:Td、Tm分别为电磁和机电时间常数,一般应用情况下Td<Tm。[4]
| ${T_d} = \frac{L}{R}$ | (6) |
| ${T_m} = \frac{{R \times J}}{{{K_e} \times {K_t}}}$ | (7) |
式(6) 和(7) 中:R为绕组电阻,L为电感,J为转动惯量,Kt为转矩系数,Ke为反动势系数。[4]
对式(5) 进行拉普拉斯变化得:
| ${W_D}\left( s \right) = \frac{{1/{C_e}}}{{{T_m}{T_d}{s^2} + {T_m}s + 1}}$ | (8) |
| ${C_e} = \frac{{N \times P}}{{60 \times a}}$ | (9) |
式中:N为电枢总导体数,P为极对数,a为支路对数。
2 PID控制策略 2.1 PID控制原理PID控制算法以其结构简单、参数易整定、稳定性好等优点,成为工业控制的主要技术之一,也是自控系统中应用最广的一种控制方法。PID控制主要应用于线性系统,尤其是当难以得出精确的数学模型且控制器的结构和参数必须根据人工经验和现场调试来确定时,应用PID控制最为方便。
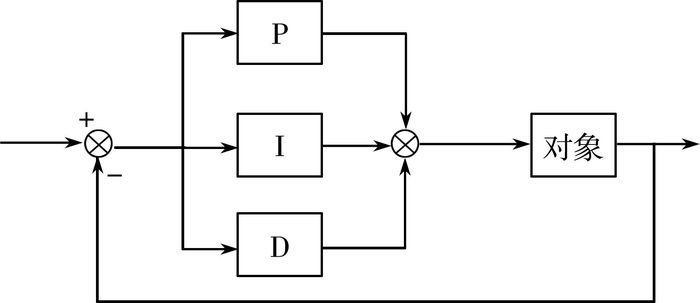 |
| 图 3 PID控制原理 |
2.2 PID控制规律
简单地说,PID控制器是一种线性控制器,根据给定值与实际值构成的偏差,将偏差的比例、积分、微分通过线性组合构成控制量u对被控对象进行控制。从本质上讲,PID控制就是一种偏差控制,其控制精准、响应快。但由于被控对象的时变性、非线性和不确定性等其他特性,传统的PID控制难以达到很好的效果。
PID控制器的传递函数一般形式为:
| $G\left( s \right) = {K_p} + \frac{{{K_i}}}{s} + {K_d}s$ | (10) |
式中:Kp为比例增益;Ki为积分增益;Kd为微分增益。
2.3 PID仿真对于电磁时间常数Td和机电时间常数Tm的测量,工程中有直接法、反动势发和启动电流法等。本文采用直接计算法来获取Td和Tm的数值。
电机参数选择:在直流伺服电机中,本文选取R=1.61、L=0.215、J=0.0074、Ke=0.015、Kt=0.038、Ce=0.125、Td=0.134、Tm=20.8。根据经验试凑整定法,得出一组PID参数:P=15、I=0.76、D=0.053。P参数必须要大一些,I参数适合区间为0~1。
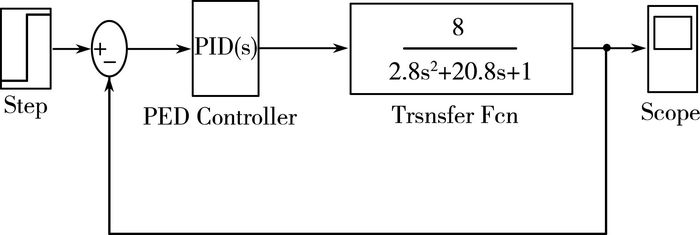 |
| 图 4 PID 系统图 |
根据Matlab/Simulink仿真平台,得到如图 5所示曲线。
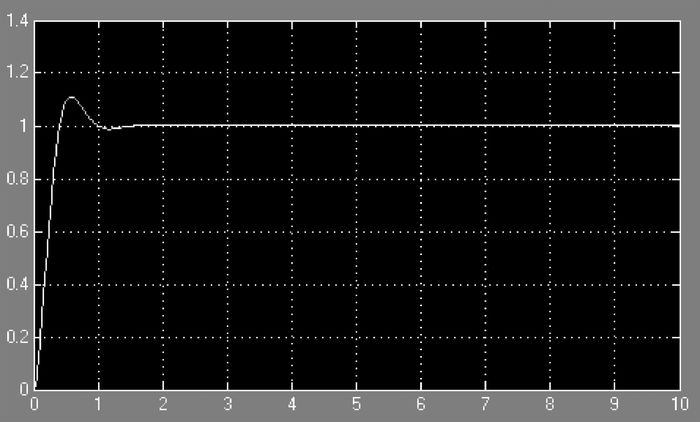 |
| 图 5 PID算法仿真图 |
由图 5可知:PID控制精度高、调节时间快、响应时间快,但仍存在系统波动大、控制性能不稳定、超调量大的缺陷。为克服上述缺陷,引入智能算法中常用的模糊控制理论。
3 模糊控制策略模糊控制作为一种新型的控制方式已经成功地用于各种工业过程控制中,其优点包括:
① 不需要建立精确的数学模型,适当运用模糊规则和隶属函数即可在工业控制领域实现智能化模糊自动控制;
② 模糊控制具有较强的鲁棒性,被控对象参数的变化对模糊控制的影响不明显;
③ 与传统的PID控制器相比,模糊控制器结构简单、便于操作、成本低廉、性价比高[5]。
如图 6所示,模糊控制器主要由以下四部分组成:
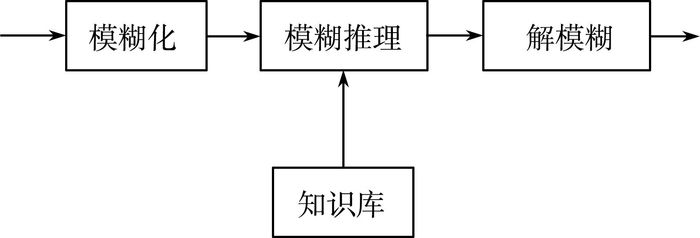 |
| 图 6 模糊控制器的组成 |
1) 模糊化接口。简单地说,就是将精确的量变化成模糊的量,确定输入、输出的基本论域,然后运用量化因子将精确量实际论域变换到基本论域上,再用合理的隶属度函数来表示模糊集合。
2) 知识库。知识库中最重要的就是模糊规则语言,它是由一系列“if...then”语句来表示实际过程中的控制规则,这些规则一般都是专家的经验和知识,具有主观性。所以在设计一个模糊控制器时,控制效果的优劣取决于模糊规则的设计。
3) 模糊推理机。模糊推理是一种不确定的推理方法,也是一种近似推理,是模糊逻辑系统的核心部分。模糊推理机是根据模糊控制规则和给定的条件,推理得到合理的控制输出量。常用的推理方法有Mamdani法、Tsukamoto法等。
4) 解模糊接口。需要一种转化方法,将模糊推理出的控制量转化成实际控制所需的精确量。目前主要有重力法和加权平均法(如下式所示)。
| $k = \left( {\sum\limits_{i = 1}^9 {{\beta _i}{k_i}} } \right)/\sum\limits_{i = 1}^9 {{\beta _i}} $ | (11) |
本文研究的无刷直流电机数学模型传递函数为:电机模型参数和上述PID仿真一样,采样时间选取T=0.1 s。
| $G\left( s \right) = \frac{{1/0.125}}{{20.8 \times 0.134{s^2} + 20.8\mathit{s}{\rm{ + 1}}}}$ | (12) |
本文设计的二维模糊控制器是双输入单输出,输入误差e,误差变化率ec,输出控制量u。误差e的范围控制在[-1 1]内,那么输入变量e和ec的论域均可取[-1 1],同时取u的论域为[-2 2],其模糊子集设为{NB(负大), NS(负小), ZE(零), PS(正小), PB(正大)},量化等级为{-2, -1, 0, 1, 2},隶属度函数都用高斯型。
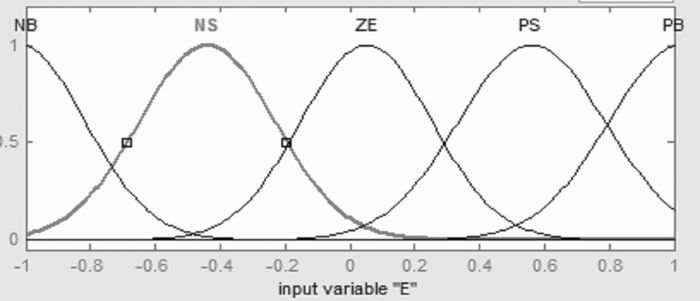 |
| 图 7 输入变量e、ec隶属度函数 |
4.3 模糊规则
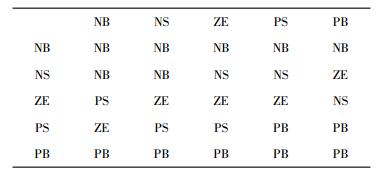
模糊规则是影响控制精度的重要环节,本研究针对控制对象G(s),根据工程经验和专家经验,建立如表 1所示的模糊规则。控制规则的多少会影响控制系统性能,但不是越多越好,应根据需要设定控制规则的条数。由于控制对象是直流电机,不需要过多的控制规则,所以本文选择25条经典规则。
| 表 1 模糊规则表 |
 |
在规则编辑器中激活规则浏览器,以3D图形形式描述模糊推理系统的推理过程。如果要单一地观察某一输入变量对输出的关系,可屏蔽另一变量。模糊推理曲面图(图 8)描述的是该模糊推理系统的输入输出特性。
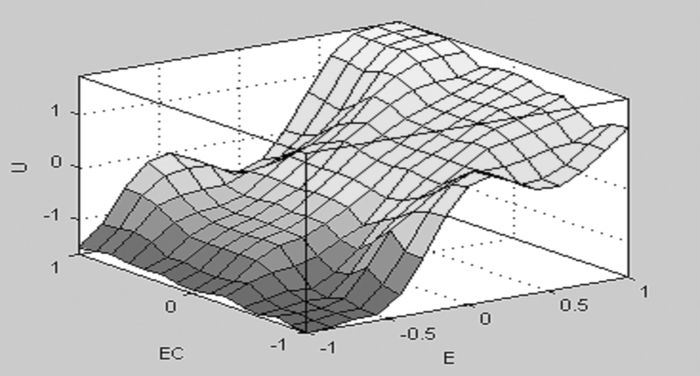 |
| 图 8 模糊推理系统输入输出特性曲面 |
4.4 模糊仿真系统
在Matlab/Simulink环境下,根据上文设计的模糊规则并严格按照电气原理搭建模糊控制器(如图 9所示)。
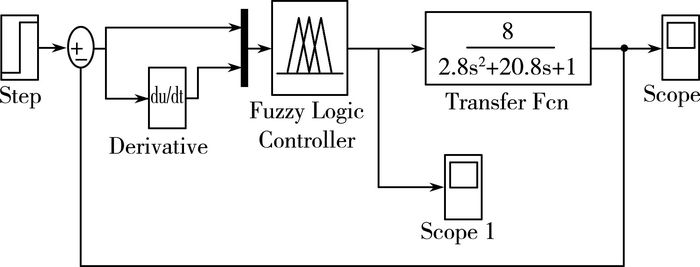 |
| 图 9 模糊系统图 |
根据Matlab/Simulink仿真平台,得到如图 10所示曲线。
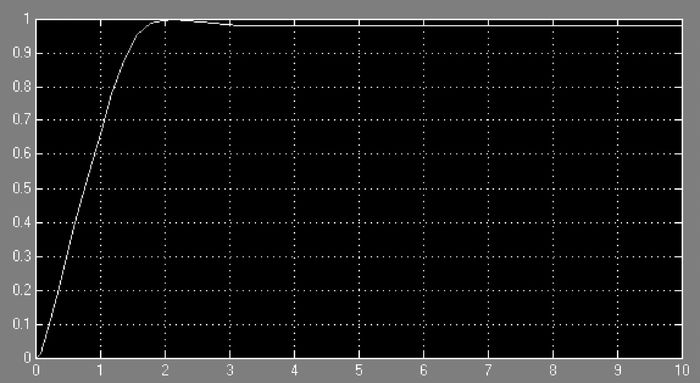 |
| 图 10 模糊算法仿真图 |
由图 10可知:控制效果基本能达到预期要求,模糊控制下阶跃响应曲线非常平稳,基本无超调、无震荡,控制输入也保持在要求范围内,这样的控制性能是合理的。
5 结论本文简述了智能车系统组成,选取直流电机为主要研究对象,对其建立数学模型。设计智能算法,通过Matlab/Simulink对模型仿真,最后再对比两种算法的优劣。模糊控制算法相比于PID算法在直流电机稳定性方面更有优越性,这也是模糊控制算法比PID控制算法应用更为广泛的原因。但若结合PID算法和模糊算法的各自优点来设计控制器,控制性能会更优,所以对于优化控制算法的后续研究尚有待进行。
| [1] |
邓广大, 李占英. 基于Cortex-M3内核的智能循迹小车设计方案[J]. 科技创新与应用, 2013, 13: 17. |
| [2] |
张晓峰, 等. 电磁智能车循迹算法[J]. 计算机系统应用, 2014, 23(12): 189. |
| [3] |
梁光胜, 等. 基于互补滤波的两轮自平衡车姿态控制[J]. 测控技术, 2015, 34(5): 73. |
| [4] |
董期林, 等. 基于模糊自整定PID控制器的直流电机伺服系统的仿真研究[J]. 机床与液压, 2009, 37(2): 117-118. |
| [5] |
黄军辉, 傅沈文. 模糊控制理论的发展及应用[J]. 中国科技信息, 2006, 12: 303. DOI:10.3969/j.issn.1001-8972.2006.01.272 |
| [6] |
何胜方. 定量排料控制系统模糊控制MATLAB仿真研究与实现[J]. 安徽冶金, 2008, 1: 18. |
 2017, Vol. 31
2017, Vol. 31

