| 机械臂视觉相机标定的研究与仿真 |
通俗地说,摄像机的标定就是从通用的世界坐标系转换到像素坐标系的过程。基本坐标系包括世界坐标系、相机坐标系、图像坐标系、像素坐标系,也就是说标定的过程就是从世界坐标系到像素坐标系投影并求得投影矩阵的过程。标定的过程主要分为两部分:第一部分是从通用坐标系到相机坐标系的三维点到三维点的转换,包括R、t等相机的一些外部参数;第二部分是从相机坐标系到像素坐标系的三维点到二维点的转换,包括K等相机内部参数。本文主要通过传统的线性标定法和张正友棋盘格标定法进行研究和仿真。
1 针孔摄像机模型针孔相机模型是相机模型中最常见也是最实用的一种线性模型,它的主要原理是:物体发出的光线,在经过模型的小孔后,会在聚焦屏上生成倒立的像。极小的孔就会使得物体上个点的光只能达到各自的像点,并且不会重叠,这样就会获得更清楚的像。摄像机的模型图如图 1所示[1]。
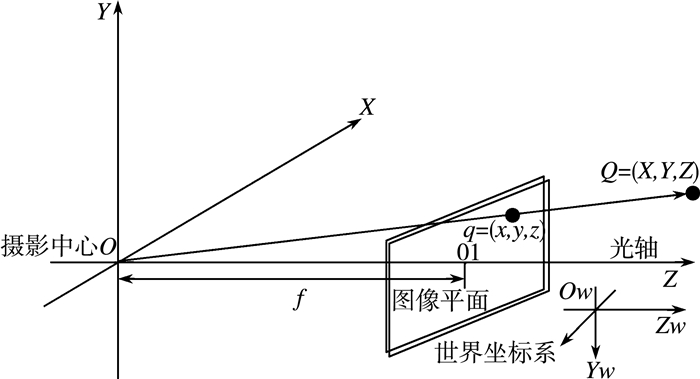 |
| 图 1 针孔相机模型示意图 |
1.1 相机坐标系到像平面坐标系转换
在相机坐标系O-XYZ外的一点Q(X, Y, Z)被投影到像平面上q(x, y, f)点,按照相似三角形定理可得:
| $ \frac{x}{f} = \frac{X}{Z},\frac{y}{f} = \frac{Y}{Z},即\;x = \frac{{fX}}{Z},y = \frac{{fY}}{Z} $ | (1-1) |
这就是投影变换的过程。可以用3*3的矩阵来表示:q=MQ,其中:
| $ q = \left[ {\begin{array}{*{20}{c}} {xZ}\\ {yZ}\\ Z \end{array}} \right],M = \left[ {\begin{array}{*{20}{c}} f&0&0\\ 0&f&0\\ 0&0&1 \end{array}} \right],Q = \left[ {\begin{array}{*{20}{c}} X\\ Y\\ Z \end{array}} \right] $ | (1-2) |
最终会得到变换矩阵为:
| $ Z\left[ {\begin{array}{*{20}{c}} x\\ y\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} f&0&0\\ 0&f&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} X\\ Y\\ Z \end{array}} \right] $ | (1-3) |
由图 1可知,像平面坐标系和像素坐标系在一个平面上,可以用简单的二维坐标系表示出它们的关系,如图 2所示[2]。
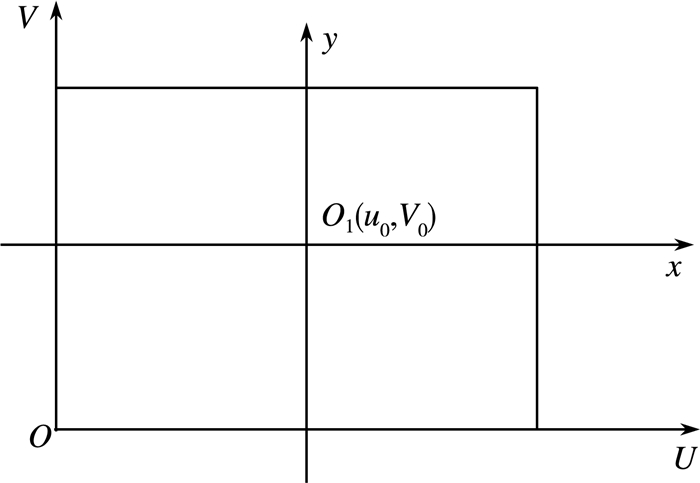 |
| 图 2 像平面和像素坐标系的关系图 |
在像素坐标系中,设每个像素的尺寸为dx*dy,在图像平面上的(x, y)在像素坐标系下为(u, v),两者存在如下对应关系[3]:
| $ \left\{ \begin{array}{l} u = \frac{x}{{dx}} + {u_0}\\ v = \frac{y}{{dy}} + {v_0} \end{array} \right. $ | (1-4) |
由图 1可知,通用坐标系用(Ow-XwYwZw)表示,用来描述相机的具体位置。通过世界坐标系可以计算出相机在任何位置的坐标。
2 线性标定法直接线性标定法(DTL)是采用图一的摄像机模型进行研究的[4],用矩阵转换来表示三维空间的点与二维空间的点的对应关系,这个矩阵用D来表示,它是一个3行4列的矩阵。
设I(XW, YW, ZW)和J(XC, YC, ZC)分别是通用坐标系、相机坐标系下的一点,(x, y)和(u, v)分别是图像坐标系下的像坐标和像素坐标,R和T分别为旋转矩阵和平移矩阵(相机外部参数),它们之间存在如下转换关系[5]:
| $ s\left[ {\begin{array}{*{20}{c}} x\\ y\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {f000}\\ {0f00}\\ {0010} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_c}}\\ {{Y_c}}\\ {{Z_c}}\\ 1 \end{array}} \right] $ | (2-1) |
| $ \left[ {\begin{array}{*{20}{c}} {{X_c}}\\ {{Y_c}}\\ {{Z_c}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} R&T\\ O&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_w}}\\ {{Y_w}}\\ {{Z_w}}\\ 1 \end{array}} \right] $ | (2-2) |
| $ \begin{array}{l} s\left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{1}{k}}&0&{{u_0}}\\ 0&{\frac{1}{l}}&{{v_0}}\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {f000}\\ {0f00}\\ {0010} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} R&T\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_\mathit{\boldsymbol{W}}}}\\ {{\mathit{\boldsymbol{Y}}_\mathit{\boldsymbol{W}}}}\\ {{\mathit{\boldsymbol{Z}}_\mathit{\boldsymbol{W}}}}\\ 1 \end{array}} \right]\\ = A\left[ {\begin{array}{*{20}{c}} R&T \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_w}}\\ {{Y_w}}\\ {{Z_w}}\\ 1 \end{array}} \right] = M\left[ {\begin{array}{*{20}{c}} {{X_w}}\\ {{Y_w}}\\ {{Z_w}}\\ 1 \end{array}} \right] \end{array} $ | (2-3) |
| $ A = \left[ {\begin{array}{*{20}{c}} {{f_x}}&0&{{u_0}}\\ 0&{{f_y}}&{{v_0}}\\ 0&0&1 \end{array}} \right] $ | (2-4) |
| $ M = \left[ {\begin{array}{*{20}{c}} {{m_{11}}{m_{12}}{m_{13}}{m_{14}}}\\ {{m_{21}}{m_{22}}{m_{23}}{m_{24}}}\\ {{m_{31}}{m_{32}}{m_{33}}{m_{34}}} \end{array}} \right] $ | (2-5) |
矩阵M是三维空间点到二维空间点的转换矩阵[6]。在矩阵A中的fx、fy都是相机的焦距,所以说A就是相机的内部参数。根据以上三个公式我们就可以得到转换矩阵M的线性方程[7]:
| $ \begin{array}{l} {Y_w} + {m_{13}}{Z_w} + {m_{34}} - {m_{31}}{X_w}u - {m_{32}}{Y_w}u - \\ {m_{33}}{Z_w}u = {m_{34}}u\\ {m_{21}}{X_w} + {m_{22}}{Y_w} + {m_{23}}{Z_w} + {m_{24}} - {m_{31}}{X_w}v - \\ {m_{32}}{Y_w}v - {m_{33}}{Z_w}v = {m_{34}}v \end{array} $ | (2-6) |
式(2-6)中共有12个系数,在进行求解的时候一般会将m34设为1,这样就简化了运算,然后通过最小二乘法去求的矩阵M,进而会得到相机的内部参数,也就是得到了三维坐标系和二维坐标系的对应关系。
3 张正友标定法张正友标定的过程是不需要人为的去移动标定板,只是通过相机对标定板按照不同的角度进行拍照,其大体步骤如下[8-9]。
3.1 外参、内参计算过程涉及的参数包括:
s:通用坐标系转换到图像坐标系的尺度因子;
A:相机的内部参数矩阵;
(u0, v0):像素的主点的坐标;
α、β:像素、焦距的融合比例;
γ:径向畸变参数;
R、t:旋转平移矩阵。
设在二维相机坐标系下的点的坐标为n=[u, v, 1]T,在通用坐标系下对应的点为N=[X, Y, Z, 1]T,可以得到坐标转换的对应关系式sn=A[R, t]N。其中内部参数矩阵为:
| $ A = \left[ {\begin{array}{*{20}{c}} \alpha &\gamma &{{u_0}}\\ 0&\beta &{{v_0}}\\ 0&0&1 \end{array}} \right] $ | (3-1) |
| $ \begin{array}{l} sn = A\left[ {\begin{array}{*{20}{c}} R&t \end{array}} \right]Ns\left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right]\\ \;\;\;\; = A\left[ {\begin{array}{*{20}{c}} {{r_1}}&{{r_2}}&{{r_3}}&t \end{array}} \right]\left[ {\begin{array}{*{20}{c}} X\\ Y\\ 0\\ 1 \end{array}} \right]\\ \;\;\;\; = A\left[ {\begin{array}{*{20}{c}} {{r_1}}&{{r_2}}&{{r_3}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} X\\ Y\\ 1 \end{array}} \right]\\ \;\;\;\; = A\left[ {\begin{array}{*{20}{c}} {{r_1}}&{{r_2}}&{{r_3}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_W}}\\ {{Y_W}}\\ {{Z_W}} \end{array}} \right] \end{array} $ | (3-2) |
因为标定是2D平面,可以让Z方向的值为0,可以得到:
| $ \begin{array}{l} s\left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right] = A\left[ {\begin{array}{*{20}{c}} {{r_1}}&{{r_2}}&{{r_3}}&t \end{array}} \right]\left[ {\begin{array}{*{20}{c}} X\\ Y\\ 0\\ 1 \end{array}} \right]\\ \;\;\;\;\;\;\;\; = A\left[ {\begin{array}{*{20}{c}} {{r_1}}&{{r_2}}&{{r_3}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} X\\ Y\\ 1 \end{array}} \right] \end{array} $ | (3-3) |
令H=[h1 h2 h3]=λA[r1 r2 t],于是对应关系可以写为:
| $ sn = HN $ | (3-4) |
由于H是一个Homographic的齐次性矩阵[10],有8个未知数的未知方程,分别有4个对应点对应着这8个方程,这样就可以求出矩阵H。然后就可以根据H=[h1 h2 h3]=λA[r1 r2 t]得到:
| $ \left\{ {\begin{array}{*{20}{c}} {{r_1} = \lambda {A^{ - 1}}{h_1}}\\ {{r_2} = \lambda {A^{ - 1}}{h_2}}\\ {{r_3} = {r_1} \times {r_2}}\\ {t = \lambda {A^{ - 1}}{h_3}}\\ {\lambda = \frac{1}{{\left\| {{A^{ - 1}}{h_1}} \right\|}} = \frac{1}{{\left\| {{A^{ - 1}}{h_2}} \right\|}}} \end{array}} \right. $ | (3-5) |
| $ \left\{ {\begin{array}{*{20}{c}} {h_1^T{A^{ - T}}{A^{ - 1}}{h_2} = 0}\\ {h_1^T{A^{ - T}}{A^{ - 1}}{h_1} = h_2^T{A^{ - T}}{A^{ - 1}}{h_2}} \end{array}} \right. $ | (3-6) |
| $ \begin{array}{*{20}{c}} {B = {A^{ - T}}{A^{ - 1}} \equiv \left[ {\begin{array}{*{20}{c}} {{B_{11}}}&{{B_{21}}}&{{B_{31}}}\\ {{B_{12}}}&{{B_{22}}}&{{B_{32}}}\\ {{B_{13}}}&{{B_{23}}}&{{B_{33}}} \end{array}} \right]}\\ { = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{\alpha ^2}}}}&{\frac{\gamma }{{{\alpha ^2}\beta }}}&{\frac{{{v_0}\gamma - {u_0}\beta }}{{{\alpha ^2}\beta }}}\\ { - \frac{\gamma }{{{\alpha ^2}\beta }}}&{\frac{\gamma }{{{\alpha ^2}\beta }} + \frac{1}{{{\beta ^2}}}}&{\frac{{v\left( {{v_0}\gamma - {u_0}\beta } \right)}}{{{\alpha ^2}\beta }} - \frac{{v_0^2}}{{{\beta ^2}}}}\\ {\frac{\gamma }{{{\alpha ^2}\beta }}}&{ - \frac{{v\left( {{v_0}\gamma - {u_0}\beta } \right)}}{{{\alpha ^2}\beta }} - \frac{{v_0^2}}{{{\beta ^2}}}}&{\frac{{{{\left( {{v_0}\gamma - {u_0}\beta } \right)}^2}}}{{{\alpha ^2}\beta }} + \frac{{v_0^2}}{{{\beta ^2}}} + 1} \end{array}} \right]} \end{array} $ | (3-7) |
| $ b = {\left[ {\begin{array}{*{20}{l}} {{B_{11}}}&{{B_{12}}}&{{B_{22}}}&{{B_{13}}}&{{B_{23}}}&{{B_{33}}} \end{array}} \right]^T} $ | (3-8) |
| $ {h_i} = {\left[ {\begin{array}{*{20}{l}} {{h_{i1}}}&{{h_{i2}}}&{{h_{i3}}} \end{array}} \right]^T} $ | (3-9) |
根据式(3-8)和(3-9)可得:
| $ \begin{array}{l} h_i^TB{h_j} = V_{ij}^rb\\ {V_{ij}} = \left[ {{h_{i1}}{h_{j1}}\quad {h_{i1}}{h_{j2}} + {h_{i2}}{h_{j1}}\quad {h_{i2}}{h_{j2}}\quad {h_{i3}}{h_{j1}}} \right.\\ {\left. { + {h_{i1}}{h_{j3}}\quad {h_{i3}}{h_{j2}} + {h_{i2}}{h_{j3}}\quad {h_{i3}}{h_{j3}}} \right]^T} \end{array} $ | (3-10) |
| $ \begin{array}{l} h_1^T{A^{ - T}}{A^{ - 1}}{h_2} = 0\\ h_1^T{A^{ - T}}{A^{ - 1}}{h_1} = h_2^T{A^{ - T}}{A^{ - 1}}{h_2}\\ \left[ {\begin{array}{*{20}{c}} {V_{12}^T}\\ {{{\left( {{V_{11}} - {V_{22}}} \right)}^T}} \end{array}} \right]b = 0 \end{array} $ | (3-11) |
由式(3-10)可知矩阵V是一个2n*6的矩阵,可以利用最小二乘法对b进行估算。B矩阵中有6个未知量,即可得出[11]:当观测平面n≥3时,b有且仅有唯一解;当n=2时,γ=0;当n=1时,仅能对α、β进行估算,此时像素主点的u0=v0=0。内部参数通过Cholesky分解得到:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{v_0} = \left( {{B_{12}}{B_{13}} - {B_{11}}{B_{23}}} \right)/\left( {{B_{11}}{B_{22}} - B_{12}^2} \right)}\\ {\lambda = {B_{33}} - \left[ {B_{13}^2 + {v_0}\left( {{B_{12}}{B_{13}} - {B_{11}}{B_{23}}} \right)} \right]/{B_{11}}} \end{array}\\ \begin{array}{*{20}{l}} {\alpha = \sqrt {\lambda /{B_{11}}} ,\beta = \sqrt {\lambda {B_{11}}/{B_{11}}{B_{22}}} - B_{12}^2}\\ {\gamma = - {B_{12}}{\alpha ^2}\beta /\lambda } \end{array}\\ {u_0} = \gamma {v_0}/\alpha - {B_{13}}{\alpha ^2}/\lambda \end{array} $ | (3-12) |
通过相机拍摄了n张不同角度的棋盘图片,每一幅图片中都会有m个特征点。假设第i幅图片的特征点Mj在摄像机矩阵的投影为:
| $ m\left( {K,{R_i},{t_i},{M_{ij}}} \right) = K[R|t]{M_{ij}} $ | (3-13) |
其中K表示摄像机的内部参数矩阵A。Ri和ti分别代表第i幅图片的旋转和平移矩阵。最大似然函数的构造形式如下[12]:
| $ \begin{array}{l} L\left( {A,{R_i},{t_i},{M_{ij}}} \right) = \prod\limits_{i = 1,j = 1}^{n,m} f \left( {{m_{ij}}} \right)\\ = \frac{1}{{\sqrt {2\pi } }}{e^{\frac{{ - \sum\nolimits_{i - 1}^n {\sum\nolimits_{j - 1}^m {{{\left( {m\left( {K,{R_i},{t_i},{M_{ij}}} \right) - {m_{ij}}} \right)}^2}} } }}{{{\sigma ^2}}}}} \end{array} $ | (3-14) |
根据上式可知,如果L=Lmax,使用多参数的非线性系统的Levenberg-Marquardt算法进行迭代,求得最优解[13]:
| $ \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{{\left\| {m\left( {K,{R_i},{t_i},{M_{ij}}} \right) - {m_{ij}}} \right\|}^2}} } $ | (3-15) |
张正友标定法只解释了径向畸变,因为它是最大的一种影响畸变。其数学表达式为:
| $ \begin{array}{*{20}{l}} {\hat u = u + \left( {u - {u_0}} \right)\left[ {{k_1}\left( {{x^2} + {y^2}} \right) + {k_2}{{\left( {{x^2} + {y^2}} \right)}^2}} \right]}\\ {\hat v = v + \left( {v - {v_0}} \right)\left[ {{k_1}\left( {{x^2} + {y^2}} \right) + {k_2}{{\left( {{x^2} + {y^2}} \right)}^2}} \right]} \end{array} $ | (3-16) |
上式中的(u, v)是没有发生畸变的理想情况下的像素坐标,
| $ \left\{ {\begin{array}{*{20}{l}} {\hat u = {u_0} + \alpha \hat x + \gamma \hat y}\\ {\hat v = {v_0} + \beta \hat y} \end{array}} \right. $ | (3-17) |
它的矩阵形式如下[14]:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\left( {u - {u_0}} \right)\left( {{x^2} + {y^2}} \right)}&{\left( {u - {u_0}} \right){{\left( {{x^2} + {y^2}} \right)}^2}}\\ {\left( {v - {v_0}} \right)\left( {{x^2} + {y^2}} \right)}&{\left( {v - {v_0}} \right){{\left( {{x^2} + {y^2}} \right)}^2}} \end{array}} \right]\\ \left[ {\begin{array}{*{20}{c}} {{k_1}}\\ {{k_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\hat u - u}\\ {\hat v - v} \end{array}} \right] \end{array} $ | (3-18) |
令Dk=c,可以得到:
| $ k = {\left[ {\begin{array}{*{20}{l}} {{k_1}}&{{k_2}} \end{array}} \right]^T} = {\left( {{D^T}D} \right)^{ - 1}}{D^T}c $ | (3-19) |
使用LM算法计算下列函数的最小值,即可以得到优化的结果:
| $ \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{{\left\| {\hat m\left( {K,{k_1},{k_2},{R_i},{t_i},{M_{ij}}} \right) - {m_{ij}}} \right\|}^2}} } $ | (3-20) |
线性标定法的仿真是通过7×6的棋盘格来提取图像中的角点坐标,提取图如图 3所示[15]。
 |
| 图 3 角点坐标提取图 |
本文选取了5×6个角点进行验证,其数值如表 1所示。
| 表 1 角点在像素坐标系的坐标数据 |
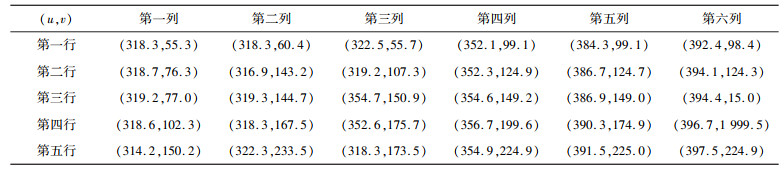 |
此时可以通过MATLAB求解M的方程,其结果为:
| $ M = \left[ {\begin{array}{*{20}{c}} {1.479\;63}&{ - 0.002\;3}&{143.74}\\ {0.003\;9}&{1.460\;7}&{65.437}\\ {0.000\;0}&{0.000\;2}&{1.000} \end{array}} \right] $ |
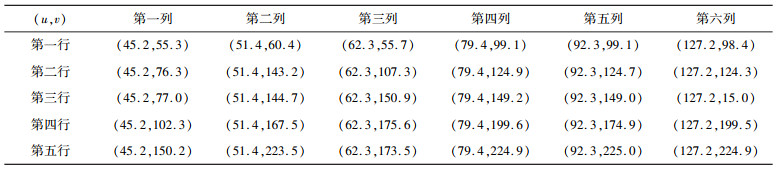
世界坐标系下的角点坐标数据如表 2所示。通过表中数据可以看出像素坐标和机械臂坐标系的平移关系,同时还可以通过MATLAB求解出世界坐标系下的方向轴上的误差:
| 表 2 世界坐标系下的角点坐标数据 |
 |
| $ err = \left[ {\begin{array}{*{20}{c}} {0.007\;3}\\ {0.006\;4} \end{array}} \right] $ |
张正友标定法通过相机拍摄了棋盘格各个角度的图片,在MATLAB自带的标定库中进行仿真,相机位姿对应的各个标定如图 4所示。
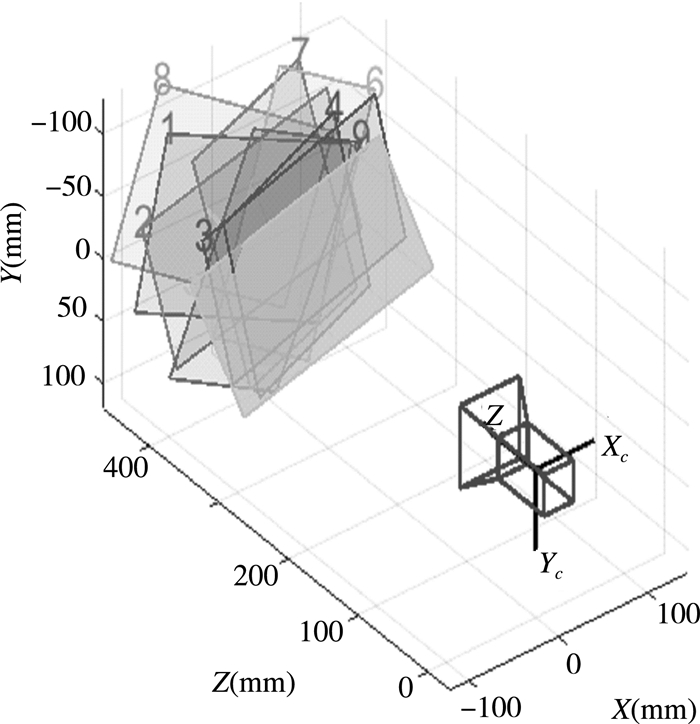 |
| 图 4 相机位姿对应的各个标定图 |
此时会在MATLAB的工作区得到转换映射矩阵A:
| $ A = \left[ {\begin{array}{*{20}{c}} {107.1}&0&{193.1}\\ 0&{88.91}&{235.8}\\ 0&0&1 \end{array}} \right] $ | (4-1) |
图片的外部参数矩阵即旋转平移矩阵为:
| $ \left[ {\begin{array}{*{20}{c}} R&t \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.001\;8}&{0.994\;7}&{166.73}\\ {0.963\;2}&{0.001\;7}&{96.27}\\ { - 0.0637}&{0.000\;21}&{604.33} \end{array}} \right] $ | (4-2) |
畸变系数和误差分别为:
| $ c\_err = \left[ {\begin{array}{*{20}{c}} {0.002\;3}\\ {0.001\;9} \end{array}} \right] $ |
| $ k = \left[ {\begin{array}{*{20}{c}} {{k_1}}\\ {{k_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.001\;22}\\ {0.002\;37} \end{array}} \right] $ |
主要通过自己设定的7×6的标定纸, 通过MATLAB软件对标定纸的角点的坐标进行提取,可以分别得出像素坐标系下和世界坐标系下的角点坐标数据,根据两者坐标的关系可以求出线性标定法的误差。张正友标定法需要对标定纸进行不同的角度拍照,根据这些不同角度的照片计算出其映射矩阵,再根据相机参数可以直接求出此方法的畸变参数和误差大小。
| [1] |
王运哲, 郑凯. 机器视觉中相机标定方法的研究[J]. 机械管理开发, 2019, 34(5): 81-82. |
| [2] |
GRIFFITHS D N, BURNINGHAM H. Comparison of pre- and self-calibrated camera calibration models for UAS-derived nadir imagery for a SfM application[J]. Progress in Physical Geography, 2019, 43(2): 15-17. |
| [3] |
邓明华, 陈云红, 王晶晶. 基于单目视觉的移动机器人SLAM系统构建[J]. 南方农机, 2019, 50(1): 20-21. DOI:10.3969/j.issn.1672-3872.2019.01.015 |
| [4] |
杨幸芳, 张梦文, 严凯, 等. 一种基于参数约束关系的工业相机的线性标定法[J]. 微型机与应用, 2014, 33(11): 38-40. DOI:10.3969/j.issn.1674-7720.2014.11.012 |
| [5] |
王丽.面向建筑物重建的摄像机自标定方法研究[D].南昌: 南昌航空大学, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D346813
|
| [6] |
江泽涛, 吴文欢. 基于本质矩阵的摄像机自标定方法[J]. 中国图象图形学报, 2010, 15(4): 565-569. |
| [7] |
吴俊君, 胡国生. 室内环境仿人机器人快速视觉定位算法[J]. 中山大学学报(自然科学版), 2013, 52(4): 7-13. |
| [8] |
张曦, 黄亮, 徐洋, 等. 基于MATLAB中calibration toolbox的相机标定的应用研究[J]. 微型机与应用, 2011(14): 31-33. DOI:10.3969/j.issn.1674-7720.2011.14.012 |
| [9] |
张铖伟, 王彪, 徐贵力. 摄像机标定方法研究[J]. 计算机技术与发展, 2010(11). |
| [10] |
申心兰, 王仲, 刘常杰, 等.一种基于棋盘格的高精度分区域相机标定方法[J].2016, 7(4): 342-349. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cskxyyq201604006
|
| [11] |
黄琬婷, 胡小平. 一种基于张氏标定法的单目相机改进标定算法[J]. 导航与控制, 2019, 18(1): 105-111. DOI:10.3969/j.issn.1674-5558.2019.01.014 |
| [12] |
李迪, 张孙亚, 吴培浩, 等. 用于分拣机器人的改进标定方法[J]. 广东轻工职业技术学院学报, 2017, 16(1): 1-5. DOI:10.3969/j.issn.1672-1950.2017.01.001 |
| [13] |
刘博宇, 赵洋, 杨进华. 一种改进的摄像机线性标定优化方法[J]. 长春理工大学学报(自然科学版), 2016, 39(4): 90-96. DOI:10.3969/j.issn.1672-9870.2016.04.021 |
| [14] |
PIROVANO W, REIJDEN A, FEENSTRA K, et al. Structure and function analysis of flexible alignment regions in proteins[J]. BMC Bioinformatics, 2009, 10(3): 21-33. |
| [15] |
KORB O, MONECKE P, HESSLER G, et al. PharmACOphore:multiple flexible ligand alignment based on ant colony optimization[J]. Journal of Cheminformatics, 2010(5): 3-7. |
 2019, Vol. 33
2019, Vol. 33


