| 风力发电并网逆变器直接功率控制改进策略的研究 |
随着社会经济的飞速发展,人类对能源的需求量与日俱增。风能作为一种资源丰富、清洁无污染、可再生的能源,已成为我国改善能源结构、应对气候变化问题的主要替代能源。
目前,我国风电并网技术成为风电发展的主要研究方向。其中,并网逆变器的控制策略是并网逆变技术的决定因素。
并网逆变器常用的控制策略包括:直接电流控制、间接电流控制和直接功率控制[2-4]。直接电流和间接电流控制策略需要PWM调制模块以及复杂的控制算法。传统的直接功率控制[5]对逆变器输出的瞬时无功功率和有功功率计算并调节,该方法更为简单,但是传统的直接功率控制方法导致直流电压、功率在启动暂态过程中产生较大波动。通过引入虚拟磁链直接功率的控制方法,用虚拟磁链估算对电力系统进行分析,以SVPWM[6-7]方式取代了传统直接功率控制系统中的功率滞环和开关表。该研究省去网侧电压传感器,避免了检测误差问题,提高了系统的稳定性,实现了电压利用率高、输出波形谐波含量少、动态响应快等优点。并通过MATLAB环境下的仿真模型,对系统进行仿真,验证了改进策略的可行性。
1 三相并网逆变器的DPC控制策略 1.1 三相并网逆变器主电路结构及数学模型三相并网逆变器主电路拓扑结构如图 1所示,其中ea、eb、ec为交流侧电网电压。在三相电网电压平衡的条件下:
| $ {e_{\rm{a}}} + {e_{\rm{b}}} + {e_{\rm{c}}} = 0 $ | (1) |
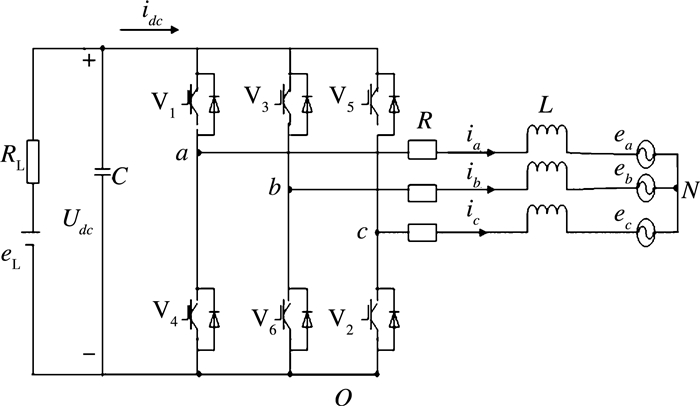 |
| 图 1 三相并网逆变器主电路拓扑结构图 |
图 1中:C为直流侧电容,RL为负载,eL为直流电源,Uao、Ubo、Uco为三相并网逆变器输出电压,UNO为电网电压的中性点与直流母线的负极之间的电压, O、N点分别为下桥臂共源极点和电网电压的中性点。
由图 1所示的三相逆变器主电路拓扑结构图,定义三相逆变桥单极性二值逻辑开关函数:
| $ \begin{array}{l} {S_{\rm{k}}} = \left\{ \begin{array}{l} 1\;\;{\rm{上桥臂导通,下桥臂关断}}\\ {\rm{0}}\;\;{\rm{上桥臂关断, 下桥臂导通}} \end{array} \right.\\ \left( {{\rm{k = a, b, c}}} \right) \end{array} $ | (2) |
对电网侧用基尔霍夫定律,可得逆变器在三相静止坐标系(a, b, c)下电压回路的数学方程式:
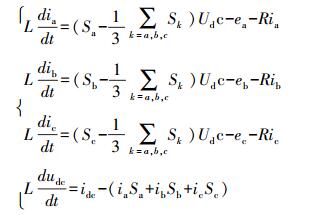 |
(3) |
式中:ia、ib、ic为三相并网逆变器侧输出电流,Udc为直流电压,UNO为电网电压的中性点与直流母线的负极之间的电压,R、L分别为滤波电抗器的电阻和电感。
根据坐标变换理论,将三相静止坐标系(a, b, c)变换成两相静止坐标系(α, β)下的数学模型。三相并网逆变器在坐标系(α, β)上的数学方程为:
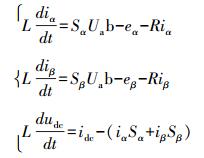 |
(4) |
式中:
三相并网逆变器传统的直接功率控制电路为电压定向的直接功率控制(VO-DPC),该控制结构框图如图 2所示。图中采用电压传感器方案,消除了电阻R的影响,采用双闭环的结构,基本原理为:根据检测到的电网侧的电压ea、eb、ec和电流ia、ib、ic,经过3/2变换,得到两相静止坐标系中的电压Uα、Uβ和电流iα、iβ,再根据功率估算模块得到瞬时估算功率P和Q,给定有功功率值P*直流外环电压设定,无功功率值Q*设定为0,将P、Q与Pref、Qref的比较差值送入功率滞环比较器,得到开关信号SP、SQ,Q*设定为0。扇区划分由Uα、Uβ确定,得到扇区幅角θ=arctan(Uβ/Uα),由θ的位置得到扇区信号θn。由SP、SQ、θn选择开关表中所需的Sa、Sb、Sc控制主电路开关。
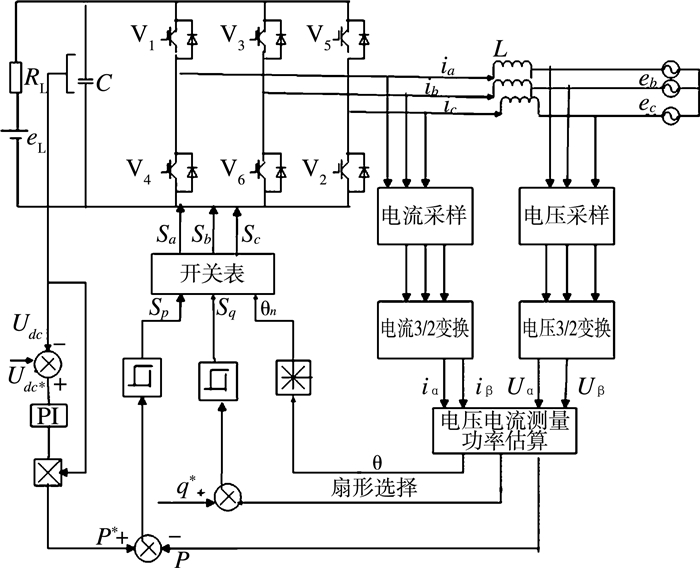 |
| 图 2 三相并网逆变器电压定向的直接功率控制图 |
1.2.1 瞬时功率的确定
常规的对有功功率和无功功率的计算都是在平均值和向量的基础上定义的,在此采用瞬时功率的方法确定。综合文献[8]、[9]的研究,三相逆变器在两相静止坐标系中的瞬时功率可以表示为:
| $ \left\{ \begin{array}{l} P = {u_\alpha }{i_\alpha } + {u_\beta }{i_\beta }\\ Q = - {u_\alpha }{i_\beta } + {u_\beta } + {i_\alpha } \end{array} \right. $ | (5) |
SP、SQ按照下列规则确定[4]:
| $ {S_P} = \left\{ \begin{array}{l} 1\;\;{\rm{ }}P < P* - {H_{\rm{p}}}\\ 0{\rm{ }}\;\;P > {P^*} + {H_{\rm{p}}} \end{array} \right. $ | (6) |
| $ {S_Q} = \left\{ \begin{array}{l} 1{\rm{ }}\;\;Q < Q* - {H_Q}\\ 0{\rm{ }}\;\;Q > {Q^*} + {H_{\rm{p}}} \end{array} \right. $ | (7) |
式中:Hp为有功功率滞环比较器的环宽,Hq为无功功率滞环比较器的环宽;它们决定了功率的控制精度。
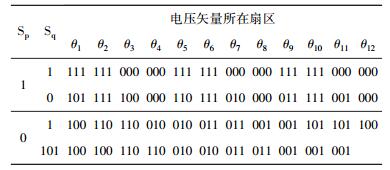
1.2.3 开关表的制定开关表[10]的开关状态,即Sa、Sb、Sc取值由SP、SQ、θn确定,θn由公式(8)确定。为使逆变器输入电压矢量得到优化,将(α、β)平面分为12个扇区,如图 3所示,开关表见表 1。
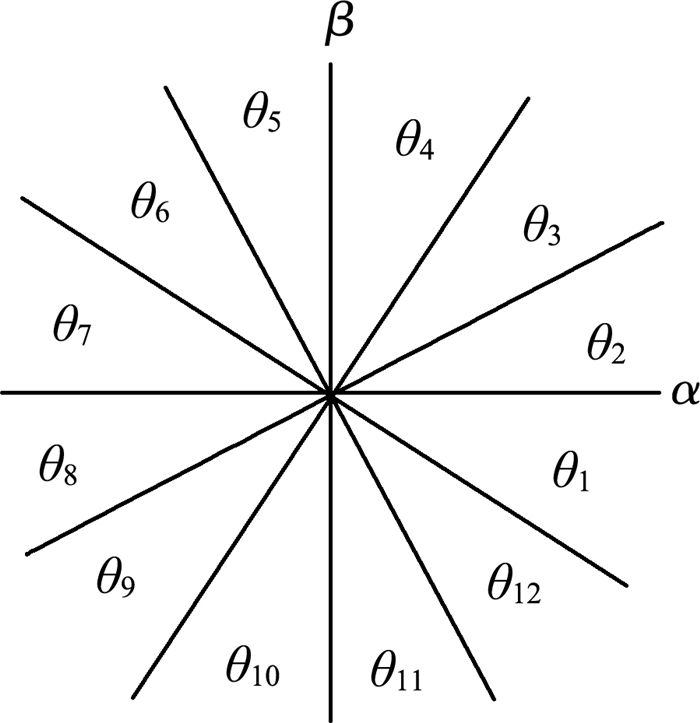 |
| 图 3 直接功率控制系统输入空间划分 |
| 表 1 传统直接功率控制开关表 |
 |
Sa、Sb、Sc的取值取决于所需的U,U为离散值的取值U0~U7,由Sa、Sb、Sc和Udc决定,即Sa、Sb、Sc=000~111(U0~ U7),可以表示为:
| $ \left| U \right| = \left\{ \begin{array}{l} \sqrt {2/3} {U_{{\rm{dc}}}}\;\;\;({U_1} \sim {U_6})\\ 0\;\;\;({U_0}或{U_7}) \end{array} \right. $ | (8) |
根据图 2和开关表 1构建了三相并网逆变器传统直接功率控制系统在MATLAB环境下仿真模型。仿真参数为:直流母线电压为600 V,交流侧电网电压的有效值为220 V,电网频率为50 Hz,交流侧电抗器电感为10 mL,直流侧电容为2200 μF,系统输出功率为2.5 kW。
图 4为a相并网电流及电网电压;图 5为直流母线电压Udc;图 6为瞬时有功功率P和瞬时无功功率Q。
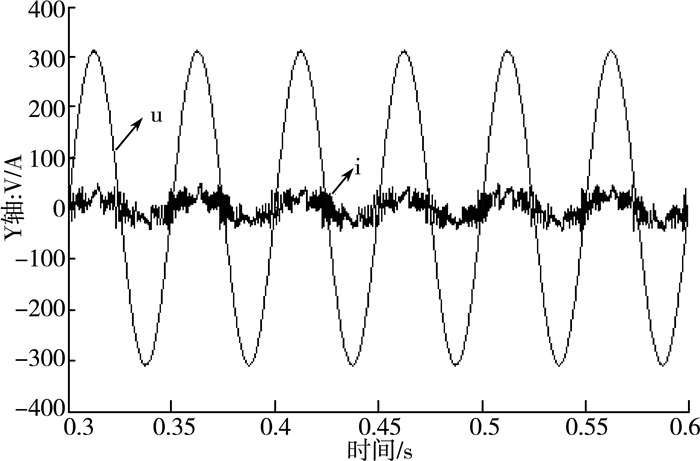 |
| 图 4 a相并网电流及电网电压 |
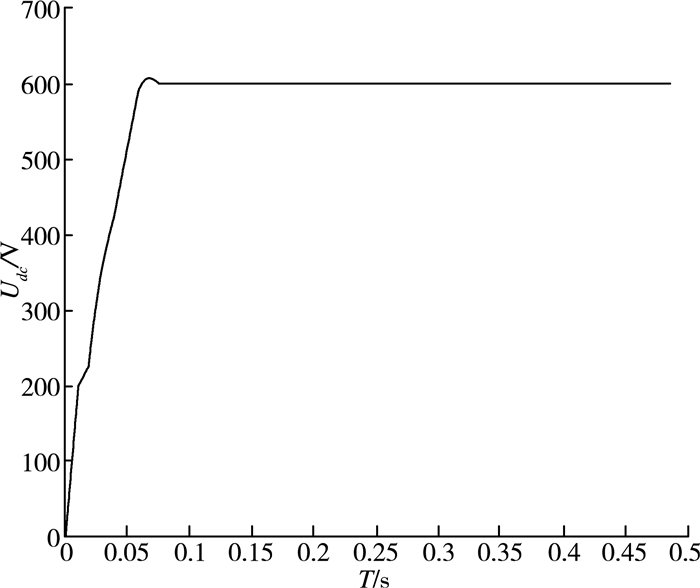 |
| 图 5 直流母线电压Udc |
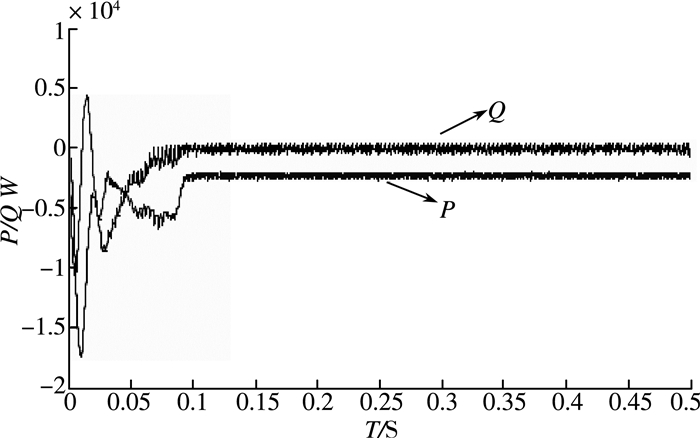 |
| 图 6 瞬时有功功率P和瞬时无功功率Q |
从图 4、5、6可以看出:逆变电流与电网电压同频同相,所以单位因数为1,逆变器向电网回馈功率,实现逆变。直流母线电压Udc也基本稳定在600 V,但在启动过程中,a相并网电流出现谐波,瞬时有功功率和瞬时无功功率也出现较大波动,即动态性能不稳定。
2 改进的三相并网逆变器DPC控制策略 2.1 虚拟磁链的估算为消除电网侧电压传感器[11],提出一种改进的DPC控制策略,即三相并网逆变器采用类似于交流电机磁链观测方法,构造虚拟电网电压磁链矢量。那么电网电压矢量
假设在三相电网电压平衡条件下,忽略线路电阻,由方程式(4)所得的两相静止坐标系下的电压坐标方程为:
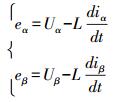 |
(9) |
式中:Uα为交流电压α轴分量,Uβ为交流电压β轴分量。因Ψ=∫edt,对上式积分可得:
| $ \left\{ \begin{array}{l} {\mathit{\Psi} _\alpha } = \smallint {U_\alpha }dt - L{i_\alpha }\\ {\mathit{\Psi} _\beta } = \smallint {U_\beta }dt - L{i_\beta } \end{array} \right. $ | (10) |
式中Ψα、Ψβ分别为电网电压合成矢量虚拟磁链在α、β轴的分量。稳态时,虚拟磁链合成矢量滞后于电网电压空间矢量的电角度π/2。
| $ \theta = {\rm{arctan}}\frac{{{\mathit{\Psi} _\beta }}}{{{\mathit{\Psi} _\alpha }}} $ | (11) |
式中θ为电网电压虚拟磁链合成矢量角。
为解决因积分初值引入直流分量的问题,用一届低通滤波环节取代积分环节。
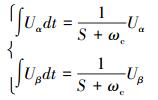 |
(12) |
式中ωc为电网电压角频率。
2.2 虚拟磁链的瞬时功率的估算根据
| $ e = \frac{{d\mathit{\Psi} }}{{dt}} = \frac{{d{\mathit{\Psi} _\alpha }}}{{dt}} + j\frac{{d{\mathit{\Psi} _\beta }}}{{dt}} + j\omega ({\mathit{\Psi} _\alpha } + j{\mathit{\Psi} _\beta }) $ | (13) |
根据:
| $ \left\{ \begin{array}{l} P = {R_e}\left( {e\cdot{i^*}} \right)\\ Q = Im(e\cdot{i^*}) \end{array} \right. $ | (14) |
其中i*为i的共轭矢量:
| $ {i^*} = {i_\alpha } - j{i_\beta } $ |
由方程式(13)、(14)可得到电网的瞬时有功功率P和瞬时无功功率Q为:
| $ \left\{ \begin{array}{l} P = \omega \left( {{\mathit{\Psi} _\alpha }{i_\beta } + {\mathit{\Psi} _\beta }{i_\alpha }} \right)\\ Q = \omega ({\mathit{\Psi} _\alpha }{i_\alpha } + {\mathit{\Psi} _\beta }{i_\beta }) \end{array} \right. $ | (15) |
图 7为基于虚拟磁链的空间矢量调制的直接功率控制系统框图。系统由三相桥臂电流和开关信号及直流侧电压估算出虚拟磁链Ψα、Ψβ和瞬时有功功率P和瞬时无功功率Q。P、Q与有功功率的给定P*和无功功率的给定Q*(Q*=0)比较做差得到误差信号,再经过PI调节器得到Ud*和UQ*,再经过公式(11)、(16)的变化得到Uα*和Uβ*,并将其送入SVPWM调制模块来得到开关状态。
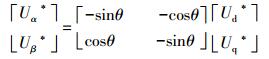 |
(16) |
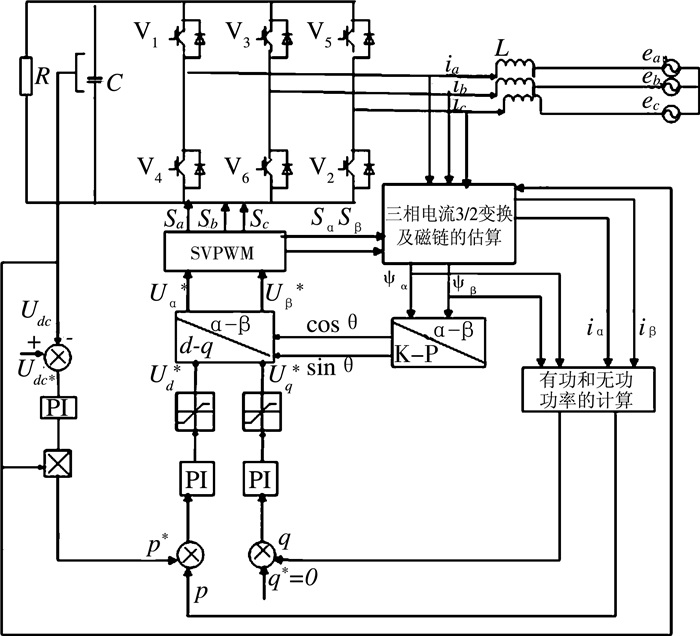 |
| 图 7 基于虚拟磁链的空间矢量调制直接功率控制系统图 |
2.4 改进策略的仿真研究
根据以上分析,按图 7所示,利用MATLAB建立仿真模型,得到以下仿真图形。参考仿真结果可以看出,改进后的直接功率控制比传统的直接功率控制具有明显优点。图(8)是并网电压的动态性能曲线,图(9)是并网电流的动态性能曲线。从两图中可以看出:当在0.3 s时,电网电压突然减小一半,交流侧电流能够根据电网电压的突变迅速做出反应,以确保向电网反馈的功率不变,并且电压、电流波形谐波较小。图(10)、(11)分别为计算得到的有功功率和无功功率,从启动到稳态过程中波动较小。从图(12)中可以看出:使用一阶低通滤波器代替纯积分环节,所得到的虚拟磁链的运动轨迹是一个圆心在坐标原点的磁链圆。
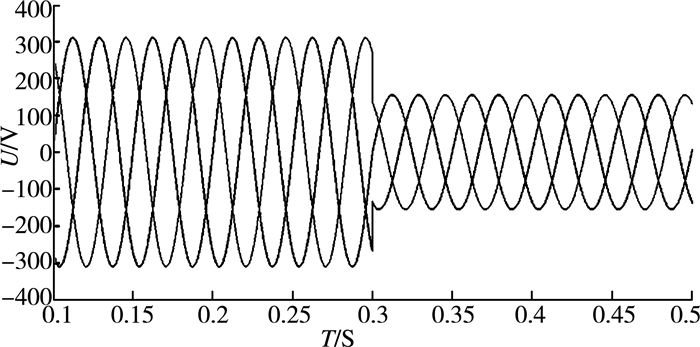 |
| 图 8 并网电网电压动态性能曲线 |
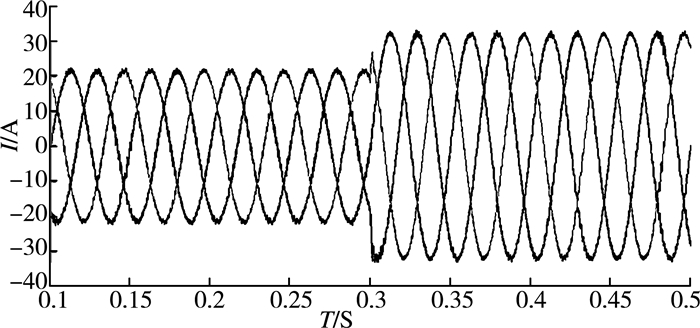 |
| 图 9 并网电流动态性能曲线 |
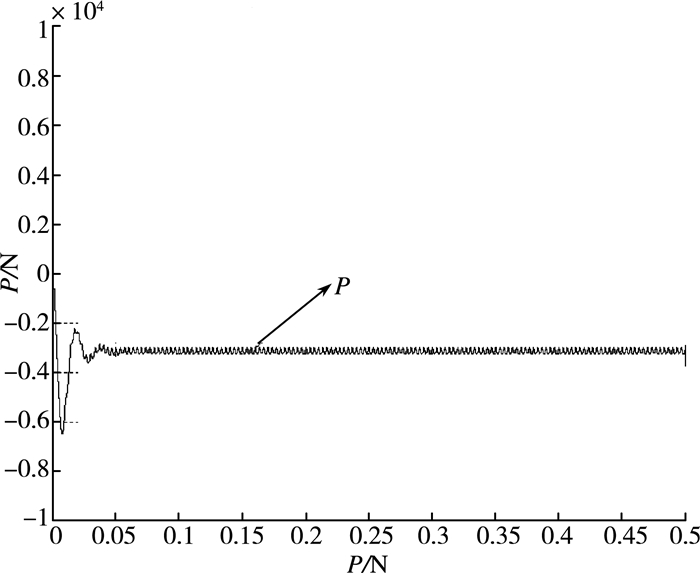 |
| 图 10 有功功率P波形 |
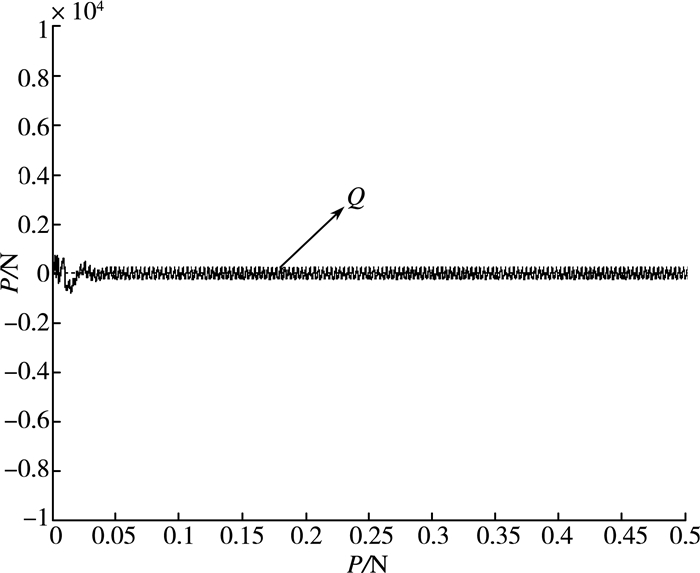 |
| 图 11 无功功率Q波形 |
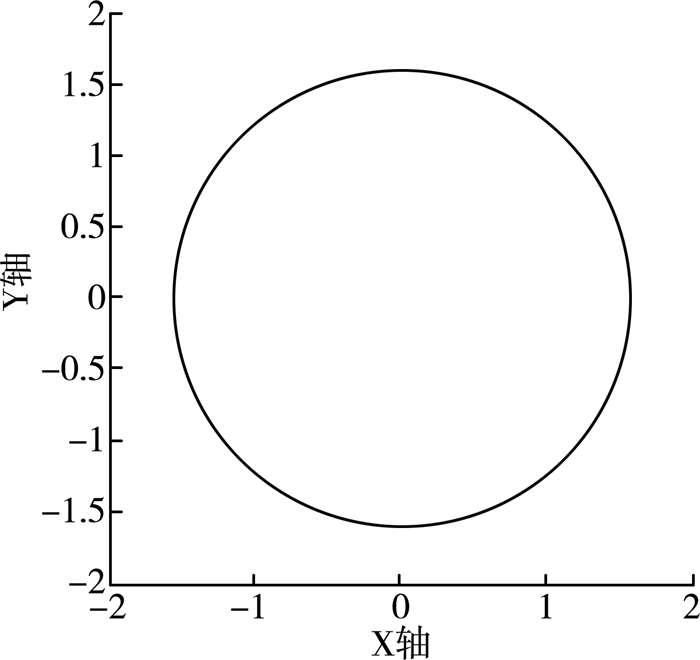 |
| 图 12 虚拟磁链的运动轨迹 |
3 结论
对传统的直接功率控制方案进行改进,采用虚拟磁链估算代替网侧电压传感器,使三相并网逆变器控制系统降低了采样频率;具有更低的电流畸变率,提高了系统的稳定性。
| [1] |
杨勇, 阮毅, 汤燕燕. 不连续空间PWM的无电网电压传感器的三相并网逆变器[J]. 电力自动化设备, 2009, 29(11): 92-97. DOI:10.3969/j.issn.1006-6047.2009.11.021 |
| [2] |
张纯江, 顾和荣. 基于新型相位幅值控制的三相PWM整流器数学模型[J]. 中国电机工程学报, 2003, 23(7): 28-31. DOI:10.3321/j.issn:0258-8013.2003.07.006 |
| [3] |
杨勇, 阮毅, 任志斌. 直驱式风力发电系统中的并网逆变器[J]. 电网技术, 2009, 33(17): 157-161. |
| [4] |
王久和, 李华德. 一种新的电压型PWM整流器直接功率策略[J]. 中国电机工程学报, 2005, 25(16): 47-52. DOI:10.3321/j.issn:0258-8013.2005.16.009 |
| [5] |
徐小品, 黄进, 杨家强. 瞬时功率控制在三相PWM整流中的应用[J]. 电力电子技术, 2004, 38(2): 30-31. DOI:10.3969/j.issn.1000-100X.2004.02.012 |
| [6] |
尹忠刚, 钟彦儒, 刘静. 基于空间电压矢量的变频器能量回馈系统研究[J]. 电力电子技术, 2007, 41(7): 6-8. DOI:10.3969/j.issn.1000-100X.2007.07.003 |
| [7] |
MOHAMED Y, EL-SAADANY E F. Robust high bandwidth discrete-time predictive current control with predictive internal model-a unified approach for voltage-source PWM converters[J]. IEEE Trans.on Power Electronics, 2007, 23(1): 126-136. |
| [8] |
王茂海, 刘会金. 通用瞬时功率定义及广义谐波理论[J]. 中国电机工程学报, 2001, 21(9): 68-73. DOI:10.3321/j.issn:0258-8013.2001.09.015 |
| [9] |
王茂海, 刘会金. 通用瞬时功率理论的完善与负载性能评价指标的建立[J]. 中国电机工程学报, 2002, 22(7): 81-84. DOI:10.3321/j.issn:0258-8013.2002.07.017 |
| [10] |
MOHAMMAD M, HASSAN R, HOSSEIN M K. High performance direct instantaneous power control of PWM rectifiers[J]. Energy Conversion and Management, 2010(51): 947-954. |
| [11] |
王焕岗, 徐文立, 黎坚, 等. 一种新型的感应电动机直接转矩控制[J]. 中国电机工程学报, 2004, 24(1): 107-111. DOI:10.3321/j.issn:0258-8013.2004.01.021 |
 2018, Vol. 32
2018, Vol. 32

